→�g�їp�͕ʕ�
���m�ʂ̕ł���̎���ɑ���n[�O�p���̒l�ɂ��ā^25.12.06�n
�O�p���̕ϊ������Ȃ̂ŗ��K�ɂȂ�܂� ���ɒP�ʉ~��Ő������Ă����̂ł킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̌`�ŁC1���Ԓ��P�̃N���X�Ă܂���Ƃ������Ƃ�����Ă����D���k�����ł�����������ƁC�̘̂b������
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^25.08.14�n
3x^(-2)��9x^(-1)y^3�̎����́A���ꂼ��2�E(���ɕ����̎w�肪�Ȃ��ꍇ��)4�ł����̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���߂ɏ����Ă���܂��悤�ɁC���̋��ނ́C�u���Z���w�T�̒P�����Ƒ������v�����������̂ł��D���Ȃ������₵�Ă���̂́C���Z���w�U�́u���̎w���v�ɂ��Ăł��D������C���Z���w�T�ɂȂ��b�����Ă��邱�ƂɂȂ�܂��D
�@���ϕ��ȂǂŁC�����̎d���Ƃ���3x^(-2)�̎�����−2�Ƃ����悤�Ȍ������͂���ł��傤���2�ł͂Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕������ɂ��ā^25.08.09�n
�R�����g���́u���m�ʂ̕ł���̎���ɑ���n[�����̕������ɂ��ā^17.1.11�n�v�ł����A�摜�������N��ł��B���łɔ����������ł������������ɂ��Ă���ƈꌾ�f�����ق����c�c�i��ʉ��́AC�͔C�Ӓ萔��f(x)=2x^2-3x+1+Ce^{-x}�ƂȂ�͂����Ǝv���̂Łj�B�{���Ȃ琔�U�����Ȃ̂ŁA�����܂Ō�������Ɩ��p�ȍ������������˂Ȃ��Ƃ��l����������܂��A�C�ɂȂ����̂ŁB
�����m��ҁn�F�A�����肪�Ƃ��D���낢��ƕ����Ă�����悤�ł����C�����������t���Ă���̂ŁC���R�C������ł��D�܂��C���w�U�ɂ͔����������Ƃ����T�O���Ȃ��̂ŁC�����������̘b�ɂ͂Ȃ�܂���D�Ⴆ�C�ǂ��ό`���Ă������������Ȃ������ϕ��������̂悤�Ȗ��ł��C���w�U�Łu�������v�Ə����Ă��邾���Łu�����̕������v�ɉ����ł��C�����Ă��܂��Ƃ������Ƃ̗�����������̂ł��D
�@�Ȃ��C���̕������̈�ʉ��́i���w�U�ł͋��߂��܂��jy=2Cx^2+4x+6�ł��D
���̃y�[�W�Ƃ��C
���̃y�[�W�ɉ������������Ă���܂��D
�@�u�ǂ��ό`���Ă������������Ȃ������ϕ��������̂悤�Ȗ��v�Ƃ��āC���̗�Ƃ��āC���̂悤�ȉߋ��₪����܂��D�i���s��j
�u������\(f(x)\)�ŁC����
\(\displaystyle f(x)f'(x)+\int_1^xf(t)dt=\frac{4}{9}x-\frac{4}{9}\)
���݂����Ă�����̂����ׂċ��߂�D�v
�i�����j\(\displaystyle f(x)=\frac{4}{9}, f(x)=-\frac{1}{6}x^2+x-\frac{5}{6},f(x)=-\frac{1}{6}x^2\pm\frac{1}{3}x+\frac{1}{2}\)
span style="color:#0000ff;">��HYML�^�O���\������Ă��܂��B�i����������CSS�ŏ����ق�������Ȃ̂ł����A���ꂾ����K�͂ȃz�[���y�[�W�ł͎�Ԃ�������܂���j
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[ ��ϕ��ɂ��ā^25.07.31�n
����ɂ��� https://www.geisya.or.jp/linear_algebra/maxima1.htm �ł���404not found�ł��B
�����m��ҁn�F�A�����肪�Ƃ��Dhttps://www.geisya.or.jp/~mwm48961/kou3/integral2.htm ���̋L�q�ŁC�f�B���N�g���̊K�w������Ă����悤�ł����C�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�x�����z�\�C�q�X�g�O�����̍쐬�ɂ��ā^25.07.17�n
�T���v���f�[�^���e�[�u���Œ���Ă���̂ŁA�����ɉ��K�Ŋm�F�ł���B��ϗǂ����ނ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̌v�Z(�܂Ƃ�)�ɂ��ā^25.07.01�n
(1)�͉������Ƃ��s�\�ł���Ǝv���܂�. �Ή����肢���܂�.
�����m��ҁn�F�A�����肪�Ƃ��DOH!�Ȃ�Ă����������肪�Ԉ���Ă���I�˒��J�Ɍ����C�������ɃG�X�P�[�v�����i%�j�������Ă��܂��āC����Ȍ�̎��C���Ȃ킿2�ڂ̍s�\������Ȃ��Ȃ��Ă����D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^25.06.28�n
���J�ȉ���ŕ�����₷���ł��I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����ɂ��ā^25.05.14�n
�S�����@�藝�ȂI�ƋC�Â��Ă���Ϙa���a�ς��|���Ȃ��Ȃ�܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����������̍����ɂ��ā^25.03.30�n
���̃y�[�W�̐������G�����ɂȂ����܂܂ł��A�ǂ݂����̂Ő���C�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogleAPIS�̐ݒ�ύX�ɔ����āC��N4�������琔�����\������Ȃ��Ȃ�CMathJax�ɏ����������ł��D�قڂP�N�����āC���T�C���`�C���U,���a�C���V�C�i�����b�j�܂ŏI�����C���݂͒��w�P�N�̕�������ƒ��ł��D�P���P�y�[�W�i�߂P�N��365�y�[�W�C�Q�N��730�y�[�W�i�߂�͂��ł�����������������C���v�Ȃǂ́C���̌�Ƃ������Ƃň������炸���
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^25.03.08�n
���̉�@�����ł͂Ȃ��A�Ȃ������Ȃ�̂�������������Ă����̂ŗǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m��錧�^wakaritai����^25.03.06�n
a�𐳂̎����Ƃ���B2�̕�����
C1: y = x^2, C2: x = y^2 + 1/4 a,���l����B����l��C1�ɂ�C2�ɂ��ڂ���Ƃ��A����l��C1��C2�̋��ʐڐ��ł���Ƃ����B�������A�ړ_�͈قȂ��Ă��Ă��悢�B
�i1�j����s,t�ɑ��A����l:y=tx+s��C1��C2�̋��ʐڐ��ł���Ƃ��Aa��t�݂̂�p���ĕ\���B�́Aa=t+1/t^2
�i2�j2�̕�����C1��C2���A���قȂ�3�{�̋��ʐڐ������Ƃ��Aa�̂Ƃ肤��l�͈̔͂����߂�B���A�����1.88988���傫�Ȑ��l�̂���
�i��w�̉ߋ���ł����j���₵�������Ƃ�����̂ł��������肢���܂��B
���̂悤�Ȗ��̓R���s���[�^�ŃO���t�B�b�N�X����A�݂ĂƂ��悤�Ȃ̂ł���a=3�̏ꍇ�ł̋��ʐڐ�3�{�ɂ��Ă̊e6�ӏ��̐ړ_�̍��W���m�肽���̂ŁA�ǂ������ߕ����������������B
�����m��ҁn�F
�A�����肪�Ƃ��D�ǎ҂���̖��ɓ�����ƁC�h��Ȃǖ{�l���g�������Ȃ���Ȃ�Ȃ����̂���`���Ă��܂��\��������̂ŁC���Ȃ��悤�ɂ��Ă��܂��D�������Cx = y^2 + 1/4 a�́C\(x=y^2+\frac{1}{4}a\)�Ȃ̂�\(x=y^2+\frac{1}{4a}\)�Ȃ̂��C�Ӗ��s���ł����C\(x=y^2+\frac{1}{4a}\)�ɉ��߂����\(a\gt\frac{3}{\sqrt[3]{4}}=1.88988\)�Ƃ����������o�ꂵ�܂��D�O���t�́C���}�ŐԐ��̏ꍇ�͇@�̌`�̋��ʐڐ��݂̂ƂȂ�C�ΐ������ڂƂ��Đ��̏ꍇ�́C�A�B�̌`�̋��ʐڐ����o�ꂵ�܂��D�Ȃ��C�ڂ������Ă͐����`�h��
ChatGPT,
Copilot ,
Gemini�̂ǂ�ɂ��Ȃ��̎�������̂܂�������ł��قړ������ĂƂ��ē����܂��D
���5��(1)�́u3�~5�~4�~3=360�v�ł͂Ȃ��u3�~5�~4�~3�~2=360�v���ȂƁB
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[��ԍ��W�C��ԃx�N�g���ɂ��ā^25.03.01�n
�������ɂ��悤�����Ă���܂��B
���Z���w�U�E�a>> �x�N�g���̓���,��ԃx�N�g��>>�y�x�N�g���̐}�`�ւ̉��p�z(2)�̉���ŁAp�x�N�g���̕��ꂪ(s+t)+c�ɂȂ��Ă��܂��B���m�F�A�X�������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂����D
���m��茧�^�e�f�B�x�A����^25.02.22�n
�ǂ����玿���������悢�̂��A�������Ȃ������̂ŁA�������玸�炵�܂��B���������āA��σ��x���̒Ⴂ����ɂȂ邩������܂��A��낵�����肢���܂��B�d���ŋ��Z�@�ւ̌����ԍ��̓��́A�`�F�b�N�����܂��B�V���̂����A���S���𑫂��Z�������l�i���ނɏ����Ă�����̂�d��ŁA���͂������̂��G�N�Z���Łj�������n�j�A�Ƌ����܂������A�Ȃ����S�������ł����̂ł��傤���H�����ĉ������B
�����m��ҁn�F�A�����肪�Ƃ��D�ʐM�ł͑��M�������Ǝ�M�������ƂŁC�����f�[�^�𑗎�M�ł������ǂ������`�F�b�N����i�d�g����̗ǂ������ŁC�f�[�^�Ɍ�����������\�����l����j���߂ɁC�p���e�B�C�`�F�b�N�T���CCRC�Ȃǂ���v���邩�ǂ�����_�����邱�Ƃ�����܂��D�������C�������₳��Ă�����e�́C����Ƃ͊W�Ȃ����Z�@�ւȂǂ̖��ŁC������Ȃǂʼn��S���͈�������ɁC�{�l�m�F�Ƃ��Ă��̔ԍ�����������ł��炤�Ƃ����`�Ŏg���悤�ł��D����͐��w�Ƃ͊W�Ȃ��C�u���ꂼ��̑g�D���Ƃ̖��v�ŁC���T���̂����̉��P���ȊO��{�l�m�F�Ƃ��Ďg����������悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̏d�S �ɂ��ā^25.02.21�n
���̒P���ȓ��ł͗����ł��܂���ł���(��)�B����ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�O���́C���ȏ��ɏ����Ă��镁�ʂ̘b�ł����C�㔼�͓�������i�����������z�ŕ��ʂł��傤�j
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^25.02.07�n
�g���₷���킩��₷���ōō��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�_���̂��łɁC1���������������Ă������̂��܂����D
���m�ʂ̕ł���̎���ɑ���n[����,���̋Ɍ��ɂ��ā^25.02.06�n
���̃T�C�g�Ő��w���w�Ԃ̂��{���Ɋy�����ł��I ����〜��w���w�̏��������͂�����ɂȂ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D2��6�����݂ŁC���Z���w�̍Ō�̕��i�����wC�̍s��j�����������Ă��܂��D3�����ɂ͒��w�Z�̐��w�����������āC���̌�ɂȂ�\��ł��D��������⍪���Ȃǂ̐����\����Web��ʏ�ōs���ɂ́C����̕��@������悤�ł����C�@FireFox�ȊO�̃u���E�U�ɑ��āCMathML���v���O�C��MathaPlayer��p���ĕ\��������@�́C2009�N���ɂ͌��Ȃ��Ȃ����悤�Ɏv���D����ɑ��āC�AGoogleAPIS������Ɏg�����@�́C�����I�ȊJ�n�錾���I���錾���Ȃ��܂܁C2024�N4���܂Ŏg���܂������C�}�Ɏg���Ȃ��Ȃ�܂����D�����ŁC�B�S�Đ��w��C�S�ĕ����w��Ȃǂ����E�߂�MathJax(MathML��jsMath���z���������́H)�����ݗ��p�\�Ȃ̂ŁC����ɏ��������Ă��܂��D�������C�������TEX����{�Ƃ����C�ו��ňقȂ�ق��o�[�W�����ɂ���Ă��قȂ�悤�ŁC1�����Ȃ��珑�������邵���Ȃ��悤�ł��D�C�M�ғƎ��̃X�N���v�g�����́C����̕ω��ɑς��Ďg���܂����C���b�N�X�����ア���C�u���E�U�ɂ���Ďg���Ȃ��ꍇ������iChrome�œ_�����Ă�Edge�ł͌��������Ⴄ���Ƃ������j�ȂǁC���Z������܂��̂��Y�܂����Ƃ���ł��D---�������҂��Ƃ������Ƃł�낵���D
���m�ʂ̕ł���̎���ɑ���n[�W���̕\�����i�I�C���[�}�j�ɂ��ā^25.01.27�n
[3]�I�C���[�}�i�܂��̓x���}�j��p�������_�̎d���́y���z�`���a���a�̂Ƃ���ł����A�w�̕������Ȃ��ꍇ�Ƃ���܂����A�y�̕������Ȃ��ꍇ�ł͂Ȃ��ł��傤���H�@�������́A�`���a���@�a���`�Ƃ��邩�H(���{�I�Ɏ��̗���s�������m��܂���B)
�y���T�z�i1�j����̍Ō�̕��ŁA���������āC�w=∅���x=∅�̏ꍇ�@�̂Ƃ���A�w=∅���y=∅�̏ꍇ���������̂ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�_���~�X�ł����̂ŁC�������܂����D�����O�̖��F(�`���a)���a �̂܂܂Ȃ�C�˂ɐ��藧���܂��D�i��ʕ\���̌������ŁC∪���ʏ�Web��ʂɎg����S�V�b�N�́m�E�Ȃ������́n�̏ꍇ�ɁC��������∪∩�ł��������Ȃ�̂��Ă��邤���ɁC��肪�ς���Ă��܂����悤�ł��j
�m���ɕςȂ̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�t�F���}�[�\�z,�I�C���[�\�z�ɂ��ā^25.01.12�n
PC�p�A�X�}�z�p�̗����ŁA"�t�F���}�[�\�z,�I�C���[�\�z"�̏͂ɖ��ߍ��܂�Ă���摜������Ȃ��Ȃ��Ă��܂����̂ŁA������悤�ɂ��Ē�����Ə�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��N�̏t�C�����Ȃ���傫�ȍs���������āC�����̕\�����@�̕ϊ���ƁiGoogle APIs→MathJax�j��2024.05.21�̓r���Ŏ~�܂��Ă����悤�ł��D�Ȃ�ׂ����������܂��D
���m�ʂ̕ł���̎���ɑ���n[�A�������̐��ɂ��ā^25.01.12�n
�X�}�z�p��"�A�������̐�"�̏͂̃y�[�W���APC�p�̖{�͂̃y�[�W����J�ڂ����Ƃ��͖��Ȃ��̂ł����A�X�}�z�p�̑��̏͂̃y�[�W����{�͂̃y�[�W�ɑJ�ڂ��悤�Ƃ����404�G���[�ƂȂ�̂Œ����Ē�����Ə�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����ʥ���Ǝ��ɂ��ā^24.12.23�n
2019�N�x�̐��Ǝ��̖���a<2�̏ꍇ�̃E�ƃG�̃E�̑O�ɂ́[(�}�C�i�X)������Ǝv���܂��B����Ȃ��Ɠ���������Ȃ��ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^24.12.03�n
�R���b�c�\�z���O���t���_�I�Ȍ`����A�v���[�`���Ă��āA���Ɋy�����q�������Ă��������܂����B�����A�u(G) �������鐫���v�̍����炩�Ȃ�摜���ǂݍ��܂�Ȃ��Ȃ��Ă���A���͂̉��߂Ɏ��Ԃ���������̂�������s���ĂɂȂ��Ă���ӏ�����������܂����B�m�F��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�́C2024�N4�����ɏI�������悤�ł��i���������L��͂Ȃ����C������j�D���T�C�g�̋��ނ̂����ŕ����⍪���̕\����Google APIs�̐����\���T�[�r�X���g���Ă������̂́C�\���ł��Ȃ��Ȃ��Ă��܂���MathJax�����ɏ����������D�Ȃ��C���������́C���Z���w�T�C�`�C�U�C�a�C�V�C���w���w�C���v���̏��ɍs���Ă��܂����C2024�N12�����݂ō��Z���w�V�̔�������ƒ��ł��D�P����100�̐��������������āC���ς�1���ɂP�ŁC�P�N��356�ŁC10�N��3560�Ői�ޗ\�z�ł��i∃∀�����Ă���`∅��j�D�R���b�c�\�z�̃y�[�W�́A�ł��邾�������Ȃ����܂��B
���m?���^�Ȃ��Ă悩�낤����n�^24.11.21�n
�A���s�������ƂĂ�������₷������ �F�X�Ȗ�肪�����ĂƂĂ��ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D�_�����łɁC�����̕\�����ł��Ă��Ȃ��ӏ����C�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�w�����ΐ��̂����ɂ��ā^24.11.17�n
���P�܂Ŏ��Ԃ͂�����܂����������ł��܂����B���肪�Ƃ��������܂���(^^)v
�����m��ҁn�F�A�����肪�Ƃ��D�����܂œ��f���邱�Ƃ������ł����C�������Ȃǂ̑_���ڂł�����C�}�X�^�[���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[��Βl�̓�������ɂ��ā^24.10.27�n
��2�ł��B���Ƃ��ẮA��Βl���悵�čl���悤�Ǝv�����̂ł����A���̕��@�ł���Ă������������ɂȂ�Ȃ������̂ŁA���̂悤�ɂ���ꍇ�ɁA�ꍇ�����͂ǂ���������̂������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��������Ƃ�\���Ă���̂����ʂ��܂��C�Ⴆ��\(\mid a\mid=\sqrt{a^2}\)�ƕό`���Ă��C���̖��������G�ɂȂ邱�Ƃ�����܂��D���̎���́C�u��悵�čl����v�Ƃ��������������Ă���l�ɐq�˂Ă��������D
���m�ʂ̕ł���̎���ɑ���n[���[�N���b�h�̌ݏ��@�ɂ��ā^24.10.21�n
�܂������\�����ł��Ă��Ȃ��Ƃ��낪����܂��B��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���䐔��C�z�����ɂ��ā^24.10.18�n
�f���炵���T�C�g���肪�Ƃ��������܂��B����Ȃ��_�͑��̃T�C�g���Q�l�ɂ��Ȃ���A�d���̋x�e���ԂȂǂɉ����Ă��܂��B�Ƃ���ŁA�u���䐔��̈�ʍ��́C�A�؎Z�̊W�łɂȂ�܂������v���̉摜�̃����N����Ă��܂��B�i���̃y�[�W������Ή���̂ł����A�O�̂��߂��̂݁j
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^24.10.17�n
���3�̏���2�̓���4�ŃJ�b�R���̕������L�ڂ���Ă��܂���Bx�̎���+�����L�ڂł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�������C����͌����Ȃ����C�����̓}�C�i�X�ł�
���m�ʂ̕ł���̎���ɑ���n[��Βl�̓�������ɂ��ā^24.10.17�n
���3�|�ʉ�2-�G.�́A�R�k�{�S�ł͂Ȃ��ł��傤���H��(�k�{�Q)�{(�k�{1)�{�k�{(�P�|�k)
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�������C(�k�{�Q)�{(�k�{1)�{�k�{(�P�|�k)=4+2�k �Ƃ���
���m�ʂ̕ł���̎���ɑ���n[�h�E���A�u���̒藝�i�������j�ɂ��ā^24.10.06�n
�\������Ă��Ȃ����������Ė�肪�ǂ߂Ȃ���ł�
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�́C2024�N4�����ɏI�������悤�ł��i���������L��͂Ȃ����C������j�D���T�C�g�̋��ނ̂����ŕ����⍪���̕\����Google APIs�̐����\���T�[�r�X���g���Ă������̂́C�\���ł��Ȃ��Ȃ��Ă��܂���MathJax�����ɏ����������D�Ȃ��C���������́C���Z���w�T�C�`�C�U�C�a�C�V�C���w���w�C���v���̏��ɍs���Ă��܂����C2024�N10�����݂ō��Z���w�a�̋�ԃx�N�g������ƒ��ł��D�P����100�̐��������������āC���ς�1���ɂP�ŁC�P�N��356�ŁC10�N��3560�Ői�ޗ\�z�ł��i∃∀�����Ă���`∅��j�D���w�V�͂��̏H�̗\��ł��B
���m���m���^�܂��܂�����n�^24.09.27�n
�����b�ɂȂ��Ă܂��B�O�p���́i�����j�̒��ŕ��͂̕\�����ꕔ�摜�}�[�N�Ȃ��Ă��ēǂݎ��Ȃ��Ƃ��낪����܂��B�C���\�ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X��MathJax�����̏���������ƂŁC��Ƃ̂��Y�ꂪ�������悤�ł��D�Ȃ�ׂ�������������ł��D�i�����Ƃ��C������Ƃ��̃X�p���Łj
���m�ʂ̕ł���̎���ɑ���n[y=sin(��−���j�̃O���t �ɂ��ā^24.09.24�n
��{�I�Ȏ���ł��݂܂���By=sin(�Ɓ|���j�̃O���t�ŁA���Ƃ��i��6�j�ł����Ay=sin2(�Ɓ|30��)�ƕό`����B���̂悤�ɕό`����ƁAy=sin(2�Ɓ|60��)�̃O���t��y=sin2�Ƃ̃O���t���Ƃ̐��̌�����30���������s�ړ��������̂ł��邱�Ƃ�������B���̏ꍇ�A�������t�ɂ��āAy=sin�Ƃ̃O���t����30�x���̌����ɕ��s�ړ������Ă���ł̓_���ł��傤���A�A�A
�����m��ҁn�F�A�����肪�Ƃ��D���͂Ƃ��āu�������t�ɂ��āA����_���ł��傤���v�Ǝ��₳��Ă��C���m�ȓ��e��`���Ă��܂���D���̂悤�ɁC���ŏ����ΐ��낪�����܂��D
�s���̗�6�̎菇�t
�@ \(y=\sin\theta\) → �A \(y=\sin 2\theta\) → �B \(y=\sin2(\theta-30^{\circ})=\sin(2\theta-60^{\circ})\)
�s�������t�ɂ����ꍇ�t
�@' \(y=\sin\theta\) → �A' \(y=\sin(\theta-30^{\circ})\) → �B' \(y=\sin(2\theta-30^{\circ})\)
��L�̂悤�ɇB�ƇB'�ł́C�\����Ă�����e���قȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�����@�i���w�U/���ȏ����x����{���5�j�ɂ��ā^24.09.23�n
�������ɗ��p�����Ă���܂��B���R�|�R�ɂ��Ăł����A�W�����̉��u�����O�v�ɂȂ��Ă���܂����A�u�����O�v�̂悤�ȋC�����܂��B���萔�ł͂������܂����A���m�F��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɉ���Əƍ�����ƁC���������̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����������̍����ɂ��ā^24.09.21�n
�����������܂������������@�͂���̂ł��傤���Himg src="https://chart.googleapis.com/chart?cht=tx&chl=x"�@�̕��������ׂĂ��܂��擾�ł��܂���B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�́C2024�N4�����ɏI�������悤�ł��i���������L��͂Ȃ����C������j�D���T�C�g�̋��ނ̂����ŕ����⍪���̕\����Google APIs�̐����\���T�[�r�X���g���Ă������̂́C�\���ł��Ȃ��Ȃ��Ă��܂���MathJax�����ɏ����������D�Ȃ��C���������́C���Z���w�T�C�`�C�U�C�a�C�V�C���w���w�C���v���̏��ɍs���Ă��܂����C2024�N9�����݂ō��Z���w�a����ƒ��ł��D�P����100�̐��������������āC���ς�1���ɂP�ŁC�P�N��356�ŁC10�N��3560�Ői�ޗ\�z�ł��i∃∀�����Ă���`∅��j�D���w�V�͂��̏H�̗\��ł��B←��q���̂��߁C���������x���Ȃ邩������܂���
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̐}�`���i�O�p�`�̌`����j�ɂ��ā^24.09.13�n
�摜���\������܂���B��낵�����˂������܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�́C2024�N4�����ɏI�������悤�ł��i���������L��͂Ȃ����C������j�D���T�C�g�̋��ނ̂����ŕ����⍪���̕\����Google APIs�̐����\���T�[�r�X���g���Ă������̂́C�\���ł��Ȃ��Ȃ��Ă��܂���MathJax�����ɏ����������D�Ȃ��C���������́C���Z���w�T�C�`�C�U�C�a�C�V�C���w���w�C���v���̏��ɍs���Ă��܂����C2024�N9�����݂ō��Z���w�a����ƒ��ł��D�P����100�̐��������������āC���ς�1���ɂP�ŁC�P�N��356�ŁC10�N��3560�Ői�ޗ\�z�ł��i∃∀�����Ă���`∅��j�D���w�V�͂��̏H�̗\��ł��B
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ɂ��ā^24.09.01�n
�����b�ɂȂ�܂��B���̂[�W�̖��4-4�̖�蕶����2��������windows8�̃N���[���u���E�U�ł͎ʐ^�̃o�O�}�[�N���o�Ă��邾���ǂ߂܂���B���lj���̕��͒��̎������������o���܂����B���������o�O�͓���҂̎d�グ�̃p�Y���Ƃ��Ċy���܂��Ē����܂����B�����Ԃ��L��Ίm�F�肢�܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�̏I���ɔ����C2024.4����MathJax�ɏ��������Ă��܂����C�����P�����Y�ꂽ�悤�ł�---Windows8�Łu���̎��v��u�O���t�v���\���ł��Ă���̂Ȃ�C������
���m�ʂ̕ł���̎���ɑ���n[���_�̍��W�ɂ��ā^24.08.30�n
���(6)�̓_A��x���W�����ł�3�ɂȂ��Ă���̂ɑ�,����ł�-3�ɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̕���������܂���
���m�ʂ̕ł���̎���ɑ���n[�R���ԑQ�����̈�ʍ� �ɂ��ā^24.08.23�n
���A���^�C���ōX�V����Ċ����� ���������b�ɂȂ��Ă���܂��@���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D��قǏ����������Ƃ���ł�
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^24.08.22�n
�x�N�g���̕\�L������Ȃ��Ȃ��Ă���̂ŁA������悤�ɂ��Ăق���
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�́C2024�N4�����ɏI�������悤�ł��i���������L��͂Ȃ����C������j�D���T�C�g�̋��ނ̂����ŕ����⍪���̕\����Google APIs�̐����\���T�[�r�X���g���Ă������̂́C�\���ł��Ȃ��Ȃ��Ă��܂��D�Ȃ��C���������́C���Z���w�T�C�`�C�U�C�a�C�V�C���w���w�C���v���̏��ɍs���Ă��܂����C2024�N8�����݂ō��Z���w�a����ƒ��ł��D�P����100�̐��������������āC���ς�1���ɂP�ŁC�P�N��356�ŁC10�N��3560�ł̗\�z�ł��D���w�V�͂��̏H�̗\��ł��B
���m�ʂ̕ł���̎���ɑ���n[���������̕ό`�ɂ��ā^24.08.21�n
���~�N�C�Y���o�Ŗ����������̂ŕ��ւ̃n�[�h����������ƂĂ��ǂ������ł��B�܂�����������Ă���Ă��ď�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����u���ւ̃n�[�h����������v����---�̕������C�_�ߌ��t�Ƃ��čō��ł�
���m�ʂ̕ł���̎���ɑ���n[ ���f�����ʂ̐}�`���i�O�p�`�̌`����j�ɂ��ā^24.08.15�n
�摜���\������Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��DGoogle APIs�̐����\���T�[�r�X�́C2024�N4�����ɏI�������悤�ł��i���������L��͂Ȃ����C������j�D���T�C�g�̋��ނ̂����ŕ����⍪���̕\����Google APIs�̐����\���T�[�r�X���g���Ă������̂́C�\���ł��Ȃ��Ȃ��Ă��܂��D�Ȃ��C���������́C���Z���w�T�C�`�C�U�C�a�C�V�C���w���w�C���v���̏��ɍs���Ă��܂����C2024�N8�����݂ō��Z���w�a����ƒ��ł��D�P����100�̐��������������āC���ς�1���ɂP�ŁC�P�N��356�ŁC10�N��3560�ł̗\�z�ł��D���w�V�͂��̏H�̗\��ł��B
���m�ʂ̕ł���̎���ɑ���n[����̋Ɍ��ɂ��ā^24.08.01�n
������₷����萔�������̂Ő�IAIIB�S�����̃T�C�g���g���ė\�K���܂����B�{���Ɋ��ӂ�������܂���B��III�̏��������͂����납��n�܂�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�����i�W���P���j���wB�̐���ɓ˓����܂����D�W�����ɐ��wB���I��点�āC�X���ɂ͐��w�V�ƍs�������Ƃ���ł��i��]�I�ϑ��܂݁j
���m�ʂ̕ł���̎���ɑ���n[���ʏ�̓����_�C�O���_�̍��W�ɂ��ā^24.06.19�n
�����Q�l�ɂ����Ē����Ă��܂��B
�y���Q�z��(1)�A�I������(-1,8)�Ƃ���܂����A��������(-5,8)�ł͂Ȃ��ł��傤���H
������J���Ɠ�����(-5,8)�ƂȂ��Ă���A�I�����ƈقȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^24.06.19�n
�߂��Ⴍ����킩��₷�������ł��ق�Ƃ��ɂ��肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ϒl�C���U�̋��ߕ��ɂ��ā^24.06.10�n
���ϒl���U�̋��ߕ��ʼn摜�}�[�N�ɂȂ��Ă��Ă킩��Ȃ��̂Œ����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D2024.4���ȍ~�̎���Ɖ͓����ł��̂ŁC���L��4���ȍ~�̉�ǂ�ł��������D�Q�l�܂łɁC���݂͐��w�U�̎O�p������ƒ��ŁC���v����ɒB����̂͑����Ă����̏H�C���w���w�͂P�N�ȏ��̌����݂ł��D
���m�ʂ̕ł���̎���ɑ���n[��ԍ��W�C��ԃx�N�g���ɂ��ā^24.06.03�n
������ς����b�ɂȂ��Ă܂��B
���̃y�[�W�A�唼�̉摜��NotFound404�ɂȂ��Ă���悤�ł��BChrome�o�[�W����: 125.0.6422.142�iOfficial Build�j �i64 �r�b�g�j���g���ĊJ���Ă��܂��B���������A�\������Ă��Ȃ����̂͐����ł��B
����������Ƃ�����̊��ŋ@�\���Ă��Ȃ��\���͂���܂����A�O��̃y�[�W�ɂ��Ă͐����\������Ă��܂����B�m�F����낵�����肢���܂��B
���m�ʂ̕ł���̎���ɑ���n[��ԃx�N�g�������ɂ��ā^24.06.03�n
�߂��Ⴍ���ᕪ����₷�������ł��I�\�ł����ԃx�N�g���ȍ~�����₪����Ɣ��x�߂ɂȂ��Ċ������ł��B
���m�ʂ̕ł���̎���ɑ���n[ �e�C���[�����C�}�N���[���������ɂ��ā^24.06.03�n
�H���\������{���ł��Ȃ��ł�
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���ɂ��ā^24.06.03�n
�H���\������A�{���ł��Ȃ��Ȃ��Ă��܂��B
�ȏ�̉F�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U��i�s���ł��D���wB,�V, �����܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏��������������܂����D1���ɐ�����100�����������āC�P�N��365�y�[�W�C10�N��3650�y�[�W�����������Ƃ������ʂ��ł��D
�@�Ǝ������̐����\�����ŕ`�������́i��L�́����j�́C�e�����܂��CiPhone, Android�Ȃ�Times New Roman�̃t�H���g�𐳊m�ɔ��f���Ȃ��ꍇ�ɁC�Ӑ}�������ƈقȂ���̂��\��������_������C�����肤�v�Ē��ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�~�̌�_��ʂ�~�E�����̕������ɂ��ā^24.06.01�n
��藓�ʼn���͂ł���̂��V�����Ėʔ����ł��I���\�����͈͓̔���̂ŏ�����܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��������Ƃ��̘a�ɂ��ā^24.05.26�n
��������Ƃ��̘a�̕���̗�肪�摜�}�[�N�ɂȂ��Ă���̂ʼn��P���Ăق����ł��B
���m�ΐ쌧�^�Ƃ肿���^24.05.25�n
�ꕔ�̃y�[�W�̉摜������\������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�S���ȍ~�C��������ł��D�͓����ł�����C���L���Q�l�ɂ��Ă��������D
���m�ʂ̕ł���̎���ɑ���n[����̗L�����ɂ��ā^24.05.17�n
���Q�́i4�j�ɐ���������܂���B�����������̕��q�E���ꂪ�t�ł͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����I�ȏڍׂ��q�ׂ�ƌ����܂����Ȃ�܂����C�u������ł��@�L�b�p���I�v�D����������������Ƃ��ɁC�����%�Ƃ��������������Ă��܂����̂ŁC���������̕��ꂪ�����Ă��܂����D
�i∀�`���J�`∅�F�_���~�X�ł����j�˒������܂���
���m�ʂ̕ł���̎���ɑ���n[�I�C���[�̕������C�ɕ������ɂ��ā^24.05.14�n
�摜�}�[�N�ɂȂ��Ă��Ă킩��Ȃ��̂ł�������P���Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V, �����܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�1���ɐ�����100�����������āC�P�N��365�y�[�W�C10�N��3650�y�[�W�����������Ƃ������ʂ��ł��D--�����\����MathML�ł���Ă���`2009�܂ŁCGoogleAPIs�ł���Ă���`2024�܂�15�N�ԍs���܂������CMathJax�ɂ��Ă��܂ōs���邩�Ƃ��������ł�
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȉ��������ɂ��ā^24.05.14�n
��3��(3)�̉̏����������������H
(x-1)(x+1)(x-3)(x+3)�ƂȂ��ď����ė~����
�����������ɂ����ł�
�����m��ҁn�F�A�����肪�Ƃ��D(x+1)(x−1)(x+3)(x−3)���I�����ł��D�u�Ȃ��āv�Ƃ͂ǂ������Ӗ����͕�����܂��C���₷����悭�C���ו��̍ו��͊e���̍D�݂��ƍl�����܂��D�i�����C���ׂ̖��ł͂Ȃ��D�j
���m�ʂ̕ł���̎���ɑ���n[�}��ϐ��\���ɂ��ā^24.05.12�n
�ސE20�N�̑ސE�����ł��B�}��ϐ��̉~�̈�_��������@���悤�₭�����ł��܂����B�e�ȉ�@���肪�Ƃ��������܂��B���N�̏d�����W�O��O�ɏ��������Ă��������ł��B�Ɍ`���̖����ēx���킳���Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D������́C�܂��܂��u�v���O���������������v�u���ł͌����ɂ������Ƃ��C��ʏ�Ŏ��������v�Ƃ����ӗ~�őO�����ɂ���Ă��܂��D�ސE��Z�Z�N�Cweb���ނ���l��葱���邱�Ƃ́C�����m��l�ڂ����Ɏ��Ă���D�ǂ��Ɍ������Ă���̂��͕�����Ȃ����C���܂Ɏ����E����Ԃ��Ă���ԐM�́C���܂Ƀ}�X�g�ɃJ�������~�܂邱�ƂɎ��Ă���D
���m�ʂ̕ł���̎���ɑ���n[�����^�̕����� �ɂ��ā^24.05.06�n
❓������܂��B��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V, �����܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�1���ɐ�����100�����������āC�P�N��365�y�[�W�C10�N��3650�y�[�W�����������Ƃ������ʂ��ł��D
�i�����������܂���.2024.05.09�j
���m�ʂ̕ł���̎���ɑ���n[�h�E�����K���̖@���ɂ��ā^24.05.06�n
❓���\������Ă��܂��d���萔�ł�����낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V, �����܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�.1���ɐ�����100�����������āC�P�N��365�y�[�W�C10�N��3650�y�[�W�����������Ƃ������ʂ��ł��D�i�����������܂���.2024.05.09�j
���m�ʂ̕ł���̎���ɑ���n[�ϕ��萔�̌����ɂ��ā^24.05.05�n
googlechrome�ʼn{�����Ă���̂ł����A�m��ł�����Ɗm��ł��Ȃ����̕������\������Ȃ��Ȃ��Ă��܂��B���m�F���������܂��ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V, �����܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���ɂ��ā^24.05.04�n
�t�O�p���̐������{���ł��Ȃ��Ȃ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V, �����܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�
���m�ʂ̕ł���̎���ɑ���n[�e�C���[�̒藝�C�}�N���[�����̒藝�ɂ��ā^24.05.04�n
���萔�ł������̂悤�ȕ\���ɂȂ錴�����䋳���肦��ƍK���ł��B�����p�\�R���͋��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V�܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�
���m�ʂ̕ł���̎���ɑ���n[�������̋Ɍ��ɂ��ā^24.05.04�n
���������b�ɂȂ��Ă��肠�肪�Ƃ��������܂��B
2024�N5��3�����_�ŋv���Ԃ�ɂ��̃T�C�g���J�����̂ł��������̂��������ɔ�����̎l�p��
�}�`���_�݂����͑S�̂����ǂł��܂���B���̃p�\�R�������̖��ł�����܂��܂���
�C�ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D2024�N4������GoogleAPIs�̐����\���V�X�e�����~�܂��Ă���悤�ŁCMathaJax�ƕ��p��������ɏ����������ł�.���ݐ��w�T�C���wA�܂ŏ����������ł��C���w�U�CB,�V�܂Ŋ�������̂́C���̉ā`�H�̌����݂ł�.���Z���w�̃g�b�v���j���[�����̈�̂��Ă�ӏ��܂ł͏������������ł�
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^24.04.30�n
❓�������Č����Ȃ��Ƃ��낪����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q���Ȑ��ƒ����ɂ��ā^24.04.25�n
�ȑO�́A�����Ƃ݂ꂽ��ł����A�قƂ�ǂ��摜�A�C�R���ɂȂ��Ă݂�܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���w�V����̏��������͂��̏H����\�肵�Ă��܂�.
���m�ʂ̕ł���̎���ɑ���n[�ȉ~�̕������̕W���`�ɂ��ā^24.04.24�n
���Q�œ_�Ɠ����ƋO�Ձ@�}�S�|�Q���̈�Ԃ����̐����@|c|,|x|<a�ł����A�}�������|c|<a�����ǁA |x|<a�́A|x|��a���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���.
���m�ʂ̕ł���̎���ɑ���n[���W���ɂ��ā^24.04.23�n
�����N����N�����Ă�ꏊ��100�J���ȏ゠��ǂݐi�߂邱�Ƃ��ł��Ȃ��ł��B�������Ă��������Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�O��̉����Ă���������Ƃ킩��܂��悤�ɁC���v����̏��������͂��̏H���ɂȂ�܂�.
�@Google�̐����\���T�[�r�X���C�~�܂��Ă���悤�ŕM�҂������Ă��܂��D���݁C�@GoogleAPIs���ˑR�T�[�r�X���~����Ɖe���͑傫���ł��D�Ȃ��C�AMathML�̕��́C�̂�MathPlayer�̃v���O�C�����C���X�g�[������Ȃ����]�Ȑ܂��������悤�ł����C2009�N���납��jsMath�ɋz������CMathaJax�Ƃ��Ă���Ă���悤�ŁC�����ނł́C�@�����߂Ȃ�A�ŕ\������悤�ɏ���������ƒ��ł��D���Z���w�T�CA�̕ӂ�܂Ői��ł��܂����C���w�V�Ƃ����w���w�܂ŏ���������ɂ́C���N��t������ł��傤--1�y�[�W�ӂ�̐��������ς�200�قǂ����āC�S���Ő���[�W����C�o�b�`�����������Ȃ悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[���䐔��C�z�����ɂ��ā^24.04.21�n
���䐔��̂Ƃ���ɁH�}�[�N�łĕ��͂������o���܂���B
������낵�����˂������܂�
�����m��ҁn�F�A�����肪�Ƃ��D�O��̉����Ă���������Ƃ킩��܂��悤�ɁC���wB�̏��������͂��̉č��ɂȂ�܂�
���m�ʂ̕ł���̎���ɑ���n[�W���̕\�킵���ɂ��ā^24.04.18�n
������~����
�����m��ҁn�F�A�����肪�Ƃ��D������K�v�Ȗ��ɂ́C��������Ă��܂��D�͂��߂̐���ɂ��ẮC����ȑO�̖{���ɏ����Ă���܂��D
���m�H���^Lim Chanhyuck����n�^24.04.18�n
�M�T�C�g��chrome�ŗ��p���Ă�����̂ł��B
�������̐��w���ɂ��߂ɂȂ��Ă���̂Ŗ{���ɂ��肪�����ł���
�ŋ߁A�䗗�̎ʐ^�̂悤�Ɉꕔ�̍��ڂ��Ƃɂ���ȑ����݂����Ȃ������Ȏʐ^�������肠��͂��̕����Ɛ����������܂���B����ŁA�d�v�ȂƂ��낪�����Ȃ������ł����Ɨ������ĕ��ɂȂ�Ȃ��Ďז��ɂȂ��č����Ă���܂��B
�ŁA����͂ǂ���������̂������Ă������������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle�̐����\���T�[�r�X���C�~�܂��Ă���悤�ŕM�҂������Ă��܂��D���݁C�@GoogleAPIs���ˑR�T�[�r�X���~����Ɖe���͑傫���ł��D�Ȃ��C�AMathML�̕��́C�̂�MathPlayer�̃v���O�C�����C���X�g�[������Ȃ����]�Ȑ܂��������悤�ł����C2009�N���납��jsMath�ɋz������CMathaJax�Ƃ��Ă���Ă���悤�ŁC�����ނł́C�@�����߂Ȃ�A�ŕ\������悤�ɏ���������ƒ��ł��D���Z���w�T�CA�̕ӂ�܂Ői��ł��܂����C���w�V�Ƃ����w���w�܂ŏ���������ɂ́C���N��t������ł��傤--1�y�[�W�ӂ�̐��������ς�200�قǂ����āC�S���Ő���[�W����C�o�b�`�����������Ȃ悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ������@�ɂ��ā^24.04.18�n
������₷���Q�l�ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����p�̎��ԑтɁCGoogleAPIs�����p�ł����Ƃ������Ƃł�����C����͍K�^�ł�
���m�ʂ̕ł���̎���ɑ���n[���䐔��C�z�����ɂ��ā^24.04.15�n
���䐔��̐������C��蕶�ɁH�}�[�N���o�Ă��܂��Ă܂� �Ή���낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle�̐����\���T�[�r�X���C�~�܂��Ă���悤�ŕM�҂������Ă��܂��D���݁C�@GoogleAPIs���ˑR�T�[�r�X���~����Ɖe���͑傫���ł��D�Ȃ��C�AMathML�̕��́C�̂�MathPlayer�̃v���O�C�����C���X�g�[������Ȃ����]�Ȑ܂��������悤�ł����C2009�N���납��jsMath�ɋz������CMathaJax�Ƃ��Ă���Ă���悤�ŁC�����ނł́C�@�����߂Ȃ�A�ŕ\������悤�ɏ���������ƒ��ł��D���Z���w�T�CA�̕ӂ�܂Ői��ł��܂����C���w�V�Ƃ����w���w�܂ŏ���������ɂ́C���N��t������ł��傤--1�y�[�W�ӂ�̐��������ς�200�قǂ����āC�S���Ő���[�W����C�o�b�`�����������Ȃ悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�������̋ɒl�C�Q�ߐ��ɂ��ā^24.04.14�n
�umathjax�Ή��v�ɂȂ��Ă���悤�ł����Amathjax�̍\�����\������Ă��邾���ň���ɐ������\������܂���B���̃y�[�W�̊m�F�����肢���������܂��ł��傤���B(�{�����̃u���E�U�FPC��MicrosoftEdge����уX�}�z)
�����m��ҁn�F�A�����肪�Ƃ��D����̓�������̂悤�ŁC�DGoogle�̐����\���T�[�r�X���C����ɍ쓮���Ă��Ȃ��悤�ł��D�i�q���P�S�}�ɑ�����������̖Y��̂ق��C�ꕔ�L���~�X������悤�ł��D�������Ƃ��s���܂��D�������炢�ɂ͕������邩���H�j�i���������܂����D�u���E�U�ɃL���b�V���f�[�^���c���Ă��܂��̂ŁC�ēǂݍ��݁m�����[�h↺�n���Ă��������D�j
���m�ʂ̕ł���̎���ɑ���n[��ԃx�N�g���ɂ��ā^24.04.14�n
��ԃx�N�g���̏͂ɂ����Đ���������і�蕶�ɁH�}�[�N���o�Ă��܂��A���̈ד��e�������o���܂���A�X�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����̓�������̂悤�ŁC�DGoogle�̐����\���T�[�r�X���C����ɍ쓮���Ă��Ȃ��悤�ł��D�i�������Ƃ��s���܂��D�������炢�ɂ͕������邩���H�j
���m�ʂ̕ł���̎���ɑ���n[2����(�W���`���O���t)�ɂ��ā^24.04.12�n
���̃y�[�W�Ɍ������\������Ȃ��悤�ł��ˁBchrome��microsoft edge�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����̓�������̂悤�ŁC�DGoogle�̐����\���T�[�r�X���C����ɍ쓮���Ă��Ȃ��悤�ł��D�i���������܂����D�u���E�U�ɃL���b�V���f�[�^���c���Ă��܂��̂ŁC�ēǂݍ��݁m�����[�h↺�n���Ă��������D�j
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̍��ɂ��ā^24.04.12�n
�x�N�g���̍��̖��łւ�ȁH�}�[�N�o�Čv�Z���o���܂���A��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D����̓�������̂悤�ŁC�DGoogle�̐����\���T�[�r�X���C����ɍ쓮���Ă��Ȃ��悤�ŁC���̃y�[�W���Ȃ�ׂ�����Mathajax�����ɏ��������܂��D�i���������܂����D�u���E�U�ɃL���b�V���f�[�^���c���Ă��܂��̂ŁC�ēǂݍ��݁m�����[�h↺�n���Ă��������D�j
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̒�`�ɂ��ā^24.04.10�n
3�N�O����{�T�C�g���{�����Đ��w�̍ĕ��������Ē����Ă��܂��B�����O����{���ڂŎl�p�ɎR�A�_�̐}�ɒu��������ĕ\������Ȃ��ӏ��������������Ă��܂��B���̍��ڂł����l�ɂȂ��Ă���ӏ����L��܂��B�ǂ̗l�Ȍ����ł����Ȃ�̂ł��傤���B�����Ă��܂��B�Ώ��@�̘A�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����̓�������̂悤�ŁC������Google�T�C�g�̓T�C�o�[�U�����āC�g���b�t�B�N���a���Ă���悤�ł��D�����\�����@Google APIs�ŕ\������ �A���ꂪ�ł��Ȃ��ꍇ�́CMathJax(MathML)�ŕ\������@�̂Q�i�K�\���ɏ����������Ƃ́C���݁C���w�T�̐����藝�C�]���藝�t�߂܂łł��܂����D���w�U�̑ΐ��̏��������́C���T�Ԑ�̗\�z�ł��D�iGoogle�̃g���b�t�B�N�O���t�Ō����C���{���̃g���t�B�b�N����r�I�����Ă���̂́C���{���Ԃł͌ߑO4���}3���Ԃ̂悤�ŁC�A�����J���̃g���t�B�b�N����r�I�����Ă���̂́C���{���Ԃł͌ߌ�6���}3���Ԃ̂悤�ł�.�j
�@�Ƃ肠�����C�ΐ��W��2�y�[�W���ɏ���������悤�\���g�݂܂��D�i���������܂����D�u���E�U�ɃL���b�V���f�[�^���c���Ă��܂��̂ŁC�ēǂݍ��݁m�����[�h↺�n���Ă��������D�j
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ������ɂ��ā^24.04.09�n
������Ƃ������ԂɁA�ؖ���ǂ���K����������A���̂���ł��܂��B�������ŋ߁H�}�[�N�������ĂƂĂ��ǂ߂��Ԃł͂���܂���B���P�ł�����̂Ȃ璼���Ē��������Ǝv���Ă��܂��B���̍��ł������悤�ȏ�Ԃ̂�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D������Google�T�C�g�̓T�C�o�[�U�����āC�g���b�t�B�N���a���Ă���悤�ł��D�����\�����@Google APIs�ŕ\������ �A���ꂪ�ł��Ȃ��ꍇ�́CMathJax(MathML)�ŕ\������@�̂Q�i�K�\���ɏ����������Ƃ́C���݁C���w�T�̐����藝�C�]���藝�t�߂܂łł��܂����D���w�U�̑ΐ��̏��������́C���T�Ԑ�̗\�z�ł��D�iGoogle�̃g���b�t�B�N�O���t�Ō����C���{���̃g���t�B�b�N����r�I�����Ă���̂́C���{���Ԃł͌ߑO4���}3���Ԃ̂悤�ŁC�A�����J���̃g���t�B�b�N����r�I�����Ă���̂́C���{���Ԃł͌ߌ�6���}3���Ԃ̂悤�ł�.�j�i���������܂����D�u���E�U�ɃL���b�V���f�[�^���c���Ă��܂��̂ŁC�ēǂݍ��݁m�����[�h↺�n���Ă��������D�j
���m�ʂ̕ł���̎���ɑ���n[�����t���m���ɂ��ā^24.04.02�n
���̃y�[�W�Ɍ��炸�ł����A�ŋߑI�����␔���̕������S�ĕ\�����ꂸ�A�摜��☓�}�[�N�݂����Ȃ̂��t���܂��i�g�єł����l�B�u���E�U�ς���̂������Ă݂܂����j�B
���ǂ�ʂ̎��ԂŌ���Əo��Ƃ�������̂ł����A���S�����肠��܂���ł��傤���H�i�ŋ߂͏o�Ȃ����Ƃ̂ق��������ł��j
�����m��ҁn�F�A�����肪�Ƃ��D2024.01.04, 01.11, 04.01, 04.02�ȂǁC�����炭�Cgoogle�̃T�C�g��DDOS�U���̂悤�ȃT�C�o�[�U�����Ă��āC�g���t�B�b�N���a���Ă��邽�ߐ��������܂��\������Ă��Ȃ��\��������܂��D
�@���̋��ނł́C�����⍪���Ȃǂ̐�����\�����邽�߂ɁCGoogle APIs���g�p���Ă��܂��̂ŁCGoogle�̃T�C�g�ɂ����ăg���b�t�B�b�N���a����Ɛ������Ԃ���܂���D2024�N�ɓ����Ă���C���̌��ۂ����X�݂���悤�ɂȂ�܂����̂ŁC���Z���w�̃��j���[��ʂɕ\�����Ă��܂��悤�ɁC�@Google APIs�ŕ\������ �A���ꂪ�ł��Ȃ��ꍇ�́CMathJax(MathML)�ŕ\������@�̂Q�i�K�\���ɏ����������Ƃ��s���Ă��܂��D�ł������̂́C���j���[�y�[�W�Ł��t���Ă��܂��D���݁C���w�T�̎O�p��̂�����܂ŗ��Ă��܂����C���w�V�܂ŒB����̂́C���N��t�v����Ǝv���܂��D
�i�Ȃ��C��L�̇@�A�̕����𗼗p���Ă���T�C�g�́C���Ɍ�����܂���̂ŁC�����ƑΏ����@�ɂ��ď����ꂽ�L���͌�����܂���ł����D�j�����t���m���̃y�[�W�ɂ��āC���ɗv�]������܂����̂ŁC�{�����ɗD��I�ɇ@�A���p�����ɏ��������܂��D�i�������������D�Ȃ��C�O�Ɉ�x�ǂ�ł���ꍇ�́C�L���V���������ɂ���f�[�^���\�������̂ŁC�ēǂݍ���(⟳)���Ă��������j�A��D��ɂ��Ă��CDDOS�U�������ꍇ�̌��ʂ͓����ɂȂ�܂����C�����������ɍU�������\���͏��Ȃ��Ƃ������f�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����@�i���w�U/���ȏ����x����{���4�j�ɂ��ā^24.03.18�n
�P�|�P�̋ɏ��l��x�̒l���Ⴄ
�����m��ҁn�F���J����∀�`�C�ԈႢ�ł����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[��������Ƃ��̘a�ɂ��ā^24.03.13�n
���2(2)�͏�����10�ƂȂ��Ă���̂œ�����1162����Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̊ԈႢ�́C�悭����댯�ȗ��Ƃ����ł��D���Ȃ킿
}{2}&chf=bg,s,fff6f6)
d&chf=bg,s,fff6f6)
������
d\}}{2}=\frac{n\{2a%2B(n-1)d\}}{2}&chco=0000ff&chf=bg,s,fff6f6)
�ł�
d\}}{2}&chco=ff0000&chf=bg,s,fff6f6)
�ł͂���܂���
�����̃~�X���₷����肪������܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ�
���m�ʂ̕ł���̎���ɑ���n[�Q���Ȑ��ɂ��ā^24.03.09�n
�Q���Ȑ�(���K�Ɠ������)��ǂ�ŋ^��Ɋ��������Ƃ������܂��B�E���R(1)�̖��Ɨ��P�̖�肪�����Ȃ̂ŁA�ʗ�����]���܂��B
�lj�
�y���4�z�̇A�A�C���̂��͈͂́A�O�����������U�ł�
�ʉ��Q�̎��̓W�J�ɂ��āA�R�ڂ̃C�R�[����
5cos^2��-9+4(shin^2��+ cos^2��)�́A9cos^2��-9+4(1-cos^2��)�̕����킩��₷���Ǝv���܂��B
�Ō�̃C�R�[���̎�5cos^2��-5�́A-5(1-cos^2��)=-5sin^2���̕����킩��₷���Ǝv���܂�
�E�i�������̕����� .�̏ؖ��j
���߂ɁC������̓_H�ƌ��_P(x, y) �ˌ��_�͓��_�ł�
�@
���U�i�Q�j
(2) �@x^2=-4x �ˁ@-4x��-4y�ł�
��V
�D�F�Ŏ�������_��x���W�́A�E�E�E
(��3/2,1) (��3/2,��3/2)�ł�
�y�V.1 �ڐ��̌����z
�E�o�Ȑ��̉����̎��@���q��x^2, y^2 �ˁ@xx1,yy1�ł�
�E�i�ڐ��̌����F�ؖ��j�ォ��W�s��
�i�K��Ȃ��j���k������̂ŁC(B)�̂悤�ɔ�����O��Ƃ����ɏؖ�������@������D�ꍇ�ɂ���ẮC(C)�ł��悢�D
�iB�j�A�iC�j�̐�������������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���R(1)�͏��������܂���.�㔼�̂��w�E�́C���ׁi��������ׂ����Ƃ������Ɓj�̘b�ł͂Ȃ��āC�D�݂̖��ł��傤�D
�E�i�������̕����� .�̏ؖ��j�ȉ��F������Ƃ���͒����܂����D(B)(C)�͌������ł�
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̕ӂ̒��� ==(�O�p����)�ɂ��ā^24.03.07�n
���Q�|�Q�̉�����Ԉ���Ă���
�����m��ҁn�F�A�����肪�Ƃ��D���J�`�C�ԈႢ�ł����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^24.03.01�n
�ƂĂ�������₷��
���̂悤�ȃT�C�g��
�ق��ɂȂ�����
�ƂĂ��֗�
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂Ȃ�ɂ킩��͈͂ł܂Ƃ߂����̂ł��D�Ȃ��C���N�̋���������w�ŗ��n4�Ԃ̖��́C�R���b�c�\�z���ޗ��Ƃ��Đ�����ɂ������̂̂悤�ɂ�������D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��ɂ��ā^24.02.25�n
���܂őS�R������Ȃ������̂ɁA���̃T�C�g�͂�����������₷�������ł��I
��2�ŁA��蕶��x�̂Ƃ��낪�ł�x�̓��ɂȂ��Ă��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D��2�͒������܂����D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̒�`�C�傫���C�����ɂ��ā^24.02.22�n
�ƂĂ��킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̃O���t�ɂ��ā^24.02.21�n
�{���ɂǂ̒P�������ɖ𗧂��Ă��܂��I�I���肪�Ƃ��������܂��B
���2��(4)�̓�����4�ł����������Ȃ��Ɛ����ɂȂ�܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���2��(4)�̓������Ԉ���Ă��܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����̉��p����ɂ��ā^24.02.21�n
���4��2���̉���̒P���W�J���ė����ł��܂���
�Ȃ�(aX2+bX2+cX2)�̑�������3��������3 (aX2+bX2+cX2)�ɂȂ�̂������Ă���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z1�N�̂P�w���ɏK���u�������v�Ƃ����P���ŁC�u�����̕������������̘a���́C�W���̕������܂Ƃ߂ď����v�Ƃ�����������܂��D
�y��z
3x+4x=(3+4)x=7x
x+x=1x+1x=(1+1)x=2x
x+x+x=(1+1+1)x=3x
�ȂǂƏ����u�v�ł�
������
A=a2+b2+c2�̂Ƃ�
A+A+A=3A
���Ȃ킿
(a2+b2+c2)+(a2+b2+c2)+(a2+b2+c2)
=3(a2+b2+c2)
�ƍl���܂��D
�{���ɁC�����������Ƃ�q�˂Ă���̂ł����H
�����y�����ǂ܂��Ă��������Ă��܂��B
�C�ɂȂ������Ƃ������������܂��B
B�n �o�Ȑ��̐}�ł�
�u]���o�Ȑ��͓��ʂƂ������Ƃł͂���܂���D�v����X�s����3��/2<��<�Ƃ��́C�Ŏ������_P�˃�/2<��<3��/2�ł͂Ȃ��ł��傤���H
�P�s���̃�/2<��<3��/2��3��/2<��<2�ł͂Ȃ��ł��傤���H
���ꂩ��A���႘���������W(���̃y�[�W)�̗��S���Ƃ̊W��
1)�̎��@r=qe/1-e<0�̕��q�ł����A��ԍŏ��ɕ`����Ă���}�i�mB�n �o�Ȑ��̐}�ł́jAF��a������A(p+q)e�ł͂Ȃ��ł��傤���H
2)�̎������l�� (p+q)e�ł͂Ȃ��ł��傤��
[D] ���_O(0, 0)�C�œ_F(p, 0)�C����x=�|p�̕�����
�ォ��X�s�ڂ́i����͂��̃y�[�W�j�̃����N����Ă��܂��B
�ォ��15�s�ڂ́u���̂Ƃ��C��HF�fF=�ƂƁv�ˁ�F�fHF=�Ƃł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�ԈႢ�ӏ��͒������܂����i���w�E�̒ʂ�Ƃ͌���܂���j�D1)�̎��C2)�̎��@�͂��w�E�̈Ӗ���������܂���D
���m�ʂ̕ł���̎���ɑ���n[�����W���̕������̍����ɂ��ā^24.02.19�n
sin�Q35�B�{sin²125�B���̒l�̋��ߕ��������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D������̓��e�́C���̃y�[�W�̓��e�Ƃ͂قڊW�Ȃ��C�O�p���̒l�̌v�Z�̂��Ƃ̂悤�ł��D��������?�ł����C

�̋��ߕ���������e�ł����H
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̑����C�a�C���C�����{�ɂ��ā^24.02.12�n
���6�̉ŁA2x=3x+b�̕�����3x�̕�����3a�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���.
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̋��ߕ��ɂ��ā^24.02.11�n
�d���ƂȂ����ŗL�l����ŗL�x�N�g�����Q���߂��邱�Ƃ�����܂����A���̏����E���������ڂ��Ă���������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ꉞ�̉͗p�ӂ��܂����C�ǂ̃��x���̕����ǂ�ȏŎ��₵�Ă���̂��ɂ���āC���̉ɈӖ��E���l�����邩�ǂ����H
�@�܂��C����͂Q���̐����s��
A�ɂ��Ă̘b���Ƃ��܂��D���̏ꍇ�C�@�ŗL�l
λ���d�� �A�ŗL�x�N�g�����Q��

�i

�͂P���Ɨ��j�ł���Ƃ�
�A�ɂ��C
\vec{x_1}=\vec{0},(A-\lambda E)\vec{x_2}=\vec{0}&chf=bg,s,fff6f6)
������C�C�ӂ̒萔
k, l�ɂ��āC
(k\vec{x_1}%2B l\vec{x_2})=\vec{0}&chf=bg,s,fff6f6)
���Ȃ킿�C���ʑS��

�̑������_�ƂȂ�D
�@�t�ɁC���ʑS�̂����_�Ɉڂ����P���ϊ��̍s��͗�s��
O������C���̏��������̂�

���Ȃ킿

�܂�
A���P�ʍs��̒萔
λ�{�ł���ꍇ�Ɍ�����D
���̋t�C���Ȃ킿�C

�̂Ƃ��C�C�ӂ�

�ɑ��āC
\vec{x}=\vec{0}&chf=bg,s,fff6f6)
�͖��炩
�@���̘b�́C�Q���̐����s��
X�ɂ���āC���_�Ɉڂ����x�N�g���i�j�j�̎���
dim(Ker(X))�ƍs��
X�̊K��
rank(X)�̘a���C�����s��
X�̎���
n�ɓ�����
dim(Ker(X))+rank(X)=n
�Ƃ����d�v�����ƊW������D���̖��ł́C
dim(Ker(A−λE))=n=2������C
rank(A−λE)=0�܂�
A−λE�͗�s��C
A=λE�ƂȂ�D
�i���M�҂́C�����w�ȑ��ŁC���ΐ����_�̗��C�Ŋw�̒P�ʂ��C���v�͊w�̗��C�œ��v�̒P�ʂ��u�ǂݑւ��Ƃ��āv��������̂ŁC���`�㐔�͑������₵���D�����Ɏg���ꍇ�́C�u�j�v�u�K���v�u�ŗL�x�N�g���v�u�����v�Ƃ������p������Ƃ���google�����E���t�������Y��Ȃ��j
�̑��M�̎d�����킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�́C�̓_�@�\��t�����[�W�ł͂���܂���̂ŁC���𗦂Ȃǂ𑗐M����悤�ɂ͂Ȃ��Ă��܂���D�����́C��ʂɏ����Ă���܂��D����E�ӌ��͑���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̓��ςƊO���ɂ��ā^24.02.03�n
���ς��l�Ȃ̂ɁA�O�ς��x�N�g���ȗ��R���킩��Ȃ��B
�����Z�͌����@�����x�N�g���Ƃ̘a���������A�|���Z�͌����@����P�ʃx�N�g���Ƃ̐ς��������݂����ȁA�����Z�Ɗ|���Z�̍Œ���̃��[���I�Ȃ̂��������Ǝv�����ǁA
���ς̓������x�N�g���ɂ�����A�O�ς̓�����l�ɂ����Ⴄ�Ƃ����̃��[�����藧���Ȃ������肷��̂��낤���B
�����m��ҁn�F�A�����肪�Ƃ��D���ʂɐ��w�̐搶�ɂ��̎��������u����͒�`������v�Ƃ������S�ɐ��m�ȉ��Ԃ����͂��ł����C���m�ł͂Ȃ��Ă������������������������l���Ă݂�ƁD
�@���̂悤�ɒ�`���āu�����͂Ȃ��̂��v�u�g�����͂���̂�=�֗��ɂȂ邱�Ƃ�����̂��v�Ƃ����ϓ_���猩�Ă݂�ƁC�M�҂��v�����͕̂����w�ւ̉��p�ŁC3������Ԃł̃G�l���M�[���]���[�����g�́C�e�X���ςƊO�ςɑΉ����Ă���C�����ŕ\���ƂƂĂ��֗����ƌ����܂��D�͊w��d���͊w�̏d�v�@���́C�������g���ĕ\�����D�����Ŋo���Ă����ƁC����ɂ��y���݂�����܂���D�����Ŋo���Ă����Ȃ��ƁC����͈�̓����҂��Ă��饥��݂����Șb�ɂȂ�D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̍��W�i�P�����j�ɂ��ā^24.01.30�n
������̃y�[�W�̖��3�A���4�̖͔͉̓������Ԉ���Ă��܂��B
- ���R�F������9/5�Ȃ̂ɂ���Ɍv�Z����1�ƂȂ��Ă�
- ���S�F������-17/3�Ȃ̂�17/3�ƂȂ��Ă���Ɍv�Z����1�ƂȂ��Ă�B
�����m��ҁn�F�A�����肪�Ƃ��D�R�s�y�œ��Ă̌`��������������C�O�̖��̒��g���t���ė��Ă����Ƃ����悭����~�X�ł����̂ŁC�������܂����D
���m��錧�^�֓�����^24.01.26�n
�u���O�p���̒�ϕ��ł̏��A�����i6�j�ł́u12.3�v�ӂ�ɊY������̂ł��傤
���H���@�Y�t�t�@�C���F�ɂ���h���ӂ�2x�ɂ��낦��h������܂���B�ǂ�Ȍv�Z��
����ׂ̉��ׂ̈̏����Ȃ̂����������������B���肢���܂��B�v
�ŁA���Z���w�̊�{���T�C�g���玿�₵�Ă���ē��ł��B
�ȑO(2020�N)�ɂ�����ŁA���肪���炸���[���A�h���X�܂ŋL�ڂ��čs����������
��A���̍ەԐM��Ⴂ�܂����o�܂ŃA�h���X��m���Ă���܂��B
������Ȃ����́A�v�Z�ߒ��ł̌�����ɂ��Ăł��B
�Y�t�t�@�C���������������B
�Y���ӏ��́A���Z���w�V������ϕ��̏��ł́g�O�p���̒�ϕ��@�����i6�j�ł�
�u12.3�v�h�ɂȂ�Ǝv���܂������A�����������������������܂��āA���肢����
���B
�Y�t�t�@�C���́A�I�[���Ёu�}���K�ł킩��t�[���G��͂ł�p146�̓��e�@sinxcosx
��0����2�܂Őϕ�����v�ł��B�����ł̐����F�h���ӂ�2x�ɂ��낦��h�Ƃ�������
�����炸�T���Ă��鏊�Ȃ̂ł��B
�ǂ����A���J�ɂ������������B��낵�����肢���܂��B
�����m��ҁn�F����̈Ӗ���������܂����D���̂悤�ȓ��Ắu��w�ŁC���������������Ă���w�������ɁC�������Ă��鋳�����v�����������ŁC���Z�ł͕��ʂ͂��������������͂��܂���D���̌������o���邾���ł��D�ϕ��萔���ȗ�����Ă��邱�Ƃ����������悤�ɁC���̋��ނ́u�������Ă���l�����v�ł��D�i�ؖ��͗��ӂ��������ł���j

����ɂ��C������

...(*1)
�����̋��ނł́C���Z�Łu�u���ϕ��v�Ƃ��ċ����邱�Ƃ��C�u���ϕ��Ƃ������t���g�킸�ɏ����Ă���܂��D���Ȃ킿�C����(*0)���������Ă�����̂Ƃ��āC(*0)�����L��(*1)���C(*2)�ȉ��̂悤�ɉ������̂����ʂł��D

...(*0)
(*2)�F(*0)→(*1)�̓�����

�Ƃ����ƁC


=-\frac{1}{2}\cos 2x%2B C\]&chf=bg,s,fff6f6)
���������b�ɂȂ��Ă���܂��B
������́u���Ǝ��v�̃Z���^�[���ʂ̌g�єł̃y�[�W�ł́A�u�����ǂށv�������Ă������J���Ȃ��Ȃ��Ă��܂��Ă���悤�ł��B
�p�\�R���Łu���Ǝ��v�́uPC�p�v�̃y�[�W�ɔ��Łu�����ǂށv�������Ɩ��Ȃ��J���܂��B�܂��A�����u�g�єŁv�̃y�[�W�ł������Ƃ��Ă��A�u���v�́u�Z���^�[�������v�̉���́A���Ȃ��J���܂��B
���m�F���������܂��ƍK���ł��B
���Z�������\�������܂��A��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�v���O�����̏������ɂ��āC�����I�ȃ~�X������܂����̂ŁC�������܂����D�Ȃ��C����1��ǂ�ł���ꍇ�C�R���s���[�^�̃L���b�V���������ɂ���f�[�^���\�������̂ŁC�ϋɓI�ɍēǂݍ��݁i�����[�h�j���Ȃ��ƕ\�����ς��Ȃ��悤�ł��D
���m��錧�^?����^24.01.25�n
�����t�[���G�O�p���ϕ��œY�t�t�@�C���F�ɂ���h���ӂ�2x�ɂ��낦��h������܂���B�ǂ�Ȍv�Z������ׂ̉��ׂ̈̏����Ȃ̂����������������B���肢���܂��B���O�p���̒�ϕ��ł̏��A�����i6�j�ł́u12.3�v�ӂ�ɊY������̂ł��傤���H��
�����m��ҁn�F�ǂ̃y�[�W�̘b�����Ă�����̂��C�ʂ��܂���D���̋��ނŁu�Y�t�t�@�C���v���g���Ă���y�[�W�́C�ϕ��̍��ڂɂ͂���܂���D�t�[���G�O�p���ϕ��Ƃ������ڂ�����܂���D�ǂ����C���̋��ނɂ��ׂ�������C�Ԉ���Ă��̋��ނɎ��₵�Ă���̂ł͂���܂��D����Ƃ��C�P�Ȃ�p���f�B�ł����H
���m�ʂ̕ł���̎���ɑ���n[�h�E���A�u���̒藝�i�������j�ɂ��ā^24.01.25�n
��1�ɂ��āA����ɂ���-��3+i�̋Ɍ`���ւ̕ό`��,cos�̕������t�ȋC�����܂�.
�����m��ҁn�F�A�����肪�Ƃ��D�ό`��5�s����̂ŁC�ǂ̉ӏ������w�E�Ȃ̂����C�͂����肵�܂��C�悭����ԈႢ�Ƃ���
cosθ�́C��� �� f(−θ)=f(θ) ���Ȃ킿
cos(−θ)=−cosθ ←�ԈႢ
cos(−θ)=cosθ ←������
�́C���v�ł����H
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^24.01.19�n
�킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^24.01.14�n
������ʼn������͂���܂���ł������܂Ƃ߂̖��(1)�̓��ĂŁA�^��������x+7>0��x+>0�ɂȂ��Ă��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���`�㐔.���K�m�[�g�i�A���T�[�u�b�N�j�ɂ��ā^24.01.11�n
�߂��Ⴍ����킩��₷�������ł��B���肪�Ƃ��������܂��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��i�}����j�ɂ��ā^24.01.09�n
���Z�����Ƃ���\����܂���B�摜�̃����N����Ă���悤�ł����A����A�C������܂����H
�����m��ҁn�F�A�����肪�Ƃ��D1��4���Ɠ��l�CGoogle�������\���T�[�r�X���~���Ă����悤�ł��D�M�҂̕��ł��������\������܂���ł����D�i�Ȃ����Candroid�ł͕\������܂���.�j�ǐL�F�P��10���̒��C�N�����璼���Ă��܂����D
�@�m�Q�l�n�Ⴆ�CGoogle�̃T�C�g��DDOS�U�����ăg���t�B�b�N���a���Ă���悤�ȏꍇ�ɂ��Ή��ł���悤�ɁC�G���[����MathJax���\�������ݒ�ɂ�����悢�Ƃ��v���܂����C���̃G���[�����͂܂��ł��Ă��Ȃ��D�iMathML�͍��ۋK�i�Ƃ͂����ǂ��C�{�����e�B�A�̉^�c�ŁC���N���O�ɃZ���{�[������̉^�c���Ă���jsMath�ɋz�������MathJax�ɕς�����H�悤�ȋL����...Google�͈��Ƃ�MathML�͍��ۋK�i�ł����C�M�҂̔��f�Ƃ��āu�ǂ��炪��藊��Ȃ����̔��f�E�q���v�ŁC���݂܂�Google��D�悳���Ă��܂��D���Ƃ̖����T�[�r�X�Ȃ̂ŁC���~�܂��Ă�����͌����Ȃ��̂���_�ł����C�Ƃ肠����20�N�Ԗ����ɕ\���ł������т͂���D����������o������C���Ƃ̖����T�[�r�X�ł���android�́C����Ȃ�����g���ׂ��łȂ����ƌ����邩�ǂ����Ƃ�����蓯�l�C�Ȃ��Ȃ�����̂ł��j
���m�ʂ̕ł���̎���ɑ���n[�]���藝�̂Q���������ɂ��ā^24.01.04�n
�O�p��Ɛ}�`�̂Ƃ��S�đI�����鏊�����łȂɂ������Ȃ��ł��A�ۑ�ł���̂Œ����Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���_��F�����܂����DGoogle�������\���T�[�r�X���~���Ă���悤�ł��D�ꎞ�I�Ȃ��ƂȂ�C�҂ĂΒ���͂��ł����C�P�v�I�ɒ�~�����̂Ȃ�C���̐����\���V�X�e�����ނł͐���y�[�W�g�p���Ă���̂ŁC����������ɂ́C���N��������܂��D�l�b�g���͂܂�������܂���.�i�ǐL�F�P���T���̒��C�N�����璼���Ă��܂����j
���m�ʂ̕ł���̎���ɑ���n[�����藝�i���j�ɂ��ā^24.01.04�n
�I�����鐔�����S�ā��Ȃ�ł�����
���ꂪ�ʏ�ł����A�H�ԈႦ�Ă����炷���܂���
�����m��ҁn�F�A�����肪�Ƃ��D���_��F�����܂����DGoogle�������\���T�[�r�X���~���Ă���悤�ł��D�ꎞ�I�Ȃ��ƂȂ�C�҂ĂΒ���͂��ł����C�P�v�I�ɒ�~�����̂Ȃ�C���̐����\���V�X�e�����ނł͐���y�[�W�g�p���Ă���̂ŁC����������ɂ́C���N��������܂��D�l�b�g���͂܂�������܂���.�i�ǐL�F�P���T���̒��C�N�����璼���Ă��܂����j
���m�ʂ̕ł���̎���ɑ���n[�w�����ΐ��̂����ɂ��ā^23.12.26�n
����Ȃ��ł��B�l�͂��̋L���ɃC�`�������̂��悤���Ȃ��Ǝv���܂��B���ƁA�ƂĂ�������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�X����Ȑ��O�̂P�_���^����ꂽ�Ƃ��̐ڐ��̕������ɂ��ā^23.12.10�n
���P�D�Q�i�āj���肪�Ƃ��������܂��B���܂�����ł��Ă��܂���ł����B
�wy=mx�}��(9m^2+16)�E�E�E�@�@�@�����Q��m�̒l���Cm1, m2�Ƃ���Ɓx�̐����ł����A
�����̍l���ł́A�����̒����̕��������Ȃ̂ɁA����̒l�łȂ��ƃ_���Ƃ��������A�������Ȃ��̂͂Ȃ��H���͔C�ӂ̎������ƍl���Ă��܂��B���܂��`���悢�̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
m, k�͔C�ӂ̎����Ƃ���D����@�v,�������C�^����ꂽ�ȉ~�ɐڂ��邽�߂ɂ́C
k�͔C�ӂ̒l�ł����Ă͂Ȃ炸�C

����A�����Ă��Ȃ���Ȃ�Ȃ��D�v����ɁC�A�ŕ\�����Q�̒����������Ɍ���邽�߂ɂ́C�A�ŕ\�����Q�̒����̌X��
m�̒l��

�Ƃ���Ƃ��C

�����Ȃ���Ȃ�Ȃ�����B�v
�@�Ŏ~�܂��Ă����
m, k�͔C�ӂ̎����ł����C����ȏ�i�܂Ȃ��Ƃ������ƂȂ�C�������������Ȃ��ƃS�l�Ă��邱�ƂɂȂ��💢
���P�D�Q�̉�@�ɂ��Ă̎���ɂȂ�܂��B�i�P�j�̉��̕��́@(1)�����Q��m�̒l���Cm1, m2�Ƃ���ƁCm1, m2�́Cm�Ɋւ���Q���������Ƃ���܂��B�����Łi�P�j�����́A��ӂ����ł͂Ȃ��ł��傤���H���ƁA�Ȃ��Am1, m2�́Cm�Ɋւ���Q���������ɂȂ�̂��킩��܂���ł����B������́A���͂̉ɂȂ�܂��B�i�P�j���ɂ����āA����m1=1�Ƃ���ƁAm2�͐����Ɍ���邩��m2=-1�ƂȂ�A�����̐ڐ��̌�_���W�����߂�B(0,5),(0,-5),(5,0),(-5,0)�ƂȂ��A����̓_�����ׂ͒��p�O�p�`�ɂȂ�̂ŁA�}��`���킩��ʂ�A����͔��a5�A���S(0,0)�̉~�ƂȂ邱�낪������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����̔ԍ��Ɠ��č쐬��̔ԍ�������킵���Ȃ��Ă��܂����̂ŁC�������܂����D���e�ɂ��āF�u��ӂ����v�ł͂���܂���D�u�Ȃ��Am1, m2�́Cm�Ɋւ���Q���������ɂȂ�̂��v�@���ڍs���ė��ӂ��Q�悷��F���ʂ̕ό`�ł��D���͉ɂ��ẮC���_�͍����܂����C���w�I�ɂ͕K�v�������q�ׂ��݂̂ƂȂ�C�z�_�͂قƂ�ǂȂ��ł��傤�D�_���Ƃ��Ă͎g���܂��D
�����s�^������^23.12.10�n
�Ȃ����̃T�C�g�͖����ł���ȂɌ����̂ł���?anatawa,nanimonodesuka
�����m��ҁn�F�A�����肪�Ƃ��D�܂������C������肨�b�ł����
���m�ʂ̕ł���̎���ɑ���n[�W���C�K�v�����C�\�������i����,�Z���^�[���j�ɂ��ā^23.12.04�n
2020�N�x�Z���^�[����.���w�T�E���wA�̃^�͇B���ĉɂȂ��Ă܂����A12��24�̖Ȃ̂�24�̔{���̏W���ɂ͓���Ȃ�����C���������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�K�v�����E�\����������Z���^�[��������ɂ��ā^23.12.04�n
�����P���ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^23.12.02�n
�f���ɓ�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ƃ肠�������}��������悤�ɂȂ�����C�����ł����Ƃ�����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^23.11.28�n
���3��(3)�̘A���������̉��������킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���ʂɗ��ӂ�W�J���āC��������̂͏����Ă���C�Q�̎���r�̌W���𑵂��āC�����Z����ƁCb�̂Q���������ɂȂ�܂��D
�@����҂́C���ƂȂ��D�L���d��������Ă���̂ł͂Ȃ��ł��傤���H�h���h���̍��ݓ������d���Ɍ����Ă��C�l��������Ŋy�������邭�`��♫♬♩
���m�ʂ̕ł���̎���ɑ���n[�����藝�E�]���藝�ɂ��ā^23.11.27�n
����ɂ��́B��A�̐}�`�̕���(���l���E�X�̒藝�Ƃ�)�𑝂₵�Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̐��w��
���̃y�[�W�ɂ���܂��D
���1(3) �Ȃ�100/3��4/3�ɂȂ�̂������Ă������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D100/3��4/3�ɂȂ�̂ł͂Ȃ��āC������������
2���̎������ł��邱�Ƃ���
=\sin\theta&chf=bg,s,fff6f6)
�����藧���C�]����
=(2\pi\times 16%2B\frac{4}{3}\pi)=\sin\frac{4}{3}\pi&chf=bg,s,fff6f6)
�����藧�Ƃ������Ƃł�
����̗��K���́u�S����I�v�݂����ȉ��o�͂Ȃ��̂ł���...
�����m��ҁn�F�A�����肪�Ƃ��D���e�I�ɑ�w���N�x���x���̖��Ȃ̂ŁC���܂��x���̃p�t�H�[�}���X�����Ƌt���ʂœ{�����邩�॥��Ƃ������ƂŁC���l���܂����D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^23.11.26�n
���������b�ɂȂ��Ă��܂��B�����ǂނ��Ƃ��ł��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�v���O������ύX�����Ƃ��ɁC�u��������v��script�̒���script�Ƃ�����������������ł������߁C�S�ł��Ă��܂����D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[2�����̍ő�ŏ�(2)�ɂ��ā^23.11.26�n
2�����̍ő�ŏ�(2)
�����m��ҁn�F�A�����肪�Ƃ��D�u�Ȃ��v�ȊO�̃S�~�f�[�^���������Ă��܂����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�X����Ȑ��O�̂P�_���^����ꂽ�Ƃ��̐ڐ��̕������ɂ��ā^23.11.23�n
�y���2.2�z�́i�R�j����̓W�J���ʂ́A���O�Q�����Q�P�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�r���o�߂ɒ���������܂����C���ʂ͕ύX����܂���ł���
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̋��ߕ��ɂ��ā^23.11.20�n
�������Website�ł͔��ɒ��J�Ȑ���������A�����Ƃ����b�ɂȂ��Ă���܂��B������\�ł��傤���H
�ŗL�l���d���̏ꍇ�̌ŗL�x�N�g���ɂ��ċ����Ă��������B
�s���{(4,-2,1)(-2,1,2)(1,2,4)}�A�ŗL�l��1��5(2�d��)�ƂȂ�܂��B�ŗL�l1�Ɋւ��ẮAx+z=0��y+2z=0����ŗL�x�N�g����(x,y,z)=k(1,2,-1)�ƂȂ�Ǝv���܂��B����A2�d����x+2y-z=0�����x=s,y=t�Ƃ���ƌŗL�x�N�g��(x,y,z)={s(1,0,1)+t(0,1,2)}�ƌv�Z�ł��܂��B�������Ax=s,z=t�Ƃ���ƌŗL�x�N�g��(x,y,z)={s(2,-1,0)+t(0,1,2)}�ƂȂ��Ă��܂��܂��B���l��y=s,z=t�Ƃ����ꍇ�A�ŗL�x�N�g����(x,y,z)={s(-2,1,0)+t(1,0,1)}�ƂȂ�܂��B�����3�̌ŗL�x�N�g���͂ǂ̂悤�ȊW�ɂȂ��Ă���̂ł��傤���H��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�i�l�����[���ɂ��́C����Ă��܂���̂ŁC���̉ŗ������Ă��������j�D�s��{(4,-2,1)(-2,1,2)(1,2,4)}�̌ŗL�l��1��5(2�d��)�ŁC�ŗL�l1�Ɋւ��ẮAx+z=0��y+2z=0����ŗL�x�N�g����(x,y,z)=k(1,2,-1)�C2�d��5�ɑΉ�����ŗL�x�N�g����x+2y-z=0�Ƃ������Ƃ��C�n�j�ł��D�Ƃ���ŁC���̂悤�ȁu��Ԃɂ����镽�ʂ̕������v�ɂ��ẮC
���̃y�[�W�ɉ�����Ă��܂����C�����������ڂ��������C���̒ʂ�ł��D
(1)�@1�_
&chf=bg,s,fff6f6)
��ʂ�C�@���x�N�g��
&chf=bg,s,fff6f6)
�ɐ����ȕ��ʂ̕�������
%2B b(y-y_0)%2B c(z-z_0)=0&chf=bg,s,fff6f6)
�Ə�����i←�d�v�����j�D���Ȃ��̖��Ō����C���_
&chf=bg,s,fff6f6)
��ʂ�C�@���x�N�g��
&chf=bg,s,fff6f6)
�ɐ����ȕ��ʂ̕�������

�Ə����܂��D
(2) ��Ԃɂ����镽�ʂ̕������́C���̕��ʂɊ܂܂��Q��1���Ɨ��ȃx�N�g��

��1�������Ƃ��ĕ\���Ă��悢�D�i�萔�{��s,t��ɁC�ʂ��}��ϐ��j
&chf=bg,s,fff6f6)
�@���Ȃ��̖��̏ꍇ�C�A�j
,\vec{u_2}=(0,1,2)&chf=bg,s,fff6f6)
�Ƃ����ꍇ��(x,y,z)={s(1,0,1)+t(0,1,2)}�C �C)
,\vec{u_2}=(0,1,2)&chf=bg,s,fff6f6)
�Ƃ����ꍇ��(x,y,z)={s(2,-1,0)+t(0,1,2)}�C �E�j
,\vec{u_1}=(1,0,1)&chf=bg,s,fff6f6)
�Ƃ����ꍇ��(x,y,z)={s(-2,1,0)+t(1,0,1)}�ɂȂ�܂����C�ǂ�ł��n�j�ł��i�������̂ł��j�D
�@����́C�x�N�g���̑g�C
,\vec{u_2}=(0,1,2),\vec{u_3}=(2,-1,0)&chf=bg,s,fff6f6)
��

�������Ƃ��番����悤�ɁC���ʂɊ܂܂��1���Ɨ��ȁi=���s�łȂ��j�Q�̃x�N�g��

��p����C���ʂ̕�������
&chf=bg,s,fff6f6)
�ŕ\����Ƃ������ƂɑΉ����Ă��܂��D���(1,2,-1)��(-2,1,0), (1,2,-1)��(1,0,1), (1,2,-1)��(2,-1,0)�ƂȂ��Ă��邱�Ƃɒ��ӂ��܂��傤�D�����ʂɂ́C���ʂ�����Q��1�g�̃x�N�g���Ƃ��ẮC�K�i�i�傫�����P�́j�����i�݂��ɐ����ȁj�x�N�g�����D��ŗp�����܂����C1���Ɨ��ł���i=���s�łȂ���j�Ȃ�ł�����ł��D
���v��
�u�|���Z����O�͂Q�̐��v�ł��u�ρv��1�̐��ɂȂ�D���̊|���Z�⊄��Z�̒��Ɂu�ρv������Ƃ��́A�������i�@�j��t����Ƃ悢�D
���̋L�ڂ͔��ɎQ�l�ɂȂ�܂����B�����������Đ������邱�Ƃ̑�����w�ׂ܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A�����ɂ��ā^23.11.18�n
���ꂱ��10�N���炢���Ȃ��̍쐬�����T�C�g���{�����Ă�����̂ŁA���Z���w�̃y�[�W���悭�{�����Ă��܂��B�ԈႢ��������Ȃ��ӏ����݂����̂ł��m�点���܂��B
7. �Q���������Əz�A�����̏͂ŁA��3��1.732�E�E�E������C��3�̐���������1�@x=��3-1�Ƃ��ƁA�E�E�E�@�̍Ō�̉ӏ�����2-1=[0,1,2(1,2�̏�ɐ�)]�ɂȂ��Ă��܂����A�Ō�̉ӏ���3-1=[0,1,2(1,2�̏�ɐ�)]���������̂ł͂Ȃ��ł��傤��?
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����i10�N��!?�j
���m�ʂ̕ł���̎���ɑ���n[�ʓx�@�F�O�p���̒l�ɂ��ā^23.11.13�n
������肾���ł͂Ȃ��A�F�X�Ȗ��������_���ɔr�o���Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D���_���猾���C���̂܂܂̕����悢�D��ʂɁCe-���[�j���O�ɂ����āu���x����Ă��C������肪�������Ԃɏo�肳���v�̂͂悭�Ȃ����Ƃł���C�Ƃ����̂́C4����x�̖�肪�C4,5�肾���o�肳��Ă���ꍇ�̂��ƂŁC�����ނ̂悤�ɑI�������e14�C��萔��21�������悤�ȏꍇ�Ɂu�����̏����o���Ă��܂��āC���K�ɂȂ�Ȃ��v�Ƃ������Ƃ͋N����܂���D
�@�t�ɁC�S���̃����_���ɏo�肵���ꍇ�u�����肪��ɏo��v�u�����C�]���C���ڂ̎�ނ�������肪�A�����ďo�肳���v�u�����ی��̖�肪�A�����ďo�Ă��܂��m���́C0�ɂ͂Ȃ�Ȃ��v�u����ґ��Ƀ��x���̍��Ⴊ����߂��āC�Ⴆ�C�Z�Ԃ̖�肪������܂���D�Z�Ԃ̓��������������ł��v�Ƃ���������E�w�E������Ƃ��Ɂu�Z�Ԃ̖�肪�v�Ə����Ă��܂����Ƃ������D�������C�v���O�����Ń����_���ɏo�肵�Ă�����̏ꍇ�C�Z�ԂƂ������Ƃ��C����\���Ă��Ă���̂����ʂ��Ȃ��i���̃y�[�W�̖��ł�����������������j�D���̂悤�ɁC�}�C�i�X�ʂƃv���X�ʂ𑍍�����ƁC���̂܂܂̕����悢�ƌ�����̂ł��D���Ԃɗ]�T������̂Ȃ�C���̃y�[�W�̖�����邱�Ƃ����E�߂��܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�s�����ɂ��ā^23.11.10�n
��T�͏��߂ďo������s�����ŁA��u��]�I�ɂȂ�܂����B���������߂Ă��邤���ɋ��ʈ����������Ă��܂����B�����̃~�X�ɋC��t���ĉ��Ƃ��ł��܂����B78�̑ސE�����ł��B���̋��ނɊ��ӂł��B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���N�ێ��ɂ��Ă͏�����ł����C�����I�Ȋ����Ń��e�B�x�[�V�������ێ����Ă����̂́C�Ȃ��Ȃ���ς��Ǝv���D�i�M�҂��܂߂āj������N�����ƕ��ώ����̊Ԃ̖�10�N�ɉ����ł��邩������������ϓ_���猾���C���p�E�����W�ɏo�i����悤�Ȋ����́C���e�B�x�[�V�������ێ��ł������ł����C���w�Ȃǂ͌𗬂����Ȃ��C�ꗬ�̕��ɂ���ʂ̕��ɂ�����ɂ��Ă��炦�Ȃ��̂ŁC�s���ȃW����������
���m�ʂ̕ł���̎���ɑ���n[����̑Q�����ƋɌ��ɂ��ā^23.11.09�n
���܂܂ŁA�����ǂ��o�������ɂ����܂ŁA���܂����B78�̌������ł������ӂ��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^23.11.07�n
���ɓ�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ȋ��z�����肪�Ƃ��D���ʂ̍��Z�̌����̐��k�Ȃ�C����͂��ł�����s���l�����̂́C[4] �����r�̂����肩�ȁH
���m�ʂ̕ł���̎���ɑ���n[�Q�����̓������1�ɂ��ā^23.11.02�n
���߂Ă��̃T�C�g���g�킹�Ă��������܂����B�ƂĂ�������킩��₷���A����e�X�g��ɂ����ɗ����܂����I�������ł�����̃T�C�g��肳��Ƀ��x���̍�����肪����Ǝv���̂ł����A�������W���Ƃ��Čf�ڂ��Ă���������X�ɕ����͂��ǂ�C�����܂��I���������ƃ��x���̍�����蓔����܂��������Ă������������ł��B�i���ꂪ���E���Ƃ����̂ł��������v�ł�💦�j���ꂩ������̃T�C�g�g�킹�Ă��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�������Ȃ̂ŁC�o����肵�������Ȃ����2�����̓������́C���̒��x�ł��D
���m�ʂ̕ł���̎���ɑ���n[2�����̍ő�ŏ�(2)�ɂ��ā^23.10.29�n
�m���P�|�Q�n�ŁA�ő�l�u�Ȃ��v�Ɠ��͂��Ă��A�̓_���~�ɂȂ��Ă��܂��܂��B����ɂ��u�ő�l�Ȃ��v�Ƃ���̂ŁA�V�X�e���̃G���[���ȂƎv���܂��B�i���̑��̖��ł́A�ő�l�A�ŏ��l�́u�Ȃ��v���������ꍇ�́��ƂȂ�̂Łj
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ޗnj��^�܂�����n23.10.29�n
�����������Ă���āA�����������킩�邩��ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����ʥ���Ǝ��ɂ��ā^23.10.28�n
�Z���^�[������2018�N�x�̍Ō�̃J�͏搔���ƒm��Ȃ��ď��������˘f���܂������A�S�̂Ƃ��Ă͂��Ȃ�o�������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�m���Ɂu�J�v�̕\���͂��������ł��̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�_�ƌX���������̕������ɂ��ā^23.10.16�n
��肪�_�o����ɂȂ��Ă��Ċy�����o���邱�Ƃ��o�����D
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���@�藝�̗��K����ɂ��ā^23.10.15�n
�ԗ����Ă���_�A���̎����ۂ���Ă���_���f���炵���v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���̔����@�ɂ��ā^23.10.13�n
����78�̑ސE18�N�̋����ł��B�M���̋��ށA�t�O�p���̔����ł͊w�K�̊y�����������Ȃ�����Ɍ������Ă��܂��B���w�͕������Ă���Ɛ��������ɂȂ��Ă��邱�Ƃ��킩��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ȒP�ȍ����������̉������ɂ��ā^23.10.12�n
�O��
���̉���u�`�����ĕ������Ă��������Ă���܂��B���킹�ĉȊw�U���V�Ђ̃��m�O���t
�u�����v�̈�߂̍������ƂƂ��ɁA�w�K�����Ă��������Ă��܂��B�o���Ƃ��ɗL�Ӌ`�ȉ���ł��萔�w�m���̗ƂɂȂ��Ă���܂��B���Ɏ��̂悤�Ȑ���҂ɂƂ��āA�傫�Ȏh���ł���܂��B
������m���ȂǑ㐔���_�ɋ߂����̂͒��ۓI��
����҂ɂƂ��ė����ɍ�����Ƃ��Ȃ����̂ł���܂����A������������������Ă��āA�o���Ȃ�������Ȃ����ƁA�������Ȃ�������Ȃ����Ƃ���t�ł���܂��B�܂�����Ƃ��ڂ�������u�`�����肢���܂��B�Ō�ɗ��4.1�̉����7s�߂P(mod5)�ƂȂ��Ă����̂�S=5t+3��x=7s+1�ɑ�����Ă����̂��˘f���܂����B�܂��A4.1�̉�@�͂���������Ƃ������ώG�ł������悤�Ɏv���܂����B����҂̂��߂��������Ă��������L���������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�ؖ��́C�e���̔[�����₷�����V�Ői�߂Ă��炦�悢�ł��傤�D�������̌������g���C�[���l���Ȃ��Ă��`���I�ɕό`�ł���Ƃ������Ƃ͌�����
�i�ǐL�j���������g��Ȃ��Z�����̓��Ă��t���Ă����܂���
���m�ʂ̕ł���̎���ɑ���n[�W�����_���W���`�ɂ��ā^23.10.08�n
774s�Ɛ\���܂�
�����b�ɂȂ��Ă���܂�
���̂悤�ȕ�����₷�����ޒɊ��ӂ��Ă���܂�
���āA
�h2.4�@�R�������s��ŌŗL�l���O�d���ɂȂ�ꍇ�h�̉E�����̃y�[�W��
x3+y3=0 �ƋL�ڂ���Ă��܂�
��v�Z�����Ƃ���
x3+y3=1�@�ƂȂ�A��q�̋L�ڂƂ��������܂�
���m�F���������Ȃ��ł��傤��
�܂��A���Y���̏�̍s��̂P���x1�x�N�g�����A
t(0,0,1)���Ǝv���̂ł����A
t(0,0,0)�̋L�ڂɂȂ��Ă��܂�
�ǂ��ł��傤��
�����Y��ł��܂��܂����̂�
�\�ł���A�L�ڂ̒ʂ�ƂȂ闝�R������������������Ƃ��肪�����ł�
�ǂ�����낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����i�����̂Ƃ����ǂ�ł���l�������Ƃ́I�j
���m�ʂ̕ł���̎���ɑ���n[�d�������ɂ��ā^23.10.08�n
�U�V�̔k�ł��@�l�ԉȊw�n�̏C�m����肽���ā@������ΐ��w���K�v�ƂȂ�����n�߂܂����@���T�����ςȂ��@���̏d������͂�����T�Ԏ��g��ł��܂��@�������@N�Ƃ� �̋�ʂ��o���Ȃ��I�@�Ȃ̂ł��낢��ȕ��̂g�o��ǂ܂��Ē����܂����@�M�a�T�C�g�͂��C�ɓ���ɓo�^���悤�Ǝv���܂��@���肪�Ƃ��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̑Q�����ɂ��ā^23.10.07�n
�ō�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̑傫���i�����j�ɂ��ā^23.10.06�n
������̃T�C�g�͂����ǂ����Ă��킩��Ȃ��ƒ��ׂĂ��鎞�ɂ��������ɋ��R�o�Ă��Ă���āA�{���ɏ������Ă��܂��B�ƂĂ��킩��₷���������A�������L���������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���s�����̉������ɂ��ā^23.10.04�n
��̓I�ŕ�����₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^23.10.04�n
�Ō�ɑS�č�������肪����Ƃ����Ǝv���܂��B�ł��A�߂��Ⴍ����Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����ƈ�ʍ��i�K���`�j�ɂ��ā^23.09.30�n
�ӂ��ӂ������Ȃ��炱�̖����Ō�܂ł�������A�v�Z�͂ƃX�s�[�h���オ��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^23.09.29�n
����������Ă��o�Ă��Ȃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D8�����ɐG�����Ƃ��ɁChead�����ɊԈႢ���������悤�ł��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^23.09.28�n
�ƂĂ�������₷���Ă悢�T�C�g���Ǝv���܂����I�@��萔�������Ƃ���Ƃ悢�Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�ߐ��̕������ɂ��ā^23.09.28�n
�������킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���s�����̉������ɂ��ā^23.09.28�n
���E������ƂĂ��悢�I���ނ��킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̎w���ɂ��ā^23.09.26�n
�ƂĂ�������₷�����e�ł����B���肪�Ƃ��������܂����B�i�T�S�ˈ�O���N�j
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������̕ό`�ɂ��ā^23.09.25�n
�e�X�g���ɍœK�ł������肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̒��_�i�W�J�`�j�ɂ��ā^23.09.23�n
���������̓r�����J�ɂ��邱�Ƃ�����ȂƎv���Ă��܂����B���̃T�C�g�ɏo��Ė{���ɗǂ������ł��B���n�Ȃ̂�1A2B�܂ł̂��ׂĂ̒P������Ă݂����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �̌��C�̑��a�i�������j �ɂ��ā^23.09.23�n
����������Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����藝,�]���藝�i�M�Z�ʼn������j�ɂ��ā^23.09.18�n
���݂�������Ă����o�Ă��Ȃ��ł��B���j���[�ɖ߂낤�Ƃ���ƁA
�Q�C�V���C���^�[�l�b�g�� Web �T�[�o (www.geisya.or.jp)�͂��Ȃ��̃��N�G�X�g���� URL �ɑ���h�L�������g�� �����邱�Ƃ��ł��܂���ł����B
������ URL ����͂��邩�A���̃z�[���y�[�W�̊Ǘ��҂ɂ��₢���킹��������
�Ƃ��������ɏo�Ă��܂��B���Ȃ݂ɑ��̃y�[�W�ł͖��Ȃ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����f�����������܂����D1�ڂ̃~�X�́Cscript�̒���script�Ƃ��������������Ă��܂����ԈႢ�ŁC2�ڂ̃~�X�́C�f�B���N�g���̊K�w�w��̊ԈႢ�ł����̂ŁC�e�X�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�̂��낢��Ȗ���ɂ��ā^23.09.15�n
���m�̂Ă�ł��B�������₵�ĕԐM���Ă��݂܂���B���̂悤�ȃT�C�g�����莄�Ƃ��Ă͂��������ɗ����Ċ��ӂ��Ă���܂��B�����炱�������ς������Ă�Ƃ����ȋ^�₪�łĂ��Ă��܂��܂��ā���
���̃T�C�g�����ꂩ��������܂��悤��
�����m��ҁn�F�A�����肪�Ƃ��D
���m���m�^�Ă炳��n23.09.15�n
�ԐM���肪�Ƃ��������܂� �P�ȊO�������Ȃ肽�����Ȃ���k�{�P�Ɋւ��āw���x����������ĂȂ���ԂȂ�A�uk�{�P�̂Ƃ����A�u���v�����藧�v�Ƃ͂Ȃ�Ȃ��̂ł́H�Ǝv���܂����B ���̎��́Ak�{�P�ł́u���v�Ŏ����āA�܂Ƃ߂ď����Ƃ��ɁA�u����������n=1�̂Ƃ��v�Ƃ��ē���������悢�ł����H
�����m��ҁn�F�A�����肪�Ƃ��Dn=1�̂Ƃ��C(����)=(�E��)�ł��Dn>1�̂Ƃ��C(����)>(�E��)�ł��D������C�˂ɁC(����)��(�E��)�ł��D����܂�Cn=1�̂Ƃ��C(����)��(�E��)�ł��Dn>1�̂Ƃ����C(����)��(�E��)�ł��D
�@�b���Β����Ȃ�܂����C(����)��(�E��)�Ƃ́C(����)=(�E��)�܂���(����)>(�E��)�̂��ƂŁC���ۂɂ�(����)=(�E��)����(����)>(�E��)�Ƃ������Ƃ͂���܂���D
�@����ɁC���������m�Ō����C(����)=(�E��)�Ȃ��(����)��(�E��)�����藧���C(����)��(�E��)�Ȃ��(����)��(�E��)�����藧���܂��D
�܂Ƃ߂ď����Ă��邾���ł��D
�@�u����������n=1�̂Ƃ��v�Ƃ���̂́C���z�I�ȏ������ł��D
���m���m�^�Ă炳��n23.09.15�n
�A�[�@�̖��ꗗ(B1)�ł����A���肵�����̂�k+1�����������̂ƁA�^����k�{�P�����ꂽ���̂̍����Ƃ��ā�0�Ƃ���܂ł͂킩�����̂ł����A���̏ꍇ�A�����͂ǂ�����Ď����悢�̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�s�����̏ؖ��o�߂��番����悤�ɁC�s�����ɂȂ�C��ʂ̐���n�ɂ��ẮC�����͐��藧���܂���D������i�I�H�j�����t���s�����i���j�����藧���܂��D�����x�͌����Ă݂����V�����i���Ȃ���D�Ȃ��C��������������̂�n=1�̏ꍇ�����D����ŁC���Ƃ̖��Ƃ��ẮC���Ő��藧�j
���m�ʂ̕ł���̎���ɑ���n[�w���Ƒ召��r�ɂ��ā^23.09.13�n
���́i�S�j�͑召�̏��Ԃ��t�ȋC������̂ł����ǂ��ł��傤���H���M�͂Ȃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�w�����̒ꂪ1����������(>0)�Ƃ��C�召�̏����͎w���̏����Ƌt�ɂȂ�Ƃ������Ƃ������Ă���̂ɁC�t����Ȃ����Ƌ^���Ă���Ƃ������Ƃł́C�b���ʂ��Ă��Ȃ��Ƃ������Ƃł��D
�Q�l�܂łɁCExcel���g���C�����\���ł�
^{\frac{17}{19}}=0.905..,\hspace{2}\big(\frac{17}{19}\big)^{\frac{19}{17}}=0.883..,&chf=bg,s,fff6f6)
^{-\frac{17}{19}}=1.10..,\hspace{2}\big(\frac{17}{19}\big)^{-\frac{19}{17}}=1.133..,\hspace{2}1&chf=bg,s,fff6f6)
�ɂȂ�܂��D
���2�́i1�j�̉��̌����ł̊J����Ⴢ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D��@�C���т�@�Ɨ������܂����D
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�s�����j�ɂ��ā^23.09.13�n
�Ō�ɖ�肪�ڂ��Ă���T�C�g�͏��Ȃ��A�������ȒP�ŊȒP�ȕ��K�⏉�w�ɍœK�ȃT�C�g���Ǝv���܂�(*^^*)
�����m��ҁn�F�A�����肪�Ƃ��D���N�C���w�����̐��k�������Ă����̂ŁC�n�������悤�ł�
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^23.09.11�n
�R���b�c�\�z�̏ؖ����������Ă��܂��B
https://youtu.be/UNvG7IJlHQ8
https://youtu.be/OFJAJ1jZqmM
https://youtu.be/cJdsEmD1lhw
https://youtu.be/EMDaWwYovH8
�����������]����K���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�撣���Ă��������D�Ȃ��C�M�҂͑��̕��̘_���I�Ȃ��̂��]���闧��ɂ͂���܂���D�������͖ʔ������`�Ƌ����ƊS�������Ă��炦��悤�ɁC���k�����ɍL�������Ă�����x�ł��D
���m�ʂ̕ł���̎���ɑ���n[������]����ʐ�(�Z���^�[���1)�ɂ��ā^23.09.05�n
��3���ł��B
�m�Ő����藝�Ɨ]���藝�̃Z���^�[���̏��e�X�g������̂ł��̃T�C�g�ʼn��K�����Ă��������܂����B
�g���₷�������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�̈�ɂ�����ő�ŏ��i�������j�ɂ��ā^23.09.02�n
�������p�����Ē����Ă���܂��B���12�̘A���s����������āA���̖�蕶�Ɣ���Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��Dandroid�ł͕\���������Ƃ������ƂŒ������܂���
���m�����s�^helpme����n23.09.01�n
���肪�Ƃ��������܂����B
���₪�Ԉ���Ă܂����B�u��p(1-p)/n�v�ł͂Ȃ��āA���[�g�̂��ĂȂ��up(1-p)/n�v�ł����B
�ł��̂ŁA���߂Ď����������
�u���z�̕��U���ꍇ�ɂ���ā@ np(1-p) �������� p(1-p)/n �������肷��̂����܂����s���Ƃ��܂���v�ł��B
�i�Ⴆ�A���̃T�C�ghttps://univ-juken.com/bosyudan-hyohon#i-17�̖��S�̂悤�ȁj
����Ԉ���ĂĂ��߂�Ȃ���
�ǂ������������肢���܂�
�����m��ҁn�F���̂悤�ɐ������܂������C�b���ʂ��Ȃ��̂́C�������v�̘b���܂��w��ł��Ȃ����炾�ƍl�����܂��D�܂��������v���w��ł��玿�₵�Ă��������D
���m�����s�^helpme����n23.08.31�n
���z�̕��U���ꍇ�ɂ���ā@
np(1-p)
��������
��p(1-p)/n
�������肷��̂����܂����s���Ƃ��܂���
�킩��₷�����������������B
�����m��ҁn�F�A�����肪�Ƃ��D���z�̕��U��np(1-p)�ł�.��p(1-p)/n�ɂ͂Ȃ�܂���D
����ɑ��āC��W�c����W�{�̌����i=�����ȗp��́u�W�{�̑傫���v�j�Œ��o�����W�{��p���āC��W�c�̕��ς𐄒肷��Ƃ��́C�W�{���ς̕W������'�͕ꕽ�ς̕W�����Ђ�

�̊W������̂ŁC��������g���܂��D�W�{�����W�c�𐄒肷�鐄�����v�ł́C�������ς��܂��D
Python�̔z��̊|�Z�̏����ύX�Ɋւ��鎿��ł�
���L��A:�R�[�h���Q�Ƃ�������
Q1�j�֘A�������`�㐔�w�Ɋւ���T�C�g������A�����������܂��ƗL��ł��B
def t_�z��():
print("t_�z��():")
A=np.array([[1, 2], [3,4]])
B=np.array([[5, 6], [7, 8]])
print("A=", A)
print("B=", B)
print("AB=", np.dot(A, B))
print("AB=", np.dot(B.T, A.T).T) #A ���[�[�����ł�
#print("BA=", np.dot(B, A).T) #��L���������B�����NG
t_�z��(); sys.exit()
�����m��ҁn�F�A�����肪�Ƃ��D�������python�́C�����o���Łu���������python�v���w�т܂��傤�̃��x���ł��̂ŁC�������炸�D
���āC���̂܂ܓ��������߂ɂ́C�擪�s�ɁCimport numpy as np���K�v�ł��D�����ŁC������̌��ł����Cpython�ȑO�Ɏ��Ɖ��M�̃��x���ŁC���̂��Ƃ������܂��D
�s��

�̓]�u�s���

�ŕ\�����̂Ƃ���ƁC
=^tB^tA&chf=bg,s,fff6f6)
�C���Ȃ킿�u�s��̐ς̓]�u�s��́C���������ւ����]�u�s��̐ςɂȂ�v�Ƃ������Ƃ́C�قƂ�ǂ̐��`�㐔�̋��ȏ��ɏ�����Ă��܂��D������Cnp.dot(B.T, A.T).T)��AB�ɓ������Ȃ�܂����Cnp.dot(B, A).T)��
=^tA^tB&chf=bg,s,fff6f6)
�ƂȂ��āC����s�̍��ӂƂ͓������Ȃ�Ȃ��悤�ł��D
�������݂ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̓p�\�R���p�̃y�[�W�Ȃ̂ŁC 375�~812��iPhone�œǂނ͖̂����ł��D�擪�Ɂm�g�єł͕ʕŁn�Ə����Ă���܂��̂ŁC�g�єł̃y�[�W��ǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^23.08.11�n
��萔����R�����ĂƂĂ��ǂ����K�ɂȂ�܂����I
�I������I�ԃV�X�e�����Ǝ�y�ɓ������킹���ł���̂ł��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^23.08.09�n
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��̒����ɂ��ā^23.08.03�n
�Ȑ��̒����Q�|�S�Ōv�Z���ł��Ȃ��č����Ă�����A�v�Z���̔�œ������o�邱�ƁA�������Q�Ԃ߂�
�u��������p����Ɉӂ������Ă����������ӂ��܂��B�ސE�Q�O�N�̐��w���t�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̏�@�̐����ɂ��ā^23.07.28�n
�P�ʍs��ƑΊp�s��̐����������Əڂ���🙏
�����m��ҁn�F�A�����肪�Ƃ��D�ȉ��Q�~�Q�s��ɂ��ďq�ׂ�B�@�P�ʍs���

�Ə�����C�C�ӂ�2�~�Q�s��

�ɑ��āC�ςɊւ�������@�������藧�F

�A�Ίp�s��́C�Ίp�����ȊO�̐�����0�ƂȂ��Ă���s��ŁC

�Ƃ���Ƃ��C

�����藧�D���Ȃ킿�C�Ίp�s���
n��́C�e������
n�悷����߂���D�Ȃ��C�P�ʍs��̒萔�{
kE�́C�Ίp�s��ł��邩��C�A�̐������g����
n������߂邱�Ƃ��ł���D

������
^n=\begin{pmatrix}k^n%26 0\\0%26 k^n\end{pmatrix}&chf=bg,s,fff6f6)
���ǂ����̉ӏ��ɁC�܂Ƃ߂ď����ׂ��ł���������
�ƂĂ�������₷������ł����B
�l�I�ɂ́A�����Ȃ��Ă��镔�����d�v�H�Ƃ������߂����Ă��܂��B
�����������d�v��������A���������ڗ��F�ɂ����ق��������Ǝv���܂��I
���A�ŋ����ƕ��f���Ɋւ��ċ��炭�A�܂��S�R�ł����A�m�邱�Ƃ��ł��܂����B
�ƂĂ��ǂ����ނ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^23.07.25�n
������Ղ������ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɍ��W�ɂ��ā^23.07.24�n
��ςɑf���炵�����ŗ�������w�Ɛ[�߂邱�Ƃ��ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������̕ό`�ɂ��ā^23.07.24�n
���������Ƃ��ɕ\�������܂邪�������Č��Â炢�̂ł����Ă���̂��Ԉ���Ă���̂������������Ȃ��Ă킩��Ȃ��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�@��ɂ��C�L���́����������\�������ꍇ������悤�ł��̂ŁC���{�ꊿ���́Z�ɏ��������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����.���U����(2013�`) �ɂ��ā^23.07.20�n
2015�N�x�Z���^�[�������w�UB��2��́A(2)�̎O�p�`APQ�̖ʐ�S�����߂���ɂ��Ăł����A(a^2-1)x/2a��ϕ������(a^2-1)x^2/4a�ɂȂ�Ǝv���̂ł����A�Y���ӏ��ł�x^3�ɂȂ��Ă��܂��B�m�F���������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�s���Ίp������ɂ��ɂ��ā^23.07.20�n
�v�_2�ӂ��det(A)��det(A-��E)���Ⴀ�Ȃ��ł��傤���c
�����m��ҁn�F�A�����肪�Ƃ��D���肦�Ȃ��ԈႢ�ť���������܂���
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^23.07.18�n
�Q�Ŋ��鑀��������ɁA3�{���ĂP�ł͂Ȃ��ŏ����̂Q�̗ݏ�������鑀��ɂ���A�L����̑����
�Q�̗ݏ�ɓ��B���܂��B
���
�����m��ҁn�F�A�����肪�Ƃ��D�o���G�[�V�����Łi���Ƃ̖��������ύX�������́j�͉p�ꌗ�ő�ʂ̌���������C���f���i2���j�ōs�����̂Ȃǂ�����悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^23.07.17�n
�s�����̈����Z�������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�u�ΐ��s�����ň����Z�������Ă�����́v�́C
���̎��̃y�[�W�ɂ���܂��D
��W�����(2)�ɂ��Ď��₪����܂�
A�̕�W����
157396
B �̕�W��
1,5,7,6,2,4,8,10
�Q�̐ϏW��
1,5,7,6
�Ɖ��߂��Ă����̂ł���
�U���ɓ���Ȃ�
���R�ɂ���
���w�E���������Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��DA�̕�W����15739,B �̕�W����1,5,7,2,4,8,10������ł��D…���(2)���C����҂̂悤�ɓǂޏꍇ�C���(1)(3)����̑S��������Ȃ��͂��ł����H
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^23.07.14�n
�킩��₷�������ŔY�݂��������܂����I�ƂĂ�������܂����A���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^23.06.29�n
���{�Ɛ\���܂��B�䋳�����������B����̗��Q��Y=5(x)�O�U�[�R���O�Q���Ɍv�Z���x���P�T�w�O�Q�[�R���O�Q���P�Q�w�O�Q�Ƃ��Ĕ���������܂����ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D

��

�ƕό`����͖̂����ł�
��6�Ɏ����悤�Ȗ�肪�e�X�g�ŏo�ĉ����Ȃ������̂ł����A������̉����ǂ�Ŏn�߂ė������܂����BA�ƒu�������Ƃ̎��ɂ����A��������Ƃ������z�����������ł��B�ƂĂ����߂ɂȂ�܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �O�p���ɂ��ā^23.06.24�n
�Ȃ��PF:PR=3:1�ɂȂ��ł����H
�������������B
�����m��ҁn�FFR:RP=8:4=2:1, PF:PR=3:1�Ə����Ă���܂����C���ꂪ�ǂ߂Ȃ��Ƃ������Ƃł����H
FR:RP��PF:PR�Ƃł͔䗦���ς����
���m�ʂ̕ł���̎���ɑ���n[�w�����A�ΐ����̕s��ϕ��ɂ��ā^23.06.21�n
log�̌`�̂��͕̂����ϕ��ł�������
�����m��ҁn�F�Ӗ��s���ł��D�ulog�̌`�̂��͕̂����ϕ��ł͂ł��Ȃ��v�Ə����Ă��鋳�ނɑ��āulog�̌`�̂��͕̂����ϕ��ł�������v�ƈӌ����q�ׂĂ���̂Ȃ�C����͂��̂悤�Șb�Ƃ��Đ��藧���܂����C�ulog�̌`�̂��͕̂����ϕ��ł�������v�Ə����Ă��鋳�ނɑ��āulog�̌`�̂��͕̂����ϕ��ł�������v�ƕԎ�������Ƃ����̂́C�Y��Ȃ��悤�ɕ����E�ʌo���Ă���Ƃ������ƂȂ̂��H���S�����̂ŁC�ꂢ�Ă݂��Ƃ������ƂȂ̂��H���������`�̉����́C����킵���̂őz�肵�Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��ň͂܂ꂽ�}�`�̖ʐ�(1)�ɂ��ā^23.06.20�n
���R�|�Q�̉͂P�U�ł͂Ȃ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^23.06.18�n
���4�̕ʉ�1�ɂ����āA�����͍����Ă��܂����r�������Ԉ���Ă���悤�ł��B
����=0�̂Ƃ���ŁAz�����̐ςɂ�����4�������Ă��܂����A��������2���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̓������1�ɂ��ā^23.06.18�n
���̉����������������₷���ł��B
���ꂩ�������Ă����Ƃ�����������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�i���̉��Z�ɂ��ā^23.06.15�n
���i�����̕��Ɏg�킹�Ă��������܂����B�v�Z���ǂ����Ă�2�i���̂܂܍s�������{�ŕ����Ă����̂ł����A������̂������ƂĂ�������₷���X�}�[�g�Ŋ������܂����B�������łق�̖������炷����������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����@�i���w�U/���ȏ����x����{���5�j�ɂ��ā^23.06.14�n
���3-3�̉���ŁAa.b.c�̒l�͈̔͂�������Ɓu�ȏ���v�̕��̌�͈̔͂ƈقȂ�܂��B⚪︎�~�Ŕ��肳�����ɐݒ肳��Ă���́u�ȏ���v�̕��ȍ~�̉ƈ�v���Ă��܂��B
������ɂ������͂ƂȂ�\����܂��A�Ή������肢�v���܂��B
���w���ɓ��{��̋��ނ��Ȃ����ŁA���̃T�C�g�𗊂�ɐ��w������Ă��܂��B�v�Z�͂����A�������Ŏv�l�͂��g�ɂ��̂ŁA�{���ɏ������Ă��܂��B���̂悤�Ȍ`�ŗl�X�Ȗ����Ō��J���Ă�������{���ɂ��肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p��̒�`(1)�ɂ��ā^23.06.06�n
(7) �̖��� sin B �� tan C ��₤�Ă��܂����A�����E����� tan A �� tan C �ƂȂ��Ă��܂��B
(7) �̎O�p�`�̊pB�͒��p�ƂȂ��Ă��āA(7) �̎O�p�`�ł� sin B ��₦�Ȃ��̂ł͂Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�]�L�~�X��������܂���
���m�ʂ̕ł���̎���ɑ���n[�W�J�̏����ɂ��ā^23.06.06�n
�����������Ă��������Ă���܂��B(4)(5)(6)�̖��ł����A�I�����̐����̊|���Z�����ŁA�����@�ł��܂��B������ǂ����Ƃ������Ƃł����B�B�B
�����m��ҁn�F�A�����肪�Ƃ��D�K�v�����ʼn͈̔͂��i��ꍇ�C�g���[�X�i�V���v�[���j?�ɑ�������a��(���w�E��)�ς��g���Ƒ����Ƃ������Ƃ͌����܂��D
(x-b)(x-c)(x-d)=x^4-(a%2B b%2B c%2B d)x^3\hspace{2}\cdots\hspace{2}%2B abcd&chf=bg,s,fff6f6)
�ΐ��̒ꂪ�����̏ꍇ�̉��������킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
��̕ϊ�1,
��̕ϊ�2�����Ă�������
���\�N�Ԃ肩�Ő��w�̓������ɂ�����@��ɂԂ���܂����B���낢��ȃT�C�g��q�����܂������A�ƂĂ����͋C�̂�������Ŋy�����A�̂̂��Ƃ��v���o���������������ɂȂ�܂����B���ӂł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�d�v�ȋɌ��l(1)�ɂ��ā^23.06.02�n
�����̋Ɍ��l�̖�荡�܂Œm�炸�ɗ��܂����B79�̌������ł��B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̂��낢��Ȗ��i���w�U�j�ɂ��ā^23.06.01�n
�y���1-1�z�̓�����������̓����ł͂���܂��B�f�o�b�O���Ă�悤�Ő\����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�f�o�b�O���}�ł��D�v���O���~���O�ŁC�ϐ��̒�`��̒[�̕����i���Ō����C�ŏ��̖��ƍŌ�̖��j�́C�~�X���N����₷���ӏ��炵���ł�---10�N�قǑO�ɁC�e�X�g���_�i�����̕��̃e�X�g�j�̐��Ƃ��畷�����b
���m�ʂ̕ł���̎���ɑ���n[���f���̂��낢��Ȗ��i���w�U�j�ɂ��ā^23.06.01�n
�y���2-3�z����2��������(1�|i)x2+(a�|i)x+2(1�|a)i=0��(1�|i)x2+(a�|i)x+2(1�|ai)=0�łȂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D��蕶��������܂���
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^23.05.29�n
��肪���x���ʂɂȂ��Ă���̂łƂĂ��g���₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ō����̂����ł����C����Ȃ�̋�S�̍�̂悤�ł�
���m�ʂ̕ł���̎���ɑ���n[�ꕽ�ρC��䗦�̌���(��W�{)�ɂ��ā^23.05.24�n
�R�C���g�X�̊m�����z���ǂ̗l�ɋ��߂邩�^������������A�{�y�[�W���������B��������悤�Ə��������Ă����B���Ƀ^�C�����[�Ƀf�U�C������Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D���Z���w�T�̋��ނɂ��C��������̍l�����������Ă��āC���������l���Ă���Ƃ���ł��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^23.05.22�n
�萔�W��.�Q�K���`.��.�����������m��Ɖ��n4.(3)1�cR(x)���������C�w�����C�O�p���̑g�����̗���---�i�ȉ����F�M�ҁj---
�����m��ҁn�F���Ԃ�C���̈ӌ��E����̓R���s���[�^�̌�쓮�ő��M����Ă��܂��D����Ɗ��S�ɓ������ʂ̎����3��20���ɎāC���ނ͒�������Ă��܂��D
�@��Ȃ��Ƃ́C�ꎚ��劮�S�ɓ������ʂŁC�����R���s���[�^����C�W���T�T�b�Ԃ����āC���ނ�ǂi�ݕ��i�ǂ̌������b�����ēǂ�ł��邩�ƌ����L�^�j�܂Ŋ��S�Ɉ�v���Ă��邱�ƂŁC�ǎ҂̃R���s���[�^���v���o�C�_�[�̑��M�v���O�����Ɏc���Ă����L���b�V���̌�쓮���ƍl�����܂��D
���m�ʂ̕ł���̎���ɑ���n[����W���Ƃ́H�ɂ��ā^23.05.20�n
���R�x�����ς���W������������Ȃ��ꍇ�͂���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ̖{���ɏ�����Ă�����e�Ŕ��f���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^23.05.20�n
�{���ɕ�����Ղ�������܂����B���̃T�C�g������Ă��������Ė{���ɗL��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^23.05.19�n
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�a�W��,���ʕ���,��W���i���K���j�ɂ��ā^23.05.18�n
�ƂĂ��ړ����Ԃɂ��₷�������B
�܂��e�X�g�O�̍ŏI�m�F�Ƃ��ĂƂĂ����ɗ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�̈�ɂ�����ő�ŏ��ɂ��ā^23.05.17�n
���T@�ŕӂōő�ŏ������Ƃ��͂ǂ��Ȃ�́H
�����m��ҁn�F�A�����肪�Ƃ��D�����ꂽ���t�����ȉ߂���̂ŁC�ɒl���鎿�₩�ǂ����������Ȃ���C�Ƃ肠�������������Ă݂悤�D
�@�ɒl���Ȃ�����Ƃ́C���̂悤�ȏꍇ�ł��F����1���Ԋ撣���ē�������̈�ʍ��̋��ߕ������������Ƃ����Ă����Ƃ��ɁC�őO��ŐQ�Ă������k���C���Ƃ̏I��钼�O�ɗ����オ���āC�u�搶�C��������ĉ��ł����v�ƕ������D���̎���́C����ɒl���Ȃ��D���Ƃ��Ă��Ȃ���������C�����̓ǂݕ���������Ȃ������Ƃ������Ƃ������Ă��邾��������D���T�ł́C�ӂ̓r���ōő�ŏ�����邱�Ƃ͂Ȃ��Ƃ������Ƃ�������Ă���̂�����C�u���T@�ŕӂōő�ŏ������Ƃ��͂ǂ��Ȃ�́H�v�Ƃ́C�����P�ɐ��������Ă��Ȃ������Ƃ������ƂɂȂ�܂��D
�@�����ꂽ���t�����ȉ߂���̂ŁC�{���́C�ӂ̓r���ōő�ŏ��ƂȂ���ł͂ǂ��Ȃ�̂ł����Ɛq�˂Ă���̂Ȃ�C���4�Ɩ��5�ɂ��̂悤�ȏꍇ�̋��ߕ��������Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i�����j�ɂ��ā^23.05.16�n
y"+y'=0�Ȃǂ̎��ɓ����������̌��ʂ��O�̏ꍇ�͊�{���͂P�ɂȂ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��Dy"+y'=0�̓����������̓�^2+��=0�ƂȂ�C���̉��̓�=0, −1�ɂȂ�i�Q����j�̂ŁC��ʉ���

�ł��傤
�ƂĂ��悭�킩��܂����B��肪�ǂ��A��������J�ŁA�����ƕ�����Ȃ������l�������A����Ɨ����ł��܂����B
��b�̊�b�ŋꂵ��ł܂������A����ƈ���O�ɐi�߂܂��B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂����̘b���D���ȕ��ŁC���ނɁu�����o������~�܂�Ȃ��v�Ƃ������͋C���o�Ă��邩������Ȃ��D�ł́C������Ă�������
���m�ʂ̕ł���̎���ɑ���n[�����@�i���w�U/���ȏ����x����{���1�j�ɂ��ā^23.05.15�n
���1-1�̉�f(3)����щ������܂���B��蕶�ł�4�������̂ł����A�ł͑����Ă��܂��H
�NjL:���̃T�C�g�̂������Œǎ��Ɏ�܂����B���肪�Ƃ��������܂����B�����Ƒ����o���������...�B
�����m��ҁn�F�A�����肪�Ƃ��D���̕��̕�����������܂���
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^23.05.14�n
�ǂ������ł��B�ƂĂ����₷���ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���₷��=������₷���v��ڎw���āC�O���t�B�b�N��ʂŏd�Ȃ�̈�ߐ���p���ĕ\������ȂǁC����Ȃ�ɋ�J���ď������悤�ł��D�i�N���J�߂Ă���Ȃ��̂ŁC��c�����C���掩�^���Ă݂܂����j
���m����J/�������Ȃ���^23.05.13�n�n
���Z�Q�N���ł��B�K���������ϕ���p���ĉ�����ƍl�����̂ł������܂������܂���B�����A�h�o�C�X�����������Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D��肪���R�Ƃ��߂��Ă��āC�܂Ƃ܂�܂���D�ǂ̂悤�ȊK������C��ʍ������߂����C�Ɍ��l�����߂����ȂǂƋ�̓I�ɒ�N���邱�Ƃ��d�v�ł��D
�@���Ȃ݂ɁC����̘a�������I�ɕ\�킹�Ȃ����ł��C�ϕ��́i�敪���ς̋Ɍ��Ƃ��āj���܂���̂�����܂����C��ʓI�ɊK�������ϕ��ɉ��������̂Ȃ�C�K������Ƃ����P�����s�v�ɂȂ�͂��ł����C���݂��ꂪ���݂��Ă���̂�����C��������Ȃ��͂��ł��ˁH
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���̔����@�ɂ��ā^23.05.12�n
{sinx(arctan2x)}�́A�������S��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D�����C{sin(arctan2x)}�̎ʂ��ԈႢ���Ǝv���܂����C�܂��������̔����@������Ȃ��ƥ��
���m�ʂ̕ł���̎���ɑ���n[�a�W��,���ʕ���,��W���i���K���j�ɂ��ā^23.05.12�n
���肪�Ƃ��������܂��B������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������i�Q�����j�ɂ��ā^23.05.11�n
�ƂĂ������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�s�����ɂ��ā^23.05.10�n
�����̂ł��܂��܂Ȗ��ɑ������܂����B���E�����̂��肪�����������ʂ������炵�܂����B
�Q�����̂Ȃ��Ŗ����ɂ��đ�w�ő����܂����ˁB�S�����̈�̊m���ʼn��b�����܂�Ă��܂��B����
�̌������Ă܂��B�Ƃ͈̔͂��悭�킩��܂����B���̈Ӗ��Ɏ��܂��B�O�p�s�����킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�L�����f���̃p�b�`���l�́C�G���A�ڒ��ɕM�҂��ǂ݂܂������C�A���i�̎���̕����C�܂��܂��Ƃ��������ŁC���{��̕��ɂȂ��Ă��Ȃ�������ۓI�ł����D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̌v�Z�����ɂ��ā^23.05.08�n
���Z�ň��������e���������߁A�������₷������
�����m��ҁn�F�A�����肪�Ƃ��D���K�Ƃ������Ƃł��ˁI
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̏d�S�ɂ��ā^23.05.08�n
�O�p�`�̏d�S�̍��̗�2�ɂ��ĕʉ��B�̏d�Sy���W�̓��������������Ǝv���̂ł����A�A�A�Ԉ���Ă��狰�k�ł�
�����m��ҁn�F�A�����肪�Ƃ��D���������������Ǝv�����Ă������Ă�������
���m�ʂ̕ł���̎���ɑ���n[1���ϊ��ɂ��ā^23.05.06�n
�Ɗw�Ő��w������Ă���Љ�l�ł��B������̃y�[�W�̉����ϕ��ɂȂ�܂����B�ŗL�l�C�ŗL�x�N�g���𗘗p���ĉ������@(��w���x���͈̔͂ł͂Ȃ�)�ł̕s���_�A�s�������ɂ��ĉ������Ă���y�[�W��T���Ă��Ă�����̃T�C�g�ɒH�蒅���܂����B�Ȃ��Ȃ��ŗL�l�A�ŗL�x�N�g�����w���w�O�̃��x���Ŏg�����s�������̉��������ڂ��Ă���Q�l���Ȃǂ�������ꂸ��V���Ă��܂����B����������{���ɂ��肪�Ƃ��������܂��B
���R��ǂ��Ȃ�������A�s�ԂȂǂ��ǂ߂Ȃ��Ƃ��낪����̂ł��f���������Ƃ��낪����܂��B�@���11.1 -2 ��(�E)�̂Ƃ���ŁA���_��ʂ�Ȃ��s�������̒��ו��Ńx�N�g��x1�A�x�N�g��x2�̒u�����͂ǂ̗l�ȗ��R�ł��̗l�ɒu���Ă���̂ł��傤���H
�A���11.1�̓_���Ɉ͂܂ꂽ����i�ŗL�l�C�ŗL�x�N�g���C�s���_�C�s�������̊W�j
��(�V)�̂Ƃ���̐����ŁA������3�s����ł��āA�c�ƂȂ邩��Ƃ���̂ł������̐�����3�s�ڂ��ǂ̂悤�ɂ��ďo�Ă����̂ł��傤���H
�B�ŗL�l�A�ŗL�x�N�g�����g�����s�������Ɋւ����������ڂ��Ă��鏑��(�ł���Α�w���w���x�������̂���)�������m�ł����狳���Ă���������Ƃ��肪�����ł��B
�ȏ�ƂȂ�܂��B�ǂ�����낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�@���̏ꍇ��x1�ɂȂ�C�E�̏ꍇ��x2�ɂȂ�܂��D�A��̎������{���ĉ��̎��ɉ��������̂ł��D�B���Z�̋��ȏ���������Ă��܂����̂ŁC��w���w���x�������̂��̂͌�����܂���D��w���w�ł́C���n���n�Ƃ��u���`�㐔�v�Ƃ�������̒��̐��`�ϊ��Ƃ����ӏ��ɂȂ�܂����C�s���_��s��������}�����Ă���悤�ȏ����͌�����܂���ł���
���m�ʂ̕ł���̎���ɑ���n[�Ώ̎��̕ό`�ɂ��ā^23.05.05�n
���ʃe�X�g��(2)�̓����ŁA(x+y)^2-(x-y^2)�ŁA-(x^2-y^2)�Ȃ̂ł͂Ȃ��ł��傤���H�H
�����m��ҁn�F�A�����肪�Ƃ��Dx��2��͔����Ă��܂����̂Œ����܂���...������-(x^2+y^2)�ł�
���m�ʂ̕ł���̎���ɑ���n[�������������ɂ��ā^23.05.01�n
�g�єłł͕������������͐���̂ǂ��ɂ���̂��킩��Ȃ��̂ł��ˁB(�u���ݒn�v���s��)
�����m��ҁn�F�A�����肪�Ƃ��D�T�u���j���[�̃v���O�������ԍ����㏑�����Ă��܂����̂ŁC�������܂����D�Ȃ��C�i�������炪����I�j�C���YHTML�t�@�C���ł͂Ȃ��C����JS�t�@�C���ɃT�u���j���[�����邽�߁C�ēǂݍ��݂��Ă��C�u���E�U�̃L���b�V�����ȒP�ɂ͏��������Ȃ��悤�ł��D�i�������̔��f�ŁI�j��U�u���E�U��Google�A�J�E���g�����O�A�E�g���Ă���C�L���V�����폜���C�ēx���O�C������ƁC����L���b�V��������悤�ł����C���g�p�̃u���E�U�̉�����悭�ǂ�ő厖�ȃL���V���܂ō폜���Ȃ��悤�ɋC��t���čs���Ă��������D�ƂĂ��厖�ȋL�^�Ȃ�C���X�N������������悢��������܂���D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^23.04.30�n
�Ō�Ɂu�}�g���v�̋L�ڂ��Ȃ����߁A������낤�Ƃ��ĉ����ł������A�����ł��Ȃ������̂����悭�킩��܂���ł����B�u�ȏ���܂Ƃ߂�ƈȉ��̂悤�ɂȂ�܂��B----�B�v�Ƃ����L�ڂ�����Ƃ悢�ƍl���܂��B�����c���[�}���쐬���A�������牽���K�������Ȃ������l���悤�Ƃ��܂����B�������A�c���[�}�쐬�̓r���ō��܂��A���[���ƒ��f���Ă��܂��B�l�b�g�Ō��������Ă��܂��܂��̃T�C�g�ɂ��ǂ蒅�����̂ł����A�����I�ɂ���c���[�}��������Ă��ċ�����~�����Ă��A���̌�̐�������ǂ����Ƃ��܂������A�\�������͂ł��Ă��܂���B���Ԃ������Ă�������ǂ�ł����Η����ł���̂�������܂���B�Ƃ������ƂŃ}�g���̋L�ڂ�����A�ǂ��̂ɂȂ��Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���ǂ��������c��C���͕�����܂����C���������M�҂́i���̒N���j���̖�肪�����Ă��܂���̂Łu�_�_���܂Ƃ߂�v���Ƃ��ł��Ȃ��D������C��|����ɂȂ邩������Ȃ��Ǝv���ޗ����C����u���Ă���Ƃ����̂�����ł��D�M�҂����܂ł������Ă���킯�ł͂���܂��C���̃z�[���y�[�W�����܂ł�����킯�ł͂Ȃ����Ƃ́C�������Ă���������Ǝv���܂��D�������ȂǁC�ƂĂ��C�ɂȂ�ޗ�������܂������C���s���̂��ߏЉ�ł��܂���D����������N�����C���������̎����������Ă��ꂽ��C����ł悢���ȂƂ����v���ł��D
���m�ʂ̕ł���̎���ɑ���n[2�����̍ő�ŏ�(2)�ɂ��ā^23.04.30�n
���2�]2�̉���̃O���t�A���2�]3�̉̂��͈̔́A����炪�قȂ��Ă��邽�߂ɉ��قȂ��Ă���̂ł́H
�����m��ҁn�F�A�����肪�Ƃ��D���Ɖ��Ή����Ă��܂���ł����̂ŁC���̕���������܂���
���m�ʂ̕ł���̎���ɑ���n[�d�v�ȋɌ��l(1)�ɂ��ā^23.04.26�n
�������ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̑����C�a�C���C�����{�ɂ��ā^23.04.25�n
�����Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�T���������̉��ɂ��ā^23.04.23�n
5��������(2)�́C(x - 1)(x^2 - 4x + 13)(x^2 - 9) = 0�Ɉ��������ł���Ƃ���܂����C
���̎���W�J�����x^5 - 5x^4 + 8x^3 + 32x^2 - 153x + 117 = 0�ɂȂ�C
���̎��ƍ����܂���D
�܂����(2)�C1.1x^6 - 2.1x^5 + 3.1x^3 - 1 = 0�̏o�͌��ʂ�(1)�Ɠ����ɂȂ��Ă���C�S�������܂���D
����ɍׂ����ł����C�E����4���������̈��������`�ɂ����āu+�v�Ɓu3�v�̏��Ԃ��t�ł��D
�ȏ�3�_�C�����������D
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[Excel�Ȃǂ��g���ĘA���P�����������������@�ɂ��ā^23.04.22�n
�ޑ�A-i��(4)�̓�����x=-1,y=0,z=2,w=3�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƃ��ƁC��蕶�̉E�ӂ̌W����]�L���Ă��܂����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����������̍����ɂ��ā^23.04.11�n
�P�D�R�Γ����Fu��x�Ɋւ���Γ��������l�ɂ��� ������x��y�̂͂��ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���̋Ɍ��ɂ��ā^23.04.08�n
�����y�����q�����Ă���܂��B
���6�́i1�j�ɂ��āA�Ȃ�������3�悩�o�ꂵ�A�������Ă���܂��B���m�F����ɁA����3��̂悤�Ɏv���܂����A�������ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���炵�܂����D���̓~�X�ł��̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̍l�����ɂ��ā^23.04.07�n
����5����7�܂ł͉������Ĕ[������܂ł����Ă����K�v���������܂����B����ɂ͗��P�`�U�܂ł������藝�����Ȃ�������Ȃ��ƒɊ����܂��B���������܂Ŗ��̂P�`�V�͂T�ȊO�����ł����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̓�������ɂ��ā^23.04.07�n
��蓹��������܂��A�ēx�敪���ς̖��������Ă��܂��B�菇��ł��ĕ���₷���ł��B�ސE20�N�̋��t�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�C�́C���́C�N��ł́C������̕������[���Ə�̂悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̒��_�i�������^�₳�������j�ɂ��ā^23.04.06�n
�Q�����̒��_�̍��W(�����W��)�����C�ɓ���Ȃ�C�����܂��A���̑O�܂ł���������ł��Ă���A�����������ɂ�����Ă��ł���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ�������Ă���͓̂������Ȃ̂ŁC������������邩������܂���D
���̃y�[�W�����肩����ł��邩������܂���D…�Ƃ��Ƃ��ƁC���Ȃ��́CAndroid�Ȃ̂œǂ݂ɂ��������i���̃y�[�W�̌g�їp�́C�܂�����ĂȂ������悤�ł��D�ǂ߂���ǂ�ł��������D
���e�ɒ��ڂ̊W�͂Ȃ��̂ł����A1�B�u�ʂ̕ł���̎���ɑ���v�̂Ƃ���ō��ڂ�
�f���炵���@�悭�����ł����@���K���̂ȂƂ܂��������������Ă������Ǝv���B�ƂȂ��Ă���̂ł����A�Ō�́u���K���̂ȂƂ܁v�́u���K���̓�Փx�v�̂��Ƃ��ȂƎv���܂����@���ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���p����ꍇ�ɁC�������Ԉ���Ă���Ǝv���Ƃ��ł��C������҂̕��͂����̂܂܈��p����Ƃ��u�}�}�v�Ƃ������r���ӂ邱�Ƃ�����D���̉́u�ȂƂ��v��������܂��C�Ӗ��͕�����̂ŁC�����Ē����K�v�͂Ȃ��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�ȉ~�̕������̕W���`�ɂ��ā^23.04.02�n
���Ɖ�e���g�����ȉ~�̏������A�����̏��������c���̐��@�ɂ����܂����@�Ⴆ��
��10Cm�c5Cm�E�E��10Cm�c6Cm�ȂǁA���������������l�ȑȉ~�@���ʂ��猩�����ߊ��̑ȉ~
�ȒP�ɏ�������@���l���܂����@2023-4-1�@���ׂĂ��l�����̈�ɂ���(1/4)�̏��Ɉ��t��
�t���[�n���h�̋Ȑ��łȂ��@�@���тȑȉ~��`���Ƃ��͏c���̒��S�������炵�l�����A
�l����������̏��������1/4�̈��t���Ȑ��Ō��ԁA����ȏ������ōD�݂̑ȉ~���o����B
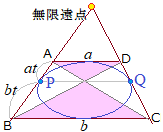 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D�f�b�T���̏K���n�߂ɕ����b����
���{��ƁZ�����i�����ƁC�l�b�g���ł͂��Ȃ�ȑO�ɂ��S���Ȃ�ɂȂ�ꂽ�Ƃ������ƂŁC�̥���搶�Ƃ����ׂ����������j�����Ȃ̂悤�Ɍ����Ă����D�u���q���߂��猩����C�ȉ~�ɂ͂Ȃ�Ȃ��D��O���ӂ����Ō�����͂����D�v���w3�N�̔��}�`�̒P���ŏK���悤�ɁC���}��P, Q�͑�`�̑Ίp���̌�_���牡�����������߂��C���̂Ƃ��CAP:PB=a:b�ɂȂ�D�����ŁCP, Q�Őڂ���悤�ɋȐ���`���Ƃ悢�D
�킩��₷���Ă悢�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̒u���ϕ��ɂ��ā^23.03.26�n
�y�⑫2�z�̉ɂ��Ăł��B
1/4��(1/t - 3t^-2t)dt�̍Ō��-2t��t���s�v���Ǝv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^23.03.20�n
������₷���č��Z�������X���[�Y�ɐi�߂�ꂻ���ł��B���肪�Ƃ��������܂�❗
�����m��ҁn�F�A�����肪�Ƃ��D�V�����Ƃ������Ƃ��ȁD
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^23.03.20�n
�萔�W��.�Q�K���`.��.�����������m��Ɖ��n4.(3)1�cR(x)���������C�w�����C�O�p���̑g�����̗���
y�f�f-4y�f+4y=xsinx �̓r����
{(3A-4C)+(-4A+3B+2C-4D)}cosx+{(4A+3C)+(-2A+4B-4C+3D)}sinx
�Ƃ���܂����A�W����x�������Ă���悤�ł��B
��������
{(3A-4C)x+(-4A+3B+2C-4D)}cosx+{(4A+3C)x+(-2A+4B-4C+3D)}sinx
�ł͂Ȃ����Ǝv���܂��B���m�F�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����i�ڂ����Ƃ���܂œǂ�ł���āC����!�j
���m�ʂ̕ł���̎���ɑ���n[���������̕ό`�ɂ��ā^23.03.20�n
�Ǘ��l����ɂ����k�����Ē����������Ƃ�����̂ł����A���[���A�h���X�ȂNj����Ă��������Ȃ��ł��傤���c���Z�����̂ɂ��݂܂���m(_ _)m����悤�ł����猋�\�ł��A
�����m��ҁn�F�A�����肪�Ƃ��D�悭�����炷���킩�邱�Ƃł����C���{�b�g�\�t�g�ɂ��SPAM���[����Ƃ��āC�s���葽���̕��̎�M���[���ɓ����̃A�h���X���c�邱�Ƃ�����Ă��܂��̂ŁC���̑��M�v���O�������璼�ڎ��₵�Ă��������D�i���k���e�����ׂČ��J�����킯�ł͂Ȃ��j
���m�ʂ̕ł���̎���ɑ���n[�������|����������3�ɂ��ā^23.03.18�n
(3)�̖����Ax��y�̎����������ł��邽�߁A-12y²-y(x�{35)�{6(x²�{2x�{3)�Ƃ��Đ��������̂ł������̏ꍇ�ǂ̂悤�ɂ��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�������P�ӏ��Ⴄ�悤�ł����C
-6(x^2%2B 2x-3)\}&chf=bg,s,fff6f6)
\}\{3y-2(x-1)\}&chf=bg,s,fff6f6)
�@���R�̂��ƂȂ���C���̉Ɠ������̏������̏�����ς������̂ɂȂ�܂�
���ډƂ͊W�Ȃ��A�֑���������܂��A����̓r�����Ɍ�A������悤�ł��̂ŁA�m�F�����肢���܂��B
���P�O�̉���S�s
�w1/P(��Q/��x�|��P/��y)=2x^2�~y/x^2�~y^2�|y��y�����̊��ł͂Ȃ��x�Ƃ���܂����A�E�ӂ̕��q��2x^2�~y�̕����͐������́|2x^2�~y���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̕��s�ړ��ɂ��ā^23.03.17�n
�{���ɂ��肪�Ƃ��������܂��B
�킩��₷���āA�d�����ɂ��݂�āA�������Ă��܂��B���͍��Z��2����������Ă��܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�̕��s�ړ��ɂ��ā^23.03.17�n
���������肪�����ł�
�X�L�}���Ԃɂ���肪�Ƃ��āA�����������A�v���Ƃ��Ȃ��̂ŏ������Ă��܂��B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���ލ쐬�҂Ƃ��Ă̂˂炢�ʂ�ł�!���������g���������}���܂�
���m�ʂ̕ł���̎���ɑ���n[�����Œ�̕����Ő����ɂ��ā^23.03.16�n
2�Ԗڂ̖��͈�����������Ɠ����͂ǂ��Ȃ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�Q�����̏ꍇ�̂������|�����������̖��́C
���̃y�[�W�̍Ō�ɂ���C���S��ł�����Ȃ��o�܂��D�������������������ڂ����ł��傤…
(2x−y−1)(x−2y+3)
��1�̍l��������蕪����₷�����Ă��炢�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ł��C����ȏ�̂��̂͌������Ƃ��Ȃ��ł��D
�@�����Ƃ��C�����m�̒ʂ�CGoogle�ł��̖���ǂ݂�����C���o�Ă���Ƃ����̂���ԕ�����₷�����@��������܂��C����������Ă��邢��킯�ł͂Ȃ��ł��傤�D�i������₷�����ǂ����Ƃ����̂́C����҂������Ă��镶�����C����҂̔��B�i�K�ɂ���ĕς��j
�@���s��ChatGTP�Ɏ��₵����C������Ă���悤�ł��FQ�u�j�q���Q�l�Ə��q�R�l�����ɕ��ׂ�Ƃ��C�j�q�Q�l���ׂ荇�����ו��͉��ʂ肠�邩�v,A�u�j�q2�l���ׂ荇�����ו����l����ꍇ�A�j�q2�l��1�̃O���[�v�Ƃ��Ĉ����A���̃O���[�v�����q3�l�ƈꏏ�ɗ�ɕ��ׂ���ɕϊ����邱�Ƃ��ł��܂��B�j�q2�l�̃O���[�v�Ə��q3�l����ׂ�Ƃ��A�S�̂̕��ו���5�l�̕��ו��̑����ł���5!�ʂ肠��܂��B�������A�j�q2�l�̃O���[�v���ł̏����͍l������K�v������܂��B���̃O���[�v���ł̏����ɂ�2�̕��ו�������܂��i�j�q1�l�ڂ���ɂ���ꍇ�ƒj�q2�l�ڂ���ɂ���ꍇ�j�B���������āA�S�̂̕��ו�������j�q2�l�̃O���[�v���ł̏������l�������ꍇ�̕��ו����������K�v������܂��B�j�q2�l�̃O���[�v���ł̕��ו���2!�ʂ肠��܂��B���������āA�j�q2�l���ׂ荇�����ו��̑����́A5! - 2! = 120 - 2 = 118�ʂ�ł��B�v �� 5!���ԈႢ������C����ȉ��͊ԈႢ
�@Bing�͍̉����Ă��܂��F�u����ɂ��́A�����Bing�ł��B?? ���̖��͏���̖��ł��ˁB�j�q2�l���ׂ荇�����ѕ��́A�j�q2�l��1�̃Z�b�g�Ƃ��čl����ƁA�ȉ��̂悤�ɂȂ�܂��B�j�q�y�A�Ə��q3�l�̕��ѕ���4! = 24�ʂ�@ �j�q�y�A���̕��ѕ���2! = 2�ʂ�@ ���������āA������24�~2 = 48�ʂ�ł��@�킩��܂������H�v
���m�ʂ̕ł���̎���ɑ���n[��ϕ��F��{�v�Z�ɂ��ā^23.03.11�n
�ÎZ����̂ɂ��傤�Ǘǂ����x���ł����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʏ�̐��ϕ��ɂ��ā^23.03.08�n
���f�ϕ��̕�����Ղ������ŁA�L�x�ȉ��K��������ƂĂ�������܂����B���肪�Ƃ��������܂��B
����Ȃ̂ł����A�i�Q�D�S�j�b4 �ϕ��l���|��i�ƂȂ�v�Z�ɂ����Đ�Βl�𗘗p���Ă̂��̂ƂȂ��Ă���܂����B�ϕ��l�̕Ίp���O�܂��̓ɂȂ邩�ǂ����͂ǂ̂悤�ɂ��ĕ�����̂ł��傤���B��͊T�_�ł̓e�[���[�W�J�𗘗p���ċ��߂Ă��蕪����ɂ��������̂Ő�����Ղ����ߕ����Љ�Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D��?�P���ɁCx����̔��~�̍����̕Ίp���ʼnE���̕Ίp��0�ƍl���܂������
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^23.03.07�n
���ɕ�����₷�����K������ώQ�l�ɂȂ�܂������肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̒u���ϕ��@�ɂ��ā^23.03.07�n
���̉��~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����C�v�Z�Ƃ����{�^���������Ή�����o�Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^23.03.07�n
���K�����͂��߂ĉ������Ƃ��͐�����50%���炢�ł������A�������������āA���x�͉��������O���㌏�����ꂼ��A�AB�Ƃ����āA�O���ے�̂Ƃ��ł����~A�Ƃ������肵�āA���̘_�����̐^���\���U�ƂȂ�������l���Ă݂�ƁA��������ƑS����ł��܂����B�_���w�ɂ��Ă͓��{��ł͂Ȃ��l�H����(�_����)�ōl����̂����R�Ȃ���őP�ł���܂��ˁB���{�ꂾ�ƍ������Ă��܂��܂�����B�ǂ��L�������肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ʃx�N�g���i�Q�����x�N�g���j�̐����\���ɂ��ā^23.03.06�n
�Ȃ��Ȃ��ǂ���肾�Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̏��@�i����Z�j�ɂ��ā^23.02.28�n
���肪�Ƃ��I�r���o�߂��킩��̏��������I�߂��Ⴂ���I
�����m��ҁn�F�A�����肪�Ƃ��D���Ƃ����Ă����i�ߋ��`�j�Ƃ��ɂ́C���k�̒��ɂ́C�т����肷��ӏ��ŊԈႤ�҂������̂ŁC������ӂJ�Ɏ����ނɎd�グ�܂���
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^23.02.27�n
�����ƊȒP�ȏؖ��͂���܂���
�����m��ҁn�F�A�����肪�Ƃ��D���������C�N���܂��ؖ��ł��Ă��Ȃ��Ƃ����̂�����ŁC���̂悤�ȗL����肪��������C�j���[�X�ɂȂ�͂��ł��D
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^23.02.26�n
���7��(2)�ŁA���̖���������̂�26���ł����j���łȂ��ꍇ�A���̖���͋U�ɂȂ�Ǝv���Ă��܂��܂��B
���l�Ɂi3�j�ŁA���̖���������̂����j���ŗ�����26���łȂ��ꍇ�A�U�ɂȂ�Ǝv���Ă��܂��̂ł����A�ǂ����ď�ɐ^�Ȃ̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D��������Ă��������D��蕶�ɌŒ�I��26���Ƃ����j���Ƃ��������Ă���킯�ł͂���܂���D�R���s���|�^�v���O�����ŁC���������t�Ɛ������j�����o��悤�ɂȂ��Ă���̂ŁC�u26���ł����j���łȂ��ꍇ�v�ȂǂƁC��蕶�ɏo�Ȃ����͂ɁC����ɏ���������Ɠ����ς��͓̂��R�̂��Ƃł��D�^�U�\�����āC�^→�^=�^�ƂȂ邱�Ƃ��m���߂�Ƃ������Ƃł��D���2023�N�͂��邤�N�ł͂Ȃ��̂ŁC3����ɂ��̋��ނ����Ă��炦�C�u1�������j���v�ɂȂ��Ă���͂��ł��D
���m�ʂ̕ł���̎���ɑ���n[�R���ԑQ�����̈�ʍ��ɂ��ā^23.02.25�n
(4)�̉���ł́Aan+1-(n+1)2^n=2(an-n*2^(n-1))�ƒu���Ă��܂����A���̎��ɍ��ӂ�2�̊K���2^(n+1)�A�E�ӂ�2�̊K���2^(n)�Ƃ���Ɠ����̊K�悪�Y���Ă��܂��܂��B
�Ȃ����̂悤�ɒu���Ă͂����Ȃ��̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�܂��C����͐��m�ɍs�Ȃ�Ȃ�������܂���D���̃y�[�W�ɂ�(4)�Ƃ����������\������܂����C���Ȃ��̎��₵�Ă�����e�́C�ǂ��ɂ������Ă���܂���D�܂����Ǝv���āC���̖��ׂ���C(5)�̉���ɂ���܂����D�i�{�j
�uan+1-(n+1)2^n=2(an-n*2^(n-1))�ƒu���Ă��܂����A���̎��ɍ��ӂ�2�̊K���2^(n+1)�A�E�ӂ�2�̊K���2^(n)�Ƃ���Ɠ����̊K�悪�Y���Ă��܂��܂��B�Ȃ����̂悤�ɒu���Ă͂����Ȃ��̂ł��傤���B�v�ː������Ȃ��ό`������ł��D

������C�萔����

�ƂȂ�ׂ��Ƃ���C
2^{n%2B 1}=2(a_n-n\times 2^n)&chf=bg,s,fff6f6)
�Ƃ���C�萔����
2^{n%2B 1}-n\times 2^{n%2B 1}=2^{n%2B 1}&chf=bg,s,fff6f6)
�ƂȂ��āC����(2’)�ƈقȂ����������Ă��邱�ƂɂȂ�܂�
����ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D������PC�p�̋��ނ����Ă�����悤�ł����C����ɂ���ƌ����Ă��C����ɂ���Ɠ����Ă�����C���w�̘b�������ۂ�Ɣ����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����̗��K���3�ɂ��ā^23.02.23�n
�����g�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝�ɂ��ā^23.02.23�n
��i�K��ǂ��Ċm���߂����Ă��܂��B�o��̌`�������h�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȑ���̘a�ɂ��ā^23.02.20�n
�����������ē����N���N�����Ă��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɑ����悤�ł����C��A�̓��e�Ȃ̂ŁC�P�̃y�[�W�ɓ���܂���
���m�ʂ̕ł���̎���ɑ���n[�������̋Ɍ��ɂ��ā^23.02.19�n
���ʂƌ��̂Ȃ��悢���āB�G��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������i���K�j�ɂ��ā^23.02.17�n
��������Ɣ������Ă���Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��DMac�̃f�X�N�g�b�v���g���Ă���̂ɁC�Ȃ��c����̈قȂ�X�}�z�p�����Ă�����̂��C�������s���ł��DPC�p���X�}�z�p���́C1���ڈ�Ԓn�i�擪�̂P�s�ځj�ɏ����Ă���܂��D
�@���ẮC�X�}�z�p��PC�p�͎����]�����Ă��܂������C�����]���ɂ���ƌ��ɖ߂�Ȃ����ƂɂȂ�̂ŁC�e���̎蓮�őI�ׂ�悤�ɂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ����������ɂ��ā^23.02.17�n
�y���P�z(2)�Łu�W�����S�����̐�������Cx�ɐ��̐��������Ă��O�ɂ͂Ȃ�܂���D�i=�ŏ���2�̑I�����͏�����j�v�Ƃ�������ɂȂ�قǂƊ��S���܂����B
�����ƌ����Α莮�̒萔����45������3�Ԗڂ̑I������������i������͒萔����24�ɂȂ邽�߁j�̂ŁA���̖��͌v�Z���Ȃ��Ă�4�Ԗڂ��������ƕ�����܂��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�����܂œǂ߂�C�\���ł��D
���m�ʂ̕ł���̎���ɑ���n[ ��ʊp�̒�`�ɂ��ā^23.02.16�n
�킩��₷���ł��B
���̂悤�ȋ��ނ����߂Ă��܂����B
�쐬���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�V�т̗v�f�����Ȃ��珉���I�ȗ��K���s������M�҂̓��ӋZ�ł�
���m�ʂ̕ł���̎���ɑ���n[���̂̑̐��ɂ��ā^23.02.15�n
���������b�ɂȂ��Ă���܂��B
�y���Q�z(2)�ŁA�ʉ��ƌ����邩�͕�����܂��A�܂�-2��x��0�͈̔͂��Ƃ��Čv�Z���Ă�����(1/2)(4/3)��*2^3�A�ϕ��͈͂�0��x����2�݂̂ɂȂ�A�v�Z�~�X�����邾�낤�Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�i�T�o���i�����̃p���f�B�Łj�u�����͂��̎��R��!�v
���m�ʂ̕ł���̎���ɑ���n[��Βl�t�̊��̐ϕ��ɂ��ā^23.02.15�n
�y���R�z�̃O���t��`�����Ŏ���ł��B�i�C�j�@�j�̋�Ԃ��A�}�����ꂽ�O���t�ɂǂ̂悤�ɑΉ����Ă���̂��C���[�W�ł��܂���ł����B0≤x<2�́i�C�j�A�j�̓���\���Ă���悤�Ɍ����܂��B
�����m��ҁn�F�A�����肪�Ƃ��Di) ii)�̍��v��(�C)�̋�Ԃł��D�����ڂŕ�����₷���悤�ɁC�s�Ԃ�5mm�قǍL���܂����D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��Œ�`�������ɂ��ā^23.02.14�n
���1��a�����߂�ہA�u�ϕ���Ԃ̉��[�Ə�[���������Ƃ��́C��ϕ��������ł����Ă��ϕ��͂O�v�Ƃ����Ƃ��납��A
�wa~a��Ԃ�f(t)�̐ϕ��x=a^2-3a+2=0�Ƃ��Ă��܂����A�f����a~a��Ԃ�ϕ������
a^2-3a+2-(a^2-3a+2)�ƂȂ��Ă��܂��A=a^2-3a+2�ɂ͂Ȃ�Ȃ��悤�Ɏv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D??�u�f����a~a��Ԃ�ϕ�����v�Ƃ������Ƃ��C�ǂ��������ƂȂ̂��ʂ��܂���D���̖��ł́C��
f(x)�������ĂȂ��̂ŁC�f���ɐϕ����邱�Ƃ͂ł����C���̓��Ă̑O�������̂悤�ɂ܂�
f(x)=2x−3�Ƃ������ʂ𗘗p�����Ƃ������Ƃł��ˁD���̏ꍇ�C���̋��ނ̉��̕����i���̎��̎��j�̂悤�ɂ��āC�m���߂邱�Ƃ͂ł��܂��D
dx=(x^2-3x)-(a^2-3a)\]&chf=bg,s,fff6f6)
��蕶�ɂ��C���ꂪ
-(a^2-3a)=x^2-3x%2B 2&chf=bg,s,fff6f6)
�ƂȂ邱�Ƃ���C
=2&chf=bg,s,fff6f6)
�Ƃ������Ƃ͌����܂��D
�@�ua~a��Ԃ�ϕ������a^2-3a+2-(a^2-3a+2)�ƂȂ��Ă��܂�=a^2-3a+2�ɂ͂Ȃ�Ȃ��悤�Ɏv���܂����B�v←����ł����̂��I������0�ɂȂ�܂��D
���Q�i�Q�j�ɂ��āA����́i-2�j�~1-2^n/2^n�ȍ~�̌v�Z�ł����A���͈ȉ��̂Ƃ���v�Z���܂����B
�y(-2�j���ɒ����Ēʕ���������ł��z-2^n+1/2^n�~1-2^n/2^n��2^n-1/2^n+1�B
�����ʕ�������̕���ǂ����̊|���Z2^n�~2^n��2^n+1���ƍl���܂����B�����̕��ꂪ2^n-1�ƂȂ�o�߂��킩��܂���B�v�Z�ߒ��̂����������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D?? ���������|���Z������C�ʕ��Ƃ����b�͏o�Ă��Ȃ��Ǝv���܂����H
���m�ʂ̕ł���̎���ɑ���n[�Q�����̕��s�����E���������ɂ��ā^23.02.13�n
������Ղ������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕����̋��ߕ��ɂ��ā^23.02.13�n
�S���������́w������[�x�Ő����o���Ă��܂��܂����i�j�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��p�ΐ��ɂ��ā^23.02.11�n
����p�ΐ��́y�����z
N �� n+1 ���̐����@�� 10n�|1��N<10n
�Ŏ~�܂��Ă��܂��܂����B
���̏�́y�傫�Ȑ����̌����z�̗�Ɣ�r����ƁA10n��<10n+1�ł͂Ȃ��ł��傤���c�H�H
�����m��ҁn�F�A�����肪�Ƃ��D�ɒ������܂����D�����Əo���̕���������܂���
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^23.02.11�n
����ɂ��́B�������ɂ͂Ȃ��ڂ���������������Ă��Ă悭�킩�芴�ӂ��Ă��܂��B
���āA���K���i�S�́j��������ł����Ax���}���̂Ƃ�y=(x+2)x(x�|3)(x+1)(x�|2)=�����@�̍Ō�́A�{�� �[���ł͂Ȃ��A�{�����傾���ɂȂ�̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D±���ɒ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�v���O���~���O�̌�(6.1)�ɂ��ā^23.02.10�n
���s���邪�����Â炢�Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�����������傫�����܂���
���m�ʂ̕ł���̎���ɑ���n[�����W���������̋������ɂ��ā^23.02.09�n
����ł��B���̂悤�Ɏ����W���̕������̉��̂���1���������Ƃ��ė^�����Ă��鎞�A�K�������̕��f�������Ɏ����܂����H�܂��A�L�q���̖��ŁA�����̕��f�������ɂ��̂Łc�Ɖ�������ʖڂł����H
�����m��ҁn�F�A�����肪�Ƃ��D�u�K�������̕��f�������Ɏ��v�ƌ����܂��D�u�����̕��f�������ɂ��̂Łv�Ə������Ƃ��Ɍ��_�����w�Ȃ�C�i�ƂĂ���x���̉ӏ������ۂ̕�����ڂɂȂ��Ă��w�Ȃ̂Łj��K�v���Ȃ��ƍl������悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�O�p��̑��݊W(���̕ό`) �ɂ��ā^23.02.09�n
�S�S�ő�w���悤�Ǝv���Ă���҂ł��B�O�p��̑��݊W�R�́A�P�|tan2A/1�{tan2A�̉���̂Ƃ���ŁA�P�|sin2A/cos2A/1�{sin2A/cos2A����Acos2A�[sin2A/cos2A�{sin2A�ɕό`����Ƃ��낪�ǂ����Ă��킩��܂���B�ǂ̃y�[�W��ǂ߂����̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��DHELP���猩���镪��ƕ��q�̂��ꂼ���cos2A���|���܂��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����.���U�B-�O�p��(2015�`) �ɂ��ā^23.02.09�n
�y2018�N�x�Z���^�[����.���w�U�EB�z��1���(2)�̖�蕶��114�x�Ƃ���܂����A144�x�̂悤�ł��B
�܂��A(3)��(�L)�łȂ���/6�ɂȂ�̂�������܂���ł����B�i�V���v���ɕ����̌v�Z�������+2��/15�ɂȂ�A��������̕ό`��������܂���B�B�j������Ē�����ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�e�X�]�L�~�X�ł��̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̂Q�{�p����,���p�����i���K���j�ɂ��ā^23.02.07�n
���1���Ⴄ���@�ʼn������Ƃ����̂ł����A�ǂ�������������v���܂���ł����B�����������������܂��ƍK���ł��B
cos2��=2(cos��)^2-1=2*(-2/3)^2-1=-1/9�@�c(1)
(sin2��)^2+(cos2��)^2=1��(1)���A
(sin2��)^2=1-(-1/9)^2=80/81
���͑�O�ی����A
sin2��=-4��5/9
�����m��ҁn�F�A�����肪�Ƃ��D������3�ی��̊p�ł���Ƃ��C2���͑�3�ی��̊p�ɂ͂Ȃ�܂���D
(A) �܂��́C������₷���Ⴉ��F180��<��<270���̂Ƃ��C360��<2��<540���͑�1�ی��܂��͑�2�ی��̊p�ŁCsin2��>0
(B) �����ƈ�ʂɒʂ��鐳�m�ȏ������ł́F360��n+180��<��<360��n+270���̂Ƃ��C720��n+360��<2��<720��n+540���͑�1�ی��܂��͑�2�ی��̊p�ŁCsin2��>0�ɂȂ�܂��D
�@�ŋ߂̋��ȏ��ł́C���܂茩�܂��C���̂悤�Ȗ��́C���ȏ����x���̒���{�ł��D
(1) ������2�ی��̊p�̂Ƃ��C��/2�́u��1�ی��̊p�v�܂��́w��3�ی��̊p�x��90��<��<180���̂Ƃ��u45��<��/2<90���v�C−270��<��<−180���̂Ƃ��w−135��<��/2<−90���x
(2) ������1�ی��̊p�̂Ƃ��C3���́u��1�ی��̊p�v�܂��́w��2�ی��̊p�x�܂��́s��3�ی��̊p�t��0��<��<30���̂Ƃ��u0��<3��<90���v�C30��<��<60���̂Ƃ��w90��<3��<180���x�C60��<��<90���̂Ƃ��s180��<3��<270���t--���W������܂�
(3) ���l�ɂ��āC������3�ی��̊p�̂Ƃ��C��/2�͑�2�ی��̊p�܂��͑�4�ی��̊p�ɂȂ�܂��D--���ꂪ�ł���C�����ł����Ƃ������ƂŁD
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������Q�ɂ��ā^23.02.04�n
���i5�j���͂�m���������܂ōs����Ƃ͂ƂĂ��v���܂���B�B
�����m��ҁn�F�A�����肪�Ƃ��D�������Z���̐����Ȋ��z���Ǝ��܂����D���߂Č����Ƃ��́u�ǁv�̂悤�Ɍ����܂����C���������p�^�[�������x�����K������w�Z��\���Z������悤�ł��D1��ł��������Ƃ�����C�Q��ڂ́u�P�Ȃ镜�K�v�ɂȂ�̂ŁC�u���C�o���[�v�ŏI����Ă����D�������C�����ɂ͎������ԂɌ��肪����C���ł�����ł��\�K���Ă������Ƃ͂ł��Ȃ��̂ŁC�l�̉��{���͖Ԃ��L���Ă����Ƃ����l�����Ó��ł��傤�D�Ȃ��C���������ό`�́C�ƊE�ł͕��ʂ̂��Ƃ̂悤�ł����C������o���������Ŏ�悤�ȑ�w�́C?����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[2�����̍ő�E�ŏ��i�\�����K�j�ɂ��ā^23.02.03�n
��9�₪�o�Ă��āA�S�ĊԈႢ�ɂȂ�Aundifined�Əo��͉̂��̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�v���O�����̃~�X�ł������Ԃ̏��߂ƏI���Ń~�X�̋N����₷���Ƃ����Ă���D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���������i���K�j�ɂ��ā^23.02.03�n
�����܂ŕ��������̉����ǂ�ł������炸�����Ă����̂ł����A��b�̊�b�̊�b���������ăX�e�b�v��ʼn��������ƂŁA���������������ł��܂����I
�{���ɒ��J�ɍ���Ē������肪�Ƃ��������܂��I
-�ƕ����̂Ƃ����1�₸�ԈႦ�܂����A�m���ɊԈႦ�₷���ł��ˁI���J�ɉ����ė��K�撣��܂��ˁI
��҂��肪�Ƃ��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����.���U�B-�}�`�ƕ�����(2013�`) �ɂ��ā^23.02.02�n
2013�N�x�@��1��̃R〜�T�̉�����Ȃ��悤�ł��B
���Ȃ݂ɁA�R=4,�T=3,�V=2,�X=5,�Z�H=4�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���߂ɒ����܂�
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^23.02.02
�Ō��(I).(J)�̕����̍l���������g�̃��|�[�g��_���ɓ��ꂽ���̂ł����A���v�ł��傤���H�܂��A���p�͂��̃T�C�g�ł��Ə�����������낵���ł��傤���H���������Ăق������Ƃ�������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���쌠�@��32�� ��1���ɂ��u ���\���ꂽ���앨�́A���p���ė��p���邱�Ƃ��ł���B�v�Ƃ���Ă���C�o���̖����Ȃǂ̏��������Ă���悢�l�����Ă��܂��D�Ȃ��C�w�����|�[�g�ɑ��ẮC�R�s�y�Ȃǂ�h�����߂ɁC�������e�̂������L���̗L���ׂ�\�t�g���w�������Ă��邱�Ƃ������C�o���������Ȃ��Ƌt�Ɏw�E����鎞��̂悤�ł��D
�@�������C���͐����_���܂Ƃ��Ɋw���Ƃ͂Ȃ��C���̌��e��N���ɍ��ǂ��Ă�������킯�ł��Ȃ��̂ŁC���������ǂ����̕ۏ͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�W���C�K�v�����C�\�������i����,�Z���^�[���j �ɂ��ā^23.02.01�n
�����������Ă��������Ă���܂��B
2018�N��(1)��B�ł����A������������u�R�̖v�ł͂Ȃ��āu�R�̔{���v�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���������̃~�X�͑傫���I
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^23.01.31
���Z�����Ŏg�킳���Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��H�~�̕����������Z�����ɏo�肷��w�Z������??
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^23.01.31�n
�y���3�z(3)�̉���ŁA
�wr=1, b=6���x�A�wr=5, b=2���x�ƒu���Ă������R��������܂���ł����B�������̂قǂ��肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�A���������@�A�������ƁC����r=1, b=6��r=5, b=2�ɂȂ�Ə����Ă���̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�~�̕����� �ɂ��ā^23.01.31�n
���2-1,���2-2�̖�蕶�Ɂw3�_�x�Ƃ���܂���2�_�̂悤�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڐ��̕������ɂ��ā^23.01.31�n
������₷�������ł��I���肪�Ƃ��������܂�(_ _)
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���f�ϕ��C�����藝�C�t���l���ϕ��ɂ��ā^23.01.31�n
�d�ˏd�ː\����܂��A�������u�W�����_���̕��ɂ��v�̏�̎��ɂ��āA����͎O�p�s�����ɂ��uR^2 "-" 1�v�����m�ȕ\���ł͂Ȃ��ł��傤���B
����Ƃ���낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���f�ϕ��C�����藝�C�t���l���ϕ��ɂ��ā^23.01.31�n
���������b�ɂȂ��Ă���܂��B
������Ƃ��������ԈႢ���Ǝv���܂����A�u���R�ƂS�v�ɂ����āu�W�����_���̕��ɂ��v�̈��̐����Ɂuexp(iz)�v�͂���Ȃ��̂ł͂Ȃ��ł��傤���B
��قǂ̑��M�ɊԈႢ������܂����B
�u���R�ƂS�v�͊ԈႢ�ł����B�������́A�u��T�ƂU�v�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̌��̂��ƂȂ̂��C�悭�킩��܂���D
���m�ʂ̕ł���̎���ɑ���n[�m���̃Z���^�[��������ɂ��ā^23.01.29�n
�Ɨ����s�̍Ō�̖��̓����������Ă������������ł�
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ�O�ɍ�������ނŁC�m���ɁC������r���ۂ��I��蒼���܂����C���Ԃ�������̂ŁC�Ƃ肠�������Ăͥ�������

�Ƃ���D���q�́C��0�̏ꍇ��

�C��2�̏ꍇ��
=52&chf=bg,s,fff6f6)
�@�ȏォ��C

���������b�ɂȂ��Ă���܂��B
���4�ł����A�\�������̂��ʓ|�ȃY�{���Ȏ��ɂ͑g�����̕����y���Ǝv���܂����B�ʉ��Ƃ��Đ������������������܂��ƍK���ł��B
�a��20�ɂȂ�g�����́A(6,6,6,2)(6,6,5,3)(6,6,4,4)(6,5,5,4)(5,5,5,5)
�����͏��Ԃ�4C1,4P2,4C2,4P2,1�ƕ\���āA�a��35�B
�S���ۂ�6^4��1296�B�䂦�ɋ��߂�m����35/1296�B
�����m��ҁn�F�A�����肪�Ƃ��D�L�q�����Ă̏ꍇ�C�Z���~���Ƃ������Ƃɂ͂��Ȃ��̂ŁC�N���ǂ�ł��킩��₷�����ǂ����ŁC�����_��t����ł��傤�D�u�����͏��Ԃɥ���v�͐����s���ł��傤
���m�ʂ̕ł���̎���ɑ���n[�t�s��(2)�ɂ��ā^23.01.28�n
���܋t�s��Q�A�R�����܂������@���o�Ă���悤�ł��B�h�����ĕM�Z���Ă݂܂��B����19�̊w���ɂƂ��Ă͋��|�Ƃ�����̂ǂ��ł����B������60�N�O�̂��Ƃł��B�̐l�ɂȂ�ꂽ���{�����ɂ��������ɋ������ɍs���悩�����Ǝv���܂��B�R���R�̉�@�ɓ���܂����B������̎�p�̌��ǂ̂������ڂ����ē��̉�]�������č�����ł��B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�s���ɂ��ā^23.01.28�n
���ȏ�̐����s��̋t�s���M�Z�ŋ��߂���@���킩��܂���B��w�̋��ȏ��@�㐔�w�w�ɂ͋L�ڂ���Ă��܂��B�����Ă��������B�����ĂȂ��肢�ł��݂܂���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�̌��C�̑��a�i�������j�ɂ��ā^23.01.28�n
���5(2)�������܂����B�����͍����Ă�̂ł����A����̉������ƈႤ�悤�ł��B�l�����͂����Ă邩���������������ł��B�i�܂��A����̃A�v���[�`���悭������Ȃ������̂ŁA�������������������ƍK���ł��B�j
80=2^4*5^1������A
(a,b)�̑g�����́A(39,1)(19,3)(15,4)(9,7)�Ɗe�召����ւ���8�B
72=2^3*3^2������A
(c,d)�̑g�����́A(23,2)(17,3)(11,5)(8,7)�Ɗe�召����ւ���8�B
45=3^2*5^1������A(14,2)�܂���(8,4)��m,n�̎w���Ɋ܂܂�Ă���Ηǂ��B14�͂ǂ���ɂ��܂܂�Ă��Ȃ��̂ŁA(8,4)�ƂȂ�B
�ȏ�����g�����́A(a,b)�̑g������(15,4)�����̋t�A(c,d)�̑g������(8,7)�����̋t�ł���B
a≥c�Ȃ̂ŁA(a,b)=(15,4)�A(c,d)=(8,7)�B
�����m��ҁn�F�A�����肪�Ƃ��D�L�q�����Ă̏ꍇ�C�Z���~���Ƃ������Ƃɂ͂��Ȃ��̂ŁC�N���ǂ�ł��킩��₷�����ǂ����ŁC�����_��t����ł��傤
���m�ʂ̕ł���̎���ɑ���n[�ǎғ��̗͂��p�ɂ��ā^23.01.26�n
�킩��₷��������Ă����������肪�Ƃ��������܂��B
����o���ĉ������X�^�C���͔��ɂ킩��₷���ł��B
�ЂƂ��퐶���ɖ𗧂�������邱�Ƃł���ɂ킩��₷���Ȃ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~����C���ジ�����ɂ��ā^23.01.26�n
(10)(13)�Ȃǂɂ���u1�v�f���Œ肷��v���삪�s���Ƃ��܂���ł����B
(13)�̒�ʂ̐F(6�ʂ�)��I�ԑ�����v�Z�ɓ���Ă��Ȃ��Ă��������o����͉̂��̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴆ��(10)�Łu1�v�f���Œ肷��v����������Ɂu�ďd�Ȃ���̂��S���ʕ��Ɛ�������v60�ʂ�ƂȂ��āC�듚�ł��D�~����Ƃ����P���ł̗p��͕W���I�Ȏg�����ɍ��킳�Ȃ��Ȃ炸�C�u�����v�̎g�����Œʂ��Ɛ��������Ăɂ͂Ȃ�܂���D���l��(13)�̒�ʂ̐F���Œ肷��Ƃ�����������Ȃ���C180�ʂ�ƂȂ��Č듚�ł��D
���m�ʂ̕ł���̎���ɑ���n[�������E�L�����E�������̕s��ϕ��ɂ��ā^23.01.26�n
�l�X�ȗ��p�ӂ��Ă��ĂƂĂ��킩��₷���B���Œm���̊m�F���ł��ĂƂĂ��ǂ��Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^23.01.24�n
������2��_���Ă��钆�w2�N�ł��B���\���߂ɂȂ�̂ł��ꂩ��������Ǝg���Ă��Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���C�������̔����ɂ��ā^23.01.23�n
���̂����������炢���A�ڂ��`�J�`�J���܂��B
�ł��A�Q�l�ɂȂ����̂ł悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������3 �ɂ��ā^23.01.23�n
���1(�R)���f�����ɑ���...������^�R�Ƃ���B���A�������ꂼ��Ɍ`���ŕ\���D�i���{���� �H�w��2016�N�j�̖��ł����A(��)�̉�������������߂������ŏI����Ă܂��B���̓�����cos�{īsin���Ǝv���܂��B�m�F���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D♦��♥♫∀�`�����ƂƁ`∳♣♬∅♠�C�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������̕s��ϕ��ɂ��ā^23.01.22�n
Chrome�ʼn{�����Ă���܂����A(6)�̂݉�ł����ލۂ�x,4,2���\������܂���(�E�F�u��Ńp�X���[�h��ł����ނƂ��Ƀp�X���[�h��₪�o�Ă���悤�Ȋ����ł�)�B
������\�����l�����܂���(�ȑO���̖����������Ƃ���Chrome���������L�������A����Chrome���ǂݎ�蓚����\��������)�ꉞ���̃R�����g��Ƃ����Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����[���b�ł��D�u����Chrome���ǂݎ�蓚����\�������v�Ƃ������Ƃ͉\�����Ⴂ�Ǝv���Dandroid�Ȃ�Chrome�̑傫�Ȃ����b�Łu�������L�������v�Ƃ������Ƃ͂��蓾�邩������܂���D�܂��C�l�b�g���[�N�̓r���o�H�i���Ȃ��̌g�т��瓖���ނ�����T�[�o�܂ł̂ǂ����j�ŁC���x���ǂ܂��f�[�^���L�����ďo���d�g��(proxy)���g���Ă���ꍇ�ɁC������G���ɂ͑O�Ɏg�����l�̃f�[�^���o����������܂���D�{���̂Ƃ���͂悭�킩��܂���D
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̍l�����ɂ��ā^23.01.21�n
�Ɍ��ƒ�ϕ��̊W�̖��͎��M�����܂��B���肪�Ƃ��������܂��B�T�N�P���Q�P��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^23.01.19�n
�������傢�ނ����̂ق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɏ����Ă���ڎ��̏��߂���Q�y�[�W�ڂ�����₳�����ł��D�i��ōs���Γ���Ȃ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�W���̕\�킵���ɂ��ā^23.01.17�n
�����g�킹�Ē����Ă���܂��B
���3.1�̉ŁAA={x|1��x^2��3,x�͐��̐���}�̗v�f��{1,2}�ƂȂ��Ă��܂����A{1}�������Ȃ̂ł͂Ȃ����Ǝv���A���A�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^23.01.16
�܂��ł킩��₷���ł��ق�Ƃɏ�����܂���🙏🙇��️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Ԑ}�`�̗p���ɂ��ā^23.01.16�n
���̈��ꓚ���ƁA���̌�ɂ��������������ł���̂ɑ��āA�^�b�v���Ď����Ŏ��ۂɈ��ꓚ�ł���̂ŁA���̎��͎����Ȃǂɂ��g����ȂƎv���܂���☺
�����m��ҁn�F�A�����肪�Ƃ��D
���m?���^?����^23.01.15�n
���T�̐V�ے��Œlj����ꂽ�C��������̃y�[�W������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����C�u���Z�Ő��w�T�����ŏI�����鐶�k�����v�Ƃ����w�K�w���v�̉������ƁC���Z�̎��Ƃłǂ������戵���ɂȂ�̂��C�\�z�����˂Ă��܂�������U�C��B���K��Ȃ����k������w�Z�͏��Ȃ��H�Ƃ���ƁC��B�œ��v�I�����E������ڂ����K�����C�����ň����Ȃ����T�Ǝ��̉�������Ƃ����W�������͂ǂ�Ȃ��̂Ȃ̂��H�l�����ł�
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^23.01.12�n
���̍l�����͖ʔ����ł��B�V���������������Ă��������Ă��肪�Ƃ��������܂��B
�@(G)�ɂ�����2^p/3^q��n�ɂ��āA�ؖ�����ĂȂ��̂ɒ藝�̂悤�ɂȂ��Ă邽�߁A�ؖ����A�ڂ��Ăق����ł��B
�m���ɁA7��9�Ȃǂ̎��͂�����������܂��A���̎��ɐ��藧������ʓI�ɂ��Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�w���@�Ŏ����Ă������ł����C�����w�ȑ��̂����̂������u�������̏ؖ����ł��܂����v�ȂǂƂ����̂͌����܂����̂ŁC����ƂȂ�����������x�̕\���ɂ��Ă��܂��D
�@�悭���邱�Ƃł����C�������̐��������������L���������Ă���ƁC���w�}�j�A�̂悤�ȕ�����u�ؖ��ł�������ǂ�łق����v�Ƃ����A�����悭�܂��D�i���܂łɉ��������܂����D�j����́C������肾���̓����ł����C�M�҂͐����_�̐��Ƃł͂Ȃ��̂ŁC���̂悤�Ȏ���E��ẮC��{�I�ɒf���Ă��܂��D�P�ɁC�����������Ă����������߂̖���N�������s���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̈ړ��ɂ��ā^23.01.12�n
�Ō�̖��̉���ɂāA���̒��_��(p,q)�ƒu�����������āu���ꂽ�I�v�Ɗ����܂����B
(���ʓI�ɍ����Ă܂������A)����a,b,c���g���ăS���S���v�Z���Ă��܂��A�Z���X�̂Ȃ���Ɋ����܂����B
�ǂ����ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^23.01.12�n
��ԍŏ��̎��A(x�|p)2+(y�|q)2=r2�E�E�E(#1) �͒��S(p,q)�ł���ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���������܂ލ����v�Z�ɂ��ā^23.01.11�n
���12�ł����A�������}�C�i�X�Ō���Ă���̂ɁA�A�j�C�j�̎����v���X�ŏ������Ă���܂����A�����̊��Ⴂ�ł����狳���Ă��������B�����2�d�����̖��ɂ��܂����B1��11��21��
�����m��ҁn�F�A�����肪�Ƃ��D�̕��̕�����������܂���
���m�ʂ̕ł���̎���ɑ���n[���������܂ލ����v�Z�ɂ��ā^23.01.11�n
��10��78�̔N��ɂ͑�ς��������Ba�ʼn����Ăق��Ƃ����瓚����x�ŕ\���B����ɂ͊�̔��Ȃnj����Ă����Ȃ��Ȃ�܂����B���܂ł悭���Z�̋��t�����܂����Ɣ��Ȃ��邾���łȂ��A���̂悤�ȋ��ނɂ����Ƒ������荇������Ǝv���܂��B���肪�Ƃ��������܂��B����
�����m��ҁn�F�A�����肪�Ƃ��������܂��D������āC���p�����o���Ă��܂����C���Ƃł͂�������������͈����Ă��炸�i���R�I�j�C�y�������w�D�悢�q�̊G�{�݂����Ȏ��ƂŁC�ǔF��K50�l�u���������t�����āu�Ƃقفv�̂悤�Ȏ��������܂������������l����C���̍��́u�ł��Ȃ����k�̓��Ă��c���Ă���C���́E�����̕v�Ȃ̂ł����C���v�f�[�^�������c���Ă��Ȃ����Ƃ��c�O�ł��D
�@�����I�Ɍ����C�u�Q���̐��k���C�W���̊w�K���s���v�u�W���̐��k���C�Q���̊w�K���s���v����ǂ�����FaceBook�����サ�Ă���Ƃ����Ă��C�����Ă���̂͂Q���̐l�Ƃ����̂����Ԃł��傤�D������C���J���ނƂ��ẮC�W���̎��Ԃ𓊓����Ă���Q���̏�ʐw���ӎ������y�[�W����炴��������Ȃ��Ƃ������ƂŁC�ꍇ�ɂ���Ă͋t�p�^�[���̕������l�����蓾�܂��D�����O�e�[���^�Y�Ƃ̍l�����Ƃ���
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^23.01.11�n
�Q���s����(D=0)�̖��(7)�Q���s����2x²+12x+18��0�̉����
�ux=3�����i�v�́ux=-3�����i�v���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[ ���������܂ލ����v�Z�ɂ��ā^23.01.10�n
��T�͂������茩�߂����Ă��܂����B�ǖ₾�Ǝv���܂��B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[3�_�̍��W�����_�̍��W�ɂ��ā^23.01.08�n
���f����ƊԈႦ�܂��B�V�W���̑ސE�P�X�N�̌����Z�̐��w�����ł��B�����O�͍s�̌v�Z�����Ă��܂����B���͓��Ɏ��g��ł��܂��B�R�_�����}�`�͉~�Ǝv�����݂�����A�O���̎R���搶�̎��ƂɎ肱�����Ă��܂����B���߂Ă��̖c��Ȏ������������L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��O���܂�̕��̏ꍇ�C�Ƌ��X�V���x�̐ݒu�E�p�~�ɊW�Ȃ��C�Ƌ����L���Ȃ܂܌p���̂悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�ݏ捪�ɂ��ā^23.01.07�n
�ォ��2�i�ڂ̐����ɂ���A�ꍇ�����̏����Ɂua>0�ł�����n�����̋����̂Ƃ��v�ua>0�ł�����n�����̊�̂Ƃ��v�����ꂼ��2������܂��B����2�́ua�@���@0�ł����āc�v������������
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����2�ɂ��ā^23.01.05�n
�����U��[��蒼��]�������܂���B�u���E�U��googlechrome���g���Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ϐ����������\���Ă��邩�J�ɃR�����g���Ă����Ȃ��Ɓu�������������v���O�����ł��C�Q�T�Ԃ��o�ĂΑ��l�̃v���O�����ɂȂ�v�ƌ������̂́C�J�[�j�n�������b�`�������̂��C�ڂ����͊o���Ă��Ȃ����C����������|�̉��߂͕��������Ƃ�����D�Ƃ���ŁC�e�iHTML�j�̒��Ɏq�ijavascript�j�̃v���O�����������Ă����āC�e�̒��ł̓R�����g�A�E�g���Ă���ꍇ�ɁC�q�������C�ɐ����Ă����Ƃ́C�V�����́D�Ƃɂ����C�������܂����D
���m�ʂ̕ł���̎���ɑ���n[����������...�ϐ��ϊ��ɂ��������ɂ��ā^23.01.03�n
�������p�����Ă��������Ă���܂��B
���6�̓������I����3�Ő����ɂȂ�܂����A����ł͑I����2�������ƂȂ��Ă���܂��B
������l����ɁA�I����3�̌�A�ł́A�Ǝv���̂ł����A�������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[����������...�ϐ��ϊ��ɂ��������ɂ��ā^23.01.03�n
���������b�ɂȂ��Ă��܂��B��A�ł͂Ǝv���̂ł����A(I)�����`�̔����������̗��x^2y'�|xy+2y^2=0�̈�ʉ���y=x/log(x^2+C)�ƂȂ��Ă��܂����A��������y=x/logx^2+C�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ͒�����v���܂����C�u�ǂ��܂ł����ꂩ�v�����Â̕�����ڂ�
%2B C}&chf=bg,s,fff6f6)
�ɒ����܂���
���6-(1)�Łu�`�����萔k�̍ŏ��l�v�ɑ���̗����ɔY��ł܂��B
�����ǂނ�k��A�ƂȂ�����ɑ���3��A�ł�����������
k��3�����藧�A�Ƃ������ɓǂݎ�ꂽ�̂ł����A
���̂悤�ȍl���͏펯�i�Ƃ����������������Ă��邩�s���j�ƈ����ėǂ����̂ł��傤���H
�}��`���ƌ����Ƃ��邱�Ƃ̃C���[�W�͂Ȃ�ƂȂ��͕�����܂����E�E�E
�i���1-(1)�̉悤�Ȏ��ό`�ŏo�����Ǝv���܂�����k��2A-3�Ƃ����悭������Ȃ��W�ɂȂ�܂����j
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɁC�_����あ�Ă���悤�ɂ������āC�������肵�Ȃ��D���̗��Łu��������������̂́Ca:b:c=x:y:z�v�i�������C�P��0�̂Ƃ��́C�Ή����鍀��0�Ƃ���j�̏ꍇ�ŁC���ꂪ�E�ӂ̍ő�l�C���ӂ̍ŏ��l�̏ꍇ��Ή�����Ƃ������Ƃł���������܂����������l�����F��蕶�̕\����ς��܂����̂Ō��Ă�������
���m�ʂ̕ł���̎���ɑ���n[�W�J�����̉��p����ɂ��ā^22.12.19�n
�lj����i6�j�̉����s�ڂɂ���-a�{b�{x��x�͂ǂ����痈�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�L�̓~�X�ł��̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����.2��������.2����(2013�`)�ɂ��ā^22.12.16�n
�y2013�N�x�Z���^�[����.���w�T�E���wA�z��2��́iii�j���悭�킩��܂���B�Ȃ����̂悤�ɓ�����̂��B�����Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă��������ƕ��������ł����C�Ђ炪�Ȃ́u���v�̂悤�ɐ^����������������[���ő�ɂȂ�C�A���t�@�x�b�g�́uJ�v�̂悤�ɐ^�����E��������ΉE�[���ő�ɂ���܂��D���_�̂����W�i���j��8/7�ŋ�Ԃ̕���1������C���[a��8/7−0.5�ȉ��Ȃ�C���[�ōő�ɂȂ�܂�
���m�����s�^��������^22.12.14�n
���̃T�C�g�͋�Google�T�C�g�̂܂܂ł��傤���B�ł�����V�o�[�W�����ɊȒP�ɕς�����̂ŕς������������Ǝv���܂��B�m���ڍs�����܂Ŏc�莞�Ԃ����Ȃ������悤�ȁc
�����m��ҁn�F�A�����肪�Ƃ��DGoogle�ɂ͗l�X�ȃT�[�r�X��������,�s�J�T�̂悤�ɃT�[�r�X���I���������̂�����悤�ł�������������C���Ɏg�����̂����m��܂��D���āC���w�E�́u��Google�T�C�g�v�Ƃ́Cworkspace�̂悤�Ȃ��̂ł��傤���H������ɂ��ẮC���łɋ��o�[�W�����͏I�������Ə�����Ă��܂����C���̋��ނ�2022�N11���ɍ��n�߂����̂ł��D
�@���m�ȗp��͔���܂��C���̋��ނ�Google workspace�ł͂Ȃ�,Google�u���K�[�̃y�[�W�ł����Google�u���O�����̂����I�����邩�������Ƃ����\������܂����C��荇�����P�ł��������čL���Ȃ��̂��̂ɂ��Ă��܂��D���̂悤�ɂ���ƁC���N��ɋ��ނ��~�����Ǝv���l�Ɋۂ��Ɠn���Ă��g���邾�낤�Ƃ������Ƃł��D
�@�b���Β����Ȃ�܂����C����҂̃f�W�^����Y�Ƃ�����肪�����āC���̎��������܂蒷���Ȃ���������Ȃ��ȂƎv������ŁC�q���⑷���z�[���y�[�W�������p���ł����\������̏ꍇ�CGoogle�̖����y�[�W�Ɍ��J���Ă����C���炭�́C�ǎ҂����p�ł��邩������Ȃ��D�����google�u���K�[���I���������ɂȂ�����C��]�҂ɔz���Ă��܂��Ƃ����\�z�ł��D
���m�ʂ̕ł���̎���ɑ���n[���̎w���̒�`�ɂ��ā^22.12.09�n
�����Ƃ��낪�����ō��̋���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^22.12.09�n
(4)��2��ڂ͐���BC�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D����C���̉���ō����Ă��܂��D������x�����ǂ�ł�������
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^22.12.04�n
�M�҂���͐��w�̐���Ƃ��Ȃ�ł����H�I�߂��Ⴍ����킩��₷���Ċ����e�X�g80�_���܂����I�I�I���������b�ɂȂ��Ă܂�☺️���ꂩ�����낵�����肢�v���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���\�N�ԋ����Ă��܂������C���͋����Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[���Ғl�ɂ��ā^22.12.03�n
������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڐ��̕������ɂ��ā^22.12.02�n
�����ɂȂ�ׂɂ́A����v�Z���Ȃ��Ƃ����Ȃ��`���A
�ƂĂ��ǂ��ł��I���肪�Ƃ��������܂�‼︎‼︎‼︎‼︎‼︎‼︎‼︎‼︎
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���w�h�ɂ�����O�p��̒�`�i���K�j�ɂ��ā^22.12.01�n
�ނ�������
�����m��ҁn�F�A�����肪�Ƃ��D??
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^22.12.01�n
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K���ɂ��ā^22.11.30�n
�����m��Ȃ����w���ł������A�ܕ����炢�ŊK��ɂ��Ă̊ȒP�ȗ������\�ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�������i�Q�����j�ɂ��ā^22.11.28�n
�����y�������p�����Ă��������Ă���܂��B���10�̊�������肢�������̂ł����c�B���肷���̎��Ō��\�ł��̂ł�낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���t�g�������J�Ȃ̂ŁC��������ƑΉ����悤�Ǝv���܂����C�H�܂����C����������Ă���̂ɓǂ�ł��Ȃ��H�̂��ȁH
�@�ŏ��́u���P�v�̑O�Ɂu���̑I�����̂����Ő��������̂��N���b�N���Ă��������D�v�Ə����Ă���܂��悤�ɁC�I�������N���b�N���Ȃ��ƍ̓_���ʂ�������o�܂���D�I�������N���b�N����̓_���ʂƉ�����o�܂��D�قƂ�ǂ��ׂẴy�|�W�����̂悤�ȃv���O�����ɂȂ��Ă���̂ŁC�����P�Ɂu���Ă��邾���v�ł́C���̋��ނ̔��������Ă��Ȃ����ƂɂȂ�܂��D���̋��ނ͉����^�v���O�����ɂȂ��Ă��܂��D�����̂Ƃ����낵���D
���m�ʂ̕ł���̎���ɑ���n[�R�����̍ő�l�E�ŏ��l�ɂ��ā^22.11.27�n
��P�ɂ��āAx>�N�ł͂Ȃ�>=�N�ł͂Ȃ��ł����H1���͈͂ɓ����Ă���͂��ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���w�E�̓_�ɂ��ẮC���ꂾ��������Ƃ��̒ʂ�Ȃ̂ł����C���Z�̐��w�Łu��Ԃ̏ꍇ�������d��������v���Ƃ́C��ϕ��̏ꍇ�������Ĕ����܂��D���Ȃ킿�C�u0<a��1�v�ua��1�v�̂Ƃ��̂悤�ɁC�P�̒l���Q�̋�Ԃɏd�����ē��镪�����́C���܂���D�i=��������R�c�͍��Ȃ��j�D������C�A,�G,�J�̂悤�Ɂu����C�ȉ��^�v�ŕ����Ă�����C�ua>1�v�ł������ϕ��̏ꍇ�����C��̋�Ԃɂ����̋�Ԃɂ��P�l�����鏑���������邱�Ƃ�����܂����C����͋�Ԃ̒[���܂܂�Ȃ��L�`�ϕ��̐������ʓ|������Ǝv���܂��D�i���̗�O�Q�Ɓj

�́C

�̗��Ƃ������邪�C��Ԃ̒[���܂܂�Ă��܂܂�Ȃ��Ă��C��ϕ��̒l�͓���������C�ȒP�ȏ������ŏ���
**�i ����CPC���̏Ⴕ���Ƃ��ɁC����̃��[���������Ă��܂��܂����D���e�́C�ŗL�l�ɉ����ČŗL�x�N�g������בւ�����C�s��̑Ίp�������ʂ���ł���̂́C���������C��a��������Ƃ����w�E�ł��� �j**
�����m��ҁn�F�A�����肪�Ƃ��D���ނɏ����ĂȂ����Ƃ��������̂́C�f���炵�����@�͂ł����C�P�̍s��̑Ίp���́C�u�ŗL�l�ɉ����ČŗL�x�N�g������בւ��ɉ����āv���ʂ������܂��D����Ă݂���킩��܂��D
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̋��ߕ��ɂ��ā^22.11.22�n
�y���̑��C�ŗL�l�C�ŗL�x�N�g�����K�p�̖��z��
�i1�j��=7 �̎��̌ŗL�x�N�g���ł����A
��j����� s(5 4) �Ə����Ă��悢
���j����� s(4 5) �Ə����Ă��悢
���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��ϕ��F��{�v�Z�ɂ��ā^22.11.20�n
�O���t��������ė~�����I
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�Ɂu���ݒn�ƑO��̍��ځv�Ƃ����`�Ń��j���[������̂ŁC��������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̏d�S�ɂ��ā^22.11.19�n
�킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�u�������m���ɐg�ɒ����邽�߂̖��v�Ɓu���ȉ��̋L�q�͋��ȏ����x���ł͂���܂���D����Ǝv������ȗ����Ă��悢�v�Ə����Ă�����ɕ����Ă���̂ŁC�u�������m���ɐg�ɒ����邽�߂̖��v���ł���悢�D�u����Ǝv������ȗ����Ă��悢�v�Ƃ������́C����Ǝv������ȗ����Ă��悢�̂ŁC���ʂɂ����镽���܂ł́C�K�������ۏł��܂���D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����̉��p����ɂ��ā^22.11.17�n
�lj�����(6)��
a+b+c=S, �|a+b+x=A, a�|b+c=B, a+b�|c=C�Ƃ��� �i�����j=SAB+SBC+SAC�|ABC =SA(B+C)+BC(x�|A)
��
B+c=2a, S�|A=2a������@(S-A)
��
B+C=2a
�i�����j=SA�~2a+BC�~2a=2a(SA+BC)
SA=(b+c)2�|a2=b2+2bc+c2�|a2
BC=a2�|(b�|c)2=a2�|b2+2bc�|c2
SA+BC=4bc �䂦�ɁC�i�����j=2a�~4bc=8abc�E�E�E�i���j
���̕����͏�̂悤�ɂȂ�̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��Dc→C,x→ S �������܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̓����ɂ��ā^22.11.17�n
�y�����Ɏ肪�͂�����Ŋy���������Ă���܂��B�������肪�Ƃ��������܂��B
�����A
��̕\�S�ɂ����āC���_�x�N�g����
��a=(40, 50, 60)...
�̂�����ł����A�\�S�Ƃ����̂́A�\�R�̂��Ƃł͂���܂��H
���m�F���������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�s�̊�{������p�������������ɂ��ā^22.11.16�n
���11�̉��́A���̌`���Ɓu�[�v���Ȃ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�K�v����,�\�������i�������j�ɂ��ā^22.11.15�n
���10�̏���s�̕����̌������t�ɂȂ��Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������i�Q�����̕������j�̒�ϕ��ɂ��ā^22.11.15�n
���̉A�r������m�肽���B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă���̂ɏ����ĂȂ����̂悤�Ȋ��z���ŁC��H�Ǝv���܂������C������������܂����D���Ȃ��́uiPhone�Ȃ̂�PC�p�̉�ʂ����Ă���̂ŁC�E�����������Ă��Ȃ��̂ł��v�D���̃y�[�W�̐擪�ɁC�傫�ȕ����Łu�� �g�єł͕ʕŁv�Ə����Ă���̂ɏ]���āC�g�єł����ĉ������D
���m�ʂ̕ł���̎���ɑ���n[�y���������ɂ��ā^22.11.11�n
�y���������ŏ��̐������F�̕����i��L��*1�`*4�̐����j�ŁA������4�s�ځB
���ꕪ�q�ɋ����H�̃��[�g�������镔���̕��ꂪx�ɂȂ��Ă��܂����An�ł���ˁB
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���������̕ό`�ɂ��ā^22.11.10�n
���̕����Ɓ@�����������Ȃ��`�ɂ����炭�Ȃ��Ă���Ǝv���܂�💦
���2�̂�����(3)�ł���
�����������̕����̕������{���|�̂Ƃ����v���X�ƊԈ���Ă�Ǝv���܂��̂ŁA�m�F���肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�u���2�̂�����(3)�v�Ƃ́u���2�̉���(3)�v�Ƃ���C���w�E�̓��e���m�F�ł��܂���D
���Ȃ킿�C
^2-\frac{9}{4}%2B 7=(x-\frac{3}{2})^2%2B\frac{19}{4}&chf=bg,s,fff6f6)
�Ő����ł��D�u�����̕������{���|�̂Ƃ����v�u�}�C�i�X�v�Ə����Ă��܂��D�v���X�ɂȂ�̂́C��蕶�ɏ��߂���t���Ă���萔��+7�����������ʂł��D
2020�N�̉�(1)�B=234�ł͂Ȃ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�Ƃ������́C�r���o�߂̍ŏ��̎��ł��ˁD�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�������i�Z���^�[����:2015�`�j�ɂ��ā^22.11.04�n
2018�N�̖��(3)�̖�蕶�B�]�肪1�A�ł͂Ȃ��A2�ł͂Ȃ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D(2)�̉Ŏ����Ă��܂��悤�ɁC144x=7y+1�ƂȂ�Ƃ��́Cx=7k+2(k�͐���)�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^22.11.03�n
���߂Ă��ז����܂����B�킩��₷������ł����B
���p�J�n�i�����U�̉���j�Q�_(a, b), (c, d)��ʂ钼���̕������������Ȃ�l����ƁC�_���Q�������ă|�C���g���i�肫��Ȃ��̂ŁC�P�_(a, b)��D��I�ɍl����D
���Ȃ킿�C�Q�ڂ̓_(c, d)�͌X�������߂邽�߂̍ޗ������Ɏg���D���p�I��
�X���Ƃ��ؕЂ��킩���Ă��钼������A��_��ʂ钼���̓��o�̉���ŁA���ɂ��̕������f���炵���Ǝv���܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^22.11.02�n
��肪�킩��₷���A�������m�肽���Ǝv���Ă�������������Ă��ĂƂĂ����肪���������ł�
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������i�Q�����̕������j�̒�ϕ��ɂ��ā^22.11.01�n
x��sin�Ƃɒu���ϕ��ł���͉̂����s�v�c�ł����A����͒�`��ɒ��ӂ���ł���Ƃ������Ƃł���ˁH�i...�ȉ���...�j
�����m��ҁn�F�A�����肪�Ƃ��D���̂܂܌v�Z����ł���ϕ����C���Ƃ���ɒu���ϕ��Ōv�Z����̂́C�������ʂȈӐ}������ꍇ���Ȃƥ��
���m�ʂ̕ł���̎���ɑ���n[�ׂ荇�����ѕ��E�ׂ荇��Ȃ����ѕ��ɂ��ā^22.11.01�n
���8�ɂ��Ď���ł��B
2�F�������ƁA�K��3�F���������ƂɂȂ�
��(�`���a)=��(�a���b)=��(�b���`)=��(�`���a���b)
�Ƃ����W�ɂȂ�̂ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���8�͂����������ł͂���܂���D�Ԉ���Ė��9�̎�������Ă���̂ł�����C���9�̉����ǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[Python�Ő�����������(2)�ɂ��ā^22.10.29�n
�����Q�l�ɂ����Ă��������Ă���܂��B���Python�ō��Z���w���Ċw�K���Ă�����̂ł��B�i���ł�70��ɓ˓����Ă��鐢��Ȃ̂ŁA�����g���`���J���Ȏ��₩������܂��A�����ق��c)
���̋L���Ƃ͒��ڊ֘A���܂��A����̑Q�����Ɋւ��鎿��ł��B
Sympy��rsolve()�Ƃ�����������A�Q���������ʍ������Ƃ��ł��܂��B(...�ȉ���...)
�����m��ҁn�F�A�����肪�Ƃ��D������̓��e�͋��ނƒ��ڊW����܂���̂ŁC�ł��܂���D�ŋ߂́CSpam���[����Ƃ��āC�l���Ƃ̕ԐM�������Ă��܂��̂ň������炸�D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g����͂̌����ɂ��ā^22.10.28�n
���w�҂ł��Bgrad(�ӃՁj�̌��������̃T�C�g�Ō�����܂����B���o�ߒ����܂߂ċL�ڂ���Ă���A��Ϗ�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���\�N�Ԃ�Ɍ��������Ă݂܂���
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i�����j�ɂ��ā^22.10.27�n
�ƂĂ�������₷��, �̌n�I�ɂ܂Ƃ߂��Ă���̂ŗǂ����K�ɂȂ�܂����B
���ȏ��ł͌��������d������Ă��邽��, �킩��ɂ����Ƃ��낪����܂�����, ������̃T�C�g�̂������ŗ����ł��܂����B�i���ȏ��������킯�ł͂Ȃ�, �������������Ƃ��낪���ȏ��̗ǂ����j
���̈�Ӑ��Ȃǂׂ̍������͋��ȏ��ɏ�����Ă���̂Ŋ撣���ė������܂��I
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�o�Ȑ��ɂ��ā^22.10.26�n
�킩��₷���Ă�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^22.10.26�n
(x+1)3=x3+3·x2·1+3·x·12+13=x3+3x2+3x+1
(2x+3)3=(2x)3+3·(2x)2·3+3·(2x)·32+33
=8x3+36x2+54x+27
[VI]�@�@(a+b)3=a3+3a2b+3ab2+b3���̎��ŁA�r���ɂR�����邪�o�Ă���̂��ŏ��ƍŌ�ɂ͂R���o�ė��Ȃ��̂��A�Ȃ����Ȃ̂����킩��Ȃ��̂ŏڂ����ڂ��Ē�����Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
^2&chf=bg,s,fff6f6)
��

�Ƃ͈Ⴄ�D
^3&chf=bg,s,fff6f6)
��

�Ƃ͈Ⴄ������̐������K�v�ȏꍇ�́C�������̎g�����𒆐S�ɁC���w�Z3�N�̋��ނ��猩�Ă��������D
���P�P�́i�B�j�̉������킩��ɂ����B�Ȃ������Ȃ邩�A�l�����������Ă����ƕ�����₷���Ȃ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����Ŗڈ�t�ł�
���m�ʂ̕ł���̎���ɑ���n[�����̕��s�����ɂ��ā^22.10.25�n
���Z���w >> ���Z���w�U�E�a>> �_�ƒ����t�Q�����̕��s�����ɂā@�Ԉ�����Ƃ��́C�E�̗���A�ł��Ă���蒼���ɂ͂Ȃ�܂���@�Ԉ�����Ƃ��́C�uHELP�v�Ɓu�ĊJ����v�̃{�^�����\������܂��D�uHELP�v������ꍇ�ł����Ȃ��ꍇ�ł��u�ĊJ����v�{�^���������Ή𑱂��邱�Ƃ��ł��܂��D�Ƃ����Ă���܂����{�^���͕\�����ꂸ�A�܂��E��A��?���邱�ƂŐ����ɂł��Ă��܂��܂�
�����m��ҁn�F�A�����肪�Ƃ��D��ʂ̉��̕����������Ă���ƁC�{�^���͌����܂���D�{�^���͏�̕��ɂ���܂��D
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^22.10.25�n
��3.2�ł����A(z-x)3��𑫂��Ă����ƁA�E�ӂ�0�ɂȂ�̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�E�ӂ�0�ɂȂ�Ƃ����ؖ��������Ă���̂�����C�u�E�ӂ�0�ɂȂ�̂ł����v�Ɛq�˂�̂͂��������ł��D
���̎���́C���X����܂����C(...)�̕����������ĂȂ���킩��Ȃ��̂ł͂Ȃ��C(...)�̕��������ł����Ă��C����ɍ�����O���|����ƁC���̒l�͂O�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^22.10.25�n
���3��(3)���킩��܂���B��������Ă��A�Ȃ������Ȃ�̂����킩��܂���B
�ǂ����Ă������������ł��B�Ȃ��Ă���ׂ����r���̎��A�v�Z�Ȃǂ�����L�ڂ��Ăق����ł��B
��낵�����肢���܂��B
�i�lj��j ��3.2�Ɩ��3��(3)�ɂ��āA�����A�킩��Ȃ��Ǝ��₵���҂ł����A�Ȃ�Ƃ������ł��܂����B
���̂悤�ȉ����������������悢���̂��ƃr�b�N�����܂����B�����������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���ɏȗ��͂���܂���D�����ǂ�ł��킩��Ȃ��Ƃ������ƂȂ̂ŁC���̖��͂����ȂƑ����������Ƃ������ƂŁC���̖������ꂽ��ǂ��ł����D���̃y�[�W�́C�S�̂����p���ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̔����ɂ��ā^22.10.24�n
��2�ł��B��������������܂Ƃ܂��Ă��Ė��������ĂƂĂ��g���₷���ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��2�ŎO�p���̔��������ƍ�3�ł́C�Ή����₷����
���m�ʂ̕ł���̎���ɑ���n[�P���s�����i��{���j�ɂ��ā^22.10.24�n
�ƂĂ��g���₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ϐ����̋ɒl�ɂ��ā^22.10.24�n
�������ɂȂ�܂��B��T�|�P�̋ɏ��l�́[�P�W�ł͂Ȃ��A�|�W�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�������i�Z���^�[����:2015�`�j�ɂ��ā^22.10.24�n
2015�N�̖��(3) ���F�̉ォ��7�s�ځ@m+1=2n �̏���5n����Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����_�C�O���_�̍��W�ɂ��ā^22.10.23�n
�e�X�g��Ɏg�킹�Ă��������܂����B���肪�Ƃ��������܂�😭
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ƃ��̑����ϊ����ɂ��ā^22.10.21�n
�������n�̓_�Ƃ��̑����킩���n������1���ϊ������܂�Ƃ������Ƃł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł��D�������C���̓_��\���x�N�g�����݂��Ɉꎟ�Ɨ��łȂ���Ȃ�Ȃ��i�Ⴆ�C�Q�����s�Ƃ��C���̃x�N�g���ŕ\����悤�ȑg���킹�łȂ��C�W���s��t�s���܂�m�s��0�n���Ƃ������ɂȂ�܂��j
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^22.10.19�n
�ؖ������Ă���̂͋C�������悢��. ���肪�Ƃ�.
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ƃ��̑����ϊ����ɂ��ā^22.10.21�n
�������n�̓_�Ƃ��̑����킩���n������1���ϊ������܂�Ƃ������Ƃł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł��D�������C���̓_��\���x�N�g�����݂��Ɉꎟ�Ɨ��łȂ���Ȃ�Ȃ��i�Ⴆ�C�Q�����s�Ƃ��C���̃x�N�g���ŕ\����悤�ȑg���킹�łȂ��C�W���s��t�s���܂�m�s��0�n���Ƃ������ɂȂ�܂��j
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^22.10.19�n
�ؖ������Ă���̂͋C�������悢��. ���肪�Ƃ�.
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �������i�Z���^�[����:2015�`�j�ɂ��ā^22.10.19�n
2019�N�Z���^�[�����́i�R�j�Z
���悭�킩��܂���B
�Ⴆ�Aa=5�Ƃ����a+2=7�Ȃ̂ōő���͂P�H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƃ��ƁC���̓~�X������܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q�ߐ��̕������ɂ��ā^22.10.18�n
���ɑf���炵���B���̃T�C�g���������ʏ�ʂɕ\������Ăق����B�T���̂Ɏ��Ԃ��������Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w�����ΐ��̂����ɂ��ā^22.10.18�n
��肪���Ă���Web��ʼn����₷���`���̂��ߔ��ɂ��肪�����B���K�ɗp���Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̕s��ϕ��ɂ��ā^22.10.13�n
�R�O�N�Ԃ肭�炢�ɐ��R������Ă���A�f���炵���T�C�g�ɏo��܂����B���肪�Ƃ��������܂��B
��T�ł����A�u���ϕ����s���̌�̂Q�s��
�C���e�O����sin3x dx���C���e�O����(1�|cos2x)sinx dt
�ƂȂ��Ă���܂����A�Ō��dt��dx�ł͂Ȃ��ł����H�����Ԉ���Ă���܂�����\����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[���� ��2�B.�x�N�g��.�O�p���ɂ��ā^22.10.10�n
�������ɗ��p���Ē����Ă���܂��B
�y2020�N�x�Z���^�[����.���w�U�EB�z��4��i�I����j(4)�ɂ��āA
���1�s�ڂ�OC�x�N�g����OD�x�N�g���̓��ς̋L���������L���ɂȂ��Ă���悤�Ɏv���܂��B
�܂��y2018�N�x�Z���^�[����.���w�U�EB�z��4��i�I����j�i4�j�ɂ���
�Ō�̉@�g,�i,�j,�k���u(3a-4)/ 2�v�̂悤�ȋC���v���܂��B
���萔�ł͂������܂������m�F�̒��A�X�������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�������C2018�N�x�ɂ��ẮC�����̎d�������
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̐}�`�։��p�ɂ��ā^22.10.10�n
���̃y�[�W�ł̓x�N�g��������킷��啶���A���t�@�x�b�g�̂������ɂ������ď����Ă���̂�F��E���@���f���ɂ����B�ق��̃y�[�W�ł́@�A���t�@�x�b�g�̏�ɏ����Ă���̂ł���Ȃ��Ƃ͂Ȃ��̂ł����B�Ƃ肠�����t�H���g��傫�����Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ�Chrome�œǂނ��Ƃ�O��ɂ��Ă��܂��D10�N�ȏ�O����Firefox�ɂ͑Ή����Ă��܂���D�i�y�[�W�������߂��āC�X�̃y�[�W�ɂ͏�����܂��C�x�N�g���̖�����̉��ɗ���̂́C�S���̕s��ł��D�jChrome�ł̂ݍ쓮�`�F�b�N���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���̔����@�ɂ��ā^22.10.09�n
1�ԉ��̃X���C�h�i�Q�l�j���̂悤�Ȍ���������̉�cos�̂͂���cot�ɂȂ��Ă��܂���A
�����m��ҁn�F�A�����肪�Ƃ��D���Z�ł��i�w�Z�ł́C

�͕��ʂɏK���ł��傤�D���̃y�[�W�́C�����`��w���N�x�����̋��ނł��D�u�K�����k�ƏK��Ȃ����k�����āC�悭���₪����L���v��
���̃y�[�W�̏��߂̕�(*4.2)�̎��ɂ܂Ƃ߂Ă���܂��D�Ȃ��C���Ȃ����l����

�̔����́C
�t�O�p���̔����@�̍ŏ�(2)�Ɍf�ڂ��Ă��܂��̂ŁC�Ⴂ�͂킩��ł��傤�D
�������Ɏg�p���Ē����Ă���܂��B
�y2014�N�x�Z���^�[����.���w�U�EB�z��4��i�I����j
�i�Q�j�̖�蕶���Ōォ��4�s�ځAOP�x�N�g���̑傫����₤�ӏ��ɂ���
��Βl�L�������Ă��Ȃ��悤�Ɍ����܂����B
���m�F�̂قǂ�낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^22.10.07�n
���Ƃ̗\�K���K�ɖ���ƂĂ��𗧂��Ă܂��I�I�������肪�Ƃ��������܂��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������̉��K�ɂ��ā^22.10.05�n
���̃y�[�W�ɂ�ax^2+bx�̌`�̖�肪�����ł��ˁBax^2+bx+c�̌`�̖��𑝂₵�Ă���������Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�萔�����Ȃ��ȒP�Ȗ��ŗ��K���Ă���C�萔���̂�����ł����K����Ƃ�������ŁC���̃y�[�W�̖��7���玟�̃y�[�W�ɂ����Ē萔���̂����肪����ł��܂��D�u�����̌��Ă���1�̃y�[�W�ɂ��ׂĂ̖�肪�����ĂȂ���Ȃ�Ȃ��v�Ƃ����v�����݂́C�g�т��g���Ă���ǎ҂ɑ����悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�������i�L�����j�̕s��ϕ��ɂ��ā^22.10.02�n
�݂ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D�u�g�їp�͕ʕŁv�Ə����Ă���܂��悤�ɁCiPhone��PC�p�̉�ʂ�ǂނ͖̂����ł��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i�����j�ɂ��ā^22.10.02�n
�d�C��RLC��H�ŁA�����������Ƃ����̂�����܂��ˁB���̔��ʎ��������̌`�⑬���ɊW����Ƃ����̂��\�������ł��Ȃ������̂ŁA���̃y�[�W�����܂����B���̗��K���܂ł��ƁA��̕����̕����ł������ȋC�����Ă��܂����B���ǐU�����N���邽�߂ɂ͔��ʎ������łȂ���Ȃ�Ȃ��B�d���̏ꍇ�Ɍ�������ԑ����Ƃ����̂́A��ʉ��Ɍ����x�̈ꎟ�������̌��ʂȂ̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�P�������Č����Cy’’�̌W����1�ɂ����Ƃ��Cy’�̌W���͒�R�E�����ɊW���Cy�̌W���͕����͂ɊW���C�U���ɑΉ�����ƍl����Ƃ悢�ł��傤�D����

�̂悤�ɂȂ�Ƃ��C����

�������̎d���ɊW���肵�C����

���U�����Ȃ��W����悤�ȁi50�N���O�̋L���Ȃ̂ŁC�A�o�E�g�Șb�ł�����j
�y����
�����m��ҁn�F�A�����肪�Ƃ��D�����������e�ɂ��ċL�q���Ȃ��ƁC���ɂ���
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.09.30�n
�}�W�Ŗ������Ă܂��B���肪�Ƃ��������܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȉ��������ɂ��ā^22.09.30�n
���x������Փx�̖��ł����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̌v�Z(�܂Ƃ�)�ɂ��ā^22.09.27�n
�җ���߂��āA���Ǝ������邽�߂ɕ����n�߂܂����B(10)�Ŏ肱����܂����B�L�����̔��z���o�Ȃ������ł��B�܂��܂��ł��B�撣��܂��B�f�G�ȃT�C�g�����肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�N���������������u�l�̈ꐶ�́C�������Ȃ��̂Ȃ璷�߂���C����������ɂ͒Z�߂���v�D�җ�̍��ɂ͂������ȂƎv���܂������C���ۂɂ́C����Ȃ����Ԃ������Ă��ł��Ȃ����Ƃ����邩�������D�ڕW����قǍi�荞�܂Ȃ��ƁC10�N�₻����w�͂��Ă��C���ʂ��`�ɂȂ�Ȃ����Ƃ����邩���D
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�:�ϐ��ϊ�.���R�r�A���ɂ��ā^22.09.24�n
2�����A3�����̏ꍇ�͖ʐρA�̐ς̌v�Z���x�N�g���O�ρA6�ʑ̑̐ς̌v�Z�ƃ��R�r�A������v���邱�Ƃ��ؖ��ł��܂����A4�����̏ꍇ�͂ǂ��Ȃ�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�O�ς͂R���������̘b�ŁC�����ɂ͊W�Ȃ��C���R�r�A���͕Δ����ɊW���Ă��āC�������ɂ��Ă���`�ł���D�����ɂ͒��ڂ̊W�͂Ȃ��Ǝv����D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̐��������ɂ��ā^22.09.22�n
�悭�킩��Ȃ����Ƃ��ǂ����ǂ�ŃN�\���Ƃ������܂���
�������������ǂ݂ɂ����v
�����m��ҁn�F�A�����肪�Ƃ��DWindows�̏ꍇ�́uCtrl+(+)�v�CMac�̏ꍇ�́uCommand+(+)�v�ɂ��g��\������܂��i�ɉ����Ă���Ɋg�傳���j�D���ɖ߂��ɂ́uCtrl+(-)�v�uCommand+(-)�v�ł��D����́C�g��k����(100%=1�{)�Ŏg���l�������ł��傤�B
���m�ʂ̕ł���̎���ɑ���n[�ɍ��W�ɂ��ā^22.09.21�n
�ǂ��ł��Ă���B���ɂȂ�܂����B�V�S��
�����m��ҁn�F�A�����肪�Ƃ��D�c��̐���̐擪�������C�X���[�N�H�[�^�[�܂œ��B�Ƃ������ƂŁC�����͌�납�炱��������Ă��������Ȃƥ��
���m�ʂ̕ł���̎���ɑ���n[���w�h �ɂ�����O�p��̒�`�i���K�j�ɂ��ā^22.09.19�n
�f���炵�����ނ����肪�Ƃ��������܂��B���ƂȂ̊w�ђ����Ƀs�b�^���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^22.09.19�n
�̓_�ł͍����Ă���A�Ԉ���Ă��邵��������Ȃ��̂ŁA������������悤�ɂ��ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���Ɂu

�v�Ƃ����{�^�����ڗ��悤�ɒu���Ă���܂��̂ŁC������N���b�N����ƁC�r���o�߂������܂��D
������ڂ����A��萔�������̂Ŏ��K�ɂƂĂ��𗧂��܂��B�����A�o��ŕ�����ۂɂ̓X�}�z�ł̃y�[�W���g���̂ł����A�X�}�z�ł��ƃ��j���[�ɕ\������Ȃ��y�[�W������������悤�Ɏv���܂��B���̃y�[�W�������ł��B�X�}�z�ł̖ڎ���������ׂẴy�[�W�ɔ�т₷���悤�ɂ��Ăق����ł��B��낵�����˂������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�E�̓_�ɂ��Ď��o�͂���̂ł����C�e�y�[�W�Ō�����T�u���j���[�����S�ɂ��āC�X�}�z�őS�̃��j���[�����Ȗ��i���w�T�C���wA�Ȃǁj�����ɂ���ȂǁC�ȗ����̕��@�����߂Ȃ��ƁC���ږ����ォ��lj������Ƃ��ɂ����Ⴒ���Ⴗ��̂ŁC�����������ɐ��肪���ł��D���̏H�ɂ͂��������������肳����\��ł�
���m�ʂ̕ł���̎���ɑ���n[��������(��{)�ɂ��ā^22.09.14�n
���������̃y�[�W�ł������畽�������ɂ��ĊȒP�ɊT�v�������Ăق����B�ǂ��䂤�`�ɂ��Ȃ��Ƃ����Ȃ����Ƃ����䂩��
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�Ɂu���ݒn�ƑO��̍��ځv���\������Ă��܂��D���ꂪ�T�u���j���[�ɂȂ��Ă��܂��̂ŁC�P�O�̃y�[�W�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�_�ƌX���������̕������ɂ��ā^22.09.13�n
�ƂĂ��ʔ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����ɍ������Ȃ��`�ւ̕ό`�ɂ��ā^22.09.13�n
�o��̎d�����w���v�����ɂ킩��₷���ł�
���ɂ͓��ɊW����܂������������Ă�������S�Ă̖��������I������ۂ̃A�j���[�V���������`�x�[�V�����ɂȂ�܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^22.09.12�n
���𑝂₵�Ă����Ɨǂ��Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D������₵�܂���
���m�ʂ̕ł���̎���ɑ���n[��ʍ��̋L���ɂ��ā^22.09.07�n
������ƑO�̃y�[�W�ł͑S�p�����ł�OK�������̂ŁA������ł�OK���Ǝv�����͂����Ƃ���A�ԈႢ�ɂȂ��Ă��܂��܂����B��{�I�ɂ͐����͔��p�œ��͂��Ȃ���Ȃ�Ȃ������̂ł��ˁB�B�B
�����m��ҁn�F�A�����肪�Ƃ��DInternet Explorer�̑S�����i2000�`2005�̍��j�́C�ǎ҂̉�ʂ������ϊ����[�h�ɂȂ��Ă���C����������I�ɊO���Ƃ����R�}���h��g�ݍ��ނ��Ƃ��ł��܂������C�������̃R�}���h�͎g���Ȃ��D
�@���āC�S�p�����́u�����v�ł͂Ȃ��u�����v���Ƃ������Ƃ́C�����w�Z�ōŏ���9�N�ԏK���͂��ł����C���l����͂���Ƃ��ɑS�p�����œ��͂��鎙�����k������ꍇ�ɁC���̂Q�̗���̂����ꂩ�őΉ����Ȃ���Ȃ�Ȃ��Ȃ�܂��D(1) 2�x�ƊԈႤ���Ƃ��Ȃ��悤�Ɂu����������v�@(2) Microsoft Excel�œ��͂���Ƃ��̂悤�ɁC�s�p�ӂɑS�p�����œ��͂����Ƃ��́C�\�t�g�I�ɏ���ɏ��������Ĕ��p�����ɂ��āC���i�ɂ��Ă��܂��D
�@�q���̐��������Ƃ���(1)�̗���ł�����čs�����悤�ł����C���q����̎���i���̂����Ƃ͌���Ȃ��H�j���}���C(2)�̗���ɗ����āC����ɓ��Ă����������āC���}���Ă��̂������̐���������ł���悤�ł��D���̗���ɗ����āC�S�p���������͂��ꂽ��C����ɔ��p�����ɏ��������Ă��܂��v���O������g�ݍ���ł��܂����C������20�N�ȏ�O�ɍ쐬�����[��������C�S�����������ł��Ă���Ƃ͌���Ȃ��Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̍��ɂ��ā^22.09.07�n
�O���t�\���̐F�ݒ�ɂ��Ăł��B���̃f�B�X�v���C�̐ݒ�̂����Ȃ̂�������Ȃ��̂ł����A�F�����邷���邽�߂���ڂ��`�J�`�J���Ă��Ă��܂��A�ڐ���𐔂���̂��h���Ȃ��Ă��܂��܂����B�N�̂�����������܂���E�E�E�B�u���F�̂悤�Ȋ����Ɍ����Ă��܂��̂ł����A���������瑤�Ńf�B�X�v���C�ݒ��ς��邱�ƂőΉ��ł��邩�������ł����狳���Ă������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D(1)�e���̃p�\�R���ɂ���ĈႢ�܂����C��ʂ̊O�ɖ��邳���u+�F��������v�u�|�F��������v�̃{�^�����t���Ă�Ƃ��́C�����2�C3���Β����ł��܂��D����ɁC�\�t�g�I��0������100���܂Ŗ��邳�����邱�Ƃ��ł��܂��D(2)�R���g���X�g���ア�ƌ����Ȃ��l������̃R���g���X�g�������ƌ�����l�������邪�C����l��������D�������l�̊������i���j�o�[�T���f�U�C���j�́C�|�����C�ڕW�Ƃ��Ă͂悢�b�ł����C�B���ł���̂��Ƃ����ƁC�Ȃ��Ȃ�������ƂɂȂ�܂��D
�@�ꉞ�C�R���g���X�g�������܂������C������𗧂Ă�����炪�����Ȃ��W�ł��̂ť��
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̒�`�C�傫���C�����ɂ��ā^22.09.07�n
�����ƕ����̂悤�ȁA�p��̉��������̂��ƂĂ��悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނł́C�����ƕ�������ʂ��鍂�Z���ȏ��̑������Ő������܂������C��w���ȏ��ł͂��̋�ʂ����Ȃ����������܂��i�����ƌ������Ӗ��Ɏg���j�̂ŁC�����ꂽ��������ǂݎ��K�v������܂��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.09.06�n
�S�Ă̋������c���[�Ɍ���邱�Ƃ͎����Ȃ̂ŁA������A����~2�Ȃǂ��āA�����ɂ��Ė߂��Ȃǂ̍�Ƃłł���̂ł͂Ȃ����B�i������ɂ̓A�C�f�A�͂��邪�A���s�ł��Ȃ� �j
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.09.05�n
�R���b�c�̗\�z
�R���b�c�̗\�z �F�@�C�ӂ�0�łȂ����R�� a ���Ƃ�Aa �������Ȃ��ɂȂ�܂�2�Ŋ���B
a����Ȃ�3�{���ĂP�𑫂��B�@������J��Ԃ��ƗL����łP�ɓ��B����B�@
1 �ɓ��B����ƁA1��4��2��1 ���J��Ԃ��B
�h�P�h��ڎw�����̕��т����܂��B
1
��
5 �� 21 �� 85 �� 341 �� 1365 �� 5461�� 21845 ⇐
�� �� �� �� ��
�� �� 227 �� 909 ⇐ �� 14563 ⇐
�� �� �� �� ⇧
�� �� 151 �� 605 ⇐ 7281 �� 29125 ⇐
�� �� �� ⇧ ⇧
�� �� 201 �� 805 �� 3221 �� 12885 ⇐
�� �� ⇧ ⇧
�� �@�@�@ �@113�� 453 �� 1813 �� 7253 �� 29013 ⇐�@�@�@�@�@�@�@�@
�� ⇧ ⇧ ⇧
3 �� 13 �� 53 �� 213 �� 853 �� 3413 �� 13653 ⇐
�� ⇧ ⇧ ⇧
17 �� 69 �� 277 �� 1109 ��4437 �� 17749 ⇐
�� ⇧ ⇧ ⇧
11 �� 45 �� 181 �� 725 ��2901 �� 11605 ⇐
�� ⇧ ⇧ ⇧
7 �� 29 �� 117 �� 469 �� 1877 �� 7509 ⇐
�� ⇧ ⇧ ⇧
9 �� 37 �� 149 �� 591 �� 2389 �� 9557 ⇐
�� �� ⇧ ⇧
�� 99 �� 397 �� 1589 �� 6457 ⇐
�� ⇧ ⇧
49 �� 197 �� 789 �� 3157 �� 12629 ⇐
⇧ ⇧ ⇧ ⇧
��̐��̕��т����܂��B
�@�P�@( 3 x 3 ) + 1 = 10 ���@10 / 2 = 5 ���ŏ��ł��B�R���b�c�̑���� 3�́A���� 5 �ɐi�݂܂��B
�@�@�@( 5 x 3 ) + 1 = 16 ���@16 / 24 = 1 �� 3 �� 5 �́A1 �ɒB���܂��B 1 �́A 3 �� 4 �� 2 �� 1 �Ō��ɖ߂�܂��B
�@�@�@����1 �A 5 �A3 �̕��тɁA�������̔z�u�����܂�( ⇪ ��́A�X�ɑ����ʒu�������Ă��܂��B)�B�@�@
�@�Q�@�}�̊e��a�́A3�{����1�������i3a+1�j�A��ɂȂ�܂�2�Ŋ���ƁA��� (��) �ɉ����ĂЂƂ�̐��A
�@�@�@���͉��ɐi��ō��[�̂ЂƂ�̐��ɐi�݂܂��B
�@�R�@��a�̉E�ɂ́A1 �������� �i4a+1�j�������܂��B3�{����1�������A��ɂȂ�܂�2�Ŋ���ƁA�S�č��[
�@�@�@�̐��̂ЂƂ�̐��ɐi�݂܂��B������̐���菬�������ł��B
�@�S�@��a��n�����R���Ƃ��āi3n+1�j�̏ꍇ�́A�i4a-1)/3�����ɑ����A���̐����傫�����ɂȂ�܂��B
�@�T�@��a�� �i3n+2�j�̏ꍇ�́A�i2a-1)/3�����ɑ����A���̐���菬�������ɂȂ�܂��B
�@�U�@��a�� �i3n�j�̏ꍇ�́A���ɕt�����͂���܂���B�e�c��́A(3n) �̐��ɒB���ďI���܂��B
�@�V�@�e�c��́A�i3n+1�j�܂��́i3n+2�j�Ŏn�܂�A�E�� �i3n+2�j�A�i3n�j�A�i3n+1�j�̌J��Ԃ��������܂��B�@
�@�W�@���[������e�c��́A�i3n+1�j�Ŏn�܂�A���ꂼ��E�Ɂi3n+2�j�A�i3n�j�A�i3n+1�j�̏��ɌJ��Ԃ���
�����܂��B���[�́i3n�j�ŁA�E�Ɂi3n+1�j�A�i3n+2�j�A�i3n�j�̏��ɌJ��Ԃ��������܂��B
�@�@�@�E�� �i3n+1�j �̐�����A�܂��c���ɐL�тĂ����܂��B
�@�X�@�C�ӂ̐�a��n�����R���Ƃ��āi4n+1�j�̏ꍇ�́A����Ŏ��g��菬�������ɐi�݂܂��B
�P�O�@�C�ӂ̐�a��n�����R���Ƃ��āi4n+3�j�̏ꍇ�́A(4a+1)�̍��Ɉʒu���A(4a+1) ��菬�������ɐi�݂܂��B
�P�P�@�S�i�����g���A�z�u��������Ղ���������鎖��t�������܂��B�@
�@
�R���b�c�̗\�z���x�����܂��B
T.Maeda (220627�n�`�����)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[����ʥ���Ǝ��ɂ��ā^22.09.03�n
�y�Z���^�[����2017�N�x ���w�T�EA ��P��z�́i�E�j�̖₢�Ɋւ��Ă̋^��ł��B����ł͍��ӂ��@X�̂R��{�W/X��3��@�ɂȂ��Ă��܂����A�₢�ł͍��ӂ��@X�̂R��{�Q/X��3��@�ɂȂ��Ă��܂��B�����ǂƂ���A�₢�̕����Ԉ���Ă���悤�Ɏv���܂��B���̃T�C�g�ł��@X�̂R��{�W/X��3��@�ł����B����͖₢���Ԉ���Ă���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���̕��ɓ��̓~�X������܂����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.08.31�n
���R�i�R�j�Ɓi�S�j�̈Ⴂ���킩��܂���B
���Ɂ|�Q���i�R�j�ł́�b�ƂȂ�̂Ɂi�S�j�ł͌W���ɂȂ�̂��킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D
���������킩��͂��ł���
(3)
(x^2-2\times x%2B 2^2)=x^3%2B 2^3&chf=bg,s,fff9f9)
←���ꂪ���
(x^2-2\times 2\times x%2B 2^2)&chf=bg,s,fff9f9)
��

�ɂȂ�Ȃ�
(4)
(x^2-1\times x%2B 1^2)=x^3%2B 1^3&chf=bg,s,fff9f9)
(x^2-2\times 1\times x%2B 1^2)&chf=bg,s,fff9f9)
��

�ɂȂ�Ȃ�←���ꂪ���
��8�E���̗�A�ォ��4�s�ځA�|2nrn�|n(n+1)rn+n(n+1)rn+1�Ƃ���܂����A�|2nrn�|n(n+3)rn+n(n+1)rn+1���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̓��Ă̂܂܂ō����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����藝,�]���藝�i����,�Z���^�[���j�ɂ��ā^22.08.31�n
2021�N�x�̋��e�@���2�A����2�̃j�ɂ��āA���Ԉ���Ă��܂����̂ŘA�������Ă��������܂��B�����͇@���Ǝv���܂��A���}�Ȋm�F�A���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̍��������ɂ��ā^22.08.31�n
���⎸�炵�܂��B���Ԃ̂��鎞�ɂ����Ē����Ă��܂��B���Z����S��������Ȃ����������R�c�R�c����Ă���ƂȂ�ƂȂ������o���A�����ꕔ�ł͂���܂����A������l�ɂȂ��ė��܂����B���肪�Ƃ��������܂��B���āA�O�p���̍��������̖��5�̎����Đ}�ł����A���4�̃R�s�[�̗l�ȋC�����܂�?�Ԉ���Ă�����݂܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�I�b�g�b�g�C������R�s�y�ɂȂ��Ă��܂����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̓�������ɂ��ā^22.08.28�n
���6�Ԃ̉�2n�܂ł̘a�Ōv�Z����Ă��āA���Ɠ������قȂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��Dn+1����3n�܂łō�����2n���ɂȂ�܂�
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̓�������ɂ��ā^22.08.28�n
���6�Ԃ̉�2n�܂ł̘a�Ōv�Z����Ă��āA���Ɠ������قȂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��Dn+1����3n�܂łō�����2n���ɂȂ�܂�
���m�ʂ̕ł���̎���ɑ���n[ 3n+1���i�R���b�c�\�z�j�ɂ��ā^22.08.27�n
�Ō�̊ȒP�Ȗv�Z�̎��̓����͂P���Ǝv���̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�w���@�ɂȂ��Ă��āC���ĂP�ɂȂ�͖̂������Ə����Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[�������i�L�����j�̕s��ϕ��ɂ��ā^22.08.25�n
��ԏ�̗��́i�A�j�̂Q�ڂ̕ό`�̂��̎w���� -2�{1 �ł͂Ȃ��A -2 �ł͂Ȃ��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^22.08.23�n
������₷���ĂƂĂ��𗧂��Ă��܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^22.08.22�n
(5)�̍��ӂ�log�̍��ɂ��Ă�����̂�log�̌W���ł��傤���H����Ƃ�log2x���w���Ȃ̂ł��傤���B�����炭��������͌v�Z�������Ă킩����̂��Ǝv���̂ł����A���̓��O�Ɋ���Ă��Ȃ��̂ł킩��܂���c
�����m��ҁn�F�A�����肪�Ƃ��D�w�����ΐ��ɂȂ��Ă�����̂́C
���̂[�W�ɂ܂Ƃ߂Ă���܂��D
�Ō�̖�肩��I������I�Ԗ��ŁA�����i�߂Ă݂���Ay=-1/2x��x-y=2���c���āA�I��ł��ԈႢ�ɂȂ�܂��B�o�O�������璼���Ă��������Ȃ��ł��傤���B���˂������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D6����1�̊m���ŁCx-y=2��2��o�ꂷ��悤�Ȃ̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^22.08.18�n
�u�j���ɂ��Ⴆ�v�������ĕ�����₷���ł��I
���肪�Ƃ��������܂�!
�����m��ҁn�F�A�����肪�Ƃ��D���Ɛ��N��ɂ́C���̂悤�ȗႦ�͎g���Ȃ��Ȃ邩������܂�����̂Ƃ���CWeb���ނ�����X���X���ŃZ�[�t�ł����C�ǂ��炩�Ɍ��߂����Ȃ��l�����邩������Ȃ��̂ŁC�l�̐��ʁC���ЂȂǂ̑����Ɋւ���b��́C���Ɏg����Ⴊ�Ȃ��Ƃ��ȊO�͐G��Ȃ������ǂ��悤�ł��D�i���Ԃ�C���ȏ��ł́C�����Ȃ��ł��傤�j
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̕��s�����C���������ɂ��ā^22.08.18�n
3�Ԃ̖��̂悤�ȕ��͕K��x�̕��Ōv�Z���Ȃ���Ȃ�Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D3�ԂƂ͉��̂��ƂȂ̂�������܂���̂ŁC2�̏ꍇ�ɕ����Ď����܂��D3�Ԃ���3��\���ꍇ�C�ux�����߂�v�Ƃ�����肾����x���v�Z����͓̂��R�ł��D3�Ԃ����3��\���ꍇ�C��������0�̃x�N�g���Ƃ̓��ς�����Cx�����������c��͓̂��R�ł��D
���m��㌧�^�n���ł͂���܂���^22.08.13�n
https://www.geisya.or.jp/~mwm48961/koukou/s12jg502.htm
�̖�肪�S10��Ə����Ă���܂����A8��ŏI����Ă��܂��܂��B���w���̐��w���W���Ƃ���lj����Ăق����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D8��ɂ��܂����D���w���̎Z���͈����܂���D�����I�����̗��ꂩ��C���s�̘b��͈����Ă��܂��C�o�J���Y���̃t�@���ł��邱�Ƃ��炢�͏����Ă�����Ă����Ȃ��ł��D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^22.08.11�n
�������p�����Ē����Ă���܂��B
�~�̕�����3�y���1-2�z�ɂ�����
�u���������̕ό`���s���ƁC(x�|1)2+(y�|2)2=13�ɂȂ邩��C
�@���S�̍��W��(1, 2)�Ŕ��a���h��10�h�̉~�E�E�E�i���j�v
�ƂȂ��Ă���܂����A�����́h��13�h�ł͂Ȃ����Ǝv���܂��B
���m�F�̒��A�X�������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���f���̂P���������\���}�`�ɂ��ā^22.08.09�n
���Q�̉���������̂ł����A�Ȃ����̂悤�ɂ���p,q,r �̐�������܂�̂���������܂���B���ɒ��ڂ��Ă���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���̖�肾��������̂ł͂Ȃ��C���̃y�[�W�̑O���珇�ɂ݂Ă��������D
���m�ʂ̕ł���̎���ɑ���n[N�i���̏����ɂ��ā^22.08.08�n
�킩��₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ލ����^�ׂ傤�͂��������炳��^22.08.08�n
���w�̃C�I�����Ƃ�mol�Ƃ��̌v�Z��g�����E���q���E�Ƃ��̖����ق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���Z���w�͂������\�N������Ă��܂���D���@���w�͒�^�I�Ȗ��������Ă�����W���u1���Ԃ��v�Ƃ��������̕��ʂ̏����ɂȂ�C�L�@���w�͍\����}�ɕ`���Ƃ�����Ƃ����Ȃ���o�肳��������Ă����Ƃ�����ƂɂȂ邩�ȁD�g�����h�Ȗ��W������͂��ł��D
���m�F�{���^�ʁf�G�k����^22.08.07�n
����A��苤�ɂƂĂ�������₷���A�f���炵���T�C�g���Ǝv���܂��B�������̕��������Ői�߂Ă���̂ł����A�I�[�i�[�l�͍��ケ�̃T�C�g�̕����ł̂悤�ȃT�C�g������邲�\��͂���܂��H�������̃T�C�g�̕����ł�������Њ��p�������ł��B�܂����̃T�C�g�̂悤�ȕ������T�C�g�����ɂ���̂ł���A�I�X�X���̃T�C�g�������Ă���������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��X�̏K�������Z�����́C���ȏ����g�킸�ɁC�K�v�ɉ����Ĕ��ς̌����������Ȃ���s�����̂������̂ŁC���݂̋���ے��̂����ƍ����܂���D�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̋Ɍ��ɂ��ā^22.08.06�n
����x���W��y���W��Ή������A�O���t��p���čl����_�����܂܂ł����ƕ�����Ȃ������̂ł����A���̕ł�ǂ�ŗ������邱�Ƃ��ł��܂����I���肪�Ƃ��������܂��B
�܂��A�쐬�ɂ��Ď���Ȃ̂ł����A���̃O���t��p���Ď��ۂ̓��Ă������Ƃ������Ƃ͏o���Ȃ��̂ł��傤���H�L�q���̉ł͂�͂��̂悤�ɕ��������g���ď����Ȃ�������Ȃ��̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�҂̈Ӑ}���ǂ��ł����Ă��C�قƂ�ǂ̍̓_�҂͕K�v�����͖�������Ă��邪�\������������Ă��Ȃ��Ƃ��Č��_����ł��傤�D���Ȃ킿�C��������Ƃ���C�����������Ƃ��Ă̖����������̉������Ȃ����Ƃ͎����邪�C���ۂɂ��̒l�Ɏ������邱�Ƃ�������Ă��Ȃ��Ƃ���,�����ȉ��̓��_�ɂ���ł��傤�D��͂�C�������铙�䐔��Ƃ̔�r�͕K�v�ł��D
���m�ʂ̕ł���̎���ɑ���n[�A���P���������̉������i�܂Ƃ߁j�ɂ��ā^22.08.04�n
��C3��D3�̖��̍����̕������s��ɂ��čs�����߂�]���q�W�J�ŁA45�ɂȂ闝�R���킩��Ȃ��̂ł��̃X�e�b�v�������Ă��������B�Ȃ�������115�ɂȂ��Ă��܂��܂� (������̂��Ƃł�)
︳2 3 6 -2 ︳
︳1 4 -2 4 ︳
︳4 1 7 5 ︳
︳3 7 3 2 ︳
�����m��ҁn�F�A�����肪�Ƃ��D�s�̒l���v�Z����ɂ́C(A)
�]���q�W�J�ɂ����@�C(B)
�s�̊�{�����Ȃǂ��m���ɐg�ɕt����K�v������܂��D�i�Ȃ��C�R�������s��̏ꍇ�́C�T���X�m�T�����n�̕��@������j
�@���̕������ʂ��ԈႦ�Ă���ꍇ�́C�������Ă��C�����܂��i3�s4��̕������t�j�C→���̏ꍇ�ł�95�ɂȂ�D
(A)

��1��ɉ����ēW�J�����




3���̍s�ɓW�J���T���X�i�T�����j�̕��@�ōs���ƁC
2×6−(−43)+4×20−3×30=45
(B) �s��{�ό`�ŁC�P�̗�̐����łȂ�ׂ�������0�����i�����ł�1��ڂ�2�s�����āC1�s�C3�s�C4�s��1��ڂ̌W����0�ɂ��邱�Ƃ��l����j

→1�s−2�s�~2�C3�s−2�s�~4�C4�s−2�s�~3

→1��ڂɉ����ēW�J����→

→1�s�ڂ�5�ł�����C2�s�ڂ�3�ł�����→

→2�s−1�s�~5,3�s−1�s�~(−2)→

→1��ڂɉ����ēW�J����→

���ň�x���̖��ɐi��ł��܂��Ƃ��̑O�ɉ������������������Ƃ��o���Ȃ��č���܂����B��������̖�肪�����_���ʼn�����V�X�e���͂ƂĂ��ǂ������̂ŁA��������肪���ɕ\�������悤�ɂȂ�A�Ȃǂ��Ă���������ƂƂ��Ă����肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.08.04�n
������₷���ĂƂĂ��ǂ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�����_���W���`�ɂ��ā^22.07.26�n
���2.3.3 �E�������炢�ŁA
☓ x2=t[2,-1,0]
☓ x3=t[1,0,1]
�� x2=t[2,1,0]
�� x3=t[1,1,-1]
�ȍ~�͐������ł��B
�ׂ��������܂ŗᎦ����Ă�����ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X2�ӏ��������܂���
���m�ʂ̕ł���̎���ɑ���n[�s���Ίp������ɂ��ɂ��ā^22.07.26�n
���2�i3�j��
4 1 4 5
1 -1 �ƂȂ��Ă��邪�A�������� 1 -1 �ł͂Ȃ����B
���̖��ɂ����āA�����̉E�������A
6�E7���ł͂Ȃ��A5�E7���i��:n��j�Ǝv����
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X2�ӏ��������܂���
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^22.07.25�n
�y���������C�����悩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A�������̐��ɂ��ā^22.07.24�n
���̉́A�ǂ��ɒ���Ă��܂���
�����m��ҁn�F�A�����肪�Ƃ��D�S����̏ꍇ�C�i���ꂪ����������j������o�Ȃ��ݒ�ɂȂ��Ă��܂������C�����̏ꍇ�ł�������o��悤�ɂ��܂����D
���m�ʂ̕ł���̎���ɑ���n[�����^�̕������ɂ��ā^22.07.24�n
�ƂĂ��킩��₷���A���̂������Ő����藝�������ł��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̐��ɂ��ā^22.07.23�n
�ƂĂ��Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�]�u�s��C�Ώ̍s��C�Ίp�s��C�O�p�s���ɂ��ā^22.07.20�n
(tA)^2�������ł���Ƃ�A�������ł��闝�R�������Ă������������ł��B🥺
�����m��ҁn�F�A�����肪�Ƃ��D�قڑ����\�̈�����ɂ���Ƃ��������ł����C���ꂪ�A�ɂ����Ĉ��ݍ��݂ɂ����̂́C�c�Ɖ����t�ɂ��Ă��s�̒l���������Ƃ������ƥ�����̃y�[�W��(5)���g���Ă��Ȃ����炩�ȁH
���̃y�[�W�́Z4 (a)(b)�������
=det(A)&chf=bg,s,fff9f9)
���(a)
=det(A)det(B)&chf=bg,s,fff9f9)
���(b)
������
^2\}\ne 0&chf=bg,s,fff9f9)
�Ȃ��(b)�ɂ��
\ne 0&chf=bg,s,fff9f9)
�C�����(a)�ɂ��
\ne 0&chf=bg,s,fff9f9)
�����藧�D
���5�̐}�͔��ł͂Ȃ��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�Ɂu���f��G�F�ނ����������㩁v�̘b�������Ă���܂����C���Ȃ��́C����㩂ɂ͂܂��Ă��܂��H�u�Q�̉ʕ���3�̔��ɓ����v�̂ł͂Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�����̏ؖ��j�ɂ��ā^22.07.16�n
���1�̂���k�{1�́A�Ȃ�A�ɂȂ�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D��������琬�藧����ł��D(A)�Ƃ������́u�������̌`�v���Œ肵�Ă��܂�����ϐ���p�����㐔�̋c�_�ɂȂ�܂���D�F������D���̎����\���Ă�����e������̂ł��D
&chf=bg,s,fff9f9)
���(#1)
&chf=bg,s,fff9f9)
���(#2)
=\frac{1}{2}(k%2B 1)(k%2B 2)&chf=bg,s,fff9f9)
���(#3)
=\frac{1}{2}(k-1)k&chf=bg,s,fff9f9)
���(#4)
(#2)�����藧�Ƃ��C(#1)��
n=k�̂Ƃ������藧�D
(#3)�����藧�Ƃ��C(#1)��
n=k+1�̂Ƃ������藧�D
(#4)�����藧�Ƃ��C(#1)��
n=k−1�̂Ƃ������藧�D
�Ō�ɉ��p�����o�����ق����ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D�͂��߂Ɂu���p�I�ȓ��e�����҂������́C���̃y�[�W�����Ă��������D�v�Ə����Ă���܂����C���w�T�̒i�K�ł̎w���@���̉��p���́C�������̓W�J�ł��D��������C���p������������C���̃y�[�W�ɐi�߂悢�̂ł��D�ʂ̌�����������C���̃y�[�W�͒��w�Z�̕��K�ŁC�{������Ȃ����ڂł����C�������̓W�J�̏����Ƃ��āu�w���@����Y��Ă��܂����l�����K���邽�߂̃y�[�W�v�ł��D������̎w���C�����̎w���Ȃǂ͐��w�U�̓��e�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̒u���ϕ��@�ɂ��ā^22.07.15�n
���m�ʂ̕ł���̎���ɑ���n[�s��̌v�Z�ɂ��ā^22.07.10�n
�s���p���ĎO�p���̉��@�藝���ȒP�ɓ��o�ł���炵���̂ł����A
�s��̐ς̌�����p���Ă��A�E��i1�C2�j�ƍ����i2�C1�j���t�ɂȂ��Ă��܂��ĉ����܂���B
�����Ă������������ł��B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��Dxy���W�n���Œ肳��Ă��āC���̍��W���_(x,y)����_(x', y')�Ɍ��_�̂܂��Ɋp�Ƃ�����]�ړ�����Ƃ��̊W���́C
���̃y�[�W�ʼn�����Ă��܂��D
 ���(#1)
���(#1)
�Ȃ��C�����ړ������ɁCxy���W�n�����_�̂܂��Ɋp�Ƃ�����]����Ƃ��́C���ʓI�ɕ������_�̂܂��Ɋp−�Ƃ�����]�ړ����������ƂɂȂ�D
%26 -\sin(-\theta)\\ \sin(-\theta)%26 \cos(-\theta)\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}&chf=bg,s,fff9f9)
 ���(#2)
���(#2)
���Ԃ�C������̉��@�藝��(#1)�̂��Ƃ��ƍl������D
�@���_�̎���Ɋp��������]�ړ����Ă���C����Ɋp��������]�ړ�����ꎟ�ϊ��̍s��́C


�@���_�̎���Ɋp��+��������]����ꎟ�ϊ��̍s���
%26 -\sin(\alpha%2B\beta)\\ \sin(\alpha%2B\beta)%26 \cos(\alpha%2B\beta)\end{pmatrix}&chf=bg,s,fff9f9)
�@����炪�C��v����͂�������
=\cos\alpha\cos\beta-\sin\alpha\sin\beta&chf=bg,s,fff9f9)
=\sin\alpha\cos\beta%2B\cos\alpha\sin\beta&chf=bg,s,fff9f9)
�ƂĂ��킩��₷��������肪�Ƃ��������܂���
�lj����̓������킹��̓_���o����͖̂{���ɏ�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̏d�S,���S,�O�S,���S�ɂ��ā^22.07.09�n
�f���炵���ł��B�_A���_O�ɂȂ�Ƃ����t��������Ƃ������ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��DO���O�S�Ȃ�`�Ɉ�v���邱�Ƃ͂Ȃ��C���_�Ȃ��

�Ƃ���Β����ɂł���̂ŁC�ʓr�������ƂɈӖ�������Ƃ͍l�����Ȃ��D
��S�ł����A�u2)�̂悤�ɒP�������i�����j�łȂ������̂����Ԃ�p���ĕϊ�����͕̂s�C���ł��邪�v�Z�͈�v����B�v�Ƃ���܂����A��Ԃ͒P�������i�����j�łȂ��Ƃ����Ȃ��ƏK���܂������B����
�|����2�ł͓���������Ă���Ǝv����ł����B
�����V�U�̕S���ŁA��Ő��w���y����ł���҂ł��B�w�E���Ԉ���Ă����炷�݂܂���B���w��
��������K���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�茳�ɂ��鐔�w�V�̋��ȏ��iK�ЁCD�ЁCT�ЁCS�Ёj�Łu�ϐ��ϊ��͒P���ȋ�Ԃōs��Ȃ���Ȃ�Ȃ��v�Ə����Ă�����̂́C�P������܂���D��ϕ��͌��n���ɏ�[�̒l�C���[�̒l�������Ĉ��������́i�萔�j�Ȃ̂ŁC�l����������Β�ϕ��͓��������ƂɂȂ�܂��D
,\hspace{2}a=g(\alpha),\hspace{2}b=g(\beta)&chf=bg,s,fff9f9)
�̂Ƃ�
dx=\underset{\small{\alpha}}{\int^{\beta}}f(g(t))g^{\tiny{\prime}}(t)dt&chf=bg,s,fff9f9)
�߂��Ⴍ�����肠���Ė��W�Ȃ��g���炷��Ƃ��肪�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��������(��{)�ɂ��ā^22.07.06�n
�S�R������Ȃ������̂ŁA������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̒�`�ɂ��ā^22.07.06�n
���ʂ̌v�Z�őΐ�(log)���g�p���Ă���A�ΐ��̃T�C�g�������Ă��Ă��̃T�C�g�ɍs�������܂����B
������K���Ȃǂ����蕪����₷�������ł��B
����ɂ�������log[2]3=1.584...�ł����Alog[2]3���ǂ̂悤�Ɍv�Z���Ă�����1.584..�����߂���̂�����̓I�ɋ����Ă������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D

�̌v�Z�́u��̕ϊ������v���g���Čv�Z���܂��D
��12�ʼn��Ő�̓z�ł���C���o�Ă�����ł����H
���ڂőI�Ԏ��͕��ʂ�P�ŁA2��ڂł��ジ�̖@���g���Ή��Ƃ��Ȃ��Ȃ���ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�e���Ŕ[�����₷�����W�b�N��I�ׂ悢�ł��傤�D�Ⴆ�C�u�������̂��܂܂��Ƃ��̏���v�̑����́C�ǂ̋��ȏ��ł��u�g�����v�Ő������܂�����ԍ��D�̂��炢���ɒ���������C���̋��ނł́u����v�Ő������邱�Ƃ������ł��D�����镨�̕����[�����₷�����k�������D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����̗��K����ɂ��ā^22.07.03�n
�e�X�g���O�ŏł��Ă��̂ŏ�����܂����I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ����̃O���t�ɂ��ā^22.07.02�n
����Ȃ�ł������3��1���^�ɂȂ��Ɖ������Ƃ͂ł��Ȃ��ł���ˁH
�����m��ҁn�F�A�����肪�Ƃ��D����͌��ʘ_�ɉ߂��Ȃ��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƌW���̕����ɂ��ā^22.06.30�n
b^2-4ac�̕����̏��̕���������s��b/a�̌�Ax�������Ă���C�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^22.06.29�n
�������ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����̗L�����ɂ��ā^22.06.29�n
���������ȒP�ɏڂ��������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�ۂ��O�p�C���������C�F������Ȃǂ͂ǂ����߂��Ă悢�̂����C����ł��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^22.06.28�n
���K��肪���������Čo���l�������ŏオ��܂����I���肪�Ƃ��������܂��B�����悩������ł����̂ł����A�ł̍Ō�ɂ܂Ƃ߂̖��̂悤�Ȗ���10��قǏo���Ă������������Ǝv���܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^22.06.28�n
�������킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^22.06.27�n
��b�I�Ȋm�F�ɂȂ�ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^22.06.27�n
�킩��₷���A�Q�l�ɂȂ�܂����B���肪�Ƃ������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉��ƌW���̊W�ɂ��ā^22.06.27�n
�F�̉e�����A�����ǂ݂ɂ��������ł��B
���e�͑f���炵���ł��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^22.06.27�n
���x�A�����b�ɂȂ��Ă܂��B
�ԈႢ���ЂƂw�E�����Ă��������܂��B
�u�������ɂ��W�J�y���2.8�z�̓����́Aa��4���2��@�ł��B
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~�ƒ����̈ʒu�W�ɂ��ā^22.06.26�n
�����g���ĕ�����₷���������Ă��āA���ɏ�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̐��������ɂ��ā^22.06.25�n
�킩��₷������ɂ������ӂ��Ă��܂��B
�w�E���炢�����܂��B
(B)�����}�`���g�����@�@�ŁA
(1)(2)(3)��������Ɓ@�̉�
(1+m^2)+(1+m'^2)=(m-m')^2�ł����Ă��܂��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�u(A)�O�����̒藝���g�����@�v�ł͂��̘b���o�Ă��܂����C�u(B)�����}�`���g�����@�v�ł͂��̘b�͏o�Ă��܂���H
���m�ʂ̕ł���̎���ɑ���n[�s�����Ɨ̈��ɂ��ā^22.06.25�n
���s�����Ȃ��̂œǂ݂ɂ��������ł��B
�����m��ҁn�F�Ӗ��s���ł��D���s���i�s�Ԃ̊W�j�̂��ƂȂ̂���s�������̂��ƂȂ̂��H������̏ꍇ�ł��C�ύX�̗\��͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^22.06.25�n
�u��Ԃƒ����v�ɂ��čl���Ă��鎞�ɔq�ǂ����Ă��������܂����B
�ǂ�ł��Ĉ�ۓI�������̂��A���t�Ɛ����ƃC���X�g�̃o�����X�̗ǂ����f���炵���Ǝv���܂����B
�i�����̗����̂��߂̃C���X�g��C���[�W�̏d�v���ɉ��߂ċC�Â��܂����j
���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������i���K�j�ɂ��ā^22.06.24�n
���ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2���Ȑ��̋ɕ������Ɣ}��ϐ��\���ɂ��ā^22.06.23�n
���T�́i�Q�j�A�O�p���̍����~�X���Ă܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[����̋Ɍ��ɂ��ā^22.06.23�n
�Q�����̋Ɍ��͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����̋Ɍ�(����)�Ƃ������ڂ����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�ɕ������ɂ��ā^22.06.21�n
���R�̉�����Q�ڂ̑I�����́Axy=2�@�̊ԈႢ�ł���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D

�̉����ǂ�ł��炤�ƁC

�ł悢�Ƃ������Ƃ�������܂��D
20����9�̏z������m�肽���ł�
�����m��ҁn�F�A�����肪�Ƃ��D�ʂɌ������Ă���킯�ł͂Ȃ����C���̃y�[�W��ǂl����C���̃��x���̎��₪�o�Ă��邱�Ƃ������ł��D
�P��0.9999����ł��D���l�ɂ��āC�Q��1.99999����ł��D������C9/20=0.45=0.44999���
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.06.19�n
��2-2�ɂ��Ď��₪����܂��B
�萔����4y^{2}-3�Ƃ���܂����A�����4y^{2}�Ƃ����萔����-3�Ƃ����萔����2������ł���̂ł����H����Ƃ����ڂ����������܂܂Ȃ����͐��Ɠ��l�Ɉ������߁A4y^{2}-3�Ƃ���1�̒萔���ɂȂ�̂ł����H�܂��A�萔���̌W���͂��̐����́A������0�Ƃ���܂����A�萔��4y^{2}-3�̌W���Ǝ��������߂�Ƃ����牽�ɂȂ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D(4y^{2}-3)�Ƃ���1�̒萔���ł��D�������������Ȃ��ƕs�����Ƃ���搶�����邪�C�M�҂͂Ȃ��Ă�������Ƃ�������ō̓_����D4y^{2}-3�̌W����(4y^{2}-3)�C������0
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^22.06.18�n
�����Ă������������̂ł���
(a/b)>(c/d)����(e/f)>(g/h)�̂Ƃ�
(a+e)/(b+f)>(c+g)/(d+h)
�͐��藧�ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D��������Ă݂āC��������ȂƎv������C�ؖ��ł��Ȃ����Ƃ������F������������Ƃɐ�ւ��Ă��悢�D
(1) �܂��C�����̒��ɕ��̐����܂܂�Ă���C���藧���Ȃ���́C�ȒP�ɍ���D

�̂Ƃ�

�ł��邪

�ƂȂ邩��C�ؖ����������͐��藧���Ȃ��D
�@�@���ɁC�����͂��ׂĐ��̐��ł���ꍇ

�̂Ƃ�

�ł��邪

�ƂȂ邩��C�ؖ����������͐��藧���Ȃ��D
�@�ȏ�ɂ��C���藧���Ȃ�.
������̃T�C�g�͏����������̂ł����A���̒��F�̎��ŏ����Ă���|�C���g��������A�Ō�̌����ߌ`���̖��Ŋw�K�ł�����A�������킩��₷���Ă悩�����ł��B
���邾���Ŗ������Ă��܂����Ƃ������̂ŁA�����߂̖��͎��ɂƂ��ď����n�[�h�����Ⴍ�Ď��g�݂₷�������ł��B�܂������b�ɂȂ邩�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̐}�`�։��p�ɂ��ā^22.06.17�n
���S�́i4�j�̉�����o�ė��Ȃ��̂ł���......
�����m��ҁn�F���̂悤�Ȃ��Ƃ͂���܂���D���������āu����v�Ƃ����{�^�����N���b�N���܂��傤
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��i�}����j�ɂ��ā^22.06.17�n
��{�I�ȎO�p��(�}����)�@�ɂ��Ăł�
���1�Ȃ̂ł����I������I�������Ƃ��ɕ\�������G��
������\���Ă��邩�s������\���Ă��邩������ɂ����ł�
�����m��ҁn�F�A�����肪�Ƃ��D����́u�s�����v�Ƃ������Ƃł�����ǎ҂������Ȃ��悤�Ɂu�o�b�J���[���C��蒼�����v�Ȃǂ̃n�b�L�����߂���\������������̂ł��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.06.14�n
�R���b�c�\�z�́A���wIIB�̒m���ŏؖ��ł��܂��B���{�̃v���v�����g�T�[�o�[Jxiv�̐��w�̕���ɘ_�������J���܂����B��낵��������_�E�����[�h���Ă����������B��i�@�\�L�łR���|����1�������鎞�̌����̑������Ғl�iA�j��2�Ŋ��鎞�̌����������Ғl�iB�j���r����ƁAB�̌������Ғl��A�̑������Ғl�Ɠ������傫���̂ŁA������ɔ��U���Ȃ��ŁA�Ō�͌���1�ɂȂ�B����1�͏\�i�@��1������Ō�͂P�ɂȂ�Ƃ����ؖ��ł��B�r���Ń��[�v�ɓ���Ȃ��́A�R���b�c�\�z�̐��l�́A�K������Ȃ̂ŁA��ʍ������߂āA������g���Ĕw���@�ŏؖ����Ă��܂��B���Z���̗�݂ɂȂ�Ǝv���܂��B���{�@�^
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^22.06.14�n
�ƂĂ��킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̔����������ɂ��ā^22.06.12�n
���K����3�ԁCx+y=u�ƒu����du/dx=2x/u�ƂȂ�ȒP�ɉ����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^22.06.12�n
�����E�듚���Ԃŕ\�����Ƃɂ���đ������ɂȂ�B
�����X�L�}���Ԃɉ����̂ɂ��傤�Ǘǂ��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕�����2�ɂ��ā^22.06.08�n
�~�Ɛڐ��̕������̐}�icircle_tangent_episode3_2.gif�j�ɂ��Ăł��B
�}�̒��ŕ\�L����Ă���(p, q)�͉~�O��1�_�̍��W�Ȃ̂ŁA�\�L��(a, b)�Ƃ���̂��������Ǝv�����̂ł������m�F���������܂��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��炪�ǂ݂₷�����Ƃ������f�ŁC(p,q)�ɑ����܂����D
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̒�` �ɂ��ā^22.06.07�n
���͂����łȂ��A�}���p���Ē�`��������Ă����̂�������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������a�C�e�C���[�W�J�C�}�N���[�����W�J�ɂ��ā^22.06.04�n
�e�C���[�W�J�ł��邱�Ƃ͏�]����0�ɂȂ鎖���Ӗ����Ă���Ǝv���܂��B��]���̃����_�E�̏������I�[�_�[�̈Ӗ����悭������܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�����������Ƃ������Ă���ł��l�b�g�Œ��ׂ���悢�̂ł́H
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.06.03�n
�R���b�c�\�z���ؖ����悤�Ƃ��Ă��܂����A�Ԉ���Ă���Ƃ�������Ă��������܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ́C�y�������w���낢��Љ�̃��x���Ȃ̂ŁC��[�̐��w�ɂ͑Ή����Ă��܂���D�����ł��D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^22.06.03�n
�ȗ����������Ė킩��Ȃ��m�肽���Ƃ��낪�Ȃ��̂Ő��������Ă����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�x�N�g���̐����\���C3�_���P������ɂ�������i���Z���w�U�j�Ȃǂ��\���K�����Ă��Ȃ��ꍇ�C�P�K����炸�ɂQ�K�����悤�Ȋ�Ȃ��b�ɂȂ�܂��D����Ƃ肠�����C�x�N�g���̕��K���珉�߂Č���̂��ߓ�����
���m�ʂ̕ł���̎���ɑ���n[�h�E���A�u���̒藝�i�������j�ɂ��ā^22.06.03�n
���3��7�ɂ����ă��̒l��2/7�{isin2/7�ƕ\�L����Ă���̂ł����A����ɂă�^7=1�ƋL�ڂ���Ă��邱�Ƃ���A�����炭�����̒l��cos2/7�{isin2/7���Ǝv����̂ł����A�����Ԉ���Ă���̂ł���A���萔�ł����C�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^22.06.03�n
���3��(2)�̉���ɂ��Ăł����Aab+1=A�Ƃ������ɂ�͂�ab�̍����c���̂�
�[���ł��Ȃ����k����萔����悤�Ɋ����܂��B
���̐����́A���R��(1)��x��0��〜4���܂ŏo��̂Ƃ͈���āAa��b��2���ȓ��Ɏ��܂邽�߁A
���1��(3)�Ɠ����悤�ɂ������|���Ɏ������ޕ��������Ƃ��Ă͗��ɂ��Ȃ��Ǝv���̂ł���
�������ł��傤���B
�����n�߂�2�����ɐ������Ă��炽�����|���Ɏ������ނ��Ƃ���Ɉӎ����Ă��邽��
���̂悤�ɍl����Ȃ����Ă��邾����������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������Ƃ��D�݂Ȃǂ́C�e���̎��R�ł��D�F�X�ȉ�����������Ƃ������Ƃ��u���Ă����v�̂���ɎQ�l�ɂȂ邱�Ƃ�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^22.06.02�n
�Y��ɂ܂Ƃ߂��Ă��āA����ɖ������Ă���̂ʼn��x�����K���悤�Ǝv�킹�Ă����悤�ȍ\���ɂȂ��Ă��Ă��肪�����ł��B�F�������l�I�D���ł��B��
���̒P�������p�����Ă��������܂��B
�Ō�ɁA.�������12�ɂ��Ď��₪����܂��I
cos��tan�ɕϊ����Ă���Ƃ��낪�Ȃ������Ȃ邩������Ȃ��̂Ŋm�F���Ē�����Ə�����܂��B
��낵�����肢�\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ���������܂����D
•�܂��́C����

�C�������C���āC�����ł��ŋ߂̏������Ƃ���

�Ƃ��邱�Ƃ������D
�i��ɏ������ق��́u3�����ڂ̋t�v�Ŋo������DCSC
���̕��́C�ǂ̋L�����R�����ł��ꂢ�����C���̋t�Ȃ̂��̌��������ȒP�ȋK���ɂȂ��Ă��Ȃ��j
•�@�v����ɁC�����C�]���C���ڂ�\���O�p���̋L���ɑ��āC���̋t����\���L���������āC

�ł��D
•�@���Z�̊w�K�w���v�̂��炢�������̂��́C���m�ɂ͊o���Ă��܂��C���݁u���Z�̋��ȏ��v�u��w�������v�ł͌������܂���D�u�i�w�Z�v�u����v�u�Љ�l��excel�v�Z������Ƃ��v�Ȃǂ́C�m���Ă��ē��R�Ƃ����������Ǝv���܂��D�u��w�ł���������Ă���ɂ͂Ȃ��ł��傤�v�D���t�̒�`�����̂��ƂŁC������5�����v���܂��C�ǂ̒i�K�ŒN�������邩�C�N���ӔC�������Ă��Ȃ��悤�ł��D
•�@�����鑤�Ƃ��ẮC�u�O�p���̒P�Ȃ�t���ł����āC�Ȃ��Ă�����Ȃ��v���̂Ȃ̂ŁC���������Ǝv�����Ƃ͂Ȃ��̂ł����C��w�����̉ߋ����Љ���ł͕��ʂɓo�ꂷ��̂ŁC�u���k���s���ɂȂ�Ȃ��悤�Ɂv�����ƐG��Ă������炢�̈����ł��傤�D�Ⴆ��


�Ȃǂ͂悭�g��������ł��D
���Z�͈̔͂Ŏ���ł��B�o�Ȑ��̑Ώ̐�(��1�ی���������Ƒ��̏ی��������邱��)�̏ؖ�����舵���Ē��������ł��B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�~�C�ȉ~�C�o�Ȑ��̕W���`���Cx���ɂ��Ă������ɂ��Ă��Ώ̂ł��邱�Ƃ́C���̌`���璼���ɕ�����̂ŁC���ʂ͏ؖ����܂���D���Z�̎��Ƃł́C���Z�R�N�̎��Ǝ����͏��Ȃ��i�Q���C�R���͂قڂȂ��j�̂ŁC�o�Ȑ��̕������Ɋ��蓖�Ă邱�Ƃ̂ł��鎞�Ԃ́C�Q�C�R���Ԃł��傤�D���̂����̂P���Ԃ��C�Ώ̐��̏ؖ��ɏ[�Ă邱�Ƃ́C�قڂȂ����Ƃł��D
=\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0&chf=bg,s,fff9f9)
���(1)
�Ƃ����D�_
&chf=bg,s,fff9f9)
��(1)�����Ƃ��i�_
&chf=bg,s,fff9f9)
���o�Ȑ�(1)��̓_�ł���Ƃ��j
=\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1=0&chf=bg,s,fff9f9)
������C�_
&chf=bg,s,fff9f9)
��(1)�����D�i�_
&chf=bg,s,fff9f9)
�͑o�Ȑ�(1)��̓_�ł���j
���l�ɂ��āC
=\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1=0&chf=bg,s,fff9f9)
������C�_
&chf=bg,s,fff9f9)
��(1)�����D
�ȏ�ɂ��C�O���t�͂����Ɋւ��đΏ̂ŁC�����Ɋւ��Ă��Ώ́i����ɁC���_�ɂ��Ă��Ώ́j�ƌ�����D
�킩��₷�������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^22.05.30�n
�����̏ؖ�������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̊�{�ɂ��ā^22.05.28�n
�ŏ��̕��́u2 ��ϕ��̌v�Z��v��(1)�A��肾�ƕ��ꂪx+1�����ǁA�̕��͖`���̎��A���ꂪx�ɂȂ��Ă܂����A����̓^�C�|�ł����ˁB��u���̒����p�j�N��܂����i���j
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.05.28�n
���������߂ɂȂ�܂������ꂩ������������ӂ��ɏo���Ă���������Ɗ������ł��B/��������������ł��I�I�ł��A�ƂĂ����߂ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^22.05.27�n
�ƂĂ��킩��Ղ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��������(��{)�ɂ��ā^22.05.25�n
�킩��₷���Ď��Ɨ����̎Q�l�ɂȂ�܂��B
���@�������}�X�^�[�ł���悤�ɂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�̈�ɂ�����ő�ŏ��i�������j�ɂ��ā^22.05.25�n
�Ō�̖��Ŏ����������ɂȂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃Z���^�[�������(2007)�ɂ��ā^22.05.24�n
�ォ���Ԗڂ̖��
�J�̌��̐��������ł́|�ʼn���ł�+�ɂȂ��Ă܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�����͂��܂������C���̃y�[�W�ł͂Ȃ��āC���̃y�[�W�����p���Ă���ʂ�js�t�@�C������������ꍇ�C�R���s���[�^�̃L���V�����������ȑO�̃f�[�^���Ȃ��Ȃ��������Ƃ��Ȃ����߁C��ʏ�ŕω����ɂ������Ƃ�����܂��D�i�L���b�V�����폜��������ɒ���܂����C�u���E�U�ɂ���āC�u1���Ԉȓ��v�̃L���V���Ɍ��肵�č폜�C�ȂǂƏڍw�肵�Ȃ��ƁC���̃L���V�����폜����邱�Ƃ�����悤�ł��j
���m�ʂ̕ł���̎���ɑ���n[�Q�����̈��������ɂ��ā^22.05.23�n
�����ł͂Ȃ��A�������̉�����~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������ł͂킩��Ȃ��l�����邩��C�����������Ă���܂����C���������Ȃ���C�������ɂȂ�܂��D���Ɖ̊Ԃɓr���o�߂��K�v�Ȃ��̂ł͂Ȃ��C��葦���ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����ƈ�ʍ��i����`�j�ɂ��ā^22.05.23�n
������an+1-����p(an-��)�̌`�����Ă���̂ɁA�Ȃ����(4)��(5)�ł�an+1-����p(an-��)�̌`�����Ă���̂���������܂���B������A�����Ă��������܂���ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��Dan+n+1=bn�ȂǂƏ����Ă���̂ł�
���m�ʂ̕ł���̎���ɑ���n[�~�ƒ����̈ʒu�W�i�܂Ƃ߁j�ɂ��ā^22.05.23�n
���7-1�́u(x�|3)2+(�|1)y2=5�v�͉~�ł͂Ȃ��o�Ȑ����Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����Ɠ���̐ςɂȂ��Ă��鐔���ɂ��ā^22.05.22�n
���ɑf���炵��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̏��@�i����Z�j�ɂ��ā^22.05.22�n
�m�̗\�K���K�ɏ[�ĂĂ��܂����A�d�ԓ��ł��ł��邽�ߔ��ɗǂ��ł��B�܂���������ɂ킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������̕ό`�ɂ��ā^22.05.21�n
���������̎菇�́A�������̉��̌���(���R���w)�̓��o���̂��̂Ȃ̂ŁA���Z�ɓ����Ă�����K����̂ł͒x���ł��B���R�̓��A�W�J����������ƕ��ׂċ����Ă��������B���Z�ŋ����̂͒x���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̋��ނɂ�����܂��̂ŁC�ǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^22.05.20�n
�킩���Ă��Ȃ������̂ł킩���Ă��Ȃ������̂ł悩�����ł��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2����(�W���`�����_)�ɂ��ā^22.05.20�n
�ƂĂ��ʔ����ē��e���f�G���Ǝv���܂����ꂩ����撣��܂��B�����_�͖��������ł��B�������W���Ǝv���܂��B
���ꂩ����撣��܂�(�P�O)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^22.05.19�n
�ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.05.18�n
���₷�����A������₷���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɍ��W�ɂ��ā^22.05.17�n
�ԗ���������̂������C�ɂȂ邪�A�ǂ��B
�܂����{�I�ȂƂ���𗝉����邽�߂ɂ���������Ɠ����̉���𑝂₵�ė~�����B���w�҂ɂ�������悤�ɁB
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̑S�������������ł��D��Βl�Ƃ��O�p����������Ȃ��ꍇ�́C��Βl��O�p���̕��K������Ă����������D
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^22.05.16�n
��肠�肪�Ƃ��������܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ������ɂ��ā^22.05.16�n
��p�ΐ��ł܂����܂����Ă����̂Ŗ��������Ȃ��痝���ł���̂��ƂĂ��ǂ������ł��B
�Q�l���ƃm�[�g�������Ă��p�\�R���݂̂ŕ��ł���y���݂�m��܂����I
�Ԉ���Ă���������������̂ŕ�����Ȃ��܂܂ɂ��Ȃ��čς݂܂��B
����܂ŎQ�l�����������ĕ��������ӂ�ɂȂ��Ă��������ɋC�t���܂����B
���ꂩ������p���܂��I���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.05.16�n
�ƂĂ��悢�����ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̓��ςƊO���ɂ��ā^22.05.15�n
��{�I�ȂƂ��낪��ϕ�����₷���A���ڂ�����������Ă��āA�Ċm�F�A�ė������邱�Ƃ��o���܂����B
�����ŁA���ρA�O�ς����̗l�ɒ�`���闝�R�A�������̂ł��傤���H ���K�˂������Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D��`�͖��ŁC�ǂ����߂悤���e���̎��R�ł����C���N�ɂ킽���Đ����c����`�́C���炩�̗��_������̂ł��傤����Ⴆ�C�����w�ւ̉��p�ȂǁD���ς́C�����ɒ������Ƃ��ɁC���̒�`���ƂĂ��g���₷���Ƃ������Ƃ�������܂��D�O�ς́C�����̉�]���[�����g�ɑΉ����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������i�������j�ɂ��ā^22.05.15�n
�y���2.4�z�������(10L+1)�~7�iL�͐����j=10M+1�iM�͐����j���Ԉ���Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�_�ƌX���������̕������ɂ��ā^22.05.13�n
�����̏����Y�ꂿ����Ă��̂ŏ�����܂������肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���ƕ����ɂ��ā^22.05.13�n
������͂���肷���߂��Ă��ĕ�����Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�܂Ƃ߂̃y�[�W����ǂނƗv�������ĂȂ��D��{�̃y�[�W����ǂ�ŁC�ł���悤�ɂȂ��Ă���܂Ƃ߂̃y�[�W������Ă��������D�����ɖڎ����t���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.05.13�n
���������y�������܂�❗️
�����Ƃ����Ɖ�������❗️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.05.13�n
�����͂������|�������Ȃ̂ł����Ȗ��������Ċy�����Ǝv����悤�ɂ������ł��@�@���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ɂ��ā^22.05.12�n
����ł��B
�����̖��ŕ������������̒m�����K�v�������̂ŐU��Ԃ��Ă��܂����B
��Q�̉E�ӁA1/2�ł�����闝�R�����Ȃ̂�������܂���ł����B
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��P����

������
&chf=bg,s,fff9f9)
�ł��D�悋����
}=\frac{2}{k(k%2B 2)}&chf=bg,s,fff9f9)
������
}=\frac{1}{2}(\frac{1}{k}-\frac{1}{k%2B 2})&chf=bg,s,fff9f9)
�ɂȂ�܂��D
�W����4�p�^�[���̃x���}�ɕ\�����Ǝv���̂ł����iA��B���d�Ȃ��Ă�����́AA�̒���B���܂܂�Ă�����́AB�̒���A���܂܂�Ă�����́AA��B���ʁX�ł���ڂ��Ȃ����́j�����܂��ăh�E�����K���̐��������Ă���������Ə�����܂��c
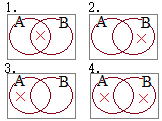 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D�Q�̏W����}������ꍇ�C���ȏ��Ȃǂɕ`����Ă���u�o�ዾ�̂悤�Ȑ}�v�����ׂĂ̏ꍇ��\���Ă��܂��D�ȉ��C�~��͂�������W���ł��邱�Ƃ�\���Ă�����̂Ƃ��܂��D1.��A��B=∅�ɑΉ����C2.��A��B�ɁC3.��A��B�ɁC4.��A=B�ɑΉ����܂��D���̂悤�ɁC�o�ዾ�̂悤�Ȑ}�ɂ��ďq�ׂ�C���̓��ʂȏꍇ�����ׂĊ܂܂��̂ŁC�ʂɋc�_����K�v�͂Ȃ��Ƃ����̂��C�ʏ�̐����̎d���ł��D�~��W����\���Ƃ��������̎d�����S�����ʂł��D
(4)�̉�������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����lj����܂���
���m�ʂ̕ł���̎���ɑ���n[�����̏ؖ��ɂ��ā^22.05.10�n
�����ڂ��߂�����e�Ɋ������ǂ܂����Ă��������Ă��܂��D���ŋ߁C�����̓��e�����Ƃ��܂����D�ؖ����Ŋׂ�₷���ԈႢ�ɂ��āC���ȏ��ɂ͋L�q������܂���D�܂��C��������Ƃň�ؐ������Ȃ�����������̂��낤���C�Ǝv����..
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��v�Z�ɂ��ā^22.05.10�n
��l�ɂȂ��Ă���log�̌v�Z�������Ȃ��Ă͂Ȃ�Ȃ��Ȃ肱����̃T�C�g�ɍs�����܂����B������킩��₷�����K���Ŏ��M�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^22.05.09�n
�Ȃ�قǂł��I�킩��܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.05.07�n
�������킩��₷���A���₷���ăX���[�Y�Ɋw�K�ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝�C�{�p�����C�R�{�p�����C���p�����ɂ��ā^22.05.07�n
���߂ɂȂ�܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����ƈ�ʍ��i����`�j�ɂ��ā^22.05.07�n
(9)�͂ǂ̂悤�ɂ��ĕό`�����̂ł����A�����������ł��܂������܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�萔�W���̏ꍇ�łȂ���C������������U��Ǝ��s���܂��D���̂��Ƃ́C���߂̕�����q�ׂĂ��܂��D�ł͂ǂ����̂��H���ꂪ�����ł��Ƃ������̂����҂����ɁC���̔w�������Ă���ΐg�ɕt�����Ƃ�����̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�������s�̊m���i���wA�C�������j�ɂ��ā^22.05.07�n
�y���3�z(1)�̉ł���2/27�Ȃ̂�1�\�o��25/27�ł͂Ȃ�5/27�ɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�:�ϐ��ϊ�.���R�r�A���ɂ��ā^22.05.07�n
��������J�ŁA�T�����ƂȂ��Ō�܂ŏo���܂����B�悢���ނ����肪�Ƃ��������܂��B���āA��3�̉���Łud/dr(sin(r^2))=2rcos(r^2)������v〜�ɂÂ����ӂւ̐ϕ���0��1��Ԃ̒�ϕ��ɂȂ��Ă��܂����A�{���͕s��ϕ��ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�s��ϕ��ɒ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^22.05.06�n
���ɁC�w���v�Z�̘a���Z�������ق�����낵���̂ł͂Ȃ��̂ł��傤���H�i�ォ��ڐ��ł��݂܂���j
�����m��ҁn�F�A�����肪�Ƃ��D���̕ł͐��w�T�̍ŏ��ɁC�W�J����������̑O��ƂȂ�w���@�����܂Ƃ߂����̂ŁC�w�����̘b�͐��w�U�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�Q�����ɂ��ā^22.05.06�n
�y���T�z(2) �̖�蕶�A��n�Q�̌Q�������Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�m���̌v�Z�i�������j�ɂ��ā^22.05.05�n
�y�ޑ�1.2�z�̉�(�@)�ŃA�j�ƃC�j������������Ƃ��̏����3!/�i2!��1!�j�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��`�������ω�����Ƃ��̍ő�ŏ�1�ɂ��ā^22.05.05�n
���2��1��t�̂Ƃ��C�ŏ��l��f(t)=(t�|1)^2��t=1���܂܂��̂ŋ��t��x��t+1���At=1�̎��A�܂�
f(1)=0���ŏ��l�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��Df(t)=(t�|1)^2��t=1���������f(1)=0�ɂȂ�Ɠǂނ̂ł������ʂɊ�����Ԃɕ����Ē��ׂ�Ƃ��ɁC�A�����ł͉E�̋�ԂɊ܂߂Ă��C���̋�ԂɊ܂߂Ă������l�ɂȂ�܂��D�Ƃ���ŁC���w�U�C���w�V�̒�ϕ��������C��ԕ����́u����Ȃ��v�u�d���Ȃ��v������̂���{�ŁCt��1, 1��t�̂悤��1���E�ɂ����ɂ��܂܂��悤�ȏ������͔����܂������������R�c�͏b�̖��������̖������C�͂����肵�Ă���Ƃ��������N�����Ȃ��悤�ɂ��܂��D������1��t�̂Ƃ��C�ŏ��l��f(t)=(t−1)^2�ʼn������͂Ȃ��̂ł��D������������Ɋ܂߂鏑�����́C���Ə��Ȃ��ł�
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.05.03�n
������������ ���肪�Ƃ��������܂�(*�E�ցE)*_ _)
�����m��ҁn�F�A�����肪�Ƃ��D�o�b�p�̉�ʂ�iPhone�œǂނƁC�����������Ȃ�܂��D�u�� �g�єł͕ʕŁv�Ƌ���ȕ����ŏ����Ă���܂��悤�ɁC�X�}�z�ł͕ʂ̃y�[�W�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�ݏ捪�ɂ��ā^22.05.03�n
��{����Z�p�Ҏ����̕����ɁA���������o�Ă����̂�
���ׂĂ����炱�̃T�C�g�ɂ��ǂ蒅���܂����I
�ƂĂ����ɂȂ�܂����A���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^22.05.02�n
(17)
�Ԉ���Ă�Ǝv���܂��B
8a^3+27b^3�ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����i�����͒����������ȁ`#�j
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�...�ϕ��̈悪�ϐ��Ɉˑ�����ꍇ �ɂ��ā^22.05.01�n
��ς킩��₷����肠�肪�Ƃ��������܂��B���ׂȂ��Ƃŋ��k�ł����A��1�̉A2x^2��ϕ��������ʂ�2x^2/3�ƂȂ��Ă��܂����A��������2x^3/3�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������P�ɂ��ā^22.05.01�n
�ƂĂ�������₷�������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�o�Ȑ����ɂ��ā^22.04.30�n
��ϕ��ɂȂ�܂����B�o�Ȋ��̃O���t���Ƃ��Ă��킩��₷�������ł��B
�m�F�ł����AV�y�o�Ȑ����̐��������@�藝���z�̖��4��HELP�̉���ŁA�o�Ȋ��̉��@�藝��cosh(���[��)=cosh��cosh��+sinh��sinh���ƂȂ��Ă��܂����A��������cosh(���[��)=cosh��cosh���[sinh��sinh���ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�s��̑����C�a�C���C�����{�ɂ��ā^22.04.29�n
���Ƌx��ł����̂Ŏ��Ԃ���悤�Ɋ撣�肽���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O���t�̕��s�ړ��ɂ��ā^22.04.28�n
���������͓����肪����܂����A2�����͊ȒP�ł��B����Ȃ��̂ł��������H����p�Y���̂����50�N�Ԃ肮�炢�Ɋy����ł��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��{���͂₳�������C�����������܂��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.04.27�n
[3n+1���i�R���b�c�\�z�j�ɂ��ān
2022.04.26�Ɂu(J) �̍Ōォ��Q�Ԗڂ̎�����A�D�D�D�v�Ŏ��₳���Ă����������҂ł��B
�����̉A���肪�Ƃ��������܂����B
(I) �̍Ō�̎����P�����ɂȂ��Ă���A�Ŋ�������������邱�Ƃ͗������Ă��܂��B
�O��̎���ł́A(J) �ɂ�����Ōォ��Q�Ԗڂ̎��ŁA13�~3/5�~8 ������ 13 �������ł��Ȃ��āA
�T���Ă��܂������A�q���g�����������ččl���A�������܂����B
����̎���́A������e�ł����A(J) �ɂ����āA�h...�h�������Ȃ��ꍇ�A���Ȃ킿�A�����Ȃ�A
13�~3/5�~8 �̍����o������ꍇ�ł��B
���̏ꍇ�́A���13 �͖ŏ����ł��܂����A���5�͎c��̂ł͂Ȃ��ł��傤���H
���Ȃ킿�A5�~2p' = 3q' �ƂȂ�ƍl���܂��B
����āA�h�D�D�D�h������ꍇ�ƂȂ��ꍇ�̂Q�ɏؖ�����K�v������̂ł͂Ȃ��ł��傤���H
�܂��A�����A���̍l�����������ꍇ�A�c���� 5 �ł͂Ȃ��A3 �̏ꍇ�A�����鎮��
����s�\�ɂȂ�̂ł́H�ƍl���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���̂P�ʂ�����@������C3n+1��肪�m��I�ɉ������Ƃ����̂Ɠ������ƂɂȂ邪�C�M�҂ɂ͂܂������Ă��Ȃ��D�v�Ə����Ă���悤�ɁC���������́u�b��v�u��������v�u�M�҂��l�������v�ł����������Q�l�ɂ��ēǎ҂��Ǝ��̐����l���Ă��������̂��x�X�g�ł�������E�I�ɗL���Ȃ��̂悤�Ȗ�肪���ۂɏؖ��ł�����C�ǂ����Ńj���[�X�ɂȂ�ł��傤.�����łȂ���u�܂������Ă��Ȃ��v�̂ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.04.26�n
(J) �̍Ōォ��Q�Ԗڂ̎�����A�Ō�̎���������闝�R�𗝉��ł��܂���B
���Ȃ킿�A2^p' = 3^q' �ƂȂ�ɂ́A�Ōォ��Q�Ԃ߂̎��̍��ӂ́i2^p' / 3^q'�j�ȊO�̕�����
�P�Ƒz�肵�Ă��邱�ƂɂȂ�܂��B�����̕����̗��R�������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D(I)����ǂ߂C�ŏ�����Ƃ������ƂŁC�����疵���ɂȂ��Ĕw���@�ɂ��C����Ȃ��Ƃ͂Ȃ��Ƃ������Ƃł�
���m?��/�H����/22.04.25�n
���a�x�N�g���P���̎���ł��B�Ȃ��p�����߂���͂Ȃ��ʓx�@���g��Ȃ��ł����H�i�����Ă���Q�l�����S���x���@�\���ɂ��Ă��܂��B�j
�����m��ҁn�F�A�����肪�Ƃ��D�ʓx�@�͐��w�U�Ńx�N�g���͐��wB������C�x�N�g���̓��ς��K���Ƃ��Ɍʓx�@���K���Ă���Ƃ͌���Ȃ�����D�͂����茾���C�ʓx�@���K�v�Ȃ̂́C�O�p���̔��ϕ����o�ꂷ��Ƃ������琔�w�V�ŏK���悭�C���w�U�Ōʓx�@��������Ƃ����̂́C�w�K�w���v�̂̐v�~�X�ł��傤����N�ł��m���Ă��邪���E�����͌����Ȃ������D�ސE���������͋������̂Ȃ�������C�D���ɕ����ł���D�����܂��C�ʓx�@�𐔊w�V�ɉƁC���w�V�̕��ʂ������߂����_������D�����w�K�w���v�̂ŁC�x�N�g���͐��wC�ɗ���̂ŁC���w�U���K�����ゾ����C�p�x�͌ʓx�@�ł��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^22.04.25�n
�₳��������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ʃx�N�g���ƎO�p�`�i�������j �ɂ��ā^22.04.25�n
�y���1�z��(3)�̓����́�PBC:��PCA:��PAB=5:9:11�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^22.04.24�n
�ƂĂ��킩��₷���y�[�W�ɂ������ӂ��Ă��܂��B
�ǂ����玿��𑗂�����̂������炸�A���݂܂������ɏ������Ă��������܂��B
���̃y�[�W�ł́A�ړ_�̍��W����ڐ��̕����������߂���@��������Ă��������܂������A
�ڐ��̕���������ړ_�̍��W�����߂邱�Ƃ͂ł���(��������������)��ł��傤���B
���蕗�Ɍ�����.
�ڐ��̕�������ax�{by=r² �� �ړ_��(a,b)
�����藧���B�Ƃ��������ł��傤���B ��낵����Ή�����Ɗ������ł��B
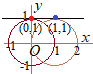 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D2�̉~�̋��ʐڐ��Ƃ������̂����邱�Ƃ��l����ƁC�ڐ������܂��Ă��C�ړ_�͌��܂�Ȃ����Ƃ�������܂��D�Ⴆ�C���}�̐ڐ��́C�ړ_(0,1)�ʼn~

�ɐڂ���F

�Ƃ������邪�C�ړ_(1,1)�ʼn~
^2%2B y^2=1&chf=bg,s,fff9f9)
�ɐڂ���F
(x-1)%2B 1\cdot y=1&chf=bg,s,fff9f9)
�Ƃ�������
�Ƃɂ���������₷���I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^22.04.20�n
��������ɂ킩��₷���ăe�X�g�O�ɏd�܂���
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�i�e�w��ԁj�ΐ��v�Z�ɂ��ā^22.04.19�n
�ΐ��v�Z(�e��)���ƂĂ��y���������ł��B�ԈႦ��Ǝ����I�Ɋ֘A��肩����������ɂȂ�̂ŁA�ƂĂ��͂��t���܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g����͂̌����ɂ��ā^22.04.17�n
�u2. �i�u���Ɠ��ρC�O�ς�p�����\���v�̒��ߕ����ɂ���
(V�E��)W�̂Ƃ��낪�Ԉ���Ă��܂�
���Z�q�͊e�����ł͂Ȃ��A���Z�q�S�̂�W�̊e�����ɂ�����܂�
�C������낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���������w���ł͏K��Ȃ��āC�~�~�N�O�ɍH�w���̐�y�̏h�����`���Ĉȗ��Ȃ̂ŁC����������o�����߂���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^22.04.14�n
�萔�W����K�A���^��Ď����^������������̓ǂݕ�������������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�������O�ɂȂ�Ƃ��́C�Ђ炪�Ȃ̋�����ꂽ�����ǂ݂₷���̂Łu�萔�W�������A����K��Ď����^������������v�Ƃ��u�萔�W���̘A����K�����^������������v�ȂǂƂ������Ƃ������悤�ł����C�L���[�s�[.�R�[��.�S�[���h.�A���t�@.�v���X�Ƃ��i���j�O�H����UFJ��s�̂悤�ɁC�_�ǂ݂��邱�Ƃ�����悤�ł��D�萔�W��.��K.�A��.��Ď��i���j.���^�i���`�j�܂ł̏����͂��낢�날��ŁC������������������ɂ���C�Ӗ��͒ʂ���悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ�(�W�J)�ɂ��ā^22.04.12�n
���͍��Z����s�o�Z�������̂ł��̃T�C�g�������Ċw�юn�߂܂������A���ɂ킩��₷�����A�������Ə����Ă������o���y�����Ăǂ�ǂ�i�߂�܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�������ǂ��̂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.04.13�n
���t�Ő��������ق����݂₷����������Ȃ��ł��E�E�E
�������肾�ƌ��t�̐������Ȃ��̂ʼn����ɂ���������A�Y��Ē��߂Ă��܂��q������̂ŃT�|�[�g���Ă��������Ȃ�H�v�������������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�u�I�������N���b�N����̓_���ʂƉ�����o�܂��v�Ə����Ă����ˁD���Ȃ���Ή���͏o�܂���D
���m�ʂ̕ł���̎���ɑ���n[�s��̑����C�a�C���C�����{�ɂ��ā^22.04.12�n
�ƂĂ�������₷�������ł��B/ �W���̕������݂��炩�����ł� / ����͂���ہA�S�p�ɑΉ����Ă��Ȃ��Ƃ��낾�������s�ւɊ����܂����B/�������킩��₷���A��蕔���������̓��e�������ł��Ă��邩�ǂ����������ɂ킩��悤�ȁA�K�v�����������Ă���`�Ȃ̂ŁA�ƂĂ������Ǝv���܂����B/���`���Ŏ����œ������m�F�ł��邱�Ƃ��ǂ��_���Ǝv���܂����B/�����ł���/�ǂ̖��łǂ̌������g���̂��������킩��ɂ����C������/�S��������Ȃ��̂ɂǂ�ǂ�i�ݏ������p�ꂪ��ь����悭�킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D��Z�Z�Z�Z�Z�傩�ǂ����̐V�������K�Ŏg���Ă���悤�ł��D�O�̃y�[�W��ǂ܂��ɁC������Ȃ��ȂǁC��w���炵���Ȃ����z�������
��?��/�H����^22.04.11�n
�m���̉��@�藝�C�]���ۂ̊m��(8)�Ƃ����y�[�W���J���܂���B404�G���[�ł��B�����m���̕��K���������ł��A�C�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�J�݈ȗ����̏�ԂŁC�ǂ�ł���l�͂ǂ�����ēǂ̂��H�������܂���
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^22.04.10�n
�y��Q�z�����C�L���̍������̕\�����ςł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��ςȂ̂ł����H
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^22.04.10�n
�ƂĂ��킩��₷���ł��B������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~����C���ジ�����ɂ��ā^22.04.09�n
��10��ɂ��Ă̎���ł��B�g�~�`�h�ɕ��ׂ�͉~������g��Ȃ��ł����i6!���i6-1�j!�j�A���̂��Ƃ�/2!3!�̈Ӗ���������܂���ł����A/10�̈Ӗ����ł�...
�����m��ҁn�F�A�����肪�Ƃ��D�ʉ��̕��q��5!�ɂȂ��Ă����ˁD��́C�u�������̂���Ƃ��̏���v�������Ă������Ă�����������u�~����v�Ɓu�������̂�����Ƃ��̏���v�̗����ɊW�����肪����Ƃ��ɁC�ǂ�����ɋ����Ă�����͏o�܂����C�������ŏo���Ȃ��Ƃ������Ƃ͂ł��܂���D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.04.08�n
���������̖��肪���������Ȃ��ł����H
�������ŏI�I��1�ɂ��邱�Ƃ��ؖ�������ł��B
3�{����Ӗ��͂Ȃ�ł����H
��������ɂ��Đ������炷���Ƃ�ړI�Ƃ���Ȃ��
n+1������ł�������͂��ł��B
���{���悤�����+1����������ɂȂ�܂��B
�����ɂȂ�ΕK�������Ɍ���܂��B
�J��Ԃ��ΕK��1�ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̖�肪�����Ȃ��Ƃ��Ɂu��肪���������v�Ƃ����̂́C�C�\�b�v����Ŏ��Ȃ��������X�b�p�C�ƌ������L�c�l�̌������Ɠ������ˁD�ʂ̖��Ȃ瓚�����܂��Ƃ����Ă��C���̖��͉����Ă��Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J �ɂ��ā^22.04.06�n
���2.7�@�̉���Ɂ@(A�|3x)(A+x)=A2�|3xA�|3x2�@�Ƃ���܂����A�@(A�|3x)(A+x)=A2�|�QxA�|3x2�@�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�V���肪�_���Ȃ��ł́C��͂�ԈႢ������������܂����D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂ̕������ɂ��ā^22.04.03�n
4.�_�ƕ��ʂ̋���"�ɂ���A
�y���z(1)���s��2����2x-3y+4z-5=0,2x-3y+4z+5=0�̊Ԃ̋��������߂�B
�̉ŁA������v�Z�������ʂ���30�ƂȂ��Ă��܂����A�������́�29�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D����������܂����D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂ̕������ɂ��ā^22.04.03�n
���w����1���̊w�K�̂��߂Ɏg�킹�Ē����Ă���܂��B�̒��J���A�l�X�ȕʉ������邱�Ƃɉ����A���l���Ղ����A�ǂ̃T�C�g�������ɂ킩��₷���ł��B���������܂ŗ������[�܂�܂����B���肪�Ƃ��������܂��B
���āA����ł��B�ȉ��̗��ŁA�̐��l������Ȃ��C���������܂��B�m�F�����肢���܂��B
4�_�ƕ��ʂ̋����̗��
(1) ���s�ȂQ����2x�|3y+4z�|5=0, 2x�|3y+4z+5=0�̊Ԃ̋��������߂�D
���́�2�Ƃ���܂����A�r�����̕������̒��̕���̌v�Z�̐��l���ς���ė���Ǝv���܂��B
(2) ���s�ȂQ����x+y/2+z/3=-1,x+y/2+z/3=1�̊Ԃ̋��������߂�D
��(-3,0,0)�Ƃ���܂����A(0,0,-3)�ł́H�܂��A���̌�̌v�Z���ς���Ă���̂ŁA�������ς��Ǝv���܂��B
(3) 6,2���ʂ̂Ȃ��p
���6.2
2����x-2y+z-3=0,2x-4y-3z-2=0�̂Ȃ��p�����߂Ă��������D
������̓r�����̕��q�̐��l���قȂ��Ă���悤�Ɏv���܂��B���l���ς��ƁA�Ȃ��p�����藧���Ȃ��̂ł͂Ȃ��ł��傤���B
(4) 7,2���ʂ̌��p������镽��
���7�̉�(1)�ōŏ���P1��(-1,0,1)�A���̌��P1��(-1,1,1)�ƂȂ�قȂ��Ă��܂��B(-1,0,1)���������̂ł͂Ǝv���܂��B
�ȏ�4�_�A���m�F����낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D(1)(4)�������܂����D(2)(3)���w�E�̂悤�ȋL�q���Ȃ��C�܂��́C�ԈႢ���Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[���̎w���̒�`�ɂ��ā^22.04.02�n
�ǂ����ނ����肪�Ƃ��������܂�
���͌��ݒ���ł����w���@���╉�̒l�̗ݏ悪�ƂĂ��C�ɂȂ��Ă����̂łƂĂ��ǂ��@��ł���
�܂������ȕ���̋��ނ�����Ă�������Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.04.02�n
�lj����(19)�͓������Ԉ���Ă��܂��B�����炭�ʂ̖��̉̂悤�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.04.01�n
�lj�����(19)
���̎��ɂ�X��Y�̕������g���Ă�̂ɓ����ł�a��b�ɂȂ��Ă��܂��B�ԈႦ�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^22.03.31�n
�͂��߂܂��āB����50��O���̉�Ј��ł��B�V���h�~�̂��ߎ��X���w�E�����̖����l����悤�ɂ��Ă��܂��B�Ⴋ���Ɋo�������Ƃ�30�N�ȏ���o�Ă��Y��Ȃ����̂ł��ˁB�X���X�������܂����B
�������A��Ƃ苳����ď����̑����ł��ˁB���ɐ��w�I�Ȏv�l�͂Ƃ����̂͗��n�����łȂ��A���n�ɂƂ��Ă��L�p�Ȃ̂ɁB
�{���̓�d�����͏����̎���͒��w�ł��K�����L��������܂��B���̉ے��́u���w3�v�܂Ō��܂������A�����̍��ɔ�ׂĂ��Ȃ�폜����Ă���P��������܂��ˁB�s���ϊ����Ȃ��̂ł����H
���ꂩ������̑̑��Ƃ��Ĕq�ǂ����Ē����܂��B
�h��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���Ȑ�(���K�Ɠ������)�ɂ��ā^22.03.31�n
���Q
���Ɋ��ɐ����u67�v�������Ă��܂��Ă��܂��D
������}�[�N�̉ԍ��̂�����ł���C�J�i���������ł��傤��
�������P�ɓ����Ă��܂��Ă���̂ł���C���̓������Ԉ���Ă��܂��D
����ɂ́u47�v�Ƃ���C���ۂɂ����炪�������ł��D
����Ɍ����Ή���̒ʂ��蕶���炵�āu�}�v�����ׂ��ł��i�����}�}�ł����炷�݂܂���j�D
�����m��ҁn�F�A�����肪�Ƃ��D�u�����}�}�v�ł�������\���ꂽ���앨�����p����ꍇ�C���ꐫ�ێ����̐N�Q�ƂȂ�Ȃ��悤�ɁC�\��������ɕύX���Ȃ��悤�ɂ��Ȃ���Ȃ�܂���D�D67�͓��Y��w���w�肵���}�[�N�̔ԍ��ł��D�D��±�ł��D6��4�C7��7�Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[���̂̑̐��ɂ��ā^22.03.30�n
�g�������`�̐ϕ��Ő��w�U�͈̔͂ŋ��߂���̐ς̖��́C�ʂ̃y�[�W�ɂ���܂��h�A���̕ʂ̃y�[�W���N���b�N������404�G���[���o�Ă��܂���
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[ 3n+1���i�R���b�c�\�z�j�ɂ��ā^22.03.29�n
111,111,111 �͓�����1�ɂȂ�Ȃ��Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
111111111��333333334��166666667��500000002
��250000001��750000004��375000002��187500001
��562500004��281250002��140625001��421875004
��210937502��105468751��316406254��158203127
��474609382��237304691��711914074��355957037
��1067871112��533935556��266967778��133483889
��400451668��200225834��100112917��300338752
��150169376��75084688��37542344��18771172
��9385586��4692793��14078380��7039190��3519595
��10558786��5279393��15838180��7919090��3959545
��11878636��5939318��2969659��8908978��4454489
��13363468��6681734��3340867��10022602��5011301
��15033904��7516952��3758476��1879238��939619
��2818858��1409429��4228288��2114144��1057072
��528536��264268��132134��66067��198202��99101
��297304��148652��74326��37163��111490��55745
��167236��83618��41809��125428��62714��31357
��94072��47036��23518��11759��35278��17639
��52918��26459��79378��39689��119068��59534
��29767��89302��44651��133954��66977��200932
��100466��50233��150700��75350��37675��113026
��56513��169540��84770��42385��127156��63578
��31789��95368��47684��23842��11921��35764
��17882��8941��26824��13412��6706��3353��10060
��5030��2515��7546��3773��11320��5660��2830
��1415��4246��2123��6370��3185��9556��4778
��2389��7168��3584��1792��896��448��224��112
��56��28��14��7��22��11��34��17��52��26��13
��40��20��10��5��16��8��4��2��1
���m�ʂ̕ł���̎���ɑ���n[�w���������ɂ��ā^22.03.28�n
���̃T�C�g�Ƃ͈Ⴂ�A��肪��������A�ƂĂ������₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^22.03.28�n
�̍D�����������w�B�����ƕ��n�s���앶�����ł������A���Z���ƌ��50�N�Ԃ�ɉ����Ă݂��猋�\�v���o���āA�p�Y���̂悤�Ŗʔ����͂܂肻���B�B�����T�C�g�ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g����͂̌����ɂ��ā^22.03.27�n
���J�b�R�͑傫���Ȃ��Ă��� �� ���J�b�R���傫�����Ăق����ł�(���h���̂��߂�)
�E1�ԍŌ�̃�(�Ӄ�)�̌v�Z��, �v�Z�̂Ƃ�����ʼnE�ӂ�grad�����ɂ���ׂ����ȂƎv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D���������������܂����D�Ō�̎��́C�u��蕶�v�ƈقȂ鎮�ł͉ɂȂ�܂���D
���m��ʌ�/tomy����/22.03.27�n
��قǎ��₵�����̂ł��B
�Y���̃y�[�W���Ɏ���ł���ꏊ����������܂���ł����̂ŁA������Ŏ��₳���Ă��������܂����B
https://www.geisya.or.jp/~mwm48961/linear_algebra/line_plane2.htm
����������܂���ł����̂ŁA�⑫�������܂��B
1. 1�_��ʂ�����x�N�g���ɕ��s�Ȓ����̕������̈ȉ��̍��ڂł��B"�@"���͈��p�ӏ�
"�_A�i1,2,3�j��ʂ�C�����x�N�g��u=(4,0,6)�ɕ��s�Ȓ����̕����� �̕W���`����L�̌�����p���Č`���I�ɏ�����x-1/4=y-2/0=z-3/6�E�E�E(1)�ƂȂ邪�A���̎��̑�2�ӂ́u���ꂪ0�ɂȂ��Ă��邩��C���q��0�ɂȂ���̂�\���v�D���Ȃ킿�Cx-1/4=z-3/6,y=0�E�E�E(2)"
�Ō��y=0�̉ӏ���y=2�ł͂Ȃ����Ǝv���܂������A�������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�����C�������܂����D�ʐM���̌̏�������܂����D
���m��ʌ�/tomy����/22.03.26�n
���߂ɂȂ��肠�肪�Ƃ��������܂��B
��Ԃɂ����钼���̕�������1.1��1��(2)�̎���y=0�Ƃ���܂����Ay-2/0=0�Ȃ̂�y=2�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�u��Ԃɂ����钼���̕�������1.1��1��(2)�v�Ƃ������̂���������܂���D�Ȃ����̃y�[�W���玿�₹���ɁC��ʓI�Ȏ���̓��������K�˂Ă�����̂����C�^��ł���
���m�ʂ̕ł���̎���ɑ���n[�m���̃Z���^�[��������ɂ��ā^22.03.21�n
2002�N�x���P�`�ǎ�����P��(2)---�ꕔ���p ��(2)�̑�����������Ȃ��ł��B�����������Ă������������ł��B���x����Ă�
(��0��)��12/400
(��2��)��4/400�{36/400�{36/400��76/400
(��4��)��3/100��12/400
12/400�{76/400�{12/400��1/4
�ƂȂ��Ă��܂����ɍ����`�ɂȂ�܂���c
�����m��ҁn�F�A�����肪�Ƃ��D13/25���(��2��)�̏ꍇ����2�����Ⴂ�܂�.
�@�������Ă���Ă���̂��C�����炸�ɂ���Ă���̂��C���ȏ����x���ł܂Â��Ă��܂�����ʏ�́C�m���̌v�Z���C�g�ݍ��킹���g�ݍ��킹�ōs���Ƃ�����C���Ȃ��͏�����ł�낤�Ƃ��Ă���̂ŁC��2���ɂ��ẮCA:������,�������̗��������߂�K�v������܂��DB�����l�D
�@�������Ă���Ă���̂��C�����炸�ɂ���Ă���̂��C���ȏ����x���ł܂Â��Ă��܂�����ʏ�́C�m���̌v�Z���C�g�ݍ��킹���g�ݍ��킹�ōs���Ƃ�����C���Ȃ��͏�����ł�낤�Ƃ��Ă���̂ŁC��2���ɂ��ẮCA:������,�������̗��������߂�K�v������܂��DB�����l�D
���m�ʂ̕ł���̎���ɑ���n[�a�̖@���ɂ��ā^22.03.21�n
�\�K�ł��̃T�C�g���g�p�����Ē����Ă���҂ł��B���̂悤�ȃT�[�r�X���������������肪�Ƃ��������܂��B
���āA���1�Ɋւ��Ď��₳���Ă������������̂ł����A�召�̃T�C�R��2�𓊂����Ƃ��ɏo��ڂ̑g�ݍ��킹��36�ʂ�ł���܂����A�I������45,55�����闝�R�������ł��܂���B
12,15�Ȃǂ́u36�ȉ��̐��v�ɂ���Ƃ悢�̂ł͂Ȃ����Ǝv���܂����̂ŁA�A�������Ă��������܂����B
�������̂قǂ�낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D36�ȉ��ɂȂ�Ƃ������Ƃ������邩�ǂ�����q�˂邱�ƂɈӖ�������܂��D�P�ł́C�Ⴄ�Ƃ킩���Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̌v�Z�ɂ��ā^22.03.22�n
������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[Excel��p�����听�������ɂ��ā^22.03.20�n
�G�N�Z����PCA�������悤�Ǝv�������A���܂����B
�����Ɣq�����������ł��̂ŁA���̊��Ⴂ�����邩������܂��A�ȉ��A�������ł��傤���H
�����ۂ̍�Ɓi�A�j
���@���U�E�����U�s��̌ŗL�x�N�g�������߂�
(1)�@��1�听���̌ŗL�x�N�g�������߂�
��@��������F$E$20 = 1
���@��������F$C$20 = 1
�����ۂ̍�Ɓi�G�j
���@���W���s��̌ŗL�x�N�g�������߂�
��@�}��C19�Ɂ@=MMULT(B14:D16,B19:B21�j
���@�}��C19�Ɂ@=MMULT(B14:D16,A19:A21�j
�����m��ҁn�F�A�����肪�Ƃ��D�\����Ȃ��̂ł����C10�N�ȏ�O�ɍ쐬�������ނ̂��߁C���̌��Excel�ł̓��j���[����̓�����⍀�ڂ̖��O���ς���Ă��āC����킵���Ȃ�܂��̂ŁC���̃y�[�W���i�O��̊֘A����y�[�W���j������ɍ폜���܂�����������炸���������������D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^22.03.21�n
PC�ł��J���Ȃ��悤�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�t�@�C������������܂���
���m�ʂ̕ł���̎���ɑ���n[�ɑ�l�C�ɏ��l(�ɒl)�ɂ��ā^22.03.21�n
(7)��x=1-��2���������Ƃ��̋ɏ��l�̒l���Ԉ���Ă��܂��B
�������肢���܂��B
-2��2-3
�����m��ҁn�F�A�����肪�Ƃ��D���̓���������ɊԈ���Ă���悤�ł��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̒�`�ɂ��ā^22.03.21�n
�ƂĂ��킩��₷���A�悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂ̕������ɂ��ā^22.03.16�n
4. �_�ƕ��ʂ̋����@
��� (2) ���s�ȂQ���ʂ̊Ԃ̋��������߂�
�ŁA-3,0,0 �� x + y/2 + z/3 = -1 ��̓_�ƂȂ��Ă��܂����A
�ԈႢ�ł͂Ȃ��ł��傤���B/ ���6.2 �́A���ł͖������Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����������̍����ɂ��ā^22.03.16�n
�����낢��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l�C�s��`�̋Ɍ��ɂ��ā^22.03.14�n
���̉�����ق����ł��B���킩��܂���B�����A�����b�ɂȂ��Ă��܂��B
�����m��ҁn�F�����l������������Ă����܂����C�u�g�єł͕ʕŁv�Ƒ傫�ȕ����ŏ����Ă���̂�����C����������Ă��������D�V���[�v�E�A�N�I�X��Android��PC�ł����Ă��C�����Ă���͈͂������߂��āC�E����������Ă���̂ɁC�ǂ߂Ă��Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�g�����i���͑�j�ɂ��ā^22.03.13�n
�߂��Ⴍ���ᕪ����悤�ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ς̔���,������,���̋Ɍ�,���̘A���C�Ɍ����ɂ��ā^22.03.10�n
���������b�ɂȂ��Ă���܂��B���̃y�[�W�̖��̉�����ڂ������肢�������܂��B/���̃y�[�W�̖��̉�����ڂ������Ă������������ł��B/���̃y�[�W�̖��ł�����̃X�}�z�̊W��A���͂ł��Ȃ������╶��������܂��B�ł��̂ʼnł��Ȃ����߁A�������܂���B���ق����ł��B
/���̉����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����l������������Ă�����悤�Ȃ̂ŁC�܂Ƃ߂ĉD�u�g�єł͕ʕŁv�Ƒ傫�ȕ����ŏ����Ă���̂�����C����������Ă��������D�V���[�v�E�A�N�I�X��Android��PC�ł����Ă��C�����Ă���͈͂������߂��āC�E����������Ă���̂ɁC�ǂ߂Ă��Ȃ��悤�ł��D�܂��C�V���[�v�E�A�N�I�X��Android�œ��͂ł��Ȃ������Ƃ������̂͂���܂���D������W�I�{�^���͂���1�I��������́C�`�F�b�N�{�b�N�X�͕����I��������̂ŁC�N���b�N�i�^�b�v�j�ɂ���đI�����C�������������ނ��̂ł͂���܂���ŋ߂́C�s�����̏��ނȂǂł����p����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �O�p���E�w�����E�ΐ����ɂ��ā^22.03.10�n
�R�������ɂȂ邱�Ƃ������悤�ł��ˁB�ʔ����ł���B
�����m��ҁn�F�A�����肪�Ƃ��D�����I�ɂ͂��̂悤�Ɍ����邩������܂��C���ʂɖ�������[1]���ł������Ȃ邱�Ƃ��m���Ă���C���̃y�[�W�ł��C���ۂ�[1]�������Ȃ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^22.03.10�n
����킩��₷���Ă܂��B���_�ɂ��Ē��_�B
�����b�N�X�R���e���c���ǂ�����ł���ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�܂��Ƃ�,2017�N�������ɏ��q�������Ɏg��ꂽ���t�炵��
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.03.10�n
�킩��₷�������ł��B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��������(��{)�ɂ��ā^22.03.07�n
���K���̉��������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D��������t���Ă��܂��D�u���̑I�������琳�������̂�I��ŃN���b�N�v�Ə����Ă���܂����C�ǂ�Ȏg���������Ă���̂ł����H���Ă��邾���ł́C�f�W�^�����ނ̎����̓_�@�\��S���g���Ă��Ȃ����ƂɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̍��ɂ��ā^22.03.06�n
�ƂĂ��悩�����ł��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��v�Z1�ɂ��ā^22.03.06�n
���肪�Ƃ�
����Ƒΐ��𗝉����邱�Ƃ��ł��܂����B
����ň��S���Đ����ł������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����s�ǂŋC�ɂȂ��Ă��邱�Ƃ��������悤�ť�����ݍ��߂Ă悩����
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��ň͂܂ꂽ�}�`�̖ʐ��ɂ��ā^22.03.05�n
�吨�ɉe���͂Ȃ��ł����A���4��x�̉��̕��q��-1�}��c�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�R���ԑQ�����̈�ʍ��ɂ��ā^22.03.04�n
�ƂĂ��킩��Ղ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����̋Ɍ��ɂ��ā^22.03.03�n
�����A�q�������Ă��������A�Q�l�ɂ����Ă��������Ă���܂��B�Q�l���������̃T�C�g�̂ق�������₷���A�e�ŁA���J�ɐ�������Ă���܂��B���肪�Ƃ��������܂��B�ݖ�ɂ����āA����̍Ō�̕����ɂ��āAlim�ɂ��Ă��������ڂ���������Ă������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���������ڂ����v�̈Ӗ���������܂���ڂ����������Z���w�͈̔͂���E���邱�ƂɂȂ�̂ŁC�����w�Z�w�K�w���v�̂����ł́u�Ɍ��ɂ��ẮC�����I�ɗ�����������x�ɂƂǂ߂�v�悤�J��Ԃ��q�ׂ��Ă���D
���m�ʂ̕ł���̎���ɑ���n[�ς̔����ɂ��ā^22.03.03�n
�u�Ԉ�����ꍇ�CHELP���I�ׂ܂��v�̂ʼn��Ă��Ȃ���C�o�܂���D�Ȃ��C���Ȃ���Android�Ȃ̂�PC�p�̉�ʂ����Ă��܂����C���Ă���͈͂��������ām����n�Ƃ����{�^�����\������Ă��Ă��C��ʓ��Ɍ����Ă��Ȃ����Ƃ�����܂��D�g�єł͕ʕłƏ����Ă���̂ŁC�g�єł����Ă��������D
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�--�ϕ������̕ύX�ɂ��ā^22.02.28�n
���K���܂ł��Ă��āA�������[�܂�܂����B�i��w��N���j
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����t���m���ɂ��ā^22.02.25�n
��{�I�Ȏ������킩��₷�������Ă��菕����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����2�ɂ��ā^22.02.23�n
�t���獂�Z���ɂȂ�܂��B���ʂ̊w�Z���i�x���ƂĂ������ƕ��������ŗ\�K�����Ă��܂��B�����m���I����Ă��܂����ނ��Ȃ��̂łƂĂ����ӂ��Ă��܂��B�s���ł������Ȃ�Ƃ��撣�ꂻ���ł��I�킩��₷���ł��I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.02.23�n
�u�R���b�c�̖��v�ɊS�̂�����A�K�� !!!
���{���
�p���
Yahoo �� Google �̌����G���W���ł́A�������X�g�ɍڂ�Ȃ��̂́A���̂ł��傤�H
�����m��ҁn�F�A�����肪�Ƃ��D
���肪�Ƃ�
�ƂĂ�������Ղ��Ă��肪����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.02.20�n
�킩��₷���ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���Ȑ��̐ڐ�,�ɐ��ɂ��ā^22.02.17�n
�X�����������Ă鎞�̐ڐ��̕������̉�������Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ�قǁC���̕����̓��e�������̂ŁC����lj����Ă����܂��D
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l�C�s��`�̋Ɍ��ɂ��ā^22.02.17�n
�������ƂĂ��킩��₷���Ă悩���������̂��Ƃ̌v�Z��肪�����藝�����[�߂邱�Ƃ��ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڐ��C�@���̕������ɂ��ā^22.02.17�n
���������
�����m��ҁn�F�A�����肪�Ƃ��D�����ƒ��J�Ȍ��t�ɂ��܂��傤�D�u�v�Z�v�����{�^���������C�r���o�߂̌v�Z�Ɖ��o�܂��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.02.17�n
������������������₷���ėǂ������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̂�����Ƃ��̏����ɂ��ā^22.02.17�n
��3��a,a,a,b,b,c �̂U�̕�������בւ��Ăł��鏇��̂��� b ���݂��ɗׂ荇���Ă�����̂̑��������߂�D
b��1�g������1�I�Ŋ���Ɖ������Ă��܂������Ab1,b2�ƐU�蕪�����Ă���킯�ł͂Ȃ��̂�2�I���d������悤�ȋC������̂ł����A�Ȃ��Q�I�Ŋ���Ȃ��Ă悢�̂��������Ă���������Ə�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��Da,a,a,b
1,b
2,c�Ƃ����`��b�ɋ�ʂ�����ꍇ�ɂ́Cb
1,b
2��ׂ荇�킹��
�@�@a,a,a,(b
1,b
2),c�̂T�̂��̂���ׂ�ƕ��@��

�ł����Cb
1,b
2�̋�ʂ͂Ȃ��̂ŁC�����2!�Ŋ�����

�Ƃ��Ă��悢�D
�@����Ȃɓ���������l���Ȃ��Ă��C�ub���݂��ɗׂ荇���v�̂�����u�܂Ƃ߂ĂP�̑傫��B������v�Ƃ���C���߂���

�łł��܂��D���̓��Ẳ���ɂ́C���ꂪ�����Ă���܂��D
(I)�̉���i�����j�̉E�����̓�s�ځA����an+1-2an��1���Ȃ��݂����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������̏��@�i����Z�j�ɂ��ā^22.02.13�n
������܂���
�I�����C�����Ƃł킩��ɂ������Ƃ��������̂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^22.02.13�n
�ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�y���������ɂ��ā^22.02.13�n
�i�y���������ƂQ���������j�y���R�z�ɂ��Ď��₳���Ă��������B
�u�̉��ł��邱�Ƃ������邩��v�̉��O�s�ڂ���l�s�ڂɂ����āAn�̎������������Ă���̂ł����A���ꂪ�ǂ����Ă��킩��܂���B
���ꂪ�������Ƃ���ƁA(x_n+2^1/2*y_n)^(n-1)=1�ƂȂ�̂ł�����a�����o���Ă���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���č쐬���Ȃ̂�Y��Ă��܂��āC�r���łق����炩���ɂȂ��Ă����悤�ł��D���X����̒��Ԃ���������܂��D
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^22.02.12�n
���̖��͓����̖��̒��ł�������ނɓ���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D����̂���b������C���������ԈႤ�ƁC�S���ɐ����l�̓G������Ă��܂��ꍇ������D�̎d����I�ԕK�v������D
�@���������C��֍Z�ł͈��������̂悤�Ȏ��̕ό`��P���Ŗ₤���Ƃ͏��Ȃ��ł��傤�D�������C����̋��ʃe�X�g���w�̂悤�ɁC����̖��͓��ʓ�����̂ł͂Ȃ��Ă��C���ԓ��ɑS����������Ƃ͂ł��Ȃ����T��̖��̂悤�ɁC�ǂ̖����̂Ă邩�̔��f�ō��ۂ�������饥��Ƃ������ʂ�����̂ŁC�P�茩�������ŁC������ǂ����c�_����Ǝ̎��Ԃƍ���Ȃ��Ȃ�D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕����� �ɂ��ā^22.02.12�n
b��d�̎��́Ay��b�ł�����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����ł����ł����Cb=d�Ȃ̂�����Cy=d�ł��悢�D
�@�Ȃ�,b=d�̂Ƃ��́C�Ⴆ�C(2, 3), (4, 3)�̂悤�ɂQ�_�̂����W���������ꍇ������C�����ɕ��s�Ȓ��� y=3�ɂȂ�܂����C����3��(2, 3)��3�Ȃ̂�(4, 3)��3�Ȃ̂��́C�ǂ���ł��悢
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����2�ɂ��ā^22.02.12�n
���_���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̐��ɂ��ā^22.02.11�n
���Z���ł��B�s�e�X�g�͈͂������̂ł������W���Ȃ����̃y�[�W�Ŗ�艉�K���ł��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���Z�ōs����������悢�Ǝv���܂����C�Ȃ������ʂ̋��ȏ��ł͏����Ă��܂����܂܂ɂȂ��Ă���D
���m�ʂ̕ł���̎���ɑ���n[�����̎w��(�L�����̎w��)�ɂ��ā^22.02.11�n
�u�w���@������w���̒�`�����߂܂��B�v�̃����N�������ƃG���[�y�[�W�ɔ��ł��܂��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^22.02.11�n
��̕\��tan�V�[�^��3/4��7/4�̒l���[1/��R�ɂȂ��Ă��܂����A�|�P�̊ԈႢ�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�\���傫���Ȃ��āu�R�s�y��㩁v�ɂ͂܂����悤�ł�.�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^22.02.10�n
�����̏������̊w�K�ɂ��Ȃ��đf���炵���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�̑��ƌ����ɂ��ā^22.02.09�n
�������߂���A���������߂���Ƃ��ꂼ��R�v�Z���K���ł��A�͂��t���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ϊ��~�X�̌��F�u�����v�̓t�B�����ʐ^�̘b�Łu�����v�����̌��ɂȂ���̂�\��
���m�ʂ̕ł���̎���ɑ���n[ ���������i���p���j�ɂ��ā^22.02.08�n
�R.�P�̉ŁA�|�R�i�R���j�i�|�Q���j�i�|�P�j�̊|���Z���R���|�Q���|�P�̑����Z�ɂȂ�菇���킩��܂���B���������A�ӂ��Ă������Q�Ԃ�E�E�E�E
�����m��ҁn�F�A�����肪�Ƃ��D�u�Q�Ԃ�v�͖ʔ������ϊ�����R�E�����R�c�͏b�R�c�ɐQ�Ԃ����ȂǂƂ����D
���āC
(a^2%2B b^2%2B c^2-ab-bc-ca)&chf=bg,s,fff9f9)
�̌����ɂ����āC

�Ƃ����ƁC���ӂ�
^3%2B (-2y)^3%2B (-1)^3-3(3x)(-2y)(-1)&chf=bg,s,fff9f9)
�ƂȂ�C�E�ӂ�
\{(3x)^2%2B (-2y)^2%2B (-1)^2-\cdots\}&chf=bg,s,fff9f9)
�ɂȂ�܂��D
���i4�j�́Z�����������̂����ԖڂɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ꂪ1�����������̂ŁC������������4�Ԗڂ́C�w���̑傫��������S�ԖځC���Ȃ킿�w���̏�����������Q�ԖڂɂȂ�܂��D�q���g���ɂ��������Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^22.02.07�n
���3-�i2�j�̓���������Ă���悤�ł��B3�̎�����-2+5/2+3/2��0�ƂȂ�A������2.
�����m��ҁn�F�A�����肪�Ƃ��D-2+5/2+3/2��2�ɂȂ�܂�
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^22.02.07�n
�Ƃ��Ă��킩��₷�������I���̒P�����Ȃ������̂ł��������������₷���X�}�z�Ŋy�ɏo���܂���!!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���Ȑ��i���K�Ɠ������j�ɂ��ā^22.02.06�n
�y���2�z�̐����́�47�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D5��67�͑�w���}�[�N�V�[�g�ō̓_���邽�߂̔ԍ��ŁC(�}��47, 0)���ɂȂ�Ƃ������Ƃ́C���̉�ʂɏ����Ă���܂��D
�@����Ƃ��C�}�͂���Ȃ��Ƃ����咣�����Ă�����̂Ȃ�C���̑O�ɏ����Ă����������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^22.02.06�n
�������L�������Ƃ��u�����I�v�Ȃǂł͂Ȃ�����☓�ŕ\�����ق����킩��₷���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��v�Z1�ɂ��ā^22.02.06�n
�߂����Ⴂ���T�C�g�ł��I���ӃJ���Q�L�J��
�����m��ҁn�F�A�����肪�Ƃ��D�w���ӃJ���Q�L�J���x�i�����J�^�J�i������̕\���j�́C��Ҍ��t�ŃA�C�h���O���[�v�E���̋Ȗ����C���c�́u���ӊ����J�Łv�̉��p�łƂ��Ďg����炵����������ł����i�u�P�w�G�v���ォ�ȁj
���m�ʂ̕ł���̎���ɑ���n[�w�����C�ΐ����̓����ɂ��ā^22.02.05�n
(5)��(6)�̏ؖ� lim[h��0]�̂��͂��ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^22.02.03�n
���ȏ���[�N�����Ă�������Ȃ�������肪�����ŗ����o�����Ⴂ�܂����A���肪�Ƃ��������܂�!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȋ��̓����ɂ��ā^22.02.02�n
���3��(1)�̈�ԉE�̍��̕����̕����̕����x�͂���Ȃ��Ǝv���܂��B�Ԉ���Ă����炷�݂܂���B
�ƂĂ��ǂ����K�ɂȂ�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���3��(1)�Ƃ����̂��ǂ̖��Ȃ̂�������܂���D���ɑ��Ƃ͂ǂ�̂��ƂȂ̂��A�܂�(1)�Ƃ����L���͂ǂ��ɂ��g���Ă��Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�ȉ~�̕������̕W���`�ɂ��ā^22.02.02�n
���Q �@�œ_�̓����ƋO�� �}�S���̐����@�}���C|c , x|<a ������C�Q�ڂ́��́������藧�D���悭�����ł��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�u�}���C|c| , |x|<a ������C

�͐��ɂȂ邩��C�Q�ڂ́��́C�t�����ɂ����藧�D�v�Ƃ������Ƃł��D|�@|���ȗ����߂����悤�Ȃ̂ŁC�lj����܂��D
�w�Z�ŏK���Ĉꉞ������悤�ɂ͂Ȃ������̂̂��܂��������X�s�[�h���x���A�Ƃɂ������ꂾ�I�Ƃ悢����T���Ă��܂����B������ƂĂ�������₷���ƂĂ��Q�l�ɂȂ�܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�v���O���~���O�̌�(2.1)�ɂ��ā^22.02.02
�u�l�v���u�R���s���[�^�v�ɓ`������e���u���߁v�Ƃ����܂��B�Ƃ���Ă��܂����A
�u�l�v���u�R���s���[�^�v�ɏ�����������e���u���v�A������������@���u���߁v�Ƃ����܂��B�ł͂Ȃ��ł��傤���H
�`������e�ɂ̓f�[�^�Ɩ��߂̓��ނ����邱�ƂƁA����Ɍq����܂��̂ŁB
�����m��ҁn�F�n�A�����肪�Ƃ��D���w�Z�P�C�Q�N�������̋��ނ́u���w�Z�v���O���~���O����̎���v�Ɋ�Â��č쐬����̂��悭�C�Ⴆ�C����R���s���[�^�͐l�����߂�^���邱�Ƃɂ���ē��삵�܂��B�[�I�Ɍ����A���̖��߂��u�v���O�����v�ł���A���߂�^���邱�Ƃ��u�v���O���~���O�v�ł�����ȂǂƋL�q����Ă��܂��D
�@���Ȃ��̒�`�́C���Ɋ�Ŏ�����邱�Ƃ͂ł��܂���u�l�v���u�R���s���[�^�v�ɏ�����������e���u���v�ƒ�`����C�l����l�ցC���W�I�C�e���r�C�V���Ȃǂ̃��f�B�A����l�ցC�R���s���[�^����l�ցC����`��������̂����̒�`����O��Ă��܂������łȂ��C����Ƃ͕ʂɃf�[�^���o�ꂷ��̂���ł��D�u���w�Z�v���O���~���O����̎���v�����������ƂȂ�ׂ������ł���Ƃ܂ł͌����܂��C�������k�̔��B�i�K�ɉ����āC���w�������Ɍ����ׂ���������I�Ԃ��Ƃ��d�v�ł�
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�̂��낢��Ȗ���ɂ��ā^22.02.01
�������킩��₷���Ĉꂩ��������Ă���Ă���̂Ŏ��K���ނɃs�b�^���Ȃ������ނ��Ǝv���܂��B�w�Z�ŋ��t�Ȃǂ�����Ă���̂ł����H�w�Z�̑�l�C�̐��w�̐搶�̘b���v���o���܂��I���̋��ނ͂��������ꂢ�ɂ܂Ƃ܂��Ă��Ďg���₷���ł��B�i���w�I�A�[�@�̃y�[�W��ǂ̂ł����j��̎��_����ł͂Ȃ����p�I�ɖ��������Ă��đ�ϕ��ɂȂ�܂����B�܂���萔����������̂őS�̑������ނ̂ɑ傢�ɖ𗧂��܂����B�܂����̂ق��̃y�[�W���l�X�Ȑ}��Ƃ炦�����Љ��Ă��ăC���[�W�����݂₷�������ł��B
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^22.02.01
������₷���A�ƂĂ��𗧂��܂����I���肪�Ƃ��������܂����I
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���ɂ��ā^22.01.31
-1+3i
�����m��ҁn�F�n�A�����肪�Ƃ��D���̃y�[�W��ǂl�����̎��������Ƃ�����C���̃y�[�W�̓��e���S�R�����ł��Ȃ������Ƃ������ƂɂȂ�܂��D����������I���܂łɂR�S�b�ł����̂ŁC�������������ǂ�ł��Ȃ��̂ł͂Ȃ��ł��傤���D

�̋��f����

�L���ŏ�����

���x����T���Ă����̂ŏ�����܂����I
���肪�Ƃ��������܂��I
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^22.01.31
�킩��₷�������ł�
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^22.01.31
�ƂĂ��悩����
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^22.01.30
�����������Ă܂��B���ӁB
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��s��C�P�ʍs���ɂ��ā^22.01.30
�s��̗ݏ�v�Z�����f����Ƒ�ςł��B���̓_����@�\�Ɋ��S���܂��B
�����m��ҁn�F�n�A�����肪�Ƃ��D���̏ꍇ�̊����͉��悢
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕�����2�ɂ��ā^22.01.28
���ہ��O�ڂ̐}�̍��W�͊ԈႢ�ł����H
�����m��ҁn�F�n�A�����肪�Ƃ��D���ۂR�ڂƂ͉��̂��ƂȂ̂��D�ۂ͂Q�����Ȃ��D�~�̒��S�̍��W�ƌ������̂͂��邪�C�ۂ̍��W�Ƃ������̂͂Ȃ��D�����������̘b�����Ă���̂��ʂ��܂���
���m�ʂ̕ł���̎���ɑ���n[���[�w��C�����̏����ɂ��ā^22.01.28
��Q�j���̗�
0000�͎s�O�ǔԂ̑��k�����Ȃ�ł��ˁB���m���ʔ����ł�
�����m��ҁn�F�n�A�����肪�Ƃ��D���w�����̐��k�������̂ŁC����l�^��p�ӂ��Ă����Ȃ��ƁC�Q���Ă��܂��̂ť��
���m�ʂ̕ł���̎���ɑ���n[�P�̋����R�捪���ɂ��ā^22.01.27
��{�I�Ȗ��������Ƒ��₵�Ăق����ł�
�����m��ҁn�F�n�A�����肪�Ƃ��D���P���T�肠��Ƃ������Ƃ́C�������Ă��܂����H
���m�ʂ̕ł���̎���ɑ���n[�s���ɂ��ā^22.01.27
���̃T�C�g�ō�����
�����m��ҁn�F�n�A�����肪�Ƃ��D���Z�̐��w����s����Ȃ������̂́C�������b�ł�
���m�ʂ̕ł���̎���ɑ���n[��Βl�t���̒�ϕ��ɂ��ā^22.01.27
��ώQ�l�ɂȂ�T�C�g������Ă����������肪�Ƃ��������܂��B���R��dx��dt�ł͂Ȃ��ł����H
�����m��ҁn�F�n�A�����肪�Ƃ��D���e�I�ɂ́C���\�傫�ȃ~�X�ł����C�������܂���
���m�ʂ̕ł���̎���ɑ���n[�}��ϐ��\���Ƃ��ɂ��ā^22.01.27
�Ō�̖��Ay=0�̂Ƃ�x=-1�܂ł͂킩���ł����ǁA���̌��(y=0,x=1�͕s��)���킩��܂���B�����y=0�̂Ƃ�x=-1��(2)�͂����ł�����(1)��y=0.x=-1�ɂ͂Ȃ�܂����ˁH�Ȃ��x=-1,y=0��������Ȃ��̂����킩��Ȃ��ł��B
�����m��ҁn�F�n�A�����肪�Ƃ��D�Q�����̌�_�́u�A���������v�̉��ɂȂ�̂ŁC�����̎������Ȃ���Ȃ�܂���D(2)���ŁCy=0�̂Ƃ�x=-1�Ȃ�C(1)���炻���łȂ����̂��o�Ă��Ă��C���ɂ͂Ȃ�܂���D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓�������ɂ��ā^22.01.27
���f���̓����S�̂����̐��̖��̑O�ɓ��B���܂����A�i�|���I���̂悤�ɍ��g���Ă��܂��B77�̌����Z���t�ł����A�l���̒��ł���ȂɏW�����ĕ��������Ƃ͂Ȃ������Ǝv���܂��B�R���i���|���ĕ\�ɏo���Ȃ����ɂ���܂����A���̗l�Ȍo���������Ē������肪�Ƃ��������܂��B���ӂ��܂��B�P���Q�V��
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������a�C�e�C���[�W�J�C�}�N���[�����W�J�ɂ��ā^22.01.25
�F�X�ȏ��ŏo�Ă���x���k�[�C���E�I�C���[�����ǂ�������܂���
�����m��ҁn�F�n�A�����肪�Ƃ��D��`�ł�����C���̒i�K�łȂ��Ƃ����͖̂����ł��D�悭�o�Ă��镪��ɐi��ł���U��Ԃ�Ώ\���ł��D
���m�ʂ̕ł���̎���ɑ���n[�������a�C�e�C���[�W�J�C�}�N���[�����W�J�ɂ��ā^22.01.25
(5.2) �� cosX �� �� �̎����Ⴄ�Ǝv���܂�
n=1 ����n�߂�� cosX = +(x^2/2!) -(x^4/4!) ... �ɂȂ��čŏ��̂P�������Ă��܂��܂�
n=0 ���珉�߂Ă��̂悤�ɏ����������ǂ��Ǝv���܂�
�EcosX = ��(n=0,��)(-1)^n * (x^2n / 2n!)
�EsinX = ��(n=0,��)(-1)^n * (x^(2n+1) / (2n+1)!)
�����m��ҁn�F�n�A�����肪�Ƃ��D(4.2)�̍Čf�ł����C�P����Ă���Ƃ��낪����܂����̂Œ����܂����D�Ȃ��C�����W�Ȃǂł́Cn=0���珑�����Ƃ������ł����C���Rn=1���珑�����Ƃ��ł��܂�
���m�ʂ̕ł���̎���ɑ���n[�P�̋����R�捪���ɂ��ā^22.01.25�n
�_�l�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̓Ɨ��ɂ��ā^22.01.25�n
�����g�킹�Ē����Ă܂��B���̕���̐����̓W�J�����ɂ����ł��B���������P���Ă��ꂽ���Ϗ�����܂��B�@
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɂ́C�������W�J���Ȃ��C�����̓W�J������܂���D���ɂ����Ƃ́C�����̑傫���C�F�̂悤�ȊO�`�I�Ȃ��ƂȂ̂��C�b�̐i�ߕ��̂��ƂȂ̂����s���ł��D
���m�ʂ̕ł���̎���ɑ���n[�������̏��@�i����Z�j�ɂ��ā^22.01.24�n
�킩��₷���I�I
���肪�Ƃ��������܂�o/|_
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������1�ɂ��ā^22.01.24�n
2�_�Ԃ̋��������̓������P�܂Œ��܂����B�㔼�̎��������A����������O�ɑ����݂��Ă��܂��B
�����܂ʼn����ė܂��o�܂����B���������A���������͈ȑOYutube�̖{�c�̐��w�Ŋw�K�������Ƃ�����܂������g�ɂ��܂���ł����B�M���̂��炵�����ނɏo����肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̒u���ϕ��ɂ��ā^22.01.24�n
��4�́��̂Ƃ��낪���܂łɂ����Ƌ^��Ɏv���Ă������ƂȂ̂ŁA�Q�l�ɂȂ�܂����B���肪�Ƃ��������܂����B
�ł��A���̂��Ƃ̏ؖ��͂ǂ̂悤�ɂ���悢�̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D
1. ���R�Ђ̋��ȏ��ł́C����������̂悤�ɋL�q����Ă���C�ϊ���
&chf=bg,s,fff9f9)
���P�����ł��邱�Ƃ͗v������Ă��܂���D���Ȃ킿
&chf=bg,s,fff9f9)
�������\�ł���Ƃ���D
,\hspace{2}b=g(\beta)&chf=bg,s,fff9f9)
�̂Ƃ�
dx=\underset{\alpha}{\int^{\beta}}f(g(t))g\apos(t)dt\]&chf=bg,s,fff9f9)
������C
&chf=bg,s,fff9f9)
���P�������܂��͒P�������ł���K�v�͂Ȃ��D�i���w�I�ɂ́C�ȏ�Ős������Ă��܂����C�ǂ����Ă��ڍׂ��������ꍇ�́C���̂悤�ɕό`�ł��܂��j
2.
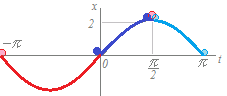
��}�̏ꍇ
)g\apos(t)dt=0\]&chf=bg,s,fff9f9)
������i�����q������܂����������J���X���ق�����ƁC���߂��牽���Ȃ��������ƂɂȂ�j
)g\apos(t)dt=\underset{-\pi}{\int^{0}}f(g(t))g\apos(t)dt%2B\underset{0}{\int^{\frac{\pi}{2}}}f(g(t))g\apos(t)dt\]&chf=bg,s,fff9f9)
)g\apos(t)dt\]&chf=bg,s,fff9f9)
3. �܂�
)g\apos(t)dt=0\]&chf=bg,s,fff9f9)
������
)g\apos(t)dt%2B\underset{\frac{\pi}{2}}{\int^{\pi}}f(g(t))g\apos(t)dt=0\]&chf=bg,s,fff9f9)
)g\apos(t)dt=\underset{0}{\int^{\frac{\pi}{2}}}f(g(t))g\apos(t)dt\]&chf=bg,s,fff9f9)
)g\apos(t)dt=\underset{0}{\int^{\frac{\pi}{2}}}f(g(t))g\apos(t)dt\]&chf=bg,s,fff9f9)
�����Q�Q�����Q�ɒ���P����U�̒��łS����U�͊��������o���Ă��܂������A�̈�̖��1����3�ɂ͋ꂵ�݂܂����B�܂����M������܂���B�������Ȃ�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�g�����@�ɂ��ā^22.01.22�n
�g�����@��2���ȏ�ł��ō����W����1�ȊO�ł�����܂��B��������ނ���A����̑��Z�⌟�Z�̗��p����ł��B�ڐ��A���s�ړ��A�`�����n�E�X�ϊ��A��
�����m��ҁn�F�A�����肪�Ƃ��D�{���̏��߂ɏ����Ă��܂��悤�ɁC�M�҂͂P���̏ꍇ���܂߂đg�����@�s�v�_�҂ł��D
���m�ʂ̕ł���̎���ɑ���n[���f���̂P���������\���}�`�ɂ��ā^22.01.21�n
���f���̈ꎟ�����̕\���}�`�̖��P�������I���܂����B���̋��ނɏ��߂ďo��������Ă��܂��B
�x�N�g���ŗ��������܈�ł����B�S�苭����g�ɒ������܂��B�L��������܂��B��������J�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̋O�Ղ̕�����2(�ϊ�)[�����Z���wC]�ɂ��ā^22.01.20�n
(�R)�͏W���͂��v������܂��B4��قǂ�蒼���܂����B���]�͓���ł��B�Ȃ����̐߂̈ړ��A���]�A�g��̗������p���������̂ł��������ł��܂���B�O���t�̈ړ��ƈႢ�܂����B�ǂ̎�������ł���悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�₳���������������ŁC����g�ɒ����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������Q�ɂ��ā^22.01.19�n
���i�����Ɋ��p�����Ē����A��ς��肪�Ƃ��������܂��B
�O�Ղ̕�����2�i���_�Q�j�y�[�W�A�m���2�n�́m�n�Ԏ��ł̉�������W�s��
�u(x�|1)(x�|2)+(y�|1)(y�|1)=1 �ɂȂ�D�v�̕����ł����A
�u(x�|2)(x�|2)+(y�|1)(y�|1)=1 �ɂȂ�D�v���Ǝv���܂��B
��x���m�F�������܂��悤���肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ڂ������܂Ō��Ă���Ă��肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�K�������ɂ��ā^22.01.19�n
��艉�K���M���ł�🔥
�����m��ҁn�F�A�����肪�Ƃ��D�����C���̔M���w���Ƃ����Ӗ��̔M������
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^22.01.17�n
�V���v���ŗǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̑Ώ̎��C�l�̑���ɂ��ā^22.01.16�n
���I�ԁA��I���A�S�������Ȃ�good�ƖJ�߂���B���̎w���@�͂��C���N�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^22.01.16�n
�P�O�⒆2�◎�Ƃ��܂���(�S)(�V)�ł��B���f���̌v�Z�Ƃ������ƂŊÂ����Ă���Ǝv��ʃ~�X�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��Œ�܂�萔 �ɂ��ā^22.01.16�n
��ϕ��ł���킳���萔�̊w�K��ʂ��Đϕ��̗͂���i�Ƃ����C�����ɂȂ�܂��B�}�`��ǂݎ��͂͂��܂ЂƂł��B�V�V�̂��Ɛ��w���t�Ƃ��Ă��̋��ނ��w�K�ł������Ƃ͗L��ł��B�E�C�����炢�܂����B���ӂ��܂��B
�����m��ҁn�F�n�A�����肪�Ƃ��D�I��̔N�ɐ��܂ꂽ�l�́C���̂��������Ȃ��D���͂����ƎႢ���ł����C���N�p�~�\��̋����Ƌ��X�V���x�́C���a29�N�ȑO�ɐ��܂ꂽ�������C�܂����i��E���u�t�E���w�ȂǂŁj�܂������C������Ƃ͑z�肵�Ă��Ȃ�����??�悤�ŁC�Ƌ���X�V�u�K�̎�u���K�v�Ȏ҂ɓ����Ă��Ȃ��D�i�����Ȋw�Ȃ̂������y�[�W�ɂ́C�u���a30�N4��1���ȑO�ɐ��܂ꂽ���ɂ��ẮA�h�{���@�Ƌ���������Ă��Ȃ�����A�ŏ��̏C���m�F�����͐ݒ肳��Ă��܂���̂ŁA�X�V�u�K����u�E�C�����Ȃ��Ă��A������������̋����Ƌ���͗L���ƂȂ�܂��B�v�Ə�����Ă���j
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̕��s�����C���������ɂ��ā^22.01.16
�Ȃ�Ł�i25t^2�j��25t�ɂȂ��
5t����
�����m��ҁn�F�n�A�����肪�Ƃ��D����������Ƃ���C

�ƌ����ׂ��ł��D���������C���Ȃ��͕������̕ό`���������Ă��܂����C���̏�ʂ͕������̕ό`�ł��D
�iA:�������̕ό`�Ƃ��Ắj

�ӁX�Q�悷���

�ӁX��25�Ŋ����


�iB:���ӂ̕�����������ό`����ꍇ�́j

����������

�ӁX�Q�悷���

�ӁX��25�Ŋ����


�@���̒��x�̕ό`�́C�ڂ̎q�Z�i���������łł���v�Z�j�ɂ��܂��傤�D�Ȃ��Canonymous������Ƃ����ė��\�Ȍ��t���g���̂͂悭�Ȃ����Ƃł��D
������1/x�̐ϕ����ΐ����ɂȂ�Ƃ���Ő^���ɐ�Βl���t�����R�͉����낤�Ǝv���Ă����B���̃T�C�g�̐�����q�����A�ΐ����̔������l����Ƃ��ɐ^�������A��������̏ꍇ�ł�����1/x�ɂȂ�Ƃ������������J�ł킩��₷����ώQ�l�ɂȂ�܂����B
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����W��,�A��,�����\�ɂ��ā^22.01.14
�Ⴊ�킩��₷������
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̎w��(�L�����̎w��) �ɂ��ā^22.01.13
�ƂĂ��킩��₷���Ă��������ł���
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����,���̋Ɍ��ɂ��ā^22.01.12
�����w���t�ł����A���Z�A��w�Ɨ�����ɗ��āA���ɑł�����ł��܂���ł����B���R�P���P�Q�������M�a�̋��ށ@�A�Ɍ��C���s�^���̒藝�ɏo����K�Ɏ��|����܂����B�̐���܂Ŋm���߂��L��ł��B�f���炵�����ނ�L��������܂��B���̏ꍇ�͂悢���t�A�悢���ނɏo������Ƃ��\�͂����߂��܂��B
�����m��ҁn�F�n�A�����肪�Ƃ��D���E�����̍��͎G�p�����߂��āC��������c�Ǝ��Ԃ�n00���ԁi�v�����C������. n=1�Ƃ͌���Ȃ��Ƃ��낪���낵���j�Ƃ������Ƃ���ԉ����Ă����悤�Ɏv���܂��D������C���ތ����s���̂܂��Ƃ�����Ȃ������̂́C���݂����܂�������܂���D
���m�ʂ̕ł���̎���ɑ���n[���w�h�ɂ�����O�p��̒�`�i���K�j�ɂ��ā^22.01.07
��15��̉ŁAsin(-270��)��-1�ƂȂ��Ă��܂����B
sin(-270��)��sin90���ƂȂ�A���̏ꍇx=0,y=r�ƂȂ邽�߁Asin90��=1�ƂȂ�Ǝv���܂��B
���m�F��낵�����˂������܂��B
�����m��ҁn�F�n�A�����肪�Ƃ��D�i�告�o�����R���̏���������ɏ����Ă݂��j��15��̍̓_�͍����Ă��邪�C�̉�����̕������t�ɂȂ��Ă���ƕ��������t���C���ׂČ���ƁC�̉�����̕������t�ɂȂ��Ă��邱�Ƃ�������C���������D
���m�ʂ̕ł���̎���ɑ���n[�O�p�s�����ɂ��ā^22.01.06
���5�͂Ȃ�cos�Ƃ�0-180�����ׂĖԗ����Ă���̂ɁA�����̕��͂킴�킴�͈͂̏��Ȃ�sin�Ƃŏo���Ă���̂ł��傤��?
�����m��ҁn�F�n�A�����肪�Ƃ��D�����ɉ���������Ă���܂����Ccos��−2�̕����͏�ɕ��ł�����C�� (cos��−2)(2sin��−1)<0 �ƂȂ�̂́C2sin��−1>0�̏ꍇ�ł��D���(cos��−2)<0 ����(2sin��−1)>0 �̘A���ł��D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����̗��K����ɂ��ā^22.01.05
�ƂĂ����₷�������ł��B�o�������Ƃ��������K�o���ėǂ������ł�
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��v�Z1�ɂ��ā^21.12.27
�킩��₷�������ł��B�Q�l�ɂȂ�܂����I
�����m��ҁn�F�n�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���s��������̐������ɂ��ā^21.12.26
���Ɍv�Z���A�s���̂������l���g��Ȃ����̂�lj����Ăق����ł��B
�����m��ҁn�F�n�A�����肪�Ƃ��D��������]�Ȃ̂����`���܂��C���ʉ����g�킸�Ɉ�ʉ������߂����Ƃ������Ƃł�����C���̕��̇U��V�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�������i�L�����j�̕s��ϕ��ɂ��ā^21.12.25
(2) iii)���������(**)��3�s������Adt/dx��dx/dt�ł͂Ȃ��ł����H
�����m��ҁn�F�n�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ڐ��̕������ɂ��ā^21.12.24
1�█�̉�����Ȃ��Ƌ��ȂƂ��낾�Ƃ����ς�킩��Ȃ��̂ł��萔�����|�����܂����A�����Ē��������ł��B
�����m��ҁn�F�n�A�����肪�Ƃ��D�u�v���u�v�D�v�Z�Ƃ����L�����N���b�N����C�r���̌v�Z���\������܂��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.12.24
F = x ^ 4 - 6x ^ 2 + 1 �̕���������������Ē��������ł�.
�����m��ҁn�F�n�A�����肪�Ƃ��D�S�����Ȃ̂ŁC�Q�������g���ĕ����������܂����C���̃y�[�W�̖�肪�ς�ł���l���C���̂悤�Ȏ��������͕̂ςł��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^21.12.23
���߂܂���
������
��������ċt�Z��������}������̕��я��̋��ʐ������o�����@�͂ƂĂ��f���炵���Ǝv���܂����B
�ł��AXx3+1�ŋ����ɂȂ�Ȃ���ΐ��͑傫���Ȃ�܂����A�����������ꂪ�����̂ł��������2�Ŋ����̂ŕK��1�ɂȂ�̂ł͖����ł��傤���B
�����m��ҁn�F�n�A�����肪�Ƃ��D�c�_���G�߂��ďؖ��ɂ͌����܂���D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^21.12.22
���鐮����(x-1)^2�̂悤�Ȗ�肪�~�����ł��I��낵�����肢���܂�
�����m��ҁn�F�n�T�u���j���[�Ŏ��̍��ځC���̎��̍��ڂɂ���܂�---iPhone��PC�p�̉�ʂ����Ă���ꍇ�C�T�u���j���[���\������܂���.�X�}�z�p�̉�ʂ����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[���̎w���ɂ��ā^21.12.21�n
����A���̖������g�����Ƃ����̂́A�����̓��{�l���w�ҁ@����F�ܘY���]�˖��{�C�R�̒���`�K���ŃI�����_�l���w�҂���w�G�s�\�[�h����ɂȂ�܂��B���ꂩ����̂̐��w�҂Ɍh�ӂ����߂Ċw��ł��������ł��B
�����m��ҁn�F�E�E�E
���m�ʂ̕ł���̎���ɑ���n[�R�������P�_�Ō���邽�߂̏����ɂ��ā^21.12.19�n
��肨�����ʼn������̂ŁA��藝�����[�܂����B
���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^21.12.15�n
3.(1)1����3.(3)1�܂ōŏ��ɒu��y��A��B���t�ł͂Ȃ��ł��傤���B
�����m��ҁn�Fsinx��cosx�����O�ɏ����Ȃ���Ȃ�Ȃ��Ƃ��C��͋���������ɁC�j�q�͏��q�����O�ɕ��Ȃ���Ȃ�Ȃ��Ƃ��Ƃ������܂�͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̍��ɂ��ā^21.12.15�n
�����}�����̂������킩��₷������Ȃ藝���ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[N�i�@�ɂ��ā^21.12.07�n
���̍��Z���w�̕��ɖ𗧂ĂĂ��܂��B��{�I������y�ɁC�����[���w�ׂ�̂ŁC��Ϗ������Ă��܂��B���wA�ɁC�u�}�`�v�̖�肪�S������܂���B�ǂ�������悢�̂ł��傤���B���������������B
�����m��ҁn�F�A�����肪�Ƃ��D����ے��̉����ɉ����āC2021�N���w���C����ȑO���C�Ȍォ�ň������ς��ꍇ������܂����C�������Z�ŋ����Ă����Ƃ��́u���wA�̐}�`�͋����܂���ł����v�D
���wA�̋��ȏ��́C3�P�ʗp�i�T��3���ԋ�����j�Ƃ��č���Ă��܂����C�e�w�Z�ł��̂�������2�P�ʂ����I��ŋ�����D�����Ƃ͂����茾���C���w�T�Ɛ��wA�����킹��6�P�ʂɂ��ĂP�l�̒S���҂�������--��������C�P�ʐ��̏��Ȃ����w�T�Ɏ��Ԃ�������--�������C�P�ʔF��͕ʂ̉ȖڂƂ��čs��Ȃ���Ȃ�Ȃ��D���wA�̐}�`�́C���w�Z�ŏK���}�`�̕��K�������C�܂����Z���w���̂Ƃ��Ă͌�ɂȂ�����̂����Ȃ��C���H�̂悤�Ȋ����ł��D
�@���̋��ނł́C���w�Z�̐��w�ɖڎ�������Ă���܂��D�ӂ̒����̔�C�ܐS�C�`�F�o�̒藝�E���l���E�X�̒藝,�~�ɓ��ڂ���l�ӌ`�Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�`�F�r�V�F�t�̕s�����ɂ��ā^21.12.08�n
���̃T�C�g�́A��肪�����ڂ��Ă���̂ł悭���p�����Ă�����Ă��܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��̒����ɂ��ā^21.12.07�n
1.3�̒u���Ή��\�̉���ds/dt�̊ԈႢ�ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�傫�Ȑ��ł͌����܂��C�ߊ�̘V��̗����̂����ł�����������܂���
���m�ʂ̕ł���̎���ɑ���n[�w���������ɂ��ā^21.12.06�n
�P�O��0.9����Ăǂ�����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�u�ǂ�����ł����v�ł́C�q�˕����c�t�ł��D(1)�u�����\���Ă�����e�́H�v,(2)�u���l�̋��ߕ��́H�v�Ȃ�C�����邱�Ƃ��ł��܂��D
(1) �w���̕����������ŏ�����Ă���

�́C�����̎w�����g����

�Ə������Ƃ��ł��C�ݏ捪���g���ď�����

�ɂȂ�܂��D
(2) ���l�����߂�ɂ́CMicrosoft Excel���g���̂��y.�i�Ȃ��C�w���E���k�̏ꍇ�C������Office�����Ȃ��Ă��CWeb��ʏ�ŁuExcel Online�v�Ƃ������̂��ŗ��p�ł���F���[���A�h���X������Ύg����FExcel Online�Ō����j���[�N�V�[�g��̂ǂ����̃Z���� =10^0.9�Ə������߂C�L������10�����x�ŁC7.943282347 �ƕ\�������D���ۂɂ́C���������̋ߎ��l��������Ă���̂ŁC�����𑝂₹�C����ɐ��m�ɂ͂Ȃ�D7.943282347242818^10�́C�قڂق�1000000000�ɂȂ�܂��D
sin��=sin�� �̕������ƂĂ�������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�g�����ɂ��ā^21.11.30�n
�X�l�̐l���`�̕����ɂS�l�C�a�̕����ɂR�l�C�b�̕����ɂQ�l�������@�́C9�b4�E5�b3�E2�b2�ʂ聁1260�ʂ�ł�.
�X�l�̐l���S�l�C�R�l�C�Q�l�̂R�g�ɕ�������@�́C
9�b4�E5�b3�E2�b2�ʂ聁1260�ʂ�ł�.
�ŏ��̖��ł���1260�~6�ł͂����Ȃ��̂ł���?
�����m��ҁn�F�A�����肪�Ƃ��D���̉E���ɉ���������Ă���ʂ�u�S�l�̑g�͂`�ɂ������ꂸ�C�R�l�̑g�͂a�ɂ������ꂸ�C�Q�l�̑g�͂b�ɂ�������܂���.������C���������߂�ꍇ�Ɠ����ɂȂ�܂�.�v
�@������C���Ȃ��̍l�����͊Ԉ���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�ȉ~�̕������ɂ��ā^21.11.28�n
�������̉E���̐�����'����'���A���t�@�x�b�g��'����'�ƌ��ԈႦ�₷�����̂Ȃ̂�,�ς��������悢�̂ł͂Ȃ��ł��傤��.���̏ꍇ�͑ȉ~�̌������̂�S���m��Ȃ������̂�,�����������߂�i�K�܂ō���������ԂɂȂ��Ă��܂��܂���.
�����m��ҁn�F�A�����肪�Ƃ��D
1��
l�͂悭���Ă��܂��DPC��X�}�z�ł́C�@��ɂ���Ďg����t�H���g���قȂ邽�߁C���܂�i�荞�t�H���g���g���ƕ\���ł��Ȃ��\��������܂��D�e�@��̓��ڃt�H���g�Ɉˑ����Ȃ�Google Web�t�H���g�Ƃ����̂�����܂����C�ǂ̎��̂��g���Ă��C�悭���Ă���͓̂������Ƃł��D
�@���̃T�C�g�ł́C���̐��w���ނƓ��l��
l��
o��
1��
0�ƕ���킵������C�u�ǂ����Ă��K�v�̏ꍇ�������Ďg��Ȃ��v���Ƃɂ��Ă��܂��D�ǂ����Ă��K�v�ȏꍇ�Ƃ́C

�̂悤�ɁC
l���L���Ƃ��ĕK�v�ȏꍇ�Ƃ�

�̂悤��,
k, l, m�����̏��i�I�����_�q��̏��j�Ƀp�����[�^�Ƃ��Ďg����ꍇ�Ȃǂł��傤�D
�@�]���āC���������C
l��
o�͏����ĂȂ��̂ŊԈႤ������͂���܂��C
1���������ĂȂ��Ƃ��ɁC����ł�����킵������Ƃ�����
1�ȂǂƏ����ƁC�u�q����n���ɂ��Ă���̂��I�v�u�C�����Ƃ��達�v�ƍl����l�������Ȃ�ł��傤�D������C���Ȃ��̗v�]�ɂ͑Ή��ł��܂���D
�萔�W����2�K���`����������(��)
���4.(3).1�̖�肪���x����Ă����������ɂȂ�Ȃ��̂œr���o�߂������Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������������܂����D�m���Ɍv�Z���ς킵���ł����C���Z�����Ȃ�Cmaxima���g���āCode2('diff(y,x,2)-4*'diff(y,x,1)+4*y=x*sin(x), y, x);�Ə������߂C�����o�܂��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̌v�Z�ɂ��ā^21.11.21�n
������₷���w�ׂĂƂĂ��ǂ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^21.11.17�n
���7�́i3�j�ɂ���
a,b,c�̑召�W�͒�܂��Ă��܂����Aa,b,c�̕�������܂��Ă��Ȃ��̂ŁA�Ή����镽�����̑召�W����܂�܂���B�Ⴆ��a=1,b=2,c=3�ł���Ίe���̕������̑召�W��1,4,9�ƕς�炸��肠��܂��Aa=-3,b=-2,c=-1�ł���Ε������̑召�W��9,4,1�ƂȂ�̂ŁA�`�F�r�V�F�t�̕s������K�p����ƁA�o�ia���+b���+c���j/3�p�~�o(a+b+c)/3�p<=(a���~c+b�O��+c���~a)/3�ƂȂ��Ă��܂��܂��B����ƁA�̂悤�ɘA�����ă`�F�r�V�F�t�̕s������K�p�ł��Ȃ��C�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɂ��������̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����̗��K����ɂ��ā^21.11.15�n
�d�Ԃ̒���A�R�[�q�[��Ă�Ԃɂ����p�ł��ďd�Ă��܂��`☺️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�̏����ɂ��ā^21.11.14�n
��w�ł��B�q���ɍ��Z���w����������悤�A���ł������撣���Ă��܂��B�������܂��Ă��܂������A�����̃O���[�̈ꌾ�R�����g���S�ɋ����āA���܂ł̂Ƃ��돇���ɐi��ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̒�`�ɂ��ā^21.11.13�n
�h����x�N�g�����ŗL�x�N�g���ł���Ƃ��C���̒萔�{�i�O�{�ȊO�j�͂��ׂČŗL�x�N�g���ƂȂ�h������̋L�q�ɂ��āA���̒萔�{�Ƃ����̂́A���̍s��A�̊e�v�f�������ō\������Ă���ꍇ�A�萔�{���s���C�Ӓ萔�͕K�������Ƃ����F���Ő������ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�x�N�g���̐����Ƃ��Ď����͈̔͂܂ōl���邩�C���f���͈̔͂܂ōl���邩�́C�g���l�̑I���̖��ŁC�ǂ���łȂ���Ȃ�Ȃ��Ƃ��������̖��ł͂Ȃ��Ǝv���܂��D
�@�Ⴆ�C�e�����������ŕ��ʏ�̊e�_�����_�̎����-90����]������P���ϊ��̍s��

�ɑΉ�����ŗL�l�C�ŗL�x�N�g����
�ŗL�l

�C�ŗL�x�N�g��

��

�ŗL�l

�C�ŗL�x�N�g��

��

�ƂȂ邩��C�s��̐��������ׂĎ����ł��u�A�j�x�N�g���̐�����ŗL�l�f���͈̔͂ōl����ꍇ�v�́C��L�̓��Ă̂悤�ɂȂ�C�u�C�j�x�N�g���̐�����ŗL�l�͈̔͂������͈̔͂Ɍ��肷��ꍇ�v�́C���Ȃ��ƂȂ�܂��D�܂��C������őz�肳��Ă���悤�ȁC�s��̊e�����C�ŗL�l�C�ŗL�x�N�g���i�̂P�j�����ׂĎ����ł���ꍇ�ł��C���f���̒萔�{�����e�͈͂ɓ����C���f���𐬕��Ƃ���x�N�g�������邱�ƂɂȂ�܂��D
�ׂ����������J�ŗǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�i���j�ɂ��ā^21.11.08�n
��萔�𑝂₵�Ăق���
�������킹���ł���̂��֗�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�N�������̌����ɂ��ā^21.11.06�n
�ŏ��̗v�_1��X=�̕��q�����A�c�ɂ��@���ł͂Ȃ����@�����Ǝv���܂��B
��ς킩��₷���A�v�_���܂Ƃ߂��Ă��肢���d�Ă��܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^21.11.04�n
�������ȑ�w��w�����Ɗ�]�ł�
�K���o�ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^21.11.03�n
����f(x)���Q�̂Q�����Ŋ���ƁA�ǂ���̗]����萔�ɂȂ�Ƃ��̉�@���ڂ��Ă���������ƍK���ł��B
��f(x)=P(x)(���@)�{(�萔)
=Q(x)(���A)�{(�萔)
=R(x)(���@)(���A)�{(�O�����ȉ��̗]��)
�ƂȂ�Ƃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����̐搶�̒��ɂ́u�F�܂Ō��킹��Ȃ�=�����͎����ōl����悤�Ɂv�Ƃ������Ƃ�����D�F�X�ȏꍇ�ɂ��ė��K���Ă���̂�����C�ʂ̖��̓������ꂼ��q�˂Ȃ��Ă��C�ސ��ʼn�����悤�ɂ��ׂ��ł��D�����łȂ���C�w�K�s�\���ł��D
�Ⴆ��,f(x)��x2−x�Ŋ������]�肪3�Cf(x)��x2+x−2�Ŋ������]�肪4�̂Ƃ��Cf(x)��(x2−x)(x2−x−2)�Ŋ������]���5/2x3−3x2−5/2x+3
���m�ʂ̕ł���̎���ɑ���n[���v���X�ϊ��̊�{�ɂ��ā^21.11.02�n
���3�́i3�j��a=-1,b=c=1/2���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̂P�O�̌W����r�ɊԈႢ������܂����̂ŁC������̕���������܂���
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.11.02�n
�т����肷�邭�炢�A�킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��i�܂Ƃ߂P�j�ɂ��ā^21.10.25�n
�ΐ����̕s��ϕ��@���7 ���̗�3�߁@(logx)^2�̉ł����A�I������̍ŏ���x�͑S�̂����ʂł�����A�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��Dx�ł����邱�Ƃ��ł��܂����C������Ȃ���Ȃ�Ȃ��Ƃ������Ƃł͂Ȃ��D���̌�ɂǂ��ό`���邩�ɂ���ĕς��C������ϕ����s���ꍇ�́C�ς̌`�łȂ������g���₷���D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^21.10.25�n
�Ō��(J) �̍Ō�̎��ł������ӂ�13������̂�
�P�~�R�O�Q�^�Q�O�V�ɂȂ�̂͂킩��̂ł���
�Ō�̎��@�~�E�E�E�~�i�P�R�~�R�j�^�i�T�~�W�j
�͂P�ɂȂ�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�w���@�ł�����C���̉��肩�疵�����邱�Ƃ������Ă��܂��D�P�ɂ͂Ȃ�܂���D����������Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�~����C���ジ�����ɂ��ā^21.10.25�n
�y�U�z�͉��łS�E�R������̂��킩��܂���B
�S�l�̏��q�̌��Ԃ͂S�ŁA���̌��Ԃɒj�q�Q�l�����邩��A�S��2����Ȃ���ł����H
 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D���q�����炻�̂����Ԃ́u���ꂼ��ŗL�̋�ʂ̂�����ȂɂȂ�̂Łv�C
4C
2�̂悤�ɒj�q�Q�l���̏ꏊ�����߂邾���ł́C�j�q�̏ꏊ�͌��܂�܂������ւ�����ʂ̕��ѕ��ɂȂ�܂��D�Ⴆ�C�}�̍������ł�
a��
D�Ǝ���Ȃ��܂��C�}�̉E�����Ȃ�
a��
D�Ǝ���Ȃ��܂��D
�p�����[�^��u�������̏����l�Ɉˑ������������o��悤�Ȃ̂ŁA���̜��ӓI�Ȋ������ǂ������������̂��Ƃ����^�₪�o�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������ɂ͉��������P����͂����Ǝv������ł�����̂ŁC���̃y�[�W�ōs���Ă��邱�Ƃ������ł��Ă��Ȃ��悤�ł��D
�@�悭������Ō����u�����������ɂ͂����P�̉�����܂�v�̂ł͂Ȃ��u�����������ɏ���������^����C�����������Ƃɉ�����܂�v�D
��Ɠ�(2)�̉E�����ɏ����Ă���O���t�ł́C�������̉��͑�������܂����C�����l���^����ꂽ�Ƃ��\���o�[�͂���ɍł��߂����Ɏ�������Ƃ������ƂŁC�����l�Ɉ˂炸�ɏ�ɂP�̒l�Ɏ�������̂́C�P���������̂悤�Ɂu���������P�����Ȃ��ꍇ�v�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̔����������ɂ��ā^21.10.22�n
���������b�ɂȂ��Ă܂��B�P�_���f���������̂ł���
�����`�̗��1�̉��́Alog�̐^�����ɐ�Βl���܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�Ă��˂��Ɍ����C���̒ʂ��,�����������ł�����������������̉��̏ꍇ�ɂ́C���ӂ��ׂ����Ƃ������āCx>0�̏ꍇ�ƁCx<0�̏ꍇ�ƂŁC�萔��C���������Ƃ͌���Ȃ��i�A���łȂ�����C�����ŕʂ̒萔���ɂȂ�̂����ʁj�Ȃ̂ŁC������ǂ����������ƥ��
���m�ʂ̕ł���̎���ɑ���n[�w������ΐ����̓����ɂ��ā^21.10.21�n
���������߂���́i�P�j���A�������Ă���̂�✕�ɂȂ�܂��B���P���X�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�S�p�����C�P�C���C�w�C��C��C�T�Ȃǂ͐����Ƃ��Ĉ����܂���D���l�́C���p�����i1�o�C�g�����j�œ��͂��Ă��������D���̃y�[�W�ɂ��Ă����l�ł��D
���y�[�W�ɂ���ẮC�ǎ҂̕X��}�邽�߂ɁC�S�p�����ŏ������܂ꂽ���̂p�����ɏ��������č̓_����v���O�������g�ݍ��܂�Ă���ꍇ������܂����C�u�֗����v�ƍl����ꍇ�ƁC�u���Ă����������Đ����ɂ���̂͂��������v�Ƃ����l���������蓾�܂��D
���m�ʂ̕ł���̎���ɑ���n[�m���̊�{�ɂ��ā^21.10.21�n
�܂̒��ɐԋʂQ�C���ʂQ�C�ʂQ�̌v�U�������Ă���D���̒�����P���R����o���Ƃ��C�Ή��Ԃ̏��ɏo�Ă���m�������߂�D�������C���o�����ʂ͌��ɖ߂��Ȃ��D���̖��́A�Ή��Ԃ̏��ŏo���Ȃ��Ƃ����Ȃ�����p���g����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�D�������Ⴆ�Εʂ̂��̂Ƃ��Đ�����Ƃ��́C����Ő����C�g�������������ł���悢���̂́C�g�����Ő�����Ƃ����̂���{�ł��D
���m�ʂ̕ł���̎���ɑ���n[�Ή��̂Ȃ��ꍇ�̂������ɂ��ā^21.10.21�n
���v�������̂ɑ�ώQ�l�ɂȂ�܂��B
�G�N�Z���̕��̓c�[���ƃG�N�Z����(TTEST)��P�l���v�Z�����ۂɁA���̓c�[���ŁA�ht-����: ���U���������Ȃ��Ɖ��肵���Q�W�{�ɂ�錟��h�I���ɁAP�l���Ⴄ�͉̂��̂ł����H
�ǂ��炪�A���m�Ȍv�Z�l�ɂȂ�܂����H
������������K���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̉��̕����ɁC���R�x�̉��߂̈Ⴂ�iWelch����Ƒ��̕��@�ł̃��f���̈Ⴂ�j�ɂ��ďq�ׂĂ��܂��̂ŁC�Q�l�ɂ��Ă��������D
�@���߂̈Ⴂ�Łu�ǂ��炪�A���m�Ȍv�Z�l�v�Ɩ₤�̂́C�₢�����H�H�Ȃ��C���l�������Ɉ���Ă��C*p<.05���ۂ����H���Ⴄ���Ƃ͏��Ȃ����Ƃ͂��̃y�[�W�̉��[�Ő��l�����Ƃ��Ď������q�ׂ܂����D
���m�ʂ̕ł���̎���ɑ���n[�����藝�E�]���藝�ɂ��ā^21.10.21�n
�Ȃ��AAC��BG��90�x�ɂȂ�̂�
�����m��ҁn�F�A�����肪�Ƃ��D���͊������܂��D�ǂ̖��ɑ��鎿��Ȃ̂��C���ԍ��������܂��傤�D�����C��P��ɑ��鎿��Ȃ�C�uAC��BD�͒��p�Ɍ����Ƃ���v�Ɩ��ɏ����Ă��邩��ł��D�������Ȏ���͂��蓾�Ȃ��I
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^21.10.19�n
�F���X���ł�
�����m��ҁn�F�A�����肪�Ƃ��D���w�̖��Ȃ̂Łu���ꂢ�ł�����́C���₷�������悢�v�Ƃ����l���ł��D�Ⴆ�C�Ԃׂ̗ɗΐF���g���ƁC��芄���̐l�������ɂ����Ɗ�����炵���̂ŁC����͔�����D
���m�ʂ̕ł���̎���ɑ���n[�g�����i���͑�j�ɂ��ā^21.10.18�n
���Q���̖��͍ŏ��ɂX���T�����Ȃ��Ă�����ł����H
���Ȃ��Ă������R���m�肽���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�X�l����T�l��I�ԕ��@�̐��v�����߂Ă��C���̖�肪�q�˂Ă��邱�ƂƈႤ���̂������܂܂�Ă��܂��D
�@�m���̖��Ȃ�C�u�X�l����T�l��I�Ƃ��Ɂv�u�j�q��3�l�C���q���Q�l�v�����Ă���m���͊�炩�ȂǂƂ�����肪���蓾�܂����C���̖��͊m���̖��ł͂���܂���D
�@�g�����̖��Ƃ��āC�j�q3�l�Ə��q2�l��I�ׂC���v�T�l�ɂȂ�Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��i���wII.�������j�ɂ��ā^21.10.16�n
II�y�萔�{�A�a�E���̐ϕ��̕ό`�����z(1)�̗� �̍Ō�̎�
= (1/3)x^3 +�@(3/2)x + 2x^2 + C
�́A��������
= (1/3)x^3 + (3/2)x^2 + 2x + C
�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�}�~�X��������܂���
���m�ʂ̕ł���̎���ɑ���n[�Ɨ��Ȏ��s�̊m���C�������s�̊m���ɂ��ā^21.10.15�n
�ƂĂ��ǂ����A��������肪�Ƃ��������܂��B
����͂���}�X�����������̓~�X�ɋC�����ɂ����̂ł��������傫���Ȃ�Ί������ł�
���͋C�ɂȂ�Ƃ���͂���܂���
�����m��ҁn�F�A�����肪�Ƃ��D��ʂ��g�傷��i�Y�[���C���j�ɂ́CWindows�ł́uCtrl�v�u+�v�Ƃ��܂��D���Ȃ��̂悤��mac���safari���g���Ă���ꍇ�́C�uoption�v�ucommand�v�u=�v�Ƃ��܂�
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^21.10.14�n
�߂��Ⴍ���n���ȉ��ł��ƂĂ��킩��Ղ������ł��܂���
�{���ɂ��肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^21.10.12�n
����2�̏ؖ��ŁA����1�̌��ʂ�p������@�����ɂ������肫��
�ƂĂ����ӂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̔����ɂ��ā^21.10.05�n
���K�Ƃ��Ďg�킹�Ă��������Ă��܂��B
���1�́i4�j��y'=6cosx^3-5cosx�������ƂȂ��Ă��܂����A���̏�Ԃ܂Ŏ���ό`����͕̂��ʂȂ̂ł��傤���H�i���ʁA�Ƃ����̂͗Ⴆ�Ίw�Z�̒���e�X�g���w�Ȃǂ��w���Ă��܂��j
����Ƃ��A���p�҂Ƃ��Ă��̂悤�Ȏ��ό`���ł���悤�ɂȂ��Ă�����������������A�Ƃ������Ƃł��傤���H
���l�Ƃ��Ă�y'=cosx*cos2x-2sinx*sin2X�ł����ʂ͐����ɂȂ肻�����ȂƊ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�I�������瓙�������̂�T���Ƃ������Ȃ̂ŁC���ɏ]���݂̂ł��D�Ȃ��Ccos�ɑ�����Ƃ�sin�ɑ�����Ƃ������Ƃ��C�悭����܂�
���m�ʂ̕ł���̎���ɑ���n[�A���^�m�����z�ɂ��ā^21.10.05�n
�v�_���܂Ƃ܂��Ă���A�����������Ȃ��炩�ݍӂ��������ł���̂ŁA�w�K���Ղ��ł��B
�y�[�W���������ƁA�ǂ܂Ȃ��Ă͐i�߂Ȃ��X�g���X�ł��Ȃ���C�������܂�����B
�͍ڂ��Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�g�̕t���Ă���I�����̂ǂꂩ�P��I�ׂi�N���b�N����j�CHELP�Ƃ��āC����Ɖ��o�܂��D
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�s�����̏ؖ��j�ɂ��ā^21.10.04�n
�Ō�̖��ŁA�H�ɐ��������ē����邩�ǂ����m�F�ł���Ȃ�āA�����܂����B
���͍Ō�̖��͂�����W�Ɠ����Ȃ̂ł����A�����ɍڂ��Ă��铚���̏o���������A������̕����[���������܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����������̕ϐ��ϊ��ɂ��������ɂ��ā^21.10.03�n
�ϐ��ϊ��̗��ԗ��I�Ɉ����Ă��ĂƂĂ�������܂��B�܂Ƃ߂Ă��������Ăق�Ƃɂ��肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.10.01�n
��S.�R�̐^�̕����́A�}�C�i�X���ƃ_���ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���e�͈͂ɓ���邱�Ƃ������ł�
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̕����ϕ��@�ɂ��ā^21.09.30�n
�ƂĂ��ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�����ρi�����j�ɂ��ā^21.09.29�n
���W�����̓��ς̗����ڂ��ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���j���[�������炻�̑O�̃y�[�W�ɏ����Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[�Q�����̓������1�ɂ��ā^21.09.29�n
���W���ʏ�ɂQ�̕�����C1:y=2x2�|4x+3��C2:y=�|2x2+5x�|6������DC1�����_�Ɋւ��đΏ̈ړ�������������C3�Ƃ���DC2�͂ǂ̂悤�ɕ��s�ړ������C3�ɏd�Ȃ邩�D
�̃O���t��C2,C3���t���Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̒��_�i�W�J�`�j�ɂ��ā^21.09.29�n
�����g���Ă̊J�݂��킩��₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�J��→���
���m�ʂ̕ł���̎���ɑ���n[�������̕������ɂ��ā^21.09.25�n
y��x�̓��̂Ƃ��̕�������90�x��]���������̂��C�ɂȂ��Ă����̂ł��������ɗ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��s�����ɂ��ā^21.09.23�n
�̓_���ĖႦ�邵�A������t���Ă��ĕ�����Ȃ���肪�����Ă������ɉ����o���ď�����܂��I�I�I
����̓_���ĊԈႦ���Ƃ������������ė������āA����1������������Ďv������A���������������A��������Ȃ��ʼn������Ƃ��o����̂łт����肵�܂����I
����ł����̃T�C�g�Ŗ������܂����Ċ����ɂ��悤�Ǝv���܂��I
�{���Ɋ��ӂł��c�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȉ��������ɂ��ā^21.09.21�n
��P�i�R�j�ɂ��Ăł��B�ȉ�������p(�|a+b+c)2=a2+b2+c2�|2ab+2bc+2ca�Ƃ���܂���-2ac�ł͂Ȃ��̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��Βl�t���̒�ϕ��ɂ��ā^21.09.20�n
�ޑ�3.3�̃O�����@�����O�̂Ƃ��@�����O�@�}1�Ɛ}�R�͈Ⴄ
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��Βl�t���̐ϕ��ɂ��ā^21.09.19�n
��Βl�t���̐ϕ��̖��Q2014�N�x���Q��������
�����O�̂Ƃ��@�e�����O
�Ȃ������Ȃ��́H
�����m��ҁn�F�A�����肪�Ƃ��D��蕶�̕����ł́C���̖��ɏ����ĂȂ����Ƃ͏����܂���D���ɁC���Ă̕����ł�
dx=0&chf=bg,s,fff9f9)
�́C���R���藧���܂����ɉe�����܂���D
��3��
=[cos(x�|��)��] �|[cos(x�|��)�|2]
�̎��̑傩�����̑O��5���Ȃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�u���ϕ�(�s��ϕ�)�ɂ��ā^21.09.19�n
�ƂĂ��킩��₷���ĕ��ɂȂ�܂��B
x��t�Œu���ϕ����悤�Ƃ��āA�u����̎���x���c���Ă��܂����ꍇ�ŁA
t=ax²+bx+c �̂悤�Ɏc����x��t�Œu���̂���ςȏꍇ�͑��̕��@��T�����ق��������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����K�������\���ɓ`����Ă��܂���

�ɂȂ�悤�ȏꍇ�C
���̃y�[�W��I.6�`I.8�̂悤�ɕϊ����܂�����������C���̕s��ϕ��͋t�O�p�����g���̂ŁC���Z�ł͈����܂���D�Ȃ��C�������Œ�ϕ��̏ꍇ�́C���Z�͈͓̔��ł��D
�ƂĂ��Q�l�ɂȂ�܂����B���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�L��2�̊O�����ɂ��ā^21.09.18�n
��Βl=��Βl�@�̊O�������悭�킩��܂���I�E�ӂɁ}��t������ۂ��̂ł����������肱�Ȃ��ł��B�̂ŁA���ӂ���Βl�̂Ƃ��̊O�������f�ڂ��Ă���������Ƃ��肪�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������݂̒ʂ�u�E�ӂɁ}��t����v�����ł��D����ȏ㌾�����Ƃ͂Ȃ��ł��D���̃y�[�W�̖��Ɣ�ׂă��x�����Ⴂ�߂��܂��D
���m�ʂ̕ł���̎���ɑ���n[�g�����i���͑�j�ɂ��ā^21.09.17�n
���̂����������Ă�����Ă��܂��B��S�̖��ł����A�}�̂P�C�R�C�V�C�̎O�p�`�́A
�T�C�V�C�R�C�Ɠ����O�p�`���Ǝv���̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�ӂƋ^��������Ƃ����邩������܂��u�~����v�u���ジ����v�̕����̒��ŁC�������́u��]���ďd�Ȃ���̂͂P�Ɛ�������̂Ƃ���v�Ə�����Ă���Ƃ��́C���ʂȐ������ɂȂ�܂����C�����łȂ���C�`�������ł��ʂ̂��̂Ƃ��Đ����܂��D����5��̑Ίp�����C�u��]���ďd�Ȃ���̂͂P�Ɛ�������̂Ƃ���v�Ƃ���3�{�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�ɍ��W�ɂ��ā^21.09.15�n
�ɍ��W�ƒ��s���W�i�f�J���g���W�j�̋�ʂ����̗��K����S������ė����o����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^21.09.15�n
���̏�ō̓_���Ă���ď�����܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^21.09.15�n
�悭�킩��܂����B���肪�Ƃ��������܂�!!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��i�܂Ƃ߂Q����O�p���j�ɂ��ā^21.09.14�n
���5�̈�ԉ��B���Ƀ}�C�i�X��Y��Ă��܂���
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�N�������̌��� �ɂ��ā^21.09.13�n
���K��肪�L�x�ɂ���̂ŁA��w�̃e�X�g��Ƃ��Ďg���ėǂ������ł��B���̉������Ă���J����悤�ɂȂ��Ă���̂��g���₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��Œ�`�������ɂ��ā^21.09.13�n
��ςɓ��������ł����B�ǂ����ނł��B�d�����w������72�˂���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�������ɂ��ā^21.09.11�n
�K������ɑ�Q������Ƃ����̂�m��܂��� �d�����I����Ă������C���]���ɂȂ�܂� ���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����2�ɂ��ā^21.09.10�n
�قƂ�ǂ̐l����O��ɖ��Ȃ̂͑�O��x�Ɂu���̖��v�������Ȃ�����H�Ƃ��ł͂Ȃ��ł���ˁB�B�B
�����m��ҁn�F�S�R�Ⴂ�܂��D���S�́m���̖��n�͂T���āC���5�́m���̖��n��2�����C���6�́m���̖��n�͂R�����C�Ō�̖��ɉ��Ȃ��̂́C�Ȃ����Ƃ������Ƃł��D
�@�ǎ҂̃��x�������߂��邩��Ƃ��C��萔���\�z�O�ɑ�������Ƃ������͂Ȃ�\
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��ň͂܂ꂽ�}�`�̖ʐ��ɂ��ā^21.09.09�n
��S�̓������A�ǂ����Ă�19/3�ɂ����Ȃ�Ȃ��̂ł����A�{����20/3�������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̍��ɂ��ā^21.09.09�n
���Ӂz
�P�D���̊W�͂Q�̃x�N�g���̎n�_��������Ă���ꍇ�������藧���C�E�}�̂悤�Ɏn�_��������Ă��Ȃ��ꍇ�ɂ͂Ƃ͂Ȃ�܂���D
���̕����̌����Ă���Ӗ����킩��܂���B���Ƃ��n�_�������Ă��Ȃ��Ă��A��a�̋t�x�N�g������b�̎n�_�܂ŕ��s�ړ�����ΐ��藧���܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�u���s�ړ�����ΐ��藧�v���Ȃ킿�u���s�ړ����Ȃ���ΐ��藧���Ȃ��v�ƌ䎩���Ō����Ă��܂��H
���m�ʂ̕ł���̎���ɑ���n[�O���t�̕��s�ړ��ɂ��ā^21.09.08�n
�킩��₷���L�����肪�Ƃ��������܂��B�O���t�̕��s�ړ��̏ؖ��ɂ��āA�u���O���t��̓_ (X , Y) �� y=f(x) ��ɂ��邩��CY=f(X) �c(1)�����藧�D�v�͐}�����Ă�y=f(x)�ɂ���̂�(1)�����藧�Ƃ킩�����̂ł����A�V�O���t�̎������߂�Ƃ��ɁA�V�O���t�̍��W�ł���(x,y)���Ȃ����O���t�̊�y=f(x)�ɑ�����Ă���̂��킩��܂���B�����������y=f(x)�͐V�O���t�Ƌ��O���t�̗����ŕς��Ȃ���ʌ`��\�����Ȃ̂ő���ł���̂�������܂���B�ł��ǂ�ȏ�Ԃɂ�y=f(x)���K�p�ł���Ȃ�A�ړ��O�E��̃O���t�̎��ȂǕʁX�̎������̂ł͂Ȃ��A���̍��W�ɂ���O���t�̎��͑S��y=f(x)�Ə��������C�����Ă��܂��܂��B�����l����Ƃ킩��Ȃ��Ȃ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���𒊏ۓI�E�`���I�ɒ�N���āC���ۓI�E�`���I�ɉ������悤�Ƃ���Ɠ���Ȃ�܂��D�����Ɨy���ɋ�̓I�Ȗ��ŁC�ǂ��Ȃ�̂��l����Ƃ悢�ł��傤�D
�Ⴆ�C

���(A)�̃O���t��̓_��(X, Y)�Ƃ��C(A)�̃O���t��x������3�C��������4�������s�ړ����Ăł���O���t��(B)�Ƃ����
^2&chf=bg,s,fff9f9)
���(B)



^2&chf=bg,s,fff9f9)
�����̐}�������đΉ��W���l����ƕ�����ł��傤�D
���̐����ɑ��āuf�͂ǂ��ɍs�����H�v�ȂǂƎ��₵�����k�����ۂɂ����̂ɂ͋�����
p�Ȃ��q�̐^�U�̕����ɂ����āup���U�ł���Ȃ�p��q���^�ƂȂ�v�Ƃ���Ă��܂����A����͊ԈႢ�ł͂Ȃ��ł��傤���H
�����ɊȒP�Ȕ���������Ă���̂ň�NJ肢�܂��B
x��2��2x=7 �Ƃ��������A�Ƃ���(x�͎����Ƃ���)
x��2�ł����Ă�A�͐^�ƂȂ�Ȃ��B
�v�����x��2���U�ł����Ă��AA�͐^�Ƃ͂Ȃ�Ȃ��B
�����p��q��p���U�ł����p��q�͐^�ƂȂ�Ƃ����̂͊ԈႢ�ł���B
(Q.E.D)
�M�҂���͖��ƂȂ��Ă���ӏ��𐔊w�I��`�Ƃ���������Ă��܂����A���ۊw�Z�Ŏg���Ă��鋳�ȏ��ɍڂ��Ă�����A���w���������Ă���l�����̒��ł̓X�^���_�[�h�Ȃ��ƂȂ̂ł��傤��?�^��Ɏv���܂����̂ł�������������K���ł��B�o�[�g�����h���b�Z���̗���k�ق̂悤�ɂ����������܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���S�ʼn��ƍl���悤���C���Ȃ��̎��R�ł��D���̖���Ƃ��̗��̖���̐^�U����v����͂����ƍl������C���w��̒�`��M�������Ȃ��Ƃ������Ƃł���C���Ȃ��̎��R�ł����C��������t�ɏo���ĕ\������C����ɂ��Ă��炦��Ƃ͌���܂���D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �ꍇ�̐��E�m���ɂ��ā^21.09.07�n
�������Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ���C����͏o�܂���D
���m�ʂ̕ł���̎���ɑ���n[�t���ɂ��ā^21.09.06�n
y=x+2����x�̌��̎����Ȃ�x+2���́|2�ɂȂ�̂ł���
�����m��ҁn�F�A�����肪�Ƃ��D����̎d���������ł��D���������C�ǂ̉ӏ��̘b�Ȃ̂��������Ȃ��ƁC�_���ł��܂��C������̓��e�͏����Ă���܂���D�����I�ɏd�Ȃ���e�́C���Q�̑�P��ɂ���܂����C�����Ă��邱�Ƃ͈Ⴂ�܂��D
�@��ʂɁC�������̑Q�ߐ��̕����������߂�ɂ́C�����̖��W�̗p��ł����u�������͕x�m�̎R�v�Ɗo���āC���q�̎���������̎��������������Ȃ�悤�ɕό`����̂���{�ł��D

���̃y�[�W�̍��ɂ���T�u���j���[����u�������v�Ƃ������ڂ��ɕ����Ă����K�v������܂��D
�����̂ق������e�����ׂđ����Ă��܂����B�����ɗ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȉ��������ɂ��ā^21.09.06�n
��3��(3)�̓����Ȃ̂ł����A(x²�|1)(x²�|9) �������ł͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����ɂ͂Ȃ�܂���D���̎��ƁC���������������Ƃ��������Ă��C�u��������ȏ�́C�^����ꂽ�W���͈̔͂ň��������ł��Ȃ��v�悤�ɂȂ��Ă��Ȃ���u�����������Ȃ����v�̉��ɂ͂Ȃ�܂���D���Ԑ����������̂܂ܒ�o���Ă��_���Ȃ̂́C���R�ł��D
���m�ʂ̕ł���̎���ɑ���n[sin��+cos�� �� sin�� cos���ɂ��ā^21.09.06�n
��2�́u�C�v sin�V�[�^������cos�V�[�^�̒l�Ⴄ�Ǝv���܂� 2���̂�[��2������2���̃��[�g2�Ȃ̂�
2����2��1�ɂȂ�܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ�܂���
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^21.09.05�n
���ɁA����{������1�ɂȂ邩��`���Ăق����ł��@�i�\�Ƃ��Łj
�����m��ҁn�F�A�����肪�Ƃ��D100�ȉ��C1000�ȉ��̑������͂����ɕ\�Ŏ����Ă���܂��D�S�������Ƒ��߂���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�K���}��,�x�[�^���ɂ��ā^21.09.03�n
��ϋ����[�����e����������A���肪�Ƃ��������܂��A�Ƃ��ɖ��1-5�ɂ��Ď��̋^����ق�Ƃ��ɃA�b�T�����������Ă���A�������܂����Bn=2�̂Ƃ��̓����͌덷����K�E�X�ϕ��ȂǂŌ�����������łĂ���̂ł����An>3�ƂȂ�Ɠr�[�Ɍ������炸�A�r���ɕ��Ă���܂����B�܂��ɂȂ�قǁA�Ƃ��������ŁA������Ă݂���Z���ł������\�ł���_�ŁA�{���ɑf���炵���Ǝv���܂��B
�i�ȉ��l�I�Ȃ��Ɓj���͖{���ɂ����ĕs��ϕ��̂������ŋ��߂悤�Ƃ��Ă���A�s���S�K���}����p���邱�Ƃŕ\���\��wikipedia�ɂ���܂����[���ł����ɂ��܂����B����Ŏ��͂œ��o�ł������ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���ɂ��ā^21.09.02�n
�P�D�ΏۂƂȂ��Ă��鍀�ځi���f���j�� �u���ݒn�ƑO��̍��ځv���A
�ڂ���������Ă���̂ŁA���ɎQ�l�ɂȂ�܂��B
�Q�D���f���́u�����g�����v�́A�u�ʂ̕Łv�ň����Ƃ������Ƃł����A
��̓I�ȏꏊ�������Ŏ�����Ă���ƁA��Ϗ�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���f���́u���̍��ځv�Ŏg���܂��Ƃ����悤�Ȃ��̂łȂ��C���f����������Ă���قƂ�ǂ��ׂĂ̍��ڂŎg���̂ŁC�ʂɎw�E����͖̂����ł���������C�͂ǂ��Ŏg���̂��H�Ɛq�˂�ꂽ��C����悤�Șb�ł�
���m�ʂ̕ł���̎���ɑ���n[��������(��{) �ɂ��ā^21.09.01�n
�������킩��₷�����A�o���Ȃ��������������𗝉��ł��Ċ������ł��I���肪�Ƃ��������܂��A�A�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�E���E���ɂ��ā^21.09.01�n
����̎g��������K���̉���������Əڂ����m�肽���ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̑O��̃y�[�W�����Ă�������
���m�ʂ̕ł���̎���ɑ���n[�R�_��ʂ�~�̕������ɂ��ā^21.08.30�n
���4�̉~�̕������̕W���`���Ԉ���Ă��܂��B
x^2+y^2�|2x�|6y-3=0�ł���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�Ȃ��W���`���Ԉ���Ă���̂ł͂Ȃ��C��ʌ`���Ԉ���Ă���ƌ����ׂ��ł��D
���m�ʂ̕ł���̎���ɑ���n[���̎w���ɂ��ā^21.08.27�n
����ł��B
�i�Q�O�Q�~�S�O�R�j
�������ԒP���Ȍ`�ɂ����
�Q�O�U�ɂȂ�܂����H
������W��
�i�S�O�Q�j�O�Q
�������ԒP���Ȍ`�ɂ��Ȃ���
�i�S�O�Q�j�O�Q���S�O�S�Ƃ������̂ł���
���̉͂Q�O�T���ȁH����Ƃ��R�Q�Ɠ�����ׂ����H�ƔY��ł����̂łS�O�Q�Ƃ����ɋ����܂����B���낢��ȃT�C�g�������̂ł����[���ł���������Ȃ��������߂������p�����Ă��������Ă��邱����̃T�C�g�Ɏ��₳���Ă��������܂����B
���̋^��_�Ƃ��Ă͉��̗ݏ�Ƃ��Ďw�����v�Z���ׂ��Ȃ̂��i�S�̗ݏ�Ƃ��āH����Ƃ��f���Q�̗ݏ�Ƃ��āH�j�A��ԒP���Ȍ`�Ƃ����͎̂w�����g�����`�i�Q�O�T�j�Ȃ̂�����Ƃ������i�R�Q�j�ŕ\���ׂ��Ȃ̂��H�܂��A������ԏ��߂Ɏ�����������̏ꍇ�ǂ̂悤�ȉɂȂ�̂��H�i�S�̗ݏ�Ƃ��āH�Q�̗ݏ�Ƃ��āH�j�͂��܂����̖��W�̖�肪�I�O��Ȃ̂��H��������������Ǝv���܂��B
���X�Ǝ��炵�܂����B
�����m��ҁn�F���e���O�_�O�_�Ő��k�̎���Ƃ͍l���ɂ����ł��D�ˉi�T�����j�C2^6�˂Ȃ�܂���C2^5�ˈႢ�܂�
�������╪���̌v�Z�Łu�ȒP�ɂ��Ȃ����v�Ƃ��������o�����Ƃ͂���܂��i����Ȃ�ɊȒP�ł���悢�j���C�u��ԒP���Ȍ`�ɂ��Ȃ����v�Ƃ��������o�����Ƃ͍l���ɂ����ł��D���������C���w�̂��̕�������p��Łu��ԒP���Ȍ`�v�Ƃ͉����Ƃ������Ƃ���`����Ă��Ȃ��̂ɁC�u��ԒP���Ȍ`�ɂ��Ȃ����v�ł͈Ӗ�����܂�܂���D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��i���wII.�������j�ɂ��ā^21.08.27�n
�������̐ϕ��̌����ɉE���ɂ����P�|�R���Ԉ���Ă���Ǝv���̂ł����B�B�B
�����m��ҁn�F�A�����肪�Ƃ��D�u�E���ɂ����P�|�R�v�Ƃ������̂���������܂��H�H
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��i�܂Ƃ߂P�j�ɂ��ā^21.08.26�n
�y���S�z�̍ŏ��̖��ɐ����͂���܂���?�I�����ɉ������悤�ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^21.08.26�n
��a��b����ab (a�Cb�͎���)�Ƃ����̂�0 ��a����0 ��b�ł��邽�߂̕K�v�\�������ł����H
��-2=��2��-1=��2i�Ƃ��������Ɉ�a�����o���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���̎��̃y�[�W�ɏ����ڂ������������܂��D
���̐��̍����������P��i���g���ĕ\���̂́C�K�{�E��{�ł����玩�R�Ɏg�����Ȃ���悤�ɂ��Ă������Ƃ���ł��D
���1�́@4a2+2(b+c)2+2(b�|c)2�@�̂Ƃ���ł���2(b+c)2�̂Ƃ����āA+2(b+c)a�|2(b+c)a�|2(b�|c)a+2(b�|c)a��0�ɂȂ�܂��H�@������Ă���������Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���ꂪ�O�ɂȂ邩��C���̂��̂̌v�Z�������Ă���C���ꂪ����ł�
���m�ʂ̕ł���̎���ɑ���n[�s��ƂP���ϊ��ɂ��ā^21.08.19�n
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����W���ɂ��ā^21.08.19�n
���P�ł��B�����������p����lj����Ă��������B
�����m��ҁn�F�u���P�ł��B�v�Ƃ����̂��@�ɕt���D
���m�ʂ̕ł���̎���ɑ���n[���̎w���ɂ��ā^21.08.18�n
���ɂ킩��₷���ł��B
��12�͉�������Ă���Ɨ����ł������̂ł��B�킩��₷�������L��������܂��B�킪�܂܂������Đ\����Ȃ��̂ł�����12�̂悤�ȕ��G�Ȗ����������肩�lj����Ă���������Ƒ�ς��ꂵ���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͕��̎w���̒�`������������̂ŁC����̖���������Ƃ��Ă��C���G�Ȗ�����ׂ�ƁC�y�[�W�̂˂炢�ƍ���Ȃ��Ȃ�D���G�Ȍv�Z��
���������y�[�W�������������D
���3(1)�̈����Z�������Ƃ�r^3�̌W����3�ɂȂ��Ă��܂��������Ă��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�����ƂƁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[��,�������̓����ɂ��ā^21.08.13�n
���ݕ����̓ƏK�����Ă��鍂��҂ł��B��b�I�Ȍv�Z���T���Ă����Ƃ����ϕ�����₷���A�m���ߖ�������A�g�ɂ������ł��B�{���ɂ��肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�N��̂��ƂȂ�C�������������Ă��Ȃ�����
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^21.08.13�n
�R���b�c�\�z���l���Ă����w2�N�̐��c�Ɛ\���܂��B
4n+1�Ɍ��y���Ă�����ɏ��߂ďo��A��l�łɊ������Ă���܂����B
��3n+1���̏���������
�}�Q�̃c���[2�ɂ͂��ׂĂ̊��1�o�ꂷ��
�����A��������������������u���������v��������Ԃōs���l�܂��Ă���܂��B
����d�����Ȃ����Ƃ��d���������߃��[�v���Ȃ��ؖ��ɋl�܂��Ă��܂��܂����B
�i���݂܂���A�ڂ������e�͂����ł͍T�������Ă��������B�j
���ꂪ�ؖ��ł���I�I�Ǝv������Ő��UB�܂ł̒m���ɂ��ǂ������������Ă��܂��B
���Z�������ƂƎv���܂����A��w�̎�҂ɂ��m�b�����݂��肦�Ȃ��ł��傤���B
�����\�ł�����ԐM����������ƂƂĂ��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���R�̂��ƂȂ���C�M�҂́C���̖�����������Ă��܂���D�قڎ��ŁC���Ԃ��ɂ͗����Ȃ��Ǝv��
���mMichigan�^�Ȃ������^21.08.13�n
��������ɂ킩��₷���A�������Z�����������ɋ��ȏ��ł͗����ł��������Ă������삪���������Ɨ����ł��܂����B
�C�O�ɂ��ē��{�̋��ނ��Ȃ��Ȃ���ɓ���Ȃ��̂Ŕ��ɏ�����܂��B
�e�y�[�W�̗��K��肪�����̗���x�̊m�F�A�������K�ɂȂ�̂Ŗ��W�I�Ȗ������ʂ����Ă���Ă��Ă��肪�����ł��B�i���������킪�܂܂ŋ��k�Ȃ̂ł����A���W���Ȃ��Ȃ������Ȃ��Ȃ̂ŗ��K������̃y�[�W�Ȃǂ�����Ƃ߂��Ⴍ���Ⴄ�ꂵ���ł��c�j�{���ɂ��̃z�[���y�[�W�ɂ͏������܂����B���ꂩ������p���܂��I�I�I���肪�Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.08.10�n
��肪���X�Ƀ��x�����グ�Ă����āA���Ɏ��g�݂₷���ł��B�܂��A��█�ɉ�������Ă��ĊԈႢ�₷���|�C���g���킩��̂�������܂��B��{�̖��������̂��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�������^hide����^21.08.08�n
�����̒�`�̐����Ł@y�f, f�f(x)�@�̓j���[�g���̋L�@�ł���ƍr��Ă��܂����A���O�����W���̋L�@�̊ԈႢ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�r��͕ϊ��~�X���ȁH�p��͒������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^21.08.08�n
�T�R�Βj���ł��B���̑̑��̂��߂ɍ��Z���w���v���o�����Ǝv���A���̃T�C�g�𗘗p�����Ă��������Ă��܂��B���͋ɂ߂Ċ�{�I�Ȃ��̂ŁA��{�̊m�F�Ƃ����Ӗ��œK���ƍl���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɕ������ɂ��ā^21.08.08�n
�����͊w���ł͂Ȃ����w�̕��K�����Ă���30��Љ�l�ł����A�v�Z�̉ߒ����ڂ����ڂ��ĂĂ킩��₷�������ł��B
�������ŗ����ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�i���j�ɂ��ā^21.08.07�n
�ƂĂ��悩�����ł��B
���ꂩ����g�킹�Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�����s�^���^21.08.06�n
�{���ɂ͊W�Ȃ����ƂŐ\����Ȃ��̂ł����A���̃T�C�g�̃A�C�R���͐ݒ肳��Ă��Ȃ��̂ł��傤���B���S�Ɏ��̎�ł���܂����A�u�b�N�}�[�N�ŃA�C�R�������邱�ƂŒT���₷���A�܂��F�X�ȃA�C�R��������ł���̂�����̂��D���Ȃ̂ňĂ��o�Ă���Ί������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���͗]�T���Ȃ��̂ť��
���m�ʂ̕ł���̎���ɑ���n[�����{���|���̒l�ɂ��ā^21.08.05�n
���w���w���x���ɂƂ��āA�����ւ�Q�l�ɂȂ�܂��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^21.08.04�n
�Y��Ă��̂ł��傤�Ǘǂ������ł��A���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^21.08.04�n
�m�̏h��ŕ�����Ȃ��Ƃ��낪�������̂ŁA������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ʒu�x�N�g���̉��p�ɂ��ā^21.08.04�n
���i�P�j�̃C�̍Ō�̖��̉�����ƈ�v���Ă���̂ɎP�}�[�N���o�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���p���������l�ł��D�i�R,�O,�V,�B,�Q�͐��l�ł͂Ȃ��C3�͐��l--���Ԃw�Z�ŏK���܂��j
���m�ʂ̕ł���̎���ɑ���n[�Q�_�����ԃx�N�g���ɂ��ā^21.08.03�n
�C���v�b�g�����łȂ��A�E�g�v�b�g���ł���̂Ŏ����̗���x���c���ł��ď������Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^21.07.30�n
�h��łǂ����Ă��킩��Ȃ���肪�����āA�����Ă������������̂ł����A
a=3+��15, b=|a²-7a| �Ƃ���B
(1) a²-7a�̒l�����߂�B
(2) b����a�̒l�����߂�B
(3) -b²<abx-a²<b²����x�̒l�͈̔͂����߂�B
�����m��ҁn�F���̎���C�h��̓����������ċ��ׂ�������l��C����ɘ_���������Ėׂ���l�����āC���������ƌ����Ă��܂����C�l�b�g��̌f���ȂǂŖ����œ��������邱�Ƃ��C����Ӗ��ł͈������Ƃł��傤.�i�q���̗͂��t���Ȃ��̂ɐ��т����ǂ��Ȃ�̂ŁC�d���̂ł��Ȃ��w�����̗p���Ă��܂����ƂɂȂ�j�D����Ȃ킯�ŁC����ς��ē��������q�ׂ�D

�̂Ƃ��C(1)

�̒l�C(2)

�̒l�����߂�.(3)

�̒l����x�̒l�͈̔͂����߂�B
�i�j(1)

^2=8\rightarrow a^2-4a%2B 4=8&chf=bg,s,fff9f9)
=2-2\sqrt{2}&chf=bg,s,fff9f9)

(2)

���l�ɂ��āC

(3)


���R�m���������̊m���n[ ��3�� / �S3�⒆ ]�ɂ���
�P�Ԗڂ̂�����������ƂȂ�ꍇ�̐��� 2 �ʂ�@���@��Ԗڂ̂���������ƂȂ�m���@2/5�@�@�c�@
�Q�Ԗڂɓ�����ꍇ�̐��� 1 �ʂ�@�@�@�@�@�@�@���@��Ԗڂ̂���������ƂȂ�m���@1/4�@�@�c�A
�@�@�@�@����āA�@�A����@2/5�~1/4 = 1/10
�ԈႢ�Ƃł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�����قŎ��₳��Ă��C�ԈႢ�E�ԈႢ�łȂ��̂ǂ���̈Ӗ��Ȃ̂��C�����ł��܂���D���l�Ƃ��Ắu����ł悢�v�ƌ����܂��D
�@�����C���̍��ڂ́u�m���̊�{�v�Ȃ̂ŁC�@����̏���ƕ��q�̏���v�Z���܂��D���̒i�K�ł́C�A�Ɨ����ۂ̏�@�藝�C�i��ʂ�=�]�����ۂ́j��@�藝���C�܂��K���Ă��Ȃ��ꍇ�̉������������Ă��܂��D�����̐��l�͓����ł��D
�@�@��

�@�A��

���1��L�̈ʒu�x�N�g����(b�x�N�g��-a�x�N�g��)/2�ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��͕��s���ł��D���̂悤�Ȋ��Ⴂ�������̂ŁC���̃y�[�W�̐擪�ɗv�_(2)�Ƃ��āC�}���t���ĉ�����Ă��܂��D������̂悤�ɊԈ���Ă͂����Ȃ��Əq�ׂĂ��邱�Ƃ��C���̂܂ܒ����ŊԈ���ė����炾�߂ł��D
���m�ʂ̕ł���̎���ɑ���n[�s��̂����ɂ��ā^21.07.28�n
�s��i�P�@�Q�@�R�@�S�j��n��͂ǂ̂悤�ɋ��߂�Ηǂ��̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�����s��łȂ���s��̂���͒�`����܂���D������

�Ƃ������̂͂Ȃ����Ƃɒ��ӁD����̏����ԈႢ���������Ƃ��āC

�̏ꍇ�Ȃ�C���̃y�[�W�̖��5�̂悤�ɂ��Čv�Z���邱�Ƃ͂ł��܂��D�������C�ŗL�l�C�ŗL�x�N�g�����������̕������܂ގ��ɂȂ�̂ŁC���ɕ��G�Ȃ��̂ɂȂ�܂��D
�g���₷�����ނł��肪�����ł��D
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^21.07.28�n
���K���lj����肢���܂�🥺
�����m��ҁn�F�A�����肪�Ƃ��D�������|�����������̖ڎ������ǂ��Ă��炤�ƁC�Ⴆ��
���̃y�[�W�̖�S�ɂ́C��肪�����ɏo�܂��D
�S�̓I�ɂ�������Ɛ������ꂽ�L�q�ŋɂ߂ĕ�����₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�ߐ��̕������ɂ��ā^21.07.26�n
�߂�������ɗ����܂��B
���肪�Ƃ��������܂��B
�v�]�Ƃ��ẮA
������~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�v�Z�Ə����Ă���}�[�N���N���b�N����ƌv�Z�����\������܂��D
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̋��ߕ��ɂ��ā^21.07.19�n
�r���������J�ɋL�ڂ���Ă����Ϗ�����܂����B
�����̌�Ɏ��ۂɗ�肪����L�ڌ`���Ŏ��p�I�ŏ�����܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.07.18�n
��{���璚�J�ɐ���������A�Ō�܂ŗ������ĉ����i�߂��܂����B
���Ԃ�����قǂ����炸�悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ������ɂ��ā^21.07.18�n
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^21.07.16�n
(x-3)2-8=0�̉������������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�W�J����

�̌`�ɂ��Ă���C���̃y�[�W�̉������߂�v���O������ 1 −6 1����������Łm�������߂�n�{�^���������ƁC���������܂��D

�@���̌v�Z�̓r���o�߂�


�@�Ȃ��C���w�Z�ł͎��̉��������K���܂��D
^2=8\rightarrow x-3=\pm\sqrt{8}=\pm 2\sqrt{2}&chf=bg,s,fff9f9)

���������b�ɂȂ�܂��B��ϕ��ɂȂ��Ă��܂��B
���R�́i�R�j�ɂ��Ď���������Ă��������B
����ɂ�����Ōォ��Q�s�ڂ�b�̎w���̌v�Z "-1/2 - 2/3"�Ƃ���܂����A�ŏI�s�ł͂��̌��ʂ�"1/6"�ƂȂ��Ă��܂��B�����"-7/6"�ł͂Ȃ��ł��傤���B
���萔�ł�������������������K�r�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɂ��܂�����Ȃ��̂ŁC���̕������������܂���
���m�ʂ̕ł���̎���ɑ���n[�J�C�Q�敪�z�ɂ��ā^21.07.11�n
(4)�@�m�J�e�S���[�̕����n�ɂ���
���R�x��4�ł͂Ȃ��A2�ɂȂ�̂ł͂Ȃ��ł��傤���H�@�����͕ς��܂��B
��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���Әa�������āC3�~3�̕����\�ŗ^������f�[�^�̎��R�x��(3−1)×(3−1)=4�ł�
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̓��ςƊO���ɂ��ā^21.07.11�n
2.�x�N�g���̊O�ρ@�́@�i�Q�j�����ɂ���`�@�̉����
�u�܂��A��{�x�N�g���E�E�E�v�@��e1���i�P�C�O�C�P�j�́i�P�C�O�C�O�j�̌�A�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���R���̗ݏ�̋t���̘a �ɂ��ā^21.07.10�n
����A1+1/3^4+1/5^4+1/7^4...����/96�ɂȂ邱�Ƃ̓��o���@�ɂ��Ď��₳���Ă����������҂ł����A���ȉ������܂����B
�{���`���̇H�ƇI���𑫂���2�Ŋ���Ƃ������ƂɋC�Â��܂����B
���}�����܂ŁB
�����m��ҁn�F�A�����肪�Ƃ��D�V���S���ɉ��L�̒ʂ���Ă��܂������H�u���E�U���L���b�V����ǂ�ł��āC�V�������������Ă��Ȃ��̂��ȁH
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^21.07.08�n
�Ƃ�ł��Ȃ�������₷���ł��I
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D�i���[���V�X�e���̌̏Ⴉ�����C��Ȃ��Ƃ��N�����Ă��āC�S���������ʂ̃��[�����V���P�O���t���ő��M����Ă��܂�??�j
���m�ʂ̕ł���̎���ɑ���n[Excel�F���W���C��A�����ɂ��ā^21.07.05�n
���W��r�̎��̕��ꂪ�A(yk-m)^2�ƂȂ��Ă��܂����A(yk-n)^2�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��,�������̓����ɂ��ā^21.07.05�n
���4�̐ς̔����@�ʼn����ꍇ�̕�����
Y�L=1�~(2x+1)^-¹+(x�[3)�~(-1)(2x+1)^-²�~2 �ł͖����ł��傤���H�A^-¹�������Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���ƌW���̊W�ɂ��ā^21.07.04�n
�ʔ����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���R���̗ݏ�̋t���̘a�ɂ��ā^21.07.04�n
���m�ʂ̕ł���̎���ɑ���n[���R���̗ݏ�̋t���̘a�ɂ��ā^21.07.04�n
(11.1)�̓t�[���G�W���Ɋւ���p�[�Z�o���̓����ƌĂ��D->(11.3)�ł�?
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�g�����i���͑�j�ɂ��ā^21.07.03�n
�̌��Ƒ��a
540�̐��̖͑S���ʼn����邩�B�܂��A���̖̗ւ����߂�B
�Ƃ��Ƃ��ł��傤���B�����������炷�݂܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�ց��a�D�ǂ����ɏ���������ł������C�����悤�Ȃ̂ł��̂��������܂��D�Ȃ��C���w�̖������Ƃ��Ɂu�U���̌������v�Ƃ����c�_�������āC�i�U���̌����Ƃ����̂͂Q��_�Ԃł̒�ϕ��̌����j�u�o���Ă������k�͂T�b�ʼn����邪�C�o���Ă��Ȃ��������k�͎��Ԃ��������Ă������Ȃ��v�悤�Ȗ����o���ƁC���w�̎������u�v�l�͂f�����v�u�P���ȈËL�͂����f����悤�ɂȂ�v�Ƃ������Ƃ������܂��D���q�˂ɂȂ��Ă���u�̌��v�u�̑��a�v��₤���́C���傤�ǂ��̋c�_�ɓ��Ă͂܂�C�o����T���������悢�Ɣ��f�ł�����ł��D�������C�����͌����Ă��C���Ƃ��ďo�肳���ꍇ�͂���̂ŁC�������͎����Ă����܂��D
�@

�̖́C�P��540���̂��܂߂�

�i�������C
0��a��2, 0��b��3, 0��c��1�͐����j�Ə�����D
a=0,1,2�̂R�ʂ�C
b=0,1,2,3��4�ʂ�C
c=0,1��2�ʂ��g�ݍ��킹��ƁC�̌���24��
���ɁC
(1%2B 3%2B 3^2%2B 3^3)(1%2B 5)&chf=bg,s,fff9f9)
��W�J����Ɩ̑��a�ɂȂ邩��C�̑��a��7�~40�~6=1680
����@�̎����ɏo�܂���
�����m��ҁn�F�A�����肪�Ƃ��D�����͂W���ł��傤
���m�ʂ̕ł���̎���ɑ���n[�ꕽ�ρC��䗦�̐����ɂ��ā^21.07.02�n
������₷���ď�����܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^21.07.02�n
�ƂĂ��������ł����B���w�����Ȃ̂ŁA���̃��x���̖��͂ƂĂ����肪�����ł��B�������������̖��𑝂₵�Ă���������ƁA���肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�U�̓����̒�`�ł́C�u���𑝂₷�Ɗ�Ȃ��v�̂ł��D���K���Ƃ��ĂQ�����C�R�����Ȃǂ����͍̂\��Ȃ��̂ł����C���̃y�[�W�ɂ��镪�����△�����Ȃǂ́C�قڊw�K�w���v�͈̂̔͂���E�������̂ł��D�́C��������܂łɁC���Ԕz���̓s���Ŕ����̌������g���������̌v�Z�̑O�܂ł����i�ނ��Ƃ��ł��Ȃ������搶�����āC��`�ɏ]���Ė������̔��������߂�Ƃ��������o��������N���ł��Ȃ������D��`���g���Ĕ�������̂́C�R�����ł��琳�𗦂��Ⴂ�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^21.07.01�n
�����������Ă�̂ɍ̓_������ƕs�����ɂȂ��Ă��܂��܂�
�����m��ҁn�F�A�����肪�Ƃ��D���̉��ɓ�������ɑ��铯���������ڂ��Ă���D�S�p�����͐����ł͂Ȃ����琳���ɂȂ�܂���Q��U��Ȃǂ͓��{�ꊿ��
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^21.07.01�n
�d���g�ݍ��킹�̏Ɩ��̕�����8!�Ƃ͂ǂ�����o�Ă����̂ł��傤���H�����Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�{���ɕ�����Ȃ��̂Ŏ��₵�Ă���̂ł��ˁI5+3=8�ł�
���m�ʂ̕ł���̎���ɑ���n[�������i�Q�����̕������j�̒�ϕ��ɂ��ā^21.06.29�n
�Q�l�̗��̏ڂ�������������Ƃ����Ȃ��Ǝv���܂����B
�S�̂Ƃ��ĂƂĂ��킩��₷���Q�l�ɂȂ�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�Q�l���̉���́C�R�e�R�e�Ə������͐}�Ŏ����܂���
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^21.06.28�n
��w3�N���ł��B���N���ĉɂȂ̂Ő����P������낤�ƌ��f���A���������K���悤�Ƃ��̃T�C�g�ɒH�蒅���܂����B�ǖ₪����������Ȍ��ŕ�����₷�������ł��B������܂����B���̖��������������Ă������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̂�����Ƃ��̏����ɂ��ā^21.06.28�n
���̂������킩��₷������
���������e�X�g�Ȃ̂łƂĂ����ɗ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������a�C�e�C���[�W�J�C�}�N���[�����W�J�ɂ��ā^21.06.27�n
�悭���T�C�g�𗘗p�����Ă��������Ă���܂��B��ς����b�ɂȂ��Ă���܂��B
�ǂ�ł��Ĉ�^��Ɏv�����Ƃ��낪�������̂Ŏ��₳���Ă��������܂��B
��2.6�̉̐���an�̕��q��3��n�悪���Ȃ��̂͂Ȃ��Ȃ̂ł��傤���H�H
���̗�2.7�������3��n�悪�������Ă���̂ŋ^��Ɏv���܂����B
�����̕��s���ł������ϐ\����Ȃ��ł�!!!!!m(__)m
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p��̑��݊W�ɂ��ā^21.06.26�n
���1(�U)�����I����������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̕ӂ̒���(�O�p����)�ɂ��ā^21.06.26�n
�ƂĂ��킩��₷�������ł��B���������܂łł��Ȃ����������ł���悤�ɂȂ�܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.06.25�n
�킩��Ղ������ł��A���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̌v�Z�ɂ��ā^21.06.25�n
log9 64
�����m��ҁn�F�A�����肪�Ƃ��D���ꂪ�ǂ������܂������H����Ȃ��ƕ�����܂���D���̎��ɂ��ẮC�����Ă�������܂��D
���m�ʂ̕ł���̎���ɑ���n[�����t���m���ɂ��ā^21.06.25�n
����ɂ��́B���J�ł���Ȃ���璷�ɂȂ炸�킩��₷������C���肪�Ƃ��������܂��B
���āC�m�����������m�� �� �Q�l�̎q���Ɋւ�����ɂ��Ď��₪����܂��B
��R�F���Ȃ��Ƃ��P�l���q���Q�l�Ƃ����q�̊m��
��S�F���ւɏo�Ă����P�l�����q�������P�l�����q�̊m��
�ł����C�ŏ��͓����m���ɈႢ�Ȃ��Ƃ����v�����݂����𗣂�Ȃ��܂܂ł����B���ǁC�ȉ��ɏq�ׂ�l�����Ŏ����Ȃ�ɗ�����������ł��܂����������ł��傤���H���m�F���������܂��ƍK���ł��B
��R�FU={(��,��) (��,�j) (�j,��) (�j,�j)}�e�����̋N������͓��l�Ɋm���炵�������Ȃ��Ƃ��P�l���qA={(��,��) (��,�j) (�j,��)}�C�Q�l�Ƃ����qB={(��,��)}��n(A��B)/n(A)=1/3
��S�F���ւɏo�Ă����q���������ɒu��U={(��,��) (��,�j) (�j,��) (�j,�j)} �e�����̋N������͓��l�Ɋm���炵�������ւɏo�Ă����̂����qA={(��,��)(��,�j)}�����P�l�����qB={(��,��)}��n(A��B)/n(A)=1/2
�ȏ�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���S�Ȃ铚�ėp���ł��D
���m�ʂ̕ł���̎���ɑ���n[�W���̗v�f�ɂ��ā^21.06.25�n
�������L�c�L�c�ŏ������ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^21.06.24�n
�ƂĂ��������Ă��܂��A�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2���Ȑ��̋ɕ������Ɣ}��ϐ��\���ɂ��ā^21.06.24�n
���4�@(3)�@�̎Q�l���Ă�xy�������W (x-2)^2 + y^2 = 1 �ɂ��� C(1,0)�𒆐S�Ƃ���A�ƂȂ��Ă���܂����AC(2,0)�ł͂Ȃ��ł��傤���B
�V�D2���Ȑ��̔}��ϐ��\���z�̗����̔}��ϐ��\���ŁAy�̍��W��\���ϐ���x�ɂȂ��Ă���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^21.06.23�n
�s�����ɂȂ��Ă����ق��̕������^�b�v�����琳���ɂȂ��Ă��܂��V�X�e���͕ς����ق��������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
��x�ł��ԈႢ����炩���Ă��܂�����҂��C��x�Ɨ�������Ȃ��悤�ȎЉ�V�X�e���i�L�����Z�������j�́C�Ԉ���Ă���D�����Ԑ����Ă���ƁC���x���Ԉ���Ă���C�悤�₭����������������悤�ɂȂ�̂��D�i�������C���Ȃ�������Șb�����Ă���̂ł͂Ȃ����Ƃ͕������Ă��܂��D�֏悵�āC�����̎v�����q�ׂ��܂łł��j
���m�ʂ̕ł���̎���ɑ���n[�������̂�����Ƃ��̏����ɂ��ā^21.06.22�n
��b�̊m�F�Ƃ��Ĕ��ɗL���I�ł���❕
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^21.06.21�n
����̕K�v�����Ə\�������ō������Ă��̂����ꂾ���ʼn������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^21.06.20�n
���������F���g�����ق��������Ǝv���܂��B
������܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.06.19�n
�킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ς̔����ɂ��ā^21.06.17�n
�����ς���肪�����ėǂ���������
�����m��ҁn�F�A�����肪�Ƃ��D
��?�^?����^21.06.14�n
��ʍ� aₙ �� aₙ = (1 + 2 + 3 +⋯+ n) / n² �ŕ\����閳������ {aₙ} �̎����E���U�ׁC��������ꍇ�͂��̋Ɍ��l�����߂�D
�����m��ҁn�F�������N�ł��邩���������C���������������C����Ȃ̂��ԈႢ�̎w�E�Ȃ̂��������ĂȂ��D�u���߂�v�Ƃ͉��l�̂���Ȃ̂��ȁH����ɕԓ������炨�������ł��傤
���m�ʂ̕ł���̎���ɑ���n[�ς̔����ɂ��ā^21.06.14�n
������܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^21.06.13�n
���̃y�[�W�̗��3��
�u�����������@�́@�������@�ł��邽�߂̉������ł����v�Ƃ������ɂ��Ď���ł��B
�����́uma=ma�v��m,a,b�Ɋւ�������ł���̂ɑ��A�ua=b�v��a,b�Ɋւ�������Ȃ̂ŁA�ϐ��̐����Ⴄ�̂ō������Ă��܂��B
���̖��̑S�̏W����{(m,a,b)|m��R,a��R,b��R}��{(a,b)|a��R,b��R}�̂ǂ���ł����H
�����Ă�������̖�蕶�̂ǂ����画�f����悢�̂ł����H(�ϐ��̐����Ⴄ�Ƃ��͑����ق��ɍ��킹��Ƃ����Öق̗���������H)
���͈ȉ��̏����@���g���܂����������Ă��܂����H
{(a,b)|a��R,b��R}�ł���Ƃ���ƁA�u�������m�����݂���ma=mb�Ƃ�����v�Ƃ��邩�Am���Œ肵��0�ł��邩�Ȃ������͂����肳����K�v������͂����A�Ȃ��Ȃ�ma=mb�̂܂܂���a,b���w�肵�Ă��^�U�����܂�Ȃ��̂ŏ����Ƃ��ĕs�K�����炾�B����Ă��̃p�^�[���͖����B
�����m��ҁn�F�A�����肪�Ƃ��D���ɏ�����Ă��Ȃ��ϐ��́C�C�ӂ̒l���Ƃ�܂��D����͒��w�Z�Q�N�̒����̕������̂Ƃ��ɏK���Ă��܂��D
�@�Ⴆ�C�_(3, 0)��ʂ�Cx���ɐ����ȁi�����ɕ��s�ȁj�����̕��������C x=3 �Ə����܂��D
�@��������C�����炵���������ɁC�܂�œ_��\���Ă��邩�̂悤�ȍ��o���o���邩������܂��Cxy���ʁi2�����̕��ʁj�ɂ����āCx=3�Ə����ꂽ�������́Cx=3(���͔C��)�Ƃ������Ƃ�\���܂���������̂Ȃ����Ƃ͏����Ȃ��Ƃ������ƁD���������āCx=3�Ƃ������������\���_�́C�Ⴆ��(x=3, y=0), (x=3, y=1), (x=3, y=2), (x=3, y=3), ���(x=3, y=−1), (x=3, y=−2), ������͐����Ɍ��肳�ꂸ�ɕ����Ȃǂ��\�i�������Cxy���ʏ�ł́Cx���͎����j�D���̂悤�ȓ_���Ȃ��ƁCx���ɐ����ȁi�����ɕ��s�ȁj�������ł���D���ꂪ�Cx=3�Ƃ������������\���}�`�ł��D
�@���l�ɂ��āCxyz�R������Ԃɂ����āCx=y�Ƃ����������́Cz�͔C�ӂƂ������Ƃ�\���Ă���Cx=y,(z�͔C��)�Ƃ������ʂ�\���܂��D����ɑ��āCzx=zy��z(x-y)=0��z=0�܂���x=�́Cz=0��x��y���Ƃ���(1, 2, 0)�Ƃ����悤�ȓ_���܂ނ��ƂɂȂ�Cx=y�̕��ʏ�ɂȂ����ƂɂȂ�܂��D
�y�v��z�����ĂȂ��ϐ��́C�C�ӂ̒l������Ƃ������Ƃ�\���D
���m�ʂ̕ł���̎���ɑ���n[�Q�����ƈ�ʍ��i�K���`�j�ɂ��ā^21.06.12�n
�C�̕����̌\�˂̏����ł����A�����ւ�킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�C�̕��Ƃ����̂��C�L�����đ傫�����Ă悭������܂��i�����o�邵�������ށj�C�Ƃ肠�������肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2���Ȑ��̋ɕ������Ɣ}��ϐ��\���ɂ��ā^21.06.11�n
�y���T�z��(3)�̉�
�Q�Ɓ{�S�͈̔͂͂P�V�^�S�܂ŁH
�����m��ҁn�F�A�����肪�Ƃ��D�Q�Ɓ{�^�S�Ə����Ă�����̂��C�Q�Ɓ{�S�Ɠǂސl�͂ǂ�Ȑl�Ȃ̂��H�u���E�U��������\���ł��Ȃ��ꍇ→�Ȃ��C�������K���Ă��Ȃ��l→�Ȃ��C�����̑��Ƃ���→���ꂾ��
���m�ʂ̕ł���̎���ɑ���n[ �����藝�i���j�ɂ��ā^21.06.09�n
������������ɂ͓r�������ڂ��ė~����
�����m��ҁn�F�A�����肪�Ƃ��D������̂��Ƃ́C�������Ă���̂ł����H�����P�C�X�}�z��PC�p�̉�ʂ�������C�S�̂������Ȃ��D�X�}�z�̓X�}�z�p��ʂ�
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J �ɂ��ā^21.06.07�n
(6�ŁA�ŏ��u������Ȃ����v���Ďv�������lj����s�ڂ̕����̊��������Ă��˂��ł悭�킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^21.06.07�n
���1�̖��Ɩ͔͉̖�肪�Ⴄ
�����m��ҁn�F�A�����肪�Ƃ��D�u���̊����̒�`�ɂ��������Ĕ������Ȃ����B�v�Ƃ������ɂ����āC��肪���̊��ł���̂ɑ��āC�����̓����ɂȂ�͓̂��R�̂��ƂŁC�u���1�̖��Ɩ͔͉̖�肪�Ⴄ�v�Ȃǂƌ�����o���͂Ȃ��D�܂��C�X�}�z�p�̋��ނ��ʂɂ���Ǝ����Ă���̂ɁCPC�����̉����̍L�����̋��ނ�android�g�тœǂނ��Ƃ̈Ӗ����������D
���m�ʂ̕ł���̎���ɑ���n[�ɍ��W�ɂ��ā^21.06.07�n
�y���R�z��(3)��HELP��sin�Ƃ����������B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^21.06.07�n
2.(3)1�̓�����e�̎w����px�ɂȂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�m���̊�{�ɂ��ā^21.06.06�n
�d�݂̖��́A�O�̃T�C�R���ƈ���čd�݂��ꂼ��ɋ�ʂ��Ȃ��̂�����N���蓾�邷�ׂĂ̏ꍇ�͕\��0,1,2,3��4�ʂ�ƍl����̂ł͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�d�݂̖��ƌ����Ă��C��3�̍d�݂̖��Ȃ̂����2�̍d�݂̖��̂��ƂȂ̂�������܂��C�ꉞ��3�̘b�Ƃ��ē����܂��D
�@�Q���̍d�݂𓊂���Ƃ��C�\��0,1,2��������܂���D
�@�܂��C�����ɏ����Ă��܂��悤�ɁC�u�m���̌v�Z�ł́C�ڂɌ�������x�̑傫���̂��̂ɂ͋�ʂ�����Ƃ���D�i�����ǂ��ǂ�Ȃɐ��m�ɍd�݂�����Ă��e�X�̍d�݂ɂ͋�ʂ�����Ƃ���D�j�v���d�v�ł��D����ڂɌ�������x�̑傫���̐��E�Ŋm�����v�Z����Ƃ��C�u���́v�͕K����ʂ��܂��D�ꍇ�̐��̐������Ƃ��ď����g�����̖��ł́C�������̂�����Ƃ��̐��������K���܂����C�m���̌v�Z�ł́u���͕̂K����ʂ��܂��v�D��������łȂ��ƁC�����̐��E�ŋN����b�ƍ���Ȃ��Ȃ�܂��D
�@����ɑ��āC�ʎq�̐��E�ł͓���̂��̂͋�ʂł��Ȃ��Ƃ�����舵�������蓾�܂����C���Z���w�̊m���ł́C�u���́v�Ƃ͖ڂɌ�������x�̑傫���̂��̂Ɍ��܂��Ă���C�F��`���ǂ�ȂɎ��Ă��Ă��C���̂͋�ʂ��܂��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.06.05�n
�F�X�Ȏ�ނ̖�肪������Ƃ��Љ��Ă��āA�}���ŕ��K���鎞�ɂ҂�����ł����B�������킹�������ɂł��ĂƂĂ��g���₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\������ �ɂ��ā^21.06.04�n
��R�̖�肠�肪�Ƃ��������܂�m(*_ _)m
�����Ɨ~���������I(*�L︶`*)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���P���������̉������i�܂Ƃ߁j�ɂ��ā^21.06.03�n
�܂��ł߂��Ⴍ����킩��₷���ł��� ���肪�Ƃ������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W �ɂ��ā^21.06.03�n
����3�Ԃ̓�����15�ł͂Ȃ�16���Ǝv���̂ł���
�����m��ҁn�F�A�����肪�Ƃ��D���ɏ����ꂽ���Ɋ���Ă���l�́C���R�Ƃ����Œ�I�Ȃ��̂�����ƍl���邩������܂��C�u��蒼���v�Ƃ����{�^�����N���b�N���Ă��炤�ƕ�����悤�ɁC���̖��͂P�̖��ł͂���܂���D��2800�ʂ�̑g���킹�̒�������Ɠ����R���s���[�^�őI��ł���̂ŁC�u����3�Ԃ̓�����15�ł͂Ȃ�16���Ǝv���v�ƌ����Ă��C���������Ă����Ȃ��ƁC���̘b�Ȃ̂��ʂ��܂���D�Ȃ��C���̖��ł̓R���s���[�^�̖��Ɖ̑g�͍����Ă��܂��̂ŁC���̖��ł��C���Ԃ�C���Ȃ����Ԉ���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[����C�g�����i�͖����j�ɂ��ā^21.06.02�n
�ƂĂ�������₷����������Ă���Ă��肪��������
help�������������Ă��܂��̂����P�_���ȂƎv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D��聃�q���g��Help��������Ƃ����o���G�[�V�����̒��ŁC��������Ă��Ȃ��ƍ���l�������D�����ł́C�q���g�͉��܂�ł��Ă͂��������ƍl����l�������D���ǁC�ŋߍ쐬�����y�[�W�ł́C�{�^���̃��x��������ɂ��邱�Ƃ������D���̃y�[�W�����x��������ɏ���������\��D
���m�ʂ̕ł���̎���ɑ���n[�O�Ӂ��p�ɂ��ā^21.06.02�n
���d��ŋ��܂�t�O�p���̊��\�̌v�Z��PC�ŏ����_��5�ʂ��炢�܂Ōv�Z���������̂ł����A������������܂���̂ŁA�q���g�����^���������B
���̌��������݂���ƁA�]��(COS��)����p�x(�x)�����߂�֗��Ȍ����ɂȂ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ȉ��Ɂu�����v�Ƃ��Ď�������̂́C���Ȃ����]��ł�����̂Ƃ͈Ⴄ�悤�ł��D���������C�O�p���C�t�O�p���C�w�����C�ΐ����Ȃǂ́C�ϐ�x�̗L����̎l���v�Z�ɂ���ĕ\�����Ƃ͂ł����C���������̘a�Ƃ��ĕ\����C���z���ɂȂ�D������C�t�O�p�������߂�֗��ȁi�L����̎l���v�Z�ŕ\�����j�����́u�Ȃ��v�D��̓I�ɂ�
&chf=bg,s,fff9f9&chs=370x35)
���(**)
�����p���āC�\��
−1<x<1�ƂȂ�
x=0.1, 0.2, ...�Ȃǂɂ��āC

�̒l�����߂����\������Ă����āC�����ǂނƂ����̂��ÓT�I�Ȏg�����ł��D
�@PC�����p�ł���Ƃ��́C�@Excel�Ȃ���[�N�V�[�g��ACOS()�ɂ��CACOS(0.1)=1.470628906, ACOS(0.2)=1.369438406�Ȃ� �Ajavascript�Ȃ��Math.acos(0.1)=1.4706289056333368, Math.acos(0.2)=1.369438406004566�Ȃ� �BMaxima�Ȃ��acos(0.1)=1.470628905633337, acos(0.2)=1.369438406004566�ȂLJCPython�Ȃ��acos(0.1)=1.4706289056333368, acos(0.2)=1.369438406004566 �DR�Ȃ��acos(0.1)=1.470629, acos(0.2)=1.369438�Ȃ�
�@�����͏�L��(**)�̌������g���āC�L�������̌��������߂邽�߂ɏ\���ȍ����̘a���狁�߂����̂ƍl����悢�ł��傤�D
�z�肵�Ă�����͈̔͂���E���Ă���Ƃ͎v���܂���
�m�肽�����Ƃ��L��܂��̂œ��e�����Ă��炢�܂�
�d�q�H�w�̃��T�[�W���}�`���l���Ă��܂�
x = sin(��t)
y = A sin(��t + B)
���`���Ȑ��́u�ȉ~�ł���v�ł�낵���ł��傤���H
�œ_ F F' �� X����ɂȂ��ł���
���̏ꍇ�� �ȉ~�̕������́H
�ŁA�ŏI�I�ɒm�肽���̂�
(x,y) �̑���l�͂��������܂����i�d�q��H�̐��l�V�~�����[�V�����Łj
���̑���l����
y = A sin(��t + B)
�� A, B �����߂���@�ł�
�E�Ⴂ���͋��߂�ꂽ�C������̂ł���(�̂͂悩����--������)
�E���͂����ς�ł�
�����m��ҁn�F�A�����肪�Ƃ��D
&chf=bg,s,fff9f9)
&chf=bg,s,fff9f9)

�́u�ȉ~�ł��v
excel�ȂǂŁu�U�z�}�v�ɂ���ƁC�����C�������C�ΐ��C�w�����ւ̋ߎ������o�܂����C���̏ꍇ��

������̂ŁCexcel�ɒ��ڎ�����������͖̂����ł��傤�D

����

����A���͂ɂ�����

�����߁C

�Ɣ�r����̂͂ǂ��ł��傤��
���2�A����A���ő�l�A�E�j0.5�����ł͂Ȃ��A0.5�����̂Ƃ��́E�E�E�@�@�@0.5�����̂Ƃ��A�ő�l�́E�E�E�ł͂Ȃ��ł��傤���B�����ď��������Ƃ�������܂��A�ԃX�P�[��a�̌��ݒl�Ƃ������At�̌��ݒl�Ȃ̂ł́E�E�E�@�@�Ƃ������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�W�����_���W���`�ɂ��ā^21.05.30�n
�ŗL�l3�d���ŌŗL��Ԃ̎�����1��3�~3�s��͑��݂��܂����H����ꍇ�̓W�����_���W���`�łǂ̂悤�Ȍ`�ɂȂ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D
 →��=2�i�R�d�j�C�ŗL��Ԃ͂P��
→��=2�i�R�d�j�C�ŗL��Ԃ͂P��
 →��=2�i�R�d�j�C�ŗL��Ԃ�2��
→��=2�i�R�d�j�C�ŗL��Ԃ�2��
 →��=2�i�R�d�j�C�ŗL��Ԃ�3��
→��=2�i�R�d�j�C�ŗL��Ԃ�3��
�W�����_���W���`�����߂�ߒ��ŌŗL�x�N�g�������3�ڂ̃x�N�g�������߂�Ƃ��A���łɃW�����_���W���`�ƂȂ����s�g���Ă���(���2.4.1�A2.4.3)�̂��悭�킩��Ȃ�����
���߂��������̂����̉ߒ��ɏo�Ă���̂Ō��Ǔ��o���悭�킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�������Ă�����̂��g���āC������Ȃ����̂�\���Ă����Ƃ����̂́C���w�ł͕��ʂ̂������Ǝv���܂���
���m�ʂ̕ł���̎���ɑ���n[.�����ƍ����ɂ��ā^21.05.30�n
�Ƃ��Ă�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃Z���^�[��������ɂ��ā^21.05.30�n
�X�}�z�Ŗ��������ƁA���������߂�Ȃ��Ƃ����Ȃ��̂ŁA�����������Â炢�ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̃Z���^�[��������ɂ��ā^21.05.30�n
�ŏ��̖��ŁA���ꂼ��ƂȂ��Ă��镔��������̂ŁA�������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D���u���ꂼ��v�ɒ����܂����D
���m�ʂ̕ł���̎���ɑ���n[�m���̊�{�ɂ��ā^21.05.30�n
���Q�m�d�݂̊m���n[ ��3�� / �S3�⒆ ]
(3)�@�P���̍d�݂�����������āC�\���Q��o���Ƃ���ŏI�����̂Ƃ���D�S�����Ƃ��ɏI��ɂȂ�m�������߂�D
������̖��͗Ⴆ��1��ڕ\�A2��ڕ\�̏ꍇ�A3��ڈȍ~�͓����Ȃ����Ƃ���A����������W�c�ƂȂ鎎�s������ƍl����̂����R���Ǝv���܂����B���̑O��ōl����ƁA���s��4����܂łőS11��ł���A���̒��œ�����̃p�^�[����6�p�^�[���̂��߁A6/11���������Ǝv���܂����B���̓_�ɂ��Ă����������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���l�Ȋm���炵���̌����������߂̐������ɂ��āC���̉��ɏ����Ă���܂��̂ŎQ�l�ɂ��Ă��������D�Ȃ�11��Ƃ����������͕ςł��D�܂��C�ʏ�̊m���i�����t�m���ł͂Ȃ��m���j�́C�X�^�[�g�n�_���������Ɍ������ē���������ꂽ���̂ŁC�r���܂Ō��Ă��琔������ς��邱�Ƃ͂ł��܂���D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^21.05.30�n
�O�����B�����������炢�����ɂȂ�܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^21.05.28�n
�w���v�Z���ӂɂȂ�܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�i���j�ɂ��ā^21.05.28�n
�������Ɍ���āC����͂킩��₷�������̂ŏ�����܂����C
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��`�̋Ɍ��ɂ��ā^21.05.27�n
���n�o�g�̌o�ϊw�����ł��B
�{���ɏ�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�E�]���藝�ɂ��ā^21.05.27�n
����ɂ��́A�������̃T�C�g�𗘗p�����Ē����Ă���܂��B�����肪�Ƃ��������܂��B
�O�p��Ɛ}�`�A�O�p�`�������A�Z���^�[���⑴�̑�3���2000�N�̖��ɂ��āA�Ō�̖ʐς̖��ɂ��Ăł��BS2��BD�ECD�Esin BCD�Ƃ���܂����A������BD�ł͂Ȃ��ABC�ł͂Ȃ��ł��傤���H
���m�F���肢�v���܂��B������̊��Ⴂ�ł�����\�������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�ԈႢ�ł����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���f���ɂ��ā^21.05.27�n
������܂���
�����m��ҁn�F������܂���ł́C������܂���D���w����������Ȃ��̂Ȃ�u����͂������낤�v�Ƃ������ƂɂȂ�܂����C�債�����Ƃ������ĂȂ��̂ɁC���Z�Q�N���������ǂ�ŕ�����Ȃ��̂Ȃ�C�����܂���������Ȃ����v�ł����H
���m�ʂ̕ł���̎���ɑ���n[�w���s�����ɂ��ā^21.05.24�n
�Ƃ��Ă�������܂����B���S���ăe�X�g�ɗՂ߂܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���k�C���^Atamol����^21.05.24�n
�c�ɂɂāC�����́i���́j�i�w���Z�ɒʂ��C���嗝�ȇT�ގu�]�ł��D��2�ł��D
���́C���w�ɂ����āC������ǂ����߁C�����C�{����Nj�����̂��D���ł��D�܂��C���ꂱ�������w���w�ԏ�ōł���Ȃ��̂ł���C�ʔ����ł���C�i��ʑw�ɂ�����j�����ł���C�����ߓ��ł���ƍl���Ă��܂��D����C�ËL�������ł��D���_�C�{���𗝉������Ȃ����ނ͌����ł��D�������ËL������l�������ł��D�������ËL����l�������ł��D�v�������Ȃ��C�����ɂ����鎞�Z�̂��߂ɍŒ���͊o���悤�Ƃ����Ă��C��͂���ł��D�c�c���̗l�Ȏ��ł����C���̃T�C�g�����ɂƂ��āC�ہC�w�ǂ̎��ɂƂ��āC���z�I�Ȃ��̂ł��D���w�҂���Ȑl��������悤�Ȃ��̂ł����Ă��C�K�������ȋc�_�������ĉ�����C�������f���炵���C�ɓ����Ă��܂��D���̏�C���x�ȓ��e�ł����ɕ�����Ղ��Z�߂��Ă��܂��D�V���ł��D
�����֒H�蒅�����o�܂ł����C�����C���́s�_�ƒ����̋����̌����t���o�����Ȃ��ĉ����グ�Ă��܂����D���̈Ӗ�����ł����D�`���i���ɂƂ��Ắj��Ȃ��̂ŁC���G�ȏؖ��̎菇��H���ē��o���悤�Ƃ��Ă��C������ł��邱�Ƃ͎����ł����D���̗l�ɔ��ɍ����Ă������C���̃T�C�g�ɍs��������܂����D�`���Ă݂�ƁC�T�C�g�̕��͋C����C���ɕM�҂̈Ќ����������܂����D���鋰�铖�L�����X�N���[�����Ă����n�ǂ���ƁC���͑M���܂����D�䂪�����܂����D���̒��̞B���ȗ��_���q����܂����D���̒��őS�Ă��q����܂����D�����J���܂����D��̕����Ӗ������̂ɂȂ�܂����D���̐��E���ς��܂����D�������āC���͐V����̎����̗l�ȕ�����𗝉����鎖���o���C�u�e���`���N�̌����i�C�������g�����̂ŏ���ɖ��t�����j�v�̓X���X���Ɠ��ɓ����ė��܂����D�����`�C�������ǂ���D�{���ɏ�����܂����D���炭�����ł�����������Ă��Ȃ���C���̐�̐l�����u�l�݁v�ł����������m��܂���D�_�ƒ����̋��������߂��Ȃ������������|���ƂȂ�C��Q�ƂȂ��Ă��������m��܂���i���ꂪ�����̑S�Ăł͂Ȃ����낤���j�D�L�������܂��I���ꂩ����X������肢���܂��I
�Ō�ɁC���Ɉ��ۂ炵����Ԃł����C�������ł����p�I�ȁC�������炵���֗��Ȍ�����f��������i�C�����̓e�N�j�b�N��������C�����C�f�ڂ��ė~�����ł��D�����܂ł͓���Ă��C���炩�̌�����藝�C���G�ȉ�@�ɂ��āC������藧���C�u�ǂ����Ă����Ȃ�̂��v�Ƃ������^��������o����l�ȋL������������҂��Ă���܂��D
�i���ɖ��f�Ȓ����ƂȂ��Ă��܂������Ƃ����l�ѐ\���グ�܂��D�j
�����m��ҁn�F�A�����肪�Ƃ��D���w�ȊO�̘b���[�����Ă���悤�Ȃ̂ŁC��������߂����Ɍ���Ȃ��u�����v���I
�@�������{�ȗ��̒����W�����Ƃ��x���銯���̊j�Ƃ��Ă̕��V�i�@�w���j�Ȃ獡���I�ȈӖ�������Ǝv���܂����C������q�̓����̎|�����ܖ���������Ă��܂������T�Ƃ����̂́C�Ȃ��H����u�����ł����ł��Ȃ�����=�Ⴆ�ΉF���J���v�Ƃ����ڕW�Ȃ�C�����I�ɂ������ł��܂����C�Z��Ƃ��������ŁC��s���Ȃ��Q�{�̐�����Ƃ������S�Ɍ������b�Ȃ̂��D���V�́C�S�R�y�C���Ă��Ȃ��̂ł͂Ȃ����H
�@���ɂ����낢��ȉ\�������āC�Z��Ɏ�ɂ́C�S���̖��𐳉����悤�ƍl���Ă͂����Ȃ������X�C���ԓ��ɂł����肪�����Ă���킯�ł͂Ȃ��̂ŁC�̂Ă���Ǝ̂ĂȂ����́u�d�����v���d�v���ƌ����Ă��饥�����́C�L�����A�����ɋ��߂���\�͂ƕ������Ă���Ƃ������Ă���D
�@���Ȃ��̐i�H��]�ɔ����Ă���̂ł͂���܂���D�w�K���Ԕz���v��̉\�b����������ł��̂ŁC����邩�ǂ����́C���Ȃ�����ł��D
���m�ʂ̕ł���̎���ɑ���n[ �}��ϐ��\���ŕ\���ꂽ���̓����ɂ��ā^21.05.23�n
�}��ϐ��̓����ɂ��Ă������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����������������悢�������Ǝv���܂����D�Q������Ŏ��I�ɈقȂ�ǖʂ�������ꍇ�́C�\�ߗ\�K���Ă����Ȃ���Ȃ�܂��C���̂悤�ȓ��ʂȎ���Ȃ���C���܂�����I�Ɋo������e�͑��₳�Ȃ������悢�Ǝv���D
���m�ʂ̕ł���̎���ɑ���n[�����̎w��(�L�����̎w��) �ɂ��ā^21.05.23�n
�ƂĂ��Q�l�ɂȂ�A�܂������o���Ă���邠���肩��A����w�̗D�������������A�T�����������Ŏ��Ƃ́A�Q�Ă����x������߂����Ă��ꂽ���̃T�C�g�Ɋ��ӁI
�����m��ҁn�F�A�����肪�Ƃ��D5���Ԗڂ��̈�łU���Ԗڂ����w��������C�����ȏ�̐��k���Q�Ă��܂��D���k�͉��������Ȃ��D���Ԋ��S�����A�z�Ȃ������Ǝv���D
���m�ʂ̕ł���̎���ɑ���n[�P���ϊ��ɂ��ā^21.05.22�n
1���ϊ�����肾�����̂ŁA�ƂĂ��킩��₷�������ł��B
���w���ł��悭�킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��W�{�̏ꍇ�ɂ��ā^21.05.22�n
��4�̉ŗp����ׂ����U�́A��W�c�̕��U�ł͂Ȃ��ł��傤���H���ŗ^�����Ă���W�{���݂̂����ł͉ł��Ȃ��ƍl���܂����A�������ł��傤���H��낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��W�{�̏ꍇ�́C�s�Ε��U�ƕW�{���U�́C�قړ������Ƃ݂Ȃ��C���̃y�[�W�̗v��ɏ����Ă��邚�̒l��p���Ē��ׂ܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̏��@�i����Z�j�ɂ��ā^21.05.21�n
������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̊K���ɂ��ā^21.05.21�n
�߂��Ⴍ����킩��܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^21.05.20�n
��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^21.05.20�n
�߂��Ⴍ����킩��₷���ł��B
�l�I�ɋ��ȏ������킩��₷���̂ŁA��w�Ɍ����Ă��̂����Ƃł��ガ�傤�̕��K��悵�イ�����Ă��������Ǝv���܂��B���肪�Ƃ��������܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̊�{�ɂ��ā^21.05.20�n
�L���������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^21.05.20�n
�Ō�̉���ł����A���p�O�p�`��`���ƁA�Ȃ�12�A16�A5�Ȃǂ̐��l���o�Ă���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D
���w�Z�ŏK���܂�
���̖��ł́CC����AB�Ɉ����������̑���H, BH=x�Ƃ���ƁC�O�����̒藝�ɂ��C13
2−x
2=20
2−(21−x)
2
������Cx=5, AH=21−5=16, CH
2=13
2−5
2���CH=12
sinx/x�̋Ɍ��̏z���Ȃ��_�@�������Ă��������I
�����m��ҁn�F�A�����肪�Ƃ��D�z����_�@�͏K���Ă��Ȃ��͂��ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.05.19�n
�ƂĂ��킩��Ղ��A���߂Ȃǂ������Ă킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�̋����R�捪���ɂ��ā^21.05.18�n
�ւ̍l�������̌n�I�ɐ�������A��C�ɖ�肪�X���X��������悤�ɂȂ�܂����I���肪�Ƃ��������܂����B����Ƃ������b�ɂȂ�܂��B��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.05.18�n
������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���s�����̉������ɂ��ā^21.05.17�n
�{�^���������Ɠ������o��������g���₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����������ɂ��ā^21.05.15�n
���Ɋւ��Ă͂ƂĂ��ǂ��Ɗ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���ɂ��ā^21.05.13�n
�悭�킩��Ȃ��č����Ă������ǁC�����������₷���ė����ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���̓����ɂ��ā^21.05.12�n
X,y�����ꂼ��t�ŕ\����Ă���y��x�̎��ŏ����ƂȂ��Ă���ꍇ�ǂ���������ł���
�����m��ҁn�F�A�����肪�Ƃ��D������������̂ł����C�ł��Ȃ����͂ł��܂���������C�ł��Ȃ����Ɂuy��x�̎��ŏ����v�Ə����Ă���C��肪���������Ƃ������ƂɂȂ�܂��D
�y��z
^2&chf=bg,s,fff9f9)
�y��z

�F�ʏ�C���̂悤�Ȗ��ł������ŕ\���Ƃ͌���Ȃ�
�y��z

�F�ʏ�C���̂悤�Ȗ��ł������ŕ\���Ƃ͌���Ȃ��D
�ƂĂ��킩��₷���I�I(o>�������m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̕��s�ړ��ɂ��ā^21.05.10�n
����܂ł�������o��̂����̃T�C�g�ƈ���ĂƂĂ��ǂ��Ǝv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^21.05.09�n
�ƂĂ��ǂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.05.08�n
��1.3�̓���a��8��b��3�悶��Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�A�̎w���@����
^3=a^6&chf=bg,s,fff9f9)
�ł��D�����

�ɂ��Ă�����C���͍����܂���D
��������̌���Ƃ͂Ȃ�ł����H�����ł́H
�����m��ҁn�F�A�����肪�Ƃ��D�u��������̌���Ƃ͌����Ȃ��v�ƌ������Ƃ��Ɂu���C�������v�ƌ��t�V�т����Ă���悤�ɒ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�s��̂����ɂ��ā^21.05.07�n
�ƂĂ��g���₷���ĎQ�l�ɂȂ�܂����B�L�������Ă��Ǝv���܂��A���ꂩ��������b�ɂȂ�܂��B���낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�}��ϐ��\���ɂ��ā^21.05.07�n
�y�n�Ɖ������m�̒��ԂŁA���w�̕������Ă��܂��B�������ނɎg�킹�Ă������������̂ł����A���͂���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�������Ɍ��J���Ă�����̂�ǂ�ł����������Ƃ��C������Ċw�K�����Ƃ��邱�Ƃ��C�S����肠��܂���D�ނ��늽�}�ł��D��ʘ_�Ƃ��Č����C���ނ��R�s�[���āC�V���ɂ�����u���Ȃ̒��앨�Ƃ��āv�ʂ̃T�[�o�Ɍ��J����̂̓_���ł����C����ȊO�̕��@�Ȃ�C���p������C���̒��앨�̃A�C�f�A�� �Q�l�ɂ��ĐV���ɏ����������ʂ̋��ނ��쐬���Ă��C�������͂Ȃ��Ǝv���܂��D
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^21.05.05�n
���2��(2)�̂Ƃ���ł��B
�Ȃ�������(A�|8)(A�|15)�|120�ɂȂ�̂����킩��܂���B
�ł���Ή�����ق����Ǝv���Ă���̂ł����A�A�A
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^21.04.29�n
���Ȕ͈͂łق����炩���ɂ��Ă�ƒɂ��ڂɂ������̂ł��肪�Ƃ��������܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̌�_�ɂ��ā^21.04.29�n
�y�����̕������z
���f�����ʂɂ����āC�_A(z1)��ʂ�C���f��z2�ɕ��s�Ȓ����̕�������
z=z1+tz2�@�it�͎����j �Ƃ��邪���f��z2�ɂ͕���������̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�������CZ2(z2)�ɂ��āC����OZ2�ɕ��s�Ȓ����Ƃ����Ӗ��ł����C�E�ɐ}�������Ă���̂ŁC������Ǝv���܂������
���m�ʂ̕ł���̎���ɑ���n[ �s��ƂP���ϊ��ɂ��ā^21.04.29�n
�ԗ��I�ɂ����J�ŕ�����₷�������B���肪�Ƃ��������܂����B��Q�D�Q�|�R�i�Q�j�ł͂��f���|�Q���{�S���ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
����錧�^�y���܂߂���^21.04.29�n
���_�̍��W�����̂S�_�̎��ł̕���oab�ɓ_c���牺�낵��������H�Ƃ�����W�́A(1,2,0)�̗l�ł�����@��������܂���B�������������Bo={0,0,0} a={3,4,-1} b={-1,2,2} c={5,0,4}�̏ꍇ�ł��B
�����m��ҁn�F�A�����肪�Ƃ��DOAB��ʂ镽�ʂ̕�������Ax+By+Cz=D�Ƃ�����
O��ʂ邩��D��0�CA��ʂ邩��3A+4B−C=D, B��ʂ邩��−A+2B+2C=D �� A=C, B=−C/2, D=0 �� 2x−y+2z=0
���ʂ̖@���x�N�g����(2, −1, 2)������_C��ʂ�OAB�ɐ����Ȓ����̕�������
&chf=bg,s,fff9f9)
����OAB�Ƃ̌�_��
2(2t+5)−(−t)+2(2t+4)=0���t=−2
x=1, y=2, z=0
2log(x�{1)��log(x�{1)^2�͐������̂ɁA�t�A�܂�Alog(x�{1)^2��2log(x�{1)�͌��ƕ��������Ƃ�����܂��B����͂Ȃ��ł����H�܂��A���̕ӂ�̒��ӂ��Ȃ���Ă���̂�l�͍��܂Ō������Ƃ��Ȃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɏd�v�Ƃ��ď����Ă���܂��悤�ɁC

�����藧�̂́C

�̏ꍇ�Ɍ���܂��D
���������āC
&chf=bg,s,fff9f9)
�Ə����Ă���Ƃ��C

������C
^2&chf=bg,s,fff9f9)
�ɕό`���邱�Ƃ͂ł��܂����C
^2&chf=bg,s,fff9f9)
�Ə����Ă���Ƃ��C

�Ƃ͌���Ȃ�����i�Ⴆ�C

�̂Ƃ��C
^2=\log(-2)^2=\log 4&chf=bg,s,fff9f9)
�j������C
&chf=bg,s,fff9f9)
�ɕό`�����Ƃ͂ł��Ȃ��D
�@���̃y�[�W�̑����ɁC
�y��z
%2B\log_6(x-3)=\log_62&chf=bg,s,fff9f9)
���(1)��
(x-3)=\log_62&chf=bg,s,fff9f9)
���(2)
�Ɠ����ł͂���܂���Ə����Ă���̂́C���������Ӗ��ł��D
��y�ɉ����āA�ƂĂ�������₷���L������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^21.04.26�n
�ƂĂ��������ނł��I
�ŏ��͊ȒP�Ȃ��̂����X����Ȃ��Ă���
��肪�������܂��I
����ɁA�ɐ���������V�X�e�����ƂĂ������Ǝv���܂����I
�����̌v�Z�ߒ��̃~�X���킩��̂łƂĂ�������܂����I
�N���[���̂悤�Ő\����Ȃ��̂ł���
�Ō��(10)�̖��ł������������Ă���Ǝv���̂ł����A�A�A
���̒��������肢�������ł��I
�ق�Ƃɕ��ɂȂ�܂����I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D10���O�ɏ������������ɁC�ꊇ�ϊ��̃~�X���������悤�ł��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^21.04.26�n
���m�ʂ̕ł���̎���ɑ���n[ ���������i���p���j�ɂ��ā^18.5.15�n
���3��2�̐������ڂ���
�ɂ��āA(x�|y)3+(y�|z)3+(z�|x)3�|3(x�|y)(y�|z)(z�|x)
=�y(x�|y+y�|z+z�|x)�z(�c)=0
�����Ă͂߂����Ƃ̒P���ȁy�z���̑��������ł���
������炾���ł͌v�Z���ĂO�ɂȂ邱�ƂɋC���t���ɂ����̂ł͂Ȃ����Ƌ��l�������܂����B
���X�����Ă������������̌`�ɉ��^�I�ɂȂ�A�����������P���ȍ�Ƃ����������Ă��܂��܂��B
����ׂ����A�c���ׂ����E�E�E
�����m��ҁn�F�A�����肪�Ƃ��D���p���ł��̂ť��
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.04.25�n
�ƂĂ��A�킩��₷������ǂ��Ǝv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������i�Q�����j�ɂ��ā^21.04.24�n
���m�ʂ̕ł���̎���ɑ���n[�������̋Ɍ��ɂ��ā^21.04.18�n
�������p�����Ă��������Ă���܂��B
���Ƃ��Ɛ��w�͓��ӂł͂���܂���ł������A������̃T�C�g������悤�ɂȂ��Ă���A�������ł���悤�ɂȂ��Ă��܂����B���肪�Ƃ��������܂��B
���Z�����Ƃ��닰�k�ł����A�뎚���ȂƎv����ӏ��������܂����̂ł��������܂��B
���Z���w�V�@�́@����̋Ɍ��̃y�[�W�A�y�����܂ł̗v��z�i�Q�j�̕��͂ɂ��āA
�u�`�C���q�C���q���`�v
�Ƃ̋L�q������܂����A�u���q�v�̂�������́u����v�ł͂Ȃ��ł��傤���H
�����Ԃ̂��鎞�ɂ��m�F�A���A���X�������肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^21.04.17�n
�����Ȃ̂Ɋۂ����Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�����͔��p�����ŋL�����Ă��������D�S�p�����i�Q�o�C�g�����C���{�ꊿ���E���ȁE�J�i�j�͕s�ł��D����R���s���[�^��ŁC�����͔��p�����łȂ���Ȃ�Ȃ��̂́C�قڏ펯�ł����C���������ނɂ���Ƃ��ɁuA.���̋��ނ̂悤�ɑS�p������s�����Ƃ�����́v�uB.Excel�̂悤�ɁC�S�p�������i�擪����j�������܂ꂽ��C���p�ɏ��������Ă��܂��v�̂Q�̗��ꂪ���肦�܂��D���̋��ނł��쐬�N��ɂ���āC��������܂����C�����ł͏��߂ɒ��ӏ�����t���܂����̂ŁC����ɏ]���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�������i�L�����j�̕s��ϕ� �ɂ��ā^21.04.16�n
(1.2)�́y2�z�̖��̓����Ԉ���Ă��܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���̎���̎d��������Ƃ��́C���������������Ǝv���������q�ׂĂ��������D
���m�ʂ̕ł���̎���ɑ���n[�w�����A�ΐ����̕s��ϕ��ɂ��ā^21.04.16�n
�ŏ��J�������������ĂƂĂ����ɂ����ł��B
�����m��ҁn�F�A�����肪�Ƃ��DiPhone�ło�b�p�̉�ʂ�������C���͏����������܂��D�擪�Ɂu�� �g�єł͕ʕŁv�Ə����Ă��܂��̂ŁC�ʕł����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�s��̑����C�a�C���C�����{�ɂ��ā^21.04.15�n
���Ƃ̕��K�ɂȂ�̂łƂĂ��ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�S���ɍs��̎��Ƃ����Ă��饥������܂����I
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^21.04.14�n
���̃T�C�g�ŏ��߂ďd�ϕ����w�т܂����B�ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^21.04.13�n
�Ⴆ�C
y''+ay'+by=4e3x+5cos 2x
�̓���������߂����Ƃ�
y''+ay'+by=e3x
�̓����y1��
y''+ay'+by=sin 2x ����������������������������������cos2x�ł���ˁH
�̓����y2�����ꂼ�ꋁ�߂Ă����ƁC
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�s��̑����C�a�C���C�����{�ɂ��ā^21.04.13�n
���ňꏏ�ɖ��������Ă����`�ʼn�����Ă����̂��킩��₷���Ă悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^21.04.13�n
���������b�ɂȂ��Ă���܂��B�������Ԉ���Ă����炷���܂��A [1] ����̗L�����̗ޑ�̉���ŁA4���ڂ̕���̗L�������猴���֍s���Ƃ��A����̕��������Ȃ̂ŕ��q�̕������t�]���Ȃ��̂ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă���Ӗ��͕�����̂ł����C���̖��ŕ������}�C�i�X�Ȃ̂ŁC�������ς��܂�
���m�ʂ̕ł���̎���ɑ���n[�Q�_�����ԃx�N�g���i�L�������j�̉��Z�ɂ��ā^21.04.12�n
�Ă��킩��₷�����������������L�������1�y�[�W�ł���Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D���j���[�Ŏ��̍��ڂɐi�߂悢�����̂��Ƃ��Ǝv���܂�����������ƁC���Ȃ��̏ꍇ�́C��ʂ̋���iPhone��PC�p�̃y�[�W�����Ă���̂ŁC����x���W���\�����ꂸ�C�T�u���j���[�������Ă��Ȃ��悤�ł��D�X�}�z�p�̃y�[�W�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[���������i���K�j�ɂ��ā^21.04.11�n
�����T�C�g�ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ϐ������`.�����������̉������ɂ��ā^21.04.09�n
�ق�Ƃ��ɋv���Ԃ�ɔ���������������������
�S���肪�����Ȃ��B�قƂ�ǖY��Ă���B�l�b�g�ł��̋L�������Ďv���o�����B�{���ɂ킩��₷���B���ƉE�̑Δ䂪���L���Ƒ傫���Ⴄ�B
���E���r���Ȃ���ǂݐi�߂�Ƃ���Ȃ������ł���B���Њ撣���Ă��������B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t���ɂ��ā^21.04.09�n
x=1�̋t�����Ă���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�u����܂����H�v�ɑ���́u����܂���v�D
�@��������x=1�͊��ł͂Ȃ��̂�[y=�ł��Ȃ�f(x)=�ł��Ȃ��̂ŁCy�̒l���o�Ă��Ȃ�]�C���̋t���l�����Ȃ��Fy�̒l�ɑ���x�̒l�����߂悤�ɂ��Cy����`����Ă��Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^21.04.05�n
���߂܂��āB�t����m�ɒʂ��̂ł����A��ԏ�̃N���X�ɓ��������߁A�Ɗw�ł�����x�̊�b�͌ł߂Ă����˂Ȃ�܂���B�ǂ̒P���ł����J�ɏ����Ă���̂ŁA���̃T�C�g��傢�Ɋ��p���Ă���܂��B������܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̒��_�̍��W�ɂ��ā^21.04.04�n
���̉����������A�������������ɂ����Ȃ��Ă��܂��ꍇ������B
�����m��ҁn�F�A�����肪�Ƃ��D�u�g�єł͕ʕŁv�Ə����Ă���̂ɁCiPhone�ł킴��PC�ł������玚��������������̂́C���R�̂��Ƃł��D
���������msato����^21.04.03�n
�ڂ���������肪�Ƃ��������܂��B�i����@�̌����̎���ŁB�j���ꂾ���̍ޗ�������Ȃ�Ƃ��Ȃ肻���ł��B�Ƃɂ����撣���Ă݂܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̘b��������܂��C���͋C�I�Ɉ�ԋ߂��̂��u��]�̒藝�E�����藝�v�Łup(x)���������̂Ƃ��Cp(��)=0 �� p(x)��x−���Ŋ�����v�ł��D���̏ꍇ�́C�������Ƃ����O����g��Ȃ���Ή����Ȃ����Ƃɒ��ӁD�i�ȉ��͐��U�̎��ƂŌ������e�j
(→)p(x)�͑�����������C�P����x−���Ŋ������]��͒萔�ɂȂ�D������q�Ƃ����ƁCp(x)=Q(x)(x−��)+R�Ƃ�����D���̂Ƃ��Cp(��)=0 �Ȃ��R=0�ƂȂ邩��C�]���0���Ȃ킿�C������D
(←)p(x)=Q(x)(x−��)+R�Ƃ���Ƃ��Cp(x)��x−���Ŋ�����Ȃ�C�q��0�ɂȂ�D���������āCp(��)=0�@��Q.E.D.��
���m�ʂ̕ł���̎���ɑ���n[�W�J�����ɂ��ā^21.04.02�n
�������m�F�ł��邾���łȂ��A���K�܂ŏo����Ƃ��낪�ǂ������ł��B
�y���������������Ƃ��ł��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`��w���w��b�ɂ��ā^21.04.01�n
�Љ�l�̂��̂ł��B�W���́up�˂��v�̋L�����ȑO�ǂ܂��Ă��������܂����B���̋L�����Ȃ���A���܂������ł��Ă��Ȃ������ł��傤�B�@�_����������Ă���̂ł����A���̑O�ɁA����@�̌����ł����������i���j��p�i���j���̒藝�͗L���Ȃ̂ł����A������E�ɂ͍s����Ƃ��܂��Ă��Ȃ��A�E���獶�ւ�����̂��A������N�ȏ�l�������Ă��܂��B�Ɗw�Ȃ̂ŗ����l���Ȃ��A�A�A�B���ꂩ��A���y�����������i���j�z��p�i���j��L�Ǝ��Ă͂��܂����A������ƈӖ��͈Ⴄ�݂����ł��B������A�Ȃ��E���獶�֍s����̂��l���Ă��܂��B�܂�Ȃ��A���y�������z�̕����͍l���Ȃ��Ă��悭�Ȃ�̂��B�l�b�g�ł���Ƃ��A�Q�l���ł͂ǂꂾ���T���Ă����܂����̂悤�Ȃ��̂�������܂���ł����̂ŁA�����ƈ����Ă��Ȃ��Ɛ\���܂����B�����悯��A���̔Y�݂������Ă��������B���������m�ł��肢�\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��Dp(x)�Ƃ����L��������\���Ă���̂��𐳊m�Ɍ��߂Ă���l����Ƃ悢�ł��傤�D���ꂪ�B���̂܂܂��ƁC���̋c�_�����Ă���̂��C�Ō�܂Ō��܂�Ȃ�����ł��D
(A) p(x)�����Z�ȏ�ŕ��ʂɏK������Ɖ��߂���ꍇ�i��������p(x)���^�U�ɒ�܂閽��łȂ���C�S�̂ɂ��Đ^���U���Ȃ��Ȃ�j
�@�Ⴆ�Cp(x)��(x−1)(x−2)=0��\���ꍇ�C�ux=1����(x−1)(x−2)=0 �� (1−1)(1−2)=0�v�͐��藧�D
�u(1−1)(1−2)=0 �� x=1����(x−1)(x−2)=0�v�́u0�~(−1)=0�@�ˁ@x=1����(x−1)(x−2)=0�v�͐��藧���Ȃ�.�i��j���̉��肩��͂��̒l�ɂ��ĉ������܂�Ȃ��D
(B) p(x)���R���s���[�^�v���O�����ȂǂŒʏ�p������^���W���Ƃ��Ĉ����ꍇ
C,javascript,python�ȂǍׂ��ȏ����͈Ⴄ���C�T�ˎ��̂悤�Ɉ���
if p(x) == 1 //������p(x)��1��������
q(x) = 2 //q(x)��2�Ƃ���
else //�����łȂ����
q(x) = 3 //q(x)��3�Ƃ���
�ʏ�C���Z�ȏ�̐��w�Ő^�U�ɉ����ĕ���ꍇ�C��L�̂悤�ɍl����p(x)���^�Ȃ��q(x)=2,�U�Ȃ��3�ƍl���邪�C�R���s���[�^�v���O�����Ȃǂł͐^�͂P�Ƃ͌���Ȃ��D�t��0���U��\���C1,2,3,...-1,-2,...�v�����0�ȊO�͂��ׂĐ^�Ƃ���D�����Ŏ��̂悤�ȃv���O���������ʂɎg����D
if p(x) //������p(x)��0�łȂ����
q(x) = 2 //q(x)��2�Ƃ���
else //�����łȂ����
q(x) = 3 //q(x)��3�Ƃ���
�@���̏ꍇ�C���鎮p(x)���Ƃ���x−1�Ƃ́C���Z�ȏ�̕��ʂ̐��w�ł́C�P�Ɍ��t�̎g�������Ԉ���Ă���ɉ߂��Ȃ����C�_���̐��E�ł́C���̎��̒l��0�ɂȂ�Ȃ�x�̏W���i�^���W���j��\�킷���̂ƌ��߂�D
�@�����ŁC���̖��ɖ߂��āC�ux=1����(x−1)(x−2)�v����L�̂悤�Ȑ^���W���ōl����ƁC�ux=1���ix��1����x��2�j�v�͋�W���C���Ȃ킿���ӂ͋U�ƂȂ邩��C����ux=1����(x−1)(x−2)�v�ˁu(x−1)(x−2)�v�͐^�ƂȂ�D
�@�t�ɁC(x−1)(x−2)�́ix��1����x��2�j�ɓ���������C�u(x−1)(x−2)�v�ˁux=1����(x−1)(x−2)�v�͐��藧���Ȃ��D
�@�v���,���Ȃ��́u���̒藝�͗L���v�ƌ����Ă��܂����C�M�҂͕��������Ƃ��Ȃ��D
���̓��e�́A���Z�̋��ȏ��ɍڂ��Ă��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D��������u���W�v�Ƃ����A�������t���ł����C���w�U��������p.59�C���w�K��p.48�C�[�ъ�p.61�Ȃ�
�˓`���I�ɂ͑�w�����̏\���ԁi���͂��j�ɂȂ��Ă���̂ŁC�蔲���͂ł��܂���D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^21.03.30�n
a = {-6, -1, -1}�Ab = {5, 4, -1}�A�� = {4, 7, -5}��3�����O�p�`�ɂ��āA�@���x�N�g���́A{-20, 44, 38}�ƂȂ�܂�����1�_�̍��W���^����ꂽ�Ƃ��̒����̎��̋��ߕ�������܂���B�������������B�������Q�l�ɍl����Ηǂ��̂ł��傤���B1�_��3���ʂ̌�_�ō��W{-(79/63), 199/63, -(209/63)}�ɂȂ�B���邢��rst�Ƃ��ċ��܂���{ 65/126, -(2/21), 73/126}�ɐ���̂��s���ł��B�����̎��̋��ߕ����������������B����̋��߂Ă����͊O�S���̍��W�ł����A���e�Ƃ����l�����͏o�Ă���̂ł��傤���H
�����m��ҁn�F���̃y�[�W�̖����P��ł������Ă��玿�₵�Ă��������D���������C���Ȃ��́u�@���x�N�g���v�ƌ����Ă��܂����C�����̕����������߂�̂Ȃ�u�ʂ�_�̍��W�v�Ɓu�����x�N�g���v���w�肳��Ă��Ȃ���Ȃ�܂���D�������́C�u�Q���ʂ̌���̕������́v�Ƃ����`�Ŏ��₪��܂�Ȃ���Ȃ�܂���D
�@�u�킽���͉������₵�Ă���̂ł��傤���v�ȂǂƂ�������͎t�����܂���D
�@�u�����Ă��C�Ȃ����ꂪ���Ȃ̂�������Ȃ��v�u�ǂ�Ȗ��ɑ��铚���Ȃ̂���������Ȃ��v��Ԃł́C�ɑ���Ď���͎t�����܂���D

��

�͓������̂ł��D���ꂪ�C���Ȃ������߂Ă��铚�ł��D���rst,���H�Ca = {-6, -1, -1}�̋L���͎g��Ȃ�
�����������Ă�����Ă��܂��B���1.2�ł����A����1/3��́A���̉E��(x+1�j1/2��̎w����
�Ȃ��Ă���悤�Ɍ����܂��B�i������ƕ����������������܂��j���̃p�\�R�����Â�����ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D

��

��

�͒N�̂��̂��Ƃ����^���͂��蓾�܂����C

��

�ƑS�����Ă��܂���
������ƂĂ�������₷���A���ӂ��܂����I
����͖����Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�����z�\�C���Γx�����z�\�ɂ��ā^21.03.24�n
����ɂ��́B
���Γx���Ɋւ��鎿�₪����܂��̂ŁA�A���v���܂����B
���w���̋��ނł��ƁA�u�����𑵂���v�Ƃ����Ӗ��ŁA���Γx����0.2�ƌv�Z�ł����Ƃ��Ă��A0.20�Ə������Ƃ�����܂��B
����ɂ��Ăǂ��v���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���ʂ̘b���Ǝv���܂��̂ŁC�Ȃ����₳���̂���������܂���D
���m�ʂ̕ł���̎���ɑ���n[�t�s��̋��ߕ��ɂ��ā^21.03.23�n
T�^�s��̋t�s��̋��ߕ��̐��������Ă���������Ƒ�ς��肪�����ł��B
������낵������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ́C��w���N�x���x���̐��`�㐔�����������̂ŁC�d�q��H�̐v�Ȃǂ̐��I�Ȃ��Ƃ܂ł͑z�肵�Ă��܂���D�����ނ���l����̂́C�s��{�ό`�Ȃǂ̕��@�ŋC���ɑg�ݗ��Ăčs�����@�ł��D
�@

�̂Ƃ�

(a%2B 2b)}\begin{pmatrix}a%2B b%26 -b%26 -b\\-b%26 a%2B b%26 -b\\-b%26 -b%26 a%2B b\end{pmatrix}&chf=bg,s,fff9f9)
�Ȃǂ̎����̒Ⴂ�s��Ȃ�Cmaxima�ɏ������߂Γ_���ł���悤�ł�
����́A�Ȃ��Ȃ��ɁA�ڂ����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^21.03.22�n
�헪�Ղ��ď����Ă���Ƃ��̍l�������ǂ��킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�u���Ձv�͕ӂƊp�̂����l���������Ă�����̂Ɋۂ�t�����肷����̂ŁC�����������u���ɂǂ����U�߂邩�����܂�v���̂ł��D�����ɏ����Ă���悤�ɁC�ӂƊp�̂P�g�Ƒ��̊p�ia,A,B�j���������Ă���C�c��P�̕Ӂib�j�͐����藝�ʋ��܂�D���̃y�[�W�̗]���藝���K���ƁC�ӂƊp�̂P�g��������Ȃ��Ƃ��͗]���藝�ɂȂ�D���̐}������C����������킪���Ă���Ƃ������Ƃł�
���m�ʂ̕ł���̎���ɑ���n[�R���������̎������̌��i�����W���j�ɂ��ā^21.03.21�n
a�̒l��ς�����̂��킩��₷���āA�ƂĂ����ɂȂ�܂����B
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D�����Ō����̂����ł����C���̃y�[�W�͂���Ȃ�̗͍�Ȃ̂ł�
���m�ʂ̕ł���̎���ɑ���n[�K���ɂ��ā^21.03.21�n
���Z���w�K���Ă���Љ�l�ł��B�ƂĂ��킩��₷�������Ȃ̂ł������p�����Ă�����Ă��܂��B���肪�Ƃ��������܂��B���̃y�[�W�́y�悭����ԈႢ�z�́u���v�̗�ł����A(3-2�I)�̂悤�ɁA���ʓ���2��!�����Ă��܂��Ă���悤�ł��B�v�Z���ʂɈႢ�͂Ȃ��ł����A(3-2)�Ƃ������ɊK��L�������Ă���ꍇ�̐����Ȃ̂ŁA��L���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�I���Q�t���Ă��܂����̂Œ����܂���
���m�ʂ̕ł���̎���ɑ���n[�ݏ捪�ɂ��ā^21.03.20�n
���K���ŁA��������������̂�����Ăق����ł��B
�����悩������Axxxxx@xxxxx�ɁAE���[���Ŗ��𑗂��Ă��炦�܂��H
���A��1�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ɏ����Ă��܂��悤�Ɂu�����i�L�����j�̎w�����g������ݏ捪�͕s�v������v�ݏ捪�̖��������邱�Ƃɂ͈Ӌ`���Ȃ��ł��D�܂��C�l���ɘA������邱�Ƃ́C���ݍs���Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƌW���̕����ɂ��ā^21.03.19�n
�����o���Ă邩�s���������̂ŁA���K�����ڂ��Ă��������ď�����܂����B�܂��A�����Ɖ�������̏�ł����ɂ킩��̂͂ƂĂ������Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̍��������ɂ��ā^21.03.18�n
�����̕����̐������ƂĂ��ׂɂȂ�܂���
���́H���l����̂���߂Ă������ʁA��������肭�o�����y���������o���Ȃ��Ȃ��Ă��܂���
�����̕������������Ǝv���܂���
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̋O�Ղ̕�����[�����Z���wC]�ɂ��ā^21.03.18�n
�����Ƃ���͊�b�������߂����Ă����Ƃ���A���ƊԈႦ�Ă�����ł��ł��邱��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȑ���̘a�ɂ��ā^21.03.13�n
�y��5-2�z�̓����̕����{����Ȃ��ł���
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ΐ����̃O���t�ɂ��ā^21.03.13�n
���R�́i���j�Ԉ���Ă���悤�Ɏv���܂��B��̂R�ƂS������ւ���Ă���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ݏ捪�ɂ��ā^21.03.10�n
�ƂĂ�������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
����錧�^������������^21.03.13�n
�L��������܂��BP1=(2,5,3),P2=(-4,2,-1),P3=(1,-3,2)�ł̎O�p�`�̊O�ډ~�̒��S���W�����߂���ɂ��āA�������肢���܂��B�O�S�̍��W��x=291/1435,y=3869/2870,z=407/287�ł��邱�Ƃ�����܂����B�ł́A���̎��̔��a�͂ǂ̗l�ɋ��߂���̂��������������B�܂��A�O��̗����ł���Ƃ͎v���Ȃ��́u���_(-1,7/2,1)��ʂ邱�Ƃ��g���Čv�Z�v�ɂ��Ă��v�Z�ߒ��̂������肢���܂��B
�u���������v�ł��BP1=(2,5,3),P2=(-4,2,-1),P3=(1,-3,2)�ŎO�p�`�̊O�ډ~�̒��S���W�����߂�������₵�Ă��܂����A��̒��_(-1,7/2,1)�̋��ߕ��͉���܂������v�ł��B���W��x=291/1435,y=3869/2870,z=407/287�ɂȂ�܂������A���a�͂ǂ̗l�ɋ��߂�ꂽ�̂��͉���܂���B���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�A���������F-29x -2y +45z =67����@, 6x +3y +4z =17/2����A, x +8y +z =12����B�̉��́Cx=−291/1435,y=3869/2870,z=407/287�ł��D
(-1,7/2,1)�̎g������(-1,7/2,1)��ʂ�C�x�N�g��P2P1=(6,3,4)�ɐ����ȕ��ʁFP2P1�̐��������ʂ̕�������6(x+1)+3(y-7/2)+4(z-1)=0��6x+3y+4z=17/2�ˇA
���l�ɂ��āCP1P3�̒��_(3/2,1,5/2)��ʂ�x�N�g��P3P1=(1,8,1)�ɐ����ȕ��ʁFP3P1�̐��������ʂ̕�������(x-3/2)+8(y-1)+(z-5/2)=0��x+8y+z=12�ˇB
�R�_P1,P2,P3��ʂ镽�ʂ̕�������ax+by+cz=d�Ƃ����ƁC2a+5b+3c=d, -4a+2b-c=d, a-3b+2c=d�C������-29x+2y+45z=67����@
�@�A�B�̘A���������̉��͏�L�̒ʂ�D���a��(-291/1453-2)^2+(3869/2780-5)^2+(407/287-3)^2�̃��[�g=��118767/(2��1435)�F�ǂ̒��_�ƒ��S�̋��������߂Ă�����
�@�����Z�̖��ɂ��ẮC�������ς킵�߂���D��w�̖��ɂ��Ă͂₳���߂���D�w���ɉ���������ł͂Ȃ��D�@�B�̐v�̂悤�ȉ��p����ł����o����Ȃ����ɂȂ��Ă���
�@���Ȃ��̓��Ă�x���W�̕������t�ɂȂ��Ă���C���ꂪ�������Ƃ����O��ʼn��x�����M���Ă��������Ă��C�Ӗ�������܂���
����錧�^������������^21.03.13�n
�s�����̎���ɂȂ�܂��B�������������B
P1,P2,P3�ō��O�p�`�̊O�ډ~�̒��S���W�����߂���ł��B��̓I�Ȑ�����P1=(2,5,3),P2=(-4,2,-1),P3=(1,-3,2)�ł��B
P1P2�̒��_(-1,7/2,1)��ʂ邱�Ƃ��g���Čv�Z����悤�ł����A���̐����͂ǂ̗l�ɎZ�o�ł���̂��������������B
�܂��A3���ʁF-29x -2y +45z =67, 6x +3y +4z =17/2, x +8y +z =12�̌�_���Z�o������@�ɂ��Ă����肢���܂��B������낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������̍Z��������Ă����Ȃ��ƁC�Ή��̎d�������܂�܂���D�Ⴆ�C�㔼�̖��́u�A���������������悢�v�����ł��D�����C���Ɏʂ��ԈႢ������̂��C��������q���R������S���̕����ɂȂ�D
�@�O���̖��́C���Z�ɂ��Ă͓�߂��ŁC�R������Ԃł̕��ʏ�̎O�p�`�̊O�S�Ƃ������ƂŁC�x�N�g�����g���ĉ����̂��ߓ��ł��傤�D�������C����҂��u���_(-1,7/2,1)��ʂ邱�Ƃ��g���Čv�Z����悤�ł����A���̐����͂ǂ̗l�ɎZ�o�ł���̂��v�ƌ����Ă��邱�Ƃ��l����ƁC����҂̊w�͂Ɩ��̎�������߂��Ă��āC�������Ă������ł���Ƃ͎v���Ȃ��ł��D
���m�ʂ̕ł���̎���ɑ���n[�P���s�����̉������ɂ��ā^21.03.08�n
�Ⴆ��4=2x�k��������2=x�ł͂Ȃ�-2=x�Ƃ��������o������ux��-2�ł͂���܂���v�ƌ����܂����A4<2x�k��������2<x�ł͂Ȃ�-2<x�Ɖ����o���Ă��ux��-2���傫������܂���v�Ƃ͌����Ȃ��̂ŕs�����������ŋ�����̂͂ƂĂ���ς��Ǝv���܂�����������ĕ��ŋ����ƌ�������Ɋw�ׂ܂��ˁB
�Ƃ���ł��̃y�[�W�ł͕s�����̗��ӂɊ|���Z���������̏������@�̏ؖ��H�Ƃ��������������܂�ڂ����͉������Ă��Ȃ��Ǝv���܂��������������ؖ���NjL����\��͂���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�T�u���j���[�̖ڎ��ɂ���܂��D�i���Ȃ��̏ꍇ�CiPhone�ł���̂�PC�ł̋��ނ�ǂ�ł���悤�ł����CiPhone�ł͕��̃X�N���[�����W��ǂ߂܂���̂ŁC�X�}�z�ł̕���ǂ�ł��������j
���m�ʂ̕ł���̎���ɑ���n[���W���ɂ��ā^21.03.08�n
�y���2.1�z
���̕��ς͂Q�ł͂Ȃ��R�B
���W���̌v�Z�̓r���������������B
����ƕ��q�̗����ɂT���|����Ȃ�P�^�Q��P�O�B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���( = �������Ă����D�Ƃ������́C�L�[�{�[�h���P����ă`���_�[�������Ă���)
���m�ʂ̕ł���̎���ɑ���n[�N�������̌����ɂ��ā^21.03.07�n
�ŏ��̗�1.1�ŁA�s�̌v�Z���s���Ă��镔���Ɍ������܂����B
x=�`�̕��q��-49�Ə����Ă���܂����A-46�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�o�Ȑ��̕������ɂ��ā^21.03.05�n
���̂̊ԈႢ������B
�����m��ҁn�F�A�����肪�Ƃ��D�Ӗ����ʂ��܂���D���̂ɂ��Ắu������Ƃ͈قȂ�Cweb��ʂł͖����̂̂悤�ȃq�Q�t�������͓ǂ݂ɂ����̂ŁC�S�V�b�N�̂̕����ǂ݂₷���ł��傤�v�Ƃ����悤�ɁC�D�݂̖����������Ƃ͂���܂����C�ԈႢ�Ƃ����c�_�͂߂����ɂȂ��ł��傤�D�܂��C�ϐ��́C���w���ȏ��Ŏg����a, x�ɂȂ�ׂ��߂�Times New Roman�C�^���b�N�ɂ��Ă��܂����C���������Ƃ����c�_�ɂ͂Ȃ��݂܂���D������ɂ���u�ǂ̕������ǂ����v�Ƃ����`�ŋ�̓I���ړI�Ɍ���Ȃ��ƁC�b���ʂ��܂���
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^21.03.04�n
���肪�Ƃ��������܂���😊
��肪�ǂ������ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�N�������̌����ɂ��ā^21.03.04�n
���2.2�̓������Ⴂ�܂��Bx.y.z��(0.1.2)���Ƃ������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ɕ������ɂ��ā^21.03.03�n
�������킩��₷���ł��B��肪����̂������ł��ˁB����������������J���Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�E���E���ɂ��ā^21.03.03�n
���������b�ɂȂ��Ă���܂��B
�t�E���E��́y���̃y�[�W�̗v��z�̐}���������Ȃ��ł��B���P�̒���낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�܂��C���Ȃ����������Ǝv���}�������Ă�������
���m�ʂ̕ł���̎���ɑ���n[�����W���ɂ��ā^21.02.28�n
�ƂĂ�������₷���ł�
�w�K�̎菕���Ƃ��Ċ��p���Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̌�_��ʂ钼���̕������ɂ��ā^21.02.25�n
2�����̌�_��ʂ�A�ʂ̒����ɕ��s�Ȓ����̕������̋��ߕ���m�肽���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D2����A,B�̌�_��ʂ�C�ʂ̒���(C)�ɕ��s�Ȓ����̕����������߂�ɂ́C
�A)�@���̋��ނň������悤�ɁC2����A,B�̌�_��ʂ钼���̕�����������āC���ꂪ(C)�ɕ��s�ƂȂ�悤�ɁC�萔k�̒l�����߂���@
�C)�@�_(x1, y1)��ʂ�C����(C)�ɕ��s�Ȓ����̕����������߂���@
�Ȃǂ��l�����܂��D����̓��e����ʉ����Č��������悤�Ƃ����C�P���Ɍ�_�����߂āC�������g���ĉ��������ȒP�ɂȂ�܂��D
�@�C�j����́C�Ⴆ�C�Q����x+y=3, x−2y=0�̌�_��(2, 1)������C���̌�_��ʂ�C�ʂ̒���5x−6y+7=0�ɕ��s�Ȓ����̕�������5(x−2)=6(y−1)�ƂȂ�܂�
���m�ʂ̕ł���̎���ɑ���n[���Ғl�ɂ��ā^21.02.24�n
�y���U�z�̉���̃G�j�P��ڂɕ\���R���o��m�������������B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������|����������(1����)�ɂ��ā^21.02.23�n
���̒��肪�Ƃ��������܂��B���Z��������T�I��������w3�N���ł��B���Z���w�̏��������Ă����̂ł����A�ƂĂ����ɂȂ�܂����B�����̖���菭��������������̖�肪����ΐ�������Ă݂����ł��B���ԐM���҂����Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ڎ��ɉ����Đi��ł��炦�C�������ɓ���Ȃ�܂�
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̑Q�����ɂ��ā^21.02.21�n
�u�]�Z�Őϕ��Q�������p�o�Ȃ̂łƂĂ��Q�l�ɂȂ�܂����I
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.02.20�n
�ƂĂ�������܂��܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^21.02.20�n
�d���R��̕������ĂāA�����̎w���̈������悭�킩��Ȃ������̂ł����A�Q�l�ɂȂ�܂����B�悭�A�킩��₷�������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ԃx�N�g���ɂ��ā^21.02.19�n
�y2�_�Ԃ̋����̌����z�́i����j�̎O�����̒藝
��j�����O�Q�������O�Q�{�����O�Q
���j�����O�Q�������O�Q�{�����O�Q
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^21.02.19�n
���Z���̎��ɂ�������Ɨ����o���Ȃ������̂ł����A�����Ȃ���Ȃ�Ȃ�����ƂȂ��Ă�����ŕ������Ă��������܂����B���̐悪�K�v�����Ƃ����L�[���[�h�◑�̃C���X�g�͖{���ɕ�����₷�������ł��B�z�F�̕ύX�܂łł���Ȃ�āA�D�����Ɉ��Ă��܂��ˁB�D���Ȕz�F�ɂ��Ċy�����C���ŌJ��Ԃ������A�S����ł���悤�ɂȂ�܂����B�{���ɂ��肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̌v�Z�ɂ��ā^21.02.18�n
�ԈႦ�Ă������������₷���Ă����o����
�����Ɩ�萔�𑝂₵�ė~����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�s�����ɂ��ā^21.02.18�n
���3�̓�����30��<��<90��,90��<��<150���ƂȂ��Ă��܂���30��<��<150���ƂȂ���̂͊Ԉ���Ă���̂ł��傤
�����m��ҁn�F�A�����肪�Ƃ��D��=90���̂Ƃ��́Ccos��=0, sin��=1�ƂȂ��āC���̕s���������������C���ӂƉE�ӂ��������Ȃ�܂��D������_���ł��D
���m�ʂ̕ł���̎���ɑ���n[�x�C�Y�̒藝�ɂ��ā^21.02.18�n
���3�ł����AP(C)Pc(E)��0.03�~0.01�ƂȂ��Ă��܂����u�����@E�ŕa�CA�Ɛf�f�����m���v��10%�Ȃ̂�
P(C)Pc(E)��0.03�~0.1�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^21.02.18�n
��ώQ�l�ɂȂ�܂����BK⁷�͂�²�i��+1�j²�i�i3��(��+1�j-4�j���i��+1�j+2�j/24�Ōv�Z�ł��邱�Ƃ킩���Ă����̂ł����AK⁹�̕����20�������̂ł��ˁA���������܂�K⁹�̃p�Y���������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���R�`���^����������^21.02.17�n
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l�C�s��`�̋Ɍ��ɂ��ā^21.02.17�n
���K���̎�ނ��܂�ׂ�Ȃ��o�肳��Ă��Ă悩�����ł��B�q���g���킩��₷�����ό`�ł����B
�s��`�Ƃ����łȂ����̂���ʂ��₷���������Ǝv���܂����B���ԂƎP�}�[�N�����킢���ċC�����オ��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^21.02.17�n
�悩�����ł��B�������A�����������K��肪����c�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W���C�ɓ��鐶�k�͌��\���܂����C���̃y�[�W�͍��Z���w�̐��K�̎��ƂƂ������́C�u�ԈႢ�����̃����|�C���g�A�h�o�C�X�v�ł��D������C�����|�C���g�C�ꌾ�ŊԈႢ���Ă��炦�C����܂łƂ������ނł��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̕����ϕ��@�ɂ��ā^21.02.17�n
i�ƒu�����̂͐ϕ��萔����Ȃ��̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D��3����(4)�̂悤�ɁuI�̌��ʂ����̌`�ɂȂ��Ă���C�Ō�ɂ܂Ƃ߂ĂP����C��t���܂��v�D
���m�ʂ̕ł���̎���ɑ���n[�K�������ɂ��ā^21.02.16�n
���鐔���An�Ƃ������AAn+1/An��Bn�̂悤�ɂȂ鐔��(��n+1���̐����n���̐��Ŋ��������A���̏�������ɂȂ�悤�Ȑ���)�̎��́A�����ۂɂǂ̂悤�ȕ��j�𗧂Ă�Ηǂ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���̎��₪�C�K������̋��ނ��痈�Ă��܂����C�K������Ƃ͂��܂�W������܂���D�܂��C��ʍ����O�ɂȂ�Ȃ�����CAn+1/An��Bn�̂悤�ɂȂ鐔����l���邱�Ƃ͂˂ɂł��܂����C������l���郁���b�g�����邩�ǂ����D�Ⴆ�C�R���ԑQ�����œ������������قȂ�Q�̉������ꍇ�ɁC�����^�̈�ʍ����Ē�`���邱�Ƃ͂���܂����C���̏ꍇ�ł��P�Ȃ�An+1/An��Bn�̂悤�ɂȂ鐔����g�����Ƃ͂���܂���.
�@���������C��̓I�Ȗ��Ŏ��₵�Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�藝�C�����藝�ɂ��ā^21.02.16�n
���m�ʂ̕ł���̎���ɑ���n[�s��̐��ɂ��ā^21.02.15�n
��w�ŏK���ƕ������̂ŁA��3�̂����ɗ\�K���悤�Ǝv���A���̃y�[�W���������Ă��炢�܂����B
�{�ł͐������킩��ɂ��������̂ł����A������͂ƂĂ��킩��₷�������̂ŁA�悩�����ł��B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�s��͕��n�ł����n�ł��K�v�Ȑ��̒��ł����C���f�����ʂ͗��n�̌ł��������g��Ȃ��悤�Ɏv���܂��D���Z���w����s�����āC���f�����ʂ������Ԃ�̂́C�[���̂����Ȃ��b�ł��D
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l�C�s��`�̋Ɍ��ɂ��ā^21.02.13�n
�����Ɍ��炸�A��������ł͂Ȃ������Ă��������Ȃ��ł��傤���H�Ԉ���Ă���\�L���������Ă����������Ȃ�Ȃ̂��킩��Ȃ��ƁA�������ǂ��ԈႦ�Ă��邩�킩��Ȃ��̂ł��Ă��炢�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă���̂ɁC�C���t���Ȃ��̂́C�����͂��̎��R���H������Ƒ��v�ł����H�Q�Ă��Ȃ��ł��傤�ˁH
���m�ʂ̕ł���̎���ɑ���n[�ő����,�ŏ����{��,���[�N���b�h�̌ݏ��@�ɂ��ā^21.02.12�n
���U�̖������[�O���b�g�̌ݏ��@�ɂ��Ē��ׂ����Ƃ������Ƃŗ��p�������܂����B�u�������킩��₷���B�v�Ƃ̂��ƂŁA���������悤�ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̃x�N�g���������ɂ��ā^21.02.12�n
����3�̏ڍׂȉ�
���wA�̃`�F�o�̒藝�C���l���E�X�̒藝�ʼn������@
(2) CP:PD�����߂�
��j����APF
���j����BPF
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�W�����_���W���`�ɂ��ā^21.02.11�n
���ɂ킩��₷���A��������J�őf���炵���B
��肪�L�x�Ŗ��̉�������p�^�[����������₷���B
���ЂƂ����̂܂܌p�����Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������P�ɂ��ā^21.02.11�n
�������킩��₷�������ł��B
�̓_�@�\�����邽�߁A�ǂ������ł��I
�m�ŁA�A�|�Z�j�E�X�̉~���K�����̂ł����A�ڂ��������Ă��������Ȃ��ł��傤���H
���Z���w���K���n�߂�1�N�̒�2�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��ǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[�J�C�Q�敪�z�ɂ��ā^21.02.11�n
�䗦�̑��d��͂ɂ��Ă̓J�C��挟��ł��邱�Ƃ����������肪�Ƃ��������܂����B���߂������e��A-L�܂ł�12�̉��H�@������A���̂��̂̕s�ǔ����䐔�P�`25�ł���A�s�ǖ����䐔12500�`18500�Ɋւ��ĕs�Ǘ���L�Ӑ����T���Ō��肷�邱�Ƃł��B���������v�Z���s���܂������AA-L�܂ł̂P�Q�Q�̓��A�s�ǔ����䐔�����ғx����1.98����2.51���x�ƂȂ�Q������܂��B�����̒ʂ�C�G�[�c�̘A�����0.5���v���X���āA2.48����3.01�ƂȂ�A�S�ȏ�ɂȂ�܂���B��́A�Q�l��������Ɓi1/��1�{1/��2�j/2�Ə�����Ă�����e�����܂������A�s�ǖ����䐔�̑䐔��12500�Ƃ����ꍇ�ɕ���l�����ɏ������Ȃ�܂��B�S�ȏ�ɂ��邽�߂ɁA���0.5�łȂ����Ƃ��S�𑫂�����������肷�邱�Ƃ��ł���̂ł��傤���H�@��ς��Z�����Ǝv���܂����A������������ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�J���S���[��12������̂�����C�G�[�c�̕�͎g���܂���D�J�e�S���[�̕����ł��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̊�{�ɂ��ā^21.02.11�n
��Βl���܂ގw�����̒�ϕ����悭������܂���A����tanX �̒�ϕ��Ƃ�����Ă����Ə�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�O���F��̓I�ɖ��������Ă����Ȃ��ƁC���������܂���D�{���C�w�����͐��̒l�����Ƃ�܂���̂ŁC��Βl�L�����g���̂͂Q�ȏ�̊��̈����Z�ɂȂ��Ă���悤�ȏꍇ�ł��D�㔼�F�s��ϕ���������Έ��������ł������
���m�ʂ̕ł���̎���ɑ���n[�����t���m���ɂ��ā^21.02.10�n
��萔���L�x�Ŋy���������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ή��̂Ȃ��ꍇ�̂������ɂ��ā^21.02.10�n
��ς킩��₷��������g���ė������₷���L��������܂��B�����₳���Ē����܂��B����Ŕ䗦���������e������܂����A��̌Q�̔䗦�̌�����@�͗����ł��܂����B�����Ŏ��₪�������܂��B�܂��A���H�@A�CB,C,D,E,F,G,H,I,J,K��ޗL�肨�̂̂̉��H�@�Ő��Y�������Ƃ��̕s�ǐ��������Ă��܂��B���̏ꍇ�ɗL�Ӑ����T����A=B=C=D=E=F=G=H=I=J=K�̋A�������̌�����s���ꍇ�̕��@�ɂ��Ă�����������ƍK���ł��B�e�g�ݍ��킹�Ń{�[���t�F���[�ɂ��L�Ӎ��̒����Ƃ����̂�����̂ł����A�Q�l����ǂނ�P�l�Ɍ�����������|����P�l�Ŕ��f����BP�l������������Ŋ�����P�l�Ŕ��f����Ƃ������@������܂����A�i�P�j�|����̂��A����̂��ǂ��炪�������̂��H�@�i�Q�j�ق��̕��@�Ō��肷����@������A���̕��@�ɂ��Ă�����������K���ł��B��ς��Z�����Ǝv���܂����A�ȂɂƂ���낵�����肢�\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��Dt����́u�Q��ނ̃f�[�^�v�́u���ϒl�̗L�Ӎ��v�ׂ�̂Ɏg���D�u�䗦�̌���v�̓ԂQ��Ȃǂɏ����Ă���܂��D������,�u�R��ވȏ�̃f�[�^�v�́u�䗦�̗L�Ӎ��v��������̃y�[�W�Ŏ��₷��̂͂��������ł��D
�@�R��ވȏ�̃f�[�^�̕��ϒl�̗L�Ӎ��Ȃ番�U���͂ŁC�䗦�̗L�Ӎ��Ȃ�J�C�Q�挟��ōs���Ɗ�������������Ղ��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�o�Ȑ����ɂ��ā^21.02.09�n
�Ȃ��coshx��1�ȏ�ɂȂ�̂��C�ɂȂ��ăl�b�g�T�[�t�B�����Ă��炱���Ŕ����������ł��܂����B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̃x�N�g���������ɂ��ā^21.02.09�n
���Q�@�́@AP=OB+sBF�́AAP=AB+sBF���Ǝv���܂��B�ׂ����b�ł����B
�܂��A�b�����_�Ƃ��Ăb�`��a,CB��b�x�N�g���Ƃ��ĉ����Ă����������A�ݖ�ǂ���ɓ������Ǝv���܂��B�@(�̂����Ɍ����Ă��݂܂���)
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�������܂����D�㔼�F�D�݂̖��ł����āC�ǂ������̖��ł͂Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�}��ϐ��\���ɂ��ā^21.02.09�n
���������R�|��
�����P/�����Q�{�P�̊T�`���肢
�����m��ҁn�F�A�����肪�Ƃ��D�ʏ�p������L���ŃA�X�^���X�N*�͊|���Z��\���܂�.��������ƁC���₪��������x=2t�ɂȂ�C�ȒP�ɏ����ł���D
�@�����C�A�X�^���X�N���ݏ��\���Ă���̂Ȃ�C

�̊T�`�Ƃ������ƂɂȂ�܂��D���̂悤�Ȗ��̊T�`�́CExcel��x=−3�`3�i0.1���݁j�Łu�Ȑ��t���U�z�}�v��I�ׂC�ȒP�ɕ`���܂��D
n�i�@�̉��K���͂Ȃ��Ȃ���������Ȃ������̂ł����A������̃T�C�g�ł̖��ɂƂĂ��������܂����I
��萔�����\����̂��������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���ԑQ�����̈�ʍ��ɂ��ā^21.02.08�n
��Ɠ�(7)
��j�����P�^�S
���j�����S
���^�S���P�����烿���S�B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^21.02.07�n
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�ƌX���������̕������ɂ��ā^21.02.04�n
�킩��Ȃ��Ȃ����Ƃ��Ɏg�킹�Ă��������Ă���܂��B
��ς킩��₷���A���肪�����ł��B���ꂩ����g�킹�Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����C�g�����i�͖����j�ɂ��ā^21.02.04�n
��낵�����肢�������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^21.02.03�n
�������̃T�C�g�l�ɂ����b�ɂȂ��Ă��܂��B
�̓_���ʂ̃C���X�g���Ɠ��ōD���ł��B
1�ԏ�̖�蕶���A�u�I��ŃN���b�тȂ����D�v�ɂȂ��Ă��܂��B�뎚�ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�`�F�r�V�F�t�̕s�����ɂ��ā^21.02.03�n
�`�F�r�V�F�t�̕s������f���藝�ƃ��[�}���[�[�^���Ō����Ƃ��̉�͐��_�ł͂ǂ̗l�ɕ\�L���ׂ��ł��傤��?
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͓��v�̊�{�������Ă���̂ŁC�����_�̂��Ƃ͐����_�������Ă���Web�L���ׂĂ��������D
���m�ʂ̕ł���̎���ɑ���n[�_�`�̎���̉�]�ɂ��ā^21.02.02�n
(3)(4)�͖��m�������ӂ����ɂ���悤�ɗ������Ȃ��Ɠr���Ōv�Z�ł��Ȃ��Ȃ��ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D���̂悤�ɂ������K�v�͂Ȃ��Cz�����ӂɗ��Ă��C���������ɉ����Ă��炦�C���ɂȂ�܂��D�Ⴆ�C���P(3)�ŁC

��

��90����]�������̂ƍl����C
i&chf=bg,s,fff9f9)
���
=3%2B i%2B i%2B 2&chf=bg,s,fff9f9)
�C

(�S)�̉�������A�N���b�N���Ă��\������܂���B(�����Good���\�������悤�ł�)
�����m��ҁn�F�A�����肪�Ƃ��D(4)�͖��1,3,4�̂R����܂��D������œ_������ƁC�ǂ�(4)������ɍ쓮���܂��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^21.02.02�n
��肪���Ă���̂��ƂĂ��ǂ��ł��I
�悭������܂����I���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�]���藝�ɂ��ā^21.02.01�n
���ʊp���Ȃ��悤�ɐ����������āA���ʊp���܂ޒ��p�O�p�`�ƁA�����������Ăł������p�O�p�`�ŎO�����̒藝���g���Ɖ������̂ł����A����ł����Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�⏕���̈������ɂ���ẮC���w���w�ʼn����邱�Ƃ�����܂����C���̉����������ʼn����Ă����ƁC�]���藝���g�ɒ����Ȃ��Ȃ�̂ŁC�}�̂Ȃ����ɑΉ��ł��Ȃ����Ƃ�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̒��_�̍��W�ɂ��ā^21.01.31�n
�����̂Ƃ�����v�Z�~�X�ŕs�����������B�����������A����͂��Љ��P�������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����2�ɂ��ā^21.01.30�n
IPad��Safari�ŗ��p�����Ă�����Ă��܂����A�T�C�g�̍������������炢��Ă��܂��āA�����܂���B
���P����낵�����肢���܂�🍀
���������ɍ̓_���Ă����T�C�g���T���Ă����̂ł������Ȃ��āA����ƌ����܂����I�g���₷���ł��B���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��DiPhone, iPad, Android�̂���������Ȃ������܂��D�������������Ȃ��Ƃ����̂́C��ʑ�����@�̖��n�ł��傤�D�Ȃ��CiPhone, iPad�ŃT�C�h���j���[�̈ꕔ�������Ȃ����Ƃ͎����ł����C����͋��ނ��̂��̂ł͂Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^21.01.30�n
���������āA���p�O�p�`�̃t�H�[���������_���ɏo�肳�ꂽ�̂ƁA�T�C���A�R�T�C���̓ǂ݊ԈႦ�����āA�P�A���X�~�X��h���w�ѕ������Ȃ��Ƃ����Ȃ��ƂƊ������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[maxima�̏����I�ȑ���15����Q�����O���t�̕`�����ɂ��ā^21.01.30�n
�O���t�ɕ`���ׂ������A�Ⴆ��6���������ł���Ƃ��āA���̈�̃s�[�N�Ƃ�����̃s�[�N�̒l�̍����ɂ߂đ傫���ꍇ�̑Ή��Ƃ��ďc���iy���j��ΐ��ڐ��ɂ��Ĉ�̃O���t�ɕ\�����邱�Ƃ�����܂����A������ΐ��ڐ��ɂ�����@�������Ă��������B
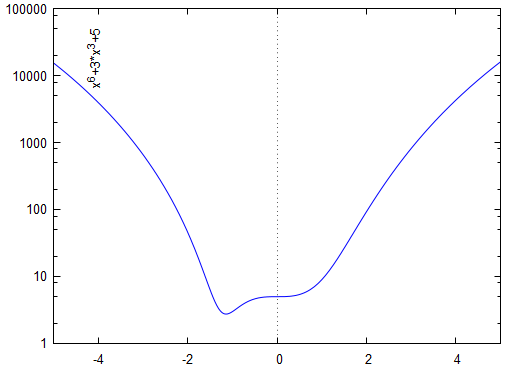 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��DwxMaxima�̃y�[�W���玿�₳��Ă��܂��̂ŁCwxMaxima�̂Q�����O���t�ł�����ΐ��ڐ��ɂ���ɂ́H�Ƃ������Ƃɂ��ē����܂���
�v���b�g→�Q�����v���b�g�ŕϐ�y�̉E�̕��ɂ���u�ΐ��ڐ�����g�p�v�Ƃ����`�F�b�N�{�b�N�X�Ƀ`�F�b�N������ł��܂��D�������C���w�̏펯�Ƃ��āC���ꂪ�g����̂́Cy���W�����̒l�ƂȂ�͈͂����ł��D
���}�́Cwxplot2d([x^6+3*x^3+5], [x,-5,5], [logy])$ �Ƃ��āC�`�����ꍇ�̃O���t�ł��D
�@Excel�ł����W,y���W�̑g����ׂ��\�i0<x��5, ����0.1��50�̃f�[�^�j����C�U�z�}��I�����Ă���C���̏����ݒ�őΐ��ڐ���I��ł����l�̌��ʂ������܂��D
���肪�Ƃ��������܂��B
�Q�~�̌�_��ʂ�~�E�����̕������̃y�[�W�A�P�ڂ̉����
�ux2+y2+ax+by+c=0 �c(1)x2+y2+dx+ey+f=0 �c(2)
���Q�_�Ō����Ƃ��C������
x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0�c(A)�v
�Ƃ���܂����B���L�_�����Ƃ߂�̂�
x2+y2+ax+by+c���j(x2+y2+dx+ey+f)��
x2+y2+ax+by+c�[�j(x2+y2+dx+ey+f)���O�ɂȂ�̂���
�Ǝv���A�u�Ȃ��A�����̂ł����v�Ƃ�������ł����B
���������Ƃ����\�������������������̂ł��傤���d�˂Ă̎���Ő\����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D
�A��������


���(1)

���(2)
�������āC(1)(2)�̉��i���L�_�̍��W�j�����߂�ꍇ�́C(1)(2)��x
2��y
2�̌W����������Ă��邩��C(1)−(2)�Ƃ���C1�����������āC�����(1)�܂���(2)�ɑ������C�������܂�Ƃ����̂��C���L�_�̍��W�����߂�Ƃ��̕��ʂ̗���ł��D
�@�Ƃ���ŁC���̖��́C���L�_�̍��W�����߂Ă���̂ł͂Ȃ��C�~�̕����������߂Ă���̂�����Cx
2��y
2�̌W���������Ă��܂��Ă͌����q���Ȃ����ƂɂȂ�܂��D���Ƃ́C���̃y�[�W�ɏ����Ă�������ǂ�ł��������D
�Q�̉~�̌����Q�_�����߂�Ƃ��ɁA�Ȃ��Q�̉~�𑫂��̂ł��傤���B
�������ƒ����̌����ꏊ�́A�����̎��������ā��O�ɂȂ�ꏊ���ڂ���w�̍��W�ɂȂ�܂���ˁB�~�P����~�Q���~�i�j�j�������̂��Ђ��āA�j���P�̂Ƃ��́A�����Q�̓_��ʂ钼���ɂȂ�B�Ƃ��Ă��ǂ��̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��Df(x,y)+k·g(x,y)=0��f(x,y)+k’·g(x,y)=0�Ƃ�k=−k’�̌`���I�ȈႢ�����ł�.�����C���̎���̎d���͈����F�u�Q�̉~�̌����Q�_�����߂�Ƃ��ɁA�Ȃ��Q�̉~�𑫂��̂ł��傤���B�v�Ƃ����Ă��C�ǂ̃y�[�W�̉��̘b�Ȃ̂����ʂ��܂���D���E���ŁC���邢�́C���̋��ނ̕M�҂��u�Q�̉~�̌����Q�_�����߂�Ƃ��ɁA�Q�̉~�𑫂��Ă���v���̂悤�ɒ������܂����C���̂悤�Ȏ����͂Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[��ԍ��W�C��ԃx�N�g���ɂ��ā^21.01.28�n
�y���V�z��DHF�̏d�S���f�Q�Ƃ���܂����A��CHF�ł͂���܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�����E�V���~�b�g�̒������@�ɂ��ā^21.01.28�n
���3�|1�@b3(t)=a3(t)-(a3,u1)u1-(a2,u2)u2�ƂȂ��Ă܂���
a2 -> a3�ł͂Ȃ��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����i�����W���j�ɂ��ā^21.01.26�n
���3��(2)�A(3)�ɂ��āB�o�Ȑ��H�ƌĂ����̂��o�Ă��Ă�悤�Ȃ̂ł����A����͐�1�EA�͈̔͂Ȃ̂ł��傤���B�E�̃O���t���番����Ə�����Ă�悤�ɃO���t������킩��̂ł����A�O���t�̏��������킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D

�̌`�̑o�Ȑ��͒��p�o�Ȑ��ƌĂ�C�����̃O���t�Ƃ������C���w�Z�ŏK���܂��D

�̌`�̑o�Ȑ��́C����ے��̔N��ɂ���ĕς��C���w�T�ɂ��������ォ��C���̂悤�ɐ��w�V�Ŕ����̑O���Ƃ��ď����G��邾���܂ŁC�d��→�y���܂őҋ��͑傢�ɕω����Ă��܂��D
�@�{���̂��Ƃ��͂����茾���C�����Ă���l�������ꍇ�������Č����邱�Ƃ�����܂����C�����I�Ȏ�舵�����猾���C

�̌`�̃O���t�̏��������K���Ă���̂�����C�O���t�̕��s�ړ��𐔊w�T�̂ǂ����ŐG���C�ʂ̗��K�����Ȃ��Ă��u�ł���悤�ɂȂ��Ă���v�Ƃ������Ƃł��傤�D������C���w�T�̒i�K�ŁC�Z���̒�������łȂ���C���̂悤�ȉ��p��肪�o�Ă��w���v�̈�E�Ƃ͌���Ȃ��ł��傤�D
(1)

�̃O���t��`��.�@(2)�@

�ƂȂ�̈��}������D(3)�@
(y-3)\gt 2&chf=bg,s,fff9f9)
�ƂȂ�̈��}������D
������������グ�Ď���ό`������@�͑�ς��߂ɂȂ�܂��B�f�G�ȉ�����肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̓������1�ɂ��ā^21.01.26�n
�����̍l�����Ԉ���Ă����狳���Ă��������B
���3(2)�ɂ���q=-p�Ȃ�p=-q�Ƃ��ł���Ǝv���܂��B���̏ꍇ������p=4,q=-4�ɂ��Ȃ�Ǝv���̂ł��B�I�������i���Ă����̂œ������i���܂������A�I�������Ȃ������ꍇ�ǂ�����L�蓾��Ƃ������Ƃł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��̍l���͊Ԉ���Ă��܂��Dq=-p�Ȃ�p=-q�Ƃ��ł��܂����C������p=4,q=-4�ɂ͂Ȃ�܂���D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.01.26�n
���ɂ킩��₷������ł����I
���Z�͐��ے��������̂Ő��w���w�ԋ@�����܂���ł����B
����30��㔼�ł����A������^���ɕ��������Ǝv��������̃T�C�g��K�₵�܂����B
�Ō�̕ł܂Ŋw�ђʂ������Ǝv���܂��B
�����b�ɂȂ芴�ӂ��Ă��܂��B��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�ϕ��C�����藝�C�t���l���ϕ��ɂ��ā^21.01.25�n
���̂������킩��₷���ď�����܂����B�}�����₷���āA�ǂ̃T�C�g�����Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ������ɂ��ā^21.01.24�n
�q���ɋ����Ă���̂ł����A�ǂ����K�ɂȂ�܂����B���������Ă悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̔N��̐e�q�Łu��������v�u�����Ă����v�̂́C������
���m�ʂ̕ł���̎���ɑ���n[�ΐ��s�����ɂ��ā^21.01.23�n
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���䐔��̘a�ɂ��ā^21.01.23�n
���䐔��̃V�O�}�����ŔY��ł��܂������A���������ĕ|�����̂������Ȃ�܂����B�{���ɂ��肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W���̗v�f�̌��ɂ��ā^21.01.22�n
����������̃T�C�g�ŕ������Ă�����Ă���܂��B���肪�Ƃ��������܂��B
���1�A2�A3�ł����A
�w3�Ŋ����鐔��N=3m�Ƃ�����
1��N=3n��100�x�@
�̂悤�ɂ��Ƃ�������ւ���Ă���̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���邩��ɂ���炵���ԈႢ�ł����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^21.01.22�n
i�̌W���̂v�Z�������ɑI�ׂĂ��܂�����
�����Ƌ������ꂼ�ꐳ���̂S�p�^�[�����I�����������ق���
�v�Z�~�X���������Ƃ��ɋC�Â����Ƃ�������̂ł͂Ȃ��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�w�̓Z���u�̔���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^21.01.22�n
�S��������Ƃ��̉摜�͂����g�ō���Ă���̂ł��傤���H��������G���Ǝv���܂��B
�i�����ł₷�Ȃǁj
�����m��ҁn�F�A�����肪�Ƃ��D���߂̍��i2000�N�̍��j�́C�ǎ҂��ދ����Ȃ��悤�ɐF�X�G�������Ă��܂������C�ŋ߂͂ނ���P�������Đ��낪��������Ƃ��ē`��邱�Ƃ��d�����Ă��܂��D
�@�������ǂ̃y�[�W�Ɂi�����ł₷�j�Ə������̂��C�����o���Ă��܂��C�i�����ł₷�j�́C�قځu��������Ⴂ�v�̈Ӗ��Œn�����̊ԂŎg���C�i�������₷�j�́C����̊ւȂǂ��z���Ă��鑼���̐l�i���̂ڂ肳��j�ɑ��āC�u��������s�ցC�悭��������Ⴂ�܂����v���炢�̈Ӗ��i�ォ��ڐ��ł͂Ȃ��j�炵���ł��D�z���Ƃ͓����z���Ƃ������ƁD�l�b�g�ɂ͑��̐���������Ă��邪�C�M�҂��������Ă���͈̂ȏ�̐��ł��`��F�G�w�ł���
���m�ʂ̕ł���̎���ɑ���n[����{.�x�N�g���̓��ςƍs��̐��ɂ��ā^21.01.21�n
�ł��邾���S��PDF�ɂ��ė~�����ł��I
���Q�l���Ȃǂ�����(iPad�œǂ߂�悤�ɂ��Ă���)�̂ŁAPDF�ɂ��Ă�������Ə������肵�₷���ł��B�߂���N�`���Q�l�ɂȂ��Ă܂��I���w�͓��ӂł�����w�ɓ������r�[�H�H�ƂȂ��Ă��܂����̂ł�����ŕ������Ă��������Ă܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��DPDF�ɂ���ƁC�t�@�C���̃T�C�Y���傫���Ȃ�܂��D�e����PDF������̂͊ȒP�ŁC���→�v�����^�[��PDF�t�@�C���ɕς���D
���m�ʂ̕ł���̎���ɑ���n[�w���������ɂ��ā^21.01.19�n
�O�Ԃ̓����[�P�ɂȂ�܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�S�p�����œ��͂��Ă�����̂ŁC���l�ł͂Ȃ��u���ȁv�u�J�i�v�u�����v�̕����u�[�P�v�ɂȂ��Ă��āC�듚�ɂȂ��Ă��܂��D
�@���l�͔��p�����œ��͂���̂���{�ł����C�Ƃ肠�����C�S�p�����œ��͂����ꍇ�́C���p�ɒ����č̓_���邱�Ƃɂ��܂����D�������C�����Z�̕����C���̕�����\���}�C�i�X�̓n�C�t���u�|�v�łȂ���Ȃ�܂���D�悭����"���̋L��"�ł͐����ɂȂ�܂���̂Œ��ӁF���[�}�́u�[�v�C�A���_�[�o�[�́u�Q�v�C�����̂����u���v�C�����o�[�u�\�v�C��t�́u�P�v�Ȃǂ͂�����������̃}�C�i�X�ɂ͂Ȃ�܂���D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̃O���t�ɂ��ā^21.01.13�n
�듚�̃O���t��\������@�\���~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D��낤�Ǝv���ł��鎖�ł��C�߂�����͋y���邪���Ƃ��Ƃ����C�O���t�������Ⴒ���Ⴕ�āC������ɂ����Ȃ�̂ŁC����͂��܂���
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^21.01.13�n
��3.2�̉���ŁA���̋}�ɉE�ӂ�0���o�ꂵ���̂����킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�O��C���܂����悤�ɁC
(\cdots)&chf=bg,s,fff9f9)
�ɂ����āC

�̂Ƃ���
&chf=bg,s,fff9f9)
�̂Ƃ���ɉ��������Ă��C�O���|����ƂO������C�E�ӂ͂O�ɂȂ�܂��D
�@�����ŁC

�ƒu�������Ă݂��
�@
(\cdots)&chf=bg,s,fff9f9)
�ɂ����āC
%2B(y-z)%2B(z-x)=0&chf=bg,s,fff9f9)
������C

�ɂȂ�܂��D�܂�
^3%2B(y-z)^3%2B(z-x)^3-3(x-y)(y-z)(z-x)=0&chf=bg,s,fff9f9)
�ɂȂ�܂�
�u���������ꏊ���͔͉ƈႤ�ꍇ�ł��A�����͈ꏏ�ɂȂ�܂����H ������_ �����Ă���r���ŕ����������Ⴒ����ɂȂ蕪����Ȃ��Ȃ��Ă��܂��̂ł����A������₷��������@�Ȃǂ���������Ē��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�������͎����̓s���ōs�����̂ŁC�ŏI�I�ɂ͌��ɖ߂��Ȃ���Ȃ�Ȃ��D���ɖ߂��C�r���o�߂�����Ă��C���ʂ͈�v���܂��D
�y��z
^2&chf=bg,s,fff9f9)
��W�J����Ƃ��ɁC(1)

�Ƃ����ƁC
^2=x^2%2B 2xc%2B c^2&chf=bg,s,fff9f9)
���ڂɗ��܂�Ό��ւƖ߂��F
^2%2B 2(a%2B b)c%2B c^2&chf=bg,s,fff9f9)

(2)

�Ƃ����ƁC
^2=a^2%2B 2ay%2B y^2&chf=bg,s,fff9f9)
���ڂɗ��܂�Ό��ւƖ߂��F
%2B (b%2B c)^2&chf=bg,s,fff9f9)

(1)(2)�͓�����
�@�����������Ⴒ���� �� �����I��낤�Ƃ��āC������ɏ����ĊԈႤ�Ƃ����̂��N�ł���肻���ȗ��Ƃ����ł��D���₷��=�ԈႢ�ɂ����悤�ɁC�u�u�������Ȃǂ𗘗p�v���āC�u��x�ɑ����̏��������Ȃ��v�悤�ɍH�v����̂��R�c�ł�
��b�͂��邽�߂Ɏg�킹�Ă��������Ă���܂��B
���̊ԈႢ�ł���A�\����܂��E�E�E��9��@�O�C�P�C�Q�C�R�C�S�C�T�̂U�̐������瑊�قȂ�R�̐��������o���āC�R���̐��������Ƃ��C�R�̔{���͉��ʂ�ł��邩.
�i�A�j�O���܂ނ��́o�O�C�P, �Q�p�o�O,�P,�T�p�o�O,�Q,�S�p�o�O,�S,�T�p�̂S�ʂ�ł����A�R���̂R�̔{���Ȃ̂ŁA�ō��ʂɁo�O�p�͎g���Ȃ��̂ŁA���̊e�X�ɂ��āA���ו��͂Q�E�P�E�P���Q�ʂ�
�ƂȂ�̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�m���̖��́C���ۓI�ȕ\�����m���߂�̂�����ꍇ������܂����C���̖��̂悤�ɋ�̗Ⴊ�ȒP�ɓ_���ł���ꍇ�́C��̗�ł����ׂ�ׂ��ł��D
�o�O�C�P, �Q�p�̏ꍇ�C�S�̈ʂ̒u�����́C�P�ƂQ�̂Q�ʂ�D���̊e�X�ɂ��āC�\�̈ʂ̒u�����́C�c��̂Q�ʂ�D�P�̈ʂ̒u�����́C�c��P�ʂ�D�䂦�ɁC�Q�~�Q�~1��4�ʂ�
��̗�F120, 102, 210, 201
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^21.01.11�n
��3.2�́u���̎���(z�|x)3�𑫂��Ă����ƉE�ӂ��O�ɂȂ�܂��v�ʼn��̋}��(z-3)3���o����̂��A���̋}�ɉE�ӂ̃[�����o�ꂷ��̂���������܂���B�����������牽������{�������Ă���̂�������܂��A�����Ē����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�܂��C�������������茩�邱�Ƃ��d�v�ł��D
(\cdots)&chf=bg,s,fff9f9)
�ɂ����āC

�̂Ƃ��͉E�ӂ��O�ɂȂ�܂��D������C
^3%2B(y-z)^3%2B(z-x)^3-3(x-y)(y-z)(z-x)&chf=bg,s,fff9f9)
�Ƃ���C
%2B(y-z)%2B(z-x)=0&chf=bg,s,fff9f9)
������E�ӂ�0�ɂȂ�܂��D
�@���Ȃ��͂��������C�s������Ă��܂���D
�ƂĂ�������킩��₷���āA�ǎ��Ȗ�肪�W�܂��Ă���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^21.01.11�n
���ɂȂ�Ȃ��ق������₷���ł��B���e�͂킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���݂ł�WEB���ނ��X�}�z�Ō���l��8���C�p�\�R���Ō���l���Q�����炢�ł��傤�D�i�g�݂Ȃ��̈��̌������ɂ��邱�Ƃ́C�}�łȂǂ̔z�u���ς���Ė����ł��D
�@�p�\�R���p�̋��ނ́C�X�}�z�p�̋��ނ̓���i�g�݂ɒ��������̂ł��D������C���̗v�]�ɂ͓������܂���D
���m�ʂ̕ł���̎���ɑ���n[�m���ϐ��̕ϊ��ɂ��ā^21.01.10�n
����web�y�[�W�ł́A�u���E�U�̋@�\�ɂ��A�����̑傫����傫�������菬����������A�����ł���̂ł����A���̃y�[�W�ł͂ł��܂���ł����B�R���s���[�^��ʂ̉𑜓x�́A�[���ɂ��l�X�œK�ȕ����̑傫����������Ă��܂��̂ŁA�����ł��Ȃ��ƍ��邱�Ƃ�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��X�̃p�\�R����Windows�Ȃ̂ŁC[Ctrl]+[+]�i�R���g���[���L�[�������Ȃ���{�L�[�������j�ňꔭ�ł��D�����Ƒ傫���������Ƃ��́C�����P��[Ctrl]+[+]�ł��D���Ƃɖ߂��ɂ́C����[Ctrl]+[−]�ł��D�������mac�ł�Command�L�[��[Ctrl]�L�[�̑��肩�ȁH
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������Q�ɂ��ā^21.01.10�n
���5��m�������������x^2+y^2���Ăǂ����玝���Ă������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����̂Ƃ��낪���̖��̐_���E�鉜�`�ł��D�u�K������m�ɂ��ĉ����Ȃ��Ă��悢�D�Ƃɂ���m���������邱�Ƃ��l����D�v�Ə����Ă���܂��悤�Ɂu���Ƃ�����m������������@�͂Ȃ����H�v�ƍl���܂��D��������ƕ����m2+1�����邩��C���q�ɂ�m2+1����ꂽ��C�ł��Ă��ꂵ���̂ɂȁI�ƍl���܂��D�����ŁCx2+y2������Ă݂܂��D��������ƁC�\��Ƃ͏�������āC�u�Ŋ��S�ɂ͏����Ȃ����C�P�͖ŏ����āC�c�������̂�x�ŕ\����v���ƂɂȂ�C���͕ʂ̌`�ʼn������邱�ƂɂȂ�܂��D
�@�����Łu�ǂ����玝���Ă������ł����H�v�ɑ��铚�́C�u����łł���Ƃ������Ƃ��������Ă����킯�ł͂Ȃ����C�����ɐF�X����Č����C�������Ă݂���C�^�悭�ł����v�Ƃ������ƂɂȂ�܂��
���m�ʂ̕ł���̎���ɑ���n[2����(�W���`�����_)�ɂ��ā^21.01.09�n
�y�����w�K�ł��܂����B��{�����o�肵�Ă��炦�āA���̃R���e���c�H���̍��ځH�͑S����ł��܂����B�����A�l�I�Ȃ��Ƃ���ł́A�����̍��Z������ɁA���w�͓��ӉȖڂł͂Ȃ������̂ŁA���ӎ������܂Ƃ��āA���炭���w�̕����牓�������Ă��܂����B���̐��w�w�K�T�C�g�̂����ŁA�Ăъw�K�ӗ~�����߂��܂����B���w�̏d�v���́A���{�l���w�ҁ@���R�[�搶�́u�V���w���@�v���u�k�Ѓu���[�o�b�N�X����ǂ��ƂŁA�w�тȂ����̏d�v���𗝉��ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�ɂ��ā^21.01.08�n
���Ɖ��M���g�킸�ɂ����̃L�[�{�[�h�������g�p����̂ŁA�w�K�����₷���ł��B����̂Q�����̃O���t�̑I����Ŕԍ��̓��̓~�X�̕s���������܂����B��{���Ƃ��āA�I�𐔂����炵�āA��萔�𑝂₵�Ă��ꂽ�����A�w�K�ӗ~�����܂�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�S���ł��u�܂���ł������邩��悭�Ȃ��v�Ƃ����������̔ᔻ������̂ł�����C�I���������炷�̂͂܂����ł��傤
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^21.01.06�n
����������ĂȂ��������Ǝv���܂�����������Ă�������܂���B
���������ׂ��������Ă�����Ă������ł���
�����m��ҁn�F�A�����肪�Ƃ��D������������ė���������Ȃ��Ƃ��͊�{��肩���蒼���������Njߓ��ł�
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.01.06�n
��3�ł����A�ÎZ�ł����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���ȏ�̈��������ɂ��ā^21.01.05�n
������₷���ĂƂĂ��w�ׂ܂����B�����ɉ�������Ă��Ă��肪���������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^21.01.05�n
������₷�������ł��B���肪�Ƃ��������܂�(*�L�ցM*)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�����ρi�����j�ɂ��ā^21.01.04�n
���ς̒�`��cos���̗p���邱�Ƃɂ��Ăł����A�����@���̐������ő�̗��R�̋C�����܂��B
sin�Œ�`����Ȃ�A�Ƃ̕������t�ɂȂ�ƁAsin�Ƃ̒l�̕������t�ɂȂ�܂���ˁB
�������ς��ƁA�p�x�̉�]�������t�ɂȂ�A�������Acos�Ȃ�t�ɉ�]���Ă������͋t�ɂȂ�Ȃ��̂͑傫�ȓ����̂悤�ȋC�����܂��B
���ƁA�x�N�g���̂Ȃ��p���A�O���ł͂����Ă��A��������̂������̂悤�ȋC�����܂��Bcos�Ȃ�Acos�Ɓ�cos�i360���|�Ɓj�ł��̂ŁA�i���܂肢�Ȃ��Ǝv���܂����j�Ȃ��p���ꌩ60���Ɍ�����ꍇ�ɁA300�����I�ƌ����Ă����Ȃ��Ȃ�悤�ȋC�����܂��B
���ς́A�ꌩ�|���Z�̂悤�Ȃ��̂ł��̂ŁA�����@�����������Ȃ��͈̂����ɂ����C�����܂��B
���ƁA�x�N�g���̓��ρi��`�̐���������Ƃ���j�̃y�[�W�ɁA���M�{�^��������܂���ł����̂ŁA�����炩�玸�炵�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�����ρi�����j�ɂ��ā^21.01.04�n
����������ς����߂���@�Ƃ��āA�]���藝���g�����@������܂��B
�i�Ȃ��p�̑ΕӁj^2���ia�x�N�g���̑傫���j^2�{�ib�x�N�g���̑傫���j^2�|2�ia�x�N�g���̑傫���j�ib�x�N�g���̑傫���j
������A�������g���ĕ\���āA���ӂ���A���ʂ̂��̂���������ƁA���ꂢ�ɓ��ς̎��������c��܂���ˁB
���z�@���́A����܂��Ă���ؖ����邱�Ƃ��ł��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^21.01.03�n
�ƂĂ�������₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̂������|�����������ɂ��ā^21.01.02�n
�����Ȃ����Ă����w���ł��A���������ł����肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ƒ����̈ʒu�W�ɂ��ā^21.01.02�n
��1�̓���A�ɂ��āA�~�ƒ����̋��L�_�̌��ƁA���ꂼ��̕������̘A���������̎������̌�����Έ�ɑΉ����邱�Ƃ��A�u���G�`���v�Ȃǂł͂Ȃ��A������Ɠ��l�ό`��p���Ę_���I�Ɏ��������Ă��������ׂ����Ǝv���܂����B(���Z���w�͎Z�������狖����Ă���̂ł����H)
�����m��ҁn�F�A�����肪�Ƃ��D�����������ɕ��s�łȂ�����Cx���W�̎������̌��Ƌ��L�_�̌����P�P�ɑΉ����邱�Ƃ́C���Z���Ȃ疾�炩�ł��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̌v�Z�ɂ��ā^20.12.28�n
���̎��������������ɂ����ł��B����ƁA�����̌`�⑾���Ȃ�(�ׂ����ė~�����ł��B)
���K��肪���Ă���̂͒蒅���Ă��邩�m�F���邱�Ƃ��ł���̂ŗǂ��Ǝv���܂��B
�w�i�����F�ɂȂ��Ă���̂��ƂĂ��C�ɂȂ��ďW���ł��܂���B���⍕�ɂł��܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�l���Ƃ̔z�F�̍D�݂܂ł͑Ή��ł��܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^20.12.25�n
�ƂĂ�������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ő����,�ŏ����{��,���[�N���b�h�̌ݏ��@�ɂ��ā^20.12.24�n
���̋��ȏ��ł͗������Ă܂����A��֑�w�u�]�҂ɂ͕K�v�s���Ȃ̂ŁA���߂ɂȂ�Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^20.12.24�n
�ō��ł��I���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^20.12.24�n
�������ۂɉ������Ƃɂ���āA���g�����܂����B
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̒�`�C�傫���C�����ɂ��ā^20.12.23�n
�e�y�[�W�Ƀy�[�W�̃g�b�v�ɖ߂�i�y�[�W�̐擪�ɃX�N���[������j�{�^��������ƕ֗��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D90���ȏ�̃y�[�W�ŁC�擪�ɖ߂�{�^����t���܂������C�L���b�V���������̉e���ŁC���ʂ����f�����܂łɎ��Ԃ�������ꍇ������悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕�����3�i�}��ϐ��\���j�ɂ��ā^20.12.21�n
�͂��߂܂��āB���4�ɂ��āB
���ό`���v�������R���L�q����K�v�͓��R�����ł����A�Ȃ��v�������������Ő����ł��Ȃ��Ƒ��̖��ւ̉��p���S�������Ȃ����̏ꗽ���̉ɂȂ�̂ł͂Ȃ����Ɗ뜜���܂��B
m²���܂ޔ}��ϐ��\���́A�܂�m²���������A����m������������@�������̗ޑ�ɉ��p�������Ǝv���܂��B��������Ζ{���(2)����m²=2m/y-1�ɕό`�����i�K��(y�Ŋ����Ă邩��)y��0�̕K�v���������܂��By=0�̎���(2)���m=0�����炱���(1)�ɑ������x=1�ƂȂ�܂��B���Ƃ�(1)�ɏ�L��m²=2m/y-1�������āA��������ό`����m=y/(x+1)�ɂ���(x=-1��(1)�ɑ�������2=0�ƂȂ�s�����ł��邱�Ƃ���x��-1�Ȃ̂�x+1������ɗ���͖̂��Ȃ�)�A�����(2)�ɑ�������x²+y²=1(y��0)�������܂��B�����O�q��y=0�̏ꍇ���瓾��(x,y)=(1,0)�ƍ��킹��A1�_�������~�������܂��B
�u�v�������R�������Ő����ł���v���������w�͂Ɍq����ƍl���鎄�Ȃ�̈ӌ��X�Əq�ׂ����Ă��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�������̕������ɂ��ā^20.12.20�n
�Ƃ��Ă��킩��₷���ł��I
�N�C�Y���������킩��₷���y�����o������Ǝv���܂����B
���肪�Ƃ��������܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�}��ϐ��\���ɂ��ā^20.12.19�n
�ƂĂ�������₷�������ł��B�K�v�����̏\�������m�F���邱�Ƃ�S��������悤�ɂȂ�A�����̒��Ŋv���I�Ȑi���ƂȂ�܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�ƒ����̋����̌����ɂ��ā^20.12.18�n
�ƂĂ�������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^20.12.17�n
�ǂނ̊y����
�����m��ҁn�F�A�����肪�Ƃ��D
��?�^?����^20.12.15�n
�E���Ɍ��A�����Ɍ����l����̂͊����A�����Ă��Ȃ��Ƃ��ł����A�����A�����Ă��邩�ǂ����͉E���Ɍ��ƍ����Ɍ����l���Ē��ׂ܂���ˁH���X����ɂȂ�܂��H
��낵�����肢���܂��B
�����m��ҁn�F���ނ�ǂ�ł���C���蓾�Ȃ��悤�Ȏ��₪�����Ă��܂��D
�����������Ɠǂ�ł��玿�₵�Ă��������D��b���y���ނƌ������ʂ̖ړI��������ł�����C���̃T�C�g��
���w�I�A�[�@��n=k+1�����藧��������Ƃ��A�킴�킴�v�Z���Ȃ��Ă��悢�ł��傤���B������x�ȒP�Ȍv�Z�������ĕ��G�ɂȂ�����ŏI�I�Ȏ����E�ӂɏ����������Ԃ��Z���ł��܂����A�Z���̖�肶�Ⴀ��܂����������Ǝv���̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���̂����́Cn=k+1�̏ꍇ�ɐ������邱�Ƃ����肵�Ă��邱�ƂɂȂ�C�_���ł��D
�@�ʏ�C��������C���͎����C���w�����Ȃǂł́u������������邱�Ƃ��ؖ����Ȃ����v�Ƃ����`�Ő��w�I�A�[�@�̏ؖ���肪�o�肳���Ƃ��́C��肪�Ԉ���Ă��邱�Ƃ͂߂����ɂȂ��ł��傤�D������C�w���́C���͐������͂����Ɓu�Â���v���Ƃ��ł��܂��D�������C���Ȃ������w�̘_�����o�������Ƃ��C����藝�����藧���ǂ������܂��ؖ�����Ă��Ȃ��Ƃ��C���������Ă��܂��Ɓu�C���`�L�v�ł��傤=���������Ƃ��C�������Ȃ����Ƃ��C���ׂďؖ��ł��Ă��܂��D
��?�^?����^20.12.14�n
���x�����߂�Ȃ����B�Ɍ��l���o���Ƃ��ɁA�����x^2-4�ŕ��q��x-1��X���Q�ɋ߂Â���Ƃ��́A����̊��l�͑��݂��Ă��炸�\�z���邱�ƂɂȂ�܂������q�͂��̂܂ܑ���������l��p����Ǝv���܂��B
���q�ƕ���ňقȂ���݂����ł����A���ۂ͈�̊��ł���ˁB�Ɍ��l�ł͈�̉��̑�����s���Ă���̂ł��傤���H����͐��m�ȋɌ��l�ƌ�����̂ł��傤���H��낵�����肢���܂��B
 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D���ꁨ0�C���q��1�C������±���ł��D
���}�Q��
�K�E�X�L���̂��Ƃŋ����Ă������������ł��B���ǂ͈��X�ɋ߂Â��̂�����A����X���܂܂�Ă�����̊K�i��̃O���t�̕����̗p����̂ł͂Ȃ��̂ł����H�Ȃ���������̋Ɍ��l���l����̂ł��傤���H
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���S�N�������Đ��w�҂��x�X�g�̒�`�ɍi�荞��ł���̂ɁC�����̍D�݂ŏ���ɒ�`��������ƍ����̂��Ƃł��D
(1) �E���Ɍ��l�����݂��� (2) �����Ɍ��l�����݂��� (3)����炪��v�����Ƃ����̒l���Ɍ��l�Ƃ���D
�Ⴆ�C
=[x]\hspace{5}(x=1)&chf=bg,s,fff9f9)
�ɂ���
=1\]&chf=bg,s,fff9f9)
�C
=0\]&chf=bg,s,fff9f9)
�@����炪��v���Ȃ�����C�Ɍ��l�͑��݂��Ȃ��D
�@���l��
=1&chf=bg,s,fff9f9)
�ł��邱�Ƃ́C�ȏ�̘b�Ɩ��W�ł��D
�q�������Ă��������܂����B
�܂��^�₪�c���Ă���̂ł����A�v���X0�͎�肤��l�Ȃ̂ł��傤���H������͗L���m��l�ł͂Ȃ��Ƃ������Ƃ́A�v���X0����肤��l�ł͂Ȃ��Ƃ������߂ł����ł��傤���H�H
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
\]&chf=bg,s,fff9f9)
�̂��Ƃ�
\]&chf=bg,s,fff9f9)
�Ə����C
\]&chf=bg,s,fff9f9)
�̂��Ƃ�
\]&chf=bg,s,fff9f9)
�Ə����D
���ʂȏꍇ�Ƃ��āC
\]&chf=bg,s,fff9f9)
�̂��Ƃ�
\]&chf=bg,s,fff9f9)
�Ə����C
\]&chf=bg,s,fff9f9)
�̂��Ƃ�
\]&chf=bg,s,fff9f9)
�Ə����D
�@�v�����,

�́C�Ɍ����l����Ƃ��̋߂Â������ȗ��I�ɋL�����������̂ŁC����̒l��\�����̂ł͂Ȃ��D
�Ɍ��l���o���Ƃ��A�v���X0���l����Ƃ��́A�v���X0�ɂ����ۂ͋߂Â������Ŏ�肤��l�ł͂Ȃ��̂ł����H
���ʂɑ�����ē��������߂�Ƃ��͎��ۂ͎��Ȃ��l�������ē������Ǝv���܂����A�A���������ł͂Ȃ��ꍇ�A�v���X0�Ȃǂ��l���ċɌ���\�z����Ǝv���܂��B���̓v���X0�͎�肤��l�Ǝv�����̂Ō��ǎ�肤��l�Ōv�Z���Ă����Ă�̂ɋɌ��l�Ƃ�����̂��Ǝv���܂����B�v���X0�ł����Ȃ�̂�����0�ɋ߂Â��Ƃ��������K���Œl���ω����邾�낤�Ƃ������ƂŋɌ��l���o����̂ł����H��������ƁA���ۂɎ�肤��l��������ꍇ�Ǝ��ۂɎ��Ȃ��l��������ꍇ�����݂���Ƃ������Ƃł����H��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���o���Ɏ��₵�Ă��炤�����C
�A���̒�`��ǂ�ł��炦�Ε����邱�Ƃł��̂ŁC��������ɓǂ�ł��������D
���3(1) 2���ڂ̕������t�ɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������Ƃ��Ă��邱�Ƃ̈Ӗ���������܂���D2���ڂ̕������t�ɂ��Ė�肪����Ă���--���ꂪ�ǂ������܂������H
���m�ʂ̕ł���̎���ɑ���n[�Q�����̕��s�����E���������ɂ��ā^20.12.12�n
���T�@����̓r���Aiz₁�́�3iz₁���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���̂̑̐� �ɂ��ā^20.12.11�n
������Ȗ�ȕ������Ă�����Ă��܂��B���삳��Ă��邱��HP�ł����A�悭�����܂łł�����̂���
���������S�������܂��B���w�̂���HP�͂������I�ł����A�����HP�̋ɂ݂Ȋ����ł��B
����HP���삠�肪�Ƃ��������܂��B���̕��̏�ł͂������𗧂��Ă���܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��̒l(�}����)�ɂ��ā^20.12.10�n
�I�𐧂łƂĂ��i�߂₷���ł��B�O�p��̐����̕\����������Ƃ킩��ɂ������Č�Łu�O�p�Ђ͂��������v�Ƃ����\���������ƌ������邵�Ƃ킩�����̂ŁA�Ⴄ�\���ɂ��Ăق��������ł��B�ł��A�����Ă��̃T�C�g�͂��Ղ��ďd�Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��Œ�`�������ɂ��ā^20.12.10�n
�ϕ��̂����̕��삾�����ɋ�肾�����̂ł���������₷���ĂƂĂ�������܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
��?�^�݂邭����^20.12.10�n
�v���X0���}�C�i�X0�����l����̂́A�Ɍ��l�Ɗ��l���قȂ邩��Ƃ����������ƂĂ��킩��Ղ������ł��B���肪�Ƃ��������܂��B
�܂��^�₪����̂ł�낵�����肢���܂��B
�v���X0���}�C�i�X0�����l����͕̂��ꂪ0�ɂȂ����ꍇ���Ǝv���܂����A���ꂪ�P�ŁA���q��0�|0�ƂȂ����Ƃ��̓v���X0���}�C�i�X0���͍l�����A�O�ŏI���܂���ˁH
����́A���ۂ̓v���X0��}�C�i�X0�ł͂Ȃ��ŏI�I�ɂ͂O�ɋ߂Â��̂�����O�ʼn���Ƃ������ƂŁA���ꂪ�O�|�O�ɂȂ����Ƃ��́A�ǂ̂悤�ɂO�ɋ߂Â��̂����ς���Ă��邩��v���X0���}�C�i�X0�����C�ɂ���Ƃ������Ƃł����H
�܂��A�v���X������}�C�i�X������͂���܂����A������v���X0�݂����ȋL�q���Ȃ��̂͂Ȃ��ł����H
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�����������̒ʂ�ł��D�㔼�F�Ȃ��Ƃ������́C�Ӗ����Ȃ��Ƃ������Ƃł��D

�C

��

���萔�̏ꍇ�ɍl���܂����C�����̏ꍇ�ɂ��̂悤�ȋL���͎g��Ȃ��D
�Ɍ��̖��ŁAlimx��2�ix-2�j�Ȃ�A���̂܂ܑ������̂ɁAlimx��01/x�Ȃ�v���X0���}�C�i�X0�����l���āA����͂��Ȃ��Ǝv���܂����A���̍��͂Ȃ�ł����H����0�ɋ߂Â��̂�����A��Ɠ�����������������̂ł͂Ȃ��̂ł����H�Ɍ��l�͍Ō���C�ɂ����������A�v���X�̖��������l����̂��}�C�i�X���������l����̂��Ō�͊W�Ȃ��Ȃ�̂ł͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D
(1) �u
\]&chf=bg,s,fff9f9)
�Ȃ�C���̂܂ܑ������v�̂́C���}�Ɍ����u����ł��邩��v�ł��D���������Ă��˂��Ɍ����C
=x-2&chf=bg,s,fff9f9)
�Ƃ������ł́C���l
=2-2=0&chf=bg,s,fff9f9)
�ƋɌ��l
=\lim_{x\rightarrow 2}(x-2)=0\]&chf=bg,s,fff9f9)
�Ƃ�����������C�Ɍ��l�̑���Ɋ��l���g����Ƃ������Ƃł��D�m�Ȃ��C���l�ƋɌ��l���������Ƃ������Ƃ͘A���Ƃ������ƂŁC���w�V�ŏK���܂��n
(2) �u

�Ȃ�C�v���X0���}�C�i�X0�����l���āA����͂��Ȃ��v�̂́C�v���X0���}�C�i�X0���l���đ�����Ȃ��̂ł͂Ȃ��C����ł��Ȃ����������Ȃ��̂ł��D���������Ă��˂��Ɍ����C
=\frac{1}{x}&chf=bg,s,fff9f9)
�Ƃ������ł́C���l
&chf=bg,s,fff9f9)
����`����Ȃ��i���ꂪ0�ɂȂ��Ċ���Z���ł��Ȃ��j����C�Ɍ��l
\]&chf=bg,s,fff9f9)
�̑���Ɏg�����ɂ��C���l�����݂��Ȃ��̂ŁC�b�͏I���ł��D
�@���Ɍ��l

�ƉE�Ɍ��l

�Ƃ���v���Ȃ�����Ɍ��l�����݂��Ȃ��Ƃ����Ă��\���܂���D
�@���l�ƋɌ��l�����݂��āC���C����炪��v����Ƃ��A���Ƃ����̂ŁC���l�����݂��Ȃ�����Ɍ��l�̑�p�ɂ͂ł��Ȃ��ƌ����܂��D���Ɍ��l�ƍ��Ɍ��l����v���Ȃ�����Ɍ��l�����݂��Ȃ��Ƃ������܂��D
�Q�l����sin45��cos15���̒l�����߂�B�Ƃ�����肪����܂����B���͐��w�̒��ł��O�p�������Ȃ̂ŁA������Ē�����ƍK���ł��B�S���w�E���ł͖����A�\����Ȃ��ł�
�����m��ҁn�F�A�����肪�Ƃ��Dsin 45���͐��w�T�̊�{�ŁC
���̃y�[�W�ɂ���܂��Dcos 15���͐��w�U�̉��@�藝�ʼn�������ŁC
���̃y�[�W�ɂ���܂��D
1/x �̔����W�������߂�Ƃ��ɁAh��0�������Ƃ����q��0�ɂȂ��Ă��܂����Ƃ��Ē�`����Ȃ��Ȃ��Ă��܂����̂ł������̏ꍇ�͂ǂ������炢���ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̒i�K�̕ό`�ŁC���q��0�ƌ����Ă�����̂�������܂��C���������_�Ō����C�u���q��0�ɂȂ��ĕ��ꂪ0�ɂȂ邩��C�ɂ��Ɍ��l����܂�C���ꂪ�����W���ɂȂ�v�Ƃ������Ƃł��D
=\frac{1}{x}&chf=bg,s,fff9f9)
�ɂ��āC

�̂Ƃ��̔����W��
&chf=bg,s,fff9f9)
�����߂�ɂ�
(1)�@�Ȃ��C

�̂Ƃ��̔����W��
&chf=bg,s,fff9f9)
�͑��݂��܂���D
&chf=bg,s,fff9f9)
����`����Ȃ�����ł��D���������āC(2)�̂悤�ɁC

�̂Ƃ��̔����W��
&chf=bg,s,fff9f9)
���l���܂��D
(2)

�̂Ƃ�
=\lim_{h\rightarrow 0}\frac{f(a%2B h)-f(a)}{h}=\lim_{h\rightarrow 0}\frac{\frac{1}{a%2B h}-\frac{1}{a}}{h}\]&chf=bg,s,fff9f9)
}{(a%2B h)a}}{h}=\lim_{h\rightarrow 0}\frac{-h}{(a%2B h)ah}\]&chf=bg,s,fff9f9)
a}=-\frac{1}{a^2}\]&chf=bg,s,fff9f9)
��3�ɂ��āA�|3�Ɠ��͂��Ă���ɂ�������炸�����ɂȂ�Ȃ��s�������܂��B�S�p�┼�p�łȂ��Ɣ�������Ȃ��̂Ȃ�A���̂悤�Ȏw�肪���O�ɂ���Ă���Ƃ����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�S���̃y�[�W�Ƃ͌����܂��C���̃y�[�W�ɂ��ẮC�S�p���͂��Ȃ��ꂽ�ꍇ�C���p�����ɏ��������č̓_����v���O������g�ݍ���ł���܂��D������C(1) �|3�C�|�R�͂�����������ɂȂ�܂��D�Ƃ��낪�C���@��ɂ���Ă�(2)�u���[�}�v�̉��_�i����̓J�^�J�i�ŁC���̕����ł͂Ȃ��j�C(3) �A���_�[�o�[�́u�Q�v�C(4)��t�́u�P�v�C(5)�������_�u�\�v�C(6)�Z�����_�u�]�v�ɕϊ�����邱�Ƃ�����܂��D
�@���̕�����\�����̂́C������n�C�t����(1)�����ŁC�������̎��Ă���(2)�`(6)�͕��̕����ł͂���܂���D���Ȃ���iPad�̃I���X�N���[���L�[�{�[�h��(2)�`(6)�̂����ꂩ��I���̂ƍl�����܂��D
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�s�����̏ؖ�)�ɂ��ā^20.12.09�n
���Z���w�̊w�K�ɂ��̃T�C�g�����p�����Ă��������Ă���܂��B
���A�����������₷���A�܂�����
�����ϗ������₷���ł��B
�Ƃ���ŁA��ϙG�z�ł����A���m�F�������������_���������܂��B
������̃y�[�W�̗��3�̉��L�̎��Ɍ�肪����̂ł͂Ȃ����Ǝv���܂����B
�@�@= 1/(k+1)(k+2) { 2k^2+5k+2�|(k^2+4k+2) }
�������́A
�@�@= 1/(k+1)(k+2) { 2k^2+5k+2�|(2k^2+4k+2) }
�ł͂Ȃ��ł��傤���B���m�F���肢�������܂��B
����Ƃ����p�����Ă������������Ǝv���܂��B
�ǂ�����낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[��Βl�t�s�����ɂ��ā^20.12.07�n
�����Ǝv���܂�‼‼
���ɂȂ�܂���‼‼
����e�X�g�������_������ꂻ���ł�☺
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����̑��a�ɂ��ā^20.12.07�n
���߂܂��āB
�Ƃ��ǂ��Q�l�ɂ����Ă��������Ă���܂��B���\���グ�܂��B
�{�y�[�W�ɂ����ĕ\�`���ŗᎦ����Ă���_��������₷���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̂�����Ƃ��̏����ɂ��ā^20.12.06�n
((3))�̓������܂������Ă��܂��I
������������Ǝv���܂��I
�����������Ă�����Ă܂�
���ꂩ����킩��Ȃ��Ȃ����猩�ɗ��܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���܂ŁC�������g�̓������t���ĉ̊ԈႢ���w�E���Ă���ԐM�́C�قƂ�ǐ����������悤�ł����C�������g�̉��������ɁC�P�ɊԈ���Ă���Əq�ׂ��ԐM�́C���ꎩ�̂��Ԉ���Ă��܂����D�t�F�C�N�j���[�X�ƌ����t�F�C�N�j���[�X�͏I���ɂ��悤
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^20.12.04�n
�ƂĂ��킩��₷������ƁA���ӂ��ׂ��_��������Ă��Ă悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �Q�����ɂ��ā^20.12.03�n
������ǂ̃T�C�g�����킩��₷���ł�👍��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���s���� �i�������܂Ƃ߁j�ɂ��ā^20.12.03�n
������������₷���I������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝�ɂ��ā^20.12.01�n
Sin165�x�̂悤��30�A45�A60�ŕ\���Ȃ���̂����������ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D

�ł�����C��6�ɏ����Ă���܂��D
�����������K��肪������͂��t���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^20.11.30�n
���݂܂���3�͈͂ł����A
Log(x-a)+a=Log e^x(x-a)�ɂȂ闝�R�������Ă������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��Ɛ^�����͂����菑���Ȃ��ƁC�Ⴄ�b�ɂȂ�̂Œ���
�m�m�~�̎O�i���сn

�ɂ��

���������āC
%2B a=\log_ee^a(x-a)&chf=bg,s,fff9f9)
�߂����ᕪ����Ղ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^20.11.29�n
[2]��d�������͂���Ȃ���ɁA
�h���̕\�Ŕw�i�F�����F�̑g�͓�d�������͂���C���F�ɂȂ��Ă�����̂͂͂���Ȃ����́C
�Ԏ��Ŏ������̂�b���������ɂȂ��Ă�����̂ł��D�h�Ƃ���̂ł����A
����͂ǂ������Ӗ��ł��傤���H
a=6,b=9�̏ꍇ���A�O���Ǝv���܂�
2��3�ŕ\���邩��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D����������d�����łȂ��̂ŁC��d�������͂���邩�H�Ƃ�����肪���݂��܂���
���m�ʂ̕ł���̎���ɑ���n[�m���ϐ��C�m�����z�ɂ��ā^20.11.28�n
�h��ŏo����Ă킩��Ȃ������̂ŁA��ώQ�l�ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�d��A����(3)�ɂ��ā^20.11.26�n
���i2�j�͉ˋ�f�[�^�Ƃ������Ƃł����A�d��A���͌��ʂ̉��߂ň���f�����܂��B�����ϐ��̈�ł��鐫�ʂ̃_�~�[�ϐ��i�j���P�A�����O�j�̌W������0.162�ł������A���̉��߂́u���̐����ϐ��ł�����\���Ɗ�b�e�X�g�����̒l�ɌŒ肵���Ƃ��A�j�ł����1�N��̐��т�0.162�|�C���g�����Ȃ�v�Ƃ��������Ő������ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���������ǂݕ����ł��邩������܂��C�P���ɁC�P�N�㐬�� = 0.606+ 0.162�~(�j)+ 0.218�~(���\��) + 0.027�~(��b�e�X�g)�̎��ɒl�������Ă��炦�C�P�N��̐��т��o��Ƃ������Ƃł��D�Ⴆ�C�j�q�C���\��3.5�C��b�e�X�g75�_�Ȃ�C1�N��̐��т�3.556�Ɨ\�z�����Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�Ή��̂���ꍇ�̂������ɂ��ā^20.11.26�n
�_�C�G�b�g�@�̌��ʂ̗�ŁAt����i�Б��j���s���L�Ӑ���5���ŗL�Ӎ�������Ƃ������ʂɂȂ����Ƃ��A����̓_�C�G�b�g�@�̌��ʂő̏d���������ƌ�����̂ł��傤���H�o�͌��ʂ���L�Ӎ������邱�Ƃ͗����ł����̂ł����A���̍����̏d�������������Ƃɂ�鍷�i�}�C�i�X�̍��j�������̂��A�̏d�������������Ƃɂ�鍷�i�v���X�̍��j�������̂��́A�ǂ������Ĕ��f��������̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�O������̕������ϒl���������̂ŕ�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^20.11.25�n
��2��̓����̃x�N�g���̎n�_���Y���Ă��܂��H
�����m��ҁn�F�A�����肪�Ƃ��DHELP�Ɂu�Ȃ��C���͂ǂ��ɕ`���Ă����Ă������ƒ�������v���Ă���Γ������̂ł��v�Ə����Ă����ˁD���炵�Ă���Ə����Ă���̂ɁC�Y���Ă��܂��Ƃ́C�܂������ł��Ă��Ȃ��\������
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^20.11.25�n
�킩��₷������Ɨ��K��肪����A�e�X�g�O�̐U��Ԃ�ɂƂĂ��𗧂��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^20.11.25�n
�u���̉��̃h�W���E��_���܂��v�������Ӗ����Ă��邩��������܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle�������͂Őq�˂���C�̂��悤�ɓ����Ă����ł��傤�D�y�����I
���m�ʂ̕ł���̎���ɑ���n[���R���̗ݏ�̘a�ɂ��ā^20.11.24�n
���m�ʂ̕ł���̎���ɑ���n[�s��̑Ίp���Ƃ��ɂ��ā^20.11.22�n
P^-1AP�̌v�Z���@���킩��Ȃ��B�ق��̎Q�l���ɂ͌ŗL�l����ׂ邾���Ə����Ă��������A����ł̓W�����_���W���`�����ۂɒʗp���Ȃ��č����Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�W�����_���W���`�́C
���̃y�[�W
[���5]�̉�s�ڂɂ��Ăł����A�s�_P,Q��x���W���W�t�ƁA���W���d�˂Ďg���Ă����܂����A���̕\�L�͐������̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̍ő�l�E�ŏ��l�ɂ��ā^20.11.20�n
�ƂĂ��A�������Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̐}�`���i�O�p�`�̌`����j�ɂ��ā^20.11.20�n
�ƂĂ�������₷����ϖ𗧂����Ă��������Ă���܂��B�h���1.2�̉h�ɂ�����sin�̑O�Ɂhi�h�������Ă���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����ɂ��ā^20.11.19�n
�Ϙa�����̗��K�������Ă�����Ă��܂��B
���ɂ��āB(�Ⴆ��cos4��sin6��)
sin(�[��)��-sin�ƂƂ����ۂɂ��镄���ƁA���@�藝���C���[�W���Ȃ��狁�߂���������(�O��̂ǂ��炩�̕�����)�������߂ɂ��镄���Ƃ��ԈႦ�Ă��܂������ł��B
(���͕Ίp�����ɂȂ�ꍇ�̒��K���킹���ɂ���Ă��邽�߂����Ȃ邾���Ȃ̂�������܂��c)�ǂ�����Ă��~�X���ɂ����Ȃ�̂��R�c������܂����炨�������������I
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����悭������܂��C��x�ɂQ�̂��Ƃ����̂͊ԈႢ�̂��Ƃł��傤
���m�ʂ̕ł���̎���ɑ���n[ �O�p�`�̌`��E�ؖ�����ɂ��ā^20.11.18�n
��7�̃q���g������ĕ�����Ƃ�������������ڂ��������Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���M���܂���
���m�ʂ̕ł���̎���ɑ���n[�o�Ȑ��̕������ɂ��ā^20.11.17�n
�߂�����킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ή��̂���ꍇ�̂������ɂ��ā^20.11.16�n
����̎���ł����A���̉��������Ă����̂ŁuHELP�v�@�\���Q�Ƃ��Ă��܂���ł����BHELP��ǂ�ŁA�����ł��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ή��̂���ꍇ�̂������ɂ��ā^20.11.14�n
���R�i�قȂ���ň�����ꗑ���o������20�̎��_�ł̑̏d�f�[�^�j��������̂ł����A���̓����ł��l���}�C�i�X�ɂȂ�܂����B
���l�̌v�Z������l���āA����͕ϐ��Q�i�a�Q�j�̕��ϑ̏d�̕����d����������ł��傤���H�i�ϐ������ւ��Ă����������ƁA���l���v���X�ɂȂ�܂����B�j
�܂��A���l�͌��ʂ̉��߂̂Ƃ���Βl���Q�Ƃ��܂����A���̖�͂�����ɂ����Ă��l�̕����͏d�v�ł͂Ȃ��Ƃ������Ƃł��傤���H�i��2�Q�ɗL�ӂȍ������邩�Ȃ������d�v������B�j
���W���̕����̉��߂ƍ������āA������ƕ�����Ȃ��Ȃ��Ă��܂��܂����B�B�B
�����m��ҁn�F�A�����肪�Ƃ��D�̓_�{�^���������ƁCHELP�{�^�����\������܂��D���Ȃ��̊��z�́C����HELP�ɏ����Ă�������e�Ɠ����ł����CHELP�͓ǂ݂܂������H
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^20.11.14�n
�����r�����ɂȂ�܂����I���ӂł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ή��̂���ꍇ�̂������ɂ��ā^20.11.14�n
������̋A�������𗧂Ă�ꍇ�A��������ł��Б�����ł��A��Ɂu��W�c�̕��ς��������������Ȃ��i���O�j�v�Ƃ�����̂Ȃ̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�u��W�c�̕��ς��������������Ȃ��i���O�j�v�Ɖ��肵����C����ȂɊO�ꂽ���Ƃ��N����m����5%���Ȃ��Ƃ������Ƃ���C��������p�����肵�Ȃ������肷��Ƃ����_�@�ɂȂ�܂��̂ŁC���Ȃ����l���Ă���ʂ�ł��D
�@�����C�u��W�c�̕��ς��������Ȃ�����������v�Ɖ��肵����C�ł͊��Ⴄ�̂������̉\��������C����Ɋ�Â��ċN����ׂ����ʂ��v�Z���邱�Ƃ́C���������ł��܂���D������C�A�������͂˂Ɂu�������Ƃ���v�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[���Ғl�ɂ��ā^20.11.13�n
���T�̉�(�C)�ɂ����āA�P��ڂɃX�y�[�h���o�āA�Q��ڂɃn�[�g���o��m���́A4/7 �~�@4/6�ƂȂ��Ă��܂����A���ۂ͓ڂ̃J�[�h�������ۂɁA�n�[�g�̃g�����v��3���ł��邽�߁A��������4/7 �~ 3/6�ƂȂ�Ǝv���܂��B
�����A���̉��ɋL�ڂ��Ă���\�Ɋւ��ẮA�n�[�g�����ڂɏo��m���́A2/7�ƂȂ��Čv�Z��i�߂Ă��邽�߁A�ɊԈႢ�͂Ȃ��Ǝv���܂��B
���Z�����Ǝv���܂����A�m�F���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ł��D���̓~�X��������܂���
���m�ʂ̕ł���̎���ɑ���n[���Z�`��w��b�̐��w�p��.����.���ɂ��ā^20.11.12�n
�y���2�z(2)lim n��1 (2-1/n)=1�ɂȂ�Ǝv���܂����A���̃y�[�W�ł͋Ɍ��Ȃ��ɂȂ��Ă��܂����Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��Dx��0 �̓]�L�~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[���C�������̔����ɂ��ā^20.11.11�n
�Ⴆ�Ε��ꂪ2(x+1)�̂Ƃ��A
�������鎞�ɓ�悷��̂͑S�́o4(x+1)^2�p�ł����H
����Ƃ��������o2(x+1)^2�p�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���ړ������(A)�u�S�̂ł��v���C(B)�����̏ꍇ�́C�萔���ォ��|����̂ŁC���̂悤�ɂ͂��܂���D
�Ⴆ�C
}&chf=bg,s,fff9f9)
�̏ꍇ�C(A)
\}-3\times 2}{\{2(x%2B 1)\}^2}=\frac{-6}{4(x%2B 1)^2}=\frac{-3}{2(x%2B 1)^2}&chf=bg,s,fff9f9)
(B)�́C�萔

���ォ��|����F

�C
^2}=\frac{-3}{2(x%2B 1)^2}&chf=bg,s,fff9f9)
�킩��₷���A�����o���܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^20.11.11�n
(9x(2x+4)
�����m��ҁn�F�A�����肪�Ƃ��D�����s���S�ŁC����̕��͂������ĂȂ��H
���m�ʂ̕ł���̎���ɑ���n[�]���藝�ɂ��ā^20.11.11�n
�Ȃ��T�C�g��URL��geisya�Ȃ̂ł����H
�C�ɂȂ肷���Ė������܂���
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂������W�N�����琢�b�ɂȂ��Ă���C���s�ɂ���n��v���o�C�_�̖��O��geisya�l�b�g�Ƃ������ƂŁC�ʂɕ��q�����|�҂��C���^�[�l�b�g���o�c���Ă���킯�ł͂���܂���D���̋��ނ̍�҂́C���������Z���w�����C�c�ɒ����l�`���̂܂܂̘V�l�i�j�j�ł�����q���̖����Ăǂ��Ȃ�I
���m�ʂ̕ł���̎���ɑ���n[�K���}���ɂ��ā^20.11.11�n
�߂�����킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s���ɂ��ā^20.11.02�n
�����I�Ȃ��ƂŒp���������̂ł����A�����s�Ɨ�̃^�e���R���ǂ������ǂ����������Ă��܂��܂��B���w�̐������[�x�A�̂悤�Ɏ��Ƃł悭�������Ă����o���₷����C���킹�Ȃǂ������̂ł��傤���A�������͓�����O�̂��Ƃ����ē����̍��Z��������Ȃ�o�����Ă����̂ł��傤��?
�����m��ҁn�F�A�����肪�Ƃ��D��C���킹�I�Ȃ��̂́C���Ɏv����������̂�����܂��C�s�Ɨ}�ɏ����Ă���̂ł�������Ă��������D
�@��������C��������o�����ɂ��āC�����Ɣj��I�ȋc�_���ł��܂��D�Ⴆ�C�������w�Z�Ŏ����Ƃł́u�c�̐��͂���\���Ă��܂�������\���Ă��܂����v�Ƃ�������،^�̎��Ƃł�����������̐搶�́u������w�����v�ɂ́C�Ԏ��ł��̂悤�ɓǂނ悤�ɏ����Ă���̂ł��D�����āu�c�̐��͂��ł��v�Ɠ��������Ă���̂ł��D�Ƃ���ł悭�l���Ă��������C�c�̐���x=3�ȂǂƂ������̒l��\���Ă��܂��D�����炘�̒l��\���Ă���Ƃ�������̂ł��D���̂悤�ɁC���ꓚ�I�ɖ�،^�Ɋo��������ł́C�_���I�ɋt�������Ă��邱�Ƃ�����̂ł��D
�@�Ⴆ�C�����Ŏ����u��͏c�ł��v�Ƃ������ꍇ�C�u�����Ɍ������Ă��闬�ꂪ�C�P��ځC�Q��ځC..�v�Ȃ̂��Ƃ����ǂݕ�������l�����łȂ��C�u��ԍ��͏c�����ɑ����Ă����v�Ɠǂސl�����蓾��̂ł��D�S���t�ł��D���̂悤�Ȗ�ŁC���t�����łȂ��C�u�Ȃ�ׂ��P���Ȏ����ƑΉ������āv�o���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�����藝�i���j�ɂ��ā^20.11.07�n
�ō��ɍō���������K���ł����B���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��ɂ��ā^20.11.02�n
�s��ϕ��̕łɂ͖�肪�����āc
��肪�S�̓I�ɏ��Ȃ��̂ő��₵�Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ڎ��͌����Ă��܂����H���͎��̃y�[�W����n�܂�܂�
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̎������0�ɂ��ā^20.11.02�n
�ׂ������Ő\����Ȃ��̂ł����A������̓��ł����A��蕶��a�ɂȂ��Ă��܂��B�i���f�����ʂ̎������O�̃y�[�W�ł��j
�����m��ҁn�F�A�����肪�Ƃ��D�b����₱�����̂ł����CHTML�����Ńt�H���g�ɂ��ĉ����w�肵�Ȃ��ƃS�V�b�N�̂ŕ\�������Ȃǂ̌��ʂƂ��āC�M���V�������̃��ƃA���t�@�x�b�g��a�������Ɍ����邱�Ƃ�����܂��D�����ɂ͊m���ɃM���V�������������Ă���̂ł����C����킵���Ȃ��悤�ɁC���̂̎w������������܂����D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������3�ɂ��ā^20.10.31�n
���1-1��(3)�A�����̕Ίp��5/3�ł͂Ȃ�5/6�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���1-1��(3)�̃��˒������܂���
���m�ʂ̕ł���̎���ɑ���n[�����t���m���ɂ��ā^20.10.31�n
���3�Ɩ��4�̈Ⴂ���킩��Ȃ��ł��B�ǂ�����������̂��w���Ă���悤�Ɋ����Ă��܂��܂��B
���4�̓�����1/3�ł͂Ȃ�1/2���Ƃ������Ƃ����܂����͂߂܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�I�������N���b�N���Ă���C�\�����������ǂ�ł��܂����H
���m�ʂ̕ł���̎���ɑ���n[�_�`�̎���̉�]�ɂ��ā^20.10.30�n
��{�҂��o���ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̗��ɖڎ��������āC1�O�̃y�[�W��������Ă���̂�����C��ɂ����ǂނ̂ł�
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��̒l(�}����)�ɂ��ā^20.10.30�n
�킩��₷���ł���悤�ɂȂ�܂����B���肪�Ƃ��������܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̘a�����ɂ��ā^20.10.28�n
���̑������ɂȂ�܂���(^ ^)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̒��_�̍��W�ɂ��ā^20.10.27�n
�ÎZ�ʼn����Ɨǂ��]�g���ɂȂ�܂��ˁI�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^20.10.27�n
��{���x���ł̎����̎�_���������邱�Ƃ��ł���悤�Ȗ�肪�����A�ǎ����Ǝv���܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̋Ɍ��ɂ��ā^20.10.25�n
���Q�̗�Q
�w����r���łr�ɕς���Ă܂����Ȃɂ��Ӗ�����܂����H
im x��-���@(��x2+2 +x )
= lim s���� ( ��s2+2 �|s )
= lim s����(s2+2)�|s2��s2+2+s
= lim s����2��s2+2+s
= 0 (�敪�q��2�C���ꁨ��)
�����m��ҁn�F�A�����肪�Ƃ��Dx����s�ɕς���Ă��邱�Ƃɂ́C�傢�ɈӖ�������܂��Dx�̂܂܂ł�−���ɍs���Ɍ��̌v�Z�Ȃ̂ŁC�v�Z���ɂ����̂ɑ��āCx=−s�Ƃ��ĕϐ���s�ɏ���������ƁCs��+�����ɍs���Ɍ��ɂȂ��āC�����Ȃǂ��v�Z���₷���Ȃ�܂��D
=\lim_{s\rightarrow\infty}(\sqrt{s^2%2B 2}-s)\]&chf=bg,s,fff9f9)
�@�����܂łŁC��−���^�́u������s��`�v�̋Ɍ��ɂȂ�̂ŁC���q�̗L�����i����̖������j�ɂ��C�s��`�ɂȂ錴���Ǝ�菜��

�@���ꁨ���C���q=2������C�Ɍ��l��0�ɂȂ�
�ƂĂ�������₷�������ł��B�������̏�ʼn����āA�̓_���ł���̂������ł��B���ƁA�킩��Ȃ�������q���g������A������Q�l�ɂł����̂ŁA�����₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^20.10.24�n
���肪�Ƃ��������܂����I������܂����I
���������̎����撣��܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R�_���꒼����ɂ��邽�߂̏����ɂ��ā^20.10.24�n
�����ƕ�����₷���������Ă�������(o_o)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �_�ƌX���������̕������ɂ��ā^20.10.24�n
��肪�t���Ă���̂��ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�e���聨�������ɂ��ā^20.10.23�n
t����̎菇���Ԉ���Ă��܂��B�Ή��̂Ȃ�t����̑O�i��F��������Ă͂����܂���B�܂�t�����Welch����ōs���܂��B
�i���܂��ɂ��̎菇���f�ڂ��Ă���e�L�X�g�͑����ł����A����̓��v�w�ł͖��m�ɊԈႢ�ł���Ƃ���Ă��܂��B�j
F����œ����U�����m�F�����̂�Student��t���肠�邢��Welch��t������s���菇�́A��i�K�Ō�����s�����ƂɂȂ邽�ߌ���̑��d���̖�肪�������L�Ӑ������ݒ��舫�����܂��B
Welch����͓����U���ɂ��Ċ挒�Ȃ̂ŁA�ŏ�����Welch������g���Ύ��O��F���������K�v�͂Ȃ��A����̑��d���̖����N���܂���B
R�Ȃǂ̓��v��̓\�t�g�E�F�A�ł��f�t�H���g��t�����@��Welch����ɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋L�����������̂�10�N����15�N�O�ŁC�ŋ߂̌X���ɂ��Ēm�点�Ē��������ɂ��ẮC��������킹�Ă��炢�܂��D�����C���T�C�g�͐��w�̃T�C�g�ł͂Ȃ��Đ��w����̃T�C�g�C���v�̃T�C�g�ł͂Ȃ��ē��v����̃T�C�g�Ȃ̂ŁC�w���̗D�ʐ��ɂ��Ĕ��f����悤�Ȑ�[�I�Ȃ��̂ł͑S�R����܂���D�ǂ��炩�Ƃ����C�w���̓��Ă��ǂ̊�ō̓_����邩��T���āC�ǂw�����s���ɂȂ�Ȃ��悤�ɍl���܂��D�[�I�Ɍ����C�̓_�҂̑����ӌ��ɍ��킹�Ă����Ƃ������ƂŁC���Ɋw���Ƃ��Đ������Ă��C���݂܂����̕����̍̓_�������h�łȂ��ꍇ�C�Љ���T����Ƃ������Ƃł��D�Ƃ���ŁC�M�҂̎����Ă���Excel�����N�������ꂽ���v�w��b�̋��ȏ����܂��C���T�C�g�̌��̋L�q�ƊT�˓����菇�ɂȂ��Ă��܂��̂ŁC�܂����������͑��}���ȁH�Ƃ��������ł��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^20.10.21�n
�m2�n�Ŏ����܂Ƃ߂鎞�̓r���o�߂������Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�r���o�߂͑S�������Ă���܂��D�����Ă���̂ɏ����Ăق����Ƃ́H
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^20.10.21�n
���2��(3)�̌v�Z�̂������ڂ��Ă����Ə�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�y�[�W�̐擪�ɏ����Ă���������̂��̂Ȃ̂ŁC�����̐����Ƃ����Ă॥�
=(ka_1,\hspace{2}ka_2)&chf=bg,s,fff9f9)
�̑��ɉ��������悢�̂��D
�v���Ă��������P�������Ǘ������Ă��Ȃ��������ƂɋC�Â��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�--�ϕ������̕ύX�ɂ��ā^20.10.21�n
���ɏ�����܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ؖ��@�Ɣw���@�ɂ��ā^20.10.20�n
�����������������o��̂ŕ�������܂��B���������C���X�g���ɂ���ĊȒP�ɓ����Ă��܂��B
���ƃL�����N�^�[�������Ƃ���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ƌW���̊W�ɂ��ā^20.10.19�n
��A�Ǝv���܂����A���Q�ŋ��߂�̂́A2���łȂ�3���������ł��ˁO�O
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�s���ɂ��ā^20.10.19�n
�r��������ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă���̂ɁC�����Ăق����Ƃ����l�̍s���p�^�[���͕������Ă��܂��D�������Ă��邾���ŁC�I�������N���b�N���Ă��Ȃ��̂ł��D�u�������ԍ���I�����Ă��������D�v�Ə����Ă���̂�����C�������ԍ���I�����āC�N���b�N���Ȃ��Ƃ����܂���D�I������C�̓_���ʂƓr���v�Z��������܂��D
���m�ʂ̕ł���̎���ɑ���n[���̘A�����ɂ��ā^20.10.18�n
����̎҂ł��B��1.3�ł����A
�C)�bx-3�b>1(�����̓s���㓙�����������Ă�������)�̂Ƃ��A��=min(�bx-3�b,1)�Ƃ����� ��=1 �ł���ˁB
���̂Ƃ� 5�bx-3�b+�bx-3�b^2 �� 5��+��^2(=6��) �̕s�����̌����͐������ł����B
��̓I��x=5�̂Ƃ������l�����������B����14 �� �E��6 �Ƃ̐�������������Ă��炦�܂����B
�܂�A�C)�bx-3�b>1�̂Ƃ����̕s�����͐������Ȃ��Ǝ��͎v���̂ł����A�ǂ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�����ł��D���M�������܂���
���m�ʂ̕ł���̎���ɑ���n[���ϐ����̋ɒl�ɂ��ā^20.10.18�n
1.�̓_���̘g���A��K�����W�� f''(a) ����K���� f''(x) �ɂȂ��Ă��܂�(4�ӏ�)�B
���̇C�̐����ɂ���(1��k��n)�́An=k���܂܂Ȃ��̂Ő��m�ɂ�(1��k<n)���Ⴀ��܂���(3�ӏ�)�B
2.�̉��(3.1)��f''(c)��f''(a)�}�Âł͂��ގ��A�E�� f(a)+�� �Ƀ_�u���_�b�V��('')�������Ă��܂��B
��5.3��(��)�̓�K�Δ���f_yy�̒l�A��������0�łȂ� 2 �ł��B
��5.3��(��)�̇A�A(-2,1)��(7-2,1)�ƂȂ��Ă��܂��B
7.�� f_y = ��g_y �̎�������܂����Af�̉��t����y�łȂ� f_x �ƂȂ��Ă��܂�(2�ӏ�)�B
8.�̗�1.1�A�� dy/dx ��d������ y/x �ƂȂ��Ă��܂�(3�ӏ�)�B
��8.4�̉�dy/dx�̎��A�E�ӂ̎��� - �͕t���܂���B(�B�ɑ��������̎��Ƃ��킹��2�ӏ�)
��8.5�̉̃A)�̂���2)�A��������(�}3,�}1)�ŁA�����̕����͋t�]���܂���B
��8.5�̃C)�A��������(�}2��5,)�ŁA2 �������Ă��܂��B
��8.5�̏�}�̑�Q�ی��A�������� 3x+y<0,x-3y<0 �ł����A�Ƃ��ɕs�����̌������t�ł�(���ꂼ��2�ӏ�����)�B
�����m��ҁn�F�A�����肪�Ƃ��D�����ł�
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��̒����ɂ��ā^20.10.18�n
����A�����w�E�����҂ł��B���̎w�E�́uy=sinh(x)�������Ȑ��ƌĂ��̂��v�Ƃ������̂ł��Bsinh�͌����Ȑ��łȂ��̂ł���A(2.1)�̎Q�l�̎��� cosh �łȂ� sinh �̎��ƂȂ��Ă���A�Ԉ���Ă��܂���Ƃ����Ӗ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Q�l���̕������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̈��������ɂ��ā^20.10.17�n
��1�̖l�ł��킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�]���藝�ɂ��ā^20.10.17�n
���̓������Ⴄ�B
���]���藝��2���������Ƃ��Ďg���ɂ́@(2)��ABC�ɂ����āC�̂Ƃ��Cc�����߂Ă��������@������3�����A�{���͂Q�ł���B
�����m��ҁn�F�A�����肪�Ƃ��D���̓����͊Ԉ���Ă��܂��Dc=2�Ȃ�O�p�`�ɂȂ�܂���D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^20.10.16�n
�x�N�g���ɂ��ĂقƂ�ǒm��Ȃ��҂ł��������o���܂����B������₷�������ł��B
�_�A�x�N�g���A�x�N�g���̘a�A�������w��ł��܂��B
�[���x�N�g���A�t�����̃x�N�g���A�����ƃx�N�g���̐ρA�x�N�g���̓��ς͊w��ł����܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���Z�̋��ȏ��ɂ���ޗ��́C�S������܂�
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^20.10.15�n
�Љ�l�ɂȂ蓪�̑̑��̂��ߕ��K���悤�Ǝv���Ă��܂������A���ȏ����̂ĂĂ��܂��Ă���A���������T�C�g�����菕����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̘A�����ɂ��ā^20.10.15�n
����̎҂ł��B��1.3�ł����A(�C)�̏ꍇ�bx-3�b����(=1)�Ȃ̂ŁA
5�bx-3�b+�bx-3�b^2 �� 5��+��^2 �� 5��+�� �ƂȂ�A��߂̕s�����̌������t�ɂȂ�̂Ő������܂����B�Ƃ����Ӗ��ł��B��̓I��x=5�������Ă��l�����������B
�����m��ҁn�F�A�����肪�Ƃ��Dx=5��������ƁC��=min(|x−3|, 1)=min(2, 1)=1�ɂȂ��ˁD���Ȃ��̏ꍇ�C�� min()�����Ă���̂Ń̕\�����e���Ⴂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��̒����ɂ��ā^20.10.15�n
2.1�̌����Ȑ���(�Q�l)�̎���e^-x�̕������Ⴄ�C�����܂��B������(-)�̎��������Ȑ��ƌĂ��̂ł��傤���B
���Ƃ͍��ׂȂ��̂ł����A2.3�̉~�̒u���ϕ� x=asin�� �� a�������Ă���A2.4�̕������̒u���ϕ��������Ɣ�ϕ����� t^2 �̌W�� 4�������Ă���(2����̊O�ɏo���O���2�ӏ�)�A3.2�̔��~�̒�ϕ��̍Ō�̊��� 2a�� �̕ϐ� �Ƃ������Ă���A�̒E��������܂��B
����ƁA���(1)�̉����(�Q�l)�ɂ��� (x��2,y��2) �͂ǂ������Ӗ��Ȃ̂ł��傤���B�������肩������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D

�itanh x�Ȃǂ�����j��o�Ȑ����Ƃ����C���̂�����

�C��ʉ�����
&chf=bg,s,fff9f9)
�������Ȑ��Ƃ���,���Α勴���x���郍�[�v�Ȃǂ����Ȑ��ɂȂ�D
�@�㔼�̎w�E�ɂ��Ă͒������܂����D
�L�`�ϕ�#1�̒l�� 1/2 �ł͂Ȃ� 2 ����Ȃ��ł��傤���B / (7)�̉���́A�����ϕ�������̎��̑�2���A��ϕ�����x�̎w���� m+1 �ƂȂ��Ă��܂����A1/x�Ƒ��E����� x^m �̌�肩�Ǝv���܂��B
/ (8)�̉���́A�����ϕ�������̎��̑�1���̌W���ɁA���� - ������܂���B�����̑�2���̌W���� n ������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�{���{�����ȁ`
���m�ʂ̕ł���̎���ɑ���n[���̘A�����ɂ��ā^20.10.14�n
�u1�ɏ\���߂��ƌ���Ȃ��������v�̐߂��{���ɐ�������̂��^�₪����܂��B
�Ⴆ�Η�1.3�́A5��+��^2��5��+�� �͐������܂����A�������� 5�bx-3�b+�bx-3�b^2��5��+��^2 ����������̂�x��3�ɏ\���߂��bx-3�b��1�̂Ƃ�((�A)�ɑ���)�݂̂ł͂���܂��B
���͏��w�Ȃ̂ł�����̃T�C�g�ȊO�̎Q�l�����ǂ��Ȃ��Ă���̂��͒m�炸�A�ǂ����P����������̒�Ă����܂��ł��܂���B���ǁu�\���߂��v���Ȃ킿�bx-3�b>1((�C)�̏ꍇ)���l�����鏑�����͖����悤�Ɏv����̂ł����ǂ��Ȃ�ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���������i2�����������Ƃ��͂��̒l�j��min(x, y)�ŕ\������
�A�j|x−1|<1�̂Ƃ�, ��=min(x, y)=|x−1|
�@��3<��2<��1<1
�C�j|x−1|��1�̂Ƃ�, ��=min(x, y)=1
�@13<12<11<1
�C�j�͓��R�߂��ĕ�����ɂ����H
���m�ʂ̕ł���̎���ɑ���n[���̘A�����ɂ��ā^20.10.14�n
�u�e�C���[�W�J�̗��p�v�̐߂� �bx-2�b ����x�o�Ă��܂����A�bx-1�b�̌�肩�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��-�_�@�ɂ��ā^20.10.14�n
����A��3.2�̋^��_���w�E�����҂ł��B�܂����A�����C������Ă��ċ����܂����B
���̃y�[�W�Ɋ�����������Ă���̂ł����A�s�x������Ǝw�E���悤�Ǝv���܂����B���P�̖��ɗ��ĂĂ��炦����������ł��B
���w�͍D���Ȃ̂ł����A�w������ׂɉ߂����Ă��܂��A���܂��̃T�C�g��ʂ��ĒǑ̌������Ă�����Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��-�_�@�ɂ��ā^20.10.13�n
��3.2�̉���� -(��+1)^2 ���o�Ă��܂����A -��^2-2�� �̊ԈႢ�ł͂���܂��B�b��^2-2�Áb< ��^2+2�� ���������߂ɁB
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q���s���� ==�i�������܂Ƃ߁j�ɂ��ā^20.10.12�n
�{�^���ЂƂŐ���A���������ĂƂĂ��i�߂₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������E�L�����E�������̕s��ϕ��ɂ��ā^20.10.11�n
���̑�6��̉�����Ԉ���Ă���
�����2�i�ڂ���3�i�ڂ̌v�Z��x�̌W������������
�����m��ҁn�F�A�����肪�Ƃ��D�Ō�̂U��7���t�ł����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃Z���^�[��������ɂ��ā^20.10.11�n
���̂܂Ƃ܂肪�R���p�N�g�ł��Ղ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^20.10.10�n
������������₷�������I�I
���Ԃ��Ȃ������̂Ő��������ɏ����Ă��鐔�����������Ė��������Ă݂���
��������Ɖ������Ƃ��ł����I
���������̕��͂��A���P�[�g�������ɓ������ēǂ�ł݂���
���͖͂��āA�����ĂƂĂ��o���₷�����������I
������܂����I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �Q�����ɂ��ā^20.10.09�n
�����̗ʂ��قǂ悭�A������������₷���A���Ղ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̓������1�ɂ��ā^20.10.09�n
�ƂĂ����Ղ��Ă������K�ɂȂ�܂���👍
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^20.10.09�n
�悩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����m�����z�Ǝ��ӕ��z�ɂ��ā^20.10.08�n
�m�����v�̏��w�҂���̃R�����g�ł��B
E(X+Y)=E(X)+E(Y)�̏ؖ��ɂ��Ă̋^��ł��B
�{�y�[�W�ɂ͈ȉ��̋L�ڂ�����܂��B
----
X, Y���Ɨ��ł��邩�ǂ����ɊW�Ȃ��C�˂�
E(X+Y)=E(X)+E(Y)�c(1)
�����藧�D
----
���̌�̏ؖ��ŁAX,Y���Ɨ��̂Ƃ��ɐ��藧�̂͂���Ȃ藝���ł���̂ł����A�Ɨ��łȂ��Ƃ��ɐ��藧���Ƃ������ł��܂���B
�Ɨ��łȂ��Ƃ��ɁA����������ƁA
p11+p12+p13+�c+p1n=p1�ƂȂ鍪���͉��Ȃ̂ł��傤���B
�t�ɁAE(X+Y)=E(X)+E(Y)�����藧���߂̏����́A
p11+p12+p13+�c+p1n=p1 (�������l)
�Ƃ������ƂȂ�A�����ł���̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���Ԃ�C�{���������ǂ܂��Ɏ��₵�Ă����܂��D�up11+p12+p13+�c+p1n=p1�v�ƂȂ�̂͂��ꂪ��`������ł��D
���1������Ă��������������͏o�Ȃ��͂��ł��D
-�l���\-
| X|Y | ���y:10 | ���p:2 | ���v |
| �j�q:1 | 4 | 2 | 6 |
| ���q:2 | 3 | 1 | 4 |
| ���v | 7 | 3 | 10 |
-�m���\-
| X|Y | ���y:10 | ���p:2 | ���v |
| �j�q:1 | 4/10 | 2/10 | 6/10 |
| ���q:2 | 3/10 | 1/10 | 4/10 |
| ���v | 7/10 | 3/10 | 1 |
��̕\��10�l�̃N���X�̒j���ʌ|�p�ȖڑI��\���Ƃ���D���̂Ƃ��C���ӏ��v��6�ɂȂ�̂́C���������̂������ɏ����ƌ��߂�����ł��D����������,�m���\�Ŏ��ӊm�����e�X�c�̘a�C���̘a�ƂȂ�̂́C�����ɘa���������ƂɂȂ��Ă��邩��ł��D���v�Ƃ͂����������̂ł��D
�킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��Œ�`�������ɂ��ā^20.10.05�n
�y���3�z�́i3�j�ɂ����āA�E�ӂ̐ϕ��̍ۂ�x�͈̔͂�0�`2����A-1�`2�ɕς���Ă��肨���炭��L���Ǝv��ꂽ���߂��A�����܂����B������̌��ł������ϐ\�������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[����̗L�����ɂ��ā^20.10.05�n
�����䂤�̍D���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�ɂ��ā^20.10.05�n
�y���������ł� / �I�������Ɠ��Ă����ۂ��ł��ł��Ă��܂� / �撣���Ă������� / �֗� / �ȒP�ł킩��₷�� �����Ɋەt�����Ă���������̂Ŏ��Z�ɂȂ� / ������S�R�킩��܂���B����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���ƂŎg�����̂��ȁH
���m�ʂ̕ł���̎���ɑ���n[��������(��{)�ɂ��ā^20.10.04�n
���ɂ킩��₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɕ������ɂ��ā^20.10.04�n
���݂܂���B����J - - -
�����m��ҁn�F�A�����肪�Ƃ��D�l���̕ԐM�́C���ݍs���Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�w�����̃O���t�ɂ��ā^20.10.03�n
�ƂĂ��킩��₷���ł��B�Ȃ̂ŁA�ΐ����̃O���t�ɂ��Ẵy�[�W������Ă���������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ł�
���m�ʂ̕ł���̎���ɑ���n[�����������i�R���j�ɂ��ā^20.10.02�n
���Q�ł���3/2����������@�Ƃ��ẮA�L�����藝��m���Ă����K�v������̂ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�u�L�����v���������C���̃y�[�W�ɉ���������˥�������Ă�����̂��C�u�m���Ă����K�v������v�Ƃ́H
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^20.09.29�n
���[�[�[�I�@���R�̂P�ł����A�w���̕��q���P�ƌ��Ă��܂��~�ɂȂ�܂����B����������������̂Œ��ዾ�Ŋg�傪�K�v���ƘV�������߂����v���Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�w����Y�����͏������������ƂɂȂ��Ă��܂��D�e���Ŋg�傷��ɂ́uCtrl �� �{�v���ɉ����D�k���́uCtrl �� −�v
�@���̂ɂ���ẮC5��6�̈Ⴂ�C8��9�̈Ⴂ�����\����������M�҂́C�ߊ�̘V��̗��������C���̃y�[�W�̃��x���Ȃ�ǂ߂�D
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^20.09.26�n
�ƂĂ��O���I�ł킩��ɂ����Ɗ�����
�����m��ҁn�F�A�����肪�Ƃ��D�o�����Ă̌��t���Ⴄ��ʂŎg���Ă݂��H
���m�ʂ̕ł���̎���ɑ���n[�R���ԑQ�����̈�ʍ��ɂ��ā^20.09.26�n
�Q�����̌W���������ł�������܂ł̕��ނ͂���Ȃ��Ǝv���܂��B�����������̉����A�����قȂ�ꍇ�Ɠ����ꍇ�̓�ŗǂ��̂ł͂���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�W���������ł���C���������ɂȂ�Ǝv������ł��܂��H�i�������Z�̒�������͈̔͂Ȃ�C�����܂ł����o�Ȃ��Ƃ͌����܂��j
���m�ʂ̕ł���̎���ɑ���n[�O�p���̕s��ϕ��ɂ��ā^20.09.26�n
�O�p�����̐ϕ��𗝉����邽�߂̏ڂ��������Ɖ��K��肪�݂����Ă���C��肾����������������邱�Ƃ��ł����B�{���Ɋ��ӂ��Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����ϕ��ɂ��ā^20.09.26�n
�����ϕ����w�ђ����ɂ������āC������[�߂邽�߂̉��K��肪�K�v�ł��������ߗ��p�����Ă����������B�K�ȃ��x���̖��Əڂ�����������Ă��邽�߁C�����ϕ��̗ǂ����K�ɂȂ����B�~�������ƁC�����������K���̗ʂ������Ɗ������B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʏ�̐��ϕ��ɂ��ā^20.09.17�n
�u�i�Q�l�j�W�����_���̕���p�����ꍇ��(2.4)�̏ؖ��v�́u���ɁC��[C2]�́C�������`�v�̉ӏ��̐ϕ��H��C2�ł͂Ȃ��AC4���������̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�K������������i�����j�ɂ��ā^20.09.16�n
(9)��R�̒lj������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ƁC����̔g�ɒǂ����Ȃ��ĥ��
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^20.09.15�n
�y���Q�z(1)
������a4+b4+c4�|2a2b2�|2a2c2�|2b2c2��������������ƁA�ƂȂ�D
�̉���A[3] ���̌������g���Ĉ�����������D��
x2�|2(b2�|c2)x+b4+c4�|2b2c2=0��
x2 "�|2(b2+c2)x" +b4+c4�|2b2c2=0
�ł͂Ȃ��ł����H
�������Ⴄ�C�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D������������܂���
���m�ʂ̕ł���̎���ɑ���n[�m���̃Z���^�[��������ɂ��ā^20.09.15�n
����Ɂ{���ʼn�����Ə�����܂��I
�����m��ҁn�F�A�����肪�Ƃ�
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�Ƃ��ɂ��ā^20.09.14�n
���߂܂��āC���w�̋��t�����Ă���܂��D
�ˑR�̎��⎸�炵�܂��Dn=k+1�̎��̏ؖ��Ɋւ��āC
��җl�́un=k�ł̉���̎��v�̗��ӂɐ��𑫂����肩�����肷�邱�ƂŁC
n=k+1�ł̎��̌`�ւƕό`����Ă��܂��D
����C�w�Z�̋��ȏ��ł́C���������un=k+1�ł̎��v�̍���(�܂��͉E��)�ɁC
����̎��������ؖ����Ă��܂��D(�����͂�����ŏK���܂������C�ǂ�����悭�������܂�)
����Ă��邱�Ƃ͓����Ȃ̂ł��傤���C���ꂼ��̒����E�Z���C�ǂ���̕������k�ɂƂ��ė������₷�����C����Ƃ��B���ɂ��Ă����Ă����Ȃ��̂��ȂǁC��җl�̌������������������Ǝv���܂��D
�����m��ҁn�F�A�����肪�Ƃ��D�w�Z�̋��ȏ��ł́C���������un=k+1�ł̎��v�̍���(�܂��͉E��)�ɁC����̎��������ؖ����Ă���Ƃ����͖̂{���ŁC�茳�ɂ��鋳�ȏ��͑S�������Ȃ��Ă��܂��D�������C���ʂȍ��Z�łȂ���C���w�I�A�[�@�̒P���̓��Ă��܂Ƃ��ɏ����鐶�k�́C�P�N���X�ɂP�l���邩���Ȃ����̃��x���ł��D�i���ȏ��̗�肻�̂��̂��o�肵�Ă������Ȃ�j�D�ʏ�C�n�������c�̂̐ŋ��ʼn^�c����Ă��鍂�Z�ŁC���悪�o��Ɓu���������Ă���̂��I�ŋ��̖��ʎg���͂�߂�I�v�ƕ������c������n���c��ł邵�グ����Ƃ����}�����o���オ���Ă��܂����C���w�I�A�[�@�̒P���́C�قڂQ�w������������ɂ���C�ǂ�Ȃɂ�����ċ����Ă��C��_�̓��Ă����łĂ��܂���D�����ŗ�_���Ƃ���ƁC�����P�ʔF��̌����݂͂Ȃ��Ȃ�܂��D�i�T�j...�䂦��n��1����������D�i←�₳������1�i�K�ŕ����_����낤�ɂ��C����ł͂ǂ��ɂ��Ȃ�Ȃ��j �i�U�j n=k+1�𗼕ӂɑ�����Ă��܂��D�i←��]�Ǝ����̍�����F�߂Ă��܂�����C���w�ł͂Ȃ��Ȃ�j
�@�����ŁC�u���m�̎��v�Ɓu���m�̎��v���͂����肳���āC�u���m�̎��v����u���m�̎��v������Ă����Ƃ������ĂɂȂ�悤�ɁC���̋��ނ̂悤�ȍ\���ŁC��\�N����Ă��܂����D�����Cn=k+1�̎����g���Ă��܂��ƁC���ӂ����Ŏ~�߂��鐶�k�͂قƂ�ǂ��Ȃ��ł��傤--�u���k�̊w�͔͂N�X�������Ă����̂ɁC�]����N�X�グ�Ȃ���Ȃ�Ȃ��v�Ƃ����S�̍\���̒��ŁC���������邽�߂ɂ́C�Ƃ��������̒��ŁC�ł��邱�Ƃ͂��ׂĂ��Ƃ������Ƃť��
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^20.09.14�n
�����e�X�g�ŕs�����͈̔͂��o�đ�̎����Ⴆ�Ȃ��ĒT���ɗ��܂����@�ォ�珇�ɂ���Ă��čŏ�����Ă��̂�
���X�ɂł���悤�ɂȂ��Ă����Ċ������������������Ă����Ɋy����������܂���
��l�ł�镪�ɂ͐��������ɂȂ�܂����@�l�͐��w�������Ȃ�ł����@���߂Ď�������T���ā@���������̂�������
�ق�Ɩ��ɂ����܂������肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ�
���m�ʂ̕ł���̎���ɑ���n[��������(��{)�ɂ��ā^20.09.13�n
�ق��̕������ꂽ�y�[�W�ƈႢ�A���`���Ŋy����
�����āA������킩��₷�����p�����Ă��������Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ�
���m�ʂ̕ł���̎���ɑ���n[�������̘a�E���ɂ��ā^20.09.11�n
���P��(3)�̓����̕����x(x+2)�ł͂Ȃ��Ax+2�Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ����C�����C���̂悤�ȁu�H�v�����Ă���̂��Ƃ�����C�قƂ�ǂ��ׂĂ̕������̖��ŊԈႤ���ƂɂȂ�܂��̂ŁC�O��̃y�[�W�����āC�������ό`��g�ɒ����Ă��������D
}\rightarrow\frac{-2}{x%2B 2}&chf=bg,s,fff9f9)
���10�̕ʉ��ŁAsin��=��3cos�Ƃ��tan��=��3�̕ό`�̍ۂɁAcos�Ɓ�0�Ƃ����sin��=1(cos�Ɓ�0)�̋L�q������Ƃ�蒚�J�ȉɂȂ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��Dcos�Ɓ�0�̏ꍇ�������ȗ����Ă��܂��̂ŁC�C�ɂȂ�����������܂��Ccos�Ɓ�0�̂Ƃ��́C��肩��sin��=��3�~0=0�ƂȂ�C��=0��,180���C�����ł�cos�Ɓ�0�����=90���ƂȂ�̂ŁC���藧���܂���D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^20.09.08�n
���̎O���������̉��ƌW�����ē����ɔ�r�I�o�₷���̂ł��傤���H�o����̂���ςŏo���邱�ƂȂ���������Ȃ��ƍl���Ă���̂ł����A�A
�����m��ҁn�F�A�����肪�Ƃ��D��w�E�w���ɂ���Ăǂ̂悤�Ȗ����D�ނ��́C�傢�ɕς��܂��D��ʓI�Ɍ����C�Ⴆ�ΐ��w�U���o��͈͂ɓ����Ă��āC���w�T�CA�CB�ƍ��킹�ĂU����x�̖��ō\������ꍇ�C���w�U�Ɋ��蓖�Ă��鍀�ڂ͂P�`�Q�ł��傤�D��������ƁC���Əؖ��C���f���ƕ������C�}�`�ƕ������C�O�p���C�w���E�ΐ����C�����ϕ��̂ǂ�����o�����Ƃ������ƂɂȂ�܂����C���N�����P������o���Ă���ƁC������������������Ď�Ƃ������ƂɂȂ�ƁC���w���Ă���u�`�����K�����藧���Ȃ��Ȃ�̂ŁC�e����ǂ�����o����������ɂ����悤�ɁC�����_���ɏo���ł��傤�D�Ƃ���ŁC���f���ƕ������Ƃ����P������o���ƌ��߂��ꍇ�ł��C���ȏ��ɏ����Ă�����x�́u�����������Ȃ������v�u�������������Ȃ����v�̃��x�����o���ƁC���̑S���������ɂȂ��Ă��܂��āC�o��̈Ӌ`���Ȃ��Ȃ�ł��傤������Z�̒�������́C�S�����ł��邩�ǂ����ƒ��ׂ邱�ƂɈӋ`�����邪�C��w�̓��w�����́C�ł���l�Ƃł��Ȃ��l���邱�ƂɈӋ`�����饥���ԗǂ����́C�e�P�����Ƃɐ��𗦂������ƂȂ�ꍇ�ł��傤�D
�@���āC�R���������̉��ƌW���̊W�Ȃǂ́C�̂�����グ���Ă�����^�I�ȍޗ��ł�����ٓ��̂������Ō����Η��Ă��̂悤�Ȃ��̂ł��D������C���ƂP��o�����Ƃ����悤�ȏꍇ�ɁC�lj�����̂ɓK���Ă��܂��D�������܂��C�����֊ցCMARCH�̂悤�ȂƂ���ŁC�o���Ă����炷���ł���悤�Ȍ`�ł͏o���Ȃ��ł��傤�D���ƌW���̊W�͓��R��������̂Ƃ��āC����ɐ������𗍂܂���ȂǂƂ����X�^�C���ɂȂ�ł��傤�D
�@���X�Əq�ׂ܂������C���q���ɔ������̎����傢�ɕω����Ă���̂ŁC�Ⴆ�ΐ��E�����ł͋��ȏ����x���̗�肪���̂܂o��ꍇ������C�t�ɁC���O�������Ƃ�����悤�ȑ�w�̈�ʓ����ł́C���ƌW���̊W���o���Ă������x�ʼn�����悤�Ȗ��͏o���Ȃ��ł��傤�D�i��w�Ɗw�����i���ĉߋ���ɓ������Ă݂�ƁC������x�̌X���͂��߂܂��j
���m�ʂ̕ł���̎���ɑ���n[���K���z(�O����K)�ɂ��ā^20.09.08�n
(2)��228�ŕs�����Ƃ���Ă��܂��܂������A�\���0.96<z<0.97�Ȃ̂�228<x<228.5�ƂȂ�A�ނ���228�������ł͂���܂��H�ۂ߂ɂ��덷���o�Ȃ��悤�A��蕶���̒l��ύX�����ق��������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��͎���̎d�����Ԉ���Ă��܂��D(2)�Ƃ������͂�������܂��D�ǂ̃y�[�W��(2)�Ȃ̂��������Ȃ���u�S�����ׂāI�v�Ƃ����Ӗ��ɂȂ�܂��D1���Ԓ������ĂT�y�[�W�ڂɌ����܂������C��ʂɘA�����z�ł��鐳�K���z��l���̂悤�Ȑ������ɂ��Ă͂߂��ꍇ�C���ʂ͏�Ɏ����l�i�����l�j�ɂȂ�C�������㐮���Ɍ������������Ă��C���m�ȈӖ�������킯�ł͂���܂���D������C�߂����̐����œ�����̂����R�ł��D
�@���ۂɂ́C�u����������i�҂�0.1%�ł�������Β�����������̏�������ł�����v�Ƃ����悤�ȋ����͂��������Ƃ������悤�ł����C����͕ʂ̐��E�̘b�ł�.
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̕ӂ̒����ɂ��ā^20.09.07�n
�����b�ɂȂ��Ă���܂��B����܂ŎQ�l�ɂ����O�p��̐����ŁA��ԕ�����₷�������ł��B
�{���ɏ�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^20.09.05�n
win10���ł̃N���[���ł�Cookie��L���ɂ��Ȃ��ƁC�������c��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł��DChrome��Cookie��javascript���L���ɂ��Ďg���Ă�������
���m�ʂ̕ł���̎���ɑ���n[���a�L�����i�V�O�}�j�Ɋ���悤�ɂ��ā^20.09.04�n
���ɂāu�P�� n��k = 1 �Ə����� n��k = 11 ��\�킷�ɂȂ��Ă���v�Ƃ���܂����C�ǂ��ł��̂悤�ȖɂȂ��Ă����̂ł����H��������ĉ������D���̏�̐M�ߐ����m���Ȃ̂��m���߂����ł��D
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ�قǁC������Ӗ��͕�����܂����C���̖{��������I�ȏ������ł����̂ŁC�������܂����D

�ł��邱�Ƃ́C���ׂĂ̋��ȏ��ɖ����I�ɏ�����Ă���C�����ĂȂ����ȏ��͂���܂���D���Ȃ킿

����ɑ��āC

�������I�ɏ�����Ă��鋳�ȏ��͂Ȃ��悤�ł��D�����C�������Ȃ��ƒ萔�������ʈ����ɂȂ�s�ւ��͂���܂��D
=a\sum k^2%2B b\sum k%2B c\sum\]&chf=bg,s,fff6f6)
�Ə����Ȃ��D

�́C���������Ȃ���ΈӖ������܂�Ȃ��C�ȂǕs�ւȂ��Ƃ�����܂����C��L���قǂɂ͕p�o�̂��̂łȂ��C�ϋɓI�ɖ�������K�v���Ȃ��悤�ł��D
���3�̒萔����-3�ł͂Ȃ��ł��傤���B���m�F����낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���F�ŏ��������߂��܂���
���m�ʂ̕ł���̎���ɑ���n[�ȉ~�̕������̕W���`�ɂ��ā^20.09.03�n
���K��肪�����o���Ă邩�m�F�o����̂ŁA�L������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƌW���̕����ɂ��ā^20.09.02�n
�ƂĂ��킩��₷������ŏ�����܂����B���肪�Ƃ��������܂��B
�ЂƂw�E�����Ē��������̂ł����A�yb�̕����z�̍��ڂ̍Ō�A�ԂŎ��������������Ă���ӏ��ŁAa=�|1��0�ƂȂ��Ă��܂����Aa=�|1��0�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƃ��ƁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̌`���ɂ��ā^20.09.02�n
joker�����������ł����H
�����m��ҁn�F�A�����肪�Ƃ��DPC�ł̕���joker�̋L�q�̒����Y�ꂪ����܂����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[���̘A���C�Ɍ����ɂ��ā^20.09.01�n
���̋Ɍ��l�ɂ��ċ����Ă��������Bx��a�ɋ߂Â��߂Â����͂��낢��i�U�����Ȃ���Ƃ����j����Ǝv���܂����A���ʂȋ߂Â����ł���E�Ɍ��ƍ��Ɍ��̈�v�݂̂������āA�����a�ɂ�����Ɍ��l�Ƃ��Ă悢�̂����C�ɂȂ��Ă��܂��B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D1�ϐ��̏ꍇ�C�傫��������߂Â����i�E�Ɍ��j�C�܂��́C������������߂Â����i���Ɍ��j�őS���ł��D������C�E����߂Â��Ă��C������߂Â��Ă��C�����l�Ɏ�������Ƃ��C�߂Â����Ɉ˂炸���̒l�Ɏ������܂��D����́C(−1)n�I�ȉ����U���`�̋߂Â��������łȂ��C(2��/3)n�I�ȍ����E�E�`�̋߂Â����C���̑��̏ꍇ�ł��C�߂Â����Ɉ˂炸���藧���܂��D
�@����ɑ��āC�Q�ϐ��ȏ�̊��̏ꍇ�C���E����v���Ă��C�c�Ɖ�����v���Ă��C�܂��ߕ�������́C�������͉�]���Ȃ���̐ڋ߂̏ꍇ�̋Ɍ��̈�v�͕ۏł��܂���̂ŁC������0�ɂȂ邩�ǂ����Ŕ��f���܂��D
�@�Ƃ���ŁC���Z�̐��w�ł́C���������u����Ȃ��߂Â��v�Ƃ͉����Ƃ������Ƃ��`�����ɒ����I�ɗ����ł���͈͂ō�����������悤�ɂȂ��Ă���̂ŁC���Ƃ��ƁC�Ɍ��́u�ؖ��v�͂ł��Ȃ��\���ɂȂ��Ă��܂��D�����ȏؖ��́C��w���w�̃Ã_�@�ŏؖ�����悤�ɂȂ��Ă��܂����C���Z���w�̓Ã_�@���K�v�̂Ȃ���肾����I��ŏo�肷��Ƃ����̏�ɂȂ藧���Ă���ƌ����܂��D
���m�ʂ̕ł���̎���ɑ���n[�ɕ������ɂ��ā^20.09.01�n
����@�������ȂƂ���ŒT���Ă��܂����C��v����̂��������Ă��Ȃ��̂ŁC���̖����̂���
���z�ɂ��������Ă��������܂��B
�E���̋ɕ��������\���}�`�̒������W�ɂ���������������Ƃ߂�B
�@�Esin�Ɓ��P/�R�@�@�@
�ǂ����������炢���̂ł��傤�B�Y�݂܂��B
�����m��ҁn�F
������

&chf=bg,s,fff6f6)
��sin�Ɓ��P/�R�ƂȂ镔���i�㑤�j
���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�藝�C�����藝�ɂ��ā^20.08.31�n
nCr������Ƒg�����̊�{�I�ȏ������������Ă���̂������I�ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�i��`��̎w�肪����Ƃ��j�ɂ��ā^20.08.30�n
��ώQ�l�ɂȂ��Ă���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�������ɂ��ā^20.08.30�n
���1��5.7.9.11���2n +3�ɂȂ��Ă��܂����ǂ�����ċ��߂���ł��傤���H
�Ⴆ��5.7.9.11��18.24.30�������ꍇ�ǂ����������ɂȂ�̂ł����B�����ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�K�����玿�₵�Ă���悤�ł����C��������O��
�����������ɕ����Ă��������D
�@����
a�C����
d�̓�������̈�ʍ���
an=a+(n−1)d�ł��D
5.7.9.11 ��
an=5+(n−1)2=2n+3
18.24.30 ��
an=18+(n−1)6=6n+12
��1��2���[���ł��Ȃ��B
����Ƒ�͐^�U��v����͕̂�����܂��B�܂�A���ɐ^���U�Ƃ������B����Ɠ����ɁA���Ƌt����W�ł�����A�y���Ƌt�̊W���^�U��v�z���Ȃ��ƕςł��B ����ŏo�Ă���u��͔����v�̖���ł́A�������@�\���Ă��܂����c����u�ၨ�����v(�^)��u�����Ȃ�����łȂ��v(�^)�c�����Ƃ��ɐ^ ���̖���F�u��łȂ��Ȃ甒���Ȃ��v(�U)�t�̖���F�u�����Ȃ��ł���v(�U)�c�����Ƃ��ɋU
�����m��ҁn�F�A�����肪�Ƃ��D���Ƌt�̐^�U�͏�Ɉ�v���C��v����Ⴊ�����Ă���̂�����u�[���ł���v�Ə����ׂ��ł��傤
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^20.08.28�n
�Ȃ�p�Ȃ�����lp�łȂ��܂��͂� ����͒�`�Ȃ̂��ǂ����܂��悭�킩��Ȃ��̂ł����A�搶�̂��̃y�[�W�̃x���}�̂悤�Ȃ��̂ʼn��ƂȂ������ł���悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D��`�͂P�����Ȃ��ł����C���l�Ƃ��������Ƃ͌����܂��D�����ƕ�����₷�������u���Ȃ���v�Ƃ́u���ł���Ƃ��ɂ��łȂ����Ƃ͋����Ȃ��v

�Ɗo����̂����ʂł��傤�D
���ɁC��Q���i�E�Ӂj���C�h�E�����K���̖@���ɂ��

�ɕό`�ł���ƍl����Ɩ����Ȃ����т��܂��D
�u���łȂ��܂��͂��v����X�^�[�g���ăX�g���Ɣ[������͓̂���ł��D
���T�̎�(3)�ɂ��Ď��₳���Ă��������B
����́A0��x��5����0��y��5����0��z��5�Ƃ������Ƃ�\���Ă���̂ł��傤���B
�����I�Ȏ���ŋ������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł�
���m�ʂ̕ł���̎���ɑ���n[��ʍ��̋L���Ɋ�����ɂ��ā^20.08.23�n
��ʍ��͂����P�Ƃ͌��邱�Ƃ͂Ȃ��H�Ǝv���Ă��܂��I
[
�K�������ɂ��ā^20.08.23�n
�K������̌�����p���āA��ʍ������߂�Ƃ��A���͂P�Ƃ͌��邱�Ƃ����Ȃ��̂ŁA���̂P�����߂�Ƃ��Ƃ���������ǂ��̂ł͂Ȃ����Ǝv���Ă��܂����A���N�R�����g������Q�l��������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ�������M���邩�́C���Ȃ��̎��R�ł����C���̔ԍ�n�����߂��Ƃ��ɁC����a
n�̒l�����܂�Ȃ��悤�Ȃ��̂͐���Ƃ͌����܂���D���Ƃ��C���������U���ďo���ڂ̐����L�^���Ă����Ƃ��C���܂ŏo���ڂ̋L�^�͐���ł����C�܂��o�Ă��Ȃ������̖ڂ̐��͐���ł͂Ȃ��D�Ⴆ�C�����ȍ~�̑�n���̓��o���ϊ�����a
n�Ƃ���Ƃ��Ca
n�͐���ł͂Ȃ��D
�@���̂悤�ɁC����̍��ԍ����w�肵���Ƃ��ɁC����̍�a
n������1�ʂ�Ɋm�肷����̂���������ŁC�����ł͂Ȃ����̂͐���Ƃ͌����܂���D
�@�����ł́C����ƌĂׂ邽�߂ɂ́C���̒l�������܂�悭�C�����\�����鎮�܂ł͌��܂�Ȃ��Ă��悢�D�Ⴆ�C
^{n-1}&chf=bg,s,fff6f6)
��
^{n%2B 1}&chf=bg,s,fff6f6)
�C
^{n%2B 3}&chf=bg,s,fff6f6)
�C
^{n%2B 5},\hspace{2}...&chf=bg,s,fff6f6)
�͂��ׂē������̂ł��D
�����Ŏ��Ɖ��M���g���Ė���1������Ă͐����Ǝv����I�������N���b�N���钼�O�ɂ́A�u������������ǂ�ȉ摜���o�Ă���̂��낤�v�Ɗy���݂ł�����A�u�Ԉ������ǂ�ȉ摜�ɂȂ�̂��낤�v�ƕs���ł�����܂��B�P��ڂ������̎��ɏo�Ă����摜�������Q��ڈȍ~���o�Ă���悤�ɐ�����ڎw���Ď��g��ł��܂��B�R���i�Ŏ��Ƃ��x�݂������P�w�������߂��Ă�����悤�ɁA���́u���Z���w�̊�{���v���g���Ċ撣�肽���Ǝv���܂��B���ꂩ�����낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ʕ����Ƙa�W���ɂ��ā^20.08.22�n
�������̓_�̏��������ƌ�����@�\�͏��߂Č��܂����I�I�������ł���✨
�����m��ҁn�F�A�����肪�Ƃ��D
���H�H�m�H�H�^20.08.22�n
���߂Ă��A�������グ�܂��B
���͗��H�n�̑�w�ɒʂ��Ă���҂Ȃ̂ł����A
�������URL
�ɍڂ��Ă�������A���₵�������A���������܂����B
���₵�����̂́A�Y�t��2���̉摜�̂悤�ȋt�O�p���̖��Ȃ̂ł����A���ꂼ��tan^-1�����A���Œu���̂͂킩��̂ł����A��������ƌ��̎��̓�+���ƂȂ�Ǝv���̂ł����A����ł͎O�p���̉��@�藝���p�����Ă��܂��B�����Ƃ��ẮA���̉��@�藝���g���A�܂��͎g�����Ƃɂ���Ď����ؖ��ł���Ƃ����̂��悭�킩��܂���B
�����̗���s���ɂ�鎿��ł����A������������ƍK���ł��B������낵�����肢�\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��+�������߂�Ƃ悢�D���@�藝�ȊO�ɑ��ɕ��@���������ł��悢���C���̖��ł͉��@�藝�̗��p����Ԋy�ɂȂ�
(7)�̖��̐}�`�I�ȈӖ��i�~�̖ʐςƂ̊֘A�Ȃǁj�͂���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D

�����͒l�Ƃ��Ă͈�v���܂����C�\���Ă���ʐς͕ʂ̂��̂ł��D
�ƂĂ�������Ղ������ł��B
����<�Q�l>�ɂ���u�d���g�����̋L���ɂ́C�Ȃ�H ���g���̂��v���ǂ������ł��B
�L���������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ׂ荇�����ѕ��E�ׂ荇��Ȃ����ѕ��ɂ��ā^20.08.22�n
���Z���w�͂ƂĂ������̂ł����A���w���w�̖�肪�ȒP�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���Z���ɒ��w�̖�肪�Ղ����͓̂��R�̂��Ƃł�
���m�ʂ̕ł���̎���ɑ���n[����-���K���z���g����ꍇ�ɂ��ā^20.08.21�n
���(2)�ɂ��āA�o��́u�ꕽ�ρ�55�A��W�����́y1�ȉ��z�v�Ƃ���A�o�������W������1�Ƃ͌���Ȃ��̂Ɋւ�炸�A�Ȃ��u�Ё�1�v�܂�u��W�������P�v�Ƃ��ĕꕽ�ς̌�����s���Ă���̂ł��傤���H�Ȃ��A�ȒP�ȗ�ŃC���[�W���i3�j�̗�(3)�ł́u��W������1�v�Ƃ���Ă���̂ŁA��(3)�ɂ��Ắu�Ё��P�v�ł��邱�Ƃ͕������Ă��܂��B��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�P�Ő��藧�ĂP�ȉ��Ő��藧�Ƃ͌����Ȃ����C�P�Ő��藧���Ȃ���P�ȉ��Ő��藧�Ƃ����Ȃ��̂́C����b�ł͂Ȃ��C���ʂ̘_���̘b�ł��D�i�K�v�����j
���_�ސ쌧�m�҂�����^20.08.20�n
������������₷���A�ŋ߂͂�����̃T�C�g������̂����ۂł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ɨ��Ȏ��s�̊m���C�������s�̊m���ɂ��ā^20.08.20�n
���ՂȂ����삪�ԗ�����Ă���A�܂��A���ǂ��ÎZ�ł�����(�v�Z�ʂ�����قǑ����Ȃ�)��肪�����育��ȉ��K�ɖ𗧂��܂����B���肪�Ƃ��������܂�m(__)m
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s���Ίp������ɂ��ɂ��ā^20.08.19�n
���̍v�̗ޑ�2.2���������Ƃ��Ă݂��Ƃ���A�ŗL����������^3-15��^2+74��-48=0�ƂȂ�܂��B�]���ĉɂ���悤�ȃ�=1,��=2,��=6�Ƃ͂Ȃ�Ȃ��̂ł����A�ǂ̂悤�ɂ��ČŗL���������������̂ł��傤���B
�ޑ�2.2�Ɋւ��āA�s��̐�������͂���ۂ�(2.2)������0�ƂȂ��Ă��܂����A�����6�Ȃ̂ł͂Ȃ��ł��傤���B
�m�F���肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���ɓ]�L�~�X������܂����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̑傫���ɂ��ā^20.08.18�n
�v���Ԃ�ɐ��`�䐔�̖��������ۂɁA���̕ӂ肩�畜�K�����Ē����܂����B
��{����Y��Ă����̂ŁA����HP�ŕ�����Ղ��������Ă���A������������܂����B
�{���ɂ��肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���s�����ɂ��ā^20.08.17�n
���̎��̎w���s�����͂ǂ��Ȃ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D��ꂪ�ȗ�����Ă��āC����̈Ӗ����m�肵�܂��C�w�������̐��̂Ƃ��͂��̃y�[�W�ŕ��ʂɈ����Ă��܂��D�ꂪ���̐��̎w�����́C���Z�ł͒�`����܂���D�܂�C���̂悤�Ȃ��̂͂Ȃ��D
�@�Ⴆ�C

�ɂ�����

�̂Ƃ��C�w���������̏ꍇ�͖�肠��܂���
^{\frac{1}{2}}=\sqrt{-1}&chf=bg,s,fff6f6)
�͒�`���ꂸ�C���l�ɂ��ĕ��ꂪ�����ƂȂ�L�����̎w���ɑ��Ē�`����Ȃ��̂ŁC�w�����Ƃ��Ē�`�ł��Ȃ����ƂɂȂ�܂��D�L�����̐���̋Ɍ��Ƃ��Ē�`����閳�����ɑ��Ă��C�r���̗L�����������炯�Œ�`�ł��Ȃ����ƂɂȂ�܂��D
1.3 �́AA^n = �̌v�Z�̍ŏI�`��A_12 �����̑�1���ڂ́A-i^n �ł͂Ȃ��A-i^(n+1) �ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�m���ϐ��C�m�����z�ɂ��ā^20.08.14�n
�i���n��w���o�ăT�����[�}�������Ă܂����AE���i�Ƃ���DeepLearning�̎��i�����ɂ��̃y�[�W�ɒH��t���܂����j�E�u�m���ϐ��ł͂Ȃ����́v�����L����Ă���_���@�����{��Ŗ��L����Ă���y�[�W�����Ɍ�������Ȃ����炢�ł��B�@ex.✕���t�^�A�A���P�[�g�̒萫�I�]���i�킩��₷���j�E�y�[�W�S�̂Ƃ��āA�G�E�\�E�F�����Ɏg���Ă��āA�킩��₷���ł��B�E����xcheck���ȒP�ɏo���Ċy�����B���݂܂���A�J�C�[���Ɍ��т����e�͂���܂��A�{���ɏ�����܂����I
�����m��ҁn�F�A�����肪�Ƃ��D������́C�[�w�w�K�̖{��ς�ł��邾���ŁC�܂��ǂ߂Ă��Ȃ��`��`
���m�ʂ̕ł���̎���ɑ���n[�s��̏�@�̐����ɂ��ā^20.08.14�n
���z�@�����K���������藧���̂ł͂Ȃ����̗Ⴊ�ƂĂ�������₷�������B���K�����ȒP�ł͂��邪�A���z�@���ƌ����@���ɂ��ė����o���Ă��Ȃ��Ɖ����Ȃ��̂łƂĂ��ׂɂȂ����B
�����m��ҁn�F�A�����肪�Ƃ��D
��??�m�Ȃ�����^20.08.13�n
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^20.08.09�n
�ƂĂ��킩��₷�������ł��m�̎��Ƃ��x��ł��܂��Ă��ĎO�p���������ł��Ȃ������̂ł����A������݂čl�����������ŎO�p����������悤�ɂȂ�܂��� ���肪�Ƃ��������܂� �{����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�T���������̉��ɂ��ā^20.08.08�n
�����A���w�n������Ƃ����w�o�g�҂ō��͐��w�̐��E�E����E�ɂ��Ă��Ȃ��҂ł����A���T�C�g�͍��Z���w�ƒ��w���w�ɂ��đ�ϗǂ��R���p�N�g�ɂ܂Ƃ܂��Ă���̂ŖڂɎ~�܂�܂����B�F�X�Q�l�ɂ����Ē����Ă���܂��B����A���w�E�������͍̂������w���R���s���[�^���p���q�R�}���_�[�̗��p�̍��ڂɂ���u�T���������̉��v�̏��ł��B���̃y�[�W��35�s�ځ`42�s�ڂɂ��鎟�̋L�q�ł��B�u�m���ʁn�q��console�E�B���h�E�܂��͂q�R�}���_�[�̏o�̓E�B���h�E�Ɏ��̌��ʂ��o�͂����Dpolyroot(c(113,-149,32,8,-5,1))[1] 1.000000+0.000000i -2.980212+0.000000i 2.931663-0.000000i[4] 2.024275-2.972515i 2.024275+2.972515i�����́C�������̉���x=1, �|3, 3, 2�|3i, 2+3i�ł��邱�Ƃ�\���Ă���D�v����͈���Ă���Ǝv���܂��B�������̉���1,3,-3,2-3i,2+3i�ł���Ƃ��ĕ������������̐ςŕ\����(x-1)*(x-3)*(x+3)*(x-2-3i)*(x-2+3i)�ƂȂ�܂����A�����W�J�����x^5-5x^4+8x^3+32x^2-153x+117�ƂȂ�܂��B(wxMaxima�Ō����܂����B)������q����̑��������𖽗߂ŕ\����polyroot(c(117,-153,32,8,-5,1))�ƂȂ�A���X�̕������Ƃ͈Ⴄ���̂ɂȂ��Ă���܂��B�����Č���Ɗm���ɂq�R�}���_�[�ɂ� polyroot(c(117,-153,32,8,-5,1))[1] 1+0i -3+0i 3-0i 2-3i 2+3i�Əo�͂���܂��B�v���ɂq�ɂ�����������̐��l�v�Z�̗L�������͏����_�ȉ�6���܂ŏo���Ă��鐔�l�ɑ��čl�@�������_�ȉ�1���ڂ̎l�̌ܓ��ɂȂ��Ă���̂�5�����̏�����o�Ă���̂������Ǝv���܂��B�ǂ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�u�T���������͉����Ȃ��v�ƌ������邱�Ƃ������̂ŁC���̃y�[�W�ł́C���ۂɐ��l�̌W����^����ꂽ�T���������������Č����邱�Ƃɂ��u�T���������͉�����v�Ƃ������Ƃ������Ă��܂��D�Ȃ��C�����錋�ʂ͋ߎ��l�ŁC�ו��܂ň�v����̂͂��Ȃ������ׂ��悤�ɒ萔����117�̏ꍇ�ł��D
���m�ʂ̕ł���̎���ɑ���n[Sn�������W���ɂ��ā^20.08.08�n
���m�ʂ̕ł���̎���ɑ���n[�����\�̕����ɂ��ā^20.08.07�n
�Ԉ�����Ƃ������������}���g��������Ă����̂łƂĂ�������₷�������ł��B���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̑Q�����ɂ��ā^20.08.07�n
���́i�R�j�̓r������e^{-x}��e^{x}�ɂȂ��Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ΐ��v�Z1�ɂ��ā^20.08.07�n
���Z�ȗ��A�ΐ��͋��ł����B��̃A�}�`���A����1���̎ɂ������čĕ��B���̃T�C�g�ɂ��ǂ蒅���S�@��]�B�������ꂽ�C�����܂����B���Z����͕��n�ł�����3�N���ɂ͐��w�V���K�C�ŏT3���ԁB
�n���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���n�ɂ��āC������߂ĕ��n�ɍs���̂́C�悭����܂����C���̋t�͂��蓾�Ȃ��ł��傤�D���n�Ő�B�Ƃ����V�Ƃ��C�Q�K�����Ă��ɂR�K�����悤�Șb�͖����Șb�ŁC�ǂ��Œ�������̂����������Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^20.08.06�n
���̉������܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�X�}�z�łɂ͕t���Ă��܂����CPC�łɂ͕t���Y��Ă��܂����̂Œ����܂���
���m�ʂ̕ł���̎���ɑ���n[�ڐ��̕������ɂ��ā^20.08.03�n
�ڐ��̕�������y1��0�̂Ƃ��X������`�ł��Ȃ��̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�C���ꂪ0�ɂȂ�̂Œ�`�ł��܂���D�������C���ʂ�x=c�`�̒����ɂȂ��āC���ʂ͐������Ȃ�܂��D
�@�ꍇ�������ď��������悢�Ƃ͌����܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̍ő�l�C�ŏ��l�ɂ��ā^20.08.03�n
���₳���ĉ������B
x+y=2�̂Ƃ�xy�̍ő�l�����߂鎞�ɁA(x+y)^2=2^2���xy=2-(x^2+y^2)/2�@xy���ő�ƂȂ�̂�x^2+y^2���ŏ��ƂȂ�Ƃ��Ƃ����l�����ł͂��܂������Ȃ��̂ł����A�ǂ��ŃG���[���N���Ă���̂ł��傤���B�X�������肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���܂������Ȃ��Ə����Ă��܂����C���܂������܂�=����ō����Ă��܂��Dx+y=2�̂Ƃ�x^2+y^2=x^2+(2-x)^2=2(x-1)^2+2��x=1(y=1)�̂Ƃ��ŏ��l2���Ƃ�܂��̂ŁCxy�̍ő�l��1�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̕��s�����C���������ɂ��ā^20.08.03�n
���s�x�N�g���̏����̂Ƃ��낪�Aa=tb�ɂȂ��Ă��܂�������Ŗ������Ă��ԈႢ�ɂȂ�������b=ta�ƂȂ��Ă��܂��B�ǂ����������ł����H
�����m��ҁn�F�擪�̏��Ɂu

�ƂȂ����

�����݂��邱�Ɓv�Ɓu

�ƂȂ����

�����݂��邱�Ɓv�͓������Ƃł��Ə����Ă����ˁD������C�ǂ����ł��悢�D�u����Ŗ������Ă��ԈႢ�ɂȂ�v�Ƃ����̂͂��������ł��D���̊ԈႢ���Ă������Ă��炢�����ł��D
�y�����w�K�����Ă��������Ă��܂��B�u�����̓W�J����2�v�̖��6�@��O��̓����Ȃ�ł���X��6��Ƃ���܂����AX��8��ł͂Ȃ��ł��傤���HA��x6�|3x4+3x2�|1�@�ŏ��̕����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�w���@���ƌ����̂������āC
^n=x^{mn}&chf=bg,s,fff6f6)
�ɂȂ�܂��D
}&chf=bg,s,fff6f6)
�ɂ͂Ȃ�܂���D
���Ƃ��C
^3=x^{6}&chf=bg,s,fff6f6)
�ł��D
���ɂȂ�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^20.08.01�n
���k���̖��͖�蕶�̈Ӗ���������Ȃ������B
�����m��ҁn�F�A�����肪�Ƃ��D�����������Ȃ������ꍇ�́C���̋��ނ̍�ҁi���j�ɊW������܂����C��蕶�̈Ӗ���������Ȃ������ꍇ�́C�������Ă��Ȃ��Ă悩�����Ƃ��������悤���Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�]�u�s��C�Ώ̍s��C�Ίp�s��C�O�p�s���ɂ��ā^20.07.29�n
�������ȑ�w�̊w�����ł��B
�R���i�Ђő�w�ŏ\���ȍu�`�����Ȃ����A���K��\�K�ɂ�����̃T�C�g���d���Ă��������Ă���܂��B�e���ڂ̍\����C�A�E�g�����ƂĂ����₷���܂Ƃ܂��Ă���A�f���炵���T�C�g���Ǝv���܂��B�l�̎���ʼn^�c����Ă���T�C�g�Ȃ̂ł��傤���H���ꂩ������p�����Ă��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���Ԍ����ɂ́C��ł���Ă���悤�Ɍ����܂����C�{���͂����ł͂Ȃ��ł��D�Ȃ��Cedge�ɂ͍����܂���.Chrome�œ_�����Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[���ʕ����Ƙa�W���ɂ��ā^20.07.28�n
����͍̓_�@�\�������Ă���̂ŁA���K�ȂǂɂƂĂ����p���邱�Ƃ��ł��ď�����܂����I������킩��₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^20.07.23�n
x^2cos(1/x)��x=0�Ŕ����ł��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�U�̋��ނ��玿�₵�Ă��܂����C�ʏ킻�̌��ł͏K���܂���D���w�V�̘A���Ɣ����\�����������Ă���C
���̃y�[�W�́y���3.2�C���3.3�z������œo�ꂵ�܂��D
�@���āC����q�˂����̂��͕�����܂����C���w�I�ɂ͍ł��d�v�Ȃ��Ƃ������Ă��āC�u�����ł���v�u�����ł��Ȃ��v�Ƃ����悤��Yes�CNo�œ���������ł͂���܂���D�X�g���[�g�Ɍ����C���������C���̊���x=0�̂Ƃ���`����Ă��Ȃ��̂ŁC�A���łȂ��C�������s�\�ł��D�������Cx=0�̂Ƃ�f(x)=0�ƒ�`����Ă���Ƃ��́C���̂悤�ɂ��āu�A���v���u�����\�v�ƌ����܂��D
=&chf=bg,s,fff6f6)

&chf=bg,s,fff6f6)
&chf=bg,s,fff6f6)
x=0�ɂ���������W���́C
=\lim_{h\rightarrow 0}\frac{h^2\cos\frac{1}{h}}{h}=\lim_{h\rightarrow 0}\left(h\cos\frac{1}{h}\right)\]&chf=bg,s,fff6f6)
������

������
=0&chf=bg,s,fff6f6)
�ƂȂ�C�����\�ł��D
�@�v��C
=0&chf=bg,s,fff6f6)
�ƒ�`����C�����\�i���A���j�ƂȂ�܂����C����ȊO�̏ꍇ�́C�A���ɂ������\�ɂ��Ȃ�܂���D
��i2�j�̉���̍Ō��AB��OC�̌��ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ς̖@���ɂ��ā^20.07.20�n
�����Â炩����
�����m��ҁn�F�A�����肪�Ƃ��DPC�p�͕ʕłƏ����Ă���̂ɁCPC�ł킴�ƌg�їp��ʂ����Ă���H
���m�ʂ̕ł���̎���ɑ���n[���a�̕\�킷��ʊp�ɂ��ā^20.07.20�n
���������������傫���]���������������A�p�b�ƌ������Ɍ��Ă݂悤���ȂƎv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�g�їp�͕ʕłƏ����Ă���̂ɁC�g�тł킴��PC�p�̉�ʂ����Ă���H
���m�ʂ̕ł���̎���ɑ���n[�������̕s��ϕ��ɂ��ā^20.07.19�n
���̃T�C�g�͗ǂ��܂Ƃ܂��Ă���̂ŁA���p���Ă��܂��B���肪�Ƃ��������܂��B
1.6�̉����������Ă���̂͏����c�O�ł��B�T�v�Ƃ��āA��r�I�ȒP�ȗ�́A���ꂪ(x^2+1)^n �̏ꍇ�A
n=1�Ɠ��l�ɁAtant=x�Œu�����āAcost��2*(n-1)��̐ϕ��ƂȂ�A�Ϙa(n�{�p)�����Ŏ����������Ă���v�Z�A
�Ƃ�������ł��傤���H
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����łł���Ǝv���܂����C���ۂ̌v�Z�͌��\�����Ȃ�悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�y�������� �ɂ��ā^20.07.18�n
Pell�@�������@�ɂ��ā@�ڍׂȋL�q���@�q�����܂����B
�@�@
�@�@�����@�o�Ȑ���́@�i�q�_�@���@���@�Ƃ肠���ā@����
�@�@ ���Ђ��@�������Ȃ�@�䋳�����������B
�@�@
�@�@���ł����@���́@�o�Ȑ���́@�S�Ắ@�i�q�_��
�@�@ �@���o(�@���ڂ���)��
�@�@�@�@�@ ����@�������@�肢�܂�;
�@�@�@�@�@
4 x^2 - 20 x y + 4 x + y^2 + 14 y + 1 = 0
�����m��ҁn�F�A�����肪�Ƃ��D�u���������_9��/�������v��^�X�k�o�Łv�u���������_�u�`�^���ؒ厡���^��g���X�v�Ȃǁu������������_�v�Ƃ����薼�̏����ɂ͏o�Ă��邱�Ƃ�����.������̖��́C�`����W�������邱�Ƃ���n�߂Ă͂ǂ��ł��傤���D���̐l�̖��������C�ɂ͂Ȃ�Ȃ���
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^20.07.17�n
���A���^�C���ɁZ�A�~�����Ă����̂Ŕ��ɕ��ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ ���ډ~�̔��a�ɂ��ā^20.07.17�n
���Ⴂ�����Ă����݂����ŁA���ډ~�̔��a�����߂���3��ڂ̓����́A3�ł����B��蕪��Ȃ̂ŁA�Q�l�ɂȂ�܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�g�����i���͑�j�ɂ��ā^20.07.16�n
���w���ł��I��������ł����A���Ƃ��S����ł��܂����I
��肪�����Ă������̑u���������o�C�ł��I�����������₷���A�ƂĂ��ǂ����ł����I
�R���r�l�[�V�����͓��ӂɂȂ�܂����I
�{���ɂ��肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����������ɂ��ā^20.07.16�n
(1)�̊��S�����`�ł��邽�߂̕K�v�\�������̏ؖ��ŕK�v���͂����̂ł����C�\�����������Ƃ���ʼn���̎��������g���ĂȂ��悤�Ɏv���̂ł����ǂ��ł����H(A)��(B)�̏��������C�܂�F(x,y)�����S�����`�̉��ɂȂ��Ă���Ƃ������Ƃ͎����Ă��܂����CP_y=Q_x�Ȃ��(A)��(B)�����藧�Ƃ������Ƃ������Ȃ��Ə���P_x=Q_y�̏\���������������ƂɂȂ�Ȃ��̂ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���F�̕����ŏ����Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[�ʐ��ɂ��ā^20.07.16�n
�O�������Ɠ��ň͂܂ꂽ�ʐς����߂�����͂���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D��������邱�Ƃ͂ł��܂����C�o���ē��Ă͂߂邾���Ƃ����g�����͂��Ȃ��ł��傤�D
�@���Ȃ킿�C2�����ɂ���
(x-\beta)dx=-\frac{a}{6}(\beta-\alpha)^3\]&chf=bg,s,fff6f6)
����@
�͂悭�g���̂Ō����Ƃ��ďd�邱�Ƃ͂���܂��D���̉�����ŁC3�����ɂ���
^2(x-\beta)dx=-\frac{a}{12}(\beta-\alpha)^4\]&chf=bg,s,fff6f6)
����A
���������Ƃ��鋳�������邩������܂��C������o���Ďg���Ƃ����̂�i�߂鋳���͏��Ȃ��ł��傤�D
�@���āC3����
&chf=bg,s,fff6f6)
��2����
&chf=bg,s,fff6f6)
�Ƃň͂܂ꂽ�}�`�̖ʐςł��낤���C3����
&chf=bg,s,fff6f6)
�ƂP����
&chf=bg,s,fff6f6)
�ň͂܂ꂽ�}�`�̖ʐςł��낤���C���ǂ̂Ƃ���
-f(x)\}dx\]&chf=bg,s,fff6f6)
�̌`�̌v�Z�ɋA�����܂��D
���}�̏ꍇ�C
(x-\beta)(x-\gamma)dx\]&chf=bg,s,fff6f6)
(x-\beta)(x-\gamma)dx\]&chf=bg,s,fff6f6)
�ƌ����v�Z���s�����ƂɂȂ�܂����C���̂܂ܒP���v�Z���Ă��悭�C�@�A�Ɉ�����
(x-\beta)(x-\gamma)&chf=bg,s,fff6f6)
(x-\beta)(x-\alpha%2B \alpha-\gamma)&chf=bg,s,fff6f6)
^2(x-\beta)%2B(\alpha-\gamma)(x-\alpha)(x-\beta)&chf=bg,s,fff6f6)
�Ȃǂƕό`���邱�Ƃ��ł��܂��D����ł����Ȃ�̌v�Z�ʂɂȂ�C���ʂ͊o������悤�ȊȒP�Ȏ��ł͂Ȃ��悤�ł��D
�g���Ȃ���ʂł͎g��Ȃ����ē�����O���
�����m��ҁn�F�A�����肪�Ƃ��D���t�V�т����Ă���킯�ł͂���܂���D�g���Ȃ���ʂŕ��C�Ŏg���āC���s���铚�Ă��|���Ď̂Ă�قǂ��邩�璍�ӂ��q�ׂ����̂ł��D
�@���̃y�[�W�̐擪�ɏ����Ă��܂����C

�̂Ƃ��ɁC
,\hspace{3}q=det(A)&chf=bg,s,fff6f6)
�Ƃ��邠��Ď҂̓��Ă����ɑ����D
D={}�̌`�������Ă�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̑O�̃y�[�W�ƌ�̃y�[�W�ɂc���g�����\�L������܂����C���̖{���Ɗւ��̂Ȃ��R�����g�̏������ɒ�����t����Ӗ����s��
���m�ʂ̕ł���̎���ɑ���n[���ډ~�̔��a�ɂ��ā^20.07.15�n
���ډ~�̔��a�����߂�3��ڂ̓������Ԉ���Ă����B�������́A2���[�g2���Ƃ������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���ډ~�̔��a�����߂�3��ځv�Ƃ������͂Ȃ���ˁD���3�ɂ͓��ډ~�̔��a�����߂���͂Ȃ��C���1�Ɩ��Q��(3)�̂ǂ���̖����ǂ̗l�ɉ����̂��q�ׂȂ��ƁC�����w�E���Ă���̂��ʂ��܂���
���m�ʂ̕ł���̎���ɑ���n[�K�������ɂ��ā^20.07.14�n
�ƂĂ��킩��₷�������ł��B
���Əڂ���������������̂ŁA��藝�����[�܂�܂����B
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̑Q�����ɂ��ā^20.07.13�n
�Q�����ɐϕ��萔�͓���Ȃ��ł������R�������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D��1�̗�ōl���Ă݂��

�Ƃ����ƁC

�̂悤�ɁC

�ɔC�Ӓ萔���܂܂�Ă���̂ŁA����ɕt�����牮�㉮���d�˂���ɂȂ�܂�
�r���o�߂̎���������Ƃ��ꂵ���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�r���o�߂̎����S�������Ă���̂ɁC���̂悤�Ȋ��z�������Ă���Ƃ������Ƃ́C���Ȃ��͑I�������N���b�N�����ɂ������Ă��邾��������ł��D�u�������ԍ���I�����Ă��������D�v�Ə����Ă���̂�����C�I�����Ȃ��ƍ̓_���ʂ����o�܂���D
���m�ʂ̕ł���̎���ɑ���n[�Q�i�@,16�i�@,���i�@��10�i�@�ɂ��ā^20.07.12�n
���w���ɂ��킩�邹�߂��ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�J�C�Q�敪�z�ɂ��ā^20.07.12�n
�\�S��2✕2�����\�̃J�C�Q��l��
X2=N(ad-bc)/abcd�Ŏ��ϊ��ł���Ǝv���̂ł����A���̏ؖ����ڂ��Ăق����̂ł����A�ǂ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����͂Ȃ�Ȃ��ł��傤�D����ƕ��q�̎��������Ă��CN���傫���Ȃ鎞�ɁC�J�C�Q�悪�O�Ɏ������邱�Ƃ͂Ȃ��ł��傤�D���ɂ��Ȃ��̐����������Ă��C���̋��ނ́u���w�v�ł͂Ȃ��u���w����v�̂��߂̂��̂Ȃ̂ŁC�����ɖ𗧂��̂����f�ڂ��Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^20.07.12�n
���̂������킩��₷���ď�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�̂��낢��Ȗ���ɂ��ā^20.07.12�n
���̉�����ׂ������ē��e���悭������Ȃ�����😑
�����m��ҁn�F�A�����肪�Ƃ��D���߂Ɍ���悤�ȃy�[�W�ł͂Ȃ��D�ǂ��炩�ƌ����C�܂Ƃ߂̃y�[�W�ł�
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�s�����̏ؖ��j�ɂ��ā^20.07.12�n
2ⁿ��n!�̏ؖ�������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��Dn��4�ɂ�����2n>n!�͐��藧���Ȃ�����i����������ł͂Ȃ�����j�ؖ��͂ł��܂���D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^20.07.11�n
�ƂĂ��킩��₷���ł��B
��̓����Ɛ������悹�Ă���������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̉��ɁC�قړ�������ɑ��������܂��D�I�������N���b�N����C�̓_���ʂƉ�����o�܂��D���Ă��邾���ł͏o�܂���D
�X���marchscanty����^20.07.10�n
�w�t�E���E��x�̗�ł͓��{��̕��͂��̂肠���Ă��܂����i�u��������X�C�J�v��u��͔����v�Ȃǁj�A���w�Ɨ��ꂷ���Ă��ė������ɂ����̂ŁA���w�I�ȗ�̂ق����������₷�����ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D������̍��ł́C���S�ʼn����l���邩�C����M���邩�͎��R�ł��D
�Ƃ���ŁC�_���C���_�̕���Ő��w�E�Z���ȊO�̓��e�����グ��ꂽ��C�u���₾�I�v�Ƃ���������������͎̂��R�ł����C�r�o�h�i���Ў����ȂǂɎg���K�������j�ł́C�悭�o�ꂵ�܂��̂ŁC���Ў��������Ȃ��悤�ł͕s���ł��D���̂悤�Ȗ�肪�o������ۂƂ������Ƃł�,���i�ł��܂���D
����C�x���g�̎Q���҂ɂ��Ď��̂��Ƃ��������Ă���D
���@���ꗿ���x�����l�͔������{���𒅂��Ă��炸�C�̃`�P�b�g�������Ă��Ȃ��D
���@���ҋq�͐̃`�P�b�g�������Ă���D
���@������t�łȂ��l�͏��ҋq�ł���D
�@���̂Ƃ��C���̂����m���Ɍ�������̂͂ǂꂩ�D
�P�D�̃`�P�b�g�������Ă���l�͏��ҋq�łȂ��D
�Q�D���ꗿ���x�����l�͓�����t�ł���D
�R�D���ҋq�͔������{���𒅂��Ă���D
�S�D������t�łȂ��l�͐̃`�P�b�g�������Ă��Ȃ��D
�T�D�������{���𒅂��Ă��Ȃ��l�͓��ꗿ���x����Ȃ��D
��
���̃y�[�W
�@�Ȃ��C���s����ے��ł́u���Ȃ���̐^�U�v����舵���Ă��܂��C��̑O�ɂ́C�����}���̋��ȏ��Łu�V�C���悯��Ή����ɍs���v�Ƃ�������̐^�U�𒆐S�Ɂu���Ȃ���̐^�U�v�������Ă��܂������C���̋��ނ̕M�ҁi���j�́C���̋��ȏ����ƂĂ��C�ɓ����Ă��܂��D�i�u1=3�Ȃ��2=4�����藧�v�Ƃ������́C�u�V�C���悯��Ή����ɍs���v�Ƃ�������������₷���j
(6.3)�̌v�Z����s�ږ����́A-c/2R�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^20.07.08�n
�������́��_�Ƃ����Ƃ���́��̒��������ė~�����ł��B
���͂ƂĂ��킩��₷���A�g���܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނɂ́C�����������Ƃ͏����ĂȂ��̂ŁC���̘b�����Ă�����̂��ʂ��܂���D���̋��ނɏ����Ă���̂Ȃ�C������������l�Ɏ��₵�Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^20.07.08�n
���2�ł����A�̓_����������Ă��v�Z�ߒ��̉��o�Ă��Ȃ����߉��������Ȃ��ł��B�v�Z�ߒ��̓������ڂ��Ă�������Ə�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�v�Z�Ƃ��������N���b�N���܂��D�������ɁC���Q(1)(2)�̓q���g�Ȃ��ł��D�Ȍ�͂���܂�
���m�ʂ̕ł���̎���ɑ���n[�s��̏�@�̐����ɂ��ā^20.07.08�n
�ƂĂ��Q�l�ɂȂ�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����̑Q�����ƋɌ��ɂ��ā^20.07.07�n
���̃y�[�W�̗��Q�Ƃ͂��݂����_�@�̗��P�̖��͓����ł����A�͂��݂����_�@�̉�ł̓��͈̔͂���>=�O�ł���̂ɑ��A���̃y�[�W�̉�ł̓�>�O�ƂȂ��Ă��܂��B�����Ŏ���Ȃ̂ł����A����=������A���Ȃ��̈Ⴂ�͂Ȃ�ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�l�X�ȏ�ʂŁC�K�v�\���ɕό`����ɂ́C�͂��݂����_�@�̂Ƃ���ŏ������悤�ɁC��>=�O�Ƃ�������悢�ƌ����܂��D�������C���̃y�[�W�ł́C�u���̐��v�Ɓu���̐��v���o�Ă��āC�ǂ��炩��I�Ԃ���������C�������������悢�i0�Ƃ����ꍇ���Ȃ����Ƃ͌����Ă���j�D
���m�ʂ̕ł���̎���ɑ���n[���L���̕ό`�ɂ��ā^20.07.07�n
���̎��ό`�ł͂����Y��ł܂���
���̃y�[�W��help��ǂނ��ƂŐ����ɒB���邱�Ƃ��ł��܂����B���肪�Ƃ��������܂�
��{�I�ɐ��Ƃɍl����悤�ł����A�����@�B�I�ȕ��@�Ȃǂ�����܂����狳���Ă��������A�l�b�g�ŒT���Ă�������܂���
�����m��ҁn�F�A�����肪�Ƃ��D�e���̃q���g�ɂ���悤�ɁC�����Ɩ�������v����悤�ɂ��܂��D����͋@�B�I�Ƃ������܂��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^20.07.07�n
�W�{���������Ȃ�قǕꕽ�ς̗L�������̌������W�{���ς̗L�������̌������傫���Ȃ�܂����A�揜���̗L�������̌����͓����Ɋۂ߂�Ƃ��邱�ƂƖ������܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�u�W�{���������Ȃ�قǕꕽ�ς̗L�������̌������W�{���ς̗L�������̌������傫���Ȃ�܂����v�ƒN�����߂��̂ł����H���Ȃ��������v���Ƃ������Ƃł����H���Z�̋��ȏ��ɂ͂��̘b�͏����ĂȂ��ł��D���̘b���C�قƂ�ǒʂ��܂���D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̒�ϕ��i��Βl�t���j�ɂ��ā^20.07.05�n
���߂Ă��̃T�C�g���{�����܂������A���������A�O���t�����₷���f���炵���ł��I
���肪�Ƃ��������܂��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A�������̐��ɂ��ā^20.07.05�n
�A������m�̐����̐ς�m�I�Ŋ����Ƃ��������̏��B
�Ō�̎��̂悤�ɂ͂Ȃ�Ȃ��Ȃ��ł����H
�ǂ����Ă����̕ό`���o���Ȃ��āA��̓I�ɐ������Ă݂��琔�������܂���ł����B
������炲�߂�Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��D�g�����������ɂȂ�͎̂����̗��Ȃ̂ŁC���Ȃ��̊ԈႢ�ł����C���̊ԈႢ�v�Z�������Ă����Ȃ��ƁC�ԈႢ���Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�K���ɂ��ā^20.07.05�n
��Ώo�Ȃ��Ǝv�����ׂ���F�B�ɋ����邭�炢�ɂȂ�܂���!�L��������܂��I���w���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l�C�s��`�̋Ɍ��ɂ��ā^20.07.04�n
���z�Ƃ���ɑ����҂���̕ԓ��ǂ܂��Ă��������܂���
��ϖʔ����ăT�C�g�����鎞�ɂ����C�����ɂȂ�܂���
���J���Ă�̂����Ǝv���܂�
���Ɩ�肠��̂��ǂ������ł��c�ԂƉJ�����ł���
�ł́A���炵�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���̔����@�ɂ��ā^20.07.03�n
������₷���ł��B���肪�Ƃ��������܂��B�����A����t���ł���̂őf���炵���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^20.07.02�n
���S�҂ł��ł���悤�Ȗ��Ŋ�b����w�Ԃ̂ɓK���Ă���Ǝv�����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̏�@�̐����ɂ��ā^20.07.02�n
�����@�������藧�������ւ̌��y���~��������
�����m��ҁn�F�A�����肪�Ƃ��D�\���������R�����Ă���܂��������܂��H�K�v�����́C������珑���ĂȂ��Ǝv���܂��H
���m�ʂ̕ł���̎���ɑ���n[�ȉ~�̕������̕W���`�ɂ��ā^20.07.02�n
�֑�
�Ƃ����P��́A�]�v�Ȃ��̂�\���P��Ȃ̂ŕs�K�ł͂Ȃ��ł��傤���H�H
����̏ꍇ�Ȃ�⑫��p�����ق����K���Ă���Ǝv���܂��B
�ׂ����Ă��߂�Ȃ����I
�����m��ҁn�F�A�����肪�Ƃ��D��͂�֑����K��ł��傤�D�u���M�̑���ɃV���[�v�y���V�����g���Ă������܂��v�ȂǂƁC����Γ��R�̂��Ƃ�t�������ꍇ�́C���ꂪ�ǎ҂ɂƂ��ĕ⑫�⒍�ӂ����y���Ƀ��x�����Ⴂ�b�Ȃ̂ŁC���ЁC�����C�َҁC�𑧂ȂǂƓ��l�ɂւ肭��������ꊴ�Ƃ��č����D�����⑫�ƕ\������ƁC�ǎ҂�������Ȃ��̂��ʏ킾�Ƒz�肳���Ƃ������ƂɂȂ�C���Ȃ茩�����Ă��邱�ƂɂȂ�D
���m�ʂ̕ł���̎���ɑ���n[�Q�i���̉��Z�ɂ��ā^20.07.01�n
�����e�X�g�ɖ𗧂��܂����I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����Œ�̕����Ő����ɂ��ā^20.07.01�n
�܂��킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D���߂Ċ��z�������l���C�������܂Řb���Ă��đ������q�ׂ�悤�ȏ�����������̂͂��������ł�
���m�ʂ̕ł���̎���ɑ���n[���ʃx�N�g���i�Q�����x�N�g���j�̐����\���ɂ��ā^20.07.01�n
�g�єł͕ʕłւ̃����N����Ă���悤�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ȏ��ł���PC�łƌg�єłŕʓ��e�Ƃ��邽�߁C�t�@�C������ς��Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[�~����C���ジ�����ɂ��ā^20.06.30�n
15�Ԃ̃T�C�R�����Ȃł��邩�Ƃ�����肪�Ȃ���ʂ�ɂȂ�̂��킩��܂���B
�i4-1�j�I��2��3�ʂ�ł͂Ȃ��̂ł��傤���B��낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����������Ă���̂ɁC�����ǂ܂��Ɏ��₵�Ă���̂͂悭�Ȃ��ł��D�R�̗��͂S�ł��C�܂�5�̗���2�ł��D
y = sin�|1 2x
�����m��ҁn�F�A�����肪�Ƃ��D���Z�ł͂��̖��͈����Ă��܂���̂ŁC����҂͂P�W�Έȏ�ł��傤�D
�@���₪����Ƃ��́C���t�Ŏ���������ׂ��ŁC�܂��C�ԈႢ������Ƃ��͌��t�ŊԈႢ���w�E���ׂ��ŁC�ʂ肪����̖����m��Ȃ��l�ɐ���𓊂����邩�̂悤�ɁC�uy = sin�|1 2x�v�̂悤�Ȃ��̂����𓊂����Ă���̂́C�R�~���[�j�P�[�V�����\�͂ɖ�肠��ł��D�悭�����m���2�n���Q�l�ɂ��āC3��2�ɏ���������Ƃ悢�D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^20.06.29�n
100�������̓�����ł��Ă���̂ł����A���ꂽ�R�b�v�̊G���o�Ă��܂��B�o�O���Ȃł����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�łU�N�C���w�Z�łR�N�ԏ��@��̎g�������K���̂ŁC�R�C�V�C�O�C�B�Ȃǂ̂Q�o�C�g�����i�����C���ȁj�͐��l�ł͂Ȃ������ŁC�R���s���[�^�ɐ��l�ƔF������邽�߂ɂ́C���p�����i�P�o�C�g�̐����j���g��Ȃ���Ȃ�Ȃ��̂͏펯�ł��D������C�����ϊ����O���Đ��l�œ�����悢�̂ł��D
�@�����܂ł��C�����̊O�����̌����ł����C���x�����Ă��Q�o�C�g�����œ��͂��ė���҂͂��܂��D�����ŁC2000�N����2010�N���܂őS���ł�����Internet Explorer�ł͊����ϊ����[�h�Ŏg���Ă���ǎ҂̃u���E�U�����̉�����Ƃ������u�����ϊ����[�h���O���v�ݒ肪�ł����̂ŁC������g���Ă��܂����C�����CInternet Explorer���g���Ă���l�����Ȃ��m���Ȃ��̏ꍇ��iPhone��Safari �n�̂ŁC�L���ɂ͂Ȃ��Ă��܂���D
�@���̂ق��C�ǎ҂��Ԉ���ĂQ�o�C�g�����œ��͂�����u����������ɂ���v�u�P�o�C�g�����ɏ��������Đ����ɂ���v�Ƃ����Â₩�����ڂ̗��V������܂����C20�N�O�ɂ͂��ꂪ�悢�Ƃ͍l���Ȃ������Ƃ������Ƃł��D�����CExcel�Ȃǂł��Q�o�C�g�����̐�������͂�����C����ɏ��������ĂP�o�C�g�����ɂȂ�̂Łu�֗��ȋ@�\�Ƃ��Ċ����v�̂��P�̍l�������ȁCGoogle�������͂ɂ�����Q�o�C�g�����ɂ����Ȃ�Ȃ��ꍇ���o�Ă���ȂǁC���f���ׂ��͑��l�ł��D
�@20�N�ȏ�ɂ킽���ċ��ނ�����Ă���̂ŁC�Q�o�C�g�����̎�舵���ɂ��ẮC��L�́u�������v�`�u�Â��v�܂ŕ�������܂����C�Ƃ肠�������̃y�[�W�ł͂Q�o�C�g�����͐����Ƃ��Ĉ����Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�O���_�̐}�`�I�Ӗ��ɂ��ā^20.06.28�n
�ËL�̖͂��ł́A����͂�{���Ȃ��悤�Ɏv���܂��B�����Ɨ��������ƌf�ڂ��Ăق����ł��B
�����m��ҁn�F�́H���̋��ނɏ����Ă��邱�ƂƉ��̊W���H
���m�ʂ̕ł���̎���ɑ���n[�O�p���̒�` �ɂ��ā^20.06.28�n
���������ׂ��������Ƃ��Ă��킩��₷���f�ڂ���Ă��ė����ꏏ�ɂ����ĂƂ��Ă�������₷�������ł� ���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^20.06.24�n
���3�̖��S�ĕ�����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�I�������N���b�N���ĉ����ǂ�ł��܂����H����ŕ�����Ȃ���C���ɂł��邱�Ƃ͂��邩�ȁH
�i�g�їp�͕ʕłƏ����Ă���̂ɁCPC�p�̕ł����Ă���H�H�j
���m�ʂ̕ł���̎���ɑ���n[�w�����A�ΐ����̕s��ϕ��ɂ��ā^20.06.23�n
2e^x �̐ϕ��͂ǂ��Ȃ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�����q�˂�̂��H�ƁC���^�₪����܂���

��̕ϊ������̐}�ɂ������̂Ƃ���Ȃ�ł����A�ʐς̔�ɂȂ�Ƃ����ؖ��ɂ͒�̕ϊ��������g���K�v������A�z�_�@�ɂȂ��Ă���C�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����I�ɂ́C�w�����̋t���Ƃ��đΐ��������܂��̂ŁC�ΐ����̐������ؖ�����Ƃ��ɁC�w�����̐������玦���̂�����ł��D�����e�����K�������S�̏����W�����ɕ��Ȃ��Ƃ������Ƃ����ŁC���w�Ƃ��ďz�_�@�Ƃ͂��Ȃ��ł��傤�D�ʃ��[�g�̏ؖ����@������ꍇ�ɂ́C���w�Ƃ��Ă͖��Ȃ��ł��傤�D���Ƃ��Cy=x−sin x>0 (x>0)���ؖ��������Ƃ��ɁCy’=1−cos x��1���g���ƁC

���ؖ�����Ƃ��ɁC���̘b���g���Ă��邩��z�_�@���ƌ����Ȃ����Ə����Ă���G��������܂����C��͊w�̎O�p�����w����Ȃ���Β�`�ł��Ȃ����Ƃ͂Ȃ��C�����������̉��Ƃ��Ă��邢�͋����̘a�Ƃ��ĕʓr��`�ł���̂ŁC�w��Ƃ��Ă͖��͂Ȃ��ƍl�����܂��D
�@�����C�����������������q�ׂĂ��Ă����C�Ȍ��疳�p�Ȑl���������ɂȂ��āC�z�_�@�łȂ����ǂ����������ӂ���Ƃ����p���͑厖����
�l�Ԃ̃q���g��-2����Ȃ���-3����
�����m��ҁn�F�A�����肪�Ƃ��D���_���猾���C���ނ̃q���g�ō����Ă��܂����C���Ȃ����Ȃ����̂悤�Ɏv���̂��H ���̎w���C�����w���̌v�Z�Ɋ���Ă��Ȃ���������Ȃ��̂ŁC���̌��ɍi���Č������Ă����Ƃ悢����
^2=a^2%2B 2ab%2B b^2&chf=bg,s,fff6f6)
������
^2=a^{\frac{2x}{3}}%2B 2a^{\frac{x}{3}}\cdot a^{-\frac{x}{3}}%2B a^{-\frac{2x}{3}}&chf=bg,s,fff6f6)

���������āC
^2-2&chf=bg,s,fff6f6)
�������������B
2�����̂������|�����������̖�4�ɏo�Ă���
10x^2+27xy+18y^2+17x+24y+6�ɂ��āB
=10x^2+(27y+17)x+18y^2+24y+6
18y^2+24y+6��(6y+2)(3y+2)
�Ƃ��Ă��܂��ł��܂���ł����B
���̏ꍇ�A���̂������|���ʼn����Ȃ������ꍇ�A18y^2+24y+6�̈��������ɖ߂邵�����@�͂���܂���?
�����m��ҁn�F�A�����肪�Ƃ��D���̒i�K�ŊԈ����������܂���D18y^2+24y+6=6(3y^2+4y+1)=6(y+1)(3y+1)�ł��D���ۂ̖��͂���6���ǂ̂悤�ɔz������C(27y+17)�����邩�Ƃ������ƂŁC27y������v���Ă��C17������v���Ă����ɂ͂��ǂ蒅���܂���D
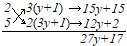
���}�̂悤�ɑg�ݍ��킹�܂��D
��������������܂���B�������Ȃ��Ƃ����Ă邩��������Ȃ��̂ŁA�����͗p�ӂ��Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D������̎��̈�����Ŋw�K���Ă���̂ł͂���܂���D����̓R���s���[�^���ނł��D�I�������N���b�N����̓_���ʂƉ��\������܂��D�������Ă��邾���ł͉����N����܂���D
���m�ʂ̕ł���̎���ɑ���n[�s���ɂ��ā^20.06.19�n
���R�����̂Ƃ���͎��܂ŏ����Ă���Ƃǂ��ŊԈႦ�Ă邩�킩��̂Ŏ����\�������Ə�����܂��D�D�D
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴆ�R�������s��̏ꍇ�C�ǂ̍s�ɉ����āC�ǂ̗�ɉ����ė]���q�W�J����̂��C�T���X�i�T�����j�̕��@�łǂ̐�����W�J����̂��Ȃǂ����͑�������C�S����ԗ�����͖̂����ł��D
���m�ʂ̕ł���̎���ɑ���n[�s��̂����ɂ��ā^20.06.18�n
3���s����~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ͍��Z�̋�����ے��ɂ������s��������Ă���Q���̐����s��܂łł��D�R���ȏ�͑�w�̐��w�ɂȂ�C�Ίp���ƃW�����_���W���`�ł̈����ɂȂ�܂��D�������Ă�̂łP�T�Ԃ��炢�ŏ�����ł��傤
���k�C���m��イ����^20.06.16�n
���̃T�C�g�����シ�邽�߂̎���ł͂Ȃ��̂ł����A�������s������낵�������������������Ɗ������ł��B�����A���̂R�����Ō����̗{��w�Z���������N�ސE���܂����B���������Ƌ��͒��w�Z�E�����w�Z�̕ی��̈�A�{��w�Z�����Ƌ��A���w�Z�����Ƌ��ł��B���Z���̍����琔�w���D���ɂȂ�A�ی��̈�̎��ɍD���ȋ��ȂɂȂ�܂����B�ސE��͌������w�Z�Ő��w�̕⏕���������Ă���A��{�I�ȓ��e���s�s�Ŏw�����Ă��܂��B���ތ�����i�߂Ă��邤���ɐ��w�̋����Ƌ����擾�������ƍl����悤�ɂȂ�܂����B�ʐM����������w�ȂǂŊw��ŒP�ʂ��擾���悤�Ǝv���܂����A�����͍��Z���̎��͐��T�A���U�a�݂̗̂��C�ł����B���V�͕��n�̂��ߖ����C�ł��B���Z���̎��̐��w�̓��e���قƂ�ǖY��Ă���̂ŁA���w�֘A�̃T�C�g��T���Ă��邤���ɁA���̃T�C�g�ɂ��ǂ蒅���܂����B���w�Ƌ����擾���邽�߂ɕK�v�ȉȖڂƂ��ē����̋��Z�n�ł��鋳��ψ���ł́u�㐔�w�v�u�w�v�u��͊w�v�u�m���_�A���v�w�v�u�R���s���[�^�v�Ȃǂ��K�v���Ɩ��L����Ă��܂��B���V�𗚏C���Ă��Ȃ������ł����A�����̉Ȗڂ���u���Ă����v�ł��傤���B���V�̗������K�v�ł��傤���B�Ƃ肠�������́A���Z�̐��w�T�{�`�A�U�{�a������Ȃ����Ă��܂��B����������������Ƃ��肪�����ł��B���Z�����Ƃ���A���ɐ\����܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���m�ɂ́C�s���{������ψ���Ŋm�F���������悢�Ǝv���܂��D���w�Ƌ����擾���邽�߂̐��w�̕K�v�P�ʁi�����ŒP�ʐ����قȂ�j�̑��ɁC�Ĕ��s����Ȃ����̋����Ƌ��Ƃ������Ƌ��X�V�̗L�����ԂȂNJm���߂Ȃ���Ȃ�Ȃ����Ƃ͑����Ǝv���܂��D
�� ��ʌ��m������^20.06.15�n
���̃T�C�g���̂��f���炵���Ɗ��S�������܂����B
�ȑO�̖���̓��e�́u�₢���v��_�����������Ă��������܂��B
�ux��0�̂Ƃ��A1/x \ne 0�ł���v�͐��������B
(�m�b�g�C�R�[�����o�͂ł���\ne �Ƃ��܂���)
���ۂɂ͐������̂ł����A�₢���ɂ���Đ������Ȃ��Ƃ�������ӊO�ɑ����Ƃ�����ۂł����B
�����m��ҁn�F�A�����肪�Ƃ��D
�����̐��k�́Cp→q�̐^�U���`���Ă��邱�̕\�̉������𗝉����Ă��܂���D���̕\�̉������ɂ́u���肪�Ԉ���Ă���C���_�����ł����Ă�p→q�͐^�ł���v�Ƃ������Ƃ������Ă���̂ł��D������C���ʂ̏ꍇ�͑S�̖���ł��C���肪�^�̏ꍇ�����ׂČ��_���^���ǂ���������悢���ƂɂȂ�܂��D
�Ƃ���ŁC�ux=0�̂Ƃ��́C1/x��0�v�͐��������Ƃ����ꍇ�ɁC���ʂ̂�����x=0�̂Ƃ��ɂȂ藧���ǂ����ׂ܂�(x��0�̂Ƃ��́C��̕\�ŐԂŎ������悤�ɐ^�ɂȂ邱�Ƃ͕������Ă��邩��ł�)�D�ux=0�̂Ƃ�1/x��0�v��x=0�̂Ƃ�����͐^�ł����C�u1/x=0, 1/x��0�Ƃ�������1/x�̒l�͑��݂��邪�C���̒l��0, 0�łȂ��v�Ƃ����咣�ɂȂ��Ă���C1/x�͒�`����Ȃ��C���Ȃ킿1/x�̒l�͂Ȃ��Ƃ��������ɔ�����̂ŁC���_���U�ł��D�ȏ�ɂ�肻�̖���͋U�ł��D
�@�S�̖���́C���ׂĂ�x�ɂ��Đ�������Ƃ��^�ŁC�P�ł��������Ȃ��Ƃ��U�Ȃ̂ŁCx=0�̂Ƃ��������Ȃ����Ƃ���U�ł��D
�悭�������F�uy=1/x�̃O���t�͑S��ԂŘA���ł���v�Ƃ������肪����Ƃ��Cx=0�̂Ƃ�������`����Ȃ��̂�����C�A�����w�`�}�������Ȃ�����U�ƌ����Ă��悢�D
[�Z���^�[���� 2008�N�x�F���w�h�E�`�i�{�����j ��Q��]�̃\�ƃ^�̓������o�܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�\�ƃ^�̓Z�b�g�ɂȂ��Ă���̂ŁC��������ł͍̓_�����C�����̉���������Ƃ��ɍ̓_����悤�ɂȂ��Ă��܂��D�\�����i�K�ł́C���������ɓ���C���ʂ͕\�������C�^�܂œ�����ꂽ�i�K�Ō��ʂ��o�܂�
���m�ʂ̕ł���̎���ɑ���n[�����_�C�O���_�̍��W�ɂ��ā^20.06.14�n
���2�i�S�j�̉���ɏo�Ă���i���m���j�Ƃ����̂́i���m���j�̂��Ƃł����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����ϊ��~�X�ł����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�m���̊�{�ɂ��ā^20.06.13�n
�U�O�ɓ͂��Ă���A�̂��v���o���Ȃ���A�������Ă��������Ă��܂��B
���āA���U�́i�Q�j�ł����A����ły���Q�̂Ƃ��A�P�ʂ�Ƃ̎��ł����A�T�C�R���ɐԁA�A�̋�ʂ����邽�߁A�Q�ʂ�@�Ǝv���A�����A�P�Q���̂P�Ƃ��܂������A�Ԉ���Ă���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D��x=1�C��y=1�C��z=2�̏ꍇ����������P�ʂ�ł�
��?�m?�^20.06.12�n
�� ��ʌ��m������^20.06.10�n
�S�̋L����������Ă��Ȃ��̂ŁA�₢���ɂ���Đ^�U���ς���Ă��܂��Ǝv���A���e�������܂����B
�ǂ��₦�U�ɂȂ�̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���������ȗ������̂͑S�̋L�������ł��D������ȗ�����Ă���ΕK���S�̋L���ł��D�Ƃ���ňꗗ�\�Ŏ����܂����悤�ɁC�u�ǂ̏ꍇ�ł��v�u���ׂĂ̏ꍇ�Łv�^�ɂȂ�̂�����C�ǂ��₦�U�ɂȂ�̂ł����Ƃ����₢�ɂ͉����Ȃ��C���̗��ĕ����Ԉ���Ă��܂��D�U�ɂȂ�ꍇ�͂Ȃ��̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�R�����̃O���t�ɂ��ā^20.06.12�n
����̐}1�`4�A���̐}3�`7�A9�̃O���t���A�����ɏd�Ȃ��������Ƃ��ĕ\������Ă��܂��B
�J�[�\���Ă�ƁA���l�ł͂�������Ȑ��O���t�ɂȂ��Ă���悤�Ȃ̂ł����c
����͎�������Google���̖��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɕ\�����ςł��D������Ƃ��͐��킾�������̂��CGoogle�̃o�[�W���A�b�v�ɔ����č���Ȃ��Ȃ����̂�������܂���D�c���䂪�����I�Ɉ�v���Ă��܂��Ă���̂ŁC�Ⴆ��y������1000�܂ł���Ƃ��ɁC��������1000�܂Ŏ��̂ʼn����������\������Ă���悤�ł��D���Ȃ�O�̂Ȃ̂�Google ChartAPI�̕��@��ǂݒ����̂Ɏ��Ԃ������肻���D�iviewwindow�̐ݒ�Œ���܂����j
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^20.06.12�n
�͎���Ƃ��Ď��g�̂ł����A���߂Ă�����Փx�̖����������Ƃ��ł��A�ۑ肪�悭������܂����B���ӂ��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�������ɂ��ā^20.06.11�n
���Z�̕��K�ŗ��p�����Ă��������܂����B
������₷�������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^20.06.11�n
�y���f���̌v�Z�K���z(2)�̗���
i^4=i2�~i2=(�|i)�~(�|i)=1
�Ƃ���̂ł���(�|1)�~(�|1)�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^20.06.11�n
���͌��݁A�ʐM����ō��Z���w���w��ł�����̂ł��B�ŋ߁A���̐��w�p�w�K�T�C�g�������āA���p�����Ă�����Ă��܂��B��肪�L�x�Ɍf�ڂ���Ă���̂ƁA�Q�[�����o�ʼnł���̂��A���̐��w�w�K�T�C�g�ƈႤ�ǂ��ł����ˁB���炭�w�K���痣�ꂽ��A���������������Ƃ�Y��Ă��A�����v�����g���Ȃ��Ă��w�тȂ������������X���[�Y�ŁA��ϕ֗��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��̒�`�ɂ��ā^20.06.10�n
���v�w�̓��发��ǂݎn�߂���log���o�Ă��܂����B�ΐ����w�̂�15�N���炢�O�ł�������Y��Ă��܂����̂ŁA�ǂ����K�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
�� ��ʌ��m������^20.06.10�n
�����܂���B������̃t�H�[�����玿�₷�ׂ��ł����B
����u(x=0�Ȃ��x=1)�܂���(x=1�Ȃ��x=0)�͐��������B�v�𓊍e�������̂ł��B���炵�܂����B
�����肪�Ƃ��������܂����B
�S�̋L����������Ă��Ȃ��̂ŁA�₢���ɂ���Đ^�U���ς���Ă��܂��Ǝv���A���e�������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�ɏ����Ă��܂����C�S��
\rightarrow q(x)]&chf=bg,s,fff6f6)
�̑S��

�́C�����Ώȗ�����܂��D���������āC
\rightarrow q(x)&chf=bg,s,fff6f6)
�Ə����C
\rightarrow q(x)]&chf=bg,s,fff6f6)
�̂��Ƃ�\���܂��D

��

�̗��ł��D�ȉ����l�D
(x=0�Ȃ��x=1)�܂���(x=1�Ȃ��x=0)�͐��������B
�����m��ҁn�F�A�����肪�Ƃ��D���_���猾���C�������D
x=0��p�Cx=1��q�ŕ\���C���̕\��������E���Ă����ƁC�ǂ̏ꍇ�ł��^�i1�j�ɂȂ�܂��D
| p | q | p→q | q→p | (p→q)��(q→p) |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
��̓I�Ȑ����Ă͂߂čl����ꍇ�́C�A�jx��0�̏ꍇ �C�jx��1�̏ꍇ �E�j����ȊO�̏ꍇ(2,3,..�Ȃ�)�ɕ�����
�A�j�̏ꍇ�C(x=0�Ȃ��x=1)�͋U�C(x=1�Ȃ��x=0)�͐^�C����������(x=0�Ȃ��x=1)�܂���(x=1�Ȃ��x=0)�͐^
�C�j�̏ꍇ�C(x=0�Ȃ��x=1)�͐^�C(x=1�Ȃ��x=0)�͋U�C����������(x=0�Ȃ��x=1)�܂���(x=1�Ȃ��x=0)�͐^
�E�j�̏ꍇ�C(x=0�Ȃ��x=1)�͐^�C(x=1�Ȃ��x=0)�͐^�C����������(x=0�Ȃ��x=1)�܂���(x=1�Ȃ��x=0)�͐^
65�̍ĕ����̎҂ŁA�Ղ��������Ɋ��ӂ��Ă���܂��B
���āA���̐��V �w���E�ΐ����̓����̃y�[�W��
��4�E�Q�̉��� y=2X/log3�@�́@y=log2X/log3�@���Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̌�_(�R�ʂ�)�ɂ��ā^20.06.09�n
�y���S�zAP:PB=5:6 CR:RA=4:5��AP:PB=6:5 CR:RA=5:4�ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̂������|�����������ɂ��ā^20.06.09�n
�S���ʼn��₠���āA�������Ă����肪����ڂȂ̂��\�������Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�X�}�z�ł̕��ɂ̓J�E���^�[���t���Ă��܂������CPC�ł̕��͂܂��̂悤�ł����̂ŁC�t���܂����D
���m�ʂ̕ł���̎���ɑ���n[�m���ϐ��C�m�����z�ɂ��ā^20.06.08�n
��w�u�t�̐������ǂ����Ă������ł����A���ɂ�������v���Ńl�b�g��������T���Ă��܂��B��肪�����邱�ƂŁA�Ⴆ�����悤�ȑ��x�ł��A�������i��ł���Ɗ����邱�Ƃ��ł��A�ƂĂ����ӂ��Ă��܂��B�u���p���v�Ɩ��ł��ē���������Ă���������ƁA�Ȃ������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂����v�͂��܂蓾�ӂł͂Ȃ��̂ŁC������͈͂ŏ����Ă��܂��D�i�����I�O�ɁC���v�͊w�̍u�`������C���w�Ƌ��̓��v�̒P�ʂ����炦���̂Ő��w�̋����ɂȂ����̂��������ȁ`�H�H�j
���m�ʂ̕ł���̎���ɑ���n[�t�E���E���ɂ��ā^20.06.08�n
�����A�����͐���������Ă���҂ŁA����ł��B���z�̊ɂ��n��i�Ⴆ�A�����O�p�B��j�𗬂��͐�͑����̏ꍇ�A�֍s���܂��B�i����������t���ŁA������x�̒������K�v�B�j�@�t�ɁA����R�n�Ŏ֍s���Ă���͐삪���鎞�A���鎞���Ɍ��z�̊ɂ����オ�������ƌ������Ƃ͏o���܂����B����������t���ł��傤���A���̉\���͂������ƍl���邱�Ƃ��\�ł��匾�����H�@�q��וF
�����m��ҁn�F�A�����肪�Ƃ��D�͐�H�w�̂悤�Ȗ{���̎��������Ă��C�M�҂͍��Z�ŕK���C�̒n�w���K���Ĉȗ��ł��̂ŁC�܂������ł��܂���D�����C���{�̉͐�ł܂������Ȑ�͂P���Ȃ��悤�Ɏv����i�ŏ��C�x�m��C������Ȃǂ̋}���ł��j�D�֍s�Ƃ͂ǂ̃��x���Ȃ̂����`���Ȃ��ƁC�Ȋw�̓y�U�ɏ悹���Ȃ��悤�Ɏv���܂��D���ʂɎԑ��̕��i�����Ă������C�召�̏�Q���Ŏ֍s������C�㗬����͂�ł����y���Œ��i�ł��Ȃ��Ȃ�ȂǁC���̗͊w�̊O�ɂ���͐�Ɠ��̎���Ƃ������̂�����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�������̕������ɂ��ā^20.06.08�n
�O���t�̊T�`�͂ǂ̂悤�ɏ����̂ł����H�K���X�̊J������킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D�}�T�Ȃǂ��g���₷����
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^20.06.07�n
�ǂ̂��炢�̎��ԑтʼn����������L�ڂ��Ē�����Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̂悤�ɍl���āC���ۂɁu�����\���v�ȂǂƋL�ڂ��Ă���y�[�W������܂����C��������ł͒N���i���w���Ȃ̂��C���Z���Ȃ̂��C�Љ�l�Ȃ̂��j�C�ǂ������g�����Łi���ƂŏK�������Ƃ̕��K�ɁC�܂��K���ĂȂ����Ƃ̊w�K�ɁC�]�g���Ɂj�g���Ă���̂����l�X�ł��̂ŁC��T�ɂ͌����Ȃ��ƍl�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^20.06.07�n
�����ʼn����͂�����邵�A�q���g��������ƂĂ�������₷���ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����^�̕������ɂ��ā^20.06.05�n
x/2+x=1/��3
��������ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D������ĉ��̌����Ɍ@�荞�߂Ή����܂����C�������ɂȂ�C�������ݓ����������̂��̂ɂȂ�܂��D�����C���̕����̎ʂ��ԈႢ������܂��D�ӂ������P�ς���ƁC�ʔ������������̖��ɂȂ�C���Z���ɏo�肷��Ӌ`�������͂���܂��D���̖��Ȃ�C�S�R�ʔ����Ȃ����ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������P�ɂ��ā^20.06.03�n
�e�X�g�O�ʼn��K���K���Ȃ���������������̂ł�����������܂���‼
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ꕽ�ρC��䗦�̐����ɂ��ā^20.06.02�n
��W�����R�O���Ƃ����A
�W�{�W�����R���ɂȂ�̂�������܂���B
��W�����ł͂R�O�����炢�̂�������ʂɂ���̂�
�W�{�ɂȂ�Ƌ}�Ɍ덷�i����j���R�����x�Ƃ������ψꉻ���Ă���̂Ɉ�a��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���S�Ɍ��藝�C���邢�̓��[�g������1�@���̂悤�Ȑ��E�̐��w�҂��F�߂Ă�����e���C����1�l�̐��`���ŃN���[��������Ƃ����̂́C��_�ł������i�I�Ȋ�Ȃ������������܂��D�悭�ǂ݂܂������H�u�W�{���ς́v�W�����Ƃ́C�����ɏ����Ă��܂��悤�Ɂu��W�c����傫�� n �̖���וW�{�����o����Ƃ��v�̘b�ŁC���x���J��Ԃ����ꍇ��"�W�{�̕W����"�ł͂Ȃ��u�W�{���ς̕W�����́C���[�g������1�@���ɏ]���v�Ə����Ă���̂ł��D���[�g�����̂P������C�W�{�̑傫����4�Ȃ�2����1�C�W�{�̑傫����100�Ȃ�10���̂P�Ƃ������Ƃł��D
�ȒP�ȗ�ōl����ƁC1,2,3,...10��10�̎���������Ƃ��C���̎����̕ꕽ�ς�5.5�C�W�����͖�2.87�ł��D���̎�������4�̕W�{��I�Ԃ�1,2,3,4�̂悤�ɏ��������̂��肪�o����C7,8,9,10�̂悤�ɑ傫�����̂��肪�o�邱�Ƃ͂߂����ɂȂ��C�قƂ�ǂ̏ꍇ���ϒl��4,5,6,7������̐����ɂȂ�܂��D���ς͂�����W�܂�Ղ��C�ɒ[�Ȓl�͏o�ɂ����D���̏ꍇ�C�W�{�̑傫��������4�ɂ��Ă���̂ŁC�W�{���ς̕W������2.87��2=��1.43�ɂȂ�܂��D����ɑ��āC�W�{�̑傫���i�W�{�̗v�f�̌��j����=100������C���̕��ϒl�́C�ꕽ�ςɂ��̂������߂��l�ɏW�܂�܂��D
���m�ʂ̕ł���̎���ɑ���n[�e���聨�������ɂ��ā^20.06.02�n
t�����1�̂̕W�{���ςɂ�錟��ō��̕s�Ε��U�̐��l���Ԉ���Ă��邩�ƍl���܂��B
�@8.81��8.753
�ƂĂ�������₷�����ɂȂ��Ă���Q�l�ɂȂ�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�P�DNo.5�̍���0.1��������Ă��܂����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�i���̉��Z�ɂ��ā^20.06.01�n
���v���O���~���O�̕����Ă���̂ł����A��i���̊���Z�̕M�Z�̎d��������܂���B���܂肪�P�ƂO�ɂȂ�͉̂����Ă��܂����A�Ⴆ�S�Q�P���Q�Ŋ���Ƃ��܂��B��������ƂS�ƂQ�͂�����ƂQ�Ŋ����̂ł����A�Ō�̂P�����͂Q�Ŋ���܂���B���ɂ��̂P���O���Ƃ��Ă��Q�ł͊���Ȃ��͂��ł��B���������ꍇ�͂ǂ���������̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D��i���̘b�͂ЂƂ܂��u���Ă����āC���w�Z�̊���Z���畜�K���܂��傤�D�q�������w�Z�̂Ƃ��Ɂu5�Ŋ����Ă�7�Ŋ����Ă�3�]��ł��������i���́j���������߂Ȃ����v�Ƃ������̐�������3�ł���̂ɁC�ǂ����̊w�Z�̒N���̐搶��38���������Ǝw�����ɏ����Ă���̂ŁC�u3��5�Ŋ���܂���C3��7�Ŋ���܂���v���ł͂���܂���Əq�ׂ��D���w�Z�ł���Ȃ��Ƃ���������C�N�������Ȃ��Ɠ����ԈႢ���o���Ă��܂��D3��5�Ŋ���Ȃ��̂ł͂Ȃ��āC����0�ɂȂ��ė]�肪3�ɂȂ�܂��D���̕\�Ŋm���߂Ă�����
| �����鐔 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ���鐔 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| �� | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 |
| �]�� | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 | 4 | 0 |
����1��5=0…1, 2��5=0…2 �Ȃǂɒ��ӂ��܂��傤�D
��4�̉���̈�ԍŌ�A2⃣�ł͂Ȃ�5⃣����Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�x���k�[�C�`�̔����������ɂ��ā^20.05.30�n
���ȏ�����ƈȏ�ɕ�����₷�����܂ł��Ă��ĂƂĂ����ʂ������܂��B�ƂĂ��@���̕��̏����ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ƂP���ϊ��ɂ��ā^20.05.29�n
�����Ɩ��̗ʂ��K�ňꎟ�ϊ��ɂ��Ă̗������[�܂�܂����B
�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���C�s��̊ȒP�ȕ��K�ɂ��ā^20.05.27�n
�s��̐ς̍��ł̕s���̎w�E�ł��B
�`���̈ꗗ�\�ɂ��Ɖ��\�̉��icolumns��(200,150,100)�ƂȂ�܂����A
����̐����ł͉��icolumns��B=(20,15,10)�ł���A�܂��E��Ꭶ�ł̕\�L��(200,100,150)��
�v�Z���ʂ����߂̕\�L�ɏ]���Ă��܂��B
���l�̓������낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�J�C�Q�敪�z�ɂ��ā^20.05.26�n
���������b�ɂȂ��Ă���܂��B
�܂��܂��A�����l�I�ɂ킩��Ȃ��̂ŁA�����Ē�����K���ł��B
�Ɨ����̌���́A�Ȃ��A�Б�����ɂȂ�̂ł��傤��?
�����A�傫���A�������ƍl���邩��ł���?
��낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂͓��v�̐��Ƃł͂���܂��C�Б�����ɂ��邩��������ɂ��邩�́C�q�ϓI�Ɍ��܂��Ă��邱�Ƃł͂Ȃ��C���͎҂����̂ǂ���ɊS������̂��C�ǂ���ׂ����̂��ɂ���Č��܂�ƍl���܂��D
�@�Ƃ���ŁC�Q�̃O���[�v�̓x���\���^�����Ă��āC�Q�̃O���[�v���Ɨ����ǂ������ׂ����ꍇ�C�u���x���̓x���\�ɂȂ�m���v�����߂Ă���̂ł͂Ȃ��C�u����ȏ�Ђǂ������m���S���̘a�v�����߂�̂��J�C2��̌v�Z�Ȃ̂ŁC�Б��ɂ���ȏ�Ђǂ������m���F���Ȃ킿�Б�����ł��傤�D
���̕\�ɂ����āCB��A�ƓƗ��ł���Ƃ��C17:3�ɂȂ�m�������߂Ă���̂ł͂Ȃ��C�u����ȏ�Ђǂ������m���v���Ȃ킿�C17:3, 18:2, 19:1, 20:0�ƂȂ�m���ɊS������C���Α����Ȃ킿�C3:17, �` 0:20�ƂȂ�m���ɂ͊S���Ȃ��͖̂��炩������C������ɂ����ƍ��������̂́H�Ƃ������ƂɊS������C�Б��ɂȂ�
X�̓��{2a x�|8a�|16
�����m��ҁn�F�A�����肪�Ƃ��D������Ȃ��̂ŋ����Ăق����Ƃ������Ƃł�����C���̂悤�ɏ����ׂ��ł��D
���̃y�[�W�̐擪(1)���1.1�ɏ����Ă���u�������Ⴂ�����ɂ��Đ�������v�Ƃ������ڂ�ǂ�ł�������
%2B(x^2-16)=(x-4)(2a%2B x%2B 4)&chf=bg,s,fff6f6)
10�Ԃւ̎���ł��B����̂Q�l����l�ƍl���āA�W�l���Q�l�R�l�R�l�ɕ�����̂ł͂Ȃ��ԈႢ�Ȃ̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�Q�l�͂P�l�Ƃ͈Ⴄ--���Z���Ɍ���Ȃ���Ȃ�Ȃ��悤�Șb�ł͂Ȃ��D
�A) [AB][��], [��][��][��], [��][��][��]←����͂R�l���̂R�g�ƌ�����
�C) [AB][��][��], [��][��], [��][��][��]←����͂R�l���̂R�g�Ƃ͌����Ȃ�
�E) [AB][��][��], [��][��][��], [��][��]←����͂R�l���̂R�g�Ƃ͌����Ȃ�
���ǃA�̌`�݂̂������ɂȂ�D
���m�ʂ̕ł���̎���ɑ���n[�����̒�`�ɂ��ā^20.05.25�n
��w�@���ł����A�p�������Ȃ�������̕��K�����Ă��܂��B�킩��₷���T�C�g�A���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^20.05.25�n
x²-1x³
�����m��ҁn�F�A�����肪�Ƃ��D���ꂪ����ł����H
&chf=bg,s,fff6f6)
��l�ɂȂ��Đ��w���Ċw�K���Ă��܂��B
�����̎��Ɏw���v�Z�����Ȃ̂ł܂Ƃ߂Ă��������ď�����܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^20.05.24�n
����ɂ��́B
��1�݂̂��ł��B
�V�^�R���i�E�C���X���s�̂��߁A�w�Z�����x�݂ƂȂ�A�w�Z���璆1���璆3�܂ł̐��w�̖��W�������܂����B(�ꉞ��B1�̐i�w�Z�ł��B ^ - ^)
�ł����A�Z�����D�����������߁A���w��❗�Ǝv���A�S�ĉ����Ă��܂��܂����A�A�A
�����āA���Z�͈̔͂��w�K���邽�߁A������n�߂����Ă��������܂����B
�ƂĂ��y�����ł�❗
�ÎZ�����Ȃ̂Ōv�Z���Ȃǂ�����K���ł��B
��낵�����肢���܂��B
�������炵�܂����B
���̂������������B
�����m��ҁn�F�A�����肪�Ƃ��D�v�Z�p���͎菑���ŕʓr�������Ă��������D�L�̊z�̂悤�ȃX�}�z�̉�ʂŌv�Z���悤�Ƃ��Ă������ł��D
���m�ʂ̕ł���̎���ɑ���n[���[�w��C�����̏����ɂ��ā^20.05.24�n
��4�ł����A1��10�̈ʂɂ�0�`9�܂ł�10��̐���������܂��̂ŁA9�E10�E9��810�̐����B�������������������Ԃ̂�111�A222�A�E�E�E�A999��9�������܂�����@810-9=801�����������ɂȂ�܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�m���̖��̕��͑�ł́C�悭�o�Ă�����{��̈Ӗ��Ɋ���Ă����K�v������܂��D�u�e�ʂ̐������قȂ���́v�Ƃ́C�P���������̂��Ȃ��Ƃ��������ƂŁC111���܂܂�Ȃ������łȂ��C112��121��211���܂܂�܂���D���Ȃ��̍l�����́C�S���������̂������܂܂�Ȃ��Ƃ��Ă��܂����C�Q�����ꍇ���܂܂�Ȃ��Ƃ����̂��u�e�ʂ̐������قȂ���́v�̈Ӗ��ł��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^20.05.24�n
35a2-13ab-12b2=(5a-4)(7a+3b)�s���������ƂȂ��Ă���܂��������Ǝv���܂�����⁉️⁉️🙄
�����m��ҁn�F�A�����肪�Ƃ��D��G�c�߂��āC�S�R���߂ł��D(5a-4)(7a+3b)���_���ƌ������Ƃ͕�����ł��傤�D(5a-4b)(7a+3b)�ł��D�������C���Ăɂ͂��炩���ߕ�������������ł���̂ŁC����ɍ����悤�ɏ����Ȃ��ƃ_���ł��傤�D�����l�����([7]a�{[3]b)([5]a�|[4]b)���Ƃ������Ƃ�������܂��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��̒l(�}����)�ɂ��ā^20.05.22�n
�ƂĂ��킩��₷���A�O�p��̊�{�͗��������B
�x�Z���̍��A�z���g�ɏ��������B
�����m��ҁn�F�A�����肪�Ƃ��D�x�Z���Ƃ������Ƃ͑�ςł��D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^20.05.22�n
�f���炵���T�C�g�ł��킩��悤�ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^20.05.22�n
f(x) = 2x; g(x) = x2; h(x) = x + 1 �̂Ƃ�,
���̍����������߂�
�����m��ҁn�F�A�����肪�Ƃ��D���₪�����ĂȂ��Ƃ������ƂɋC�t���Ă����ˁH���M�~�X�����
���m�ʂ̕ł���̎���ɑ���n[�����W���������̋������ɂ��ā^20.05.22�n
�{�錧�̍��Z�̐��w�̍u�t�����Ă��܂��B���3�̌�̗��́A���������{���I�Ȑ��������ꂽ���������Ǝv���܂��Bx��3
��{ax��2��{bx�|5��(x��2��|2x�{5)�~(x�{a�{2)�{(2a�{b�|1)x�|5a�|15�͕��f���͈̔͂ɂ����čP�����ł��邱�Ƃ��q�ׂāA���ӂ�x��1�{2i��������0������A�E�ӂɑ�����Ă�0�ɂȂ邱�Ƃ��q�ׂāAx�ɋ������܂܂�邱�Ƃ���A2a�{b�|1��0�A�|5a�|15��0�Ƃ��ׂ��Ǝv���܂��B�����A������Ŋm�F���܂����A���f���ɂ����Ă��A�����Z��|���Z�ɂ����Č���������A���邢�́A���z���͂����莦����Ă��邩�ǂ����ŁA���̍l�����́A�͈͊O�ɂ��Ȃ肤��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�k���ȉ�����ς�ł���u�������Ȃ�ȒP�ɕ�������@�F�����ߖ���p(�L�q�����Ȃ猸�_�o��)�v�Ƃ����lj��̘b�����Ă���Ƃ��ɁC�O�������b���ł��Ȃ��Ȃ��
���m�ʂ̕ł���̎���ɑ���n[��ϕ��F��{�v�Z�ɂ��ā^20.05.20�n
�����(4�̖��́A������-9�ł́A�Ȃ��ł��傤���H�ǂ����Ă�9�ɂ͂Ȃ�܂���
9�������܂�������
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă��܂�������Ȃ��Ƃ������Ƃł����H
���m�ʂ̕ł���̎���ɑ���n[���z�ɂ��ā^20.05.19�n
���z�̂��A���肪�Ƃ��������܂��B
���w�ł��o�����Ȃǂ����p�������̂Ȃ̂ł��ˁI
�m���ɏؖ��ł�����̂ł͂Ȃ��Ǝv���܂����E�E
���A��������A��낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���v�͐��w�̂悤�Ő��w�Ƃ͈Ⴄ�悤�ȥ���D
���m�ʂ̕ł���̎���ɑ���n[���z�ɂ��ā^20.05.19�n
���z���琳�K���z�ւ̋ߎ�����
np>5�@�@n(1-p)>5�ɂȂ�̂́A�Ȃ��ł���?
QC����̌���̏��ŏo�Ă��܂��B
�����A�m���Ă�����̂Ȃ�A�����Ă��������B
��낵�����肢�\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���[�Ɉ��p���Ă��܂��悤�ɁC���p��̌o�����Ȃ̂ŁC�Ȃ��Ƃ��������ɂ͍���Ȃ��ł��傤
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^20.05.16�n
��Ϗڂ���������Ă��āA�ƂĂ��Q�l�ɂȂ�܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̐��ɂ��ā^20.05.16�n
�s�x�N�g���̗ł͂Ȃ��čs���ł͂Ȃ���ł��傤��
�t���܂��R��
�����m��ҁn�F�A�����肪�Ƃ��D�P�̍s�x�N�g���C�Ⴆ��
&chf=bg,s,fff6f6)
�ɑ��āC��3��ł����s���Ƃ������Ƃ͍l���Ȃ��ł��傤�D���l�ɂ��āC�P�̗�x�N�g���C�Ⴆ��

�ɑ��āD�s���͂Q�s�ł����C�Ƃ͌���Ȃ��ł��傤�D
Excel�t�@�C����R�ɃC���|�[�g������@
�@�@���������A�S���@�\���Ȃ��̂ł����A���́H�B�i�P�j�G�N�Z���̃t�@�C������@��I��
�@(2)�@�f�[�^�Z�b�g������́�OK�̒i�K�Ői�܂Ȃ��Ȃ�B
�@�e�L�X�g�t�@�C������R�ɃC���|�[�g������@
�@�@���������A�S���@�\���Ȃ��B����
�����m��ҁn�F�A�����肪�Ƃ��D���Ă����������番����܂��悤�ɁC����Excel�̓��[�J���v���O�����Ƃ��ē���Excel20xx��O��Ƃ������̂ł��D�������p�\�ȃt���[�\�t�g�Ƃ��Ă�Excel�̂��Ƃł͂���܂���D�ǎҗl�������p�̊������Ă����₭�������D
���m�ʂ̕ł���̎���ɑ���n[�����{���|���̒l �ɂ��ā^20.05.15�n
5^2x= 3 �̂Ƃ��C5^x+5^�i-x�j�̒l�����߂Ȃ����B�̓��ĂɌ�肪����܂��B
���ӂ��悵����P^2=5^2x+2+5^�i-2x�j�ł͂Ȃ��Ap^2��5^2x�|2�{5^�i�|2x�j�ɂȂ�͂��ł���B
�����m��ҁn�F�A�����肪�Ƃ��DSNS�̐��E�ł͑傫�Ȑ��ʼn��x�������ΐ��`�ɂȂ�ƍl�����������悤�ł����C�����n�̕���ł́C�܂��������ǂ��ł��邩�C���ɂ��̂��Ƃɑ���]�����ǂ��ł��邩�Ƃ����菇�܂Ȃ���Ȃ�܂���D
^2=5^{2x}%2B 2%2B 5^{-2x}&chf=bg,s,fff6f6)
�ł��C
^2&chf=bg,s,fff6f6)
��

�ɂ͂Ȃ�܂���D
�\���ȉ��K���o����̂ŏ������Ă��܂��B
�@�ł����A�u ��x(ax+b)^n dx �v�̌`���̖�肪��������܂���ł����B���̌����Ƃ����Ǝv���܂����A���K�������̂ŗp�ӂ��邱�Ƃ͏o���Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɁC�Ȃ��ƌ����Ȃ��悤�Ȃ̂ŁC�Ƃ肠��������lj����܂��D���ڂ̕��ނ����̃y�[�W�ł悢���ǂ����͕ʓr�l���܂��D
���m�ʂ̕ł���̎���ɑ���n[�ڐ��̕������ɂ��ā^20.05.14�n
�ȉ~�̓�����y=0�̂Ƃ��̏ꍇ�킯��Y��Ă��܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�ȉ~�����łȂ��C�o�Ȑ��ł��������ł�y=0�̏ꍇ�́C�������������W������`����Ȃ��̂ŁC���̓��Ă̒��ɂ͓����Ă��܂���Dy=0�̏ꍇ�́Cx���ɐ����Ȓ����Ƃ���,�����ڂŁu�ڂ̎q�Z�v���番�������(x=a)�����ʂƂ��Ĉ�v���܂��D
���m�ʂ̕ł���̎���ɑ���n[���f���̌v�Z�ɂ��ā^20.05.13�n
��ϕ��ɂȂ�܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^20.05.10�n
���7(1)�̉���ŁCB���N����Ȃ��̂ł���CC���N����Ȃ��Ǝv���܂��B�Ȃ̂ŁCA�CD�̂ǂ��炩�ɂȂ�Ǝv���܂��B�����͕ς��܂���
�����m��ҁn�F�A�����肪�Ƃ��D����͌����邪�C�����ς��Ȃ��Ƃ����̂�������D
���m�ʂ̕ł���̎���ɑ���n[�����W���������̋������ɂ��ā^20.05.10�n
���̂��Ƃɂ��̉�@��p�������K��肪�����āA�ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ŗL�l�C�ŗL�x�N�g���̋��ߕ��ɂ��ā^20.05.09�n
���̂�����ō������Ēu���čs����Ă��܂����̂ŁA�ƂĂ�������܂����B
�@����Ȃ̂ł����A�u�ŗL�l�C�ŗL�x�N�g�������߂�ɂ́v�̍��ɌŗL������det|A-��E|=0�Ƃ���܂��B����͖l�̒P�Ȃ鏑���ԈႢ��������܂��A���Z�łƂ����m�[�g�ɂ�det|��E-A|=0�Ƃ���܂����B����ł��������������Ă���̂ŏ��̎��������Ă��܂��Ă��܂��B�Ȃɂ�������₷��������Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��Ddet|A-��E|=0��det|��E-A|=0�͑S�������ł��傤�D�Ⴆ�C�Q���̐����s��̏ꍇ
(1)
(d-\lambda)-bc=0&chf=bg,s,fff6f6)
�ƂȂ�̂ɑ��āC(2)
(\lambda-d)-bc=0&chf=bg,s,fff6f6)
�͂ǂ���ŏ����Ă������ł��D�i�ǂ���̏������ł��悢���ƂɂȂ��Ă���C���݂Ɏ茳�̎Q�l���ł́C12����(1)��4���C(2)��8������܂��D
�@��������̈Ⴂ���o��̂́C����Łu�ŗL�������v�������Ă���ꍇ�ł����C�Ⴆ�C3���̏ꍇ�̌ŗL��������
(1)

�ƂȂ���

�̍ō����̌W�������ɂȂ�C(2) �ł͕��������ɂȂ�܂��D�i���҂ɂ���āC�����̔łɂ���ĕς��C�ǂ���ł��悢�j
�@���̍��Z�ł͍s����K��Ȃ��͂��Ȃ̂ŁC�ŗL���������K�����Ƃ́C���a�̎���̘b���ȁH
���<<6>>��[1][3]�̂Ƃ��Ɂu�������Ȃ��v�Ƃ��āA�Ȍ�v�Z����Ă��܂���B
�����̎w���𗘗p���Čv�Z�𑱂���K�v���Ȃ��̂͂Ȃ��Ȃ̂ł��傤���H
P=2�̂Ƃ��́Aq=3/2�Ar=5/2�ɂȂ�͂��ł��B
��������3/2�̊K��Ȃǂ͒�`����Ă��Ȃ��̂ł��傤���A
�g�ݍ��킹�⏇��ł�n��r�ɕ����𗘗p���邱�Ƃ͒�`����Ă��Ȃ��̂ł��傤�B
���A�{���Ȃ�炩�̐��l�A���������ɂ͎��ۂɂ͑��݂���̂ł͂Ȃ��ł��傤���H
�����ɐ����Ă��Ȃ����痘�p�ł��Ȃ�������Ȃ��Ƃ����l���������܂����[�������܂���B
�����I�ɂ����炭���̑����������ۂɓW�J����ƁA���O3�̌W�����u80�v�ƂȂ�̂ł��傤���A
���ꂪ����ߒ��ŁA������������u�K��������͏���͗��p�ł��Ȃ����珜�O�v�Ƃ����悤�ȍl�������̗p����Ă���̂��A�Ȃ�ƂȂ��[�������܂���B
 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D�{�������ɑ��Ă̂ݒ�`���������C�����ȊO�ɂ��K�p���Ă�����Ƃ��āC�Ⴆ�K���}���i���}�j�Ȃǂ�����܂����C
���̃y�[�W�C��舵���͓���Ȃ�܂��D
������킩��₷���A���ɍl�����̏��łƂĂ��������Ă��܂��B
�@����ł����A���̏��������Ƃ͖����̂ł�����蕶�Ɂu�ŒZ�Łv���������͂������肷���ł��傤���H������������e��n�̍l�����ł͉����Ȃ��̂ł͂Ƃ�����₵�Ă���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���炩�̌`�ʼn���肷��ꍇ�͐����Ȃ��ƕ�����悤�ɂȂ��Ă���K�v������܂�
���m�ʂ̕ł���̎���ɑ���n[�x���k�[�C�` �����������ɂ��ā^20.05.07�n
�덷���ł����Ae^{-x^2}dx��e^{-t^2}dt�ƕς��������ǂ��Ȃ��ł����ˁH�C���e�O�����̉���x������̂Łc
�����m��ҁn�F�A�����肪�Ƃ��D���i=�O�j�ɂ���͉̂e�����܂���
���m�ʂ̕ł���̎���ɑ���n[���Ғl�ɂ��ā^20.05.07�n
��7�̉����20����13�����X��ɏオ���Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����i�������܂Ƃ߁j�ɂ��ā^20.05.05�n
���3��(3)���\������܂���B
�����m��ҁn�F�A�����肪�Ƃ��DFirefox�Ō��Ă�����悤�ł����C�������Firefox����͐���ɕ\������܂��H�H
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^20.05.03�n
(x+y)���+5(x+y)
�̉�������������܂���B������(x+y)(x+y+5)�ł����B
�ix+y)(x+y)+5(x+y)...�������番����܂���B
�����m��ҁn�F�A�����肪�Ƃ��Dx+y=A�Ƃ�����(x+y)2+5(x+y)=A2+5A
A��������o����A(A+5)
����x, y�ɖ߂��ƁC(x+y)(x+y+5)
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^20.05.01�n
���K�ɖ𗧂��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�����z�\�����ϒl,���U,�W�����ɂ��ā^20.05.01�n
�m�����v������Ȃ����Ă���Љ�l�ł��B
�킩��Ȃ���������̂ŁA�����Ă��������B
�w���̍�����m�����v�����ł��B
��낵�����肢�v���܂��B
1�y�[�W�ځA�E���̉��̉ӏ��ɂȂ�܂��B
���̂悤�ɂ��ĉ��ϐ��ŋ��߂����ϒlu�́C���̂܂܂ł͖{�����߂�ׂ����ϒl�Ƃ͈قȂ��Ă��܂����C���̂悤�Ɍ��̕ϐ��ɖ߂����Ƃ��ł��܂��D
u=x−42.5/5�@�́@x=42.5+5u
�E���̎����A�킩��܂���B(���K���z�̕W�����̎��ɑ������Ă��܂����c)
�@���̎��łȂ��A�ϊ��ł���̂ł��傤��?
�E�܂��A5�Ŋ����Ă���̂́A�Ȃ��ł���?
�@�x���Ŋ���̂ł͂Ȃ��A�f�[�^���Ŋ���̂͂Ȃ��ł���?
��̂قǁA��낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̉��ɐԂƐ̃O���t�Ő���������C����ɂ��̉��ɘg�t���Ő���������܂��悤�ɁC5�͊K�����ł��D����l�����ɔ��ɊȒP�ȗ�Ŏ��ۂɂ���Č���Ε�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^20.04.30�n
�ƂĂ��A�����T�C�g�Ȃ̂ŁA�������悢�Ƃ������܂����B
���肪�Ƃ��������܂����B
������Ă��������A���ꂩ����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����ƈ�ʍ��i����`�j�ɂ��ā^20.04.30�n
�Ƃł������Əo����̂��ǂ��@�V���h�~�ׂ̈ɗ��p���Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R�_���꒼����ɂ�������ɂ��ā^20.04.29�n
������₷���āA���₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^20.04.27�n
�l�I�ɂ͂������y���������̂ł����A����̃{�^���������ɂ͏���������݂���̂��ǂ����Ȃ̂���������ɂ��������悤�Ɏv���܂��B6��ڂ��������Ƃ������ƕ\�����o�ăr�b�N�����܂����B
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D�u���͊��ł��o�܂��v�Ə����Ă���s���ŁC����Ȃ��o��悤�ɂȂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^20.04.23�n
�@���̕��ő�Ϗ������Ă��܂��D
���Ӓv���܂��D
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^20.04.23�n
��肪�p�^�[���ʂɂ��܂��܂Ƃ߂��Ă��܂��B�O���_�ɂ��ė������[�܁B
��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^20.04.21�n
�ŋߌl�I�ȕ��̂��߂Ɏg���n�߂܂����B��ς����b�ɂȂ��Ă���܂��B���i�U�j�ł����A��x6�ł͂Ȃ�x9�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D

�́u�w���@���v�ɂ��

�ɂȂ�Ƃ������Ƃ͑��v�ł���
�M�T�C�g�̂������Ń\���o�[���g���Ƃ���Ȃ��Ƃ��ł���Ƃ����̂��킩��܂����B
�ŏ����@��(4)��E44��=SUM(E2:E41)�Ƃ����ӏ���
F44��=SUM(F2:F41)�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m��錧/����������/20.04.15�n
��Ԃɂ����钼���̕��������11�ŕʎ���ł̉�p(3,-1,6)�͂ǂ̗l�ɓ��ěƂ߂�ꂽ���l�Ȃ̂������ĉ������B
�����m��ҁn�F�A�����肪�Ƃ��D(3,-1,6)�͓_�̍��W�ł͂Ȃ��C�x�N�g���̐����ŁC���̓������͉���ɏ����Ă���܂��D
&chf=bg,s,fff6f6)
�̐����������ƂȂ�悤��

�Ƃ���ƁC
&chf=bg,s,fff6f6)
��Ԃɂ����钼���̕��������P�P�ŁA���(s+2,3s-1,4)+p(3,-1,6)=(2t-2,2,-t+1)���������Ƃō��W�擾�̌v�Z���o���邱�Ƃ����������ĖႢ�܂������܂��悭�菇�̌����������Ă��Ȃ��̂ŁAp(3,-1,6)�̓��o�ߒ������肢�������܂��B
 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D���11�Ƃ��Ȃ��̎���ɑ��铚���Ƃ́C�ʂ̖��ł��D(s+2,3s-1,4)+p(3,-1,6)=(2t-2,2,-t+1)���������Ƃ�(3,-1,6)�����Ƃ͖��W�ł��D�i���}�Q�Ɓj
�������̐}�́A�ߐ��Ɛ������͊܂ފ܂܂Ȃ��ŕ����܂����A�N�����߂����̂Ȃ�ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�N���Ƃ����₢�ɂ͈Ӗ����Ȃ��C���߂��Ƃ����p��ɂ��Ӗ����Ȃ��ł��傤�D���Ƃ��C�f�J���g���g���n�߂��Ƃ������Ƃ�������C���Ȃ��͂��̋L�����g���悤�ɂ��܂����C����Ƃ��f�J���g�ȊO�̐l��������g��Ȃ��悤�ɂ��܂����D�����̌��ʂɉ����e�����Ȃ��C���w�␔�w�j�ł��̂��Ƃɂ��Ď��₳��邱�Ƃ��C����@����Ȃ���C�g�����̂Ȃ��b�ł��D
���ɁC�����̋L���̓j���[�g�����ƃ��C�v�j�b�c���̂Q�̋L��������Ƃ����悤�ȏꍇ�ł��C���̋L�����j���[�g����C�v�j�b�c���u���߂��v�Ƃ������Ƃ͂Ȃ��ł��傤�D�ނ炪�g���n�߂��L�����֗�����������㐢�̐l�������^�������Ďg���悤�ɂȂ����Ƃ������Ƃł��傤�D
�����������ŁC���{�ł͂قƂ�ǂ̋��ȏ���Q�l���ł��̏��������g���Ă���̂ŁC����ƈقȂ�L��������Ɏg���Ɠ��ĂƂ��ĔF�߂��Ȃ��ꍇ������܂��D
�������C���{�̍��Z��
x��3�Ə������Ƃ��C��w�⑼�̍��ł�

�̂悤�ɓ�������{���ŏ����悤�ȏK���̈Ⴂ�͂���܂��D
��2 �ŁAabc���猩�āA�Ⴆ�Aa��4�̑I���������ƍl����ƁA�S�̂ŁA3��4��̑g����������ƍl���ẮA�Ȃ������Ȃ��̂��̐���������܂���A
�����m��ҁn�F�A�����肪�Ƃ��D�ua��4�̑I���������v�Ƃ����̂͊ԈႢ�ł��傤.���̉E�́u�ނ���������v�̉���Q��
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^20.04.01�n
���4��
9y^2+30y-24=(3y-2)(3y+12)
�ƈ�����������ƁA�����Ȃ��Ȃ��Ă��܂��܂��B
���������āA9y^2+30y-24=3*(3y-2)(y+4)�Ƃ���킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�v���(0)�Ԃɏ����Ă��܂��悤�ɁC���ʈ������������ł������Ă������Ƃ́C�u�������|���ȑO�v�̑O��ł��D
���m�ʂ̕ł���̎���ɑ���n[�ꍇ�̐��E�m���C�Z���^�[��������ɂ��ā^20.03.28�n
����(2)��
�@��or��and��and�k�͍l���Ȃ��Ă�����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���t�V�т����Ă���̂ł͂Ȃ��u�N���v�u�ǂ̂悤�Ɂv�i�ނ̂��𐳊m�Ɏw�肵�Ȃ���Ίm���̌v�Z�͂ł��܂���D�܂��C����(2)�Ƃ����Ă����͂Q����܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕�����3�i�}��ϐ��j�ɂ��ā^20.03.27�n
�����܂���‼�Ȃ��A�O�Ղ����߂�Ƃ��Ax,y�̎���x,y�ȊO�̑��̕ϐ��͏����̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D1�s�ڂɏ����Ă���܂��悤�ɁC�u���w�Z�ȗ��C�O���t�C�����E�Ȑ��̕������́Cx��y�̎��ŕ\�킵�Ă���D�v�v����ɁC���̕ϐ����g��Ȃ����Ƃ��̊W�����~��������ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�~�̌�_��ʂ�~�E�����̕������ɂ��ā^20.03.26�n
�}�`�����������ĕ�����₷�������ł��B���ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���w�T.�����ƍ����ɂ��ā^20.03.26�n
������₷����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌��� I �ɂ��ā^20.03.24�n
b��2��|b+3342=0�@���̉������������ĉ�����
�����m��ҁn�F���̉��ɂ���u�������߂�v���O�����v�ɐ������������߂C���͏o�܂��D
���m�ʂ̕ł���̎���ɑ���n[�Ȑ��ň͂܂ꂽ�}�`�̖ʐςR�ɂ��ā^20.03.24�n
���P�́i�Q�j�̋��߂�ʐς̉ӏ��̉E�ӓڂ̑O�̕�����+�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�i��j−�i���j�Ƃ������ƂŁC���ۂ̌v�Z�́C�u�����v�ƂȂ��Ă���E���ɏ����Ă���ʂ�ł�
���m�ʂ̕ł���̎���ɑ���n[�Q�����̍ő�l�E�ŏ��l�i��Ԃ�����ς��ꍇ�j�ɂ��ā^20.03.22�n
���2�̍ŏ��l�̉���� (�A �ɂ��āA���� t>0 �Ə����Ă��邽�߁A0��t<1 �̕������������Ȃ��A�u0�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���䐔��̘a�ɂ��ā^20.03.20�n
k��1�ł͂Ȃ���(5�Ƃ�6�Ȃ�)�����������܂��Ă��āA��k�̓��̎�����B�̖��W�ɏo�Ă����̂ł����A���̎������߂�Ƃ��ɏ�̓�������̘a�̐�Ă͂߂悤�Ƃ��Ă��A�������s����ŋ��߂��܂���ł����B�Ȃ̂ł��̃T�C�g�Œ��ׂĂ݂ē��Ă͂߂Ă݂Ă��킩��܂���ł����B���̃T�C�g�̍�җl�����̕��͂�ǂ�ł���̂Ȃ�ǂ������̎��̉��@������������������K���ł��B
�����m��ҁn�F�A�����肪�Ƃ��Dk
2�̘a�́C��������ł͂Ȃ�
(2n%2B 1)}{6}\]&chf=bg,s,fff6f6)
���g���܂��D������C�Ⴆ�Ύ��̂悤�Ɍv�Z���܂��D
-(1^2%2B\cdots%2B 4^2)&chf=bg,s,fff6f6)

���l�ɂ���

���s�U�t�ɂ���
�\�߁Z���Z���Z�ƕ��ׂĂ����āi���͐ԋʁj���̂悤�ɔԍ��D��u���܂����B
(1)(2)�Z(3)��(4)�Z(5)��(6)�Z(7)(8)
(1)�`(8)��8���̔ԍ��D�̂���2�����c��̐ԋ�2�ɂ����Ă���ƍl���܂����B
8Ⅽ2��28�ʂ�
�ƂȂ��Ă��܂��܂��B
�ǂ��ɊԈႢ������̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��́u�܂����l�����v�ɑ����āC�����Ă݂�ƁC�������̂�����������Ă��܂��D�ԋʁ���u���g�����Ƃ��āC(1)(3)��(1)(4)�͓����ł��D���l�ɁC(1)(5)��(1)(6)�C…(5)(7)��(5)(8)�C(6)(7)�C(6)(8)�Ȃǂ��������̂ł��D���̂悤��28�g�̓��œ������̂�18�g����̂ŁC���ۂɂ�10�g�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[2�����̍ő�E�ŏ��ɂ��ā^20.03.19�n
�ƂĂ��킩��₷���Ċy���������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̕��s�����C���������ɂ��ā^20.03.19�n
�킩��₷��
�ł�����������Ɠ���������������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƌW���̕����ɂ��ā^20.03.18�n
���肪�Ƃ��������܂����B�ƂĂ�������₷�������ł��B�Q�l�ɂ����Ē����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p��̑��݊W�ɂ��ā^20.03.14�n
�O�p��̑��݊W�i�Q�j�̃R�̖��Atan^2A-sin^2A�ɓ���������I�Ԗ��Ɋւ��āA��
tan^2Asin^2A�ɂȂ��Ă���̂ł�������͌�肾�Ǝv���܂��B���Ɖ̂ǂ��炪�ԈႢ�Ȃ̂��͂킩��܂����������肢���܂��B�����Ԉ���Ă����炷���܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴄ�y�[�W�̘b��ʂ̃y�[�W�Ŏ��₷��̂͂悭�Ȃ��ł��D������T���Ă����̓��e���Ȃ�����ł��D

������

����������

�������������Ȃ�
�Q�l�ɂȂ�܂����B
���Z���w�Ȃp�Y���݂�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ғl�ɂ��ā^20.03.11�n
��Ɋ��Ғl�̉�������Ă�������o�����ق��������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��DQuestion Oriented Method �Ƃ����̂������āC���w���K�̏ꍇ�ɁC���߂ɖ����N���Ă�����������߂ɂ͂ǂ�Ȓm�����K�v�ɂȂ�̂����l�������邱�Ƃɂ��C�h���̂Ȃ����}�őދ��ȍu�`������邱�Ƃ��ł��܂��D�\���m�����S���Ȃ��ꍇ�́C�����y�[�W�ɗv����̂�����C��ɓǂ߂悢�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�d�������ɂ��ā^20.03.11�n
���̕łɂ͖�肪�Ȃ��̂ɁA���j���[�ɖ߂�Əd������̕������Ԃ��Ȃ��Ă��āA�����ア���ƂȂ��Ă���̂ł����Ȃ�łł����H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��Ԃ𑪒肵�C�P���ȓ��u=���s���v�Ȃ�Ԃŕ\�����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^20.03.10�n
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂƒ����ɂ��ā^20.03.10�n
�߂��Ⴍ���ᕪ����₷�������ł��B���Ȃ݂ɍ��P�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̌v�Z����Z���^�[��������ɂ��ā^20.03.11�n
�����Ƃ��S�R�Ⴄ�̂ɂȂ��Ă��肵�ĉ����Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނł�Chrome�������ł��DEdge�́C�قƂ�ǂ��ׂƂ̃y�[�W�őΉ����܂���D�Ή����������\�������܂���D
(�ǐL)���������������璼�����D����Ԃ̕ԓ��Ƃ��܂������܂��C��������������
���m�ʂ̕ł���̎���ɑ���n[��Βl�L���t�̕s�����ɂ��ā^20.03.11�n
�킩��₷���̂ŁA���p�����Ē����Ă��܂��B�O���t���������]�\������܂��B
�����m��ҁn�F�A�����肪�Ƃ��DSVG�O���b�t�B�N�X�ɂ�����㉺�X�P�[���ϊ��ɂ��āCChrome, Firefox�ł͍쐬�����Ӑ}�̒ʂ�\������܂����CIE, Edge�ł͔��]����悤�ł��D���̋��ނł�Chrome�������ł��DEdge�́C�قƂ�ǂ��ׂƂ̃y�[�W�őΉ����܂���D�Ή����������\�������܂���D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^20.03.08�n
��Ԃɂ����钼���̕������́A�����ɑΉ������ď����������Ă�������̃R���s���[�^�v���O����(�S�C�T�_)�̓��͍�Ƃł̋^��_�s���_�����������郂�m�ł����B���Ɏ���ɓ����Ă��ꂽ�ł͊m�M�������Ƃ��o����l�ɂȂ�܂����B�R�����g���C�ɓ���܂����A�f���炵���\���̗l�ł��B������������ɗL��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
�������s�m�w������^20.03.08�n
���Z���wI�EA,2����(1),�����W��(1)�̃y�[�W�ɂ��āAPC��chrome�ʼn{������ƁA���ɕ\������郁�j���[�̗����A�L���ɂ���ĉB��Ă��܂��܂��B���i����͂��Ȃ��̂ł����A��a����������̂ŁA���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�L���̓��e�Əo�����ꏊ�͎����iGoogle�����߂�j�ŁC���w�E�̎����m�F�ł��܂������C�����[�h�i�ēǂݍ��݁j�ő��������܂�
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^20.03.08�n
��Ԃɂ����钼���̕������̏��ɂ���u���P�P�v�ł́g�_(1,2,3)��ʂ�Ȃ��ꍇ�ł̋��ʐ���(�ŒZ����)�� P(127/46, 59/16, 4) Q(14/23, 2, -7/23)��PQ=33/��46 �ɂȂ�h�̉o�ߒ��ɂ��āA����̂悤��"�J���}�t�ŃC�R�[���Ōq�����Ă��Ȃ�"�ꍇ�̕����x�N�g����"0�[��"�ɐ����Ă�����̉�������l�ɂ��肢���܂��B���T�̉������ł͎d�g�݂�����܂���B��������������������B���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����x�N�g����"0�[��"�Ƃ������Ƃ͏d�v�ł͂Ȃ�
(s+2, 3s-1, 4)+p(3, -1, 6)=(2t-2, 2, -t+1)�������ƁCs=35/46, t=30/23, p=-33/46�C�����(s+2, 3s-1, 4), (2t-2, 2, -t+1)�ɑ��������W�ɂȂ�
�͂����茾���C

�̌`�ɂ������l�͉��p��肪�ł��܂���D

�̌`���g�����Ȃ����Ƃ��d�v
�ƂĂ��킩��₷���Ė��ɗ����Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
��?�m?����^20.03.07�n
��Ԃɂ����钼���̕������̏��ɂ���u���P�P�v�ł́g�_(1,2,3)��ʂ�Ȃ��ꍇ
�ł̋��ʐ���(�ŒZ����)���łɂȂ�h�ɂ��āA
�ǂ̂悤�Ȍv�Z�ߒ���������x�N�g���Ƀ[�����t����������L���̗l�ȕ����\
�L�ɂ��ĉ������̂���������������������B���肢���܂��B
������������B
�����m��ҁn�F���[���\�t�g���g���Ē��ڎ��Ƀ��[���𑗂邱�Ƃ͂�߂Ă��������D��������ʏ�̑��M�v���O�����̂ݎt���܂��D
���[���\�t�g����̑��M���t����ƁC�ǎґ��i�P���ɉ���l�Ƃ��̃��x���j�ŃE�C���X�\���łȂ��l���P�l�ł��܂܂�Ă���ƁC�c��Ȑ��̃E�C���X���[���C�X�p�����[���������Ă���悤�ɂȂ邽�߁D��x�ł����̎��ԂɂȂ�Ǝ�������܂ʼn��N��������悤�ɂȂ�D
��?�m?����^20.03.05�n
���肢���܂��B
��Ԃɂ����钼���̕������̏��ɂ���u���P�P�v�ł̂��ƂŁA
�_(1,2.3)��ʂ�A�Q����x-2=(y+1)/3,z=4��(x+2)/2=(z-1)/-1,y=2
�̖���ɑ��A
���ʐ����̕������Ɛ���̂��Ǝv���܂����A
�_(1,2,3)��ʂ�Ȃ��ꍇ�ł̋��ʐ���(�ŒZ����)�́A����̍��Ƃ�(2.76, 1.283,
4)�ŁA������(0.609, 2, -0.304)��,���̋�����(4.8655845531116055)�Ƃ������Ƃ�
�Ȃ�܂����B
(https://mathcal.org/canvas/vector/suisen.html)���̃T�C�g�v�Z�V�X�e�����g��
�Đ������������Ǝv���Ă��܂��B
�����Z���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D������̓_�̍��W�́C�e�X
,Q(\frac{14}{23},2,-\frac{7}{23})&chf=bg,s,fff6f6)
��

�ɂȂ�Ƃ������Ƃ�OK�ł��D���̃T�C�g�̂��Ƃ͔�]���܂���
��Ԃɂ����钼���̕������̏��ɂ���u���P�P�v�ɂ��āA
�_(1,2.3)��ʂ�A�Q����
x-2=(y+1)/3,z=4��(x+2)/2=(z-1)/-1,y=2
�̓����͂R�ʼn���𗝉����悤�Ɠw�͂��Ă��܂��B
�����ŁA������̂Q�ӏ��̍��W���ǂ����Ă��m�肽���̂ł����������������B
�����Z�̒����ɁA���k�ł������}���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̍��̗��ɏ����Ă���悤�ɁC�u�����̖��ł́C�P�ɐ����ł���悭�C���ۂɌ�����Ă���Ƃ͌���܂���D�v������C�Q�����̍��W�ɂ͈Ӗ�������܂���D
�������s�mRac����^20.03.02�n
�ł��Ō�܂ł��I���A���̕łɐi�ލۂɁA��ԏ�̃��j���[�܂Ŗ߂邱�Ƃ��ʓ|�������̂ŁA��ԉ��Ɂu���̕łɐi�ށv������ƁA�������I�ɂȂ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���v�]�̈Ӗ��͕�����܂����C���̗��p���@���Ǘ��l�̍l���闘�p���@�Ƃ���v���܂����C�ǎ҂̗��p���̂ƈ�v���Ȃ��ē���v�f������܂��D���Ȃ킿�C���ނ̖ڎ������ǂ��ď��ɂ���Ă����ǎ҂͏��Ȃ��āCGoogle, YAHOO!�Ȃǂ���ʂ̃y�[�W�֒��ڗ���l�������C�u���̃y�[�W�Ƃ͉����v�����߂��Ȃ��C���������Ȃ��l�������D���ފǗ��l�̑����猾���Γr���Œlj������Ƃ��ɁC�u���̃y�[�W���ς��v�Ƃ������Ƃ�����܂��D
�@PC�œǂ�ł���ꍇ�C���̂悤�ȏꍇ�ɔ����āC���[�ɃT�u���j���[������Ă���C�O��̂[�W�ɒ��ڍs����悤�ɂȂ��Ă��܂��D�X�}�z�̏ꍇ�́C���j���[�̐擪�ɃT�u���j���[��������悤�ɂȂ��Ă��܂��D
�@Google, YAHOO!�Ȃǂ���ʂ̃y�[�W�֒��ڗ�����C�u���E�U�̏�[�Ɂu�ی삳��Ă��Ȃ��ʐM�vhttp://�Əo�܂����C���j���[�����ǂ��Ă���C���Ɍx���Ȃ���https://�ƂȂ�Ⴂ������܂��D
���m�ʂ̕ł���̎���ɑ���n[ �x�N�g���̒�`�C�傫���C�����ɂ��ā^20.03.01�n
���͂܂����w���Ȃ̂ł����A��������Ɨ����o���܂����B�ƂĂ����ɂȂ�܂����B���ꂩ������̃T�C�g���g�p�����Ă��������܂��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W���̕\�킵���ɂ��ā^20.02.23�n
�u�����̏W����2�̕\�������ł��܂��v�ł͂Ȃ��A�u�����̏W����2�ȏ�̕\�������ł��܂��v�̂ق����ǂ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�W���̕\�����Ƃ��ẮC(1) �O���I�L�@�F{1, 2, 3} �̂悤�ɏW���̗v�f�������@�C (2)�@����I�L�@�F{ x | x> 0} �̂悤�ɏ����Ɨv�f���g���ĕ\�����@�̂Q������܂��D(2)���g���ǂ�ȏW���ł��\���܂����C�����C�L�����̂悤�ɂP��ɕ��ׂ邱�Ƃ̂ł�����̂�(1)�̏��������ł��܂��D������C���Ȃ��̍l���͊Ԉ���Ă���C�R���邢�͂S�̕\�����͂Ȃ��C�u�����̏W���͂Q�̕\�������ł��邪�C�����̏W���̂悤��(2)�̏������������\�Ȃ��̂�����܂��v�D�������C

��

�̂悤�Ȍ�������̈Ⴂ�͕ʂ̂��̂Ƃ͐������C(1)(2)�Ƃ����{���I�ȕ\�L�@�̈Ⴂ��������ʂ�����̂Ƃ��܂��D
�オ�K�p����Ă��镶����i�قǏ�ɏオ���Ă���A�d�Ȃ��Č����܂��B���P��낵�����˂������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ�ȃu���E�U���g�����Ƃ������Ƃ͊e���̎��R�ł����CEdge���g���Ă���Α��̐l�ƈႤ�������ɂȂ�ł��傤�D�����ނł�Edge�ɍ��킹��\��͂���܂���D�����C�_����Chrome�ł���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̎w���ɂ��ā^20.02.22�n
(�w�{�`�j^�i�P�^�Q�j���Ăǂ����܂���?
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����s���ł��D
^{\frac{1}{2}}=\sqrt{x%2B a}&chf=bg,s,fff6f6)
���Ăǂ����܂���?�Ƃ͉��̎���Ȃ̂�����Ȃ��ƁH�H
�Q�̃v���b�g���P�̃O���t�ɕ`���ꍇ�A�ʏ킙���̃������͍����ɂȂ��Ă���Ǝv���܂��B�����A�Q�̂����P���E���̎��̖ڐ���ŕ`�������ꍇ�ɂ͂ǂ̂悤�ɂ���悢�̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�E�ɂ��邩���ɂ��邩�͏d�v�ł͂Ȃ��C�c���̒P�ʂ��قȂ�Q�̃O���t���d�˂ĕ`�����Ƃ͑z�肳��Ă��Ȃ��悤�Ɏv���D���Ƃ��C�~�h�����[�g�Ɠ��o���ς�2��ނ̃O���t���P��ʂɕ`���ꍇ�́C�Z�Z�N�����̑o����100���Ƃ��āC���̌�́u�䗦��\������v���ƂɂȂ�C�P�ʂ͋��ʂ́��ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̍��������ɂ��ā^20.02.16�n
���4�́A�Ō��3�s���Ȃ������Ȃ�̂�������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���̐����������Ă���̂�����C�ǂ�ł��炤���Ȃ�
���m�ʂ̕ł���̎���ɑ���n[sinx�Ɋւ���s��ϕ��ɂ��ā^20.02.15�n
�킩��₷���܂Ƃ߂��Ă���Ǝv���܂��B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���k�C��[3���������ɂ���]�^20.02.13�n
3���������ɒ萔�͊܂܂Ȃ���ł����H(��Ff(x)��3x³+5x²+7x+8��3���������ł͖����A�A�A�H)
�k��̉ߋ���2013�N�x���5(3)�̉ł́A3�����������Œu�����ɒ萔���������O��Řb�i�߂Ă���ł��A�A�A
�����m��ҁn�F��ʂɂ͒萔����������̂Ƃ��čl���܂����C���̖���F(0)=0������萔����0�ɂȂ�Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^20.02.13�n
���������J�Ȃ����łȂ��A��������������Ȃ��Ă����Ă��āA�ƂĂ����₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^20.02.12�n
������������₷�������̂Ńe�X�g�O���ɍQ�ĂĂ܂������A����o������悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^20.02.12�n
�������ł������肪�Ƃ��������܂�(^^)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ�2�ɂ��ā^20.02.11�n
���p�`���܂Ƃ߂Ă������̂�����ɗ�����[�߂Ă��ꂽ�Ǝv���B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^20.02.10�n
��莩�̂͂ƂĂ����₷���Q�l�ɂȂ�܂������A�r���̎��̓q���g�Ƃ��ďo���悤�ɂ��āA�ŏ��͎��͂ł���Ă݂悤�I�̕��������Ǝv���܂��B����������ƒ��J�ȕ����������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕������ɂ��ā^20.02.09�n
���̕łɒH�蒅�������́u���������ĉ��A�ǂ��͈̔́v��Ԃł������A������₷������ňꎞ�Ԍ�ɂ͂��̕ł̗��K����S�ĉ�����悤�ɂȂ�܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ�2�ɂ��ā^20.02.07�n
��9��(2)�̉ߒ����o�Ă��Ȃ��u2��+2��v�̌`�ɂȂ炸�A����ǂ��납�u2��+2��|a(a�͉����̐���)�v��u2��|2��c�v�̌`�ɂȂ��Ă��܂��P�[�X������܂��B������蕽��������������@���ǂ����Ă�������܂���B�R�c�͂���܂���?
�����m��ҁn�F�A�����肪�Ƃ��D���͂�����(2)�ɏ����Ă���ʂ�ł��D��������C���Ȃ��̏ꍇ�u�ǂ�Ȗ��ł������ؖ��ł���v�Ǝv������ł��܂��H�ؖ��p�̖��łȂ����C�Ⴆ�Έ��������ł�����́C���̒l�����ɂ����ɂ��Ȃ�̂ŁC�����������̏ؖ��͂ł��܂���F�m��n

�C

���ɂ킩��₷�����e�ŁA�����������X�e�b�v�A�b�v���Ă����̂Ŗ����Ȃ����g�ނ��Ƃ��ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^20.02.04�n
�������ł��ˁB
�N��ł����A�̂͏K��Ȃ��������Ƃ���������Ɨ����ł��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���̔����@�ɂ��ā^20.02.01�n
arcsec,arccsc�̔����̓��o���m�F�������Ĕq�����܂����Dy�̊���x�̊��ɖ߂��Ƃ���sin(y)��cos(y)�ŕ\���Ă���߂��Ƃ��낪�����ł͎v�����Ȃ��đ�Ϗ�����܂����D1�_�C�ɂȂ����Ƃ��낪����܂��āC�Ⴆ��arcsec�̔����̒��ŁCsin(y)=sqrt(x^2-1)/x�ƂȂ��Ă��܂����Csin(y)=sqrt(x^2-1)/abs(x)�Ƃ��āC���ʂ�1/(abs(x)*sqrt(x^2-1))�Ƃ���ق����ǂ��悤�Ɏv���܂����D�iWikipedia�⎄�̎茳�̏��Ёi�������K�����ϕ��i���������C�����o�Łj�j�ł����̂悤�ɂȂ��Ă��܂��D�j������������Ƃ��ɂ͎Q�l�ɂ����Ă��������܂��D���肪�Ƃ��������܂����D
�����m��ҁn�F�A�����肪�Ƃ��D

�̌X���͐��Ȃ̂ŁCx<0���ۂɂ�x<−1�̏ꍇ�ɕ������Ԉ��Ȃ��悤�ɁC�����̑S�̂܂���x�ɐ�Βl��t���Ă��鏑���������ł��D
�U�T�̎҂ɂ�������₷��������Ă��������đ�ς��肪�Ƃ��������܂��B
���āA���ʂƕϋȓ_�̖��P�́i�R�j�̂��h�̓����ł����A���q��(x^2+1)�͗v��Ȃ��̂ł͂Ȃ��ł��傤���H�����Ԉ���Ă����炲�߂�Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��D�s�v�ȉӏ���������܂���
���m�ʂ̕ł���̎���ɑ���n[�ݏ��]�ɂ��ā^20.01.28�n
���̃T�C�g�̍�҂����
�p���F�ԈႢ�̒���
�ݏ��]�̃y�[�W�ޑ�4��help(���)�ɂ���
�ȉ�help����
�����Ŗ������A���T�����̐ς𑫂�����������肷��
=a(a�|1)(a+1)( (a�|1)(a+2)+5 )
(�����܂Ō���)
�͐�������
=a(a�|1)(a+1)( (a�|2)(a+2)+5 )
�ł͂Ȃ��ł����H
���̂悤�ɂ��Ȃ��ƌv�Z������Ȃ��ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����藝�i���j�ɂ��ā^20.01.28�n
���̂�������
�����m��ҁn�F�A�����肪�Ƃ��D���{��͑��v�ł����H
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȑ���̘a�ɂ��ā^20.01.28�n
�y����z
(�R)
�A�j ��ʂɁC���{�P�����ׂ̗荇���Q���̍����C�������ɂȂ邱�Ƃ𗘗p����
���ƂȂ����藧�������ł��������̗��̂悤�ȏ������ɂȂ��Ă��āA�{���ɐ��藧�̂��m�F���Ȃ��ėǂ��̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����ɏؖ��������Ă�����
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^20.01.27�n
���Q�́i�W�j�̖��̓������Ⴄ�C�����܂��B�i�X�j���Ⴄ�C�����܂����A�����������Ă��Ȃ�������������܂���B���������ڂ����������ق����ł��B�X�O���̕�������ɉE���ɂ���悤�ɍl�����ق��������̂ł����H�����K�����̂Ɠ������ς���Ă���̂ő��}�ɉ��P���Ă������������ł��B��������ԈႢ�̏ꍇ������̂Ő搶�Ɋm�F���Ă݂܂��B���炢�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���������������͂���܂���D�X�O���̕�������ɉE���ɂ���悤�ɍl�����ق��������Ƃ������Ƃ͂���܂���.��������̂悤�ɂ͂Ȃ��Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�����������ɂ��ā^20.01.26�n
����炵��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^20.01.21�n
�������肪��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^20.01.21�n
�����ɂ���N���[���F�̕������ז��ł��B
���͖��ŕ����Ă����ė~�����Ǝv���܂����B
���ƁA����������Փx�̍�����肪�~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�^�U�̘b�łȂ��C�����̘b�ł��Ȃ��C�����̍D�݂̘b�����Ă�����悤�ł��̂ŁC���ɑΉ��͂��܂���
���m�ʂ̕ł���̎���ɑ���n[�M�����W���̌v�Z�ɂ��ā^20.01.20�n
��ς킩��₷���܂Ƃ߂ł����B���v�̃y�[�W�̂���Ȃ�[������]���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�ɂ��ā^20.01.20�n
�x�N�g���̘a�̃y�[�W�̖��Ȃ̂ł����A�I�����̓�i�ډE����Q�ڂ̑I�����́A�������ꂽ�x�N�g���̎n�_��(0,0)�ł͂Ȃ�(1,0)�ɂȂ��Ă���Ƃ������̂ł����A����͐������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D(0, 1)�ł�
���m�ʂ̕ł���̎���ɑ���n[�m���̃Z���^�[��������ɂ��ā^20.01.18�n
�Z���^�[���O�Ɋm�F�����������m���̖�肪�ԗ����Ă����ĂƂ��Ă����肪���������ł��I���肪�Ƃ��������܂��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D1��19���i���j�̓Z���^�[�����̐��w����������ˁD�撣���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^20.01.17�n
���⎸�炵�܂��B
�Q�̉~�̌�_��ʂ钼���̖��ŁAk��p�����������̏ꍇ�A���̉�@�͌�_���Q�̏ꍇ�̂ݗL�����ƕ������̂ł����A1�_�Ō���鎞�͂Ȃ��_���Ȃ̂ł��傤���H
�ǂ���̉~�̎����������̂ŁA�g����̂ł͂Ȃ����Ǝv���܂����B
��낵�����肢���܂��B🙇��
�����m��ҁn�F�A�����肪�Ƃ��D�������Ƃ��āu�Q�̉~��2�_�Ō����v�u�Q�̉~�͂P�_�Őڂ���v�u�Q�̉~�ɋ��L�_�͂Ȃ��v������܂��D�Q�̉~���P�_�����Ō����}�͕`���܂���D�����Łu2�̉~
=0,\hspace{5}g(x,y)=0&chf=bg,s,fff6f6)
���P�_�Őڂ���Ƃ��v
%2B kg(x,y)=0&chf=bg,s,fff6f6)
�́C2�~�̐ړ_��ʂ钼���ɂȂ�ƌ����邩�Ƃ����Ƃ������Ƃł�����C����͌����܂��D�i���ʐڐ��ɂȂ�܂��j
[II]�̗�ł́Ab��3y�ł���A-3y�łȂ��̂ɑ��āA[IV]�̗�ł́Ab��-7��-7y�ł���A7��7y�ł͂Ȃ��A�Ƃ������ӂ�����Ƃ����ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
^2&chf=bg,s,fff6f6)
��[�T]��
^2=a^2%2B 2ab%2B b^2&chf=bg,s,fff6f6)
�̌������g���ēW�J����Ƃ��́C

��

�ŁC[�U]��
^2=a^2-2ab%2B b^2&chf=bg,s,fff6f6)
�̌������g���ēW�J����Ƃ��́C

��

�ł����C����͍��Z�̋��ނȂ̂ŁC���̂��Ƃ��킴�킴�����K�v�͂Ȃ��ƍl���܂��D
���2�̉�����~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�͎O���Ȃ̂ł����ꓖ����܂��D�܂���肪����ɂȂ��Ă���̂ŁC����ɉ����t����Ƃ́C����̉���ɂȂ�܂��D����̉���̉���̂悤�ȉ��㉮�����҂���̂łȂ��C�����ł������͍l���܂��傤�D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^20.01.15�n
��ς킩��₷�������ǂ��ł�!���ނ�����Ă�����x���R���������̂��A����Ƃ킩��悤�ɂȂ��Ă��܂���!���肪�Ƃ��������܂���(^^)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���ɂ��ā^20.01.12�n
���\�N���O�ɕ��������Ƃ𗝉��������̂ɖ𗧂��܂����B65�B
�����m��ҁn�F�A�����肪�Ƃ��D��I
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^20.01.12�n
���w�����ȍ������n�o�g�̎҂ł��B�͓䗦�������Ƃ����I�уZ���^�[���w�͂ق�0�_�ł����B�ȒP�Ȍv�Z�Ȃ͒��w�܂ł͍D����������ł����A�P��������Ȃ�ɂꓦ���o���Ă��܂��܂����B�N���d�˂�ɂ�Z���E���w�̑���Ƃ������̂ɒz���Ă��܂����B
�܂��͐���3�������肩��撣���Ă݂悤�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���Ƒ��Ђ̂��Ƃɂ��ẮC�J�߂邱�Ƃ��C���Ȃ����Ƃ��C�v����ɔ�]�͂��܂���D
���m�ʂ̕ł���̎���ɑ���n[�W���̗v�f��p�����ؖ��ɂ��ā^20.01.12�n
�W���̗v�f��p���������̗��P�ɂ��Ăǂ����Ă��킩��Ȃ�����������܂��B
x=3(-m+2m)+4(m-n)�Ə�����Ƃ���܂����A�ǂ�������炻�̂悤�Ȏ��ɂȂ�̂����S���킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��Dx=3(-m+2n)+4(m-n)�ł����C�u�ǂ�������炻�̂悤�Ȏ��ɂȂ�̂��v�ȂǂƓ���l���Ă͂����܂���D�W��B��x=3(�@)+4[�@]�́u�`�ɏ�����v���̂̏W�܂肾����C3(�@)+4[�@]�̌`�ɏ����邩�ǂ��������s���낵�Ȃ���l����Ƃ������Ƃł��D
�@�܂��C�P���ɓW�J����Cx=3(-m+2m)+4(m-n)=m+2n�ɂȂ邱�Ƃ�������܂��D������Cx=m+2n��x=3(-m+2m)+4(m-n)�̌`�ɏ����܂��D���̉��ɏ����Ă��܂��悤�ɁCx=3(3m+2n)+4(-2m-n)�ł��\���܂���D�v����ɁC3(�@)+4[�@]�̌`�ɏ����邩�ǂ��������ׂĂ��邾���ŁC�����������̂悤�Ȍ���������̂łȂ��C���������ō��킹�Ă���Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�Q���s���� �ɂ��ā^20.01.07�n
���K��肪�t���Ă���̂��A�f���炵���ł��ˁB�������[�܂�܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[Sn�������W���ɂ��ā^20.01.07�n
��2�̉������3^2�Ƃ��镔���́A3n^2�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ʓx�@�̒P�ʃ��W�A���ɂ��ā^20.01.07�n
�ʓx�@�͂��߂Ēm��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃Z���^�[��������ɂ��ā^20.01.06�n
2007�N��1A�̍Ō��M�����߂�Ƃ���Aa^2�|6a�|3��0���Aa^2��6a�{3�Ƃ��A2a^2�|14a�{19�ɑ��������A��������������̂Ŋ������܂����I�����������ē��������X�L�������p���āA�����ǂ�ǂ�V���v���ɂ��Ă��������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �Q�����ɂ��ā^20.01.06�n
2006�N�Z���^�[���w1A�̑�2��́Ay��6x^2�{11x�|10��x��������a�Ay��������b���s�ړ����A���_��ʂ�����������߂���ŁA
y��6(x�{a)^2�{11(x�{a)�|10�{b�Ƃ�����Ab���|6a^2�|11a�{10�ɂȂ��Ă��܂��܂����Ba��b�̕����́A�ǂ����f������悢�̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�����Ă��������Dy=f(x)�̃O���t��x��������a�Ay��������b���s�ړ�����ƁC�V�����O���t�̕������� y−b=f(x−a) �ɂȂ�C�u�ǂ�����}�C�i�X�v���t�����Ƃ���{�ł��Dy�����v���X���t���悤�Ɂu�Y�����v��������Ă���悤�Ɍ�����̂́C�ڍ����邩��ł��Fy=f(x−a)+b
S=1+2/4+3/16+4/64�E�E�E�E�E�E+n/4^n-1�̘a���������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D���̂悤�Ȍ`�łP��P���œ�����ƁC���Ȃ��ɂ͉����͂������C�ʂ̖��ɂȂ�܂��ʂ̎�������Ȃ���Ȃ�Ȃ��Ȃ�܂��D�����ł͂Ȃ��āC�����ʼn�����͂�t���Ă��������D
���̃y�[�W������
�M�T�C�g�Œu���ϕ����ł���悤�ɂȂ�܂���!����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������3�ɂ��ā^20.01.05�n
���̕��������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���̕���v�Ƃ͉����Ӗ����Ă���̂��ɂ���ĉ��ς��܂��D�@�p��C�����̂悤�ȑ��̋���,�A���w�T�C���wA�̂悤�ȑ��̉ȖځC�B�x�N�g���␔��̂悤�ȑ��̒P���C�C���f�����ʂ̖��œ������ȊO
�@���ł��Ȃ��D�A�B���ڎ������ǂ��ĊY�����ڂ����Ă��������D�C�������̗]�n����
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^20.01.05�n
����������ĕ�����₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƒ����i�����W���j�ɂ��ā^20.01.05�n
���10�̂��ƂŎ��₪����܂��Bk��0�AD>0�Ƃ���̂́Ak�̕��������ł����ł��A�Q�̕s������������D<0�������Ƃ͂Ȃ�����Ak��0�AD>0�Ƃ��āA�͈͕t���̉�����������Ƃ������Ƃł����H
�����Ă��������I��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ȏ��̍\���ł́C�Q�������K���Ƃ��ɔ��ʎ����܂��K���Ă��Ȃ��̂����ʂȂ̂ŁC������̂悤�ȋ^�₪���蓾�܂��D
�@���ʎ����w��ł��猾���C�����������ʎ����g����̂͂Q���������ɑ��ĂȂ̂ŁCk��0�̏ꍇ�Ɍ���܂��D���ɁCk��0�ł���Ck<0, k>0�̂ǂ���ł����Ă��C�قȂ�Q�̎�������������C�O���t�͂����ƈقȂ�Q�_�Ō����…���̘b�̗���́C�قƂ�lĵ̉̎��̂悤�ɁC���ňËL���ď����܂��D
�@�Ȃ�HELP�ɏ����Ă���悤�ɁCk=0�̂Ƃ��͂Q���������ɂȂ�Ȃ��̂ŁC���ʎ�D�͎g���܂���D���̏ꍇ�͒����̃O���t�������ƌ����悢�̂ŁC�X����0�Ƃ��܂����C�����ɏ������悤�ɁC���̂悤�Ȃ��Ƃ͋N����܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�����̍ő�l�C�ŏ��l�ɂ��ā^20.01.04�n
�Z���^�[�̖��́A�����̏ꍇ�A�`���[�g������Ă��������łȂ����ƂɋC�Â��܂����B��{��U���ɏ���Ăǂꂾ�����p�������邩�H����v�Z�������ɍH�v���Ď��ԒZ�k�����邩�H
�Ȃ̂ŁA�Z���^�[�܂Ŋ�b����f���������A�c��̉ߋ���ŏ��7���z����ڎw���܂��I�����Ė{�Ԃ�7������������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̈ړ��ɂ��ā^20.01.04�n
������������������Ă�����Ă܂��I���肪�Ƃ��������܂��I���14�̉���ŁA(2, 3)��(0, �|2)�̂Ƃ���A(2, 3)��(0, �|1)�ł͂Ȃ��ł����H�ԈႦ�Ă��炷�݂܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������̈ړ��ɂ��ā^20.01.03�n
y��ax^2�{bx�{c���Ax���Ɋւ��đΏ̈ړ�����ƁAy���|ax^2�|bx�|c�ƂȂ��āA���̎��~(�|1)
y���̏ꍇ�Ay��ax^2�|bx�{c�ŁA�^�̕�����������ւ��A
���_�̏ꍇ�Ay���|ax^2�{bx�|c�ŁA���[�̕���������ւ��A�Ƃ������Ƃ͏d�v�ł��ˁI�l�I�ɁAx���ɑΏ̂ƁAx��k�ɑΏ̂��������āA�ԈႦ�܂��c�B
�����m��ҁn�F�A�����肪�Ƃ��D���ʂ͂��̒ʂ�ł����C���̋��ނ̍l�����Ƃ͏����Ⴄ�悤�ȁH���Ȃ��̏ꍇ�C���ʂ��o���悤�Ƃ��Ă��邩��C������ʂ��o���Ȃ���Ȃ�Ȃ��̂ɑ��āC���̋��ނł́C�@�����Ώ́Fx=X�Cy=−Y��������F−Y=f(X) �Ay���Ώ́Fx=−X, y=Y��������FY=f(−X) �B���_�Ώ́Fx=−X, y=−Y��������F−Y=f(−X)�Ȃǂ̂悤�ɁC�u�P�̕��@���o����v�Ƃ����l�����ł��D
���m�ʂ̕ł���̎���ɑ���n[���z�ɂ��ā^20.01.03�n
�m�����z�ɂ��āA�{���I�ȂƂ��납��������Ă��������āA���肪�Ƃ��������܂��I
���7�ɂ��āA�W������1���AV(X)����(X)^2��npq��1�ɂȂ��Ă��āA���U��1�ƂȂ��Ă��܂��H�����̊��Ⴂ�������炲�߂�Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɂ��̂悤�ɏ����Ă��܂����C(0��)�Ё�1←→(0��)V(x)=��2��1�Ȃ̂ŁC���U�Ōv�Z����ƁC�����v�Z�������ɍςރ����b�g������܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̕��s�����ɂ��ā^20.01.02�n
�Q�[���݂����Ŋy��������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̔����ɂ��ā^19.12.31�n
(4)�̉���̓�����4cos^3(x)-5cosx�ɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^19.12.30�n
���i�P�j(a�|2b+3c)2�@�̓����Ȃ̂ł����Ō�� 6ca �Ȃ̂ł��� 6ac�ł͂Ȃ̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�T�C�N���b�N�ȏ��ɂ��āC���߂ɉ�����Ă��܂��̂ŁC������ǂ�ł��������D��`�u���Ԃ��v���u���ʂ��v���u���ˁv���u�˂��v
���m�ʂ̕ł���̎���ɑ���n[�_�ƌX���������̕������ɂ��ā^19.12.29�n
������₷�������ł��B
�喞���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[3n+1���i�R���b�c�\�z�j�ɂ��ā^19.12.28�n
���߂ă��[�������Ă��������܂��R��itwitter�A�J�E���g�Fkousaki1112�j�Ɛ\���܂��B
�iG)�̂܂Ƃ߂ɂ���萔
1.253142144��������i���Ɏ�����
1111,0001,0110,1010,0100,1000,0000�ɂȂ�A�����3���|���Ă݂��
�S�Ă̌���"1"�̘A���ɂȂ邩�Ǝv���܂��B
�����̃q���g�ɂȂ�܂��ł��傤���c
������Ƃ���Ă݂���ʔ������ʂ������܂����̂œ��e�����Ă��������܂����B
���ډ������炢�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂��\���𖾂����킯�ł͂Ȃ��̂ŁC�����o�Ă��邩������܂��C���������Ă��������Ƃ��肪�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^19.12.27�n
���9�̓r�����Asin�Ɓ���2�ł͂Ȃ��Asin�Ɓ�-��2�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�s��̐��ɂ��ā^19.12.26�n
���`�㐔��40�N�Ԃ�ɍĒ��킵�Ă�����̂ł��B�V�O�}�L�������̋��ȏ��Ƃ͈Ⴂ�A�ƂĂ��Q�l�ɂȂ�܂����B��͂��̗�ɂ��ǂ�ׂ��ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����W���ɂ��ā^19.12.25�n
���3(1)�̂悤�ȏꍇ�ŁAa-h����a+3h�܂ł�4h�ω����Ă���ƍl���āA4�ł������Ă����Ȃ�4f'(a)�Ƃ���̂͂��߂Ȃ�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�Ӗ����猾�������������Ƃł����C���w�̓��ĂƂ��Ắu�������ό`����Ă��邱�Ɓv���d�v�ł��D�i�N���̓_���Ă����傪�o�Ȃ��悤�Ɂj
-f(a-h)}{h}\]&chf=bg,s,fff6f6)
�ɂ����āCb=a-h�Ƃ����ƁCh→0�̂Ƃ�b→a, a+3h=b+4h ������
-f(b)}{4h}\times 4=4\lim_{h\rightarrow 0}f\apos(b)=4f\apos(a)\]&chf=bg,s,fff6f6)
�Ƃ������ĂȂ�OK�ł�
�ǐL�@���Ғl�̃y�[�W�̖���S������ā@���j���[�ɖ߂�����@���j���[�̍��ږ��u���Ғl�v���Ԃ��}�[�J�[����Ă��܂��܂����B�@�����߂����C���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ς��ڂ̐F�����ɂ��ẮC���j���[�̉E�ɏ����Ă���܂����C������30���ȉ��Ȃ�ԁC50�����x�Ȃ�C70���ȏ�Ȃ�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[���Ғl�ɂ��ā^19.12.25�n
���Ғl�̖��U�̉��ɂ�����(�R)��(�T)������ 17/8 �ɂȂ��Ă܂��B
�C�����ĉ�����l���肢�v���܂��B
�T�O�N�߂��O�ɕ����Ȃ��������◝���ł��Ȃ����������@�J��Ԃ������Ă��܂��B
�ǂ���肠�肪�Ƃ��������܂��B�撣���ĕ����܂��̂Ł@������X�������肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�R���ȏ�̈��������ɂ��ā^19.12.25�n
X3��|(3t3��{4)X�{2t3��{4t =0�̉��������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��Dt��C�ӂ̒萔�Ƃ��āCx�̂R���������������Ƃ������Ƃł����H�����ʂ��Ԉ���Ă��܂��H���̂悤�Ȗ��͉����܂���D�i�`���I�ɉ������Ƃ͂ł��Ă��C�����������߂�i��ւ��g���āC���\�s�������Ȃ���Ȃ�Ȃ��j
�@X3��|(2t3��{4)X�{2t3��{4t =0�Ȃ�����藝���g���ĊȒP�ɉ����܂�
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l���W���̌����ɂ��ā^19.12.25�n
�K�v�����Ƃ��āAX���Q�̂Ƃ��A���ꁨ�O������Ɍ��l�����݂��邽�߂ɂ͕��q���O�Ƃ����Ӗ����悭������܂���B�����x�����̂Ƃ��A�悭����̍ō����̍��ŕ���A���q������Ƃ����e�N�j�b�N�I�Ȃ��Ƃ������̂ł����A�Ȃ���������̂��Ӗ����S�������炸�A�@�B�I�ɂ���Ă��܂��܂��B
���ɕs���Ȃ����A�������i�݂܂���B�ł�������̏����悭������悤�ɐ������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��DS��,T��,D�ЂȂǁC�ǂ̋��ȏ����g���Ă��Ă��C���̖������グ�鎞�Ԃ͂قƂ�ǂ���܂��C�������Ƃ��Ă͂ł��ē��R���x���̒���{�ł��D���̃M���b�v�́C���Z���Ƃ��Ă͂��ꂵ�������D
�@�܂��C

�̂悤�ȏꍇ�ɂ����āu�K�v�����Ƃ��āAX���Q�̂Ƃ��A���ꁨ�O������Ɍ��l�����݂��邽�߂ɂ͕��q���O�v�Ƃ�
�@���ꁨ�O�̂Ƃ���
�@A) ���q��
�L���̒l�C�Ⴆ��
1�ɋ߂Â��ꍇ�ɂ́C

�ƂȂ��āC���w�ŋ֎~����Ă��鉉�Z�C1��0�̋Ɍ������߂Ă��邱�ƂɂȂ�Cx<2�Ȃ��−∞�Cx>2�Ȃ��∞�ƂȂ�C���߂�l3�ɂ͂Ȃ�܂���D
�@B) ���q��
�����̏ꍇ�ɂ́C

�C���Ȃ킿

�ƂȂ�C���߂�l3�ɂ͂Ȃ�܂���D
�@C) ���q��
0�̏ꍇ�C���Ȃ킿

�̌`�����Ă���ꍇ�ɂ́C�����藝���l����Ε�����悤�ɁC��������q��

�Ƃ��������������Ă��邱�ƂɂȂ�C�ɂ����0�ɂȂ錴������菜�����Ƃ��ł��܂��D���̌��ʂƂ��āC���߂�l3�ɂ͂Ȃ�\���͂���܂����C�K�������Ȃ�Ƃ͌���܂���D
�@�ȏ�ɂ��CC)�̕��q��
0�ƂȂ邱�Ƃ��K�v�����i����A)B)�ł͂��߂�����j�ł��邪�C�\�������͕ʓr�������Ȃ���Ȃ�܂���D
�@C)�ɂ��C

�Ƃ����邩��C
}{x-2}=a=3\]&chf=bg,s,fff6f6)
���C

�Ƃ����Ώ\�����������������ƂɂȂ�܂��D
�@���Ɂux�����̂Ƃ��A�悭����̍ō����̍��ŕ���A���q������Ƃ����e�N�j�b�N�I�Ȃ��Ɓv�ɂ��ẮC
���̃y�[�W�����߂ɓǂ�ł��������D
�@�u����̍ō����̍��ŕ���A���q������v�Ɗo������@�����邩������܂��C���́u����ƕ��q���e�X�̍ő區�ł�����v�Ƃ����l�����������߂��܂��D��̓I�ɂ�
A) ���q�̎���������̎����̏ꍇ�C

�̂悤�ȏꍇ
x→10, 100, 1000,…�̂Ƃ��C���q�ł͍ő區

��

�Ƒ傫���Ȃ�̂ɑ��āC�����̒Ⴂ

��

�́C�قƂ�Ǎ��v�ɍv�����Ă��炸�C

�ȂǂƂȂ�܂��D
�@���̎���͕���ɂ��Ă����l�ł��D���ǁCx→���̂Ƃ��̕����̒l�́C����C���q�̊e�X�̍ő區�i�e���j�̑����ɂȂ�C�����̒Ⴂ���̍��i�q���j�͖��W�ł��D�����ŁC�u�ő區���m�ڑΌ������₷���悤�Ɂv�C��������q���ő區�ł�����܂��D
}{4x(1-\frac{5}{4x})}\]&chf=bg,s,fff6f6)
�@���̂悤�ɕό`����ƕ��ꕪ�q�Ƃ��i�@�j����1�ɋ߂Â�����C�u�ő區���m��v����C�����ɂȂ�܂��D

B) ���q�̎���������̎����̏ꍇ�C

�̂悤�ȏꍇ
}{3x^2(1-\frac{4x}{3x^2}-\frac{5}{3x^2})}\]&chf=bg,s,fff6f6)

C) ���q�̎���������̎����̏ꍇ�C

�̂悤�ȏꍇ
}{x^2(1%2B\frac{2x}{x^2}%2B\frac{3}{x^2})}\]&chf=bg,s,fff6f6)

���P(�P)�̉��̈ʒu�����Q�Ɣ���Ă��Č����炢�ł�
�����m��ҁn�F�A�����肪�Ƃ��DEdge�ȊO�̃u���E�U�œǂ�ł��������D�i������Chrome�ł��j
���m�ʂ̕ł���̎���ɑ���n[�v���O���~���O�̌�6.3�ɂ��ā^19.12.20�n
�P�O�O���E�ɂP�Q�O���P�O�O���P�O�O�����P�Q�O���P�O�O�����P�Q�O���P�O�O���ł��Ƃł��Ȃ��ł��܂������Ă܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɒE�֔���ɂȂ�悤�ł��D���C����ɂ��邩�ǂ����̔���v���O�������������Ă݂܂�
���m�ʂ̕ł���̎���ɑ���n[���Ғl�C�ϓ��C���U�C�W�����ɂ��ā^19.12.19�n
����w�Z�̑S�Z���k����25�l��ׂɒ��o�������A25�l�̐g�����ς�170cm�A�W������6cm�������B
���̎��A�S�Z���k�̐g���̕W�����̓_����l��I�����Ȃ����B
�@�������������̏ꍇ�́A�����_��3�ʂ��l�̌ܓ��A��2�ʂ܂ł���
�Ƃ�����肪����̂ł����A���̑I������
01�D 173.92cm
02�D 170cm
03�D 4.68cm
04�D 1.20cm
05�D 172.47cm
�ƂȂ��Ă��܂��B
���͂��̒��ɓ����������Ǝv���Ă���̂ł����A�i6.1237��6.12���Ǝv���Ă��܂��j
���܂����m�M�����Ă܂���B
���������Ȃ̂����m��Ȃ��Ǝv���āA�^�S�ËS�ɂ��Ȃ��Ă��܂�(��)
�搶�͂�������ɂȂ�܂��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���̐l�̖��ɂ͂��܂花���Ȃ��悤�ɂ��Ă��܂����C���l���̒ʂ�ł悢�Ǝv���܂�
���m�ʂ̕ł���̎���ɑ���n[�h�E���A�u���̒藝�ɂ��ā^19.12.18�n
n�������łȂ��L�����ł���ꍇ�ǂ��Ȃ�̂ł��傤��?
�����m��ҁn�F�A�����肪�Ƃ��D�w�K�w���v�̂őz�肳��Ă���͈͂���E�����c�_�ɂȂ�܂��̂ŁC���ʂ͂����ɂ͓��ݍ��݂܂���D
�@���Ƃ��C

�����̐��̂Ƃ��C

�̂悤�ɗL���w���͗ݏ捪�ɓǂݑւ��邱�Ƃ��ł��C
&chf=bg,s,fff6f6)
�����̐��̂Ƃ��C

�Ƃ��������ɂȂ�Ƌ��ȏ��Œ�`����Ă��邩��C����

�ɑ��āC

�Ƃ������̂��l���邱�Ƃ��ł��܂����C���O���

�̂悤�Ȏ��̒l�����߂邱�Ƃ͂ł��܂���D��w�������ɏo���ꍇ�́C�u���f��

�ɂ��āC

�����藧�Ƃ��C

�Ə����v�ȂǂƁC���̖��̒��ł̋L���̎g�������`���Ă���o�肷�邱�ƂɂȂ�܂��D�i���̂悤�ȕ��f��

�͂Q����C�Q�����ɂȂ�܂��F

�j��ʂɁC���f��

�C����

�ɑ��āC

�͂������ɂȂ�C�~����ɓ��Ԋu�ɕ��т܂��D
�@�����̓��̍ŏ��̐��̊p�ɑΉ�������̂����߂�ɂ́C���̃y�[�W�̉E���Ɂu�I�C���[�̌����v�Ƃ��ď����Ă�����̂��g���₷���C

�ƍl����悢�D
���2(2)�̉���ŁA�����Ȃ肱��܂ł̍��ڂŏo�Ă��Ȃ������A���̈�����������
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
�Ƃ����̂��o�Ă��܂������A���̌������o���Ă����ׂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���p���Ƃ��������Ƃ������Ă�����̂́C���Z�R�N���I���܂łɏK�����Ƃ̑S�����O��ɂȂ�܂��D�W�J�ƈ��������̗������܂܂�Ă�����ł��C�W�J�����C���̍��ڂ́C�W�J�̖ڎ��ɂ���܂��D

�̈������������́C
�R���ȏ�̈��������ɂ���܂��D�����ł͂悭�o�܂��D
����͒P�Ȃ銴�z�Ȃ̂ʼn͕K�v����܂���B
�ƂĂ��f���炵���T�C�g�ł��ˁB
�����ɂ��ẮAlim(h��0)((f(a+h)-f(a))/h)�͂��̂܂܂ł�(0/0)�ɂȂ��Ă��܂��v�Z�ł��Ȃ������Ȃ̂�f(x)=x^2�Ȃǂ̋�̓I�Ȋ��ɂ���Čv�Z����Ƃ����ƈȑO�ɏK���������������g���ĕ���ƕ��q��h���ł��āA�����ƒl�����܂�̂ŁA�u���w�͂Ȃ�ƍI���ł��Ă�̂��`�v�Ƃ����̂����Z�̎��̊��z�ł����B���Z�Q�N�̎��ɐԐۖ�E�g�c�m��́u���w�����v(�|����)�𐔊w�̐搶����Љ��ēǂ�ŁA���w�̖ʔ����Ɏ��̍��Ԃɓǂ݂ӂ��������̂ł����B���̌�A��-�_�@���K���ė�����ɂ�Ă��̍I��������������(�O�^�O�Ƃ����ÓI���v�Z�s�\�ȏ�����Ȃ�)���w�̖ʔ����Ƒf���炵�����ĔF�����Ă��܂��B��-�_�@�Ȃǂ͍��Z���ɂ����W�I���e�Ƃ��ĉ�����Ă͔@���ł��傤���H����ƁA���f���̂Ƃ���ŃI�C���[�̌������o���Ă��邵�A��������z���ł��邱�Ƃ������Ă���̂Ł@�@��^(����)���|�P�Ȃǂɂ��u���b�v�ŐG���Ƃ��D��S���h������悤�Ɏv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��-�͖����ł��D�I�C���[�̌����̓h�E���A�u���̒藝�̂Ƃ���ŏq�ׂĂ��܂��D
���m�ʂ̕ł���̎���ɑ���n[���ƌW���̊W�ɂ��ā^19.12.09�n
���U�EB�̍����������̉�����3�ڂ́u���i2�j�v�̗�3�ɂ��Ăł��B
�ŏ��̖�蕶�ɂ�x^3�|px�{q=0�Ə�����Ă��܂����A�������́{q�ł͖����|q�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���p�ł��邱�Ƃ͊m���ł����C���N�x�̖��ł��邩�L�ژR��̂悤�Ȃ̂ŁC���ׂ���͈͂Œ��ׂ܂������C���Ȃ�Â����炵���C�m�F�ł��܂���D���ƌW���̊W�Ɠ��e�������悤�ɁC����̕��̕������P�ύX���܂����D
���m�ʂ̕ł���̎���ɑ���n[�t�E���E���ɂ��ā^19.12.08�n
��P�@��������X�C�J
�܈ӂɂ͑�̖@�������Ă͂܂�܂������ʂɂ͑�̖@�������Ă͂܂��
�͌���܂���B
���̗�́u���b�v�̏ꍇ�̂悤�Ɉ��ʂȂ̂Ŋ܈ӂ̗�ɋ�����̂͌������
���₷���̂ł͂���܂��H
�܈ӂ͓����I�ɐ������Ă����Ԃɂ��Ă̂���(�o���^�̎��ɂ͂p���^)��
����A���ʂ͏��b�ł��������̂悤�Ɏ��ԓI�ȊW�ł��B�X�Ɂu�`����d
����v�̂悤�ɍs�ׂɊւ���L�q�͏�Ԃł͂Ȃ��̂Ŋ܈ӂƂ͕ʂɈ����K�v
������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�Ȃ�v�Ƃ����p�ꂪ���ʊW�ɂ��C�W���̕�܊W�ɂ��g���邱�Ƃ��g���āC���̂悤�Ȗ��Ő��k�ɍl����ޗ�����邱�Ƃ�����܂����C����͊�{�ł͂Ȃ��C�����܂ŗ������i��ł���̉��p�ł��傤�D
�u�������Ȃ���Ε����Ȃ��v�̑���Ƃ�Ɓu������Ƃ�������v�ɂȂ�
��͐������͂������C�ǂ��������������H
�@�������Ă���q���̏W���́C�������Ă���q���̏W���̕����W���ƂȂ��Ă���Ƃ������ƂŁC�������������͂Ȃ��D
�@���̂悤�Ɂu�Ȃ�v�Ƃ�������p����g���Ă͂����Ȃ��Ƃ��������ɂ����čs���̂ł͂Ȃ��C�ǂ���̈Ӗ��Ɏg���Ă��邩�f�ł���悤�ɂ��܂��D
�����̔ے�̐^���l�͂O�̎��A�ے�̔ے�(�m��)�B�P�̎��͂����̔ے�Ƃ��čl����̂ł���?
�����m��ҁn�F�A�����肪�Ƃ��D���{��Ƃ��ēǂ߂܂���̂ŁC�K���ɗp����Ȃ��Ŏ���𐄒肵�܂��D
�@�^��1�ŋU��0�ŕ\���Ƃ��C

��0�̂Ƃ�

��1�ɂȂ�C

��0�ɂȂ�܂��D�܂��C

��1�̂Ƃ�

��0�ɂȂ�C

��1�ɂȂ�܂��D
�@�ے肪���Δے�P��Ɠ����C�ے肪������m��ɂȂ�܂��D�q���̗V�тƓ��l�ŁC�u���̓l�R�łȂ����Ƃ͂Ȃ��v=�u���̓l�R�ł��v
���́u�R�̍����v�̉Ɖ�������肢�������ł�
�����ĂȂ������̂ŁA�ǂ��ŊԈ�������m�肽���ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����t���܂���
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝�C�{�p�����ɂ��ā^19.12.05�n
�킩��Ȃ���������������悤�ɂȂ�܂������肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���낢��Ȑ���̘a�ɂ��ā^19.12.03�n
���4��(1)�̉�����A���2��(1)�̉���ɂȂ��Ă���C�����܂��B�Ԉ���Ă����炷���܂���
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����{���|���̒l�ɂ��ā^19.12.02�n
�����b�ɂȂ��Ă܂��B���S�ɂ��āA�q���g��a+a^-1�̂Ƃ����a^x+a^-x�ł��傤���H�@a^x+a^-x�����߂�̂�(x + y)^3=x^3+y^3+3xy(x+y)���g���A(a^x/3+a^-x/3)^3=(a^x+a^-x)+3a^x/3*a^-x/3(a^x/3+a^-x/3)�Ƃ��ċ��߂܂����B�i�ώG�ł��݂܂���j
�Ɠ��������ɂȂ�܂����B
�����炾��a^2x/3+a-2x/3���v�Z�����Ԃ��Ȃ��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�������܂����D�㔼�F���̕ό`�����蓾�܂��D
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^19.12.01�n
p�Ȃ��q�̐^�U�̕\�Ƃ��̌�́u�i�ʂ́jp�Ȃ��q�v�Ɓu�˂�p�Ȃ��q�v�̈Ⴂ�ɂ��Ă̎���ł��B�Ⴆ��x�������Ƃ���Ƃ��ux��0�Ȃ��x��1�v�́u�˂Ɂv�Ə�����ĂȂ���U�̖���ƍl����̂ł͂Ȃ��ux��0�܂���x��1�̂Ƃ��^�A0��x��1�̂Ƃ��U�v�̌ʂɐ^�U�����܂�����A�ƍl����悢�̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�ɏ����Ă��܂����C�up(x)�Ȃ��q(x)�v�̂悤�ɕϐ�x���܂ނ��̂́C�u���ׂĂ�x�ɂ��āCp(x)�Ȃ��q(x)�v�̏ȗ��ƌ��Ȃ���܂��D
�@���ۂɂ́C�up(x)�����藧���Ȃ�x�ɂ��ẮCq(x)�����藧���Ă����藧���Ȃ��Ă��Cp(x)�Ȃ��q(x)�����藧�v�̂ŁC
�U→�^�F�^
�U→�U�F�^
�u���ׂĂ�x�ɂ��āCp(x)�Ȃ��q(x)�v���l����Ƃ��ɁC�up(x)�����藧��x�ɂ��āCq(x)�����藧�v���ǂ����ׂ�悢�D
�^→�^�F�^�i�����Ȃ��Ă���悢�j
�^→�U�F�U�i�����Ȃ锽�Ⴊ����_���j
�@����́C�ux��0�Ȃ��x��1�v�͋U�ł��Dx��0�ł����Ă��C�Ⴆ��x=0.5�̂Ƃ�x��1�����藧���Ȃ�����
���ǁA�W�{���ςƕW�{�䗦�Ƃ͂Ȃ�Ȃ̂����Ȍ��ɐ������镶�͂��~��������
�����m��ҁn�F�A�����肪�Ƃ��D�W�{�̕��ς̂悤�ɁC�P�Ɏ������Ε�������͉̂���s�v�ł��D�W�{�䗦�́Z�S�ɏ����Ă���܂��D�����Ă�����̂������ĂȂ��ƌ�����ƁC�����������ł��D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^19.12.01�n
���肪�Ƃ��������܂�
�킩��₷�������ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������Q�ɂ��ā^19.11.30�n
�����ɂ���͈͂�l��ŕ\���Ă����肪�������̂ł����A���ɂ���Ďg��������̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�q�˕����܂����ł��D���������ɂ́C���̔ԍ��������ȂNj�̓I�ɏ����ׂ��ł�.�܂��C���ɂ���Ďg��������Ƃ́C�ǂ��ɂł����錾�����ł�…���ɂ���ĈႤ�͓̂��R�̂��Ƃł����C���ɂ���Ăł͂Ȃ����e�ɂ���ċ�ʂ����̂����R�̂��Ƃł��D������C���ɂ���ĂƂ������t�͉����q�ׂĂ��炸�C�u��b�̊�F�����đP�����g�������Ă���̂ł����v�Ƃ�����ނ̗U���q��ɂ��������܂�
���m�ʂ̕ł���̎���ɑ���n[�����W��,�A��,�����\�ɂ��ā^19.11.28�n
�ޑ��(4)�̓�����-2f(a)f�f(a)�ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�������t�ɂȂ��Ă��܂����̂ŁC���̕������������܂���
���m�ʂ̕ł���̎���ɑ���n[�w���v�Z(�P) �ɂ��ā^19.11.28�n
�킩��₷���āA�y�������ł��܂��I
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕�����2�ɂ��ā^19.11.27�n
���ď�̕��̂Q�̖��̓�����y�|1=x�|3���x+7y�|10=0�łȂ��Ay=x-2���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���ď�̕��̂Q�̖��Ƃ������̂͂���܂���D���e�I�ɋ߂����̂́C��1 ����(�C)�ł����C(A)(B)���܂Ƃ߂ē����������Ƃ��ɁC2�Ƃ������͓̂��R�̂��Ƃł�
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^19.11.27�n
���Q�̂T��ڂł����A�������@�i�|1/2, 0) �ɂȂ��Ă��܂����A�w�@�Ɓ@�x�@�͋t�ɂȂ�̂ł͂Ȃ��ł��傤���H�@�܂�A���S�̍��W�́@0,-1/2 �Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���2��5��ڂ͂����������ł͂���܂���D6��ڂȂ玿��̈Ӗ����ʂ��܂��D�������C���S�̍��W��(0,-1/2)�ƂȂ��Ă���̂ŁC���₪�t�ł�…�����Ă��邩�璼���K�v�Ȃ��ł�
���m�ʂ̕ł���̎���ɑ���n[�����藝�E�]���藝�ɂ��ā^19.11.27�n
�Ō���ڂ���������
�����m��ҁn�F�A�����肪�Ƃ��DHELP�̏��ɏڂ��������Ă��܂��D�ڂ��������Ă�����̂��ڂ��������Ăƌ����Ă��C���`�ꔽ������Ȃ��ł��傤��
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^19.11.26�n
�킩��₷�����Ċ������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��̐��ɂ��ā^19.11.26�n
�ƂĂ����߂ɂȂ�܂����I�I
����Ŗ����c�t���������i�ł������ł��I
�v�_���A���܂��܂Ƃ܂��Ă���̂ŊG�{���o�Ŗ��ӓǂݕ������Ă��܂��B�_(^o^)�^
���̋��ގ��̂͂ƂĂ�������₷���̂ł����A�����C���X�g�Ȃǂ����Ă݂Ă͂������ł��傤���H
�C���X�g���Ȃǂ̃C���X�g�ł���A�t���[�f�ނł��̂ň��S�Ɏg�����Ƃ��ł��܂���I�I
�����m��ҁn�F�A�����肪�Ƃ��D�c�t�������ɍs��̊|���Z�Ƃ����̂́C�W���[�N�ł��傤���C10���ǂ߂ΒN�ł�������ƌ����̂́C�{���ł�
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^19.11.20�n
�ԐM���肪�Ƃ��������܂��B�������ŗ������邱�Ƃ��o���܂����B^ - ^
�����m��ҁn�F�A�����肪�Ƃ��D���������ԈႦ��Əォ��ڐ��̔����ɂƂ��Ă��܂��\���͂���܂����C�u�����������₪����v�Ƃ������Ƃɏ��Ȃ��炸���S
���m�ʂ̕ł���̎���ɑ���n[�Q�����̍ő�l�C�ŏ��l�ɂ��ā^19.11.20�n
��6�́i1�j�ŁA�ǂ�����1/2����ɂ��ďꍇ�킯�����Ă���̂��킩��܂���ł����B
�����悩�����狳���Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��Dx��t��x+1�Ƃ����悤�Ɂu��Ԃ̕����P�v�Ȃ̂ŁC���[�̒lx��1/2�̂Ƃ����E�Ώ̂ƂȂ邩��C���[�̒lx��1/2�ȉ��̂Ƃ��͍��[�ōő�ƂȂ�D���[�̒lx��1/2�����傫���Ƃ��́C�E�[�ōő�ƂȂ�
���m�ʂ̕ł���̎���ɑ���n[�����W��,�A��,�����\�ɂ��ā^19.11.19�n
���m�ʂ̕ł���̎���ɑ���n[�ꍇ�����̂܂Ƃߕ��ɂ��ā^19.11.18�n
���R�́A��蕶�ɁuA�̑܂Ƀn�[�g�̃J�[�h���Q���ƃX�y�[�h�̃J�[�h���R�������Ă���ꍇ�̐��͉��ʂ肠��܂����v�Ƃ��邩��AA�̑܂̃J�[�h�̍ŏI�I�ȃ����c�݂̂����āAA�̑܂̃J�[�h���ω����Ȃ��T�ʂ�̏o�߂�͑S���łP�ʂ�ƌ��āA�P�{�R���Q�{�Q���R���P�R�ʂ�ɂȂ�̂��Ǝv�����B
�����m��ҁn�F�A�����肪�Ƃ��D�s�������̂ƈقȂ���̂��Ԃ��ė���̂��C�R���Q�{�Q���R���P�Q�ʂ�ŁC�s�������̂Ɠ������̂��Ԃ��ė���̂��T�ʂ肾����C�S����17�ʂ�ɂȂ�܂��D
�ꍇ�̐��̐������Ƃ��āC�Γ��łȂ����̂�ɐ����Ă͂����Ȃ��D�Ⴆ�C�u���ɍ����ꍇ���܂Ƃ߂ĂP�ʂ�Ɛ�����v�u���ɍ���Ȃ����̂��܂Ƃ߂ĂP�ʂ�Ɛ�����v�̂悤�ɂ܂Ƃ߂Ă��܂��ƁC�ǂ�Ȗ��ł��ꍇ�̐��͂P�ʂ�Ɠ�����悢���ƂɂȂ邪�C����Ȑ�������q�˂Ă���̂ł͂Ȃ����Ƃ͖��炩
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^19.11.17�n
���2��(1)��[1]�̂�����
{a²�|(b+c)²}{a²�|(b�|c)²}
=(a+b+c)(a�|b�|c)(a+b�|c)(a�|b+c)
�̕���������̂ł��������ڂ������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
^2\}\{a^2-(b-c)^2\}&chf=bg,s,fff6f6)
\}\{a-(b%2B c)\}\{a%2B(b-c)\}\{a-(b-c)\}&chf=bg,s,fff6f6)
(a- b-c)(a%2B b-c)(a- b%2B c)&chf=bg,s,fff6f6)
�w���\�����@�킩��₷���ڂ��ĉ�����@���w�����Ȏ҂ɂ́@���肪���������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ������ɂ��ā^19.11.15�n
�`���[�g�̖��������Ă��Ă킩��Ȃ��Ƃ��낪����A�l�b�g�Œ��ׂĂ��邤���ɋM�a�̃z�[���y�[�W�ɂ��ǂ蒅���܂����B����A�r���������J�łƂĂ��킩��₷�������ł��B���ӂ̋C������`�������Ă������������A���P�[�g�𑗐M���܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�X�}�z�����ɂ͕ʂ̃y�[�W������Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[���K���z�ɂ��ā^19.11.13�n
�ƒ닳�t�����Ă��Đ��wB�̓��v�ɓ���܂����B���͊w���̎��A�����ɏo�Ȃ��Ƃ̗��R�œ��v�̎��Ƃ����܂����B������������邱�ƂɂȂ��č������Ƃ���A���̃T�C�g�ɍs�������܂����B�i�P�j����i�W�j�̉��K�����ė����o���܂����B���k����ɂƂ��č��i�Œ�_�����߂���Ȃǂ͐H�������ǂ��ł��傤�ˁB�Q�l�ɂ����Ă��炢�܂��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^19.11.13�n
�ƂĂ��悭������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ꕽ�ρC��䗦�̐����ɂ��ā^19.11.12�n
������Ղ����ł����Ǝv���܂����B
���Q�ŁA1.67��'��1.67��(150-145)/3�̌��ʁA�܂�W�{���ς̕ꕽ�ς���̍����Ђ̉��{�ł��邩�����߂����̂Ƃ��������ł�낵���ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�P���� 145=m−1.67��' �Ə���������ł����C���Ȃ��̗����Ɠ����Ӗ��ł�
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝...�ɂ��ā^19.11.10�n
�f���炵��web���ނł��ˁB���肪�Ƃ��������܂��B���ꂩ��܂ŗ��p�����Ă��������܂��B
�Ƃ���ŎO�p���̉��@�藝���瓱���������ɁAsin����cos���̐ς͂���̂ɘa���͂Ȃ��ł��ˁB
����͂܂�Asin���}cos��=?���Ȃ��̂́A��-��/2�Ƃ���(cos��sin�Ɉʑ�����/2�x��邩��j
?=sin���}sin(��-��/2)=2sin(��+��/2-��/4)cos(��-��/2+��/4)�ŗp������邩��ł��傤���H
����Ă����炷�݂܂���B��T�C�g�ł����Ƃ����ƕ������Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�̉E���ɁC����킵�������̈ꗗ�������Ă��܂��̂Ō��Ă��������D
(1)

→�����͂Ȃ�
(2)

→�����͂Ȃ�
(1)�ɂ��ẮC���Ȃ��̗\�z�ʂ�C�i�����������������Ⴄ�j
(1’)
&chf=bg,s,fff6f6)
\cos(\frac{\alpha%2B\beta}{2}-\frac{\pi}{4})&chf=bg,s,fff6f6)
�Ȃǂƕό`���邱�Ƃ͂ł��܂��D�i���������Ȃǂɂ�聁0�ƂȂ�������߂����Ƃ��Ȃǁj
���Ȃ��������Ȃ��̂��H�Ɛq�˂��Ă��C�O�p���̉��@�藝���瓱���������ɂȂ�����Ȃ��Ƃ��������Ȃ��D�K�v�ɉ�����(1’)�̂悤�Ɂu���v���Ƃ͂ł��܂��D
x²�̌W����a���܂܂�Ă�ꍇ�ŁA����������������Ƃ���a�͈̔͂̋��ߕ����ڂ��Ăق�����
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴆ�y���5�z�ł́Ca�̒l�����ɕς��āu����������������Ƃ���a�͈̔́v��������t���Ă���C�R���s�����Ŋm�F����悢�ł��傤�D0< a <1
���m�ʂ̕ł���̎���ɑ���n[�z�����̌v�Z�ɂ��ā^19.11.08�n
99999�c9����n(n�͎��R��)�͏z�����ɂȂ�̂Ȃ��,���ꌅ���V�̐�����7�~1,7�~2,�c7�~9�ɂ����ĉ��ꌅ��1�`9�̐����ŕ\����邩��A���ꌅ��7�̔{����,99999�c9�ŕ\���ĕK���z�����ɂȂ�̂ł����@�@���ꌅ��7�̔{����,99999�c9�ŕ\���Ȃ��ꍇ�́A�Ȃ��������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�\����Ȃ��ł����C���{��Ƃ��ĂقƂ�lj�ǂł��܂���D�u���ꌅ���V�̐����́v�u���ꌅ��7�̔{���́v������\���Ă���̂��s���ł��D�܂��C�P�̕��̒��Ɏ�ꂪ�������悤�ȏ������͓ǂ݂ɂ����̂ŁC�Z�����ɋ��ׂ��ł��D
���m�ʂ̕ł���̎���ɑ���n[�m���ϐ��C�m�����z�ɂ��ā^19.11.05�n
����ł��B
��1�̐}�̎��ۂ̕����Ɂu����͊m���ϐ��ł͂Ȃ��v�ƋL�ڂ�����܂����A�}�̉��Ɂu���̗�ł́v�Ƃ���悤�ɁA�Ӑ}�Ƃ��Ắu�����Ƃ��Ă���l�́u�܋��v�Ȃ̂ŁA���̎��ۂɂ����镔���́u�m���ϐ��v�ł͂Ȃ��Ƃ������߂ł悢�ł��傤���H
�Ⴆ�u�͂���v�ł͂Ȃ��āu4���v�ɂ��Ă��̉������A�Ƃ������l���m���ϐ�(���U�I�m���ϐ�)�Ƃ��ĂƂ炦�邱�Ƃ��\�Ƃ��������Ŗ��Ȃ��ł���ˁH
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�Ŏ��グ�Ă��鑼�̗�C�Ⴆ�Ό��t�^�iA, B, AB, O�j�C���Ƃ̂킩��₷���i�킩��₷��, �ǂ��炩�Ƃ����킩��킷��, ����, �ǂ��炩�Ƃ����킩��ɂ���, �킩��ɂ����j�̂悤��
���`�ړx�̂��̂́C�m���u�ϐ��v�Ƃ��Ă͎g�����C���l�ɂȂ��Ă�����̂������m���u�ϐ��v�Ƃ��Ďg����Ƃ������Ƃ𒍈ӓI�ɏ����Ă��܂��D
�@���ʁi�l��,�Q��,��,�듙�j,�i�W, �V, �U, �T�j,�i�C, �B, �A, �@�j�͖��`�ړx�Ȃ̂Ŗ����ł����C�i4, 3, 2, 1�j�ƂȂ�m�����e�X�i0.8, 0.1, 0.08, 0.02�j�Ƃ������ƂȂ�i4, 3, 2, 1�j�͊m���ϐ��ƌ��Ă悢�ł��傤�D
�P���������Ƃ�df(x)/dx≥0���������Ǝv���̂ł����A�Ⴆ���`�Ƃ������t��t��������df(x)/dx>0�Ƃ��Ȃ��Ƌt���̑��ݏ����Ƃ��ď\���ł͂Ȃ��̂ł͂Ȃ����Ǝv���̂ł����A�ǂ��ł��傤���B
�Ⴆ�Af(x)=3�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�́i�ɒl�͂ǂ����̖������H�j�Ɓi�Ȃ����Ă��܂��ꍇ�j�ɂ��Ȃ������������������Șb��������Ă��܂��̂œǂ�ł��������D
�@�m�ǂ̋��ȏ��ɂ�������Ă����{�n
(1) �J���(a, b)�ɂ�����f'(x)>0�Ȃ�Cf(x)�͕��[a, b]�͈̔͂ő�������D
(2) �J���(a, b)�ɂ�����f'(x)<0�Ȃ�Cf(x)�͕��[a, b]�͈̔͂Ō�������D
�@�m���Z�̋��ȏ��ɖ����I�ɂ͏�����Ă��Ȃ����C���ȂǂŎ�����Ă��鎖���n
(1') �J���(a, b)�ɂ�����f'(x)��0�ŁCf'(x)=0�ƂȂ�_���L���Ȃ�Cf(x)�͕��[a, b]�͈̔͂ő�������D
(2') �J���(a, b)�ɂ�����f'(x)��0�ŁCf'(x)=0�ƂȂ�_���L���Ȃ�Cf(x)�͕��[a, b]�͈̔͂Ō�������D
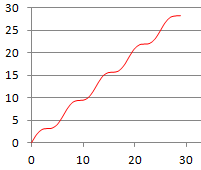
(1')�͗Ⴆ�C

���l�����ꍇ�C

�̂Ƃ�

�ł͂��邪
(x_1^2%2B x_1x_2%2B x_2^2)\gt 0&chf=bg,s,fff6f6)
�ƂȂ邱�Ƃ��番����悤�ɁC�L���̌Ǘ��_��f'(x)=0�ł����Ă��C�S��ԂŒP�������ɂȂ�܂��D
�@����ɑ��āCf(x)=3�̂悤�ɁC�u�ׂ荇���H�v�_�Ǝ���Ȃ��ŃT�{���Ă���ꍇ�if'(x)=0�ƂȂ�_���L����Ԃɖ�������ꍇ�j�́C�P�������ɂȂ�܂���
�@�܂��C���}�̂悤��

�̃O���t�ɂ����ẮCy'=0�ƂȂ�_�͖�������܂����C�L����Ԃɂ͗L�������Ȃ̂ŁC�t������`�ł��܂�
2�̐���2�_��x ^ 2 + y ^ 2 = 9�ɐG���ꍇ�Ap�����q�ƌĂ�A�����̐����i5,6�j��ʉ߂���Ƃ��Ap�����q��ʉ߂��闼���̐��̕������͉��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���x�ǂ�ł����{��Ƃ��ēǂ߂܂���D�܂��C���C���̂悤�ȏ������͍��W��\���C�_�̖��O�͂o�C�p�̂悤�ɑ啶���ŏ����܂��D
�@�ȏ�̂悤�Ȏ����C���͂����čޗ��������g���Ď����g�ݗ��Ă�Ɓux ^ 2 + y ^ 2 = 9�̂Q�̐ڐ����_�i5,6�j��ʂ�Ƃ��C�����Q�̐ړ_��ʂ�ɐ�(polar line)�̕������� 5x+6y=9�ɂȂ邱�Ƃ��ؖ����Ă��������v
�i�ؖ��j
2�̐ړ_�̍��W��(p, q), (r, s)�Ƃ����ƁC�ڐ��̕������͊e�X�Cpx+qy=9, rx+sy=9�ɂȂ�D���ɂ����Q�̐ڐ����_(5, 6)��ʂ邩��C5p+6q=9…(1), 5r+6s=9…(2)�����藧�D
(1)(2)��2�_(p, q), (r, s)�� 5x+6y=9�̕������������Ƃ������Ă��邩��C2�_(p, q), (r, s)�͒��� 5x+6y=9��ɂ���D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^19.10.30�n
���q�ǂ������Ă����Ƃ���Ŗ��V(4)�A�܂�܂ƊԈ�������������Ă��܂��܂����B�����̃~�X���������Ɠ����������������̂őI��������☓�B�n�b�ƋC�t���Ă�蒼���ė����ł��܂����B�ǖ�B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �h�E�����K���̖@���ɂ��ā^19.10.27�n
�S�̖������̖���̐����́A�G���ł킩��ɂ��������B
�l�I�ɂ́A�͂����ׂāA�����Ȃ��Ƃ��P�A�Ɠǂ݉����A�����̗ʉ��q�ɂ܂��ے�́A�r�����𐬂藧�����邱�ƂɎ���u���Ă���A�Ƃ������Ƃ𗝉����Ă���A�悭�킩��悤�ɂȂ����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̏d�S,���S,�O�S,���S�ɂ��ā^19.10.26�n
�O�S�̈ʒu�x�N�g�����A���Ԃ��ē��ڂ�����(1/4�{�̖ʐς�)������3�p�`�̒��_�ŕ\�L�������Ă��̂܂ܐ��S�̈ʒu�x�N�g���Ƃ������̂ł������܂������܂���B���肢�ł��Ȃ��ł��傤���Hm(_ _)m
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����ʂ��܂���D���Ȃ킿�C���̃y�[�W�̉��̕��ɂ���I�C���[���̊W�F

�ɂ����āC�u���Ԃ��ē��ڂ�����(1/4�{�̖ʐς�)������3�p�`�v�Əd�S�͈�v���܂����C�O�S�␂�S�͈�v����Ƃ͌���܂���D�܂��C�u�\�L�������āv�Ƃ͂ǂ��������ƂȂ̂��C�u���̂܂ܐ��S�̈ʒu�x�N�g���Ɂv�Ƃ͂ǂ��������ƂȂ̂��C�ʂ��܂���D
�s8�t�̍Ō�́�6�����闝�R���C�}�C�`�킩��܂���B
�ڂ��������Ă��������B🙏💦💦
�����m��ҁn�F�A�����肪�Ƃ��D�܂��C
�~�����K���Ă��������D���̂��̂���Ȃ�~����̑����́C����̑��������ł��D����������ɂ�����C���̖��ł͂����P�����炃����[�i12���j�̈ʒu�ɌŒ肵�āC�c��5�̏ꏊ�ɓ������̂���3�C����2����Ƃ��̏���̑���

�ƍl���Ă��悢�D
(6)��(x3�|x2+x�|1)(x3+x2�|x+1)�͂Ȃ�����x2+x�|1��x2�|x+1=A�ɓ��Ă͂܂�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D
&chf=bg,s,fff6f6)
�ɉ����^��_������܂����H�I�C�C�|���b�ɂȂ��Ă��܂���
�O���t�t���ň��̓_�ɂ����ĊȌ��ɉ������Ă��Ė{���ɂ킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�~�̌�_��ʂ�~�E�����̕������ɂ��ā^19.10.23�n
�藝�̉���T ��6�s�ڂł���Ax2+Ay2Bx+Cy+D=0 �Ƃ����L�q��Ax2+Ay2➕Bx+Cy+D=0 �ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă��܂����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[ �����_�E�O���_�̐}���ɂ��ā^19.10.23�n
�S�Ăɂ����Ă킩��₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W���̕\�킵���ɂ��ā^19.10.22�n
�L���������܂��ł����A�S�C�T�N�O�ɔ�ׂāA������ڂ����Ȃ��Ă���Ɗ����܂����B
�ƂĂ��e�ȋL�ڂł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^19.10.19�n
�Ȃ������̕������͈�̎��ŕ\���Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����ɏ����Ă��܂��悤�ɁC�u��ʂɁC�O������ԁi���R�x�R�j�ɂ����āC�P�̐����i�������ɂ�锛��j������ƁC���R�x��1�����ĂQ�����i���ʂ�Ȗʁj�ɂȂ�܂��D�������Q�Ȃ�C���R�x���Q�����ĂP�����i������Ȑ��j�ɂȂ�܂��D�v
�@(A) 3������ԂŁC�����Ȃ�=3�����D (B) 3������Ԃŕ������P�i�P�����̐����j=2����=���ʁD(C) 3������Ԃŕ�����2�i2�����̐����j=1����=�����D
��F(B)

��2����=����.
(C)

�́C���ʂƕ��ʂ̋��ʕ���=1����=�����D
�@�ȏオ��{�ł��D�������C���1�̎��ŏ����Ȃ��ƌ������Ƃł͂Ȃ��D�Ⴆ�C������O��Ƃ������C

�Ƃ����A���������́C
^2%2B (y-b)^2=0&chf=bg,s,fff6f6)
�Ɠ��l�Ȃ̂ŁC��L�̘A����������
^2%2B (5x%2B 6y...)^2=0&chf=bg,s,fff6f6)
�Ə������Ǝv���Ώ�����D
�i�������\������j�Ȃ��ł�
���̃T�C�g���Ă��`�i�w�E�j
�����m��ҁn�F�A�����肪�Ƃ��D����̌v�Z�́C�����ɏ����Ă���ʂ�u���͉\�ȕ����́C�u���p����(0�`9)�v�u�����_(. )�v�y�сu�����̃}�C�i�X( - )�v�ł��B���̑I����́C�I�������N���b�N���Ă��܂����H�܂��C�s��v�Z����`����Ȃ����̂́u��`����Ȃ��v���ł��D��`����Ȃ����̂ɂ́C���ɓ��͂���܂���D
�����Ɍ�/�����肳��^19.10.16
���́A�킩��₷���������̍H�v�������������Ă���������ƍK���ł��B
���͒���e�X�g�O�ȂǎQ�l�ɂȂ�܂��B
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ̊Ǘ��l�i���j�́C������̓I�ɒ�N���āC��̓I�ɉ������邱�Ƃ��l���Ă��܂��D�T�˗ǍD�̊��z�͗L��ł����C����y�[�W���鋳�ނ́u�y�[�W���������v�Ɂu�H�̍H�v�����������v�Ƃ́C�u�S���������I�v�Ƃ����Ӗ��ɂȂ�܂��̂ŁC����͖����ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�i���̉��Z�ɂ��ā^19.10.16�n
�ڍׂȌv�Z�ߒ��������Ē������肪�Ƃ��������܂��B
���āA2�i�������16�i���ł͕��̐���2�̕␔�ŕ\�����܂����A���̂��Ƃ͍��Z���w�͈̔͊O�̂��߁A��w�����ł͌v�Z���ʂ����ɂȂ�悤�Ȗ���2019�N���݂ł͏o�肳��Ȃ��ƍl���Ă悢�ł��傤���B
������N��ɍ��Z�̃J���L���������ύX�ɂȂ�A2�̕␔�����グ�邱�ƂɂȂ����ꍇ�͓��R�ɏo�肳�����̂Ɨ������Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ̊Ǘ��l�i���j�̗����ł́C���w�E�E������̎�|�Ƃ͊����قȂ�܂��D���������␔���g���̂́C�R���s���[�^�̓��������Ƃ��āC�����t�������������ꍇ�ŁC�Ⴆ��2�i16���ŕ\���Ƃ��ɁC�ō��ʂ�0�̏ꍇ�ɐ��̐��C�ō��ʂ�1�̏ꍇ�ɕ␔�̕��̐���\���Ƃ����悤�Ȏg�����ŁC0000000000000000(=0)�`0111111111111111(=32767)�܂�2^15=32768�ʂ�C1111111111111111=(−1)�`1000000000000000(=−32767)�܂ł͕��̐��Ɠǂޖ����ƍl���Ă��܂��D������C���w���̂Ƃ͊W�Ȃ��C���w�̒��̃R���s���[�^�̒P���łȂ�C�J���L�������ƊW�Ȃ��C���݂ł������ł��o����̂ł͂Ȃ��ł��傤���D
���m�ʂ̕ł���̎���ɑ���n[�t�O�p���̔����@�ɂ��ā^19.10.16�n
arcsec, arccsc, arccot�Ȃǂ̋t���̔����@�ɂ��ċ����Ă��炦��Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ō�̕��ɎQ�l�Ƃ��Ēlj����Ă����܂����D
���m�ʂ̕ł���̎���ɑ���n[�m���̉��@�藝�C�]���ۂ̊m���ɂ��ā^19.10.16�n
���̉����������������₷�������ł�❗️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̊�{�ɂ��ā^19.10.16�n
���́yhelp�z�Ƃ����Ƃ���̐�����������₷�������ł�❗️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s���ɂ��ā^19.10.16�n
�p��ƋL���̍��A
�l�p6�ڂ̕��ɂ��āA
�����ɂ��~���s�������������s��Ƃ����܂��B
�Ƃ���܂����A
n�~n�s������n�~n�s��̎��ł���ˁH
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^19.10.13�n
���3�̓����́A��/4��5��/4 �ł͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕������ɂ��ā^19.10.12�n
�~�O�̈�_����������ڐ�����߂�ꍇ�A�ڐ�̌X����a�Ƃ��Ď�������A�~�̕������ƘA�����āA���ʎ�D��0�Ƃ���Ă����߂邱�Ƃ͂ł��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D
���̎��̃y�[�W�ɉ�����Ă��܂�
���n�̑�w�𑲋Ƃ����T�O�䔼�̎҂ł��B���̓x�u�f�[�^�T�C�G���X�����p����P���v���O�����v�ɂ��Љ�l���J�����g�p�C���b�g���Ƃ���u���鎖�ɂȂ�܂����B���n�ł������\�Ȋ�b�R�[�X�Ƃ������ł������A�����Ȃ��T���Ă��܂��B���̃y�[�W�ɏo����āA�����S�O�N�O���v���o������A�܂ꂩ�����S������������܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ȒP�ȏd�ϕ��̌v�Z�ɂ��ā^19.10.10�n
�Q�l�̗��ɍڂ��Ă���悤�ȉ�������̃T�C�g�ł͌����炸��Ϗd�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�}��ϐ��\���ɂ��ā^19.10.08�n
����ł��B
�Ⴆ��A���i2sinx�j�{siny.B���i2cosx�j�{cosy�Ƃ����Ƃ����@�藝�̕ό`���J��Ԃ���A�^2�{B^2��4cos�ix+y�j�{5�ł��邱�Ƃ��킩��܂��B������A��1�̂Ƃ���B�̍ő�l�y�эŏ��l���l����Ƃ��}��ϐ��\���𗘗p���Ă���Ƃ�p����
A����i4�icos�ix+y�j�j�{5�jcos�ƁAB������i4�icos�ix+y�j�j�{5�jsin�Ɓi�C�ӂ̃Ƃƕ\���Ɣ��a���̂�x��y�Ɉˑ�������Ȃ̂ŕs�K�ɂȂ�̂Łu����Ɓv�Ƃ��Ă���B�j�Ƃ���A��1�̏������cos�Ɓ���1/��i4�icos�ix+y�j�j�{5�j�A�����
sin�Ɓ���i1-1/�i4�icos�ix+y�j�j�{5�j�j�Ȃ̂�B����i4�{4(cos�ix�{y�j)�ƕό`����cos�ix�{y�j�̊��ɂ���
�ő�l��2��2�ŏ��l��-2��2���ۂɑ�����Đ��藧���Ƃ��m���߂�B���̂悤�Ȕ}��ϐ��\����p����B�̍ő�l�A�ŏ��l�����߂�̂͐��w�I�ɐ������̂ł��傤���H����Ƃ��Ԉ���Ă���̂ł��傤���H�܂��A���̗��R�������ĉ������B
�����m��ҁn�F�A�����肪�Ƃ��D�ŏ��̕����ŁC4cos(x+y)+5�ɂȂ�Ȃ��悤�ł��D���������������ď����Ȃ��ƁC���������Ă���̂��s���ł��D
A=1�Ȃ�B^2��4cos�ix-y�j�{4����-2��2��B��2��2�͒����Ɍ�����
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^19.10.08�n
�u�댯�ȗ��Ƃ����ɒ��Ӂv�̗�S�ŏo�����}�C�Ȃ̂ł����A���p�O�p�`��`�����R�͕�����̂ł����A���̐��ŕ����ꂽ���ꂼ��̒�ӂ̒����͂ǂ����܂�̂ł��傤���B�����w�����ł��̂Œ��w�͈̔͂Ȃǂ������甲���Ă���܂��B�ǂ͈̔͂ɑ������镔�������������Ă��������Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z3�N�̐��w�ŁC�O�����̒藝���g���܂��D���̐}�̒�ӂ�1��:5�����߂�ɂ�
^2&chf=bg,s,fff6f6)
��ό`���āC

���̕����͎�v�Ȑ����ł͂Ȃ��̂ŁC�Ȃ��߂邾���ł悢
���̏͂̂ݗ���x���������j���[�̐F���ς��܂���B���炩�̗��R������̂ł��傤���B���������������B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɁC�L�^������v���O���������܂������Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̌�_(�R�ʂ�)�ɂ��ā^19.10.06�n
�y���S�zBQ�̉�����CA�̌�_��R�́ABX�̉�����CA�̌�_��R�ł͂Ȃ��ł���
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�����i�L�����j�̕s��ϕ��ɂ��ā^19.10.06�n
���łɁA���(���ʊȒP�ɂȂ����)��[1]�́Ax²+3x+5��0����ɐ��藧�̂ŁAlog(x²+3x+5)+C���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�������Clog|x²+3x+5|+C���ԈႢ�Ƃ������Ƃł͂Ȃ��Clog(x²+3x+5)+C�Ə�����Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�����i�L�����j�̕s��ϕ��ɂ��ā^19.10.06�n
���(1.6)��[2]�̉́Ax+2log(x-1)+C�ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D2�������Ă��܂����̂ŁC�������܂����D�������Cx+2log|x-1|+C�ł�
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^19.10.05�n
8�Ԃ��\�����Ǝv��
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴆ��

�̂Ƃ��C

������C

�ł����Ă��C

�Ƃ͌����Ȃ�����C�\�������ł͂Ȃ��D�i����͂P����ΐ��藧���Ȃ����Ƃ̏ؖ��ɂȂ�j
�t�ɁC

�̂Ƃ��C

�Ƃ���ƁC

������C�K�v�����ł��D�i�ȏ�̂��Ƃ́C�����̃q���g�ɏ����Ă���܂��j
�}�W�ł킩��₷���I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^19.10.05�n
�����������̃R�����g���ł��Ă������̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D����͂��̗�����ł��\�ł�
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J�����ɂ��ā^19.10.03�n
���U�́i�R�j�ŁA���ł�2/c�Ȃ̂��A����ł�B=3/c�ɂȂ��Ă��܂��B��27�ō����Ă����̂ł����B
���ŋ߂�����̃T�C�g������������ł��B�K�x�ɏڂ�������A���傤�ǂ������ʂ̖�萔�ŁA�����Ă��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��H���ł�2/c�Ȃ̂��A����ł�B=3/c�ɂȂ��Ă��܂���B��27�ō����Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂ̕������ɂ��ā^19.10.03�n
��肪�ڂ��Ă��ĂƂĂ����߂ɂȂ�܂���m(_ _)m
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̎w���ɂ��ā^19.10.02�n
�ƂĂ����̖��ɗ����Ă��܂��B
���ꂩ����g�킹�Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^19.09.29�n
�t���܂Őe�ɗL��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^19.09.28�n
�ق��̃T�C�g�ɍڂ��ĂȂ��Ƃ����������̂ŏ�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���̃T�C�g�ɍڂ��Ă��Ȃ��āC���̃T�C�g�ɏ���Ă��邱�Ƃ����ł������̂������Ă��炦��ƁC��鑤�̎Q�l�ɂȂ�܂�
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������2�ɂ��ā^19.09.27�n
���2�̈�s��i+i�ɂȂ��Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�]���藝�ɂ��ā^19.09.24�n
�s�^�S���X�̒藝���g��Ȃ��]���藝�̏ؖ��������ĉ������B���肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ����ǂ͈̔͂̐��w���K���Ă��邩�ɉ����āC�l�X�ȏؖ����@������܂��D�������ʏ�̍��W���g���Ď������@��x�N�g���̑傫�����g���ƊȒP�ł��D
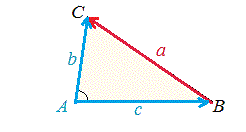
�x�N�g�����g�����@�Ƃ́C�Ⴆ���}��

�ł����C���̂Ƃ�

�Ƃ�����̂ł��D
�@�Ƃ���ŁC�s�^�S���X�̒藝���g���C�g��Ȃ��Ƃ������Ƃ͔����Șb�ł��D�����ł́C�O�����̒藝�i�s�^�S���X�̒藝�j�́u��Ԃɂ��Ă̐^���v��\���Ă���Ƃ����ÓT�I�ȗ���ŋ����Ă��܂����C�����ł͎O�����̒藝�́C���[�N���b�h�̈Ӗ��ł�2�_�Ԃ̋����́u��`�v�i���̂P�j�ƍl�����Ă���̂ŁC2�_�Ԃ̋�����
^p%2B(y_2-y_1)^p}&chf=bg,s,fff6f6)
�Ȃǂƒ�`����ƁC�藝�̌`���ς��܂��D
�@����ɑ��āC�]���藝�����Z�ŏK���]���藝�̌`�����Ă���̂́C2�_�Ԃ̋��������[�N���b�h�̈Ӗ��Œ�`�����ꍇ���ƌ����܂��D������C�M�҂̍l���ł́C�s�^�S���X�̒藝���g��Ȃ��]���藝�̏ؖ��Ƃ����̂́C�u�����I�ɂȂ��v���ƂɂȂ�܂�
������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝�C�{�p�����C�R�{�p�����C���p�����ɂ��ā^19.09.23�n
tan3�Ƃ�3�{�p�����̓��o�͊w�Z�̋��ނ�A�Q�l�����ɂ����܂�ڂ��Ă��Ȃ����̂������A
������̃T�C�g���ɂ킩��₷���A��Ϗ�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̏�@�藝�ɂ��ā^19.09.21�n
���U�́u�R��ڂ܂łɏ��҂��P�l�ɍi����m���v���u�R��ڂ��܂܂��A�P��ڂƂQ��ڂŏ��҂��P�l�ɍi����m���v�Ɖ��߂��Ă��܂��܂����B���̏ꍇ�A�R��ڂ��܂ނƗ�������ׂ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D…�܂łɂƂ����ꍇ�́C…���܂݂܂��D
�����m������^19.09.20�n
�o�Ȑ��̖���x²/a²-y²/b²=1�ɂ�����x<0,x>0�͈̔͂ɂ��ꂼ�ꋤ�L�_������y=mx-2m�̂��͈̔͂̋��ߕ����m�肽���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���ʎ��ƃ���=c/a<0���C���Ɍv�Z���Ă��ł��܂����C�}�������Β�����−b/a<m<b/a�������܂��i�������Ca,b>0�Ƃ��܂��j
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^19.09.18�n
������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̌`��E�ؖ�����ɂ��ā^19.09.16�n
����������Əڂ��������ė~����
�����m��ҁn�F�A�����肪�Ƃ��D(�q���g���ق���)�Ƃ����I�������N���b�N���܂������H
���m�ʂ̕ł���̎���ɑ���n[�_�`�̎���̉�]�ɂ��ā^19.09.16�n
��ς悭�ł��Ă���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��]�ړ��̂P���ϊ��ɂ��ā^19.09.16�n
���ɂ悭������܂����B�L��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.09.15�n
�{���ɑf���炵���ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ����� �ɂ��ā^19.09.15�n
������������₷�������ł��B
�Ō�̖��̉��������������̓I�ɂ��Ă��������ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D3���قǗ��s�ɍs���Ă������߁C���x��܂����D
���m�ʂ̕ł���̎���ɑ���n[�����藝�E�]���藝�ɂ��ā^19.09.14�n
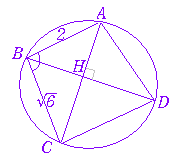
����ɂ��́B���̃T�C�g�ɂƂĂ������b�ɂȂ��Ă���܂��B
1998�N�Z���^�[�������@��IA��1��[2]�ł����A
��ABH�䁢CDH
���A�Ȃ���������̂����ǂ����Ă�������܂���B
���݂܂��A�ǂ̂悤�ɓ��o����̂��A�����������Ē����܂��ł��傤���H
��낵�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D3���قǗ��s�ɍs���Ă������߁C���x��܂����D
���Ȃ��́C����l���߂��Ă���悤�ł����C���w���Ȃ�u��u�ŕ�����܂��v�D
���Ȃ킿�C�~���p�̒藝�ɂ��
��BAC=
��BDC�C
��ABD=
��ACD�����藧�i�Β��p
��AHD=
��DHC���q�ׂĂ��悢�j
�Ή�����2�g�̊p�����������灢ABH�䁢CDH
���m�ʂ̕ł���̎���ɑ���n[�ڐ��̕������ɂ��ā^19.09.11�n
���ȏ��ɏ����Ă���悤�Ȋ�{�I�Ȓm����
���ȏ��ɂ͂Ȃ����ǖ͎��Ƃ��ŏo�Ă���悤��
���p�̒m���������Ă��������S���܂����B
���e�����J�ł��ꂵ�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���䐔��C�z�����ɂ��ā^19.09.11�n
���P(4)�̓����̑I�����́v���̂悤�ɕ\������Ă��܂�
±6 8 ±10 12
������ Windows 10�@IE11�ł�
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɁCIE 11��IE7�݊��̃y�[�W��ǂނƁCISO 8859-1�̕�������±��F�����Ȃ��悤�ł��̂ŁC�������܂����D�i�Y���y�[�W�͑�������C��x�ɂ͒����Ȃ��̂ŁC�C���t�����撼���\��j
���m�ʂ̕ł���̎���ɑ���n[�Q�ߐ��̕������ɂ��ā^19.09.11�n
lim x���� {f(x)-(ax-b)}=0 �́Alim x���� f(x)=ax+b �Ƃǂ��Ⴄ�̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���o�I�ɂ́C
=ax%2B b\]&chf=bg,s,fff6f6)
…(1)
=\lim_{x\rightarrow\infty}(ax%2B b)\]&chf=bg,s,fff6f6)
…(2)
�Ə��������Ƃ����C���͕�����܂����C���̋L���͎g���܂���D
�܂��C(1)�͂������̋Ɍ������߂Ă���̂�����C�E�ӂɂ܂������c���Ă���̂͂��������ł��D(2)���g����̂�
=3,\hspace{1}\lim_{x\rightarrow\infty}(ax%2B b)=3\]&chf=bg,s,fff6f6)
�̂悤�ȓ���̒l�Ɏ�������ꍇ�����ł��i���̂\�W�̉���ł́u�������́v�Q�ߐ��ɂȂ�ꍇ�j�D��ʂ̑Q�ߐ���y=ax+b�ɂ�����a��0�ƂȂ邱�Ƃ������̂�
=\infty\]&chf=bg,s,fff6f6)
�̂悤�Ɂ��ɔ��U���邱�ƂɂȂ�܂����C�����́��Ɓ��͓������͂���܂���D
\]&chf=bg,s,fff6f6)
�͖��炩�ł�
�@�����ŁC�������̂Ƃ���y=f(x)�̑Q�ߐ���y=ax+b�ɂȂ�Ƃ́C�������̂Ƃ���f(x)��(ax+b)�̍���0�ɋ߂Â����Ƃƒ�`����Ƃ��܂������܂�.
}{ax%2B b}=1\]&chf=bg,s,fff6f6)
�Ƃ��Ă��悳�����Ɍ����܂����C���̗�ŕ�����悤�ɁC�����̔䂪1�ƒ�`����ƒ萔���̍�������ꍇ�Ɍ����������܂���D

&pm ����͂ǂ��䂤�Ӗ��ł������ׂĂ��悭�킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ł́C���P(4)��4�����u���̋L���������Ă��܂��v���C�u���̂悤�ɂ͌����Ă��Ȃ��͂��v�ł��D
���Ȃ킿�CHTML�����̒��ŁC�����������g����±�Ə����C±�ƂȂ�܂����C&pm�ł́i�����̃Z�~�R����������Ȃ��̂Łj���������ɂ͂Ȃ�܂���D
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^19.09.05�n
���܂łŁA�����̎Q�l����ǂ݂܂������A�����ł悤�₭�����̒��ŃX�b�L���Ɨ������邱�Ƃ��ł��܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̓�������ɂ��ā^19.09.04�n
�ƂĂ��킩��₷�������ł��B���6�̈��Q��̖��ŁA1�ԍŌ�̍s��log|x|�͈̔͂�0�`1�ɂȂ��Ă��܂��������1�`2�ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����i��ꂪ�o��̂́C�����Ō�̕�����--100���̓���99�������j
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.08.31�n
�قڂS�O�N�Ԃ�ɐ��w�̕��K���n�߂܂����B�킩��₷���J�݂��Ă��������A�v���o���̂ɏ�����܂��B
�p���ł���Ǝv���Ă���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ƂP���ϊ��ɂ��ā^19.08.24�n
���Z�̎��A�ꎟ�ϊ������������琔�w���y���������̂ł��B�ŋ߂̎q�������킢�����B
�����m��ҁn�F�A�����肪�Ƃ��D���N���O�̑��Ɛ��Ƃ��������ł����C�ꎟ�ϊ����D��ۂ������l�Ƃ́H���Z���̋S��C�O�Ղ̕������Ȃǂ����ӁH
���m�ʂ̕ł���̎���ɑ���n[�O�p���̍��������ɂ��ā^19.08.24�n
����Ȃ̂ł����O�p���̍�����r sin�i��+���j�i�������|
��������
���A0������2
���j�Ƃ���܂����Ȃ�
���͏�L�͈̔͂łȂ���_���Ȃ̂ł����H
�܂����̋�̓I���l���킩��Ȃ��ꍇ�Ar sin�i�Ɓ|���j�Ƃ��čl����̂͂����̂ł����H���R�����肢���܂��B�܂��|���Ɛݒ肵���ꍇ�|���͈̔͂͂ǂ̂悤�ɂȂ�܂����B
�F�X���₵�Ă��܂��܂������������܂����ԓ��̕�����낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�i�������|
��������
���A0������2
���j�Ƃ���܂����v�Ƃ�������ł����C���̋��ނɂ́C�����͏����ĂȂ��ł��D
�@��ʂɍ��Z���������Ƃ��́C�u�|
��������
���܂���0������2
���Ƃ���v�̂������₷���D���̏�����t���Ȃ���C���͈�ʉ��ɂȂ��Ċ�������o�Ă���̂ŁC�ς킵���Ȃ�܂��D�v��Ɓu���͏�L�͈̔͂łȂ���_���v�Ƃ������Ƃ͂Ȃ��C�~��1�����Ă���p�x�̋�Ԃ��w�肵�Ă���ǂ��ł��悢���C���ۂɂ́C�u�|
��������
���܂���0������2
���Ƃ���v���g���₷���Ƃ������Ƃł��D
r sin�i�Ɓ|���j�Ƃ���͕̂ʂɍ\��Ȃ��ł��Dr sin�i�Ɓ|���j���g���ꍇ��r sin�i�Ɓ{���j���g�����ꍇ�̈Ⴂ�́C���R�̉���ɂ���܂��D
�@���̋��ނł́C

�ƂȂ�p�x��

�Ƃ��Ă���̂�����C

�ƂȂ�p�x��

����������ꍇ�ł��C�Ή�����p��T�������ł��D
�w�������肾�������w�ł����A���̃T�C�g�ɏo����Đl���ŏ��߂Đ��w�̖��������y�������킩��悤�ɂȂ�܂����B���J�ȉ���ɏ����Ă��������Ė����������ł�����ɐi��ł�������������݂ɂȂ��Ă��܂��B�����ւ��b�ɂȂ肠�肪�Ƃ��������܂��B�Ƃ���ŁA���낢��Ȉ������� �y���R�z�i�R�j�̓�����(x+1)(x-1)(x+3)(x-3)�ɂȂ�̂ł����A�I�����S�ڂ̍Ō�̕�����(x-3)����ʂł͍��[�ɂ���ĕ\������Ă���̂ł킩��ɂ��������ł��B�ŏ��u��L�ȊO�v��I��ŕs�����ɂȂ�܂����B�����ǂ�ŁA(x-3)��T�����獶�[�ɂ���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D������̃e�X�g�ł́C��ʕ\���������̂́CSafari�ł��e�L�X�g������������ɂ���ݒ肾���ŁC���̂ǂ̑g�ݍ��킹�ł����₢���킹�̂悤�ȏǏ�ɂ͂Ȃ�Ȃ��悤�ł��D���Ԃ�g�p���Ă�����̂́CW=1920,H=1080��Chrome�ŁC�������͂Ȃ��悤�Ɍ����܂���...
���m�ʂ̕ł���̎���ɑ���n[�ő�p�C�ŏ��p�ɂ��ā^19.08.23�n
3�́i�P�j�Ȃ̂ł����Ax=�Q+���[�g�R�̎��̉��Ԉ���Ă���Ǝv���̂ł����ǂ��ł��傤�H
���ۑ�����Ă��Ⴂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D�g�єł̕��͒����Ă��܂����CPC�ł̕����܂��̂悤�ł����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�g�����i���͑�j�ɂ��ā^19.08.22�n
�q���g���B����悤�ɂł���Ƃ����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ��ƍ���l�̕��������ł��傤
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��̒l(�}����)�ɂ��ā^19.08.22�n
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
��oosaka�mluka����^19.08.21�n
������̃T�C�g�̐��w�̕������{�������Ă������������ł����A���܂�ɂ��������킩��₷���x�̂����܂����B�����Ŏ���Ȃ̂ł����A���̑f���炵���T�C�g�����ۂɎQ�l�ɂ������Г�����܂����狳���Ă������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����������̂͂���܂���D���\�N�ԁC�ł��Ȃ����k�̊�F�����Ă��ĕ����������Ƃ������Ă���
�����m�y�����Y����^19.08.20�n
�����]�̒藝�ɂ��Ď��₳���Ē������̎҂ł��A�ԐM���肪�Ƃ��������܂��By�ɂ��Ăł���x�ȊO�Ƃ������ƑI���Ă��������܂����B
����̌o�܂ł����A�]�肪�ꎟ�����萔�Ƃ������Ƃ�ax+b�̌`�ŕ\����Ƃ͔[���ł��锽�ʁA���ꂾ�Ɨ]�肪x���X���ł���ꎟ���̌`�ŕ\����Ƃ������ƂɂȂ�]�肪���ɂȂ��Ă���͔̂[���ł���̂ł����j�A����Ȃɂ��܂����Ƃ����̂��H�Ƌ^�₪�N���Ă��܂����A���̂悤�ɖT���猩��Ύ����ł����鎖�ɋ^�������Ă��܂��̂͐��w�̏����I�m���������̓Z���X���s�����痈�Ă��̂ł́H�Ə���ɐ������Ă��܂���җl�͉��������ɂ��Ƃƍl�����܂����H�����đ��@�i�^��Ɋ������[������j�Ȃǂ���������ĉ������B
�@��A�^�₪�ł����Ƃ��̑��@�i�^�������������@�j�Ⴆ�A�Q�Ƃ���ۂ������߂̏��Г�����܂����狳���Ă��������B���Ȃݍ�2�ł��B�������炵�܂����B�@
�����m��ҁn�F�A�����肪�Ƃ��D���������I�Ȗ��ʂɉ�����Ƃ������ɁC�����ł͂Ȃ����C�����ł͂Ȃ����ƍ����ȋc�_�Ŗ����Ă��邱�Ƃ��������ƍl�����܂�.ax+b�����ė]�肪x���X���ł���ꎟ���ȂǂƘA�z�����͎̂��R�ł����C���w�Q�N�̒����̌X���Ƃ��ؕЂ̉ӏ����C�����������ɍς܂��Ă��܂��Ă��āC�ϐ��ƌW���̋�ʂ����Ȃ��Ȃ��Ă���悤�ł��D���������I�Ȗ��𐔑���Ί��o�͐g�ɒ����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^19.08.20�n
�͂��߂܂��ā@���߂ė��p�����Ă��炢���ꂩ������p�������Ǝv���܂����B�f���炵���T�C�g�̒��肪�Ƃ��������܂��B�@
����₪����܂��A�i��]�̒藝�j��2�����Ŋ������]�肪1����or�萔�Ƃ������Ƃ�ax+b�ƒu����Ă���̂ł����Ax�̕������Ȃ�y�i�]�肪ay+b�j�łȂ��Ή������x�Ȃ̂������ĉ������B
�܂����̋^��͂ǂ͈̔͂̒m���̕s�����炭����̂Ȃ̂��������Ă��������A��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�O�������Ď���Ă�����C��납�狅�����ł����悤�ȏՌ��̎���ł��D�m���̕s���Ƃ������Ƃł͂Ȃ��āC���̏�̈Öق̗����������Ƃ����Ƃ������Ƃ��ȁDx�̎���x��2�����Ŋ���b�����Ă���̂�����C�]���x�̎����Ƃ������Ƃł��D�i�t�Ɍ����C���Ȃ��͂Ȃ�y�̎����Ǝv���̂ł����H�Ȃ�z�̎��ł��Ȃ��Cw�̎��ł��Ȃ��Cu�ₖ�̎��ł��Ȃ��Cy�̎��ƍl����K�R���́H�j
����t�m�Ȃ���^19.08.19�n
���ʎ�b2-4ac�̃A���t�@�x�b�g�̂��Ă͂߂̎��A-x2+2ax-a-2�̂悤�ɍ���4���鎞�̑Ώ��@�������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D

�̏ꍇ�́C�萔����

������C
=0&chf=bg,s,fff6f6)
�Ƃ��āC
^2-4\times 1\times(a%2B 2)&chf=bg,s,fff6f6)
�Ƃ��܂��D
�q�����畷���ꂽ�Ƃ��ɂ�����Ƌ�������悤�ɕ����Ȃ����܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.08.16�n
���T���_���ȑ��q�̂��߂S�O�N�Ԃ�ɂ���Ă݂���ł����A�Ȃ�ƂȂ��v���o���Ă��܂����B�킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^19.08.16�n
���S�i-1�A-1�j���a2�̉��������̂ł����A�I������(x+1)2+(y+1)2=4���������߉ł��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D6����1�̊m���ŁC������肪2�d�ɏo�Ă��āC�I����������Ȃ��Ȃ��Ă����悤�ł��̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�i�@,16�i�@,���i�@��10�i�@�ɂ��ā^19.08.15�n
32�i����10�i���̎��͕ϊ����@��T���Ă����̂ɍڂ��Ă��Ȃ��Ă�������B�����Ɍ������b����Ȃ��������G���W�����������ǁA�u32�i���v�Ō������āu32�i�����ڂ��Ă��Ȃ��T�C�g����v�o�Ă���̂͂��������B
�����m��ҁn�F�A�����肪�Ƃ��D64�i���܂ł�64�i���܂łɕϊ����鎩�R������lj����Ă����܂���
���m�ʂ̕ł���̎���ɑ���n[�ʐ��ɂ��ā^19.08.15�n
�킩��₷���I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^19.08.12�n
������₷��
�S�ėǂ��Ǝv���܂�‼
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɑ�l�C�ɏ��l�ɂ��ā^19.08.12�n
�����ߖ��͊ȒP������̂ł�߂��ق��������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��Dweb��ʏ�ŕ�����\�������鐶�k�͂߂����ɂ��Ȃ��悤�ł�
���m�ʂ̕ł���̎���ɑ���n[ �����_�E�O���_�̐}���ɂ��ā^19.08.12�n
�ƂĂ�������₷�������ł��B ���ɗL��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^19.08.12�n
���z�łȂ�����ł��A�����܂���B
���7�Ȃljɂ���]��̒u�������悭������܂���B��������Ă��炦�Ȃ��ł��傤���B�܂��A�ǂ����ɏ����Ă���̂Ȃ炻�̃y�[�W�������Ă���������ƍK���ł�
�����m��ҁn�F�A�����肪�Ƃ��D��肪�Ԉ���Ă��܂����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^19.08.10�n
�V�l�z�[���������̌������҂ł����A�����̂�����Ȃ��u���������v�ɂȂ��Ă���܂��B�L��������܂��B�Q�l�ɂȂ�Ȃ��Đ\����Ȃ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D��O�C�풆���܂�̕��Ȃ�Ǘ��l�����N���ł�
���m�ʂ̕ł���̎���ɑ���n[�w�����C�ΐ����̓����ɂ��ā^19.08.09�n
�E��(2)(3)�̂悤�ȋɌ��l�ɍs�������D
�������̋Ɍ��l�́C���̋Ɍ��l�ŕ\�킷���Ƃ��ł���D
lim(n����)(1+1/n)^n
�Ƃ����̂͂������̂ЂƂɂƂ��Ĉ�˂Ŗ��炩�Ȃ̂ł��傤���B
�Ȃɂ��������Ă���̂��Ƃ�Ƃ킩��Ȃ��̂ł����A
�����������Ƃ��Ă���̂ł�����Ћ����Ă������������ł��B
�܂Ƃ��Ɋw�K��ς�ł��Ă���Ȃ�Ό���Ζ��炩�ł���Ƃ������R�ɂ��ďȂ����̂ł���A�������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̓��e�̓n�C���x���ł��D���ʂ̍��Z�������ʂ̒��ӗ͂œǂ�C������������Ȃ��ȂƎv���C1��ڂ̌��e�Ƃ��ď��������̂ł��D���ӂ��ēǂ߂C�Ȃ���悤�ɂȂ��Ă��܂��D
�܂�(3)�́C
^{\frac{1}{t}}\]&chf=bg,s,fff6f6)
������C
^{x},\hspace{5}\lim_{x\rightarrow-\infty}(1%2B\frac{1}{x})^{x}\]&chf=bg,s,fff6f6)
�ɋA�����܂��D
(2)�͉��̕��Ɂu��(11)�͎��̂悤�Ɏ������v�Ƃ������ɏ����Ă��܂����C
2)�ɂ����āC

�Ƃ����ƁC

�̂Ƃ��C

������C

�܂��C

������C

}\]&chf=bg,s,fff6f6)
}=\lim_{h\rightarrow 0}\frac{1}{\log_a(1%2B t)^{\frac{1}{t}}}\]&chf=bg,s,fff6f6)
�ƂȂ邩��C���l�ɂ���(2)�ɋA�����܂��D
�@�M�҂����Ƃł��̂悤�ɋ������킯�ł͂Ȃ��D���̂܂ܓ˂���������C1�N���X����1�l�����鐶�k�����邩�ǂ����C���̐��k�́u�A�o�����v��������܂���D
����
��L(4)��(4)'�̖��͗ޑ�ł���Ǝv���܂����A
(4�j�@ 1.96�~��/��n �� 1
(4)'�@2�~1.96�~��/��n �� 0.5
�ƂȂ��Ă��܂����A���́A(4)'�́u2�v�{�ƂȂ�̂ł��傤���H
�����Ă��������B�X�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D(4)'�ɂ́C1.96�~6.76/��(n)��0.5�Ə����Ă���̂ŁC���ӂ�2�{����2�~1.96�~6.76����(n)�ƕό`���Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[ �}��ϐ��\���Ƃ��ɂ��ā^19.08.07�n
���͂⋳�ȏ����킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̒��_�i�W�J�`�j�ɂ��ā^19.08.07�n
�}�C�i�X�����t���̕����ɂ��āA�����Ɗ������Ȃ����Č����Ă��܂��A�}�C�i�X�������Ƃ����Ƃ�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɂ͕����͂�������܂��DInternet Explorer�͌��ݐ������Ă��܂��iMicroSoft�Ђ��g��Ȃ��悤�Ɍ����Ă���炵���j�C���Ȃ������܂��D�������Ăق����ӏ�����肵�ē��e���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^19.08.06�n
❘�]�b���P�A❘�x❘���P�Ȃ�b�]�{�x�^�P�{�w�x�b���ؖ�����B
�����m��ҁn�F�����ĉ������Ƃ������ƂȂ�C���̂悤�ɏ����Ȃ��Ƃ����܂���D����ɁC����̖�肪�Ԉ���Ă��܂��D�ؖ��ł��鎮�̌`�����Ă��܂���D�ʏ�Ȃ�C�����܂łŖ�O�����̃P�[�X�ł����C���������ւ��ĉ������Ƃ͂ł��܂��D�i�܂����C�ċx�݂̏h��̓�����q�˂Ă���̂ł͂Ȃ��ł��傤�ˁj
}{\lt}\mid 1%2B xy\mid&chf=bg,s,fff6f6)
(?)←

(1-y^2)\gt 0&chf=bg,s,fff6f6)
(�ؖ��I)
y=e^at�Ɖ������肷��̂�2�K�����������������₷�����邽�߂Ƃ������Ƃł����B(���̐����ʼn������肷�邱�Ƃ��\�ł��傤���B)
�����m��ҁn�F�A�����肪�Ƃ��D�O���̎���F�����܂��Ɍ����C�����ł����C�ׂ��ȃj���A���X�ł͈Ⴄ��������D�㔼�̎���F���̐����łƂ́H�Ӗ��s���D���̎��łȂ�\
�@y=e^rx�Ɖ��肷��C�ȒP�ɉ����邪���ɂ͊ȒP�ȕ��@��������Ȃ�����C��������@�ʼn����Ƃ����������ȁD
�@���R���ۂ̎����l���瓾����悤�Ȕ����������C�Ⴆ��
y\apos%2B (0.4%2B 0.5x-0.6x^2)y=0&chf=bg,s,fff6f6)
�̂悤�Ȕ����������ł��C������

�����肷��i�����͈͂�ʂƂ���j�C�W����r�ɂ��u�قڂǂ�Ȗ��ł��v�������Ƃ��ł��܂�…�R���s���[�^�����ɓK���Ă��܂��D�������C����ꂽ������������\���Ă���̂��C�����I�Ȋ��ɒu����������̂��Ȃǂ͕�����ɂ����ł��D���̂悤�ɂ��āC���̎��ʼn������肷�邱�Ƃ͂ł��܂����C�܂��ʂ̕��G���ɍs��������܂��D�Ƃ肠���������I�ɉ����ɂ́Cy=e^rx�Ƃ����̂��x�X�g�ł��D
�@�u�w�����ɒu��������Ɣ��ς̖�肪�ȒP�ɂȂ�v�Ɗo����̂ł��D
�ƂĂ�����ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^19.08.01�n
�����������₷���A���t���ł�������Ɗm�F�o�����̂ŗǂ������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s��ƂP���ϊ��ɂ��ā^19.07.30�n
�ƂĂ�������₷�������ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ΐ��v�Z1�ɂ��ā^19.07.30�n
[ ���ʂȐ^�� 1 , a ]
�@a>0 , a��1 �ƂȂ�ǂ�� a �ɂ��Ă�
a0=1 ������ loga1=0 ����������D
a1=a ������ logaa=1 ����������D
���O���́u�^����1�̂Ƃ��́C�ꂪ���ł����Ă��ΐ��̒l��0�ɂȂ�v�Ƃ������ƁD
�㔼�́C�u��Ɛ^���������Ȃ�C�ꂪ���ł����Ă��ΐ��̒l��1�ɂȂ�v�Ƃ������ƁD
�̕����Alog1 1�́H�ƂȂ��Ă��Ȃ�Y�݂܂����B
��ɂ�1������Ȃ��Ƃ������[��������悤�Ȃ̂ŁA����͋L�ڂ��������ǂ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�{���̂P�s�ڂɁua>0 , a��1�v�Ə����Ă���̂ŁCa��1���O��ł��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i�����j�ɂ��ā^19.07.29�n
������������܂����B
�����Ȃ̂ł����Ac1=c2�ƂȂ�̂͂ǂ̗l�ȏꍇ�Ȃ̂ł��傤���H
�����̒P�U����c1=c2�ƂȂ��Ă����̂ŁA���R���m�肽���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̗l�ȏꍇ���H�Ƃ�������͂����܂��ł��D�����̗^�����ɂ���āC�����ȏꍇ������܂��D
�@�ʏ�C���Z���w���N�x�̕����ł́C�����������̉������܂œ��ݍ���ł���]�T���Ȃ��̂ŁC�ψʂɔ�Ⴗ��t�����̗͂������i−ky�j�C���C��R���Ȃ��ꍇ�iy'�̌W����0�j�C�P�U���ɂȂ�Ƃ������Ƃ��C�����₷�����邽�߂�k=��
2�Ƃ�����

�̉����p���x�ւ̎O�p��

�ŋ��߂���Ƃ������Ƃ��g�b�v�_�E���ŋ�����̂ŁC������Q�K��������

�����藧�Ƃ������Ƃ�ڂŊm�F���邾���ł��D
�@����ɑ��āC����������

�̈�ʉ������߂�ƁC

�ƂȂ�܂����C��������������
=C\sin(\omega x%2B\alpha)&chf=bg,s,fff6f6)
�Ə����邱�ƂɂȂ�܂��D�܂��ʂɂ́C�����ʑ�

��������Ă��Ă����ɂȂ�Ƃ�����C�����ʑ�0�̂��̂����Ɍ��肷���

�̉��ɂȂ�Ƃ������Ƃł��D
�U�@���̓c�[���́ut-���� : �����U�����肵���Q�W�{�ɂ�錟��v�o�͌��� �̂Ƃ���Ƀv�[�����ꂽ���U���@�i���R�x1x�s�Ε��U�P�{���R�x2x�s�Ε��U2�j/ (���R�x1+���R�x2 )�Ə����Ă���܂����A�茳�ɂ���Q�l���ł̓v�[�����ꂽ���U���i�s�Ε��U�P�{�s�Ε��U2�j/ (���R�x1+���R�x2 )�ɂȂ��Ă���܂��A�ǂ��炪�������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̎Q�l���̉��y�[�W�ɂ��������Ă���̂ł����H�ł����WEB��̋��ނŁC�Ή��ӏ���URL�Ŏ����Ă�������
���m�ʂ̕ł���̎���ɑ���n[�s��̑Ίp���Ƃ��ɂ��ā^19.07.28�n
n��̂Ƃ����n<0�̏ꍇ�͂ǂ��Ȃ�̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނł͂���0��O��Ƃ��Ă��܂��D����0�̏ꍇ�Ɋg���������ꍇ�C����͉��̂��߂Ȃ̂��i�ʏ�͐ς̉��Z�����R�ɍs�����߁j�C���炩�̒�`���s�����ꍇ�ɖ����������Ȃ��̂�����������K�v������܂��D�Ⴆ�C�s��ɂ��Ă͌����@�����������Ȃ��̂ŁC

�̂悤�Ȋ���Z�Ƃ����Ӗ���t���邱�Ƃ͂ł��܂���D�܂��C

���t�s��ƒ�`�����ꍇ�ł��C

�̋t�s��
^2&chf=bg,s,fff6f6)
�ƈ�v���邩�ǂ����C���Z�ɂ��Ă̐����������炩���ߊm���߂Ă����K�v������܂��D
�@�Ƃ肠�����C���̋��ނ̑O��Ƃ��ẮC����0�̏ꍇ�ɂ��ďq�ׂ����̂ŁC����0�ɂ��Ă͉����q�ׂĂ��Ȃ����Ƃ͊m���ł��D
����₷������ł����B�����D�ɗ����Ȃ����Ƃ�����܂��B���ʕ�����a�W�������o�������ʂɋ�W���i�Ӂj���܂܂�Ă��Ȃ��̂͂Ȃ��ł��傤���B��W���́A�ǂ�ȏW���̕����W���Ƃ���Ƌ��ȏ��ɏ�����Ă����̂ŁA���ʕ�����a�W���̌��ʂɊ܂܂��̂ł͂Ǝv���̂ł����B�킩��͈͂Œ��ׂĂ���W�������ʕ�����a�W���Ɋ܂͂���܂���ł����B�F�����Ԉ���Ă���̂ł��傤���B����Ƃ���W���́A�K���I�ɋL�ڂ��Ȃ��̂ł��傤���B����Ȏ���͎t���Ē�����ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴆ�C

��
�����W�������ׂďq�ׂ�Ƃ����ꍇ�C���Ȃ��̗\�z�̂悤��

�ɂȂ�܂����C

��
�v�f���������ׂĎ����Ƃ����ꍇ�́C

�ɂȂ�C�v�f�̌����q�ׂ�ƌ�����2�ɂȂ�܂��D���̋��ނł͏W���̗v�f���������ׂĎ������������Ă���C�u�v�f�v��I�ׂƂ������ɂȂ��Ă���̂ł��D
��r�I�ȒP�Ȃ̂ŁA���݂��������Ȃ��X�����C�J�݂����ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�ȒP�Ȃ��Ƃ͂������Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^19.07.25�n
�ÎZ�ł͖����ł��Ə����Ă��������ł����A�ӂ[�ɂ݂�ȈÎZ�ʼn����Ă܂���
�����m��ҁn�F�A�����肪�Ƃ��D�����h�͈ÎZ�ł͖����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�]���藝�ɂ��ā^19.07.24�n
Google �L���̈ʒu�������ז��ł��A�}������̒��Ƀ��C�A�E�g�����Ƃ����Ⴒ����ʼn���������������Ȃ��Ȃ�܂��B�@���P���Ă���������Ƃ��肪�����ł��B��낵�����肢���܂��B19.7.25
�����m��ҁn�F�A�����肪�Ƃ��D�y�[�W���̂ǂ̈ʒu�ɉ����o�邩�́C���ނ̍�ҁi���j�����߂Ă���̂ł͂Ȃ��CGoogle�����߂Ă��܂��D�A�_���g�C�I�J���g�C�e���Ȃǂ̃W�������͔r�����Ă��܂����C����ȊO�ł͍L������������C�ǂ��ɉ����o�邩�͌��܂��Ă��܂���D�i���Ȃ��͎ז����ƌ����܂����C�����AI�̐i���ɂ͖ڂ���������̂�����܂��D���ۂɍL�����o�Ă���ꏊ������ƁC�ǎ҂̖ڂ����܂�ꏊ�ɐ��m�ɏƏ��������Ă���̂ɂ͋����D�t�Ɍ����C�L���̏ꏊ������ƁC���ނ̍�҂��d�v���ƍl���Ă���ӏ��ł͂Ȃ��C100�l�̓ǎ҂��ł����Ԃ������ēǂꏊ�m�̑O��n��������悤�ł��j
���m�ʂ̕ł���̎���ɑ���n[�~����C���ジ�����ɂ��ā^19.07.24�n
���ł��B�u�K���X�łł������ŁA�ԐF�̂��̂�6�A�F�̂��̂�2�A�����Ȃ��̂�1����B�������~��
�~�`�ɕ��ׂ���@�̑��������߂�B�v
���̖��̓�����8�I��6�I��2�I��28(�ʂ�)�ŁA���̍l�����͕�����̂ł����A
�ʂ̉�@�Ƃ��ĐF�̋����Œ肵�ĉ��������Ɏc��̋�����ׂ鏇����l����ƁA�ԐF6�A�F1�A����1����ׂ鏇��Ȃ̂ŁA8�I��6�I��56�ƂȂ�A�����������̂Q�{�ɂȂ��Ă��܂��܂��B
����Ɠ��l�ɐԐF�̋����Œ肵�ĉ��������͐�����������6�{�ɂȂ��Ă��܂��܂��B
���̂��Ƃ���l���āA���߂ɌŒ肷�鎞�ɌŒ肷�鋅�̐F�̌��Ŋ����Ă����Ȃ��Ƃ����Ȃ��̂��Ƃ������Ƃ�
�l�����܂����B
�������A�Ȃ����̂悤�ȍ�Ƃ��s��Ȃ��Ɠ���������Ȃ��̂����S��������܂���B
����̐l�ɕ����Ă�������Ȃ��ƌ�����̂ł����A�����Ă��������Ȃ��ł��傤���B���肢���܂��B
 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D���̖��͉~����̖��Ȃ̂ŁC�ďd�Ȃ���̂�1�������Ă͂����Ȃ��D�u���̖��̓�����8�I��6�I��2�I��28(�ʂ�)�ŁA���̍l�����͕�����̂ł����A�v�Ə����Ă��܂����C����͖{���ɕ������Ă���̂��ǂ����^��ł��D
�@�����̃K���X���i��[�̈ʒu�ȂǂɁj�Œ肵����C�c��8�́u6��2�̓������̂�����Ƃ��́i���ʂ́j����ɂȂ邩��v8�I��6�I��2�I��28(�ʂ�)�Ƃ��ׂ��ł��傤�D���ɁC�̃K���X���P�i��[�̈ʒu�ȂǂɁj�Œ肵�Ăł���u�������̂�����Ƃ��́i���ʂ́j����́v8�I��6�I��56�ƂȂ邪�C���̒��ɂ͐������Ă���C��[�ɌŒ肵�����̂Ɖ�]���Ĉ�v������̂��܂܂�Ă���D������2�{�]�v�ɐ����Ă��邱�ƂɂȂ�.�i�Ⴆ���}�͂Q�ʂ�ł͂Ȃ��j
�Q�l�ɂȂ�܂����B
�Ƃ��Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D����ҁi���j�����ӂƂ��Ă��鍀�ڂł���
���m�ʂ̕ł���̎���ɑ���n[�O�p�������ɂ��ā^19.07.20�n
== �O�p������ ==�̖��́A�ォ��4�Ԗڂ�5�Ԗڂ̉��悭�킩��܂���B�ڂ���������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��������x�ǂ�ł��炤�ƕ�����悤�ɁC���̔ԍ��͓ǂނ��тɕς��܂��D4�Ԗڂ�5�ԖڂƂ����Ă��C�ǂ�ł���l���ƂɈႢ�܂��D����̓q���g�����ĉ������D�i�����Ə����I�Ȗ����C���̂����lj����Ă����܂�--�ǐL�F�lj����܂����j
���m�ʂ̕ł���̎���ɑ���n[�Q���s���� �i�������܂Ƃ߁j�ɂ��ā^19.07.15�n
���ʎ��Ԉ���Ă܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��̎���̎d���́C���������ł��D���̃y�[�W�ɂ͔��ʎ���10�قǂ���܂��̂ŁC�ǂ̎��̂��ƂȂ̂��������Ȃ���C������e������ł��܂���D��ԉ\���������̂́C���2�̂Ƃ���ɏ����Ă���D'�̒�`��ǂ�ł��Ȃ��ꍇ�ł��D���Ȃ����m��Ȃ��Ƃ������ƂƁC�Ԉ���Ă���Ƃ������ƂƂ͈Ⴄ�̂ł�
���m�ʂ̕ł���̎���ɑ���n[����̋Ɍ�(���^���^)�ɂ��ā^19.07.15�n
�L���̒l�Ɏ������鐔��̋Ɍ��ilim�yn�����z�j���l�����Ƃ�n�Ԗڂ̐���a�in�j��n�{1�Ԗڂ̐���a�in�{1�j�̒l�͏�Ɉ�v����ƌ����܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ����q�˂����̂́C�����炭���̂��Ƃ��ƍl�����܂��D

�i

�͗L���m��l�j�̂Ƃ��C

�����藧���H→����́C�������ł��D
�@���w�ł͈ꌾ�Ⴆ�C�^�ƋU������ւ��܂��D���ۂɂ́C���Ȃ��̎�������̂܂܁u���t�ʂ�Ɂv�~�߂�ƁC����Ȃ��Ƃ͐��藧���Ȃ��C�ƌ��킴��܂���D�u���t�ʂ�Ɂv�����C

�i

�͗L���m��l�j�̂Ƃ��C�˂�

�����藧���H→�S�R���藧���܂���D
�y����z
•

�̂Ƃ��C

�ł��邪�C

•

�̂Ƃ��C

�ł��邪�C

�@�ȏ�̂悤�ɁC���L���m��l�Ɏ������邩��ƌ����āC�e�����������i=�萔�l�̐���ł���j�Ƃ͌���܂���D�������C���߂ɏq�ׂ��悤�ɁC���L���m��l�Ɏ�������ꍇ�ɂ́C���̑悎�����悎+1���������l�Ɏ�������Ƃ͌����܂��D
���̂���������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^19.07.10�n
3.(3)1�̓��B����������߂镔���̌W����r9A-13B=2�ƂȂ��Ă��܂���=0�ł͂���܂���?
�����m��ҁn�F�A�����肪�Ƃ��D����̔ԍ����H3.(1)1�̂悤�ł��̂ŁC�������������܂���
���m�ʂ̕ł���̎���ɑ���n[��Βl�L��2�̊O�����ɂ��ā^19.07.10�n
���肪�Ƃ��������܂��B�ƂĂ�������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�U�z�}�̍쐬�ɂ��ā^19.07.10�n
�u�����O���[�v�̎U�z�}�v����������ł��Ȃ������B
�����m��ҁn�F�A�����肪�Ƃ��DExcel�̃o�[�W�����ɂ���邩������܂��C���݁C�M�҂͕����n��U�z�}���C���̂悤�ɊȒP�ɍ쐬���Ă��܂��D
| x | y1 | y2 | y3 |
| 1 | 1.5 | 2.5 | 1.7 |
| 2 | 3.1 | 2.7 | -1.3 |
| 3 | -1.3 | 4.6 | 3.2 |
| … | … | … | … |
→x���W�͋��ʁCy���W�͗ƂɊe�n��ʂ����D���̕\�̗�ł́C(1, 1.5),(2, 3.1), (3, -1.3),...����1�̌n��C(1, 2.5), (2, 2.7), (3, 4.6), ...����2�̌n��C(1, 1.7), (2, -1.3),(3, 3.2), ...����3�̌n��
���͈̔͂�S���I�����āC�U�z�}�i�_�����C�������C�_�Ɛ��j��I�ׂC�����n��U�z�}���ł���
[3]�Ń��A�����d���ƂȂ�ꍇ�͂ǂ������炢���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D����Č���Ή��ł��Ȃ��ȒP�ɉ����܂��D
�Ⴆ�C

�̂Ƃ��C

�̏d���ɂȂ�܂����C����łł���Q������������
&chf=bg,s,fff6f6)

�ƂȂ��āC�P�����܂��̂ŁC�����A���Q�����̈���ɑ�������

�i�܂���

�j�������ł��āC2���ԑQ�����ƂȂ�C���ʂɉ����܂��D

3�~3�s���det�̓r�������ڂ��Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�s�̃y�[�W�����Ă�������
���m�ʂ̕ł���̎���ɑ���n[�O�Ղ̕������P�ɂ��ā^19.07.09�n
�������̖��������Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
�O�Ղ̕�����3�ɏo�Ă��܂�
�u(A) ��Βl�L���P�ƒ萔�����̂Ƃ��v���A�ꍇ�������ĉ����Ă��ǂ��̂��ǂ����A�s���������B
�܂��A���̃y�[�W��(B)�̉���ɂ́Ax=0�Ax>0�̂Ƃ��ɂ́A��Βl�L����x�ŊO���Ax<0�̂Ƃ��ɂ́A��Βl�L����-x�ŊO���A�Ƃ��������������Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�ǂ���ł��悢�D�㔼�F�Ӗ��s��
���m�ʂ̕ł���̎���ɑ���n[�������̋Ɍ��ɂ��ā^19.07.09�n
���ɂ킩��₷���Ă��肪�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.07.09�n
�ڂ��������ꂽ����ƒ��ӂ��邱�Ƃ��������̂ŃX���[�Y�ɗ����o���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^19.07.08�n
�y��P�z�y��Q�z�y��R�z�y��S�z�̖��̉摜�Ɓy��T�z�y��U�z�̉���̉摜�������N��B
�y��P�z�̉��
�i��j
(1)���
�|3x<4�|1
�|3x<3
x>1
�i���j
(1)���
�|3x<4�|1
�|3x<3
x>�|1
�����m��ҁn�F�A�����肪�Ƃ��D{��x>1 → x>−1�͒������܂����D
���m�ʂ̕ł���̎���ɑ���n[��Βl�L���̊O�����ɂ��ā^19.07.06�n
�����͂Ȃ����A�����Č����A���̑召�̔�r�̂��߂ɍ����̋ߎ��l�����߂�ߒ��Ȃǂ��ȗ������ɏ����Ă���A��蒚�J�ȉ���ɂȂ�A�Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��D…�������̃��x���ŁC�����܂Ŗ߂�邩�Ƃ������͂���
���m�ʂ̕ł���̎���ɑ���n[��Βl�̓�������ɂ��ā^19.07.06�n
�y���P�z��(1)�̉��
�i��j
(x+3)(x�|2)<0���
�|3<x<4
�i���j
(x+3)(x�|2)<0���
�|3<x<2
�y���Q�z��(2)�̉��
�i��j
�C�j
y=(2x�|1)�|(x�|2)
=2x�|1+x�|2
=x+1
�i���j
�C�j
y=(2x�|1)�|(x�|2)
=2x�|1�|x+2
=x+1
�y���R�z�̉��
�i��j
�G�j �|1��x<�|0�̂Ƃ�
�i���j
�G�j �|1��x<0�̂Ƃ�
�y���R�z�́i�ʉ��P�j�̉��
�i��j
x=�|0�̂Ƃ�y=0+1+2+3=6
�i���j
x=0�̂Ƃ�y=0+1+2+3=6
�y���R�z�̉��
�i��j
x=0�̂Ƃ�y=2 �� k=0������
�i���j
x=0�̂Ƃ�y=2 �� k=2������
�y���R�z�̉���́A���Ă��Ȍ������āA�킩�肸�炩�����B
���G�Ȗ��ɂȂ�قǂ������肵������ɂȂ�̂́A����ǂ��B
���G�Ȗ��ɂȂ�قǂ�蒚�J�ȉ���ɂȂ�悤�ɐS�|���Ăق����B
�悿�悿�����̎��ɂ́A�������Ƃ��J��Ԃ����ؒ��J�ɐ�������邮�炢�����傤�Ǘǂ��B
�ȉ��́A�y���R�z�̉���ɂ��Ă̕M�҂̉��߁B
�i���āj
��Βl�L�����S���邩��A�ꍇ�����́A�u��Βl�L���̐��{�P�v�ŁA�T�K�v�ɂȂ�B
�A�j�����|�R
�����|�i���j�|�i���{�P�j�|�i���{�Q�j�|�i���{�R�j���|�S���|�U
�����|�S���|�U�́A������������Ay���ŏ��ɂȂ�̂́Ax���ő�̂Ƃ��B
�����|�R�̂Ƃ��A�����U
�䂦�ɁA�����U
�C�j�|�R�������|�Q
�����|�i���j�|�i���{�P�j�|�i���{�Q�j�{�i���{�R�j���|�Q��
�����|�Q���́A������������Ay���ŏ��ɂȂ�̂́Ax���ő�̂Ƃ��B
�����|�Q�̂Ƃ��A�����S
�䂦�ɁA�����S
�E�j�|�Q�������|�P
�����|�i���j�|�i���{�P�j�{�i���{�Q�j�{�i���{�R�j���S
�����S�́A�萔�l��������Ay�́A���̒l�ɊW�Ȃ��A���B
�䂦�ɁA�����S
�G�j�|�P�������O
�����|�i���j�{�i���{�P�j�{�i���{�Q�j�{�i���{�R�j���Q���{�U
�����Q���{�U�́A������������Ay���ŏ��ɂȂ�̂́Ax���ŏ��̂Ƃ��B
�����|�P�̂Ƃ��A�����S
�䂦�ɁA�����S
�I�j�O����
�����i���j�{�i���{�P�j�{�i���{�Q�j�{�i���{�R�j���S���{�U
�����S���{�U�́A������������Ay���ŏ��ɂȂ�̂́Ax���ŏ��̂Ƃ��B
�����O�̂Ƃ��A�����U
�䂦�ɁA�����U
���������āA�|�Q�������|�P�̂Ƃ��A�ŏ��l�S���Ƃ�c�i���j
�y���R�z�́i�ʉ��Q�j�̉���������ł��Ȃ��B
�ǂ̐�Βl�Ǝ��̂ǂ̍����Ή����Ă���̂��A�S���킩��Ȃ��B
�r���̌o�߂����̉ߒ����܂߂āA�����Əڂ����������Ăق����B
�܂��A����̎��Ɛ������̉摜��2L��4L�̐��l���ꗂ�����B
�y���R�z��(1)�̉���̍Ō�̕����́A���ᎆ�ƒ�K�������ăO���t��������Α��v�����A����ȊO�̏ꍇ�ɂ́A�Ȃ��O���t�̂P�ڂ̒��_�i0,2�j�ƂQ�ڂ̒��_�i2,12�j��ʂ���ɂȂ�̂��A�킩��Ȃ������B�\���Ƃ��ẮA�O���t�̂Q�ڂ̒��_�i2,12�j�ƂR�ڂ̒��_�i3,7�j��ʂ���ɂȂ�\��������̂ł͂Ȃ����H�A�Ǝv�����B
���̕ӂ�̎v�l�̉ߒ��������Əڂ����������Ăق��������B
�܂��A�O���t�̉摜�̐ԐF�̌X���́A�u�X���T�v�ƂȂ��Ă��邪�A�u�X���R�v�̊ԈႢ�H
�����m��ҁn�F�A�����肪�Ƃ��D����ɂ��Ă͒������܂������C��w�������̒i�K�Œ�2�̕��K�������Ă���ƌ����Ă������ł��傤�D���ԓ��ɓ��Ă������Ȃ��I
���m�ʂ̕ł���̎���ɑ���n[�����̓������1�ɂ��ā^19.07.05�n
�y�ޑ�2.2�z�ŁA
(a-(b+1)/2)^2 + (3b^2-6b-1)/4 = (a-(b+1)/2)^2 + 3(b-1)^2/4 - 2/3
�ƂȂ��Ă��܂���
(a-(b+1)/2)^2 + 3(b-1)^2/4 - 1 �̊ԈႢ�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^19.07.04�n
�Ƃ肠�����A�ꍇ�����ɂ���Đ�Βl�L�����͂������@�̒i�ɂ��āB
��(�V)�́i���āj
���́A�O���܂ސ�Βl�L�������̂܂܊O���ق��ɂ���ׂ��B
�i��j
�A)
(���̂P)�@�����|�P�̂Ƃ�
(���̂Q)�@-1�������O�̂Ƃ�
�i���j
�A)
(���̂P)�@�����|�P�̂Ƃ�
(���̂Q)�@-1�������O�̂Ƃ�
�������́A�����I�ɂ́A�S�̂��ȉ��̗���ʼn��e����ׂ��H
�i���j
�A)
(���̂P)�@-1�������O�̂Ƃ�
(���̂Q)�@�����|�P�̂Ƃ�
��(�P)�A��(�Q)�A��(�R)�A��(�S)�ɂ͂���(����)�̎���������Ȃ��(�T)�A��(�U)�A��(�V)�ł��ȗ����Ȃ��Ŏc���Ăق��������B
�ȉ��̂R�́A�M�ҍ�B
��i�T�j
���{�Q���O���������|�Q
���{�Q���O���������|�Q
���|�P���O���������P
���|�P���O���������P
�����|�Q�̂Ƃ��A�K�������P
�����P�̂Ƃ��A�K�������|�Q
��i�U�j
�����O���������O
�����O���������O
���|�Q���O���������Q
���|�Q���O���������Q
�����O�̂Ƃ��A�K�������Q
�����Q�̂Ƃ��A�K�������O
��i�V�j
�����O���������O
�|���|�P���O�����|�P�������O
�|���|�P���O���������|�P
�����O���������O
���|�P���O�����O�������P
���|�P���O���������P
��(�V)��
|x|���͂�������0�Ƃ̑召�ŕ�����
����|x|-1���͂�������|x|-1�̐����ŕ�����
�́A
|x|���͂�������0�Ƃ̑召�ŕ�����
����|x-1|��|-x-1|���͂�������|x-1|��|-x-1|�̐����ŕ�����
�̂ق����킩��₷�������B
�s���t(2)�̖��Ɖ���́A�����̈ʒu�����������B
�i��j
�|�P������1/2�̂Ƃ��C�Q�b���{�P�b�{�b�Q���|�P�b
���ȒP�ɂ����
�|�P������1/2�̂Ƃ�
2(x+1)�|(2x�|1)=3
�i���j
�|�P������1/2�̂Ƃ��C�Q�b���{�P�b�{�b�Q���|�P�b
���ȒP�ɂ����
�|�P������1/2�̂Ƃ�
2(x+1)�|(2x�|1)=3
�s���t(4)�̉��
�i��j
�C�j �|1��x<1�̂Ƃ�
�E�j 1��x�̂Ƃ�
�i���j
�C�j �|1��m<1�̂Ƃ�
�E�j 1��m�̂Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D�s���t(4)�̉���̂ݒ������܂����D���͍̗p���܂���D
���m�ʂ̕ł���̎���ɑ���n[�W���̗v�f��p�����ؖ��ɂ��ā^19.07.04�n
���2��(2)�̉�����͂̉�����4�s�ڂɁAx∉B�͏ؖ��ł������ɂȂ��A�Ə����Ă���܂��B�������́Ax��B�͏ؖ��ł������ɂȂ��A�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^19.07.04�n
�y���S�z��(3)��(4)�̉���̍ʼn��i�́A��d�������������\�L����Ă��炸�A��d�����Ƃ��Č���ĕ\�L����Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D��d�������͂���āC��d�����Ƃ��Đ������\������Ă���Ƃ����ׂ�
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓������ �ɂ��ā^19.07.03�n
[1] ����̗L�����̗ޑ�̉���̍ʼn��i
�i��j
2��3/6
�i���j
2��30/6
[2] �Ώ̎��̒l�́y���Q�z�̉���̍ŏ�i
�i��j
xy=1/(��7+��3)(��7+��3)=1/4
�i���j
xy=1/(��7+��3)(��7-��3)=1/4
[5] ���������C���������́y���T�z��[2]��(2)�̉���̍ʼn��i
�i��j
(())
�i���j
{()}
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^19.07.03�n
�y���S�z��[1]�̃L��y���T�z��[2]��(3)��y���T�z��[3]�Ŏg���������̏��@�́A�܂���ŏK���A�ƂЂƌ������Ă��ǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D�������̃y�[�W�Ȃ̂ŁC���Z3�N�������Ɛ����ǂ�ł���Ƒz��
���m�ʂ̕ł���̎���ɑ���n[�t�E���E���ɂ��ā^19.07.03�n
A���t���܂ɂ����L���AE�����E���ɂ����L���̈Ӗ��͂Ȃ�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D

�́C�����ɏ����܂����悤��all�i���ׂẮj�Ƃ������Ƃ�\���L���ŁC�����͎����Ƃ���C�Ⴆ��
&chf=bg,s,fff6f6)
�́C�u���ׂĂ�x�ɂ��āCx
2��0�v�����藧�Ƃ����^�̖���ɂȂ�܂��D�������C
&chf=bg,s,fff6f6)
�́C�u���ׂĂ�x�ɂ��āCx
2>0�v�����藧�Ƃ�������ɂȂ�܂����Cx=0�̂Ƃ����藧���Ȃ�����U�̖���ł��D

�́C�����ɏ����܂����悤��exsist�i����C���݂���j�Ƃ������Ƃ�\���L���ŁC�Ⴆ��
&chf=bg,s,fff6f6)
�́C�u����x�ɂ��āC2x=6�v�����藧�Ƃ����^�̖���ɂȂ�܂�(x=3�̂Ƃ����藧����)�D�������C�����͎����Ƃ���C�Ⴆ��
&chf=bg,s,fff6f6)
�́C�u����x�ɂ��āCx
2<0�v�����藧�Ƃ�������ɂȂ�܂����C����͋U�̖���ł��D
���Z�ł́C����

��

�͎g���܂��C���ׂẮCall�C

�Ɠ������̂����ׂĂ���̂ŁC�����͂Ȃ��ł��傤�D����C���݂���Cexist�C

�����l�ł��D
�y�Z���^�[���� 2012�N�x�F���wI�EA�i�ǎ����j ��P��m�P�n�z�̃J�L��HELP
�i��j
1<0=0.86..
0.64..=3<2
�i���j
1<0=0.866..
3<2=0.634..
�O�߂̃G�I��HELP��0.866..��0.634..�Ƃ��邩��A��̂ĂȂ�A0.86��0.63..�����A�ނ���A�ȗ������ɁA���̂܂�0.866..��0.634..�Ƃ���ق����Ó��H�܂��A�����̈ʒu�����������B
�y�Z���^�[���� 2011�N�x�F���wI�EA�i�ǎ����j ��P��m�P�n�z�̃A�C�E�G�I��HELP
�i��j
A=��2{ x(y�|��10)x+��10(y�|��10) }
�i���j
A=��2{ (y�|��10)x+��10(y�|��10) }
��������
A=��2{ x(y�|��10)+��10(y�|��10) }
�y�Z���^�[���� 2010�N�x�F���w�h�E�`�i�{�����j ��P��m�P�n�z�̃I�J�L��HELP
�i��j
�ix�̌W�����Q�̔{���̏ꍇ�j
�i���j
x�̌W���́A7������A�폜
�����m��ҁn�F�A�����肪�Ƃ��D1�ԖځF1<0=0.86..�Ȃǂ̋L�q�ɂ����āC1��0�͐����ł͂Ȃ��C�I�����̔ԍ��ł��D�����͂��̂܂܂ł��D2�ԖځC3�ԖځF�����D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ꕽ�ρC��䗦�̐����ɂ��ā^19.07.03�n
���킩��ɂ���
���������ׂ����Ƃ���܂Ő������Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D����Ŗڈ�t�ł�
���m�ʂ̕ł���̎���ɑ���n[�Ɨ��Ȏ��s�̊m���C�������s�̊m���ɂ��ā^19.07.03�n
<<���1.4>>�ŗ]���ۂ��l���܂��B�@ABC3
�l��������Ȃ��ꍇ�AABC�̂���1�l����������ꍇ�B�@1/2�~1/3�~1/4��1/24�AA�̂ݓ�����ꍇ1/2�~1/3�~1/4��1/24�AB�̂ݓ�����ꍇ2/3�~1/2�~1/4��2/24�AC�̂ݓ�����ꍇ3/4�~1/2�~1/3��3/24�A(1�{1�{2�{3)/24��7/24�A1-7/24��17/24�Ƃ���̂͊ԈႢ�ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�]���ۂ��g���ĉ������Ƃ��ł��܂�
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^19.07.02�n
5����11�̃q���g���������ɂ����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������̃��x���Ȃ̂ŁC�q���g�����낤���Ȃ��낤���C������̂�����܂�
���m�ʂ̕ł���̎���ɑ���n[�Ώ̎��̒l�i�������j�ɂ��ā^19.07.02�n
��㎮�̖�������Ɨǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă��邱�Ƃ������ĂȂ��悤�Ɍ�����̂́C���������S�O�Șb�ł��D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^19.07.02�n
�ƂĂ��������Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�̓�������ɂ��ā^19.07.01�n
���1.2���������Ē����܂����B
���2��(2)�̇U���1/2<=x<2�̏ꍇ�� x+1=2 �������������m�ɒ��Ē�����Ƃ���ɂ悭�Ȃ�̂ł͂Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�v�]�̓��e��������܂���
���m�ʂ̕ł���̎���ɑ���n[�������̓Ɨ��ɂ��ā^19.06.30�n
�w���@�̖���3�̉̃C�j�i
�i��j
����0�Ȃ��3��-��/��
�i���j
����0�Ȃ��3��-��/��
�w���@�̖���2�̉́u4�m-3�v�u4�m�{1�v�u4�m-2�v�Ȃǂ́A��́A�ǂ�����o�Ă��������A�킩�肸�炩�����B�u�������܂ލ��́A�S�ĂS�̔{���ɂȂ�A�������܂܂Ȃ����́A�v�Z����ƁA�Z�Z�ɂȂ�v�Ȃǂ̐���������Ɨǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�������܂����D�㔼�F�m�͐�����lj�
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �ꍇ�̐��E�m���ɂ��ā^19.06.29�n
�y�Z���^�[���� 2011�N�x�F���w�h�E�`�i�{�����j ��S��z��(3)�́�HELP���ɂ��āA
�v�Z���̒��ɁA
��Fp=1/3 q=2/3
���Fp=2/3 q=1/3
�����m��ҁn�F�A�����肪�Ƃ��D�����D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[����̗L�����ɂ��ā^19.06.30�n
��ԉ��̂ق��́uIII�@�i�R�捪�͔��W�w�K�j�v�̗��́A(2)�̕\�L�������Ă�B
�܂��A�ǂ����Ȃ�A���ꂪ�R�捪�̏ꍇ�̗����������ق����ǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D���ς��Q���鏋�ꂵ�����ɂȂ邪�C�ꉞ�lj����Ă����܂���
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�ɂ��ā^19.06.30�n
�y���P�z��(3)�̉�
�i��j
��96�[��243�[��54
�i���j
��96�[��24�[3��54
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Z���^�[������� �ꍇ�̐��E�m���ɂ��ā^19.06.29�n
�y�Z���^�[���� 2011�N�x�F���w�h�E�`�i�{�����j ��S��z��(3)��HELP�ɂ��āA
��Fp=1/3 q=2/3
���Fp=2/3 q=1/3
�����m��ҁn�F�A�����肪�Ƃ��D�w�E����Ă��邱�Ƃ��ʂ��Ȃ��F���߂���,p=2/3 q=1/3�ƂȂ��Ă���D�܂��C�����(3)�łȂ���(1)�̘b
���m�ʂ̕ł���̎���ɑ���n[�~�ƒ����̈ʒu�W�ɂ��ā^19.06.29�n
�A������������1���������������Ăł���2���������ɔ��ʎ���p����ƁAk�͈̔͂����߂�闝�R���C�}�C�`�킩��Ȃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������c�����ix=k�^�j�łȂ�����C�u�A���������̉��̌��v=�u���L�_�̌��v=�u��x�̌��v�ƂȂ�ix���Q����Ό�_��2�D�����P�Ȃ狤�L�_�͂P�D�����Ȃ�����L�_�͂Ȃ��F�ȏ�̘b�͂����������Ă��Œ��ׂĂ��悢�j
�@������C�Q���������̔��ʎ����g���āC���̎������̌��ׂ�Ƃ悢
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^19.06.29�n
�������|�����ł�����̂ƁA���̌������g��Ȃ���Ȃ�Ȃ����̂�����Ǝv�����A�f��������������@�͊������Ȃ��̂��B
�����m��ҁn�F�A�����肪�Ƃ��D���ƕ\������̂��x�X�g�Ȃ̂��C����Č��Ȃ���Ε�����Ȃ��Ƃ������������̂�…
�����C���̎���ɂ́u���ʂȂ��Ƃ͂������Ȃ��v�u�ŏ��̘J�͂Ő��ʂ��グ��ɂ́v�Ƃ������{�v�z�������Č����܂��D
�@���ʎ�`�C���ʎ�`���Ƃ�ƁC�y�����������Ȃ��̂���Ȃ����ȁD
���m�ʂ̕ł���̎���ɑ���n[�}�N���[�����W�J�ɂ��ā^19.06.29�n
����16�N�x�V-7�̉�����Ae^x�̃}�N���[�����W�J��x���|����悤�Ȍ`�Ɍ����܂����A���ۂ�f(n)(x)=(x+n)e^x�Ɉ���̂ŁA���̂悤�ɏ����������K�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D
}(x)=(x%2B n)e^x&chf=bg,s,fff6f6)
�𗘗p���Ă��ł��邪�C���̏ꍇ�͂�����ȒP�ɂł��ؖ����Ȃ���Ȃ�Ȃ����Ce^x�̃}�N���[�����W�J��x���|��������ȒP�ɂł���Ƃ������Ƃł��D
�ŏ��͂킩��₷�������ł��B�㔼�͎����������đS���ǂނɓ�����܂���ł���
�����m��ҁn�F�A�����肪�Ƃ��D�u�㔼�́v�Ƃ́C����6�ԈȌ�̉�����ڂ����ēǂދC�����Ȃ������Ƃ����Ӗ��H
���m�ʂ̕ł���̎���ɑ���n[�Ώ̎��̕ό`�ɂ��ā^19.06.29�n
���������A�Ώ̎��Ƃ́A�����H�A�̐������Ȃ��B
�y��{�R�z��(3.3)�̉�����Ȃ��B
�y��{�S�z�̐錾���́ux+1/x�̑������v�Ƃ����p��́A���߂ĕ��������ɂ́A�u(x+1/x)+(x+1/x)+(x+1/x)...�v��u(x+1/x)-(x+1/x)-(x+1/x)...�v�Ȃǂ̒P���ȘA���݂̂��v�������ׂāA���f�����B(x+1/x)���P�̗v�f�ƌ��Ȃ������R�Ȏ��̈Ӗ��H
�y��{�S�z�̉���́A���������A�����P�ɕ����ɂȂ��������ł͂�����̂́A(x+1/x)2���A(a+b)2�̌����ɓ��Ă͂܂�A�Ƃ������Ǝ��̂������I�ɂ킩�肸�炩�����B�܂��A����䂦�ɁA(x+1/x)�̏ꍇ�ɂ́AQ��x �|���� 1/x = �K��1�A�Ƃ����������A���߂͈�́A���̂��Ƃ������Ă���̂��A�Ӗ��s���������B���Ɂu�ς��^�����Ă��Ȃ��Ă��v�Ƃ��������́A�킩�肸�炩�����B
�y��{�S�z�̉���́un��1/x�̑Ώ̎��v�Ƃ����p��̈Ӗ����킩��Ȃ������B
�y���S�z��(3)��(4)�̉���̎��́A�y��{�Q�z�̌����Ƃ��y��{�S�z�̗�ŋ������Ă��鎮�Ƃ���v���Ă��炸�A���f�����B
�����m��ҁn�F�A�����肪�Ƃ��D�u�Ώ̎��Ƃ́A�����H�A�̐������Ȃ��B�v�F�m���ɂ����ŁC�ȒP�ɏ����邪�C���ۂ̎g�����ɑ����Č����ƁC���̕K�v���Ȃ��ƍl������D���Ȃ킿�C�Ώ̎��̕ό`�Ƃ������������Ȃ���Ȃ�Ȃ��l���C������������ė���Ƃ����̂��قƂ�ǂȂ̂ŁC�Ώ̎��Ƃ͉�����������Ȃ��l�͂܂����Ȃ��D
�y��{�R�z��(3.3)�̉�����Ȃ��B�F���ɂ���̂��v��ŁC���ۂ̖��͖��3(2)�̂悤�ɉ����D
�ȉ��́C�R�����g�Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̌v�Z�ɂ��ā^19.06.28�n
�i�r�̑O�̍��ڂ́u�����ƍ����i�����Ɨ�j�v��File Not Found�ɂȂ�B
���������̂Q����܂ލ����̉����
�i��j
��32=��9=3 �ł��邪��(�|3)2=��9=3 �ƂȂ�
�́A
�i���j
��32=��9=3 �ł��邪��(�|3)2=��9=-3 �ƂȂ�
�̊ԈႢ�H
���������̂Q����܂ލ����̗�́A�܂��A���ꂼ��ɓ�����0�ɂȂ鐔�l�������āA����������������̂Ƃ���ȏ�̂��̂ŏꍇ�������Ă���A�Ɩ������Ă���Ɨǂ������B�܂��A�����̂S�̏ꍇ�������P�ɂ܂Ƃ߂鎞�̎菇��R�c���������Ă���Ɨǂ������B
���S�̉ł́A(a+1)2��a2+2a+1�ƕ��ʂɓW�J���Ă���̂ɁA���������̂Q����܂ލ����̗�ł́A����Ƃ͂܂��Ⴄ������{�����Ƃ̗��R�ɂ��Ă�������Ɛ������Ă���Ɨǂ������B���������̂Q����܂ލ����̗�ł́A�����L�������̂܂ܓW�J�����ɊO�����Ƃɒ��ڂ��Ă���A�Ƃ����Ӗ��H
�����m��ҁn�F�A�����肪�Ƃ��D�i�r�̌��F�������܂����D�㔼�F�ԈႢ�͂Ȃ��D��̋L�q�F�����������Ƃ��Ă��邩�ʂ��Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^19.06.28�n
����(3)�́A-2��x��2�ł͂Ȃ��͉̂��̂ł����H
x��-2�C2��x�͈̔͂�x�̒l�͂��蓾�Ȃ��Ǝv���̂ł����c�B
�����m��ҁn�F�A�����肪�Ƃ��D���̉����1�y�[�W�����Ă���Ă���̂�����C1��������Ԃ��Đq�˂�Ƃ����̂́C�ǂ��ȂH
�㔼�F���R�u�܂��́v�łȂ����Ă��܂��Dx��-2�̂���2��x�̂��͓���x�ł͂Ȃ��D�����������Ƃ͒��w�Z���牽�x���o�Ă����͂��ł��D�Ⴆ�Cx2=4�̉���x=2, −2�ł����Cx=2��������x=−2�ł͂Ȃ����ƂɂȂ�Cx=−2��������Cx=2�łȂ��Dx=2����x=−2�Ƃ������̂�����͂��͂Ȃ�����,���Rx=2�܂���x=−2�Ƃ������Ƃł��D
����Ɍ����Cx��2�Ȃǂƌ����L�������������v���͂��ł��Dx<2�Ȃ�x=2�ł͂Ȃ����Cx=2�Ȃ�x<2�ł͂Ȃ��̂�����Cx��2�Ƃ����L����=��<�̂ǂ��炩����i�܂��́j�����藧�Ƃ������ƂŁC�i���j�łȂ���͂��͂Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.06.28�n
���w�̃e�X�g��Ƃ��āA�ƂĂ����ɗ����܂���
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���s�����ɂ��ā^19.06.27�n
�o���Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���ꂾ���ł͎肪����s���ŁC�����悤���Ȃ��ł�
���m�ʂ̕ł���̎���ɑ���n[���������̓�������ɂ��ā^19.06.27�n
�y���R�z��(1)�̉�
�i��j
(x2+4x)2+8x2+32x+15=(x2+4x)2+4(x2+8x)+15
�i���j
(x2+4x)2+8x2+32x+15=(x2+4x)2+8(x2+4x)+15
�y���S�z��(1)�̉�[1] ��������S�̂�����ꍇ�́A������(b�|a)3�|(b�|c)3�|(c�|a)3�̏�����(b�|a)3�Ɂ|1���O��|���ā|(a�|b)3�|(b�|c)3�|(c�|a)3�ɕό`������ɁA���߂́u�|�v�ȊO�����ʂŊ����ā|{(a�|b)3+(b�|c)3+(c�|a)3}�ɕό`����A�Ƃ��������������Ă�H
�܂��A(a-b)�Ƃ������́A�w������̎��ɂ́A(a-b)2n-1=-(b-a)2n-1�Ƃ������ɕό`�ł��A�w���������̎��ɂ́A(a-b)2n=(b-a)2n�Ƃ������ɕό`�ł���A�Ƃ����ߑ�������Ɨǂ������B
�܂��A��������ƁA���̌��(a�|c)=�|(c�|a)�Ŋ��鏊���킩��₷���Ȃ�B
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�������܂����D�㔼�F[1] ��������S�̂�����ꍇ�̑O�Ɂu
^3-(b-c)^3-(c-a)^3&chf=bg,s,fff6f6)
�ƕό`����ƌ��₷���Ȃ�D�v�Ə����Ă���܂��̂ŁC������背�x������鐶�k�́C���������Ε����邩�Ȃ�
�y�ޑ�Ɠ��z��(2.1)�̖��
�i��j
4(ab-cd)2
�i���j
2(ab-cd)2
�y��3.2�z�̉����y���R�z��(2)�̉́A�ux3+y3+z3�|3xyz=(x+y+z)(x2+y2+z2�|xy�|yz�|zx)�v�̌����ւ̑����̗l�q���P�x��������Ƃ����`�Ŏ������ɁA������(�c)�Əȗ����������킩��ɂ��������ł��B�܂��A�y�ޑ�Ɠ��z��(3.1)�̉��A���̌�����K�p�����̂��A�P�u�A�˘f���܂����B�܂��A�y�ޑ�Ɠ��z�̖��Ɖœ��Ɍ����ł������A���w�҂ɂ��D�������ɂ���Ȃ�A�v�Z�̓r���̎�����A�ȗ����Ȃ��A���̑����ό`�����̌�����K���Ɋ�Â��ĉ������̂��������������{��Ő�������A��O�ꂷ��ƁA�����Ƃ킩��₷���Ȃ�A�Ǝv���܂����B���̏�Ԃł́A���������������Ă�������A���Ƃ́A�������g�ŏ���ɍl���ĉ��߂��Ȃ����A�Ƃ����悤�ȕs�e�ŕ��C��`�I�ȑԓx���Ƃ���ǂ���Ŏf���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D2���Q�悵����4�ɂȂ�̂ŁC���̎��Ő������͂��ł��D
�y��3.2�z�̉����y���R�z�́C���̑O�Ɍ����������Ă���C���ꂵ���Ȃ��̂ł�����g���͓̂��R���ƍl���܂��D�i���p���̃y�[�W�Ȃ̂ŁC����Ȃ�Ɋ�{���K���ς܂����l������Ă���Ƃ����O��ł��j
���m�ʂ̕ł���̎���ɑ���n[�����藝�ɂ��ā^19.06.26�n
�����藝�̔�Ꭾ�Ɋ���邽�߂̍��ڂłɉL���g��������}�ɉ����āA�u�t���v�ł͂Ȃ��u�L���v���������̂ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�ėp�Ɛ�p�C��ʂƓ���̈Ⴂ�ł͂Ȃ��ł��傤���D����\���̎��Ԃł͂���܂���C��������g�����Ƃɂ���Đ��w���炪����ł��i�ނ̂��C�E���҂��ǂꂭ�炢�o��̂��̊|���ł��D�u�L���v�ʼn����ʂ��āC���Ƌ��s�{�ȊO�̐��k���C�w�K��������ꍇ�����������Ȃ����D�ǂ��炪�����܂肪�����Ɨ\�z�ł��邩�̔��f�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[ ���������i���p���j�ɂ��ā^19.06.26�n
�y���Q�z��(3)�̉��
�i��j
=(x2+2x�|12)(x2+x�|12)�c�i���j
�i���j
=(x2+2x�|12)(x2+3x�|12)�c�i���j
�y���S�z��(1)�̉��
�i��j
x4+3x2+4=(x2+2)2�|xx2�ƕό`�����
�i���j
x4+3x2+4=(x2+2)2�|x2�ƕό`�����
�y���P�z�y���Q�z�y���R�z�y���S�z�̂��ׂ�
�i��j
���̊e��
�i���j
���̊e����
�y�ޑ�Ɠ��z��(1.2)�̉�b2c���Q����
�i��j
a2b+abc+a2c+b2a+b2c+abc+abc+b2c+c2a-abc
�i���j
a2b+abc+a2c+b2a+b2c+abc+abc+c2b+c2a-abc
�y�ޑ�Ɠ��z��(1.3)�̉�
�i��j
(b+c)(a-c)(b-a-c)�c�i���j
�i���j
(b+c)(a-c)(b+a)(b-a-c)�c�i���j
�y�ޑ�Ɠ��z��(1.4)�̉�
�i��j
3��������
�i���j
2��������
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�������͕̂M�҂ł����C�����������Z�p�ɂ͐�������i�y�R�j
���m�ʂ̕ł���̎���ɑ���n[�ꍇ�̐��E�m���C�Z���^�[������襥��ޑ��ɂ��ā^19.06.26�n
�ꍇ�̐��E�m���̃Z���^�[�������(�_�̐i�ݕ�)->��2��->��(3)��ɂ���
1��ڂɌ��_�Ɏ~�܂�m�� = 1/6
2��ڂ�5�̓_�Ɏ~�܂�m�� = 1/36
2��ڂɌ��_�Ɏ~�܂�m�� = 5/36
�Ȃ̂ŁA
���������2���Ď~�܂�Ȃ��m�� = 1 - (1/6 + /1/36 + 5/36) = 2/3
������2���Ăǂ̈ʒu�ɂ��Ă�3��ڂɌ��_�Ɏ~�܂�m�� = 1/6
�Ȃ̂ŁA�ŏI�I��
3���邱�Ƃ��ł���3��ڂɌ��_�Ɏ~�܂�m�� = 2/3 * 1/6 = 1/9
�Ƃ����l�����͑��v�ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��Ǝv���܂�
���m�ʂ̕ł���̎���ɑ���n[��{�I�ȎO�p��(�}����)�ɂ��ā^19.06.25�n
�������ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��F��{�v�Z�ɂ��ā^19.06.25�n
�f���炵���A�����ƍ���Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^19.06.25�n
��������Ƃ������w�̖��́A�l�ɂ���čl�������قȂ邽�߁A���̂悤�Ȗ����o�肷�邱�Ƃ͗��_��D�܂����Ȃ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����̖��łȂ��C���ׁi��������ׂ����Ƃ������Ɓj�̔��f��S��̘b�����Ă����āC���Ȋ������Ă�����̂ŁC�������ɂ����ł��D���ʂɌ����C�������C�����v���̂͂��Ȃ��̎��R���I�ŏI���̂ł����C��͂菭���⑫���Ă����܂��D
�@��ʂɁC��→���̖���ɂ��āC����Ȃ������͉���ƌ��_�Ƃ̊W�����ł���̂�,���_�̕����������̐��`���ƈ�v���Ȃ��Ƃ��ɁC���̂�→���Ƃ������莩�̂�ے肵�����S���������܂��D���Ƃ��u�������C�p�����C�M���X�ɂ���C�����h���̓h�C�c�ɂ���v�Ƃ�������͐^�ł����C����Ɋ����܂ł́C�u�����h���̓h�C�c�ɂ���v�Ƃ����ꕔ���������Ĕے肵�����Ȃ�ȂǁD
�@�Ȃ��C��������������Ў����̂r�o�h�i�K�������j�ł́C���̗�̂悤�Ș_���E���_��肪�o�邱�Ƃ�����܂����C����p��œ��퐶���̐S���������Ă��邩��C�w�I�łȂ��C�J�K���V�C���̂��ȂǂƋ��ۂ���ƁC�����̍s���͈͂������Ȃ�܂��D���_�����Ȃ��̐��`���ƍ������ǂ�����q�˂Ă���̂ł͂Ȃ��C�_���E���_�����m���ǂ�����q�˂Ă��邱�Ƃɒ��ӁD
�i�u���������� �������f���݂�݂�킩��I��@�̋ʎ蔠�v/��������o��/P.104����̈��p�j
����A�`D���画�f���Ċm���ɂ����邱�Ƃ́C���̂����ǂꂩ�B
A �_�C�r���O���D���Ȑl�́C�T�[�t�B�����D���ł���B
B ���b�g���D���Ȑl�́C�ނ���D���ł���B
C �T�[�t�B�����D���ł͂Ȃ��l�́C�ނ���D���ł͂Ȃ��B
D �J�k�[���D���ł͂Ȃ��l�́C�T�[�t�B�����D���ł͂Ȃ��B
----------------------------------
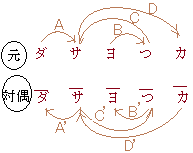
1 �_�C�r���O���D���Ȑl�́C���b�g���D���ł���B
2 ���b�g���D���ł͂Ȃ��l�́C�T�[�t�B�����D���ł͂Ȃ��B
3 �J�k�[���D���Ȑl�́C�ނ���D���ł���B
4 �ނ肪�D���ł͂Ȃ��l�́C�T�[�t�B�����D���ł͂Ȃ��B
5 �_�C�r���O���D���Ȑl�́C�J�k�[���D���ł���D
----------------------------------
�i��5�D����͉E�}�j
���炩������܂��A�������̃O���t�̊g��E�k���̉�����ڂ���������낵�����Ƒ����܂��B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
}%2B q&chf=bg,s,fff6f6)
��

��ς���Ɗg��k���ł��܂����C���Z�ł��̂悤�Ȋϓ_������グ�邱�Ƃ͋H�ł��D���l�ɂ��āC2����
^2%2B q&chf=bg,s,fff6f6)
�ɂ��Ă��C�^����ꂽ�����̒��S�ɑ��Ċg��k�������}�`���l���邱�Ƃ��ł��܂����C��������グ��̂͂��̂悤�ȍ��W�ϊ��Ƃ����e�[�}�̃y�[�W������Ƃ������Ƃ��ƍl�����܂��D
�y��1.1�z�̉��
�i��j
�a���a��
�i���j
�a��
�y���P�z��(3)�̉��
�i��j
�Ⴆ��(2x+3)(x�|4)��(�|x�|3)(�|x+4)�͓������̂�����
�i���j
�Ⴆ��(2x+3)(x�|4)��(�|2x�|3)(�|x+4)�͓������̂�����
�y���P�z��(3)��(4)�̉���̂������|���̉摜�������N��H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�R���ȏ�̈��������ɂ��ā^19.06.24�n
���1��(2)�̉��
�i��j
9x2�|+6xy+42=0�̉��������ɂȂ�
�i���j
9x2+6xy+4y2=0�̉��������ɂȂ�
���3��(1)�̉�����ρB
�������Ƃ��Q�x�A�����Ă���B
�u���W���͈̔͂ł�x2-3��x2+1�̕���������ȏ�����������邱�Ƃ͂ł��Ȃ��D�v�������H
�i�P�����{�j�i�Q���̕�������ցj�ˁi�R���͗��[�����c��j
�i�P���̕�������ցj�i�Q���̕����͈��j�ˁi�R���͗��[�����c��j
�̓��{�ꂪ�킩�肸�炢�B
�u�P�����̕����́A�e���̕�����+�ň��v�u�Q�����̕����́A�e���̕�����+��-�Ō�ցv�Ȃǂ̂ق����ǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D�O���Q��→�������܂����D�㔼�F�����ɐԂƐ̕����ŏ�����Ă�����e���ǂ��\�����邩�ł����C�l�ɂ���ĕ�����Ղ����W�b�N�ɑ���͂��蓾�܂����C�u�P�����̕����́A�e���̕�����+�ň��v�Ƃ�����ɂ͂܂Ƃ߂��܂���D
���m�ʂ̕ł���̎���ɑ���n[�R���ȏ�̈��������ɂ��ā^19.06.23�n
2x3��+16�̉��������킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D����̎d�����ςł��D�u2x3��+16�̉������v�Ƃ͌���Ȃ��D�u2x3��+16=0�̉������v�u2x3��+16�̈��������̕��@�v�Ȃ猾���܂��D���̃y�[�W�͐��w�T��3�����̈��������̋��ނȂ̂ŁC�ꉞ�C�u2x3��+16�̈��������̕��@�v�Ƃ������₾�Ƃ��܂��D
�m�n
=2(x%2B 2)(x^2-2x%2B 4)&chf=bg,s,fff6f6)
�ɂȂ�܂��D
16������3�悩�ƍl����Ɛ��w�T�͈̔͂Ō�����܂��C��ɂQ�ł�����Ɖ��ł��Ȃ����ł��D�ގ��̖��́C���w���̊Ԃɉ��x�����K����͂��ł��D
=2(x%2B 5)(x-5)&chf=bg,s,fff6f6)
(��4)��x��2�̂Ƃ��A��ϕ����̕���́A���[�g�̒���4�|4��0�ƂȂ��`����Ă��Ȃ��̂ł����A���v�ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ��Ȃ��s���C��������ł��D
�@���s�̋���ے��ł́C
=1\]&chf=bg,s,fff6f6)
�̂悤�ɐϕ���Ԃ������̏ꍇ��C

�̂悤�ɁC�ϕ���Ԃ��L�E�ł���ϕ��������̒���1�_�Ŗ����ƂȂ���́m�L�`�ϕ��n�͊w�K�w���v�͈̂̔͂���E������̂Ƃ��Ĉ������Ƃ������C�茳�̋��ȏ��ɂ��̖�肪������Ă�����̂͂Ȃ��悤�ł��D
�@���W�E�Q�l���ł́CA�u�����Ēʂ�v,B�u�L�`�ϕ��̉�������Ă��甭�W�w�K�ɂ���v,C�u���H��ʊ�ŕ��C�ŏo�肷��v��3�̑ԓx�ɕ������悤�ł��D
�@���݂́C�͔͉̌��J�Ȃǂ����߂���V�r�A�Ȏ���Ȃ̂ŁCC�̑ԓx�ʼn����ʂ��͓̂����������܂��C���͖̂�肠��܂���D

�Ƃ����Ӗ��ł��D
�y���R�z��(2)�̉�
�i��j
x4�|3x2+1=(x2�|1)�|x2
�i���j
x4�|3x2+1=(x2�|1)2�|x2
�y���R�z��(3)�̉�
�i��j
x4�|10x2+9=(x2�|3)�|4x2
�i���j
x4�|10x2+9=(x2�|3)2�|4x2
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�ŋߍ�������̂́C�l�̃`�F�b�N���ʂ��Ă��Ȃ����Ƃ������悤�ŁE�E�E
���m�ʂ̕ł���̎���ɑ���n[�w���@�̓�������ɂ��ā^19.06.22�n
�y���2.2�z�ł����A(1)�Ȃ������u(n/m)���g�\�ȕ����h�Ȃ�A(m+2n/3m+5n)���g�\�ȕ����h�v�������Ă���悤�Ɋ������܂��B����āA���ǂ̂Ƃ���A��ؖ��@�Ɣw���@�́u���E���v�Ƃ����̂��A���܂ЂƂn�b�L�����Ȃ��悤�Ɋ������Ă��܂��܂��B���܂��ؖ��ł���Ε��ނȂ�Ăǂ���ł��ǂ��̂����m��܂���...
�����m��ҁn�F�A�����肪�Ƃ��D���߂̕��́i���ۂ̎菇�j�ɏ����Ă��܂����CA�u

�v�������̂���ؖ��@�ŁCB�u

����

���疵���i

����

�j�v��C�u

����

���疵���i���w�I�펯�ɔ����邱�Ɓj�v�������̂��w���@�Ȃ̂ŁCB�̃X�^�C�����Ƃ�C�w���@�̈ꕔ�͑�ؖ��ɂȂ�܂��D

�����肷�邩���Ȃ����̈Ⴂ�����ł��D
�u���E���v��T�����Ƃ���ƒT���ɂ����ł��傤.
�y��Ȍ����z��(4)�̍��ӂ̎����Ⴄ�Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�P������Ă��܂����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.06.22�n
������ �������� �킩��₷�� ������ �ڂ����������Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D���\�ڈ�t�ł���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.06.22�n
�u�̗�𑝂₵�ė~�����Ⴆ��(3a+2b)(4a-5b)�Ƃ��ׂ��������Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D��ɏ����Ă��܂����C[V]�̓o���o���ɂ��ďW�߂�u��肩���v���g�ɕt���Ă���悭�C���ʂ��u�o����v�K�v�͂Ȃ��D�̂ŁC���ɗ��K�͂��Ȃ��Ă��悢�ƍl���Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[�������|�����������i�Q�����j�ɂ��ā^19.06.21�n
x�ɂ��Đ������鎞�A�ꎟ�̍��ɂ��ẮA�}�C�i�X�����ʂ̒��ɓ����̂ɁA�萔�̍��ɂ��ẮA�}�C�i�X�����ʂ̊O�ɏo���A���Ƃ̗��R�ɂ��Ă�������Ɛ������Ă���Ɨǂ��A�Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��DPC�ł̕��ŁC����}�̃f�B���N�g���w�肪�Y���Ă��܂����̂ŁC�����܂���
���m�ʂ̕ł���̎���ɑ���n[�~�̕������ɂ��ā^19.06.21�n
�~�̕������̈�ʌ^�ʼnE�ӂ�0�ɂȂ����C�ɂȂ�̂ōڂ��ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u��ʌ^�ʼnE�ӂ�0�ɂȂ��v�̌��t�ʂ肾�Ɗ��ɏ����Ă���܂����Cr2=0�ƂȂ���q�˂Ă�����悤�Ȃ̂ŁC���̗���lj����܂����D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^19.06.21�n
�u�����4���@���̎���������������D�v�Ɉȉ��̖�肪����܂����B
6x2+20xy+14y2+29x+49y+35
x�ɂ��Đ������āA
6x2+(20y+29)x+(14y2+49y+35)
�Ƃ���ŁA(14y2+49y+35)�̕����́A7(2y2+7y+5)����7(y+1)(2y+5)�܂ň��������ł��܂��B
�Ȃ̂ŁA�Q���ƁA(7y+7)(2y+5)��(y+1)(14y+35)�̗����̑g�ݍ��킹���ł��邱�ƂɂȂ�܂��B
���(y+1)(14y+35)�̂ق����������̂ł����A�������|�������Ă��v�Z������Ȃ��̂ŁA�Y�݂܂����B
�����m��ҁn�F�A�����肪�Ƃ��D7(y+1)(2y+5)����7���ǂ�Ƒg�ނ���2�ʂ�C���̂ǂ�Ƒg�ނ���2�ʂ�C�i�����͐��̂݁j������4�ʂ�̂����ō������̂�T���Ƃ������Ƃł��D���ɕς�������ł͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�����Œ�̕����Ő����ɂ��ā^19.06.20�n
�i�r�Q�[�V���������̃y�[�W�����E���ɕ\�������B
�����m��ҁn�F�A�����肪�Ƃ��D���ɕ\������i���̍��W��^����j�Ƌ@��ɂ���Ă͌����Ȃ����̂�����悤�Ȃ̂ŁC�E�ɕ\�������y�[�W������܂����C�s�s���͂Ȃ��ł��傤
���m�ʂ̕ł���̎���ɑ���n[�����W���ɂ��ā^19.06.20�n
�����W���A�ƂĂ��悭�킩��܂����B
��w���Ȃ̂ł����A�������蕜�K�ł��܂����B
���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̈��������ɂ��ā^19.06.20�n
���5��(1)�̉�
�i��j
�����|24
�i���j
�����|6
���5��(2)��(3)�̉́A�擪���t�ɂ��Ȃ��ꍇ�ɂ́A�������t�ɂ���K�v�����邱�Ƃ�����A�Ƃ������Ƃ������s�����A�Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�O���F�������܂����D�㔼�F����͂����ł����C�������̂�T���Ƃ������Ƃ̒��ɂ́C�g��ς��邱�ƁC������ς��邱�Ƃ��܂܂�܂�
���m�ʂ̕ł���̎���ɑ���n[�W�J�����̉��p����ɂ��ā^19.06.20�n
���Q�z��(3)�̉�
�i��j
�S��
�i���j
�O��
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.06.20�n
����������������������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̌v�Z����Z���^�[��������ɂ��ā^19.06.20�n
��ς��肪�����T�C�g�ł��B�����b�ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�̏����ɂ��ā^19.06.19�n
�y���P�z��(6)�̉�
�i��j
�Q���̍��ƒ萔���ɓ��������o�Ă���悤�ɁC�g�������l���܂��D
=(x2�|4x)2�|53(x2�|4x)+672)
�i���j
�Q���̍��ƂP���̍��ɓ��������o�Ă���悤�ɁC�g�������l���܂��D
=(x2�|4x)2�|53(x2�|4x)+672
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����2�ɂ��ā^19.06.19�n
�y���P�z��(3)�̉�
�i��j
(-2x-3y)2=(-2x)2+(-2x)(-3y)+(-3y)2
�i���j
(-2x-3y)2=(-2x)2+2(-2x)(-3y)+(-3y)2
�y���Q�z��(1)�̉�
�i��j
{x-(4y)}
�i���j
{x+(-4y)}
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂƒ����ɂ��ā^19.06.18�n
�y��Q�z��(B)�̉�����
�i��j
2a+3b+3c=0�c(3)
2a+3b(�|3c)�c(3�f)
�i���j
2a+3b+3c+d=0�c(3)
2a+3b+3c=(�|d)�c(3�f)
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^19.06.18�n
:8��0000��4���̓d�b�ԍ��Ƃ��ĕs�K���Ȃ̂�715-1��714�ʂ肪�����ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�s�K���ł͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[��ʍ��̋L���ɂ��ā^19.06.17�n
���Z���㐔��̊�b�������ł��Ȃ��������̂ł��B�w�Z�́u�����\�K�ł�����ȁv�Ǝ��Ƃł͋����Ă��ꂸ�A�ΖʂŘb���Ă��n���ɂ���邩�A���������������邾���ł��̐������ł�������Ӗ����狳���Ă���܂���ł����B
��l�ɂȂ�A�����S���N�����̂悤�ȃT�C�g�������Ă��܂����A���̃T�C�g�͓��ɂ킩��₷�������ł��B
���K���S����ł��܂����B
���������Ɏ��M�����Ă�悤�ɂȂ�܂����B
�܂��A���̋x���ɖK�ꂽ���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^19.06.17�n
���͈�Ìn�̑�w�ɒʂ��Ă��܂��B
�^���w�̕���Ńx�N�g�����g�p�����v�Z������̂ł�����͂����A������Ȃ��̂ł����A�����ł��ǂ̂悤�ɂ킩��Ȃ��̂��������炸�����Ă��܂�
���Z�̎��ɕ����A���wB�Ȃǂ�����Ă��Ȃ������̂łЂƂ����Ă������h���v�������Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D��Ìn�ŕK�v�ȉ^���������Ƃ����̂�������܂��C�x�N�g���ŏ�����Ă���������́C�����ɕ�����Ε��ʂ̕������ł��D�������ʂȂ��Ƃ͏����Ă���܂���D

��

���܂Ƃ߂ď��������̂ł��D
���̑��C��������Ō˘f�����Ƃ����邩������܂��C�ȒP�Ȗ��̐������Ȃ��Ċ�������������������܂���D
�i�s���L���Ɍ����C�u�炭�Ȃ����Ƃ��A�ꂵ���Ƃ��A�{�N�̊���v���o���Ă��������B���̖��ɂ������܂���I�v�j
�Q�l�ɂȂ�܂�����
���j�^�[�̏�ɒ�������I�@�Ǝv�����狛�ł���...
(���\�т����肵�܂�����)
�����m��ҁn�F�A�����肪�Ƃ��D���k���ދ����Ȃ��悤�ɁC�V�ѐS�ł��܂���
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^19.06.16�n
�y���V�z�̉�
�i��j
p�|3/�|2=q+8/4=r�|1/6
p�|3/�|1=q+8/2=r�|1/3
�i���j
p�|3/�|2=q+8/4=r+1/6
p�|3/�|1=q+8/2=r+1/3
�m���13�n�́A�����x�N�g�������ʂɌv�Z������}�C�i�X�ɂȂ����̂ŁA��u�A�����܂����B
���̃T�C�g�́A��{�A�������b���璚�J�ł킩��₷���ł��B
���ꂩ�珇�ԂɑS���A�ǂ�ł����\��Ȃ̂ŁA�܂��~�X�ɋC�t������A�������Ă��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�r���o�߂̕����ɊԈႢ������܂����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�m���C�Z���^�[��������ɂ��ā^19.06.14�n
�P��ŏI���̂�3�ʂ�A2��ŏI���̂�9�ʂ�A3��ŏI���̂�54�ʂ�Ȃ̂ŁA�P��܂��͂Q��ŏI���m����(3+9)/(3+9+54)
�Ƃ����l�����������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����̎d���������̂Œ��ӂ��܂��傤�D�܂��C����ɑ���Ƃ��ẮC�u�ԈႢ�v�ł��D
�@���̋��ނɂ���̂Ȃ�C�ǂ̖��̘b�Ȃ̂��������ׂ��ł��D�������߂��̂���2�₾���Ȃ̂ő�2��ɑ��鎿��Ƃ��܂��D
�@��ʂɁC����Z�������������˂Ɋm����\���킯�ł͂Ȃ��D����Ɏg�������ׂĂ̏ꍇ�̐����C�e�X�u���l�Ȋm���炵���ŋN����ꍇ�v�ɂ����m����\���܂��D1��ŏI���̂́C�S����6�ʂ�̓���3�ʂ�D2��ŏI���̂́C�S����36�ʂ�̓���9�ʂ�D����3��9�𑫂��Ă��C�����\���Ȃ��D�i��������������C1��ŏI���̂͑S����36�ʂ�̓���18��Ƃ��Ȃ���Ȃ�Ȃ��D�m�����2��ڂ̏�������������āC�S����36�ʂ�̎��s�����l�Ȋm���炵���ŋN����悤�ɂ��Ă����Ȃ���Ȃ�Ȃ��n�j
�@����ɂ��(18+9)/36=3/4�Ƃ��܂�
���m�ʂ̕ł���̎���ɑ���n[���̊p�C���̊p�ɂ��ā^19.06.13�n
�O���t���̎O�p�`�̊p�̑傫������ʊp�ŕ\�����Ƃ͂ł���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̎��̃y�[�W����ʊp�̋��ނł��D
���m�ʂ̕ł���̎���ɑ���n[�K�������ɂ��ā^19.06.12�n
�ƂĂ�������₷���Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^19.06.11�n
�ƂĂ�������Ղ������ł�
�Y�݂��������܂���
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ԍ��D�̂��炢���ɂ��ā^19.06.10�n
���3�ōd�݂̕\�����t�ł́H�Ǝv���܂������A�����ǂł͐������L���Ă�����𗠂ƌĂ�ł���Ƃ̂��Ƃł��B���w�ȊO�̂��Ƃ����ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���a�̎���̏��w�Z�ł́u�����@�P����=�G�͕\�v�Ɗo���܂������C5�~�ʂ����͂�₱�����D�G�Ɛ������������ɂ����āC�t�̕��ɂ͐����N����������D5�~�܂ł܂Ƃ߂���C�G�͕\����
���m�ʂ̕ł���̎���ɑ���n[�����̃x�N�g���������ɂ��ā^19.06.10�n
���3�Ň�ABC�̐}�̔䗦�Ɛ���BC�̓����̔䗦���Ⴂ�܂��H�܂��A��BC��7�F5�ɓ��������Ƃ��̒l�ɂȂ��Ă���C�����܂�(�����ԈႦ�Ă��Ȃ����)�B
�����m��ҁn�F�A�����肪�Ƃ��D�}�̌��������BE�̕��������悤�Ɍ����܂����C�v�Z��͂��̋��ނ̒ʂ�ł�
�@���ۏ�́C���S�ɔ䗦�ɍ����}�����������_�������₷���̂ł����C��������Ə��w�����������ő����Ă���������悤�ɂȂ�̂ŁC���₵���D�����h���̂��P�̎肩�ȂƁD�������C�������Ȃǂł��̎���g���ƁC���x���̈قȂ�c�_�����藐��āC�L�҉���ς킵���Ȃ�̂ŁC���������V�r�A�ȏ�ʂł́C�ړx�����킹�Ă����Ǝv���܂��D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����钼���̕������ɂ��ā^19.06.10�n
�y���P�z�̉̒��F�̕����Ɖ摜�̐F�̓_P�̍��W��Y��Z�̐��l���t�B
�i��j
(1,-3,1)
�i���j
(1,1,-3)
�m���U�n�̉�
�i��j
cos��=�|15/10��2=�|��3/2
�i���j
cos��=�|15/10��3=�|��3/2
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[Excel��p�����x�N�g���̌v�Z�ɂ��ā^19.06.10�n
�R�T�C�����Ȃ��Y��Ă����قǂ̑f�l�ł����A��ϕ�����₷�������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ ���������i���p���j�ɂ��ā^19.06.10�n
�قڈÎZ�ʼn����܂����B
���܂艞�p�ł͖��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D ���������i���p���j �J���č���Ă���̂ɈÎZ�ʼn����Ă��܂��Ăǂ�����˂�D�u�����̔ӌ�т͍��̂�1���ԁC�H�ׂ�̂�1���v�ƒN��������������̂Ƃ悭�����P�[�X����
���m�ʂ̕ł���̎���ɑ���n[�_�ƒ����̋����̌����ɂ��ā^19.06.10�n
���P�i�R�j�@�Ԉ���Ă���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�v���Ԃ�Ɂu��肪�Ԉ���Ă���I�v�œ˂����܂�Ă��܂��܂����D�����C���͍����Ă��邪�C���̕������Ԉ���Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[�萔�W���̂Q�K���`�����������i���j�ɂ��ā^19.06.09�n
����2����`�����������Ɋւ��āA
�Ⴆ�� y�f�f-y�f=e^x �̈�ʉ������߂鎞�ɂǂ�����Ηǂ��̂ł��傤���H
y=Ae^x�ƒu���Ĕ������đ�����Ă�����..
y�f�f-y�f=0�ƂȂ��Ă��܂������Ȃ��Ȃ��Ă��܂��܂�.
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��͋��ނ�^�ʖڂɓǂ�ł��܂���D��ʉ��̋��ߕ��Ɠ�����̋��ߕ��ƍ����Ă��܂��D�܂��C������̋��ߕ���2��܂Ŏ��s���Ă悢�Ƃ����ӏ����ǂ�ł��܂���D����Ɍ����Cy�f�f-y�f=�Ƃ����̂͂Q�K�����������Ɍ����܂����Cy'=z�Ƃ����C1�K�����������ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�K���ɂ��ā^19.06.09�n
100!���A�v�Z���邱�Ƃ��ł���݂����ł��B
https://www.desmos.com/calculator/mqguoc4xi1
�����m��ҁn�F�A�����肪�Ƃ��D�T�����Ƃ��Ă��ꂽ�ӗ~�ɂ��Ă͕]�����܂����C����́u���ʂ́v=Excel�Ȃǐ��k�����ʂɏo�=�\�t�g�Ƃ͌����Ȃ��ł��傤�D100!�̌��ʂ����Ȃ�C���̃v���O������Python�ɏ������߂Ε\������܂��D
import datetime as dt
dt1 = dt.datetime
tn1 = dt1.now()
fact1 = 1
for n in range(1,101):
fact1 *= n
print(fact1)
tn2 = dt1.now()
print(tn2-tn1)
→
9332621544394415268169923885626670049071596826438
1621468592963895217599993229915608941463976156518
286253697920827223758251185210916864000000000000000000000000
���v���Ԃ́C0.008�b���x�ł��D
�����Z�ł悭�o�肳���u100!�ɂ�1�̈ʂ���0�����A�����Ă��邩�v�i24�j�Ƃ��������̓������ڊm�F�ł���Ƃ��낪���݂���
�i�e�w��ԁj�x�N�g���̓��ς̂V�y�[�W��
�i��j
��a· ��b=|��a| |��a|cos�� ������
�i���j
��a· ��b=|��a| |��b|cos�� ������
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̐�Βl�̕ό` �ɂ��ā^19.06.07�n
�y���z�́�Q��̉̉摜
�i��j
|a+b|2=7...(1)
�i���j
|a-b|2=7...(1)
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̘a�A���A�����{�ɂ��ā^19.06.05�n
�x�N�g���̕��s�ɂ��ď����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�ł��D�����ƁC�g�єł̃��j���[�ɂ��̍��ڂ������̂�Y��Ă����悤��…
�E�y�\���m���Q�z��(2)
�i��j
���CP�Ƃ����ƁCX��AP��p:(q+r)�ɓ�������_�ƂȂ��Ă���D
�i���j
���CP�Ƃ����ƁCX��PA��p:(q+r)�ɓ�������_�ƂȂ��Ă���D
�E���S�̉��
�i��j
BP:PC=AB:AC=b:c�����藧�D
�i���j
BP:PC=AB:AC=c:b�����藧�D
�E���S�̉��
�����̉E����(4.1)��(4.2)���t.
�E���S�̉���̂R�ڂ̊p�̓��̒藝�̏ؖ��̐}
�i��j
�x�N�g��b�ƃx�N�g��c
�i���j
�x�N�g��p�ƃx�N�g��q
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ������̓~�X�̑������ЂɂȂ��Ă����悤�Ł`��
���m�ʂ̕ł���̎���ɑ���n[��_�̓�����C�x�N�g���C���f���C���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^19.06.04�n
�E���1�����i�����_�̌������Q�i�K�Ɏg���ꍇ�j�̉E�i�̂Q�摜�ڂ̎��̉��
�i��j
�́CAQ��32:12�ɓ�������D
�܂��CQBC��15:8�ɓ�������D
�i���j
�́CAQ��23:12�ɓ�������D
�܂��CBC��15:8�ɓ�������D
�E�y��ʂ�(1)�z�̖��
�i��j
AQ��BR�̌�_��X�Ƃ���D
�i���j
CP��BR�̌�_��X�Ƃ���D
�E�y��ʂ�(1)�z�̉��
�i���j
�ɂ��CBX:XR=lm+ln:km
�i���j
���ł́Al������o����Ă�̂ɁA�����ł́Al������o����ĂȂ��B
�E�y��ʂ�(2)�z�̉��
���ƍ����̗����̏��ŁACX:XP�̔䂪�t�B
�Ō�ɋt�����|���鏊���ł��ĂȂ��B
�����m��ҁn�F�A�����肪�Ƃ��D1��,2��,4�Ԃ̘_�_�ɂ��Ă͒������܂����D3�Ԃ̘_�_�ɂ��ẮC�ǂ���ł��悢�ƍl����D
���m�ʂ̕ł���̎���ɑ���n[�Q�ߐ��̕������ɂ��ā^19.06.04�n
�Q�ߐ��̎�ނ��������ŕ�����₷���A�Ō�ɖ��������ėǂ������Ǝv���܂��B
���Ɖ��₩���(������ɂ���)����(�Ⴆ�ΎO�p���ɔ͈͂��������)�����H���ɓ���Ă���������ΗL���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���̎��̃y�[�W�͌��܂������H��ʂɎO�p���͐U�����邾���őQ�ߐ��Ƃ͌��т��ɂ����C��������w�����ƎO�p���Ƃ̐ςȂ�Q�ߐ��͂��蓾�܂����C�ނ��댋�_�������₷���C�P���Ȗ��ɂȂ�܂��D
&chf=bg,s,fff6f6)
→�Q�ߐ��͂Ȃ�
\rightarrow 0&chf=bg,s,fff6f6)
������₷��������肪�Ƃ��������܂����B
�����Ȃ̂ł����A�~�̕������̈�ʌ`�i�W�J�`�j�ɁA�Ⴆ��
Dxy(D�͒萔)
�̍����܂܂�Ă����ꍇ�ɂ́A�~�̌`�ɂ͂Ȃ�Ȃ��Ƃ����F���ł�낵���ł��傤���B
�~�̕������̏��������߂���ŋ^��Ɏv���A���₳���Ă��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��Dxy�̍�������ꍇ�C�ȉ~��o�Ȑ�����]�������̂ɂȂ�܂����C���̃y�[�W�ň��������e�Ɣ�r����Ƃ��Ȃ������̂ɂȂ�܂��D2���Ȑ��Ɖ�]�̘b�ɂȂ�܂��D�Ƃ肠�����C�~�̕������ł�xy�̍��͏o�Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�s�̐����ƃN�����[���̌����ɂ��ā^19.06.02�n
�l�͒��w���Ȃ̂ł����A�Ȃ�ad�[bc�̂悤�̂ȂȂ߂ɂȂ�̂ł����H�ڂ��ɂ�������悤�ɐ������Ăق����ł��B���肢���܂�
�����m��ҁn�F���f�肵�܂��D
�� ?�m?����^19.06.02�n
���wA�́u�}�`�̐����v�������悤�ł���
�Ȃɂ����R������̂ł���
�����m��ҁn�F�A�����肪�Ƃ��D���R�͂���܂��D���wA��2�P�ʂŊw�сC3�P�ʕ��̗ʂ̋��ȏ�����2�P�ʕ����w�Z���I�����邱�ƂɂȂ�܂��D�Ƃ���ŁC���ʊw�̕����I�Ԋw�Z������Ƃ���ƁC���̕�����̂Ă����ƂɂȂ�܂��D���̉��l�ςɂ͎^���ł��Ȃ��Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�����̎w���i�L�����̎w���j�ɂ��ā^19.06.01�n
���2��(2�j�ɂ͐����͂���܂���ł���
������3�捪2���̂P�ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̎w���ƕ����i�L�����j�̎w�����Ԉ���Ċo���Ă�����悤�ł��D



�ł��D
�@��������C�����ɐ����������Ă���̂ɁC�����͂���܂���ł���…�ƁC���Ȃ݂̂��^���̏ؐl�ł��邩�̂悤�ɏq�ׂ�̂́C�������Ȃ��̂��D�|�p�̕\���̕���Ƃ��H�ו��̍D�݂̕���̂悤�ɁC�����̐^���������ł��镪��ł́u�N�����Ƃ����Ă������͂���ōs���v�Ƃ������Ƃł��܂����C���w�◝�Ȃ̂悤�ȋq�ϓI�����𑼐l�Ƌ��L���镪��ł́C���������b�̂��荇�킹������S�\�����K�v�ł��D
����ɂ��́B�����������b�ɂȂ��Ă��܂��B40���N�O�̍��Z���ł��B
����Ƒΐ������I��肻���ł��B���ɔ�������������̂ł����A���̋��ނ��Ƃǂ��ɍs�����炢���̂ł��傤���B�ڎ��̔����̍����N���b�N����Ɛ��V�̍��ڂɈڂ��Ă��܂��̂ł��B�ꉞ�����o�ł̐��U�̋��ȏ���Q�l���������Ă��܂����A���̃T�C�g�Ő搶�̉��ŕ������Ē����ƒ��肪����̂ł��B(��A��������̂��W���͂��t���܂��i�j�B�搶�̕������ip�A�h���X�Ō����Ă�̂���)�B��낵�����肢�\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�U�̑������̔������܂��Ȃ炻�̌�����C�ς�ł����琔�w�V�̐���̋Ɍ������肩��
���m�ʂ̕ł���̎���ɑ���n[ �x�N�g���̐}�`�։��p�ɂ��ā^19.05.31�n
����ɂ���E��F�����ʂ��Â炢�ł��B
�����m��ҁn�F�A�����肪�Ƃ��DEdge�ɂ͑Ή�����\�肪����܂���D������Chrome�ł��D
���m�ʂ̕ł���̎���ɑ���n[�s���Ίp������ɂ��ɂ��ā^19.05.30�n
�ŗL�x�N�g���͕����l�����邪�A�ǂ��I��ł��̂��̌v�Z�ɖ��͂Ȃ���
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ���������܂���D�ŗL�x�N�g���������̑g���琬��͕̂��ʂ̘b�ł����C���̊e�X�͒萔�{���Ă��C�K�i�����Ďg���Ă��ŗL�x�N�g���ł��邱�Ƃɂ͈Ⴂ�͂���܂���D�����̑g���琬��ŗL�x�N�g���̂����̂P�����I�ׂC���̌������������\���܂���D
�@������C�������₵�Ă����Ă̂����ʂ��܂���D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����̉��p����ɂ��ā^19.05.30�n
a,b,c�͂���̂Ȃ��ϐ��Ax,y,z�͂���̂���ϐ��Ƃ����傫�ȈႢ������A�Ƃ����_�����ĂɂȂ��Ă��Ȃ��̂��킩��ɂ����Ȃ��Ă��錴���̂悤�Ɏv���܂��B���Ƃ���x,y,z��X,Y,Z�Ȃǂŕ\������̂͂������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ������l���̂悤�ȕ����ɂ�锛��̈Ⴂ�Ƃ������̂́C�����������݂��܂���D
���m�ʂ̕ł���̎���ɑ���n[�Q�~�̌�_��ʂ�~�E�����̕������ɂ��ā^19.05.29�n
�����
p2+q2+ap+bq+c=0
p2+q2+dp+eq+f=0
�����藧�D
���������āCp2+q2+ap+bq+c+k(p2+q2+dp+eq+f)=0 �c(3)
�����藧�D�i0+0k=0 �͐��藧�D�j
�@���l�ɂ��āC (r , s) �ɂ��Ă�
r2+s2+ar+bs+c+k(r2+s2+dr+es+f)=0 �c(4)
�����藧�D
��
3)(4)�́Cx2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0 ���u�Q��_��ʂ�v���Ƃ������Ă���D
�ɂȂ�̂��Ȃ��Ȃ̂��킩��Ȃ��ł�
�����m��ҁn�F�A�����肪�Ƃ��D�傫�Ȉ��ʂ����������C���ݍ��ނ킯�ɂ��������C�f���o���킯�ɂ��������C�n����܂ł��킦�Ă��邵���Ȃ��Ƃ����̂����y�̋����ł��D�����͑����ËL����悢�Ƃ������̂łȂ��C�n����܂ł��킦��̂��K�v�Ȃ��̂�����܂��D
�@P(p,q)�������������CQ(r,s)����������������CP��Q������������=P��Q���Ȑ���ɂ���Ƃ����܂�
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�--�ϕ������̕ύX�ɂ��ā^19.05.29�n
�F�������Ă����Ă킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D�ł���Ίy�����w�ׂ�悤�ɂ������ƍl���Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[�w���s�����ɂ��ā^19.05.29�n
�����́B���̃y�[�W�̃O���t�E�ɂ��Ďf���܂��Bx���ɋL�ڂ���Ă���p��q���t����Ȃ��ł��傤���H(�Ԏ��̕����ł��B)
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�w���s�����ɂ��ā^19.05.29�n
�ł����A���4�̃q���g2�͒�1�^5�̌�A�ł���ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�ł͂Ȃ��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�ɕ������ɂ��ā^19.05.28�n
Android�œ��삵�Ȃ�
�X�^�C���V�[�g�������
�����m��ҁn�F�A�����肪�Ƃ��D�g�єł͕ʕłƏ����Ă���̂ŁC�ʕł����Ă��������D�M�҂�Android�ł͐���ɍ쓮����悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.05.28�n
�C���ɓW�J�Ƃ����\���������ł��ˁI
�����m��ҁn�F�A�����肪�Ƃ��D�Z�C�͋֕��Ƃ������Ƃ�
���m�ʂ̕ł���̎���ɑ���n[�����W��,�A��,�����\�ɂ��ā^19.05.27�n
�w�Z�̏h��v�����g�̉��ہX�����Ă������̂łƂĂ�������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����̌����ɂ��ā^19.05.26�n
����̂Ƃ��낪���������傫���Ƃ��ꂵ���ł��I
�����m��ҁn�F�A�����肪�Ƃ��DiPhone�Ō��Ă���̂ł�����C�g�їp�̃y�[�W�����Ă��������D���̃y�[�W��PC�p�ł��D
���m�ʂ̕ł���̎���ɑ���n[�������̓����ɂ��ā^19.05.26�n
[{f(x)}ⁿ]=n{f(x)}ⁿ⁻¹f�L(x) n�͐���
�����藧��
����́A�������̔����@�̌����𗘗p���ē������Ƃ��ł���炵���̂ł���
�ǂ����ł��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D����͂��܂����C���̃y�[�W��ǂ�ł��̎��₪����Ƃ������Ƃ́C���w�U���K���Ă���r���ł��邩�C�b�̎�Ƃ��ĕ����Ă��邾���i���w�V�͏K���Ă��Ȃ��j�̂悤�Ȋ����ŁC�������ʂ��Ȃ��\��������܂��D
\}^n&chf=bg,s,fff6f6)
�̂Ƃ�

&chf=bg,s,fff6f6)
�Ƃ�����

&chf=bg,s,fff6f6)
^{n-1}f\apos(x)&chf=bg,s,fff6f6)
�Q�l���2�ɂ��Ăł��B8�s�ڂ�
(4X-1)(X+1)=0�ƋL�ڂ���Ă��܂����A
(4X-1(X+2)=0�̌�A�ł���?
�܂����̃y�[�W�Ŋe�₢�ɂ��Đ�������Ɖ�@�̊m�F���ł��܂���B�듚���Ċm�F���邵���Ȃ��̂ł����H(���̃y�[�W�ł����̂悤�Ȃ��̂�����܂����B)
�����m��ҁn�F�A�����肪�Ƃ��D�i�O���j�������܂����D�i�㔼�j�{�^���̃^�C�g����help�Ƃ��Ă����̂ŁC���̈Ӗ��Ɉ��������āChelp���K�v�̂Ȃ��l�ɂ͏o�Ȃ��悤�ɂȂ��Ă��܂������C�m���ɐ����ł�������o������悢�̂ŁC�ݒ�ύX���܂����D���̃y�[�W�ɂ��ẮC�y�[�W�����������Ē��ׂ���Ȃ��̂ŁC�ʂɗv�]���������y�[�W�͐ݒ�ύX����悤�ɂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������|�����������ɂ��ā^19.05.23�n
��肪���������̓�Փx�ł�������!!!!!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�̏����ɂ��ā^19.05.23�n
������₷�����������肪�Ƃ��������܂���🎵
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����Œ�̕����Ő����ɂ��ā^19.05.23�n
�ƂĂ������������₷�������ł�❗️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^19.05.22�n
�����Ղ肱�Ă��Ă̗��K�������Ȏ�ނ������Ă悩����
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴂ���́u���Ă��āv�D�݂ł������C�ŋ߂͐����͂�����Ă��āu��������n�v�̐H�ו��ɂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̑傫���i�����j�ɂ��ā^19.05.22�n
�킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����s�����̉������ɂ��ā^19.05.22�n
���ό`�ɂ���@�ŁA�ǂ����ĕ������������ɂȂ鎞�Ɛ��ɂȂ鎞�ʼn�@���قȂ�̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�̏��߂̕��ɂ���s�����̐����U�C�V��U��Ԃ��


�ƂȂ邩��
\gt (x-2)(4-x)&chf=bg,s,fff6f6)
\lt (x-2)(4-x)&chf=bg,s,fff6f6)
�ƂȂ�܂�
������₷�������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z1�ɂ��ā^19.05.21�n
�ƂĂ��ǂ��ł�🗣❤�����ʼn�����Ƃ��낪���ɂȂ�܂��[
�������\�ł�������������ʂ𑝂₵�Ē�����Ƃ��肪�����ł��I😭💦
���w���O�N��
�����m��ҁn�F�A�����肪�Ƃ��D���ɂ��郁�j���[�����ǂ��āC�����v�Z2→����̗L����→�������̓Ɨ�→���̒l(�������̑Ώ̎�)→xn+1/xn�̒l→�Z���^�[������� �������̌v�Z→�����v�Z�̓������→��d�����Ɛi��ł�������
���m�ʂ̕ł���̎���ɑ���n[�s��ϕ��̕����ϕ��@�ɂ��ā^19.05.20�n
�e�X�g�O�Ȃ̂ł�����������܂����B
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D���Z�ł�5�����{�ɒ��ԍl���������āC6���ɓ��������K�Ƃ��������肩�ȁD��H5���ɐ��w�V�̕����ϕ�������Ă���Ƃ́C�����������ȏ����I���D�i�w�Z����
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^19.05.20�n
����̉́u�ҋ��v�����X�u��v�ɂȂ��Ă��āA�����ɋC�t�������������������B
�����m��ҁn�F�A�����肪�Ƃ��D�����ƁCPC�̊����ϊ������[�U�̂悭�g���ϊ����w�K���Ă��܂��āC����悭�g����傪���ԗl�ɂ�Ă��܂��͍̂��������Ƃł��D�M�҂ׂ͂��ׂ��̏����̂��肪�CPC�Ői�w�Z�Ə����ƁC�^����ɐ_�w�Z�ɂȂ��Ă��܂��悤�Ȃ��肳�܂�…3,4�����������܂����D
���m�ʂ̕ł���̎���ɑ���n[�ݏ捪�ɂ��ā^19.05.19�n
���̃y�[�W�̗ݏ捪⑵�̓�ڂ̃u���b�N(�w�i�F)�����F�̕����ɂ��Ăł��B
�_��3�ڂ�4�ڂ�a>0�ƂȂ��Ă��܂����Aa<0�̌�A���Ǝv���̂ł����������ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D

…(A)�Ƃ������ƂƁC

…(B)�Ƃ������Ƃ́C�������Ƃ��q�ׂĂ��܂��D
�@�قƂ�ǂ̋��ȏ���(B)�ŏ�����Ă��܂����C���F���������C��w�͂̐��k�ł͍������₷�����߁C�M�҂�(A)�ŏ����Ă��܂��D
�@(A)�̋��ނ�(B)�̋��ނ��ɓǂ�ō�������Ƃ́C���̗��������Ă����Ɨ��ɂȂ����݂����Șb����
���߂܂��āA�ŋߕϐ��W����2�K���`����������������Ă��܂����A�悭�����ł��Ȃ������A������ӂɂ��Ă̍u�`������ė~�����ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�t�b�N�X�^�̓��x�����������Ĉ����Ă��܂���D�ǂ��炩�ƌ����C���������߂��ׂ��������C�t�[���G���������Ȃǂ��R���s���[�^�ł��������Ƌ��߂ċC��ϓ���\�z����Ƃ���������ɋ���������܂��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^19.05.18�n
���܂��܂�������܂��A���S��a��5�����ŁA�ŏI���ȊO��a^3�ł������a+1/a�ŊȒP�ɂł��Aa^3*0-2�ƂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���߂�5���������^�ɂȂ��Ă���̂ŁC�m���ɂ���͐��藧���܂��D���܂��܂��ǂ����́C���̕ό`����ʂɒʂ���=�g����@��������ǂ����Ŕ��f����Ƃ悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^19.05.18�n
����̗L�����̗ޑ�ł����A�v�Z�����Ƃ���A(3*sqrt(2)+2*sqrt(3)+sqrt(30))/6�ƂȂ��Ă��܂��B��sqrt(30)/3�͊ԈႢ�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D��蕶�̍Ō�̍��̕������v���X�������炻���Ȃ�܂����C�}�C�i�X�Ȃ̂ʼn̒ʂ�ł��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^19.05.18�n
(a+b+2)(a+b-3)�̓����������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��ǂ�ł���C���̎��₪����Ƃ����̂́C���������D����́C�����g�ɒ����Ȃ������Ƃ������ƂɂȂ邩��D
���(2)���悭�ǂ�ł��琔���������ς���Ɠ������o��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.05.17�n
�킩��₷����������Ă��ėǂ��Ǝv��
�����Ɩ�����|�����������Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D�����|�����Ƃ����Ă��C���ۂɊԈႢ�₷�����łȂ���Ȃ�Ȃ��̂ŁC�Ȃ��Ȃ��v�����Ȃ�����
���m�ʂ̕ł���̎���ɑ���n[���f���ɂ��ā^19.05.16�n
���f�������[�g�ɂ������Ă���ꍇ�������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���[�g���������Ă��鐔������������C

�̋��f����

�ł���Ƃ��C

�̋��f����

�ł���Ƃ��������Ƃɂ͋��f���̒�`�����̂܂ܓK�p����܂��D���̖�������܂���D
�@��₱�����̂́C���Z�̊w�K�w���v�̂����āC��w�ŏK�������Ƃ����̂܂܋�����搶������ꍇ�ł��D�Ⴆ�C
&chf=bg,s,fff6f6)
�̂Ƃ��C

�Ə����Ƃ�����`�Ȃ��ɁC

�����߂�Ƃ����悤�Ȗ��Ӗ��ʂɏo���悤�Ȑ搶�́C�����������Ă��܂���D����͑������ɂȂ�C�f����Ȃ����̌`�ō��Z���ɂ�点��͔̂����ł��D���Z�ł͍����̒��ɐ����̎���������ꍇ�܂ł͑f��őΉ����܂����C�����̒��ɋ���������ꍇ�́C���̊ȒP�Ȓ�`��a�����Ă���C�A����������h�E���A�u���Ɏ������ނ悤�ɂ��܂��D
�댯�ȗ��Ƃ���〜�ŎO�p��ɂ��ď����Ă���܂����A�u�O�p��v�Ƃ͂Ȃ�Ȃ̂��̐������Ȃ������̂Ō˘f���܂���
�Ȃ̂Ő��F�̐}�̒��p�O�p�`���O�p��ɂȂ��āA�s���N���O�p��ɂȂ�Ȃ����R��������Ȃ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���߂̕��Ɂu���p�O�p�`�̕ӂ̒����̔��\���V�������̋L���v�Ə����Ă��܂��D
�@��������C���ۂɐ��F�̐}�̒��p�O�p�`���O�p��ɂȂ��āA�s���N���O�p��ɂȂ�Ȃ����R��������Ȃ����k������Ƃ������Ƃ́C���̕��͂������Ă��Ă悩�����Ƃ������ƂɂȂ�…���ۂɊ댯�ȗ��Ƃ����ɗ����Ă���Ǝv������C��ԏ��߂̕��̉����������x���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^19.05.16�n
�t�قȎ���ő�ϐ\�������܂���B
�y���2�z⑴�̕ʉ��ɂ��Ăł��B⋯⋯⋯�ȉ��̐����ł��B3�s�ڕs�����̉E�̃J�b�R���ł����A1/2��3�����Ă�3/4�ɂȂ�Ȃ��ł���ˁH�B2�s�ڂ̕��� bc, ac,ad���|�����4���Ǝv���̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���2(1)�ɂ͕ʉ��͏����ĂȂ��̂ŁC���e���猩��(3)�̕ʉ���������܂���
���m�ʂ̕ł���̎���ɑ���n[�����Œ�̕����Ő����ɂ��ā^19.05.16�n
�M�L�̂��Ⴄ�����Łu�͂���v�����͓�
���ׂĂ̕M�L�̂ɑΉ�����ׂ�
�ÎZ�ʼn����Ă��̂ŊԈ�����̂��ƕs���ɂȂ�
�����m��ҁn�F�A�����肪�Ƃ��D����������q�ׂĂ���Ƃ����͕̂�����܂����C�����ƈقȂ���b�������Ă͂����܂���D���݁C�C�^���b�N�̂ŏ������ނ��Ƃ��ł��Ȃ��̂ŁC�C�^���b�N�̂ŏ������߂�悤�ɂ��Ăق����Ƃ������Ƃł�����C�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�m���ϐ��C�m�����z�ɂ��ā^19.05.15�n
�m���ґf�ɑ�����������������킩��₷�����A���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�i���z�ɓ��̓~�X������悤�ł�→�ϐ��j
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.05.14�n
���肪�Ƃ��������܂���
�����̗͂�m��Ă悩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ��ɂ��ā^19.05.13�n
���⒉2�ɂ��Ď��₳���Ē����܂��B
2�s�ڂ�
(xy+1)�|(x+y)=(x�|1)(y�|1)
�Ƃ���܂����A�W�J����ƉE�ӂ̗l�ɂȂ�Ȃ��A�����A��L�ł̓}�C�i�X�̕����������Ă���Ǝv���܂��B���邢��(1-x)(1-y)���ł��傤���B40���N�O�̍��Z���Ȃ̂ŁA���x���x���ʂ��Ȃ������Ă��܂��܂������̌���Ȃ炲�������������B
�����m��ҁn�F�A�����肪�Ƃ��D�i���Ӂj�|�i�E�Ӂj�̕����ׂ�̂�����C�E�ӂ̕����͋t�ɂȂ�܂��D(xy+1)�|(x+y)=(x�|1)(y�|1)�ł悭�C(1-x)(1-y)�ł������ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����ɂ��ā^19.05.12�n
����help�ɂ����Ƃ킩��₷����������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D??
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^19.05.11�n
��3�̎������Z�̐��w���킩��Ƃ́cwwwww
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�t�̕s�����ɂ��ā^19.05.10�n
��2�ɂ��Ă��������������B
����ł�2|x+1|�q |x|-1. �������悤�ɂƂ����w��������܂��B�������{���ɂ� �E�� |x|�̐�Βl�L���̊O�����łȂ��Ax–1 �̐�Βl�L���̊O�������ڂ��Ă��܂��B�ǂ�����x-1�̊O���������ɂȂ�̂����ɂ͕�����܂���B���݂܂���������������Ί������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X������܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̍��ɂ��ā^19.05.09�n
�������킩��₷�������ł��I
���ɂǂ����ăx�N�g���̍������߂�ꍇ�Ɏn�_���m�����킹��̂��A���̎��̖��̌����͂ǂ����Ȃ̂��������^�₾�����̂Ő������肪���������ł��I
���ꂩ������w�撣��܂�💪
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �������̂�����Ƃ��̏����ɂ��ā^19.05.08�n
���܂ŕ�����Ȃ�������肪������悤�ɂȂ��Ċ�����😃�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�i�@,16�i�@,���i�@��10�i�@�ɂ��ā^19.05.04�n
16�i�@�̖���������������������ǂ���Ȃ��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W
�����ɂ��Ă̖��͂Ȃ���ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���邱�Ƃ͂���܂����C�W�����ɕς����琳�������ς��̂ŁC�����̗��K�����Ȃ��Ăͥ���Ƃ����̂́C��ɒ��w�Z�̘b�ŁC���Z�ł̉��p�̕��p�͂�����ł͂Ȃ��悤�Ȋ��������
���m�ʂ̕ł���̎���ɑ���n[��̕ϊ������ɂ��ā^19.05.03�n
�u�����̐搶�ɃJ���J���ɓ{��ꂽ�D�搶�Ƃ��ẮCb/a �ł͂Ȃ��C�ʐς̔䂾�ƌ������������悤���D�v�B�搶�̐搶�͍����ЂЂЂ��ď��Ă�̂ł��傤���H�i�j�B���ז����܁B�u�搶�̐搶�v���搶(���Ȃ��l)�̐搶�ł��B���߂�Ȃ����A�Z�����̂ɁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�藝�C�����藝�ɂ��ā^19.05.01�n
�W���̐����y��Ȍ����z(4)�ɂ���
���ł̋L�q�̌����ƁA���̉����f �h(x)��
�����o���ꂽ�����ɂ��ꂪ����܂��B
����œ����o���ꂽ���������������悤��
�v���܂����������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�藝�C�����藝�ɂ��ā^19.05.01�n
���ݒ�����эZ�̍�1�œ藝������Ă�����̂ł����A
���ȏ���prime���x���ɂ͖��[3]�̕����ɕ������܂ޏꍇ��A[5][6]��p,q.r���ꔭ�ł͋��߂ꂸ�A�z�肳���p�̐��l�ŏꍇ�������s�Ȃ��āA���̋ᖡ������ꍇ�̃^�C�v�A�܂��A�藝��p���ēW�J������x^2���o�Ă���̂͂ǂ�ȑg�ݍ��킹�̎����H�ƍl����^�C�v�͂���܂���ł����B
�������Q�l�ɂȂ�܂����B
�藝�⑽���藝��p����x^py^r�Ȃǂ́u�W�������߂�v���͂����̃T�C�g�ɂ����肪�ł��Ă���Α��v�ł��傤���H
�����蔭�W�I�Ȑ��U�i�K�ł́u�W�������߂�v��肪�������狳���ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���Ђ�̕t�����ɂ���āC���W���͑��l�Ȃ��̂��ł��܂����C���̃y�[�W�ŏq�ׂ���{�ɗ����Ԃ��ď�������C�قƂ�ǂ̖��͂ł���͂��ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̓W�J����1�ɂ��ā^19.04.30�n
(x-2)³-9(x-2)
�����m��ҁn�F�A�����肪�Ƃ��D���₪����̂Ȃ�C�W�J�������̂��C���������������̂������t�ŏ����Ȃ��ƒʂ��܂���D
���m�ʂ̕ł���̎���ɑ���n[�P�̋����R�捪���ɂ��ā^19.04.30�n
�ւɂ��ĉ���������Ă��Ȃ����́A�ւ������̎O�捪�ł��邱�Ƃ������Ă�������ׂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����������͏o���Ȃ��ƍl�����܂��D�i�������C���Ƃ�1���Ԓ��ւ̖��������Ă��āC����ɑ����̖������悤�ȏꍇ�́C�ւ����ł���̂��͈Öق̗����ɂȂ��Ă��܂��j
���m�ʂ̕ł���̎���ɑ���n[�i���f���ŕ\�����j�O�Ղ̕������ɂ��ā^19.04.30�n
(8)��4)�̉���Ƀ~�X����܂��H���Ȃ��Ƃ��I������|z-3|=3|z-2|�Ɖ����|z-3|=3|z|�͈Ⴄ�Ǝv���̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[��ʍ��̋L���Ɋ�����ɂ��ā^19.04.29�n
�̓_�ł��Ȃ���
�ł��Ȃ��Ȃ炻�[��[�@�\�����
�����m��ҁn�F���t�����������U���I�ȕ��͂ɂȂ��Ă��܂��̂ŁC�ʏ�͉��Ȃ��P�[�X�ł����C�{���ɃX�}�z�̑�����@���������Ă��Ȃ���������܂���̂ŁC�����ĉ��܂��DiPhone��Safari�ō̓_�ł��܂��D�����C���Ȃ��̉�ʐݒ�ł́C�E�̂ق��ɏo�Ă��鐳�딻�肪�����Ă��Ȃ��悤�ł��D������悤�ɂ�����@�͓��R������ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�w���@�̓�������ɂ��ā^19.04.28�n
���1,2�̂Ƃ���Łipk�{r)²��p²k²�{�Qpkr�{r²�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�r���̎���r�������Ă���Ƃ������ƂŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�P���ϊ��ɂ��ā^19.04.26�n
�f���炵���B�m�F��肪����̂��ǂ��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���ȏ�̈��������ɂ��ā^19.04.25�n
�����̐�I�̒P���̐������A�Ƃ��Ă�������₷���̂ŁA�����������p���Ă��܂��B�����������Ɨ����ł��Ċ��ӂł��B
�Ƃ���ŁA�l�͍��Z1�N���ł����A���A���Z2�N���̐��w������Ă��ǂ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���w�̓��e�͌n���I�ɏ������ē��S�ōĕҐ�����K�v������̂ŁC�K���Ă���g�ɒ����܂łɎ��Ԃ����������������܂��D������C���w�ł́C�\�K�^�̊w�K�̕����L���ł��D���ہC������эZ�ł͍��Z1�N���ō��Z2�N���̐��w������Ă���͂��ł��D
�@�����C�ڍׂȉ��K�̗��t�����s���Ȃ���i�߂Ȃ��ƁC���߂ɊԈ�������Ƃ�g�ɒ����Ă��܂��ƁC�������߂ɂ��̉��{���̓w�͂��K�v�ƂȂ�܂��̂ŁC���X�N���l���Ȃ���i�ނƂ悢�ł��傤�D�i�n�ɑ��������Ă��邩�ǂ����m���߂Ȃ���j
���m�ʂ̕ł���̎���ɑ���n[�w�����̃O���t�ɂ��ā^19.04.23�n
��4��⑷�̉Ɋւ��Ăł��B3�s�ڂƂS�s�ڂł����u�w���v�Ɓu��v�̋L�q���t�̗l�Ɏv����̂ł������̌���ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�t�ɂȂ��Ă��܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�e���聨�������ɂ��ā^19.04.22�n
�����̂��ɂ���������ɂ��ĕ�����₷��������Ă��藝�����邱�Ƃ��ł��܂����B���肪�Ƃ��������܂��B�R�s�[���鎞�A�ςȏꏊ�ŋ���Ȃ��悤�ɁApdf�����Ă���������ƂƂĂ����肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��Dpdf�ɂ���ɂ́CHTML�t�@�C���̈����I��ŁC���M����v�����^�ł͂Ȃ�PDF�t�@�C�����w�肷��Ƃ悢�̂ł����C���v�]�̓��e�͂����������Ƃł͂Ȃ��悤�ł��Dpdf�ɂ����Ƃ��ɁC���̗ǂ��ӏ��ʼn��y�[�W�ł���悤�ɂ�����@�͂���܂����C���������HTML�ł����y�[�W����Ă��܂��̂ŁC�ǂ����悤���ƍl���Ă��邤���ɉ��N���o�߂��Ă��܂���…
?�m?�^19.04.21�n
���肪�Ƃ��������܂����B���̕��̃y�[�W��������Ē����Ă�����킩��܂����B�����J�ɂ��肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ݏ捪�ɂ��ā^19.04.21�n
�������肸������Ă���Ǝv���̂ł����A�ł�����������������B���̏�̕��́u�v�_�v�́��̕����̎��ł��BX n�恁a��n��Ƃ�����������܂��B(x �͐Ԏ�)�B����͂ǂ������Ӗ��ł��傤���B���Z�����Ƃ��낷�݂܂���B���s���A���w�E��������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ�قǁC�ȗ����߂��ŁC������Ȃ��l�ɕ�����悤�Ȑ����ɂȂ��Ă��Ȃ��悤�ł��̂ŁC�⑫������{���ɂ��������݂܂��D
&chf=bg,s,fff6f6)
�ƂȂ錳�̐�

��

�̂��捪�Ƃ����C

�ŕ\���D
���Ȃ킿�C
�m�ݏ捪�̒�`�n�F

������E�ӂ�
&chf=bg,s,fff6f6)
�̏ꍇ�ɓK�p�����



����������

���R�́i�R�j
x3+y3+z3�|3xyz=(x+y+z)(x2+y2+z2�|xy�|yz�|zx)�͌����ł��ˁB
�m��Ȃ������̂łǂ����Ă����Ȃ肱���Ȃ�̂��Y�݂܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�́C�薼�ɂ������Ă���܂��悤�Ɂu���p���v�ł�…�܂�C��{��肪�ł���悤�ɂȂ��Ă���C�r���߂��I�Ƀ`�������W������ł��D�����́C
���̃y�[�W[�V]�ɏ����Ă���܂��D
����ɂ��́B����͎O�p��O�p���̏��ł����b�ɂȂ�܂����B�����͎w���ΐ����̊�b���̊�b�̂Ƃ�������ɗ��܂����B���̎w���̐���⑴��q�����ċ����܂����B���w�������Ă�����Ȃ畁�ʂɘ_�����̂ł��傤���A�Ⴆ�Ό����̐��w�U�̋��ȏ����݂�Ƃ킩��ɂ����A�Ƃ������_���Â��ł��ˁB������O������(����v���܂��A�Ǒf�l���B)�_���Ȃ���Ă��Ă킩��Â炢�����搶��������Ɛ�������Ă��܂��B�G�������ł����B���肪�Ƃ��������܂��B(�҂��)�B�u�����v✖
�u�����o�Łv���ł����B���݂Ɏ����������Ă�����̂ł͐��Up152�ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~����C���ジ�����ɂ��ā^19.04.17�n
�����グ�ė��Ԃ����Ƃ��ł��邩�ۂ��ʼn~�����ジ�������܂�̂ł����c�Ȃ��w�I�łȂ��悤�ȋC�����ă����������Ă��܂��܂��c
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ������w�ɑ��Ď����Ă���C���[�W�́C�D�L���l�ԏL���t���Ă��Ȃ��N�[���C�X�}�[�g�ʼn_����������w��Ƃ��������ł��傤���D�m���ɁC���Z���w�̑㐔�C��͕���͉��S�N���̊Ԃɐ�������Ē��ۓI�ȋL�������̐��E�ɂȂ��Ă���悤�Ɍ����܂����C���R�Ȋw��Љ�Ȋw�ւ̉��p�ƂȂ�ƁC�ǂ�ǂ�̐l�ԏL���b�ɓK�p���邱�ƂɂȂ�ł��傤�D���Ƃ��C�W�����P���̊m���Ƃ������_���E�H�[�N�̊m���̂悤�ȁC�������E���̂��̂𓊉e�����悤�ȓ��e�����w�ň����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^19.04.17�n
�������̕\�����ɂ��ċ^��������Ă��܂��B�@���͂��̃y�[�W�ɂ���悤�Ɂ@f��g(x)�@�Ƃ����������ŏK�����L��������̂ł����A�ŋ߂̋��ȏ��ł݂͂ȁA�if��g�j(x)�̂悤�Ɂi�@�j�����Ă��܂��B���̊��ʂ͕K�v�Ȃ̂ł��傤���B�@�Ȃ��čςނ��̂Ȃ�A�����Ȃ������������肵�Ă悢�Ǝv���̂ł����A�������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɍŋ߂̋��ȏ�3����������C�����Ȃ��Ă��܂��D���T�C�g�̋��ނł��C���Z�����́if��g�j(x)�����C���ɂ��Ă��܂��D
�@�����C�����W�ł͐����Ђ̂��̂ł� f��g(x)�C�Ȋw�U���V�Ђ̂��̂ł́if��g�j(x)�C��w�̋��ނł͂ǂ��������܂��D
�@���̍����ɂ��āC�����@���͂˂ɐ������邪�C�����@���͂˂ɂ͐�������Ƃ͌���Ȃ��Ƃ����Ƃ��́C�ǂ̏����ł��F
\circ h=f\circ (g\circ h),\hspace{5}f\circ g\ne g\circ f&chf=bg,s,fff6f6)
�̂悤�ɏ����܂��D�C��t���Ȃ���Ȃ�Ȃ��̂́C������t����Ƃ���
(x)&chf=bg,s,fff6f6)
��
&chf=bg,s,fff6f6)
�ňقȂ錋�ʂɂȂ�\�������邩�Ƃ������Ƃł����C����͂Ȃ��ł��傤�D
�@�L���C�ǂݕ��C���艼���Ȃǂɂ�����鐢�E�Ŏd�������Ă���ꍇ�C�Ⴆ�Ζ��������̏��ނ�����Ă���ꍇ�⍂�Z�̎��Ƃŋ����Ă���ꍇ�ɂ́C�\�L�̈Ⴂ�ɂ��Ď��₪������Ή����Ȃ��Ȃ�Ȃ��̂ŁC����ȕ��ɍ��킹������y�ł��傤�D�����ȏ�ł́C�ǂ���ł��悢�ł��傤�D
���������b�ɂȂ�܂��B���x���x����U�߂ł��݂܂���B�m�b������������K���ł��B
���̉~�̐ڐ��̕�������₤���ɂ��āB
�ȉ��̉~�̐ڐ��̕����������߂�B
�E�~(x^2)�{(y^2)=9�̐ڐ��ŁA����4x�{3y=1�ɕ��s�Ȃ��́B
���͉��̂Q�̃��[���𗘗p���Ĉȉ��̂悤�ɉ����܂��������W�̉ƍ����܂���B
�������ɂ��̖�肾�Ɛڐ��͂Q�{���܂�͂���������A���܂��܂ȓ_���玄�̍s���������������������̂͗����ł��܂����A�̓r���Ō�����[���݊O���Ă��Ȃ�����Ȃ̂łǂ����ĉ����Ȃ��̂��킩��܂���B
�����Ŏg�p�������[���B
�@ �~(x^2)�{(y^2)=(r^2)��̓_P(x1,y1)�ɂ����邱�̉~�̐ڐ��̕�������
(x1����)�{(y1��y) =(r^2)
�A �Q����y=(m1��x)�{n1,y=(m2��x)�{n2�ɂ��āA�Q���������s�Ȃ��m1=m2
���̉�
���[���@���A(x1����)�{(y1��y) =9�A���Ȃ킿����(-(x1/y1)��x)�{(9/y1)�E�E�E�B
�܂��A���̐ڐ��͒���4x 3y=1�ɕ��s�Ȃ̂ŁA���[���A����чB���AX1=4,y1=3�ł���A�B��y=(-(4/3)��x)�{(9/3)�A���Ȃ킿y=(-(4/3)��x)�{3
���̂悤�ɁA���[���͓��݊O���Ă��Ȃ�����ł��������܂���B
�ǂ����Ԉ���Ă���̂ł��傤���H
���Ȃ݂ɁA���ʎ����g�����̂�_�ƒ����̋������g�����̂ȂǁA���̉�͗����ł��܂����B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��̍l�����ł́C���̋��ނ̓��āi�A�j��(1)�̑���������̂������Ă��܂��D���Ȃ킿�C�ړ_�̍��W��
&chf=bg,s,fff6f6)
�Ƃ���Ƃ��C

�����łȂ��C
&chf=bg,s,fff6f6)
�͉~����̓_������C

���������Ȃ���Ȃ�܂���D
�@�䗦��3:4�ɂȂ���̂́C

�����ł͂���܂���D�����{�Ɍ����Ă��C�傫�����ł�

���������ł́C

�@�����̓��ŁC

�������̂́C
&chf=bg,s,fff6f6)
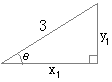
�@�}�̂悤�Ȓ��p�O�p�`�ŁC�X���C���Ȃ킿

�̂Ƃ��C

�Ɠ����鐶�k�͌��\����D����́C�����T���C���A���A���̈�킩��
���e�ȉ�����肪�Ƃ��������܂��B
���\�N�Ԃ�ɉ���������肪�������̂ł��������������S�ɖY��Ă��܂��A����������A�M�y�[�W�ɂ��ǂ蒅���܂����B���������܂ŏ������v���o���Ă���܂��B
���R�����̍�����͂���Ƃ���A�ǂ����Ă������i-1/2�j���i-1/�j�܂ł������͂ł��܂���B���̂������܂����̂�������܂��A����Ȃ��������������ݒ茅��������Ȃ��̂�������Ȃ��Ǝv�����A�����������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���܂蒷���������������ނ悤�ɂ���Ɓu��ʍ\���������v�̂ŁC3���Ő��Ă��܂����C�B��Ă��\��Ȃ��Ƃ����ݒ�Ō����������Ȃ����܂����D15�����������߂C�L�������͉������Ȃ�܂���
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�����̏ؖ��j�ɂ��ā^19.04.16�n
���5�̈�ʉ���
1�E2�E3�E...�Ek�@+�@2�E3�E4�E...�E(k+1)+...+n(n+1)(n+2)...(n+k-1)
=n(n+1)(n+2)...(n+k)/(k+1)�Ƃ����藧���������Ǝv�����܂����B
���ۂɊȒP�Ȑ��w�I�A�[�@�ł����Ă邱�Ƃ��ؖ��ł��܂���
��肪�~���������̂ŏ�����܂���
�����m��ҁn�F�A�����肪�Ƃ��D���藧���܂��D
���m�ʂ̕ł���̎���ɑ���n[�w���������ɂ��ā^19.04.14�n
�����������
�����m��ҁn�F�A�����肪�Ƃ��D�������ɗ�����́C���������������蓾�܂����C���ۏ�͂��܂茩�����Ȃ��D�Ƃ肠����2��lj����Ă����܂����D
���m�ʂ̕ł���̎���ɑ���n[�O�p���̉��@�藝�ɂ��ā^19.04.14�n
sin45����1/��2�ł́H
�����m��ҁn�F�A�����肪�Ƃ��D����҂̖��O��������Ȃ��̂ŁC�Ƃ肠�����u�̂ё��N�v�Ƃ��悤�D
�̂ё��N�C���炢�I�N�̌����Ƃ��肾�D

�͐������D
�@�Ƃ���ŁC���̎��₪�Ȃ�����̂����l���Ă݂�ƁC�̂ё��N��

��

�Ɠ������̂��Ƃ������ƂɋC�t���Ă��Ȃ�����ł��D�����炭�C�̂ё��N�́C���Z1�N��6�����ɁC�w�Z���x���Ƃ�����̂ł��傤�D���́i�����́j���Z�ł́C������ׂ����e�ɑ��Ď��Ǝ��Ԑ������|�I�ɑ���Ȃ��̂ŁC���w�̎��Ƃ�1���x��C���̌�̎��Ƃ͕t���Ă����Ȃ��悤�ɂȂ��Ă���̂ł��D�i�������Ƃ��x�������Ԃ͂Ȃ��j
�@�����炭�C�̂ё��N�����Ƃ��x���ɁC����̗L�����Ƃ������Ƃ��ς�ł��܂����̂ł��D
���̃y�[�W��ǂ�ł��������D�i���̋��ނ̍�҂́C���Z1�N�̎��Ƃ�S���Ă��Ȃ��D���Z�ɓ��w������C��2�̎��Ƃ����Ă��āC��1�̋��ȏ��́u�e���ǂ�ł����悤�Ɂv�̈ꌾ�ōς܂��ꂽ�悤�ȋL�����E�E�E�j
���N��1�ɂȂ����̂ŁA�\�K�Ƃ��ĉ����Ă܂����B
�����̉���Ȃǂ��킩��₷���ĂƂĂ��ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�i�e�w��ԁj�x�N�g���̓����ɂ��ā^19.04.13�n
�e�w��ԁA�x�N�g���̓��ρA9�y�[�W�ځA(5)�B
�p�x��120�x�Ōv�Z����Ă���悤�ł����A60�x�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�ԈႢ�ł����̂Œ������܂����i991�s�̃v���O��������771�s�ڂ̕������t�ł���…�����̍�����v���O�����ł��邱�Ƃ͊m���ł����C���G�����ă����e������D���������v���O�����͂悭�Ȃ��j
���m�ʂ̕ł���̎���ɑ���n[��ʊp�̒�`�ɂ��ā^19.04.12�n
�����b�ɂȂ�܂��B�S������I���Ɛ��l�̉ӏ����}�`�݂����ɂȂ�A�����ŏI���Ȃ��ł��B�O�p���̍ŏ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�f�B���N�g���̎w�肪�㉺�ɂ���Ă��܂����̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[��ϕ��F��{�v�Z�ɂ��ā^19.04.11�n
���3��(2)��-18�������łȂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�͊ԈႢ�Ȃ������̂ł����C�r���v�Z�ʼn������ӏ�������܂����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���a�̕\�킷��ʊp�ɂ��ā^19.04.10�n
���a�̈Ӗ����悭�킩��܂����I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^19.04.07�n
�Q�l�ɂȂ�܂��B���肪�Ƃ��������܂��B
�����W��]�݂܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���l���s�s�m���̂���^19.04.04�n
�U�~�f�|�g/J=K/3�~�k���j���ɂ������̂ł����ǂ��������������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����͒��w���̖��ł��D
���̃y�[�W��ǂ�ŁC�����ʼn�����悤�ɂ��Ă��������D
�iX+4�j2�恁�iX�{�R�j�Q��{�iX-4�j�Q����Ăǂ������̂��������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�u�������v�Ƃ������t�́C�s�p�ӂɎg��Ȃ������悢�Ǝv���D�������������C���������@�C�������H���C�������^���K���C�̂悤�ɐl�̍s���ɂ��Đ������Ƃ����p����g���̂́C����ȊO�̍s�����Ԉ���Ă���C���������ȊO�ɐ������l�����Ă͍���Ƃ����O��ɂȂ��Ă���C�悢�������͉��ʂ������Ƃ������l�ς�F�߂Ȃ����ȍl�����̐l�������D�ޗp�ꂾ�ƍl�����܂��D���_���猾���C�������͉��ʂ�ł�����C�ǂ�ł��悢�̂ł��D���̂����ŁC�ȒP�����Ȃ��͎̂��̂悤�ɓW�J���Ă��琮��������@�ł��D
�W�J����
^2=(x%2B 3)^2%2B(x-4)^2&chf=bg,s,fff6f6)
��������

�E�ӂɏW�߂�

������������
(x-9)=0&chf=bg,s,fff6f6)

���Ԏ����肪�Ƃ��������܂��I��ʊp�Ɋւ���2���e�������܂����B
�����O���炱�̃T�C�g�͂���悤�ł��ˁB�������m�����̂͂��������O�ł����B�����o�ł̐��U�̊Y���ӏ��̋L�q���������ɂ����̂ł����������ׂĂ�����A���̃T�C�g��������܂����B�悭������悤�ɋL�q����Ă��Ă��肪���������ł��B�h�V���E�g���G�������ł����i�j�B������ł܂��������Ē����܂��B��낵�����肢�v���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D2�N���炢�O����X�}�z�p�y�[�W�i�����̏������c���̃y�[�W�j�������ŗD��I�ɏo��悤�ɂȂ��āCPC�p�͕��ʂɌ������Ă��Ȃ��Ȃ��o�Ă��Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�W���ɂ��ā^19.04.01�n
A={1,3,5,7,7}�݂�����
�v�f���d������Ƃǂ��Ȃ�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͑S���̓��僌�x���̓��e�������Ă���C�����炪�m���Ă��邱�Ƃ���ח��Ă�ƁC�|�C���g���i��m��Ȃ��Ȃ邽�߁C�����Ă��܂��C������̌��ɂ��Ă͎��̒ʂ�ł��D
�@�W���ɂ��ẮC��ʂ� {x, x} = {x}�����藧���܂��D���Ȃ킿�C�����v�f���������Ă�1������̂ƌ��Ȃ���܂��D
�@���������āC{1,3,5,7,7}={1,3,5,7}�ł��D
�����̘b�́C�W�����������Ƃ̂ł���R���s���[�^�\�t�g�̌��ʂƈ�v���܂��D
���̃y�[�W�̉��̕���10.�Ƃ������ڂ̐擪��2�i���ɏW���Ƃ����^�̃f�[�^�̓����Ƃ��ď����Ă��܂��D
���Z�����Ƃ��낲�߂�Ȃ����B���̌�����Ȃ玸��v���܂��B
���i�́u���Ӂv�Ƃ����ӏ��ł����A
�u�Ɓ��|30+360�~m�v��330�ł���ˁB�Ƃ���ƁA���̉����̏W���̗v�f�ɂȂ�Ȃ��Ǝv���Ă��܂��܂������B���w�Ǒf�l�Ȃ̂Ō��������A���߂�Ȃ����B�Ȃ�m��1�ōl�����̂ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[��ʊp�̒�`�ɂ��ā^19.03.31�n
�ƂĂ��ʔ����ł��ˁI
��肪�J��Ԃ�����V�c�R�C�̂��ƂĂ��ǂ��ł��i�j�B��X�������܂��������C�ɓ���ɓ���Ă����܂��ˁB���肪�Ƃ��������܂�(^^)
�����m��ҁn�F�A�����肪�Ƃ��D���������������Ă�����Љ�l�̕��̔����̂悤�ł��D�����̍��Z���͂ƌ����C���������Ƃ�3����1���o���Ă���ΗD�G�ȕ��ł��傤…12������4���������悢���ł��傤�D1���Ԃ̎��ƂŁC�����́C���̎��Ƃ�����̂��C���ɋC��t���Ȃ���Ȃ�Ȃ��̂��Ƃ��������_��15���C�����̎��Ƃ�15���Ƃ��āC�c���20���͒x�����Ă��鐶�k�ɑ��钍�ӂƂ��C���ȏ��������Ă��Ă��Ȃ����k�ɑ��钍�ӂƂ��C�����ĕ������k�ɑ��钍�ӂƂ��C�X�}�z��Еt����悤�ɒ��ӂ��邱�ƂŔ��ł��܂����Ƃ������̂ŁC12������K�����50���̎��Ƃ͏I����Ă��܂��ł��傤�D����Ȃ���ł��D���Ƃ����藧�����烋�������ł��D
���m�ʂ̕ł���̎���ɑ���n[�t���ɂ��ā^19.03.31�n
�ƂĂ��킩��₷���ď�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�̋����R�捪���ɂ��ā^19.03.30�n
���ʂɗ͋Z�Ńւ��O�悵�Ă�1�ɂȂ�Ȃ��ł��B
������ĉ��łȂ�ł���?
����ƁA�ԐM���ꂽ�̂�������悤�Ƀ��[���ɒʒm������Ȃǂ͖����̂ł��傤��?
�����m��ҁn�F�A�����肪�Ƃ��D1�ɂȂ�Ȃ��̂͌v�Z�ԈႢ�����Ă��邩��ł��D���ɁC

��Y��Ă���ꍇ������܂��D

�̂Ƃ�



�̂Ƃ������l�ɂ��Ăł���D
�@���[���ł̕ԐM�́C�ł��邾��������悤�ɂ��Ă��܂��D���[���A�h���X���W�Ǝ҂ɘR���ƁC�X�p�����[�����R�̂悤�ɗ���̂ŁC���l���ɂ͒m�点�܂���D
���ɋ����Ăƌ����A�����ł��ǂ��킩��Ȃ��̂ł܂��������Ă��狳���悤�ƎQ�l�ɂ����Ă��������܂���
��ω���₷�����e�ł���܂�����
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����Œ�̕����Ő����ɂ��ā^19.03.29�n
���́m4�n�ŁA�������|(a�|b)(b�|c)(c�|a)�ɁA�Ȃ�̂ł����A�ǂ��������ł��傤���H
������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���̖��̓��ł͂Ȃ��āC���������̌��ʂ��ł��傤�D�|(a�|b)(b�|c)(c�|a)=(b�|c)(a�|b)(a�|c)�̉����������̂ł����H
���m�ʂ̕ł���̎���ɑ���n[�m���̏�@�藝�ɂ��ā^19.03.28�n
��5
�P��ڂ̂����ł̓A�C�R�����ł͂Ȃ�A�Ƃ�����l�������ĂQ���ւ̏ꍇ�͂Ȃ������ł��傤���H
�P���ł�A�͂������AB��C�������Ă͂����Ȃ��H
��蕶�����A���Q���ŒP�Ƃŏ����c��P����B�܂���C�̕Е��̂ݔs�ނ��Ă��ǂ��悤�ɓǂݎ�ꂽ�̂ł���
�����m��ҁn�F�A�����肪�Ƃ��D����ɏ����Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�m�W���`�n�ɂ��ā^19.03.28�n
�l�͂���������2�ł����ȒP�Ȍ��t�łƂĂ�������₷��������Ă���̂ł悭�����ł��܂����B����̐��w�̊w�K�ɋ������킫�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���݁C��1�ł��̋��ނ�ǂ�ł���H
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^19.03.27�n
���O�ł��B�@���Z���w�O�̗\�K�Ƃ��Ďg���Ă܂��B
���O�̏t�x�݂ɂ��������ǂ��P���̃����N��Z�����Ƃ��낷�݂܂�����Ē������
������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����������C�ɂȂ��Ă���悤�ł��̂ŁC���Z�����͋O���ɏ��ł��傤�D�����C���Z�ƌ����Ă����푽�l�ŁC���ϓI�ȕ��ʉȂȂ�C�t�x�݂͉p��␔�w�̐V�����������[�N�u�b�N����������āC�V�w�����X�ɂ��͈̔͂���e�X�g�Ƃ���������ɂȂ�̂ŁC��������̂��悢�Ǝv���܂��D
�@���w�ł́C�\�K�^�̊w�K����������g�ɒ����₷���C�K���Ă��Ȃ��Ă��C���T�C�g�ɂ��鋳�ނ��ł���Ƃ���͑S������������悢�ł��D�i�\�ʂ��Ȃ߂�̂łȂ��C���ۂɖ��������̂��悢�j
���m�ʂ̕ł���̎���ɑ���n[�W�J����1�ɂ��ā^19.03.27�n
[4]��(x+1)(x2�|2x+1)���킩��܂���
�Ȃ��[3]��-2���W������Ȃ��̂�[4]�͌W���ɂȂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D
�����F��`��
(x^2-2x%2B 4)&chf=bg,s,fff6f6)
�́C

�Ƃ��ĕό`�����
(a^2-ab%2B b^2)&chf=bg,s,fff6f6)
�ɓ��Ă͂܂邩��

���Ȃ킿

�ɂȂ��D
������
(x^2-2x%2B 1)&chf=bg,s,fff6f6)
�́C

�Ƃ��ĕό`�����
(a^2-2ab%2B b^2)&chf=bg,s,fff6f6)
�ƂȂ���
(a^2-ab%2B b^2)&chf=bg,s,fff6f6)
�ɓ��Ă͂܂�Ȃ�����

���Ȃ킿

�ɂȂ�Ȃ���D
�Ō�̖�茩���Ɉ����|����܂���(T-T)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��p�ΐ��ɂ��ā^19.03.26�n
������肪������Ɗ�����
�����m��ҁn�F�A�����肪�Ƃ��D�����ˁ[
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������i�O�p�`�̌`����j�ɂ��ā^19.03.26�n
http://www.geisya.or.jp/~mwm48961/koukou/complex_plane15.htm �ɍڂ��Ă���
���f�����ʏ�ŁC�R�_A(4z), B(3z+2), C(z3)�_�Ƃ��遢ABC�����O�p�`�ƂȂ�悤�ȕ��f��z�����ׂċ��߂�D
�i����������ȑ�2016�N�x�j
�̉��ǂ��I�����Ă��~�ƂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɂ����Ȃ�܂��D�L�[�{�[�h���P����āC�I�����ɂȂ�����͂����悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^19.03.26�n
�킩��₷�������ł����B���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^19.03.26�n
�ƂĂ�������₷�������B���K��������A�w�т������������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��]�̒藝�ɂ��ā^19.03.25�n
���t���Z��N���ɂȂ�܂��B�m�̗\�K���Ƃ̒蒅�ɕs�����o���Ă��܂������A���̃T�C�g�Ŗ��Ɏ��g�ނ��Ƃŗ�����[�߂邱�Ƃ��ł��܂����B
���ӂ��ׂ��_�̍������ȂǁA�������ʔ������͂Ŋy�����ǂ߂܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�V���������Ƃ��ẮC�������������������܂���
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^19.03.25�n
�e�X�g���͌����ËL������ł��傤���A�Ȍ��ł킩��₷�������Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�����̈ËL�őΉ��ł���̂́C�Z���̒�������܂łł��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^19.03.24�n
��17��HELP���̍Ō�̂Ȃ������ł����A�uy=cos3x�Ɠ����v�ł͂Ȃ��A�Ⴆ�uy=-sin3x�Ɠ����v�ɂȂ�̂ł͂Ȃ��ł��傤���D
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�O���t�̕��s�ړ��ɂ��ā^19.03.23�n
�����W����V���W�����߂鎞��Y+������(X+��)�ɂȂ�܂���ˁB�����ŋ����W��X���炘��Y���炙�ɋL���������Ă������킯�����炙+������(��+��)�ƂȂ�A���ꂪ�ړ���̃O���t�ɂȂ�̂ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D
�ړ��O�̃O���t�i���O���t�j��̓_�� (X , Y) �C�ړ���̃O���t�i�V�O���t�j��̓_�� (x , y) �Ƃ����ƁC���O���t��̓_ (X , Y) �� y=f(x) ��ɂ��邩��C
Y=f(X) �c(1)
�����藧�D
�@�_ (X , Y) �� x ���̐��̌����Ɂi�E�Ɂjp�Cy ���̐��̌����Ɂi��Ɂjq �������s�ړ��������̂��_ (x , y) ������
x=X+p �c(2)
y=Y+q �c(3)
�����藧�D
���ꂪ�O��ł�����C�����W����V���W�����߂�Ƃ��́Cx=X+p �c(2)�Cy=Y+q �c(3)�ɂȂ�CY+������(X+��)�ɂ͂Ȃ�܂���D
�u�i�R�����j��Ԃł̈ړ��Ƃ���ɑΉ�����s��̗�v�̐����ɂ���u(2)�@y���̂܂��Ɋp��������]������ړ� �v�̃Ƃ̕����͂Ђ���Ƃ�����t�ł͂Ȃ��ł��傤���H�B
�܂��s����}�C�i�X�̂��ꏊ���R�s�P��ڂ�SIN�ł͂Ȃ��ł��傤���H
�܂������Ă����炲�߂�Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��D���̐}�̂悤�ɂ����炚�̌����Ɂi����������ʼnE�Ɂj�ƁC�����ɏ����Ă��錋�ʂƈ�v���܂��D�����C���w�╨���̐��E��rot V�̌v�Z�̂悤�ɁC��]�ƌ����Ζⓚ���p�ō������Ɍ��܂��Ă���悤�ȏꍇ�́C���Ȃ��̍l���ƈ�v���܂��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^19.03.21�n
������ƂĂ��킩��₷�������ł��B�S��������������Ɏ���ɑ�����݂��̂ł����A�߂����ቖ�Ή��ŏ��܂����B���ꂩ����g�킹�Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����Ŗڈ�t�̑Ή��ł��D�i�ւƂւƁj
���m�ʂ̕ł���̎���ɑ���n[��d�����ɂ��ā^19.03.21�n
�T�N�T�N�Ɗm�F���ł��ėǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��,�������̓����ɂ��ā^19.03.20�n
���ɐ������Ă����ƁA�����@�ōŌ�̓������������Ă��܂��̂ŁA�����ߌ`����������������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^19.03.20�n
��蕶�Ł��~���\������āA��蕶���\������Ȃ��̂͂ǂ����Ăł����B�����Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D���̊��z�����������ɁC�Ԃ̑����ŏ����Ă���܂��悤�ɁuGoogle�̐����\���ɏ�Q���������Ă���͗l�v�ł��̂ŁC�������\������Ă��܂���D����̂�҂����Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[��Ԃɂ����镽�ʂ̕������ɂ��ā^19.03.19�n
���3����ɂ���A���2����ɂ���͉̂��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�R���s���[�^������ɂ����ԍ��Ɩ��̓�Փx���ォ��l���āC��������̕\������������ς����悤�ł��D�����܂����D
���m�ʂ̕ł���̎���ɑ���n[p�Ȃ��q�̐^�U�ɂ��ā^19.03.18�n
4���J�[�h���̂������ŏ�������̒�`�ɔ[��(��萳�m�Ɍ����ƁA�̂����Ȍ���������"����")�ł��܂����B
�f���炵��������₷���y�[�W������Ă������肠�肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̉��ƌW���̊W�ɂ��ā^19.03.17�n
�ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̏ؖ�1�ɂ��ā^19.03.16�n
�߂���߂��ᕪ����Ղ������ł��I�I
���w�D���Ȃ�ł����Ǐؖ��ɋ��ӎ��������̂ŏ�����܂����I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ��W�J�ɂ��ā^19.03.15�n
������Ղ�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����ɂ��ā^19.03.15�n
����ɖ������Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J����1�ɂ��ā^19.03.15�n
�������ǂ����Ă����Ȃ�̂��̉�����~�����ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D�f�t���̎���ɂ́C���q�l�͐_�l�ŁC�ǂ�Ȉӌ��ł��e���Ƃ����������嗬�ł������C����͐��X��X��������܂���D���w�Z�̘b�́C
���w�Z�̃y�[�W�Ŋm���߂Ă��������D
�x�X���݂܂�
�Ō�̖��̃I�`�L�̉�����A�`�G�̉�����������e�Ȃ̂ł����L���~�X�ł����H
����Ƃ��\�������������Ȃ��Ă���̂ł��傤���H
�Ƒ������҂ł����N���������e���\������Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D����̔ԍ����Y���Ă��܂����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����ɂ��ā^19.03.14�n
���P��(8)�ŁA1/2{cos10��+cos(�|4��)}
=1/2(cos10��+cos4��)�ƂȂ��Ă��܂����A1/2(cos10��-cos4��)�ł͂Ȃ��ł����H�@�����Ԉ���Ă���Ή�������肢�������ł��B
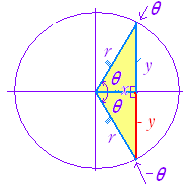 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D�܂��C���d�v�������������Ă����܂��傤�Dsin�Ƃ�tan�Ƃ͊���Ff(−��)=−f(��)�ł����Ccos�Ƃ͋���Ff(−��)=f(��)�ł��D�܂�Ccos(−��)=cos�Ƃł��D���������āCcos(�|4��)=cos4�Ƃł��D
���̃y�[�W�Q�ƁD
�@���̖�F

�ŃƂ̏ꏊ��−�Ƃ��ꏊ���C�����W�͓���������D
�y���d�v�����z
=\cos\theta&chf=bg,s,fff6f6)
�@�Ȍケ�ꂪ�o�Ă�����C�u���߂��I���̌������I�����������I�v�Ɠ��ӋZ�ɓ���Ă����Ƃ悢�D
1�ڂ̔��ʎ�D=0�ɂ��Ă��܂�����A���̌������g���ƁA�������P�����\���Ȃ��Ǝv���������Ă��܂��B���А������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���t��ǂ�������̂ł͂Ȃ��C�����Ƌ�̓I�Ɏ��E�����������Ă��������D

�̕������F
x%2B (6y^2%2B 14y%2B k)=0&chf=bg,s,fff6f6)
…(1)
�̔��ʎ�
&chf=bg,s,fff6f6)
…(2)
�ɂ��āC

�̕������F
=0&chf=bg,s,fff6f6)
…(3)
�̔��ʎ��F
^2-4(25-4k)=0&chf=bg,s,fff6f6)
…(4)
���Ȃ킿�C

…(4’)
�Ƃ���ƁC

…(4)�ƂȂ邪
^2&chf=bg,s,fff6f6)
…(2)
�ƂȂ��āC

��0�ɂ͂Ȃ�܂���D
�����ʎ��Ƃ������t�́C�Q���������ɑ��Ē�`����Ă���̂ŁC�u

�̔��ʎ��ɂ���

�Ƃ���Ɓv�Ɛ��m�ɏ����܂������C������ɂ�����C���̂悤�Ɂu�Q�����ɑ��Ĕ��ʎ��Ƃ����p����g���悢�v
�Q����

�̔��ʎ���

�ɂȂ�悤�ɂ���ƁC

�͂P�����̂Q��ɂȂ�D
���̌��ʂ́C���̃y�[�W�̍����ɏ����Ă���܂��D
�S������܂������A����x�̕\�����̂܂܂ł��B
�����m��ҁn�F�A�����肪�Ƃ��DPC�łō��v��萔�̐ݒ�ɓ��̓~�X������܂����̂Œ������܂����i10→6�j�Ȃ����̒����ɂ���āC���Ȃ��̊w�K�̋L�^�����������킯�ł͂���܂��C������s���l�ɂ͒����Ă���͂��ł��D
���m�ʂ̕ł���̎���ɑ���n[�x�����z�\�C���Γx�����z�\�ɂ��ā^19.03.07�n
�x�����z�\�ł̍ő�l�̋��ߕ��������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D����ɏ�����Ă��邱�Ƃ͓ǂ߂܂����C�Ȃ����ꂪ����Ȃ̂��������ł��܂���D���Ȃ킿�C�x���̍ő�l�͕\�������番����C�K���l�̍ő�l���\�������番����܂��D
���m�ʂ̕ł���̎���ɑ���n[���ς�p�����x�N�g���������ɂ��ā^19.03.06�n
�Q�l�ɂȂ�܂��D�y��S�z�̉�����2�s�ڂ̎��C���ӂ�3���ڂ�b�x�N�g���ł͂Ȃ�a�x�N�g��b�x�N�g���ł͂Ȃ��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă��܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�O�p��̑��݊W�ɂ��ā^19.03.05�n
�Ƃ��s�p��cosA��4����1�̂Ƃ�sinA��tanA�̒l�̋��ߕ���������Ȃ��̂ł����E�E�E�ǂ̂悤�ɉ��������̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D��Q�����Ȃ���3��4�ɏ��������邾���ł��D

�̂Ƃ��C

������


&chf=bg,s,fff6f6)

�����̎���́u��≡���ł��v�D3����1�̏ꍇ�������Ă���̂�����C4����1�̏ꍇ��3��4�ɏ��������āC�����Ōv�Z���ׂ��ł��D����������Ƃ��Ȃ��ƁC����5���̂ɂȂ�����C�܂����₵�Ȃ���Ȃ�Ȃ��Ȃ�C�����̈Ӗ����Ȃ��Ȃ�܂��D
�����̋^�₪�����ł��Ă������肵�܂����I�܂��A���Z�̓��e��\�K����̂ɂƂĂ�������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̌���.�a�ς̌����ɂ��ā^19.03.04�n
���ɗ����܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����E�\����������Z���^�[��������ɂ��ā^19.03.03�n
�\�������@�K�v�����@�K�v�\�������̃R�c���Ō�ɏ����Ă���Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�擪�ɗv��̐}�����܂������C����ŕ�����Ȃ��Ƃ��́C�T�u���j���[�����ǂ���
���̃y�[�W��ǂ�ł��������D
2�i�@�̂ɂ��Ăł�
1101(2)�~1011(2)
13�~11��143�ɂȂ鎖�͗����o���܂������A
���̎���
130=1�~128+0�~64�c�c�c�́u130�v�Ɓu128�v�͉��̐����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�i�Y���y�[�W���玿�₵�Ă��������D�����łȂ��ƒT���Ȃ��ƁC�������₩������܂���j
130��143�̃^�C�v�~�X�ł��D�������܂����D
128�͉��̐����ł����H�́C�O�̉���𗝉����Ă��Ȃ��l�̎��₾���獢��D

�̏ォ�珇�Ɏ��邾������Ă����Ƃ������Ƃł��D
(�I�_)�|(�n�_)�Ƃ�ށA�Ƃ͂ǂ��������Ƃł����H
�����m��ҁn�F�A�����肪�Ƃ��D�n�_�`�̈ʒu�x�N�g����

�C�I�_�a�̈ʒu�x�N�g����

�̂Ƃ��C�Q�_�`�a�����ԃx�N�g��

�́C�I�_�̈ʒu�x�N�g��

����n�_�̈ʒu�x�N�g��

�����������̂ɂȂ�

���̋t�ł͂Ȃ��D
��ʂ�,�����̒l�ɕω����������Ƃ��ɁC���߂̒l��

�C�I���̒l��

�Ƃ���Ƃ��C�ω��������ʂ�

�ƂȂ�D���̂悤�ɁC�ω��̗ʂ͂˂Ɂi�I���̒l�j−�i���߂̒l�j�ŋ��߂�D����̓x�N�g���ł������Ƃ������ƁD
�Z�p�x�Ƃ����߂��...�̂Ƃ���Ɋ܂܂��
�Q�����ƂQ+3��+4�Ƃ͊ԈႢ�ł����H
����Ƃ���2+3��+4�ŕ\������������̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���₵�Ă���̂ł͂Ȃ��C�ӌ��������Ă���悤�ł����C2����

�ŕ\���i�u��v�͕s�v�j����́C����܂��D
=\theta^2%2B 3\theta%2B 4&chf=bg,s,fff6f6)
�������C���̘f���̏Z�l�́C…!�ǂ����Ă�̂�`
���܂ŏo���Ȃ������a�Ϙa �o����悤�ɂȂ�܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2���Ȑ��̋ɕ������Ɣ}��ϐ��\���ɂ��ā^19.02.23�n
���������b�ɂȂ��Ă���܂��B
�P�_�m�F���������܂��B
�y�T�D�œ_���ɂƂ���Ƃ���2���Ȑ��̋ɕ������z
��Q�� �������œ_�̉E�ɕ`���ꍇ
�mB�n�mC�n �o�Ȑ��C�����������l��ecos�Ƃ̕��������ɂȂ�܂�
�ɂ�����uecos�Ƃ̕��������v�̂Ƃ��낪�����ł��Ă��܂���B
�X�������肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
�������œ_�̍��ɕ`���ꍇ

�������œ_�̉E�ɕ`���ꍇ

�ƂȂ�Ƃ������Ƃł��D�i0<e<1�̂Ƃ��ȉ~�Ce=1�̂Ƃ��������Ce>1�̂Ƃ��o�Ȑ��j
�u�S�����̘f���̏Z�l�́C�����Ă��邱�Ƃ��킩���D�v
�ƌ����Ă��܂��������Ȃ��͉��l�ł����D
�����m��ҁn�F�A�����肪�Ƃ��D�W���[�N�ɑ��ẮC�W���[�N�ŕԂ��̂��悢�D�u�R�������ł��v�ł͖���߂��邵�C�u�O���W�A�i=�W���[�W�A�j�ł��v�ł͏d�߂���D���a���������炢���K���ȃ|�W�V��������
���m�ʂ̕ł���̎���ɑ���n[�}�N���[�����W�J�ɂ��ā^19.02.22�n
���Z���ł������V�̕���Ŏg���Ă������ł����H
���̏ꍇ�A�K�v�\�������́u��f(x)��x��0�̋ߖT��n������\�v�����ŗǂ��ł����H
�L�q�̏ꍇ�̌��܂蕶��Ȃǂ���������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D���m�ȋc�_�����邽�߂ɂ́C�������a�ɐG�ꂴ��܂��C���̋��ނł͋����W�J�̔����������ɍL���G��邱�Ƃ�ڎw���Ă��܂��D�����������ނ��Ǝ~�߂Ă��������D
���m�ʂ̕ł���̎���ɑ���n[N�i���̏����ɂ��ā^19.02.22�n
�ƂĂ�������₷�������ł��I
�^�₪�������܂����I
���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
�����s�m ����������^19.02.20�n
�ȉ~�̂悤�ɁA(acos��,bsin��)�Ƃ����悤�ȉ��̍��W�̒u�����͑o�Ȑ��ɂ͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�Q���Ȑ��̔}��ϐ��\���́C
���̃y�[�W�̉��̕��ɂ���܂��D
���P�S�̉���ɂ��钸�_�̓����ɂ��Ă��������ڂ���������~����
�����m��ҁn�F�A�����肪�Ƃ��D���̖��ŕ\������������C�Ȍ����Ăŕ�����Ղ�����ł����C��̓I�ɃC���[�W����ɂ́C���ۂɃO���t��`���Ă݂�Ƃ悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�������̈ړ��ɂ��ā^19.02.19�n
�������̈ړ��̖��Ɏ���̗����Ȃ��������߂������瑗�M���܂�
���P�́i�Q�j�̓����́Ay=x^2-4x+5�ł͂Ȃ��Ay=x^2-4x-3���Ǝv���̂ł����m�F�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���̕�����
^2%2B 2&chf=bg,s,fff6f6)
�̒��_�̍��W�́C
&chf=bg,s,fff6f6)
�ł��D���̃u���t������������3�C����������−1�������s�ړ�����ƁC���_�̍��W�́C
&chf=bg,s,fff6f6)
�ɂȂ�܂��i

�̌W���͕ς��Ȃ��j
�@���������āC�������̕������́C
^2%2B 1=x^2-4x%2B 5&chf=bg,s,fff6f6)
�ƂȂ�C���̉�ʂ̏����Ă������̒ʂ�ł��D
�@�H�H
^2=x^2-4x-4&chf=bg,s,fff6f6)
�Ƃ��Ă���\������
�@���P�ł悭����ԈႢ�F
^2=a^2-2ab-b^2&chco=ff0000&chf=bg,s,fff6f6)
�ɋC��t���܂��傤�i��������
^2=a^2-2ab%2B b^2&chf=bg,s,fff6f6)
�j
54�˒��w�� �ʋ��Ȃ̋��������Ă��܂����A���̑̑��ɂȂ��ėǂ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ɨ��Ȏ��s�̊m���C�������s�̊m���ɂ��ā^19.02.16�n
�߂�ǂ������Ǝv���Ă����ǂ���������܂��Ȃ��Ƃ͂킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ꕽ�ρC��䗦�̐����ɂ��ā^19.02.14�n
����_�̏W���i�o�b�g��A�z���Ă���������j���疳��ׂɕW�{�𒊏o���āA�����̕W�{�ɗ͂������Đ܂���������܂��B�ア�͂������Ă��_�͐܂�܂��A�����͂�������Ɛ܂��_�̐��������Ă����܂��B���߂������̂́A�_�̏W���i��W���j���M���x�X�X���Ő܂�Ȃ����̗͂̑傫���ł����A�ǂ̂悤�ȕW�{���o�A�����f�[�^�A��͂��s���悢�ł��傤���H���̃y�[�W�ŏЉ��Ă����肪�g�������Ȃ̂œ��e�����Ă��������܂����B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D1�̎d���́C�����ƌ�Еt����8���ŁC�c��2�����炢���j�S�I�ȍ�ƂƂȂ邱�Ƃ������D�W�{�̒��o���@�͂��ꎩ�̂P�̑傫�ȃe�[�}�ł���C�܂���͓��v�O�̃m�E�n�E�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�d���g�����ɂ��ā^19.02.14�n
������Â炢
�����m��ҁn�F�A�����肪�Ƃ��D5�b���炢�œǂ߂鋳�ނł͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƌW���̕����ɂ��ā^19.02.13�n
�}���S�ĕ\������Ă��܂���B
�ǂ�������悢�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��DInternet Explorer 11�œǂ�ł�����悤�ł����C������̐ݒ�~�X�� Internet Explorer 7 �݊����[�h�ɂȂ��Ă��܂����̂Œ������܂��� -- SVG�O���t�B�b�N�X��canvas�O���t�B�b�N�X���g���Ă���y�[�W����������C�g�y�͈͂��L���ł����C�����璼�����ƂɂȂ�Ǝv���ƁC�C�������Ȃ肻���D�������C�����Ȃ���C�t���Ȃ��������ƂȂ̂ŁC����\���グ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�x�N�g���̐���(�}������)�ɂ��ā^19.02.12�n
�������Q�p����͕̂��ʃx�N�g���̏ꍇ�����ł����
��Ԃ̐�����3�̐����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ������Ă���̂́C���ʃx�N�g���̒P���ɂ���y�[�W�ł��D��ԃx�N�g���̘b�́C��ԃx�N�g���̃y�[�W�ɂ���܂��D
��H���R�̘b���m�F���ĉ��ɂȂ�H
���m�ʂ̕ł���̎���ɑ���n[��Βl�L���t�̕s�����ɂ��ā^19.02.12�n
��Βl�t�̕s�����ɂ��Ă̍��ځB�y��P�z�@���̕s�����������Ă��������D��2)�̂Ƃ�
?2=<x<0�̂Ƃ��Ax�{2=<?2x?1 ��
1=>x �ɂȂ��Ă��܂����E�E�E
x+2x=<?1?2 ��� 3x=>?3 ����
?1=>x �ł͂Ȃ��ł��傤���H
�����炾����
�����m��ҁn�F�A�����肪�Ƃ��D2��6������̊����ϊ��R�[�h�̃G���[�i���L�Q�Ɓj�̂��߁C���₪���m�ɉ��Ə����Ă���̂���������܂��C3����−3���炘��−1�ł��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�L���t�̕s�����ɂ��ā^19.02.11�n
��Βl�L���t�̕s���� ==
�y��P�z�@��2)�� x�{2=<?2x?�P��x�{2x=<?1?2��3x=<?3��x=<?1
�ɂȂ�܂��Hx=<1�ɂȂ��Ă��܂����E�E�E
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�R���������̎������̌��i�����W���j�ɂ��ā^19.02.11�n
�ƂĂ��d�Ă܂��I���ꂩ�����낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��DiPhone�ł��̉�ʂ��ǂ߂�̂ł����H
���m�ʂ̕ł���̎���ɑ���n[�ΐ��������ɂ��ā^19.02.09�n
�ΐ��̒ꂪx�ɂȂ��Ă���������̉������������ĉ�����
���肢�������܂�
�����m��ҁn�F�A�����肪�Ƃ��D��{�́C
��̕ϊ��������g���āC����^���Ɉړ������邱�Ƃł��D�������C�^��������>0�����ł����C��̏�����>0,��1�ł��邱�Ƃɒ���
�y��z

������
�i�j

�͒�ł���^���ł��邩��

…(1)
���ɁC��̕ϊ�������p�����


^2=4\log_{10}x&chf=bg,s,fff6f6)
^2-4\log_{10}x%2B 3=0&chf=bg,s,fff6f6)
(\log_{10}x-3)=0&chf=bg,s,fff6f6)


������(1)��������C

…�i���j
x��y�ł͂Ȃ��Ax��x2�̏ꍇ
adx4+�iae+bd�jx3+�iaf+be+cd�jx2+�ibf+ce�jx+cf
���iax2+bx+c�j�idx2+ex+f�j
�̂����������ĉ������I�I
�����m��ҁn�F�A�����肪�Ƃ��D���̒�N�̎d�������̂悤�ɕς���ƁC����������ɂȂ�܂��D�i���̌`�ł́C��肪�����Ă��܂��Ă��܂��j
����
&chf=bg,s,fff6f6)
���^����ꂽ�Ƃ��C�S����

�𐮐��W���̂Q��-�Q���Ɉ�������������@�͂��邩�H
�@���_���猾���u����܂���v�D
�i���_�㌾���邱�Ɓj
���W���̂S���������������������Ȃ�C���̋��f�����܂����ƂȂ邩��C�����ȂQ��g�ݍ��킹��Ύ��W���̂Q���������ɂȂ�܂��D�����m�Ȃ�ǂ̂悤�ɑg�ݍ��킹�Ă��悢�D���̂悤�ɂ��āC���W����4����
&chf=bg,s,fff6f6)
���^����ꂽ�Ƃ��C���̎��͎��W����

��p���āC
(dx^2%2B ex%2B f)&chf=bg,s,fff6f6)
�Ə�����Ƃ����͖̂{���ł��D
�@�Ƃ���ŁC���̃y�[�W�́u�������|�����������v�̋��ނȂ̂ŁC���̖������������W���̏ꍇ�������Ă��܂��D��L�ɂ����āC�����W���Ƃ���Ƃ��̂S���������������������Ȃ�C���̋��f�����܂����ƂȂ邩��C�����ȂQ��g�ݍ��킹��Ύ��W���̂Q���������ɂȂ�Ƃ͌����܂����C���ꂪ�����ɂȂ�Ƃ͌����܂���D���̂悤�ɂ��āC���̐����W����4������2��-2���Ɉ������������ʌ����͂Ȃ��Ca,c,d,f�̑g�ݍ��킹����C3��,2��,1���̌W�����������̂����s���낵�Ȃ���T�������Ȃ��ł��傤�D�i�������|���̈��������̖��́u�ǂ�Ȗ��ł�������v��ł͂Ȃ����Ƃɒ��ӁD�j
�i���ۂɂ́j
�@�Ƃ���ŁC4������2��-2���Ɉ��������ł�����C�e�X��2������2���������̉��̌�����p���ĉ������Ƃ��ł��邩��C��ʂ�4����������������悤�Ɍ����܂����C���_�������͂����Ƃ������ƂƁC���������Č���������̊Ԃɂ͑傫�ȃM���b�v������܂��D4���������̉��̌����i�t�F���[���̌����j�́C�ƂĂ����G�ŁC���͋��߂��܂����C�������ɂȂ邱�Ƃ͂߂����ɂ���܂���D
������������������ƂɁu�̓_����v�������Č�̑f�������Ԃ̃}�[�N���o�Ă���Ƃ���A���̕����̂������ł��傤���A���ȏ���ǂ�ŗ������ē��ōČ����āA�݂����Ȏ菇�ނƂ��ɂ͂Ȃ��S�n�悳������܂�����!
�Ȃ�Ƃ����܂����A�G�}���ƂȂ��Ċw�K�y�щ��K�̑��x�𑬂߂Ă��ꂽ�C�����܂��I
���ʂƂ��Č��ꂽ��A���R�U�T�W�i���Ƃ킩�邽�߂ɂ��Ă܂��j�����Ă܂����M�����Ă��炢�܂��ˁI
�����m��ҁn�F�A�����肪�Ƃ��D�i�����ϊ��V�X�e���̃G���[�͂܂������Ă��܂��C���[�J���Łi��M��̃p�\�R���Łj�t�ϊ��ł���ꍇ������悤�ł��̂ʼn��܂��j
���Ɂm �ς���^19.02.08�n
���wA�̐}�`���E?2?E?�`�F�o��l���E�X�̒藝?E?a?E��E?R�͂ǂ����ɂ���܂���?
�����m��ҁn�F�A�����肪�Ƃ��D
��2019.2.6�ȍ~�Ɏ�M�������z���́C�����ϊ��R�[�h�̃G���[�ɂ��C�܂Ƃ��ɓǂ߂܂���D���炭�����f�����������܂���
UTF-8�ɋt�ϊ�����ƁC��L�̂悤�Ɉꕔ�ǂ߂܂��D���̒f�Ђ��琄�肵�܂��ƁC�`�F�o��l���E�X�̒藝�̂��Ƃ�q�˂Ă�����悤�ł��D����́C���w���w��
���̃y�[�W�ɏ����Ă��܂��D
質問です…、E2%の食塩水500gに4%の食塩水を??g混ぜると9%の食塩水になる」??に入る数孁E
⤴のような問題�Eどのようにとけ�EよろしいでしょぁE��。。、E
�����m��ҁn�F�A�����肪�Ƃ��D�Q���U�������Ƀv���o�C�_�[�l�ɂ����ăT�[�o�����e��Ƃ�����C���̌��ʁCSend-mail CGI�̊����ϊ��ɃG���[�������Ă���悤�ł��D���̋��ނ̊Ǘ��l�́C���[�U�Ƃ��ăf�[�^�t�@�C�������������Ă��܂��C�v���o�C�_�l�ɑΉ����˗����邵���Ȃ��ł��D
�����M���ꂽ�����̊����R�[�h���CUnicode,UTF-8,Shift-JIS,jis,EUC,������C�؍���C��p��Ȃǂǂ�ɕϊ����Ă��ǂ߂܂���ł����̂ŁC�v���o�C�_�l�̑Ή��҂��Ƃ������ƂŁC���炭���҂����������D����܂ł͓ǂ߂܂���̂ʼnł��܂���D
���G���[�̌X���Ƃ��āCShift-JIS�̃R�[�h��UTF-8�ɕϊ�����Ă���悤�ł����C�t�ϊ����|���Ă��ꕔ�����ǂ߂܂���D
��2019.2.6�ȍ~�Ɏ�M�������z���͂��ׂĂ���ɊY�����܂��D���炭�����f�����������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^19.02.05�n
�G������!
�����m��ҁn�F�A�����肪�Ƃ��D�iandroid�Ȃ�g�їp�͕ʃy�[�W�ɂ���܂��D�����ƌ��₷���͂��ł��j
���m�ʂ̕ł���̎���ɑ���n[�x�N�g�������̌v�Z�ɂ��ā^19.02.04�n
���������o�Ă��Ȃ��B�r���v�Z������Ƃ����ƕ�����₷���B
�����m��ҁn�F�A�����肪�Ƃ��D�r���o�߂͏����Ă���܂��D�i7+3���Ȃ�10�ɂȂ�̂��C���̓r���o�߂������Ăق����Əq�ׂĂ���̂Ȃ�C�x�N�g���Ƃ͕ʂ̘b�ł��j
���m�ʂ̕ł���̎���ɑ���n[�ΐ������@�ɂ��ā^19.02.04�n
���2�̉����3�s�ځAlog�������Ă���Ǝv���̂ŁA���m�F���肢���܂��I
���Ɗw�Ő��O������Ă����w���ł����A�ƂĂ��������Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q�i�@,16�i�@,���i�@��10�i�@�ɂ��ā^19.02.03�n
�Ō�̓��́A������Ėʓ|�������̂ŁA���܂���ł������A���Ƃ́A�ƂĂ��킩��₷�������ł��B���肪�Ƃ��B�A
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̃x�N�g���������ɂ��ā^19.02.02�n
�������܂��B
���1�̉ŁA��(1)�̂Ƃ���́�AC����OB+s(��BF)��(�E�E��)�@�Ƃ���܂����A
��OB�ł͂Ȃ���AB���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[��Βl�L���t�̕s�����ɂ��ā^19.02.02�n
�����ŗ����ł��Ȃ����e���킩��₷���̂����Ă��ď�����܂����B���肪�Ƃ��������܂��B
(B)�̖��̉����(�A)�����P�̏ꍇ�A�Ȃ�(�|���{�P)�{(�|���{�Q)���R�ƂȂ�̂����킩��܂���B
����͂��Ȃ����݂܂���A�A�A�B�ł�������Ԃ̂��鎞�ɉ�������肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
�A�j

�̂Ƃ��C

������C


������C

������

��
%2B (-x%2B 2)\lt 3&chf=bg,s,fff6f6)
�ƂȂ�܂��D
���v����ɁC

�Ȃ�A���R�C

�����藧�Ƃ������Ƃ��g���܂��D
������₷������
�����m��ҁn�F�A�����肪�Ƃ��D����ł��ӌ��ł��Ȃ��C���z���ꌾ�̏ꍇ�́C�Ǘ��l���@�B�I�ȉ������Ă���悤�Ɍ����܂����C�ǂ̂悤�ȃy�[�W���u�����ˁI�v�Ȃ̂����������Ă��܂��D�y�[�W���������̂ŁC�S�̂����������ɂ͉��N��������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q�~�̌�_��ʂ�~�E�����̕������ɂ��ā^19.01.30�n
���3�̕K�v�����A�\�������Ƃ͂ǂ������Ӗ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ͍��Z���w�U�̋��ނł��D���Z���w�ł́C���w�T�E���w�`���w��ɐ��w�U���w�Ԃ悤�ɂȂ��Ă���C���w�`���w�Ȃ����k�����w�U���w��ł���Ƃ������Ƃ́C�߂����ɂȂ��ł��傤�D�܂�C���Ȃ��͒��w�����C���Z���Ɛ��Ő��w�`���K��Ȃ��������C�v������̌������璼�ڂ��̃y�[�W��ǂ�ł���Ƃ������Ƃ̂悤�ł��D
�@�K�v�����E�\�������̊ȒP�ȉ���́C
���̃y�[�W��
���̃y�[�W�����Ă��������D
�@�������C���낢��Ȗ��������Ƃ��ɁC�K�v�����Ŕ͈͂��i��C���ɂ��̍i��ꂽ�������\���������������Ƃ���2�i�\���̓��ẮC���Z���w�ł͐����C�̂悤�Ɏ��鏊�Ŏg���܂��D���ɋO�Ղ̕����������߂���ł́C�d��܂��̂ŁC���̓��Ă̏������͂ǂ����Ă��g�ɒ�����K�v������܂��D
�@����ɑ��āC�ȒP�Ȑ����̕ό`��������̉������Ȃǂ́C�u�K�v�\���ȕό`�v�u���l�ό`�v�ƌĂ�C�˂Ɍ��ɖ߂��W�ɂȂ��Ă��܂��D�����ŏq�ׂĂ���u�K�v�����ő{���͈̔͂��i��v�ό`�ł́C�u��������Ƃ�����͈̔͂ɂ����Ȃ����C���ꂪ���̏��������Ă�����̂���Ƃ͌���Ȃ��v�̂Łu���ۂɌ��̎������Ă��邱�Ƃ��m���߂�=�\�������m���߂�v���Ƃ���ł��D
�@�y���̗�z


�͌��̕������ɑ��āu�K�v�����v�ɂȂ��Ă���C�\���������i���̕������̉��ƂȂ��Ă���j�̂�

�����ł��D
�ƂĂ��킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �x�N�g���̑傫���i�����j�ɂ��ā^19.01.27�n
�Ō�ɖ�肪���Ă��ė������₷�������ł�!��������p�������ȂƊ����܂����B���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J����1�ɂ��ā^19.01.27�n
�S����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�K�v�����Ə\�������ɂ��ā^19.01.27�n
�u�d�v�v�Ƃ����o�������A�ƂĂ�������₷��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���f���ɂ��ā^19.01.27�n
���f���������m�肽���Ă��ƃT�C�g�ɂ����̂ł����A��`�����łȂ��m�F�������邱�ƂŃA�E�g�v�b�g���ł��Ȃ��Ȃ������T�C�g�ł����B���ꂩ������p�����Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������i���p���j�ɂ��ā^19.01.26�n
���1��(2)�̓����́`�Ⴆ��(2x+3)(x−4)��(−x−3)(−x+4)�͓������̂�����`
��(-x-3)��(-2x-3)�ł�����?
�����m��ҁn�F�A�����肪�Ƃ��D���1��(2)�ɂ͂��̂悤�ȋL�q�͂���܂���D(2x+3)(x−4)��(−x−3)(−x+4)�͓������̂ł͂���܂���D�����������̘b�����Ă�����̂ł����H
���m�ʂ̕ł���̎���ɑ���n[���f�����ʂ̓������2�ɂ��ā^19.01.26�n
���ł���������܂��@�@���f�����ʂ̗��2.1�̍Ōオsin�ɂȂ��Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�m���̏�@�藝�ɂ��ā^19.01.25�n
�q�������Ă��������Ă��܂��B���z�ł��B
����S��ł����T�C�R���̖ڂ̑Ώ̐�����
x+y+z+w=20
x+y+z+w=8�@(x+y+z+w=4�@�Ɓ@x+y+z+w=24���Ώ�)
w=1�̎��@x+y+z=7�@ X+Y+Z=4�@�@15�@
w=2�̎��@x+y+z=6�@ X+Y+Z=3�@�@10
w=3�̎��@x+y+z=5�@ X+Y+Z=2�@�@6
w=4�̎��@x+y+z=4�@ X+Y+Z=1�@�@3
w=3�̎��@x+y+z=3�@ X+Y+Z=0�@�@1�@�@���v 35
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����Ɨ̈��ɂ��ā^19.01.24�n
y��x�̐}���̎d�����ڂ��ė~����
�����m��ҁn�F�A�����肪�Ƃ��D�}�͍��̒ʂ�D�i�D�F�����D���E�����܂܂Ȃ��j
�i�T�j�̖���dx/dt���Ȃ��̂悤�ɂȂ�̂��킩��Ȃ��̂ŁA�ڂ��������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D
�ς̔����@�Ȃǂ��܂��K������Ă��Ȃ��悤�ł�����C��������ɓǂ�ł��������D
�������A�����̋��ނ̎�������Ă��܂������̂ł��B���t���炸�Ȏ���ŊǗ��l����̂��萔�Ƃ����f�����|�����Đ\����܂���ł����B���̋��ނ̒ʂ�ɉ�������120�ɂȂ�܂������A����x�������m�F������A��O�̖��̕ʉ������Ă��܂����B����ȕ�����ɂ����Ă������ʋ��ނ̎���ł����J�ɂ������������肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ׂ荇�����ѕ��E�ׂ荇��Ȃ����ѕ��ɂ��ā^19.01.22�n
���ŁAa b c c d d��6������1��ɕ��ׂ鎞�Aa b ������Ȃ����ו������ʂ肩�B�Ƃ���܂����B
���̃y�[�W��ǂ��c c d d��4�I�� 2�I2�I��6�ƂȂ�A����4��������ׂ�����5C2=10������������Ǝv���܂����B
������������������A6C2�~ 4�I��2�I2�I=90�ł����A���̖��ɂ͂��̃y�[�W�̍l�����͓��Ă͂܂�Ȃ��̂ł��傤���H�ǂ̂悤�ɍl��������̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�d�v�Ȏ����ȗ����Ă��܂��ƁC�Ӗ����ʂ��Ȃ��Ȃ�܂��D���̋��ނ������璲�ׂĂ����������L�q������܂���D���ۂɂ�
�i�����̎����Ă�����W�́j���ŁAa b c c d d��6������1��ɕ��ׂ鎞�Aa b ������Ȃ����ו������ʂ肩�B�Ƃ���܂����B
�i���̋��ނŁj���̃y�[�W��ǂ��c c d d��4�I�� 2�I2�I��6�ƂȂ�A����4��������ׂ�����5C2=10������������Ǝv���܂����B
�������i�����̎����Ă�����W�́j������������A6C2�~ 4�I��2�I2�I=90�ł����A���̖��ɂ͂��̃y�[�W�̍l�����͓��Ă͂܂�Ȃ��̂ł��傤���H�ǂ̂悤�ɍl��������̂ł��傤��
�Ƃ������Ƃ̂悤�ł��D�v����ɁC���̋��ނƂ͊W�̂Ȃ����Ȃ��̓��ĂƂ��Ȃ��������Ă�����W�̘̉b�����Ă�����悤�ł��D
�@�M�҂̍l���ł́C���Ȃ��̓��Ă��Ԉ���Ă���C���̖��W�̉��Ԉ���Ă��܂��D

�̂͂��ł��D
�����b�ɂȂ�܂��B�E�E���L�Ɋւ���ǐL��
1�y�[�W�ڂ����������2�y�[�W�ڂ��甽�����Ȃ��̂ł��B
�����������ƂȂ��A2�y�[�W3�y�[�W�ƃy�[�W��i�߂邾�����Ƃ��̃y�[�W�̐F�͕ς��A�������܂��B���̃p�\�R���̖��Ȃ�ΐ\����܂���B
���1�E�E4�y�[�W�܂ł��镪�ł����A���x����Ă�1�y�[�W�ڂ͂ł���̂ł����A2�y�[�W�ڂ�������N���b�N���Ă��ω��Ȃ��A�i�ގ����ł��܂���B���2�͑��v�ł��B
���̃p�\�R���̖��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ����̓_�v���O���������������悤�ł��D���N�̊ԂɁC���z�����Ƃ��ɁC�O�̃v���O�����ƃg���u�����悤�ł��D�������Ƃ͌�����܂��C�����܂��D
�m�ǐL�n���Ɖ�z�z���邽�߂̔z��ϐ��̗L���͈͂��Ԉ���Ă��܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����ɂ��ā^19.01.19�n
�W�J����2�̖��6
��3��(3)��8�ō̓_���Ă����ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D�S�p�����ɂȂ��Ă��܂��H�͔��p�����ɂ��Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�s��̑Ίp���Ƃ��ɂ��ā^19.01.18�n
P�́|1��ɂ��Ă��������ڂ��������ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͋t�s��̘b���������Ă���ǂނ悤�ɂȂ��Ă���̂ŁC�y�[�W�̐擪�ɃT�u���j���[����t�s��̃y�[�W���ɓǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[�~�̐ڐ��̕�����2�ɂ��ā^19.01.16�n
�ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[N�i���̏����ɂ��ā^19.01.15�n
�Q�i���̏������Q�{����ƌ��オ�肷�邱�Ƃ͗����ł��܂������A10�i���̏������Q�{���ē�������Ă����z�͔�Ă��܂�����������܂��B
������0.1�`0.9��10�i�����Q�i���ɒ������Ƃ������A0.5�ȊO�͏z�������ł��ˁB
x=a/10(1<a<9)
x*2=a/5={1+b/5(a>5)}or{1(a=5)}or{0+b/5(a<5)}(1<b<4)
x={1*1/2+b/10}or{1*1/2}or{0*1/2+b/10}
�����m��ҁn�F�A�����肪�Ƃ��D�܂��C�u�����v→�����D����

�̂P������

�i

�͐����j
�ȊO�́C�L����

���|���Ă������ɂȂ�Ȃ�����C���������������ɑ����i�z�����ɂȂ�j�͂����Ƃ͌����܂��D
�@���̌`�̋c�_�iN�i�@�Ƃ����L���@��ς�����C�L������←→�����������ς�邱�Ɓj�́C�悭�o�Ă��܂��D��L�Ƌt�̕ϊ��C���Ȃ킿�C1/3�̂悤�ȕ����i3�i���j�C��ʂ�1/N�iN�i���j��10�i���̏����ɒ����Ƃ��CN��2��5�̔{���ł���ꍇ�Ɍ���L����

���|�����Ƃ��ɐ����ɂȂ邩��C����ȊO�̕�����g���Ă��镪���͂��ׂĖ��������i�z�����j�ɂȂ�Ƃ������Ƃ́C�悭�m���Ă��܂��D
�x�����z�\�́A�����������Ƃ��낪�킩��Ȃ��B
�ǂ�������o�����ł����H
�v�Z���A�����ŕ\����
�����m��ҁn�F�A�����肪�Ƃ��D�������₳��Ă���̂���������܂���D��ʂɁC�x�����z�\�̖��ł͂ǂ̂悤�ɓ�������悢�̂��Ƃ����₢�ł�����C���ɂ���ĈႤ�ł��傤�D���̃y�[�W�ɂ�����1�肠����̂��Ƃł�����C�����ɂ���m�Q�l�n�Ƃ����������N���b�N�����Ƃ��ɕ\�����������ǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[��ϕ��̒u���ϕ��ɂ��ā^19.01.14�n
���m�ʂ̕ł���̎���ɑ���n[���w�I�A�[�@�i�����̏ؖ��j�ɂ��ā^19.01.12�n
�Ȃ�قǁ`�I�Ɗ������܂����A
��1�Ő�B���K���Ă��Ȃ��̂ɂ킩�����̂Ŋ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�d�ϕ�:�ϐ��ϊ�.���R�r�A���ɂ��ā^19.01.12�n
�d�ϕ��ő̐ς����܂�Ȃ�Ėʔ����ł��ˁB�}�������ĂƂĂ�������₷���ł��B���TeX�����߂ďK���܂����B�������̂悤�ȕ�����₷��������v���O���~���O�łł���悤�ɂȂ肽���ł��B
���̖��A�ȉ~�̒��̋��̑̐ς����߂Ă���̂ł��傤���H�H�ϕ��͈͂��ǂ̂悤�ɋ��߂���ǂ���������܂���B���a1�̉~��1/2�{�����ȉ~�ł���ˁH
���D(x^2+y^2)dxdy D:x^2/4+y^2��1
���D(x^2+y^2)dxdy D:x^2/4+y^2��1
�́A�ϕ��͈͂��ȉ~�Ȃ̂ł����A�~�Ɠ��l�ɋɍ��W�ϊ����ċ��߂邱�Ƃ��ł���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�ϐ��ϊ��ɂ���Ă�������͂��ł����C�����Ɗ�{��
�����`�ȊO�̗̈�ł̏d�ϕ����}�X�^�[�����Ƃ悢�ł��傤�D
�@�Ȃ��C������̖��́C���ɂ��Ă����ɂ��Ă��Ώ̂Ȃ̂ŁC��1�ی������߂ĂS�{����悭
dydx\]&chf=bg,s,fff6f6)
dxdy\]&chf=bg,s,fff6f6)
�����ŁC
dx=2\sqrt{1-y^2}\frac{4-y^2}{3}\]&chf=bg,s,fff6f6)
���g���āC��Ƃ���

���̂��Ƃ́C�O�p�����g���Ēu���ϕ��ɂȂ�悤�ł��D
�Ȃ��C�`�͋��ł͂Ȃ��C

�����_����̋����̂Q��ɂȂ�̂ŁC�����������̂ɂȂ�܂��D
�������̎Q�l�ɂ����Ă��������Ă܂��B
���̖������������āA��������T�����̂ł����A���M���Ȃ��c�����1+x��sint�ɒu���ϕ�����Ή����܂����H
��(��x)/(1+x)dx
�����m��ҁn�F�A�����肪�Ƃ��D�͂��߂ɁC���̋L���͎���ϕ��̂Ƃ��Ɏg���܂��D�����ł͎��ϐ����̕s��ϕ���\�����ʂ̋L���炪�悢�D���ɁC1+x=sin t�Ƃ���ƁCx=sin t-1��0�ƂȂ��ā�x����`����܂���̂ŁC���̕ϊ��̓_���ł��D���̂悤�ɖ��������瓦���āC�P�Ȃ镪�����ɂ���Ɖ����܂��D

�Ƃ�����



dt=2t-2\int\frac{1}{t^2%2B 1}dt\]&chf=bg,s,fff6f6)
������
���̃y�[�W��(2)iii)�̗v��ɂ���悤�ɁC

�̌`�̕s��ϕ��́C���Z���w�ł͈���Ȃ��t�O�p���ɂȂ�܂����C������g���ƌ���

������������₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����m�����z�Ǝ��ӕ��z�ɂ��ā^19.01.11�n
���3�̕��UV(Y)=E(Y^2)-E(Y)�ƂȂ��Ă��܂����A��������V(Y)=E(Y^2)-(E(Y))^2�ł́H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����i��Βl�t���j�ɂ��ā^19.01.11�n
���Q(�R)�̉���̃C�j�́u���������āA -1<=x<=1�v�͌��ł͂Ȃ��ł����H
�ꍇ������-1<=x<1�ƁA�s�����̉���x<=0,1<=x�̋��ʕ������Ƃ�ƁA-1<=x<=0�ƂȂ�̂ŁA
�u���������āA -1<=x<=0�v�Ƃ���̂��������Ǝv���܂��B
�i�܂��A����̂܂܂��ƑS�̂̉���-2<=x<=1�ƂȂ��Ă��܂��܂��B�j
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q���s�����ɂ��ā^19.01.11�n
�������ɖ𗧂Ă����Ă�����Ă܂��B
�뎚�ł��B
�`���̐���������(�Q�l)�ȉ���
�u�Q�����ɂ́u�O���t�v���Ή�����D
�@�������ڂŌ����C�Q������y=��t������Q���ւɂȂ�D�v
�̂Q���ւ͌뎚���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�敪���ϖ@�̍l�����ɂ��ā^19.01.10�n
�D�y�ÏC���Z�̔��ł��B
�@�B�I�ɖ��x���x1/���Ƃ�肪���ȂƂ���A�敪���ς̕���ς���Ƃ����̂͗ǂ��A�C�f�A�ł��ˁB
�����A�Ɍ�����ϕ��@��2�́i�l����2�j�̐����́i����2�j�Ɏ������ނ��߂ɂ͕���/����n�W�߂Ė����ɔ���Ƃ����悤�ɓW�J�����ق�����낵���̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ȃ��Ă��܂����HWeb��̃t�H���g���u���E�U�ɂ���āiFirefox�j�Ƃ����������ɂ����Ƃ����b�ł�����C�����͒����܂�
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^19.01.3�n
���ɂ���Ă͂����������邾�������`����Ȃ���������ƕ������̂ł����A���̏ꍇ�ɁA����������`�����ł��L����`������߂���@�������Ă��������B
����E�E�Ef(x)=x^2-2,g(x)=log2:x�̂Ƃ��A(g��f)(x)����`�����f(x)�̍ł��L����`������߂�B�܂��A���̂Ƃ���(g��f)(x)�����߂�B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��̎�������ł́C������
(g°f)(x)=g(f(x))=log2(x2−2)�́C
x2−2>0�������ƂȂ�̂ŁC

�ł��D
�@��ʂ̏ꍇ���C����Ɠ��l�ɍl����悭�C
g(x)�̒�`�悪�C�Ⴆ��
a<x<b�Ȃ�C
a<f(x)<b�������悢�D
���ȑO�̘A���ł�
��==���j���[�ɖ߂�
 �A�����肪�Ƃ��D�ǎ҂���̖��ɓ�����ƁC�h��Ȃǖ{�l���g�������Ȃ���Ȃ�Ȃ����̂���`���Ă��܂��\��������̂ŁC���Ȃ��悤�ɂ��Ă��܂��D�������Cx = y^2 + 1/4 a�́C\(x=y^2+\frac{1}{4}a\)�Ȃ̂�\(x=y^2+\frac{1}{4a}\)�Ȃ̂��C�Ӗ��s���ł����C\(x=y^2+\frac{1}{4a}\)�ɉ��߂����\(a\gt\frac{3}{\sqrt[3]{4}}=1.88988\)�Ƃ����������o�ꂵ�܂��D�O���t�́C���}�ŐԐ��̏ꍇ�͇@�̌`�̋��ʐڐ��݂̂ƂȂ�C�ΐ������ڂƂ��Đ��̏ꍇ�́C�A�B�̌`�̋��ʐڐ����o�ꂵ�܂��D�Ȃ��C�ڂ������Ă͐����`�h��ChatGPT, Copilot , Gemini�̂ǂ�ɂ��Ȃ��̎�������̂܂�������ł��قړ������ĂƂ��ē����܂��D
�A�����肪�Ƃ��D�ǎ҂���̖��ɓ�����ƁC�h��Ȃǖ{�l���g�������Ȃ���Ȃ�Ȃ����̂���`���Ă��܂��\��������̂ŁC���Ȃ��悤�ɂ��Ă��܂��D�������Cx = y^2 + 1/4 a�́C\(x=y^2+\frac{1}{4}a\)�Ȃ̂�\(x=y^2+\frac{1}{4a}\)�Ȃ̂��C�Ӗ��s���ł����C\(x=y^2+\frac{1}{4a}\)�ɉ��߂����\(a\gt\frac{3}{\sqrt[3]{4}}=1.88988\)�Ƃ����������o�ꂵ�܂��D�O���t�́C���}�ŐԐ��̏ꍇ�͇@�̌`�̋��ʐڐ��݂̂ƂȂ�C�ΐ������ڂƂ��Đ��̏ꍇ�́C�A�B�̌`�̋��ʐڐ����o�ꂵ�܂��D�Ȃ��C�ڂ������Ă͐����`�h��ChatGPT, Copilot , Gemini�̂ǂ�ɂ��Ȃ��̎�������̂܂�������ł��قړ������ĂƂ��ē����܂��D
 �����m��ҁn�F�A�����肪�Ƃ��D�f�b�T���̏K���n�߂ɕ����b����
�����m��ҁn�F�A�����肪�Ƃ��D�f�b�T���̏K���n�߂ɕ����b����
 �����m��ҁn�F�A�����肪�Ƃ��D2�̉~�̋��ʐڐ��Ƃ������̂����邱�Ƃ��l����ƁC�ڐ������܂��Ă��C�ړ_�͌��܂�Ȃ����Ƃ�������܂��D�Ⴆ�C���}�̐ڐ��́C�ړ_(0,1)�ʼn~
�����m��ҁn�F�A�����肪�Ƃ��D2�̉~�̋��ʐڐ��Ƃ������̂����邱�Ƃ��l����ƁC�ڐ������܂��Ă��C�ړ_�͌��܂�Ȃ����Ƃ�������܂��D�Ⴆ�C���}�̐ڐ��́C�ړ_(0,1)�ʼn~
 �����m��ҁn�F�A�����肪�Ƃ��D���q�����炻�̂����Ԃ́u���ꂼ��ŗL�̋�ʂ̂�����ȂɂȂ�̂Łv�C4C2�̂悤�ɒj�q�Q�l���̏ꏊ�����߂邾���ł́C�j�q�̏ꏊ�͌��܂�܂������ւ�����ʂ̕��ѕ��ɂȂ�܂��D�Ⴆ�C�}�̍������ł�
�����m��ҁn�F�A�����肪�Ƃ��D���q�����炻�̂����Ԃ́u���ꂼ��ŗL�̋�ʂ̂�����ȂɂȂ�̂Łv�C4C2�̂悤�ɒj�q�Q�l���̏ꏊ�����߂邾���ł́C�j�q�̏ꏊ�͌��܂�܂������ւ�����ʂ̕��ѕ��ɂȂ�܂��D�Ⴆ�C�}�̍������ł�
 �����m��ҁn�F�A�����肪�Ƃ��DwxMaxima�̃y�[�W���玿�₳��Ă��܂��̂ŁCwxMaxima�̂Q�����O���t�ł�����ΐ��ڐ��ɂ���ɂ́H�Ƃ������Ƃɂ��ē����܂���
�����m��ҁn�F�A�����肪�Ƃ��DwxMaxima�̃y�[�W���玿�₳��Ă��܂��̂ŁCwxMaxima�̂Q�����O���t�ł�����ΐ��ڐ��ɂ���ɂ́H�Ƃ������Ƃɂ��ē����܂��� �����m��ҁn�F�A�����肪�Ƃ��D���ꁨ0�C���q��1�C������±���ł��D
�����m��ҁn�F�A�����肪�Ƃ��D���ꁨ0�C���q��1�C������±���ł��D ���}�̏ꍇ�C
���}�̏ꍇ�C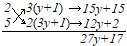 ���}�̂悤�ɑg�ݍ��킹�܂��D
���}�̂悤�ɑg�ݍ��킹�܂��D �����m��ҁn�F�A�����肪�Ƃ��D�{�������ɑ��Ă̂ݒ�`���������C�����ȊO�ɂ��K�p���Ă�����Ƃ��āC�Ⴆ�K���}���i���}�j�Ȃǂ�����܂����C
�����m��ҁn�F�A�����肪�Ƃ��D�{�������ɑ��Ă̂ݒ�`���������C�����ȊO�ɂ��K�p���Ă�����Ƃ��āC�Ⴆ�K���}���i���}�j�Ȃǂ�����܂����C �����m��ҁn�F�A�����肪�Ƃ��D���11�Ƃ��Ȃ��̎���ɑ��铚���Ƃ́C�ʂ̖��ł��D(s+2,3s-1,4)+p(3,-1,6)=(2t-2,2,-t+1)���������Ƃ�(3,-1,6)�����Ƃ͖��W�ł��D�i���}�Q�Ɓj
�����m��ҁn�F�A�����肪�Ƃ��D���11�Ƃ��Ȃ��̎���ɑ��铚���Ƃ́C�ʂ̖��ł��D(s+2,3s-1,4)+p(3,-1,6)=(2t-2,2,-t+1)���������Ƃ�(3,-1,6)�����Ƃ͖��W�ł��D�i���}�Q�Ɓj
 (1')�͗Ⴆ�C
(1')�͗Ⴆ�C �x�N�g�����g�����@�Ƃ́C�Ⴆ���}��
�x�N�g�����g�����@�Ƃ́C�Ⴆ���}�� ����ɂ��́B���̃T�C�g�ɂƂĂ������b�ɂȂ��Ă���܂��B
1998�N�Z���^�[�������@��IA��1��[2]�ł����A
��ABH�䁢CDH
���A�Ȃ���������̂����ǂ����Ă�������܂���B
���݂܂��A�ǂ̂悤�ɓ��o����̂��A�����������Ē����܂��ł��傤���H
��낵�����肢�v���܂��B
����ɂ��́B���̃T�C�g�ɂƂĂ������b�ɂȂ��Ă���܂��B
1998�N�Z���^�[�������@��IA��1��[2]�ł����A
��ABH�䁢CDH
���A�Ȃ���������̂����ǂ����Ă�������܂���B
���݂܂��A�ǂ̂悤�ɓ��o����̂��A�����������Ē����܂��ł��傤���H
��낵�����肢�v���܂��B

 1 �_�C�r���O���D���Ȑl�́C���b�g���D���ł���B
1 �_�C�r���O���D���Ȑl�́C���b�g���D���ł���B �@�}�̂悤�Ȓ��p�O�p�`�ŁC�X���C���Ȃ킿
�@�}�̂悤�Ȓ��p�O�p�`�ŁC�X���C���Ȃ킿