|
【応用】
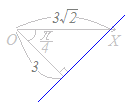
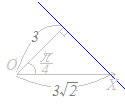
【極座標で表された2点間の距離】
(解説)極座標で表された2点A(r1 , θ1 ), B(r2 , θ2 )間の距離をlとおくと l2=r12+r22−2r1r2cos(θ2−θ1 ) が成り立つ. 右図の△OABに余弦定理を適用すると l2=r12+r22−2r1r2cos(θ2−θ1 ) が成り立つ. 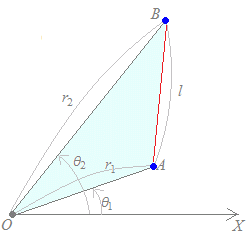 (別の解説) 直交座標(x1, y1 ),(x2, y2 )に直して,2点間の距離の公式
l=
を適用することを考えると
x1=r1cosθ1 , y1=r1sinθ1
x2=r2cosθ2 , y2=r2sinθ2 だから l2=(x2−x1 )2+(y2−y1 )2 =(r2cosθ2−r1cosθ1 )2+(r2sinθ2−r1sinθ1 )2 =r22cos2θ2+r12cos2θ1 −2r1r2cosθ1cosθ2 +r22sin2θ2+r12sin2θ1 −2r1r2sinθ1sinθ2 =r22+r12−2r1r2(cosθ2cosθ1+sinθ2sinθ1 ) =r22+r12−2r1r2cos(θ2−θ1 )
【例5】
極座標で表された点C(c, θ1 )を中心とする半径aの円の方程式は r2+c2−2rc cos(θ−θ1 )=a2 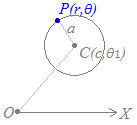 左の距離の公式において,次のように置き換えると得られます.
左の距離の公式において,次のように置き換えると得られます.
r2→r
ただし,得られた式においてrとθを変数として扱います.θ2→θ r1→c θ1→θ1 l→a
【例6】
極座標で表された点C(c, θ1 )を中心とする半径cの円の方程式は r=2c cos(θ−θ1 ) 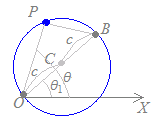 (解説)
(解説)上の【例5】においてa=cとおくと r2+c2−2rc cos(θ−θ1 )=c2 r2−2rc cos(θ−θ1 )=0 r=2c cos(θ−θ1 ) (別の解説) 右図の△OBPは直角三角形だから OP=OB cos(θ−θ1 ) したがって r=2a cos(θ−θ1 ) (さらに別の解説) 上の【例4】のグラフ r=2a cosθ を原点のまわりに角θだけ回転したものだから r=2a cos(θ−θ1 ) |
【三角関数の公式を使って変形したもの】
三角関数の公式 sin(±θ)=cosθ sin(±θ)=−cosθ a sinθ+b cosθ=sin(θ+α)
ただし,αはsinα=, cosα=
となる角
などを使って,上記の【例】(3)(4)の形に直せるものも,直線や円を表します.
【例7】
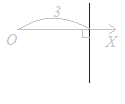
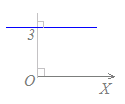
r sinθ=hは,図のように点H(h, )を通り,OHに垂直な直線を表します.
(解説)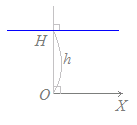 sinθ=cos(−θ) さらに,cosθ=cos(−θ)だからcos(−θ)=cos(θ−) したがって,元の方程式は r cos(θ−)=h と書き直せるから,点H(h, )を通り,OHに垂直な直線を表します. 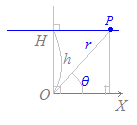 (別の解説) (別の解説)右図からわかるように,点P(r, θ)がこの直線上にあれば,r sinθ=hが成り立ち,逆にr sinθ=hが成り立てばこの直線上にあります. (さらに別の解説) r sinθ=hを直交座標に直すと,y=hになるので,y切片がhでx軸に平行な直線になります. 【例8】
r=(sinθ+cosθ)は,三角関数の合成公式を使って,次のように変形すれば,【例6】に述べた円を表すことが分かります.
(解説)r=2cos(θ−) 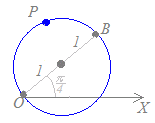 r=(sinθ+cosθ) =2(sinθ·+cosθ·) =2(cosθ·cos+sinθ·sin) r=2cos(θ−) |
|
【問題2】次の各々のグラフ(青の線で示したもの)に対応する極方程式を右欄から選んでください.
(1)解説
 |
r2+4rcosθ+12=0
r2−4rcosθ+12=0 r2+8rcosθ+12=0 r2−8rcosθ+12=0
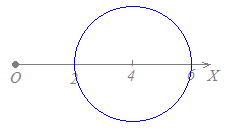
極座標の(4, 0)を中心とする半径2の円だから,【例5】においてc=4, θ1=0, a=2を代入すると
r2+42−2r×4 cos(θ−0)=22 r2+16−8r cosθ=4 r2−8r cosθ+12=0 となります. |
|
(2)解説
 |
r=2cos(θ−)
r=2cos(θ+) r=4cos(θ−) r=4cos(θ+)
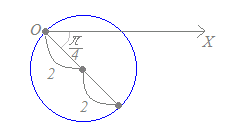
極座標の(2, −)を中心とする半径2の円だから,
【例6】においてc=2, θ1=−を代入すると r=4cos(θ+) となります. |
|
(3)解説
(別解)
cos(θ−)=sin{ −(θ−) } =sin(−θ)=sin(π+−θ) ここで,sin(π+A)=−sinAだから sin(π+−θ)=−sin(−θ) さらに,sin(−A)=−sinAだから −sin(−θ)=sin(θ−) |
r sin(θ−)=4
r sin(θ+)=4 r cos(θ−)=4 r cos(θ+)=4
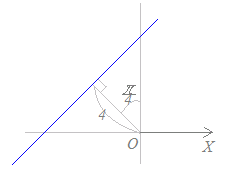
極座標のH(4, )を通りOHに垂直な直線だから,
【例3】においてα=, h=4を代入すると r cos(θ−)=4 このままでは,ちょうど合う式がないので,各々の式を三角関数の公式によって変形して比較すると cos(θ−)=−cosθ·+sinθ·←元の式 sin(θ−)=sinθ·−cosθ·←○ sin(θ+)=sinθ·+cosθ·←× cos(θ−)=cosθ·+sinθ·←× cos(θ+)=cosθ·−sinθ·←× |
|
【直交座標⇔極座標:方程式の変換】
【例9】直交座標で表されたグラフの方程式と極座標で表されたグラフの方程式とは,次の関係をもとにして互いに変換することができます.
x=r cosθ
y=r sinθ (上記から導かれるものとして,x2+y2=r2もよく使う)
x+y=2
【例10】
⇒ r cosθ+r sinθ=2
r (cosθ+sinθ)=2 r×2 (cosθ·+sinθ·)=2 rcos(θ−)=1
x2+y2=x
x2+y2はr2に直す.
xはr cosθに直す. ⇒r2=r cosθ 両辺をr>0で割る. r=cosθ |
※次のように変換できないものもあります. [直交座標に直せないものの例] r=aθ(アルキメデスの渦巻き線) [極座標に直せないものの例] x=a(θ−sinθ), y=a(1−cosθ)(サイクロイド) ⇒ r cosθやr sinθの形になっている式は直せますが,生のθが登場する式は直せません. 【例11】
r=2 sin(θ+)
右辺を三角関数の加法定理で展開して,sinθやcosθの式にする.
⇒r=2(sinθcos+cosθsin) r=2(sinθ+cosθ) r=sinθ+cosθ 両辺にrを掛けてr sinθやr cosθを「作る」 r2=r sinθ+r cosθ x2+y2=y+x |
|
【問題3】
各々の極座標で書かれた方程式に対応する直交座標の方程式を右から選んでください. (初めに極座標の方程式を選び,続いて直交座標の方程式を選んでください. 間違ったときは,問題を選び直してください.) |
x2−y2=−1 y=2x x−y=2 x2+y2=2y x2+=1 xy=1 x2+y2−x−y−2=0 |
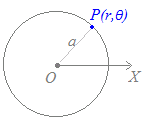 原点を中心とする半径
原点を中心とする半径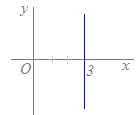 この事情は,右図のように
この事情は,右図のように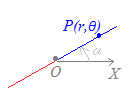 【例2】
【例2】 【例3】
【例3】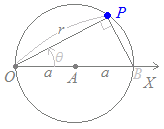 【例4】
【例4】