← PC用は別頁
|
■解説
【 要約 】 絶対値付の不等式では，
(A)の解説(A) 絶対値記号１つと定数だけのときは，次のように簡単にできる． |x|<3 の問題 ⇔ - 3<x<3 (B) 一般の場合には，場合分けによって絶対値記号をはずすことができる ○ |x| の定義： |x| は原点（ x=0 ）からの距離（ ≧0 ）を表わす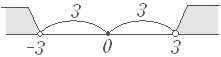．  ⇒ |x|>3 は原点からの距離が 3 よりも大きい値，すなわち右図灰色部の値になるから，x<−3 または 3<x 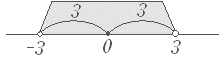 ⇒ |x|<3 は 原点からの距離が 3 よりも小さい値，すなわち右図灰色部の値になるから，− 3<x<3 |
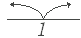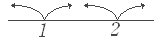(B)の解説 ○ |x−1| をはずすには，| | 記号の内部，すなわち，x−1 の正負によって分ける．⇒ x<1 と x≧1 に分ける． ○ |x−2| をはずすには，| | 記号の内部，すなわち，x−2 の正負によって分ける．⇒ x<2 と x≧2 に分ける． ○ 両方をはずすには（ア）x<1 （イ）1≦x<2 （ウ）x≧2 の３つに分ける． （答案）は次のようになる． （ア）x<1 のとき， (−x+1)+(−x+2)<3 より x>0 したがって，0<x<1 …(*1) （イ）1≦x<2 のとき， (x−1)+(−x+2)<3 より 1<3 これはつねに成り立つ． したがって，1≦x<2 …(*2) （ウ）x≧2 のとき， (x−1)+(x−2)<3 より x<3 したがって，2≦x<3 …(*3) 以上より，0<x<3 …（答） 注意点 ※ 上記のように場合分けしたとき，（ア）（イ）（ウ）の内部では，その場合分けに用いた条件を使わなければならないことに注意． 例えば（ア）で，x<1 のとき …… x>0 と出てくれば，  ※ 全体をまとめるときに，0<x<1 と 1≦x<2 は右図のように区間がつながって，0<x<2 になることに注意 この問題では，さらに 2≦x<3 だから，結局 0<x<3 になる． （ペッチン，ポッチンは下着などを指で押してつなぐ小さな金具の子ども言葉．凹型と凸型がちょうど合うようになっている．スナップボタンというのが大人の言い方らしい．） |
|
問題１ 次の不等式の解を下の選択肢から選べ． [1]|x−3|<2 |
|
【例１】 次の不等式を解いてください．
に分ける必要がある． に分ける必要がある． 両方を同時にはずすには，1) x<−2，2) −2≦x<0，3) x≧0の３つに分ける
（解説）
1) x<−2のとき | x+2 |=−x−2 | x |=−x だから −x−2≦−2x−1 x≦1 1)の範囲だから，x<−2 2) −2≦x<0のとき | x+2 |=x+2 | x |=−x だから x+2≦−2x−1 x≦−1 2)の範囲だから， −2≦x≦−1 3) 0≦xのとき | x+2 |=x+2 | x |=x だから x+2≦2x−1 x≧3 3)の範囲だから，3≦x
全体をまとめるとき，1)の範囲と2)の範囲は，x=−2において，つながることに注意
x≦−1, 3≦x…（答） 右図において， 赤線y=2| x |−1が 青線y=| x+2 |よりも上にある （または等しい）のは，x≦−1, 3≦x |
|
【例２】 次の不等式を解いてください．
2| x+1|<| x−1|
| x+1 |の絶対値記号をはずすには，
x+1<0 → x<−1 x+1≧0 → x≧−1 に分ける必要がある． | x−1 |の絶対値記号をはずすには， x−1<0 → x<1 x−1≧0 → x≧1 に分ける必要がある． 両方を同時にはずすには，1) x<−1，2) −1≦x<1，3) x≧1の３つに分ける
（解説）
1) x<−1のとき | x+1 |=−(x+1) | x−1 |=−(x−1) だから −2(x+1)<−(x−1) −2x−2<−x+1 x>−3 1)の範囲だから， −3<x<−1 2) −1≦x<1のとき | x+1 |=x+1 | x−1 |=−(x−1) だから 2(x+1)<−x+1 2x+2<−x+1 2)の範囲だから， 3) 1≦xのとき | x+1 |=x+1 | x−1 |=x−1 だから 2(x+1)<x−1 2x+2<x−1 x<−3 3)の範囲だから，解なし
全体をまとめるとき，1)の範囲と2)の範囲は，x=−1において，つながることに注意
右図において， 赤線y=| x−1 |が 青線y=2| x+1 |よりも上にあるのは， |
| 問題２ 次の不等式の解を下の選択肢から選べ． |
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る |
|
■［個別の頁からの質問に対する回答］[絶対値付の不等式について／18.6.25］
絶対値が二つ以上連なった形の不等式の解き方を載せてくださるとありがたいです
■［個別の頁からの質問に対する回答］[絶対値付の不等式について／17.6.8］
＝＞［作者］：連絡ありがとう．このページで幾つか取り上げています． 解説に別解があるといいと思います！
■［個別の頁からの質問に対する回答］[絶対値付の不等式について／17.5.20］
＝＞［作者］：連絡ありがとう． |
| 鬮ｫ�ｨ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ鬩搾ｽｵ�ｽ�ｺ鬮ｦ�ｮ陷ｻ�ｻ�ｽ�ｿ�ｽ�ｽ鬩幢ｽ｢�ｽ�ｧ�ｽ�ｽ�ｽ�ｵ鬩幢ｽ｢�ｽ�ｧ�ｽ�ｽ�ｽ�､鬩幢ｽ｢隴乗��ｽ�ｺ�ｽ�･�ｽ�ｽ�ｽ�ｽ鬩搾ｽｵ�ｽ�ｺ�ｽ�ｽ�ｽ�ｮGoogle鬮ｫ�ｶ�つ髫ｲ蟷｢�ｿ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�｢鬮ｫ�ｨ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ |
