|
■ 分数関数(有理関数)の不定積分 (例題中心) ◇◇ はじめに・目次 ◇◇○ この頁で取り扱う不定積分 この頁では次の(1)~(3),(A)(B)について解説と例を示す.実際の不定積分の計算においては(A)(B)を先に考えて,(1)~(3)で締めくくるという流れになるが,目指すべき目標の形(1)~(3)をはじめに説明する.
【基本の形】
(1) 分母がxの1次式になるもの
dx
(2) 分母がxの2次式になるものi) 分母が異なる2つの1次式に因数分解できるもの (分母=0の2次方程式が異なる2つの実数解をもつとき)
dx
ii) 分母が完全平方式( ··· )2になるもの(分母=0の2次方程式が実数の重解をもつとき)
dx
iii) 分母が( ··· )2+A になるもの (ただしA>0)(分母=0の2次方程式が虚数解をもつとき)
dx
(3) 例外的に,分子が分母の微分になっているときは,直ちに不定積分が得られる.
dx=log|f(x)|+C
【あらかじめ行っておく変形】 (A) 一般に,分数関数は(分子)÷(分母)の割り算によって商と余りに分けると,「分子の次数<分母の次数の形」 (数研の参考書で「分数式は富士の山」と呼ばれるもの) に変形することができる.この変形により,分数関数の不定積分を求めるときは,分子の次数が分母の次数よりも低い形だけを考えればよいことになる. (B) また,分母が何次式であっても分母=0のn次方程式は1次式と2次式の積に因数分解することができ (実数解の部分が1次式か重解に,虚数解の2つの組が(2) iii)の形の2次式に対応する) 部分分数分解と恒等式の係数比較法により,上記(1)(2)の形に帰着させることができる. |
【この頁では既習事項と考えている問題】 (0) 分母がxの累乗になるもの(次の形)
dx (ただし,a>0)
は,
k x−adx
の形だから,直ちに不定積分が得られる.
ア) a≠1のとき
dx= x−adx = x−a+1+C
イ) a=1のとき
dx=log|x|+C
例
ア)
dx=3 x−2dx = 3 x−2+1+C =− +C (初歩的な注意であるが ) +C ではないかと思う人は数学II「負の指数」の項目を見直しておく方がよい.
イ)
dx=5log|x|+C
※ y=log xは真数xがx>0のときだけ定義されるが,y=log(−x)は真数−x>0のとき,すなわちx<0のとき定義される.そこで,これらをまとめて
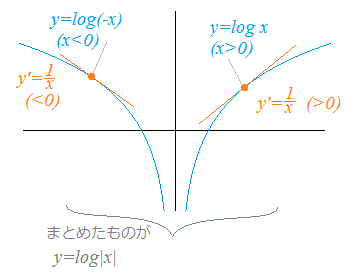 ア) x>0のとき,(log x)= イ) x<0のとき,x=−t (t>0) → y=log t (t>0)とおいて合成関数微分法によって微分すると = = − = となるから y=log(−x) (x<0)の微分もに等しい. ア)イ)をまとめると,(log|x|)= が導かれる. |