 【問題1】
【問題1】
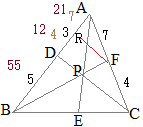
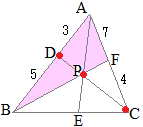
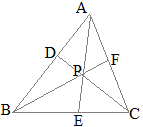
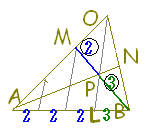
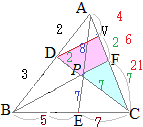
右図の △ABCにおいて, ABを 1:2に内分する点を D, ACを 2:3に内分する点を Fとし, BFと CDの交点を Pとする.さらに, APの延長が BCと交わる点を Eとする.
このとき, BE:EC, AP:PE, BP:PF, CP:PDをそれぞれ最も簡単な整数比で表してください.
解答を見る解答を隠す
Aを原点とし,  \( \overrightarrow{\rm{AB}}=\vec{b},\hspace{5px}\overrightarrow{\rm{AC}}=\vec{c} \) \( \overrightarrow{\rm{AB}}=\vec{b},\hspace{5px}\overrightarrow{\rm{AC}}=\vec{c} \)とおく.
まず,線分 BFのベクトル方程式を求める:
Fの位置ベクトルは  \( \displaystyle \frac{2}{5}\vec{c} \) \( \displaystyle \frac{2}{5}\vec{c} \), Bの位置ベクトルは  \( \displaystyle \vec{b} \) \( \displaystyle \vec{b} \)だから
) \( \displaystyle \overrightarrow{\rm{AP}}=\overrightarrow{\rm{AB}}+ s\overrightarrow{\rm{BF}}=\vec{b}+s(\frac{2}{5}\vec{c}-\vec{b}) \) \( \displaystyle \overrightarrow{\rm{AP}}=\overrightarrow{\rm{AB}}+ s\overrightarrow{\rm{BF}}=\vec{b}+s(\frac{2}{5}\vec{c}-\vec{b}) \)
(sは実数)…(1)
次に,線分 CDのベクトル方程式を求める:
Dの位置ベクトルは  \( \displaystyle \frac{1}{3}\vec{b} \) \( \displaystyle \frac{1}{3}\vec{b} \), Cの位置ベクトルは  \( \displaystyle \vec{c} \) \( \displaystyle \vec{c} \)だから
) \( \displaystyle \overrightarrow{\rm{AP}}=\overrightarrow{\rm{AC}}+ t\overrightarrow{\rm{CD}}=\vec{c}+ t(\frac{1}{3}\vec{b}-\vec{c}) \) \( \displaystyle \overrightarrow{\rm{AP}}=\overrightarrow{\rm{AC}}+ t\overrightarrow{\rm{CD}}=\vec{c}+ t(\frac{1}{3}\vec{b}-\vec{c}) \)
(tは実数)…(2)
(1)(2)の両方を満たす点 Pに対応する実数 s, tを求める:
=\vec{c}%2B t(\frac{1}{3}\vec{b}-\vec{c})) \( \displaystyle \vec{b}+ s(\frac{2}{5}\vec{c}-\vec{b})=\vec{c}+ t(\frac{1}{3}\vec{b}-\vec{c}) \) \( \displaystyle \vec{b}+ s(\frac{2}{5}\vec{c}-\vec{b})=\vec{c}+ t(\frac{1}{3}\vec{b}-\vec{c}) \)
\vec{b}%2B \frac{2}{5}s\vec{c}=\frac{t}{3}\vec{b}%2B (1-t)\vec{c}) \( \displaystyle (1-s)\vec{b}+ \frac{2}{5}s\vec{c}=\frac{t}{3}\vec{b}+ (1-t)\vec{c} \) \( \displaystyle (1-s)\vec{b}+ \frac{2}{5}s\vec{c}=\frac{t}{3}\vec{b}+ (1-t)\vec{c} \)
この連立方程式を解くと
 \( \displaystyle s=\frac{10}{13},\hspace{5px}t=\frac{9}{13} \) \( \displaystyle s=\frac{10}{13},\hspace{5px}t=\frac{9}{13} \)
(1)(2)に代入すると
 \( \displaystyle \overrightarrow{\rm{AP}}=\frac{3\vec{b}+4\vec{c}}{13} \)…(*1) \( \displaystyle \overrightarrow{\rm{AP}}=\frac{3\vec{b}+4\vec{c}}{13} \)…(*1)
(*1)により
 \( \displaystyle \overrightarrow{\rm{AP}}=\frac{7}{13}\cdot\frac{3\vec{b}+4\vec{c}}{7}=\frac{7}{13}\overrightarrow{\rm{AE}} \)…(*2) \( \displaystyle \overrightarrow{\rm{AP}}=\frac{7}{13}\cdot\frac{3\vec{b}+4\vec{c}}{7}=\frac{7}{13}\overrightarrow{\rm{AE}} \)…(*2)
(*2)の変形が分からない人へ
 \( \displaystyle \frac{n\vec{b}+ m\vec{c}}{m+n} \) \( \displaystyle \frac{n\vec{b}+ m\vec{c}}{m+n} \)
は BCを m:nに内分する点 Eです.このように分子の係数の和と分母が一致していれば,それは内分点であることを表しています.
しかし,それらが一致していなければ
 \( \displaystyle \frac{3\vec{b}+ 4\vec{c}}{13}=\frac{7}{13}\cdot\frac{3\vec{b}+ 4\vec{c}}{7} \) \( \displaystyle \frac{3\vec{b}+ 4\vec{c}}{13}=\frac{7}{13}\cdot\frac{3\vec{b}+ 4\vec{c}}{7} \)
のように変形すると(7で割って7を掛ける)
「内分比も縮尺比も分かる」「一石二鳥」なのです.
内分点までのベクトルを縮小したものが  \( \displaystyle \overrightarrow{\rm{AP}} \) \( \displaystyle \overrightarrow{\rm{AP}} \)なら,  \( \displaystyle \overrightarrow{\rm{AP}} \) \( \displaystyle \overrightarrow{\rm{AP}} \)を延長すれば  \( \displaystyle \overrightarrow{\rm{AE}} \) \( \displaystyle \overrightarrow{\rm{AE}} \)になります.
まず,分子の係数の和を分母にして,内分公式に合う式にして,その後で分数を調整するのがコツ
だから
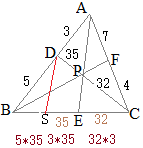
BE:EC=4:3
AP:PE=7:6
 \( \displaystyle s=\frac{10}{13} \)だから
BP:PF=10:3 \( \displaystyle s=\frac{10}{13} \)だから
BP:PF=10:3
 \( \displaystyle t=\frac{9}{13} \)だから \( \displaystyle t=\frac{9}{13} \)だから
CP:PD=9:4
→閉じる←
|
 【問題2】
【問題2】
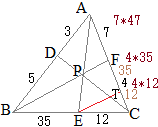
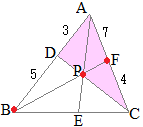
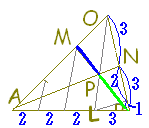
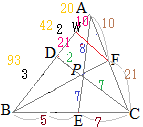
右図の △ABCにおいて, ACを 3:4に内分する点を F, BCを 6:5に内分する点を Eとし, BFと AEの交点を Pとする.さらに, CPの延長が ABと交わる点を Dとする.
このとき, AD:DB, AP:PE, BP:PF, CP:PDをそれぞれ最も簡単な整数比で表してください.
解答を見る解答を隠す
Aを原点とし,  \( \displaystyle \overrightarrow{\rm{AB}}=\vec{b},\hspace{5px}\overrightarrow{\rm{AC}}=\vec{c} \) \( \displaystyle \overrightarrow{\rm{AB}}=\vec{b},\hspace{5px}\overrightarrow{\rm{AC}}=\vec{c} \)とおく.
まず,線分 BFのベクトル方程式を求める:
Fの位置ベクトルは  \( \displaystyle \frac{3}{7}\vec{c} \) \( \displaystyle \frac{3}{7}\vec{c} \), Bの位置ベクトルは  \( \vec{b} \) \( \vec{b} \)だから
) \( \displaystyle \overrightarrow{\rm{AP}}=\overrightarrow{\rm{OB}}+ s\overrightarrow{\rm{BF}}=\vec{b}+ s(\frac{3}{7}\vec{c}-\vec{b}) \) \( \displaystyle \overrightarrow{\rm{AP}}=\overrightarrow{\rm{OB}}+ s\overrightarrow{\rm{BF}}=\vec{b}+ s(\frac{3}{7}\vec{c}-\vec{b}) \)
(sは実数)…(1)
次に,線分 AEのベクトル方程式を求める:
Eの位置ベクトルは  \( \displaystyle \frac{5\vec{b}+ 6\vec{c}}{11} \) \( \displaystyle \frac{5\vec{b}+ 6\vec{c}}{11} \)だから
 \( \displaystyle \overrightarrow{\rm{AP}}=t\frac{5\vec{b}+ 6\vec{c}}{11} \)(tは実数)…(2) \( \displaystyle \overrightarrow{\rm{AP}}=t\frac{5\vec{b}+ 6\vec{c}}{11} \)(tは実数)…(2)
(1)(2)の両方を満たす点 Pに対応する実数 s, tを求める:
=t\frac{5\vec{b}%2B 6\vec{c}}{11}) \( \displaystyle \vec{b}+ s(\frac{3}{7}\vec{c}-\vec{b})=t\frac{5\vec{b}+ 6\vec{c}}{11} \) \( \displaystyle \vec{b}+ s(\frac{3}{7}\vec{c}-\vec{b})=t\frac{5\vec{b}+ 6\vec{c}}{11} \)
\vec{b}%2B \frac{3}{7}s\vec{c}=\frac{5t}{11}\vec{b}%2B \frac{6t}{11}\vec{c}) \( \displaystyle (1-s)\vec{b}+ \frac{3}{7}s\vec{c}=\frac{5t}{11}\vec{b}+ \frac{6t}{11}\vec{c} \) \( \displaystyle (1-s)\vec{b}+ \frac{3}{7}s\vec{c}=\frac{5t}{11}\vec{b}+ \frac{6t}{11}\vec{c} \)
 \( \vec{b},\hspace{5px}\vec{c} \) \( \vec{b},\hspace{5px}\vec{c} \)は平行でなく,零ベクトルでもないから

 \( \displaystyle 1-s=\frac{5}{11}t \) \( \displaystyle 1-s=\frac{5}{11}t \)
 \( \displaystyle \frac{3}{7}s=\frac{6}{11}t \) \( \displaystyle \frac{3}{7}s=\frac{6}{11}t \)
この連立方程式を解くと
 \( \displaystyle s=\frac{14}{19},\hspace{5px}t=\frac{11}{19} \) \( \displaystyle s=\frac{14}{19},\hspace{5px}t=\frac{11}{19} \)
(1)(2)に代入すると
 \( \displaystyle \overrightarrow{\rm{AP}}=\frac{5\vec{b}+ 6\vec{c}}{19} \)…(*1) \( \displaystyle \overrightarrow{\rm{AP}}=\frac{5\vec{b}+ 6\vec{c}}{19} \)…(*1)
 \( \displaystyle s=\frac{14}{19} \)だから
BP:PF=14:5 \( \displaystyle s=\frac{14}{19} \)だから
BP:PF=14:5
 \( \displaystyle t=\frac{11}{19} \)だから
AP:PE=11:8 \( \displaystyle t=\frac{11}{19} \)だから
AP:PE=11:8
 \( \displaystyle \overrightarrow{\rm{AP}}=\frac{13\dfrac{5}{13}\vec{b}+ 6\vec{c}}{19} \) \( \displaystyle \overrightarrow{\rm{AP}}=\frac{13\dfrac{5}{13}\vec{b}+ 6\vec{c}}{19} \)
だから
CP:PD=13:6
AD:AB=5:13
AD:DB=5:8
→閉じる←
|
 【例題1】
【例題1】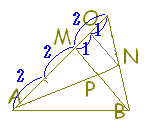
 【問題1】
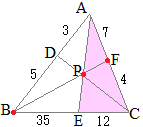
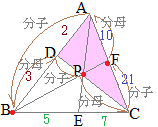
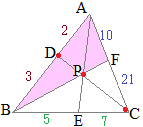
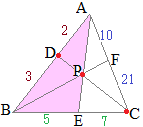
【問題1】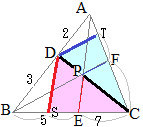 AD:DB=2:3, BE:EC=5:7のとき
AD:DB=2:3, BE:EC=5:7のとき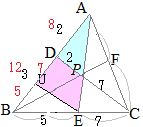
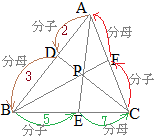
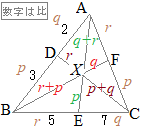
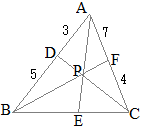
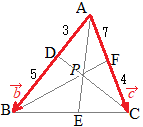
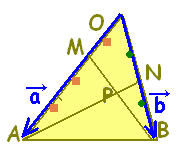
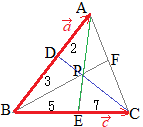 数学Bのベクトルで「2直線の交点を求める」とは,たとえば右図において原点をBにとった位置ベクトルを用いて,DCとAEの交点Pを求めるには,直線DCのベクトル方程式(1)と直線AEのベクトル方程式(2)を求め,両方を満たすベクトルをPの位置ベクトルとする.
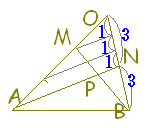
数学Bのベクトルで「2直線の交点を求める」とは,たとえば右図において原点をBにとった位置ベクトルを用いて,DCとAEの交点Pを求めるには,直線DCのベクトル方程式(1)と直線AEのベクトル方程式(2)を求め,両方を満たすベクトルをPの位置ベクトルとする.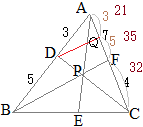 AD:DB=3:5, CF:FA=4:7のとき
AD:DB=3:5, CF:FA=4:7のとき