|
≪要点≫
y=ax(a>0, a≠1)のグラフには次の特徴があります. 1.定義域:−∞<x<∞, 値域:0<y<∞
※中学校で単に「変域」と呼ばれるものを,高校では独立変数xの値の範囲のことを「定義域」,従属変数yの値の範囲のことを「値域」と言います.
a>0,a≠1, −∞<x<∞ → y=ax>0.
2.グラフは常に点(0, 1)を通ります.xはすべての実数値をとりますがyは正の値だけをとります.
(理由)
3.各々のa (>0)について,グラフは点(1, a)を通ります.どんなa (>0)についても,a0=1が成り立ちます. したがって,x=0のとき,y=1となるので,グラフは常に点(0, 1)を通ります.
(理由)
4.グラフはx軸に限りなく近づきますがx軸に接したりx軸と交わることはありません.どんなa (>0)についても,a1=aが成り立ちます. したがってx=1のとき, y=aとなるので,各々のa (>0)について,グラフは点(1, a)を通ります.
y=0(x軸)は漸近線と呼ばれます.
5.y=axのaを指数関数の底(てい : base)といいます.
(1) 底がa>1のとき,単調増加関数になります. →図1, 2
p<q ⇔ ap<aq
(2) 底が0<a<1のとき,単調減少関数になります. →図3,4
p<q ⇔ ap>aq
(参考程度の読み物)
↓とても難しい話なので,読まなくてもよい.
実数値[例えば,πなど]に対する指数関数[a,aπ]について
有理数(整数や有理数[分数])のx,例えばx=に対して指数関数axは累乗根で定義されますが,指数関数のグラフを書くためには,x=のようにxが無理数の場合にも点が描かれていなければ,グラフに穴があいてしまいます.これをどう考えるのかについて.無理数x=については,指数関数の値は次のように有理数からなる数列の極限値で定義されると考えます. 21.4<2<21.41 21.41<2<21.414 21.414<2<21.4142 … 2=21.41421356... (以上はあくまで理論的な話で,実際にその値を求めなさいとは言いません.) このようにして,xが無理数のときでも2xの値が決まるので,y=2xのグラフは「すべてのxに対してつながっているように」描けばよいことになります. |
このページの「マイナーチェンジありカバー版」「パソコン用」ページ
(グーグルブロガー版)は,こちら⇒ 図 1 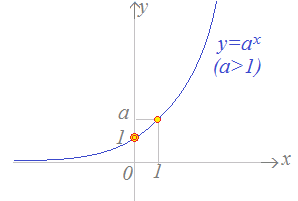 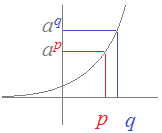 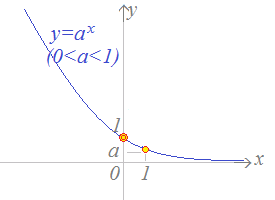 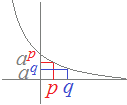 |
|
例 1(→図 5) y=2xのグラフ 1.定義域:−∞<x<∞,値域:0<y<∞
特に,グラフがx軸よりも上にあるように描き,右の方はどんどん増える雰囲気で描くこと(0<y<∞)が重要です.
2.グラフは点(0, 1)を通ります.
星座に例えれば,これは一番明るくて重要な星:アルファ星に例えることができ,この点を通っていないようなグラフを書けば,そのグラフは全くダメです.
3.グラフは点(1, 2)を通ります.
星座に例えれば,これは2番目に明るい星:ベータ星に例えることができ,この点を通っていないようなグラフを書けば,そのグラフはかなりダメです.
4.グラフはx軸に限りなく近づきますが,x軸と接触したり交わったりすることはありません.(x軸は漸近線になります.)
x軸に触っていたり,x軸よりも下に出ることがないように「慎重に,美的に」描くことが重要です.
5.関数のグラフは単調増加(全区間で常に増加=右上がり)となります.
グラフが右上がりになっているというイメージをしっかり持つことが,後に指数不等式を解くときの鍵になります.
例 2(→図 6) y=0.5xのグラフ 1.定義域:−∞<x<∞,値域:0<y<∞ 2.グラフは(0, 1)を通ります. 3.グラフは(1, 0.5)を通ります. 4.グラフはx軸に限りなく近づきますが,x軸と接触したり交わったりすることはありません.(x軸は漸近線になります.) 5.関数のグラフは単調減少(全区間で常に減少=右下がり)となります.
右下がりという点が,後に指数不等式を解くときに,多くの生徒が「うっかり間違いやすい」落とし穴になっています.これはとても危険なワナだと思って警戒した方がいいです.
|
図 5
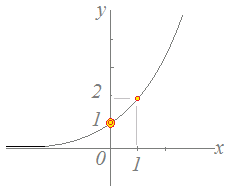
1.x軸よりも下に出ているようなグラフはまずダメです.
図 6
2.原点(0, 0)や点(1, 0)を通っているようなグラフは零点です. 4.5.直線に見えるもの(定規をあてて点をつないだもの),y=x2のように左側も持ち上がっているもの,右下がりのグラフになっているものは零点です. 3.点(1, 2)でなく少し上の方の(1, 3)を通っているように見えるグラフは少し減点されます. 4.5.波打っているようなものは程度によって減点されるでしょう. 全般に手書きなので,「重要な特徴が押さえてあれば」「微妙な手ぶれは許される」と考えるとよいでしょう. 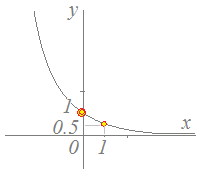 |
|
指数の大小比較 図 2, 4にように
(1) a>1のときは,関数のグラフは単調増加(右上がり)になります.したがって,
p<q ⇔ ap<aq (2) 0<a<1のときは,関数のグラフは単調減少(右下がり)になります.したがって, p<q ⇔ ap>aq 例 3次の2数の大小を比較してください.(不等号を使って表してください.)
(1)2, 2
(解答)底は2 (>1)で =<=だから 2<2
(2)0.5−0.7, 0.5−0.8
(解答)底は0.5 (<1)で −0.7>−0.8だから 0.5−0.7<0.5−0.8 |
(3),
(解答)有理数の指数(分数の指数)を使って書き直すと =3, =(32)=3 底は3 (>1)で >だから 3=3>3 >
(4),
(解答)有理数の指数(分数の指数)を使って書き直すと =(0.12)=0.1, =0.1 底は0.1 (<1)で =<=だから 0.1>0.1 > |
|
問題1次のうちで最大のものを選びなさい.
1も底2を使って表しておきます.
2−, 2, 2, 20, 2 底は2 (>1)で −=−0.5<0<=1.2<=1.33..<=1.5だから 2−<20<2<2<2 最大のものは2
1も底0.7を使って表しておきます.
0.7−2, 0.72, 0.7−3, (0), 1=0.70 底は0.7 (<1)で −3<−2<0<2だから 0.7−3>0.7−2>0.70>0.72(>0) 最大のものは0.7−3
底をとして書き直すと
( )0.3, ( )−0.2, ( )0 , (( )2)−0.5=( )−1, (( )3)−0.4=( )−1.2 底は (<1)で −1.2<−1<−0.2<0<0.3だから ( )−1.2>( )−1>( )−0.2>( )0>( )0.3 最大のものは( )−1.2=( )−0.4 |
底2を使って書き直すと
=2, =(22)=2, =(23)=2, =(24)=2 底は2 (>1)で =0.5<=0.666...<=0.75<=0.8だから 2<2<2<2 最大のものは2=
底0.1を用いて書き直すと
1=0.10, 0.1−5, =(0.12)=0.1, =(0.13)=0.1, 0.0001−1=(0.14)−1=0.1−4 底は0.1 (<1)で −5<−4<0<<だから 0.1−5>0.1−4>0.10>0.1>0.1 最大のものは0.1−5 |
|
底が異なる指数関数 図 7により
(1<)a<bのとき
(解説)
(1)y=axとy=bxはいずれも点(0, 1)を通ります.
たとえば y=2xもy=3xも点(0, 1)を通ります.
(2)x>0のとき,ax<bxが成り立ちます.(→図 7の領域B参照)
たとえば,x>0 → 2x<3x.
(3)x<0のとき,ax>bxが成り立ちます.(→図 7の領域A参照)
たとえば,x<0 → 2x>3x.
→x<0のとき(3)は要注意です.
同じxに対して x>0ならば2x<3xです. 2<3 4<9 8<27 しかし, x<0ならば2x>3xです. > > > 例 4次の数の大小を比較してください.
(1)1.910, 2.110
(解答)底は1.9<2.1で, 指数は10 (>0)で等しいから 1.910<2.110
(2)( )−1, ( )−1
(解答)底は=1.5>1.33...=で 指数が−1 (<0)で等しいから ( )−1<( )−1
参考:( )−1==0.66...<( )−1==0.75
|
図 7
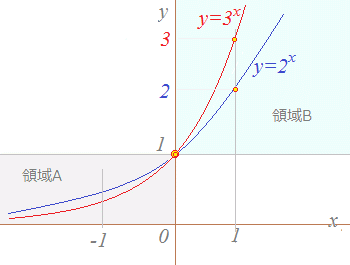
(3)230, 320
(解答)同じ指数で表すと 230=(23)10=810, 320=(32)10=910 底は8<9で 指数は10 (>0)で等しいから 810<910 したがって 230<320
(4),
(解答)同じ指数で表すと 2=(23)=8, 3=(32)=9 底は8<9で 指数は (>0)で等しいから 8<9 したがって <
(別解)
()6=(2)6=23=8 ()6=(3)6=32=9 ()6< ()6 → < |
|
図 8により
(0<)a<b(<1)のとき
(解説)
(1)y=axもy=bxも点(0, 1)を通ります.
たとえばy=( )xもy=( )xも点(0, 1)を通ります.
(2)x>0のとき,ax<bxになります.(→図 8の領域D参照)
たとえば,x>0 → ( )x<( )x.
(3)x<0のときはax>bxになります.(→図 8の領域C参照)
たとえば,x<0 → ( )x>( )xになります.
→x<0のとき (3) は要注意です.
同じxに対して, x>0ならば,( )x<( )xです. < < < しかし, x<0ならば,( )x>( )xです. ( )−1=3>( )−1=2 ( )−2=9>( )−2=4 ( )−3=27>( )−3=8 例 5次の数の大小を比較してください.
(1)0.25, 0.35
(解答)底は0.2<0.3(<1)で, 指数は5 (>0)で等しいから 0.25<0.35
(2)( )−2, ( )−2
(解答)底は<(<1)で, 指数は−2 (<0)で等しいから ( )−2>( )−2
(別解)
( )−2=( )2==1.77... ( )−2=( )2==2.25 ( )−2<( )−2 |
図 8
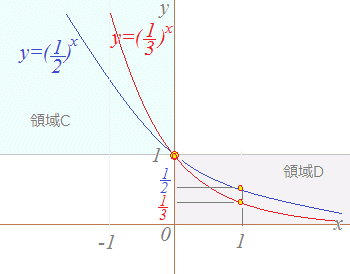
(3)0.50.6, 0.60.5
(解答)底は0.5<0.6(<1)で,指数は等しいから(0.6>0) 0.50.6<0.60.6 …(1) 底は等しく(0.6<1)指数は((0<)0.5<0.6だから 0.60.6<0.60.5 …(2) (1)(2)→0.50.6<0.60.5
(別解)
0.50.6<0.50.5<0.60.5 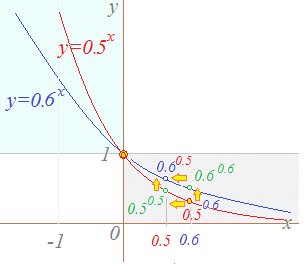 |
||||||||||||||||||||||||||||||
|
問題2次のうちで最も大きなものを求めなさい.
9−3<9−2 …(1)
9−2<8−2 …(2) (1)(2)→ 9−3<8−2
=8<8 …(1)
8<9= …(2) (1)(2)→ <
0.80.9<0.90.9 …(1)
0.90.9<0.90.8 …(2) (1)(2)→ 0.80.9<0.90.8 |
( )−<( )− …(1)
( )−<( )− …(2) (1)(2)→ ( )−<( )−
0.70.8<0.80.8<0.80.7<(1)<0.8−0.7<0.8−0.8<0.7−0.8
|