このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック
◎内側の色を変えるには，次の色をクリック
◎標準文字色を変えるには，次の色をクリック
鼠 銀 黒 青 紺 茶 緑 桃

== 必要条件と十分条件 ==
《解説》
■
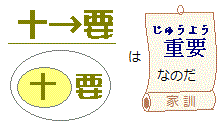
　数学で用いられる「必要条件」「十分条件」という用語は，日常生活で用いられる”必要"，"十分"とは異なるものです．
　数学上の必要条件，十分条件は，ｐならばｑ（記号では，ｐ→ｑ）という関係が成り立つかどうかで決まります．

ｐならばｑ

（記号で表わせば，ｐ→ｑ）
が成り立つとき，
「ｐはｑであるための十分条件」，
「ｑはｐであるための必要条件」
といいます．

■
　ｐ→ｑ　と　ｐ←ｑ　の両方とも成り立つとき，
「ｐはｑであるための必要十分条件」
「ｑはｐであるための必要十分条件」
といいます．

十分必要条件<とはいいません．
■
　ｐ→ｑ　と　ｐ←ｑ　のどちらも成り立たないとき
　ｐはｑであるための必要条件でも十分条件でもありません．
■
　２つの命題（１つの判断を述べた文章や式で，正しいか正しくないかが定まるものを命題といいます．）があるときに，一方が他方の必要条件あるいは十分条件といういい方をし，ある命題１つについてそれ自体で必要条件とか十分条件とかということはいえません．
［例１］
　シェパード→犬，犬→動物　です．
　そこで，犬であることは，シェパードであるための必要条件です．
　また，犬であることは，動物であるための十分条件です．
　しかし，犬だけで，必要とか十分とかの議論はしません．

［例２］
　ｘ＞１→ｘ＞０，ｘ＞２→ｘ＞１　です．
　そこで，ｘ＞１はｘ＞０であるための十分条件です．ｘ＞０はｘ＞１であるための必要条件です．
　また，ｘ＞２はｘ＞１であるための十分条件です．ｘ＞１はｘ＞２であるための必要条件です．

■
　２つの命題が与えられたとき，一方が他方の何条件であるかを判断するには，矢印を２つ作ってみて，どちら向きの矢印が成立するかで考えます．正しい推論で一方から他方が得られるとき，その矢印は「成立」すると考えます．
　
　図示できるときは，中に入っている方が十分条件です．
［例３］
　「ｍａ＝ｍｂ　は　ａ＝ｂ　であるための何条件ですか」という問題があるとき，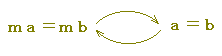
　
という図を作り，どの矢印が成り立つかを調べます．（とにかく，矢印を２つ作ることが大切です．）
○　　ｍａ＝ｍｂ　→　ｍ（ａ－ｂ）＝０　→　ｍ＝０またはａ－ｂ＝０　［ａ＝ｂに行くとは限らず，ｍ＝０に行くこともある］　
○　　ａ＝ｂ　→　ｍａ＝ｍｂ　（両辺に同じ数を掛けても等しい），
だから，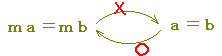
以上により，成り立っている矢印を見ると，ｍａ＝ｍｂは，矢印の先なので，ａ＝ｂであるための必要条件．

※　上の説明において，「ｍａ＝ｍｂ　→　ａ－ｂ＝０」が成り立たないことは，１つの例　ｍ＝０，ａ＝1，ｂ＝２　を示すだけで証明できます．このように，ある命題（主張）ｐ→ｑが成り立たないことを示す例は「反例」と呼ばれます．
○　ｐ→ｑ　の反例としては，「ｐが成り立ち」かつ「ｑが成り立たない」ものでなければなりません．
○　ｐ→ｑ　は　（すべての）「ｐについてｑが成り立つ」の省略なので，「１つでもｐであってかつｑでないもの」があれば，ｐ→ｑが間違っていることになります．しかし，「あるｐについてｑが成り立つ」ことを示しても他のｐについてｑが成り立つことは示せていないから，ｐ→ｑが成立することの証明にはなりません．
　このように
例を幾つ示しても成り立つことの証明にはなりません．
反例を１つ示せば成り立たないことの証明になります．
*** 採点結果は次の図で表示されます ***

正解の場合： 不正解の場合：
《問題》　次の（　）に入る語句を右の｛　｝から１つ選びなさい．（問題文中の文字は，すべて実数とします．）
（等式の問題）
１
ｘ＝１はｘ２＋３ｘ－４＝０であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
２
　ａ＝１かつｂ＝１　は　ａｂ＝１　であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
３
　ａ＋ｂ＝２　は　ａ＝ｂ＝１　であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
４
　ａ＝ｂ＝０　は　ａ＋ｂ＝０かつａｂ＝０　であるための
（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
５
　ａ＝ｂ＝０　は　ａ２＋ｂ２＝０　であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
６
　ａ＝ｂ　は　ａ＋ｃ＝ｂ＋ｃ　であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
７
　ｘ２＝９　は　ｘ＝３　であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
８
　(ｘ－ｙ)(ｙ－ｚ)＝０　は　ｘ＝ｙ＝ｚ　であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
９　整数ｎについて
　ｎが３の倍数であることは，ｎが６の倍数であるための
（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
10　整数ｎについて
　ｎが３の倍数であることは，ｎが２の倍数であるための
（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
11　
　　整数ｎについて
　ｎ２が奇数であることは，ｎが奇数であるための（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓
12　整数ｎについて
　ｎ２が３の倍数であることは，ｎが３の倍数であるための
（　　）条件
｛必要，十分，必要十分，必要でも十分でもない｝
ヒント↓

■［個別の頁からの質問に対する回答］[必要条件と十分条件について／18.9.4］
ありがとう😊 助かりました！
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／18.8.20］
このサイトいい復習になりました。ありがとう。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.12.30］
1番の回答の説明が2番の回答の説明と同じになっていますよ
＝＞［作者］：連絡ありがとう．PC版の方でコピーミスがあったようですので訂正しました．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.11.26］
なんとなく大体理解することができました。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.11.20］
一つ一つの問題に解説がついていてよかった
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.10.28］
とてもわかりやすくて、楽しく覚えられました！ ずっと分からなくて困っていたので助かりました！ 明日の模試もがんばれます！！
＝＞［作者］：連絡ありがとう．模試，頑張ってください．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.7.6］
ヒントを開くとほぼ答えが出てたのでもうすこし答えを厳しくして欲しいです。
＝＞［作者］：連絡ありがとう．様々なレベルの読者がいて，ヒントだけでなく解答そのものが欲しいという要望の方が多いです．この頁では，ヒントを開くとほぼ答えが分かるというのですから，それでヒントとしてよい働きになっていると思います．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.3.19］
最後の問題12番では、3の倍数でない数の2乗が3の倍数であることを反例として挙げればいいのですよね。 ならば√３はどうなのですか？
＝＞［作者］：連絡ありがとう．この質問については以前にもお答えしています．問題文に「整数ｎについて」と書いてあるのだから，整数の中で考えます．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.3.27］
わかりやすかったです。ありがとうございました
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.2.6］
最後の問題で、√３をｎに代入すると ｎ²が3になり 3の倍数になるのですが、ｎは√３となり3の倍数ではなくなるとですが、この考え方は間違っているのでしょうか？
＝＞［作者］：連絡ありがとう．問題文に整数ｎについてと書いてあるので，整数で考えます．「整数ｎについて」が１行上にあって見落としてしまうという話が前にもありましたので，改行しました．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.2.2］
とても分かりやすかったです！苦手を克服できました。ありがとうございました。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.1.15］
11 間違っています 反例としてルート3 ルート3^2は奇数ですが、ルート自体に奇数偶数の定義付けがされていませんので 答えは十分条件です
（追伸）　整数nでしたか… 見落としてました。申し訳ない

＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.1.10］
この辺が数1aでの不安要素だったのですが、とても分かりますいし、問題形式で理解度も深まったので安心してセンター試験に臨めそうです。助かりました。
＝＞［作者］：連絡ありがとう．受験生は大変ですが頑張ってください．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／17.1.3］
整数ｎについてをもっと見やすく目立たせたほうがいいと思います。
＝＞［作者］：連絡ありがとう．改行してあり結構目立っていると思いますが･･･この「整数について」という前提を読まなくても，意味が変わる問題は含まれていません．例えば第９問で「ｎが３の倍数であることは，ｎが６の倍数であるための（　　）条件 」という問題では，ｎが３の倍数であることはとなっているので，普通に読めばｎが小数，分数，無理数，虚数である場合はどうなるのかとは考えません特に注意書きがなくても，ｎが３の倍数であるなら整数と考えのが普通です．
■［個別の頁からの質問に対する回答］[必要条件と十分条件について／16.12.11］
8番の問題を間違えました。 解説の[十要は重要である]のやり方が役に立ちました！ 問題か沢山ないサイトが多いので、ここでは助かりました
＝＞［作者］：連絡ありがとう．
...メニューに戻る
■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります