|
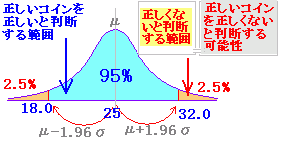
◇簡単な例でイメージ作り(1)◇ 例1 あるスポーツでは先攻後攻をコインのトスで決めている.このコインが正しく作られているか否かをテストするために,50回投げたところ,表が35回出た. このコインは正しいと言えるか?(考え方) コインのトスの結果は偶然に支配されるので,テストしたときに表がちょうど半分出るとは限らない. コインの表が出る回数は二項分布 B(n, p) をなし,試行回数が多いときは正規分布 N(np, np(1-p) )と見なしてよい.→ このコインは正しく作られていない. |
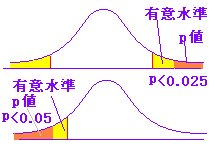
正規分布表で下図のように真ん中部分が95%になるのは(右が47.5%になるのは) p(u) = 0.475
となる u の値から,u = 1.96 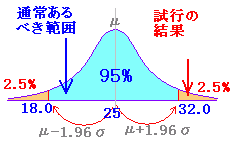
|
◇少しだけ理屈を ! (1)◇偶然に支配される世界を扱っているので,100%確実とは言えないが,コインが正しく作られていると見なす範囲をかなり広くとって確率95%で採択しているのに,その範囲に入らない. |
 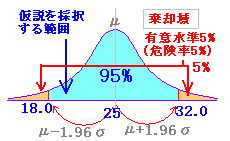 ※ 正しいものを間違っていると判断する誤りを第1種の過誤という.左の説明は,第1種の過誤を犯す危険率αを5%ないし1%にとることを表わしている. 常識的に考えれば,危険率は小さい方が望ましいが第1種の過誤を小さくとり過ぎると,帰無仮説の採択域が大きくなり「間違っているものも正しものに入れてしまう過誤」:第2種の過誤を犯す確率(β)が大きくなる.βは標本の大きさ n を大きくとることにより低く押さえることができる. 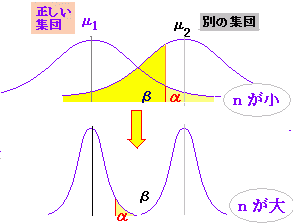 (標本数を大きくすると分布が分かれる) |
| ◇簡単な例でイメージ作り(2)◇ 例2 あるサイコロが正しく作られているかどうか調べるために600回投げてテストしてみたところ,1の目が90回出た.有意水準5%として,このサイコロが正しく作られているかどうか判断せよ.(考え方) 1の目が出る回数は二項分布 B(n, p) に従い,試行回数が多いときは正規分布 N(np, np(1-p))と見なしてよい. μ-1.96σ=82.1,μ+1.96σ=117.9 このような場合,仮説 p = 1/6 は棄却できないが,正しいとも言い切れない. |
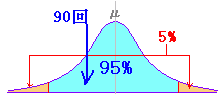 
左の解説ではサイコロが正しいときの確率分布の95%内に標本の測定値が入るかどうかで考えたが,標本分布の95%内に母平均が入るかどうかで考える解説書もある.
すなわち,左の解説は μ-1.96σ<m<μ+1.96σ・・・(1) を元に考えているが 母比率の推定: μ=100, n =600, m=90, R=n/m, p = μ/n とすると(2)は m-1.96 nが十分大きいときR ≒ p だから,これは μ-1.96 |
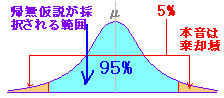
◇少しだけ理屈を ! (2)◇元の仮説を「帰無仮説」といいH0で表わす. |
元の仮説の採択される範囲が95%,棄却される範囲が5%という基準は,元の仮説に対して非常にゆるく,対立仮説に対して厳しいものとなっている. このため,元の仮説が採択されても p =1/6 であると主張するための積極的な根拠とはならない. 実際,n = 90回は,p = 1/7, p = 1/8の場合でも95%の範囲に入る. ※ 帰無仮説が採択されたら,検定は無に帰してしまう.帰無仮説が棄却されて対立仮説が採択されるときのみ検定として積極的な判断ができる. ⇒ 言いたくない方を帰無仮説に,言いたい方を対立仮説に選ぶことが重要. 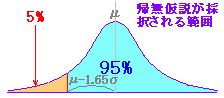 |
|
◇簡単な例でイメージ作り(3)◇ 例3 ある規格の鶏卵は重さの平均61(g),標準偏差1(g)の条件を満たすものと定められている.ある日,出荷予定の鶏卵100個を抽出検査した結果,平均が59.0(g)であったとき,この日出荷予定の鶏卵は規格の範囲内にあるといえるか.有意水準5%で検定せよ.(考え方) 帰無仮説H0:出荷予定の鶏卵の重さμ=61 |
※ m - 1.96
の範囲に入るかどうか調べる.※ 母標準偏差σが分かっているときは,これを使う. この式は, -1.96≦ 左の問題では,z = (59-61)/0.1=-20 < -1.96となって帰無仮説は棄却される. 他の解説書やソフトの利用も考えると,z値に慣れる方が分かりやすい. |
| ◇簡単な例でイメージ作り(4)◇ 例4 春に1群の稚魚であった養殖魚を2つの池に分けて飼育し,秋に100尾ずつ標本を抽出して体重を測定したところ,A池の養殖魚は平均体重20(g),標準偏差3(g),B池の養殖魚は平均体重21(g),標準偏差4(g)であった.B池の養殖魚が良く育っていると言えるか.α=0.05で検定せよ.(考え方) 帰無仮説H0:平均体重 μ1 = μ2 |
確率変数の変換に関する性質から,2つの確率変数X, Y について期待値は E(aX + bY) = aE(X) + bE(Y) 2つの変数X, Yが独立ならば,分散は V(aX + bY) = a2V(X) + b2V(Y) が成り立つ. したがって,2つの独立な確率変数については E(X - Y) = E(X) - E(Y) V(X - Y) = V(X) +V(Y) が成り立つ. そこで, 平均の差を検定するときは z = |