�i�ŏ����ƂQ���������j
�Z �y���������̎����łȂ����̂�����x���ŏ��i�o�Ȑ��̑�P�ی��̕����͒P���������ɂȂ��Ă���̂�y���ŏ��ɂȂ�j�ƂȂ�����ŏ����Ƃ����D
�Z �����܂ł̋L�q�ł́C�y���������̉������̘b�ł���Ȃ�����ۂɂ� \( x_1+ \sqrt{2}y_1 \)�Ƃ����`�̂Q��������������ƂȂ��Ă���C�������łȂ��ŏ���(x1 , y1)�����܂�C�Q�������� \( x_1+ \sqrt{2}y_1 \)�Ƃ����`�̂Q��������������ƂȂ��Ă���C�������łȂ��ŏ���(x1 , y1)�����܂�C�Q�������� \( x_1+ \sqrt{2}y_1 \)���g���Ă��ׂẲ������߂��邱�Ƃ��������D \( x_1+ \sqrt{2}y_1 \)���g���Ă��ׂẲ������߂��邱�Ƃ��������D
�@D���������łȂ������̂Ƃ��ɑΉ�����ŏ��������߂���́C���w�j�㋻���[�����ƂȂ��Ă���C����̍I���ȉ�@���m���Ă��܂�������ɂ��Ă͂����ł͐G��܂���D
�@D=61, 73, 85, 89, 94, 97�Ȃǂ̏ꍇ�ɂ́C�ŏ���(x1 , y1)�͔��ɑ傫�Ȑ��ɂȂ�܂��D���ɁC�t�F���}�[���m�l�Ɉ��Ă��莆�̒��Ŏ������Ƃ�����D=61�̏ꍇ
x2−61y2=1
�̐������́C�ŏ��̂��̂ł�x��10���̐����Cy��9���̐����ƂȂ��Ă���C�ȒP�ɂ͋��߂��Ȃ����̂ł��D
�Z D���P���̐����̏ꍇ�́C��������y���������̍ŏ��������܂�̂ŁC������g���ăy�����������������Ƃ��l���܂��D
D=2�̏ꍇ
x2−2y2=1
�ɂ����� 2y2�͋����C 2y2+1�͊�ɂȂ�̂ŁC���� x�͊
������x=1 (y=0)��������x=3,5,..�̏��Ɍ��������
32−2×22=1
�����藧����C x1=3 , y1=2���ŏ����ƂȂ�D
���̂Ƃ��C�Q����������  \( 3+2\sqrt{2} \) \( 3+2\sqrt{2} \)�ɂȂ�܂��D
^n=x_n%2B \sqrt{2}y_n\hspace{10}(n=0,1,2,3,...)) \( (3+2\sqrt{2})^n=x_n+ \sqrt{2}y_n\hspace{10px}(n=0,1,2,3,...) \) \( (3+2\sqrt{2})^n=x_n+ \sqrt{2}y_n\hspace{10px}(n=0,1,2,3,...) \)
�ƂȂ鐮�� (xn , yn )�����ׂẲ���^���܂��D
��ʉ���
^n%2B (3- 2\sqrt{2})^n}{2}) \( x_n=\dfrac{(3+ 2\sqrt{2})^n+ (3- 2\sqrt{2})^n}{2} \) \( x_n=\dfrac{(3+ 2\sqrt{2})^n+ (3- 2\sqrt{2})^n}{2} \)
^n- (3- 2\sqrt{2})^n}{2\sqrt{2}}) \( y_n=\dfrac{(3+ 2\sqrt{2})^n- (3- 2\sqrt{2})^n}{2\sqrt{2}} \) \( y_n=\dfrac{(3+ 2\sqrt{2})^n- (3- 2\sqrt{2})^n}{2\sqrt{2}} \)
�������� (1, 0)�C�ŏ����� (3, 2)
���̑��̉��� (17, 12), (99, 70), (577, 408), ...
D=3�̏ꍇ
x2−3y2=1
�ɂ����� 3y2�͋����ɂ���ɂ��Ȃ蓾�܂��C
������x=1 (y=0)��������x=2,3,4,..�̏��Ɍ��������
22−3×12=1
�����藧����C x1=2 , y1=1���ŏ����ƂȂ�D
���̂Ƃ��C�Q����������  \( 2+ \sqrt{3} \) \( 2+ \sqrt{3} \)�ɂȂ�܂��D
^n=x_n%2B \sqrt{3}y_n\hspace{10}(n=0,1,2,3,...)) \( (2+ \sqrt{3})^n=x_n+ \sqrt{3}y_n\hspace{10px}(n=0,1,2,3,...) \) \( (2+ \sqrt{3})^n=x_n+ \sqrt{3}y_n\hspace{10px}(n=0,1,2,3,...) \)
�ƂȂ鐮�� (xn , yn )�����ׂẲ���^���܂��D
��ʉ���
^n%2B (3- 2\sqrt{2})^n}{2}) \( x_n=\dfrac{(3+ 2\sqrt{2})^n+ (3- 2\sqrt{2})^n}{2} \) \( x_n=\dfrac{(3+ 2\sqrt{2})^n+ (3- 2\sqrt{2})^n}{2} \)
^n- (3- 2\sqrt{2})^n}{2\sqrt{2}}) \( y_n=\dfrac{(3+ 2\sqrt{2})^n- (3- 2\sqrt{2})^n}{2\sqrt{2}} \) \( y_n=\dfrac{(3+ 2\sqrt{2})^n- (3- 2\sqrt{2})^n}{2\sqrt{2}} \)
�������� (1, 0)�C�ŏ����� (2, 1)
���̑��̉��� (7, 4), (26, 15), (97, 56), ...
D=4�͕������Ȃ̂Ō������܂���D
D=5�̏ꍇ
x2−5y2=1
�ɂ����� 5y2�͋����ɂ���ɂ��Ȃ蓾�܂��C
������x=1 (y=0)��������x=2,3,4,..�̏��Ɍ��������
92−5×42=1
�����藧����C x1=9 , y1=4���ŏ����ƂȂ�D
���̂Ƃ��C�Q����������  \( 9+4\sqrt{5} \) \( 9+4\sqrt{5} \)�ɂȂ�܂��D
^n=x_n%2B \sqrt{5}y_n\hspace{10}(n=0,1,2,3,...)) \( (9+ 4\sqrt{5})^n=x_n+ \sqrt{5}y_n\hspace{10px}(n=0,1,2,3,...) \) \( (9+ 4\sqrt{5})^n=x_n+ \sqrt{5}y_n\hspace{10px}(n=0,1,2,3,...) \)
�ƂȂ鐮�� (xn , yn )�����ׂẲ���^���܂��D
��ʉ���
^n%2B (9- 4\sqrt{5})^n}{2}) \( x_n=\dfrac{(9+ 4\sqrt{5})^n+ (9- 4\sqrt{5})^n}{2} \) \( x_n=\dfrac{(9+ 4\sqrt{5})^n+ (9- 4\sqrt{5})^n}{2} \)
^n- (9- 4\sqrt{5})^n}{2\sqrt{5}}) \( y_n=\dfrac{(9+ 4\sqrt{5})^n- (9- 4\sqrt{5})^n}{2\sqrt{5}} \) \( y_n=\dfrac{(9+ 4\sqrt{5})^n- (9- 4\sqrt{5})^n}{2\sqrt{5}} \)
�������� (1, 0)�C�ŏ����� (9, 4)
���̑��̉��� (161, 72), (2889, 1292), (51841, 23184), ...
D=6�̏ꍇ
x2−6y2=1
�ɂ����� 6y2�͋����C 6y2+1�͊�ɂȂ�̂ŁC���� x�͊
������x=1 (y=0)��������x=3,5,7,..�̏��Ɍ��������
52−6×22=1
�����藧����C x1=5 , y1=2���ŏ����ƂȂ�D
���̂Ƃ��C�Q����������  \( 5+2\sqrt{6} \) \( 5+2\sqrt{6} \)�ɂȂ�܂��D
^n=x_n%2B \sqrt{6}y_n\hspace{10}(n=0,1,2,3,...)) \( (5+2\sqrt{6})^n=x_n+ \sqrt{6}y_n\hspace{10px}(n=0,1,2,3,...) \) \( (5+2\sqrt{6})^n=x_n+ \sqrt{6}y_n\hspace{10px}(n=0,1,2,3,...) \)
�ƂȂ鐮�� (xn , yn )�����ׂẲ���^���܂��D
��ʉ���
^n%2B (5- 2\sqrt{6})^n}{2}) \( x_n=\dfrac{(5+ 2\sqrt{6})^n+ (5- 2\sqrt{6})^n}{2} \) \( x_n=\dfrac{(5+ 2\sqrt{6})^n+ (5- 2\sqrt{6})^n}{2} \)
^n- (5- 2\sqrt{6})^n}{2\sqrt{6}}) \( y_n=\dfrac{(5+2\sqrt{6})^n- (5- 2\sqrt{6})^n}{2\sqrt{6}} \) \( y_n=\dfrac{(5+2\sqrt{6})^n- (5- 2\sqrt{6})^n}{2\sqrt{6}} \)
�������� (1, 0)�C�ŏ����� (5, 2)
���̑��̉��� (49, 20), (485, 198), (4801, 1960), ...
|
�i�Q���������Ɛ������̊W�j
�@�y��������x2−3y2=1�ɑ���
^n=x_n%2B \sqrt{3}y_n) \( X=(2+ \sqrt{3})^n=x_n+\sqrt{3}y_n \) \( X=(2+ \sqrt{3})^n=x_n+\sqrt{3}y_n \)
^n=x_n-\sqrt{3}y_n) \( Y=(2- \sqrt{3})^n=x_n-\sqrt{3}y_n \) \( Y=(2- \sqrt{3})^n=x_n-\sqrt{3}y_n \)
�Ƃ����ƁC��ʉ���
 \( x_n=\dfrac{X+ Y}{2} \) \( x_n=\dfrac{X+ Y}{2} \)
 \( y_n=\dfrac{X- Y}{2\sqrt{3}} \) \( y_n=\dfrac{X- Y}{2\sqrt{3}} \)
�Q�����́C���5��(5)���
 \( \begin{pmatrix}x_{n+ 1} \\ y_{n+ 1} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}x_{n} \\ y_{n} \end{pmatrix} \) \( \begin{pmatrix}x_{n+ 1} \\ y_{n+ 1} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}x_{n} \\ y_{n} \end{pmatrix} \)
�ƂȂ�܂��D�����X, Y��(xn , yn )�̊W���O���t��p���Ē��ׂĂ݂܂��D
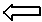
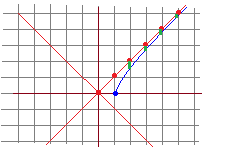
�@�܂��CX�̊e�X�͎����l�ŁC���䐔��̑悎���i���}�̐Ŏ������w������̓_�j�ɂȂ��Ă��܂��D�܂��C
 \( 2- \sqrt{3}=\dfrac{2^2-\sqrt{3}}{2+ \sqrt{3}}=\dfrac{1}{2+ \sqrt{3}} \) \( 2- \sqrt{3}=\dfrac{2^2-\sqrt{3}}{2+ \sqrt{3}}=\dfrac{1}{2+ \sqrt{3}} \)
^n=\Bigl(\frac{1}{2%2B \sqrt{3}}\Bigr)^n=(2%2B \sqrt{3})^{-n}) \( Y=(2- \sqrt{3})^n=\Bigl(\dfrac{1}{2+ \sqrt{3}}\Bigr)^n=(2+ \sqrt{3})^{-n} \) \( Y=(2- \sqrt{3})^n=\Bigl(\dfrac{1}{2+ \sqrt{3}}\Bigr)^n=(2+ \sqrt{3})^{-n} \)
������CY�̊e�X�͉��}�̐ԂŎ������w������̓_�ɂȂ�܂��D
�}�S
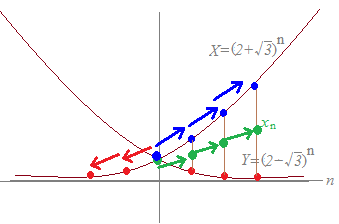
�@n=0, 1, 2, 3, ...�ƕω�����Ƃ��Cxn�́u�����l�v��X, Y�̒��_�ɂȂ�̂ŗŎ������_�̏c�̍��W��\�����ƂɂȂ�܂��D�iyn�̒l�͒��ړI�ɂ͌����Ă��܂���D�j
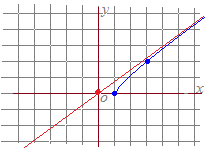
�}�T
�@���̂Ƃ��C(xn , xn )�͑Q����
 \( \begin{pmatrix}x_{n+ 1} \\ y_{n+ 1} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}x_{n} \\ y_{n} \end{pmatrix} \) \( \begin{pmatrix}x_{n+ 1} \\ y_{n+ 1} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}x_{n} \\ y_{n} \end{pmatrix} \)
�����C
������x0=1 , y0=0����X�^�[�g����ƁC
 \( \begin{pmatrix}x_{1} \\ y_{1} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}=\begin{pmatrix}2 \\ 1\end{pmatrix} \) \( \begin{pmatrix}x_{1} \\ y_{1} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}=\begin{pmatrix}2 \\ 1\end{pmatrix} \)
 \( \begin{pmatrix}x_{2} \\ y_{2} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}2 \\ 1\end{pmatrix}=\begin{pmatrix}7 \\ 4\end{pmatrix} \) \( \begin{pmatrix}x_{2} \\ y_{2} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}2 \\ 1\end{pmatrix}=\begin{pmatrix}7 \\ 4\end{pmatrix} \)
 \( \begin{pmatrix}x_{2} \\ y_{2} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}7 \\ 4\end{pmatrix}=\begin{pmatrix}26 \\ 15\end{pmatrix} \) \( \begin{pmatrix}x_{2} \\ y_{2} \end{pmatrix}=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}\begin{pmatrix}7 \\ 4\end{pmatrix}=\begin{pmatrix}26 \\ 15\end{pmatrix} \)
�̂悤�ɁC���X�Ɖ�(xn , xn )��������D
�@�t�ɁC����P�̉�x2=7 , y2=4����X�^�[�g���āC
 \( A=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix} \) \( A=\begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix} \)
�̋t�s��
 \( A^{-1}=\begin{pmatrix}2 & -3 \\ -1 & 2 \end{pmatrix} \) \( A^{-1}=\begin{pmatrix}2 & -3 \\ -1 & 2 \end{pmatrix} \)
�����X�Ɋ|���Ă�����
 \( \begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}=\begin{pmatrix}2& -3\\ -1& 2\end{pmatrix}\begin{pmatrix}7\\ 4\end{pmatrix}=\begin{pmatrix}2\\ 1\end{pmatrix} \) \( \begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}=\begin{pmatrix}2& -3\\ -1& 2\end{pmatrix}\begin{pmatrix}7\\ 4\end{pmatrix}=\begin{pmatrix}2\\ 1\end{pmatrix} \)
 \( \begin{pmatrix}x_{0} \\ y_{0}\end{pmatrix}=\begin{pmatrix}2 & -3 \\ -1 & 2\end{pmatrix}\begin{pmatrix}2 \\ 1\end{pmatrix}=\begin{pmatrix}1 \\ 0\end{pmatrix} \) \( \begin{pmatrix}x_{0} \\ y_{0}\end{pmatrix}=\begin{pmatrix}2 & -3 \\ -1 & 2\end{pmatrix}\begin{pmatrix}2 \\ 1\end{pmatrix}=\begin{pmatrix}1 \\ 0\end{pmatrix} \)
�ƂȂ��Ď������ɓ��B���邩��C�^����ꂽ���͎���������A�Ȃ��Ă���P�̌n��̉��ł��邱�Ƃ�������D
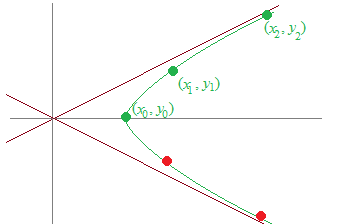
�������]���āC n=−1, −2, ..�ƕ��̐��ɓ˓����Ă��܂��Ă��C���ʕς�������Ƃ͋N����Ȃ��D���ہC�����Ă݂��
 \( \begin{pmatrix}x_{-1} \\ y_{-1}\end{pmatrix}=\begin{pmatrix}2 & -3 \\ -1 & 2\end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}=\begin{pmatrix}2 \\ -1\end{pmatrix} \) \( \begin{pmatrix}x_{-1} \\ y_{-1}\end{pmatrix}=\begin{pmatrix}2 & -3 \\ -1 & 2\end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}=\begin{pmatrix}2 \\ -1\end{pmatrix} \)
 \( \begin{pmatrix}x_{-2} \\ y_{-2}\end{pmatrix}=\begin{pmatrix}2 & -3 \\ -1 & 2\end{pmatrix}\begin{pmatrix}2 \\ -1\end{pmatrix}=\begin{pmatrix}7 \\ -4\end{pmatrix} \) \( \begin{pmatrix}x_{-2} \\ y_{-2}\end{pmatrix}=\begin{pmatrix}2 & -3 \\ -1 & 2\end{pmatrix}\begin{pmatrix}2 \\ -1\end{pmatrix}=\begin{pmatrix}7 \\ -4\end{pmatrix} \)
�̂悤�ɁC (x−n , y−n)=(xn , −yn)�ƂȂ��Ă���C��̐}�̐ԂŎ������_�̂悤�ɂ����������Ɂi�����W�̕��������t�ɂȂ����`�Łj�o�ꂷ��D�Ή�����Q���������͂������̐}�� n<0�̕����̐Ԃ̓_�ɂȂ�D
|
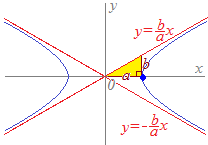



 ���P,���3
���P,���3

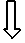 ���T,���T
���T,���T