|
■度数分布表
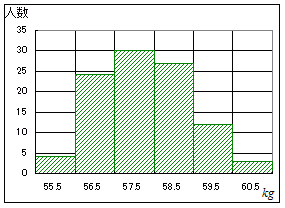
この度数分布表をグラフにすると,次の図1のようになります. この度数分布表は階級幅を(1cm→0.5cm→0.25cm→...)と限りなく細かくしていくと,縦棒の高さが限りなく低くなります.
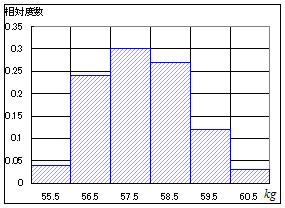
■相対度数分布表 これに対して,相対度数分布表(確率の表)をグラフにすると,次の図2の棒グラフのようになります. 相対度数分布表は,縦方向の目盛りが確率になっているだけで,度数分布表と同じ形をしています.
例えば,総人数を10000人に増やしておくとき,階級幅が小さくなるとともに,右の表の緑色で示したように人数が減り,赤色で示したように相対度数すなわち確率が減ります. 解説を簡潔にするために,階級幅を細かくしていくと相対度数分布表が曲線に近づくといってしまうことがありますが,正確には相対度数分布表が曲線に近づくのではありません. 右に続く→
|
→続き ■確率密度とは 次の表3のように,相対度数=確率の代わりに, 「確率密度=1cm当たりの確率」 を持ってきて,これを縦棒の長さにすると,階級幅を限りなく細かくしていっても,縦棒の長さはある値に近づき,曲線になってくるのです. たとえば, (A) 確率=0.04,階級幅=1→確率密度=0.04/1=0.04 (B) 確率=0.02,階級幅=0.5→確率密度=0.02/0.5=0.04 (B) 確率=0.01,階級幅=0.25→確率密度=0.01/0.25=0.04
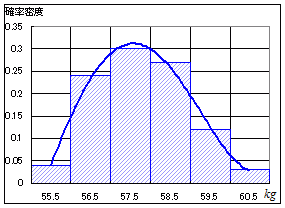
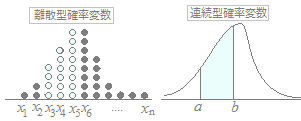
次の曲線のように,実数で定義される確率変数Xを連続型確率変数といいます.連続型確率変数では,縦の長さは確率密度を表します. 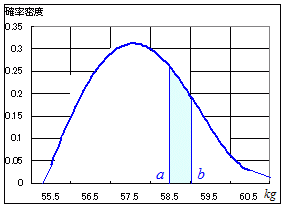
横幅のある区間の「面積が確率を表す」ので,例えばx=58.0というような特定の値をとる確率は0と考えます.
正確に測れば,体重がx=58.0000000(kg)というような人はいないが,58≦x≦58.5(kg)の人ならいると考えることになります.
このことに関連して,P(X=a)=0 (幅のない縦線だけなら面積は0) となるから,確率を表すときに,等号付き不等号で書かれていても,不等号だけで書かれていても同じ値を表すことになり, 次の2つは同じ値になります. P(a<X<b) , P(a≦X≦b) |
■筆算で計算できる簡単な連続型確率分布の例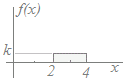 【例】 一様分布
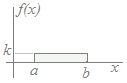
【例】 一様分布右図のように定義域a≦X≦bにおいてf(x)=k(定数)となるような確率分布を連続型一様分布ということがあります. 右図の連続型一様分布において,定数kの値を求めてください. f(x)dx=1 ←(3)
(長方形の面積が1)になるのだから2k=1 k= …(答)
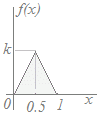 【例】
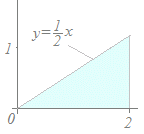
【例】右図のように頂点がx=0.5にあって0≦x≦1において定義される分布関数において,頂点の高さを表す定数kの値を求めてください. 三角形の面積が1になるから =1 k=2 …(答) 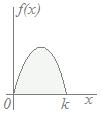 【例】
【例】右図のように区間0≦x≦kにおいて2次関数f(x)=x(k−x)で定義される分布関数において,定数kの値を求めてください. x(k−x)dx=1 ←(3)
だから(kx−x2)dx=k − = − = =1 k3=6 k= …(答) |
■筆算では計算できないもの 【例】正規分布 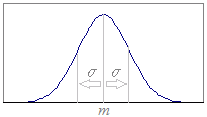 統計で最もしばしば登場するのが正規分布です.
統計で最もしばしば登場するのが正規分布です.期待値m,標準偏差σの正規分布は,右図のような形の帽子型(富士山型)をしており 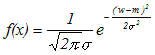  で表されます.  正規分布においてX≦aとなる確率P(X≦a)は,右図の水色で示された部分の面積になります.この図形の面積は,理論上は定積分
正規分布においてX≦aとなる確率P(X≦a)は,右図の水色で示された部分の面積になります.この図形の面積は,理論上は定積分
f(x)dx
で表されますが,
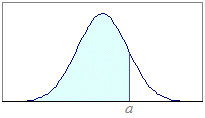 この定積分は筆算では計算できないことが知られており,数値積分によって近似値として求められます.昔はその結果を数表として印刷して使っていましたが,今日ではコンピュータの組み込み関数として求めることができます.
この定積分は筆算では計算できないことが知られており,数値積分によって近似値として求められます.昔はその結果を数表として印刷して使っていましたが,今日ではコンピュータの組み込み関数として求めることができます.
【要点】
Excelのワークシート関数を利用して,
「期待値m,標準偏差σの正規分布において,
を求めるにはX≦aとなる確率」 =NORMDIST(a,m,σ,1) とします. (※第4引数を1にすると左端からaまでの図形の面積(=累積分布関数),0にするとf(x)の値(=確率密度関数)になります.水色の部分の面積を求めるには,第4引数を1にします.) 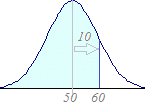 【例】
【例】「期待値50,標準偏差10の正規分布において,X≦60となる確率」(右図の水色の部分の面積)を求めるには =NORMDIST(60,50,10,1) とします.(結果は0.84134474) 【例】 「期待値50,標準偏差10の正規分布において,X>60となる確率」(上の図の白の部分の面積)を求めるには =1−NORMDIST(60,50,10,1) とします.(結果は0.15865526) 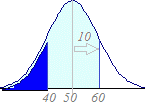
【例】 「期待値50,標準偏差10の正規分布において,40≦X≦60となる確率」(右図の水色の部分の面積)を求めるには =NORMDIST(60,50,10,1)−NORMDIST(40,50,10,1) とします.(結果は0.68268948) |
|
長方形の横の長さがb−a,縦の長さがkだから,その面積は
(b−a)k=1 したがって k= →3
三角形の面積は
ab になるから ab=1 ab=2 →2
まず,定数kの値を求めます.
kx(1−x)dx=1
により
k(x−x2)dx=1
k−=1
=1
k=6
次に6(x−x2)dx=
→5
|
【問題4】
期待値55,標準偏差7の正規分布において,X≦50となる確率をExcelを使って求めてください.(小数第4位を四捨五入して第3位まで求めてください.) 1 0.044 2 0.238 3 0.262 4 0.762 HELP  =NORMDIST(50,55,7,1)により0.237525188となるので,0.238とします.
=NORMDIST(50,55,7,1)により0.237525188となるので,0.238とします.
→2
【問題5】
期待値10,標準偏差3の正規分布において,X≧15となる確率をExcelを使って求めてください.(小数第4位を四捨五入して第3位まで求めてください.) 1 0.033 2 0.048 3 0.452 4 0.952 HELP 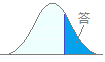 =NORMDIST(15,10,3,1)によりX≦15となる確率が求められるので,1−NORMDIST(15,10,3,1)=0.04779033から0.048とします.
=NORMDIST(15,10,3,1)によりX≦15となる確率が求められるので,1−NORMDIST(15,10,3,1)=0.04779033から0.048とします.→2
【問題6】
期待値15,標準偏差4の正規分布において,10<X<20となる確率をExcelを使って求めてください.(小数第4位を四捨五入して第3位まで求めてください.) 1 0.678 2 0.789 3 0.896 4 0.967 HELP 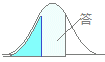 X=10となる確率やX=20となる確率は0だから,10<X<20という問題になっていても10≦X≦20でも結果は同じになります. =NORMDIST(20,15,4,1)−NORMDIST(10,15,4,1)により,0.788700322となるので,0.789とします. →2 |
|
■連続型確率変数についての期待値,分散,標準偏差
【確率】
右図の例では ○離散型確率変数がx3≦x≦x5の値をとる確率は p3+p4+p5 pk ←Σ記号で表した場合
○連続型確率変数がa≦x≦bの値をとる確率はf(x)dx ←積分記号で表される
【期待値】
右図の例では ○離散型確率変数の期待値は m=E(X)=x1p1+x2p2+x3p3+…+xnpn xkpk ←Σ記号で表した場合
○連続型確率変数の期待値はxf(x)dx ←積分記号で表される
【分散】
(*)の証明右図の例では ○離散型確率変数の分散は V(X)=(x1−m)2p1+(x2−m)2p2+…+(xn−m)2pn (xk−m)2pk ←Σ記号で表した場合
なお,V(X)=E(X 2)−E(X)2が成り立ちます.○連続型確率変数の分散は (x−m)2f(x)dx ←積分記号で表される
離散型確率分布の場合と同様に,V(X)=E(X 2)−E(X)2 …(*) が成り立ちます. (x−m)2f(x)dx=(x2−2mx+m2)f(x)dx
=x2f(x)dx−2mxf(x)dx+m2 f(x)dx
ここで=x2f(x)dx=E(X 2), xf(x)dx=E(X), f(x)dx=1
だから(x−m)2f(x)dx=E(X 2)−2m2+m2=E(X 2)−m2
=E(X 2)−E(X)2
【標準偏差】
標準偏差はいずれの場合も,分散V(X)の正の平方根で求められます. σ(X)=
= = = ■筆算で計算できるもの■ = = = 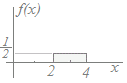 【例】 === 一様分布 ===
【例】 === 一様分布 ===右図の連続型一様分布において, ○ 2≦x≦3となる確率は f(x)dx
=dx=x=
○ 期待値は E(X)=x×dx=x2==3
(左右対称な分布では,期待値は中央になります)
○ 分散はV(X)=(x−3)2×dx=(x−3)3 =
V(X)=E(X 2)−E(X)2で計算する場合はV(X)=x2×dx−9=x3 − 9
=−9=−9=
○ 標準偏差はσ(X)==
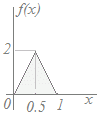 【例】
【例】右図の連続型分布において, ○ 0≦x≦1となる確率は f(x)dx=4xdx+(4−4x)dx
=2x2 + 4x−2x2
=+(2−)=1
○ 期待値は E(X)=xf(x)dx=4x2dx+x(4−4x)dx
=x3 + 2x2−x3 = +{ (2−)−(−) }
=
(左右対称な分布では,期待値は中央になります)
○ 分散はV(X)=x2×4xdx+x2(4−4x)dx−=...=
(定義通りにやればかなり長い計算になります)
○ 標準偏差はσ(X)===
|
【例】
統計において最も重要な正規分布は,次の形の関数で表されます. 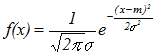 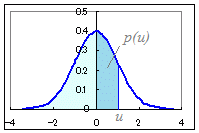 正規分布のうちで特に,期待値0,標準偏差1となる標準正規分布は,次の形の関数で表され,そのグラフの形は右図のようになっています. 正規分布のうちで特に,期待値0,標準偏差1となる標準正規分布は,次の形の関数で表され,そのグラフの形は右図のようになっています.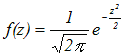
正規分布に関する「確率」「期待値」「分散」「標準偏差」を考えるときに注意すべきこととして,
y=e−x2 のような関数は「筆算では積分できない」ということです. このような場合には「数値積分」という方法で,あらかじめコンピュータで計算された数表を見て答えることになります. なお,Excelを使っている場合には,この数表も不要でワークシート関数を使って計算することができます.したがって,正規分布についての「確率」「期待値」「分散」「標準偏差」を扱うことは,原理的には複雑な積分計算ではあっても,実際上はマニュアルの使い方に慣れるだけの問題となります. ○ 正規分布についての「確率」の計算は,この頁の上の方で【要点】にまとめてあります. ○ 正規分布 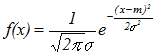 …(*A) …(*A)の期待値はm,分散はσ2,標準偏差はσになります.(*1) ○ 標準正規分布 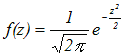 …(*B) …(*B)の期待値は0,分散は1,標準偏差は1です.(*2)
(*1)および(*2)の表現は,実際には逆でしょう.すなわち,(*1)については,期待値がm,標準偏差がσとなるように正規分布の関数を定めれば(*A)になるということです.(*A)の式に含まれる定数mやσを取り出すだけで期待値と標準偏差が求まるのは,そのためです.
また,(*2)については,「期待値0,標準偏差1の正規分布」が標準正規分布の定義です.  ○ 通常,統計・数学の教科書の巻末に付いている数表では,標準正規分布における0≦z≦uとなる確率が書かれています.(右図の濃い水色で示されたp(u)の面積に相当します.)
○ 通常,統計・数学の教科書の巻末に付いている数表では,標準正規分布における0≦z≦uとなる確率が書かれています.(右図の濃い水色で示されたp(u)の面積に相当します.)これに対して,Excelのワークシート関数 NORMSDIST(z) では,−∞<z≦uとなる確率(薄い水色の部分も足したもの)が返されます.左半分:薄い水色の部分(z<0)となる確率は0.5なので,z>0のとき,数表の値には NORMSDIST(z) −0.5 が対応します. なお,NORMSDIST(z) では,z<0のときにもその左側の確率が求められます. 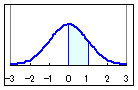 【例】 【例】標準正規分布において,0≦z≦1となる確率(右図水色の部分の面積)は,
数表では,左欄の1.0と上欄の.00(0.00の省略形)の交わる場所を読むと,0.3413となります.
Excelのワークシート関数では,=NORMSDIST(1)を求めると0.84134474となるので,0.84134474−0.5=0.3413447の有効数字を4桁とすれば0.3413となります.
※連続分布においては,z=1となる確率(右図のz=1の線分の面積)は0なので,「0≦z≦1となる確率」と「0<z≦1となる確率」「0≦z<1となる確率」「0<z<1となる確率」はすべて同じ値になります.以下の例でも同様です.
 【例】 【例】標準正規分布において,z≧1.52となる確率(右図水色の部分の面積)は,
数表では,左欄の1.5と上欄の.02(0.02の省略形)の交わる場所を読むと,0.4357となるので,右半分の面積0.5から引いて,0.0643とします.
Excelのワークシート関数では,=NORMSDIST(1.52)がz=1.52の左側の面積になるので,=1−NORMSDIST(1.52)により 0.06425551の有効数字を4桁として0.0643とします. 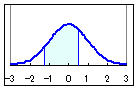 【例】 【例】標準正規分布において,−1.23<z<0.67となる確率(右図水色の部分の面積)は,
数表では,左欄の0.6と上欄の.07の交わる場所を読むと,0.2486となるので,z=0の右側にある面積は,0.2486
正規分布(標準正規分布)は左右対称で,数表にはu≧0の値しか書かれていないので,左側の−1.23<z≦0となる確率を求めるには,代わりに0≦z<1.23の値を求めます. 左欄の1.2と上欄の.03の交わる場所を読むと,0.3907となるので,z=0の左側にある面積は,0.3907 これら左右の面積を足して,0.2486+0.3907=0.6393が求める確率になります. Excelのワークシート関数では,=NORMSDIST(0.67)がu=0.67の左側の面積になり,=NORMSDIST(−1.23)がu=−1.23の左側の面積になるので,これらの差を求めるとよいことになります.=NORMSDIST(0.67)−NORMSDIST(−1.23)により 0.639222559の有効数字を4桁として0.3692とします.
これら2つの結果,0.6393と0.6392とは小数第4位が違いますが,これは数表において最後の桁が四捨五入で丸められた結果となっているために生じるもので,Excelの結果の方が詳しくなっていますが,「結果はどちらを使ってもよい」と考えてください.
♪これを言ってしまえば,もうおしまい♪==そもそも,統計で小数第4位までの精度が求められることはめったになく,例えば世論調査で内閣支持率を求める場合でも,内閣支持率が○○.○○%などというのは聞いたことがありません.せいぜい,○○%か○○.○%でしょう. |
 【問題7】 【問題7】0≦x≦2において,確率密度関数 がf(x)=xで定義されている確率 分布について,期待値と分散を求めてください. 1 期待値1,分散 2 期待値1,分散 3 期待値,分散 4 期待値,分散 HELP E(X)=x×x dx= = =
E(X 2)=x2×x dx= = =2
V(X)=E(X 2)−E(X)2=2−=
→4 |
【問題8】
標準正規分布において1≦z≦2となる確率を求めてください.(Excelを使って小数第4位まで求めてください) 1 0.1359 2 0.3414 3 0.4772 4 0.6131 HELP =NORMSDIST(2)-NORMSDIST(1)により,0.135905198となるので0.1359と答えます. →1 |

 【問題1】
【問題1】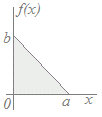 【問題2】
【問題2】