■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数について/18.7.01]
コメント失礼しますm(__)m 数3をこのサイトで学習していて思ったのですが、私は最初複素数平面から始め、その後微分法のところをやろうと思ったのですが、数3微分ではこの学習サイトの''関数''のところをやってからだなと思い関数のところを学習していたのですが、逆関数のところでlogとeが出てくる関数があって、eをやってからじゃないといけないなと思い、調べたところ微分法の範囲にあることを知り、ちょうど関数の学習をある程度終えていたので順調に学習が進んでいたのですが、媒介変数表示の微分まで来て媒介変数のところをとばしていたので、媒介変数のところを(サイクロイドのところ)までやってまた微分のところに戻ったのですが、三角関数の微分がどうやら必要ぽくってこれからやろうと思ったところなのですが、長々となってしまい申し訳ないのですが、このように、どの順番で学習を進めていけばいいのかわからなくて困ってます。どの順番で学習していくのがよいのでしょうか?
=>[作者]:連絡ありがとう.主要な(基本の)内容は,教科書の目次の順に学ぶようになっています:①2次曲線,媒介変数と極座標;②複素数平面;③数列の極限,関数の極限;④微分;⑤積分.[教科書会社によって①②を逆にする場合があります]
ただし,「融合的な内容」,例えば指数の対数乗  を考えると,指数関数と対数関数のどちらを先にやってもできないように見えますが,一巡基本を押さえてから,振り返るようにします.高い山に登るときは,まっすぐに上る一本道があるのではなく,4000M地点から5000M地点を往復して,高地順応しながら荷物を上げるように,行ったり来たりするということです.
非常にわかりやすかった。テスト前に見て良かった。
=>[作者]:連絡ありがとう.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数について/17.12.26]
たいへん勉強になっております。さて(4)について解答は -cost/sint なのではないでしょうか?
tに条件がないので、t=π/2の時、tantは定義されません。
よろしくおねがいします。
=>[作者]:連絡ありがとう.高校によって(学科によって)は, cottを習わないことがあるため,  を避けて  としたものですが,そうすると確かに北極と南極の接線は表せません.
ただそれは,tに条件がないからということではないです.他にも,赤道上でも接線はありませんが,一般に分数関数,無理関数を条件を示さずに使うときは「その式が定義される範囲で使う」ことになっています.だから,この形で書くと赤道上でも北極,南極でも接線は考えていないことになり,あなたの流儀で書くと,赤道上は助からないが北極と南極は助けられるということになります.
このような除外点を個別に検討すると,すべての問題についてtの値の範囲を書かなければならないという解釈になりますが,この教材では初歩的に媒介変数表示から微分する練習として,「関数なり導関数が意味を持つ範囲で成り立てばよい」という普通の解釈でやっています.
例3dy/dxがdx/dxになっています
=>[作者]:連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数について/17.10.24]
「媒介変数表示のときの微分」のページの例2の問題で問題文にはdx/dxを求めなさいとなっているんですが、答えにはdy/dx=~となっています。自分は微分をやり始めたばっかりなんで勘違いしているだけかもしれませんがおかしいと思いました。
=>[作者]:連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数について/17.2.15]
微分積分法の復習に大変お世話になっております。
媒介変数表示の微分[問題](5)ですが、与式のうちy=a(cost-tsint)が、回答解説と違っているようです。
解説内のy'から察するに正しい式は
x=a(cost+tsint)
y=a(sint-tcost)
ではないでしょうか。
更新をお休みになっておられたら恐縮です。
ご確認いただけたら幸いです。
=>[作者]:連絡ありがとう.問題文の方がタイプミスでしたので訂正しました.
|
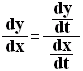 です。
です。