|
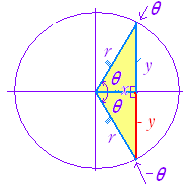
印刷物になっている三角関数表は 0°〜90°の値のみ書かれており, sin( −15°)のような値は書かれていない. 右図から次の公式が導かれ,これを利用すれば, −90°〜0°の三角関数の値を,0°〜90°の三角関数に直して求めることができる. 公式(5)
なお,1回転した位置になる 360°-θの三角関数は,この値に等しい.cos(− θ)= cosθ (cosθは偶関数) tan(− θ)=− tanθ (tanθは奇関数) |
 |
| 例 sin345°=sin (− 15°)=− sin 15°=(表より)=− 0.2588 cos345°=cos(-15°)= cos 15°=(表より)= 0.9659 tan345°=tan(−15°)=− tan 15°=(表より)=− 0.2679 |
|
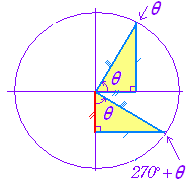
| 右図のように y 軸から測った場合は,次の公式になる.縦横が逆になるため,sinθ,cosθが入れ替わる.tanθは分母分子が入れ替わる.
公式(6)
sin(270°+θ)=− cosθ
cos(270°+ θ)= sinθ tan(270°+θ)=− |
 |
| 例 sin 345°=sin(270°+75°) =− cos 75°=(表より)=− 0.2588 cos 345°= cos(270°+75°) =sin 75°=(表より)= 0.9659 tan 345°= tan(270°+75°) =− =(表より)=− 0.2679 |
|
| ※ 上の公式(5)(6)は,0°≦θ≦90°の場合の説明に用いているが,実際にはθの値に制限なく成り立つ. すなわち,次のような関係は任意の角度θについて成り立つ: |
|
| 【要点】 sin 345°などの数値を求めるには,sinθ,cosθなどの形が変わらず符号のみを考えればよい公式(5)を用いる方が楽. 文字式の変形で公式(6)が登場するときは,sinθ,cosθ,tanθなどの形の変化に注意. |
|