■商で表される関数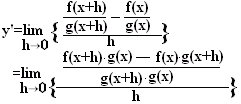 ■ここで,本来の導関数の定義: ={ f(x+h)-f(x) } g(x)-f(x) { g(x+h)-g(x) }
|
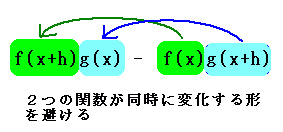
=-f(x+h){ g(x+h)-g(x) } + { f(x+h)-f(x) } g(x+h) 分子は |
■商で表される関数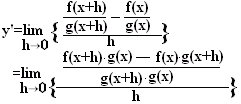 ■ここで,本来の導関数の定義: ={ f(x+h)-f(x) } g(x)-f(x) { g(x+h)-g(x) }
|

=-f(x+h){ g(x+h)-g(x) } + { f(x+h)-f(x) } g(x+h) 分子は |
|
【例1】
(解答)分子1の微分は0,分母x+2の微分は1だから
【例2】
(解答)分子3x−1の微分は3,分母2x+1の微分は2だから
【例3】
(解答)分子xの微分は1,分母x2−1の微分は2xだから |
【例題1】
解説を読むxの関数 |
|
【例題2】
解説を読むxの関数 |
【例題3】
解説を読むxの関数 |
|
【例題4】
解説を読むxの関数
ア)商の微分法でやる場合
分子は(やられてから)−(やり返す) (分母)2 を使うと イ)積の微分法でやる場合
この微分を行うには,合成関数の微分法が必要になる
|
【例題5】
解説を読むxの関数
ア)商の微分法でやる場合
分子は(やられてから)−(やり返す) (分母)2 を使うと イ)積の微分法でやる場合
この微分を行うには,合成関数の微分法が必要になる
|
[問題]
|
 |
||||
|
解説 |
|||||
|
■このサイト内のGoogle検索■ |
|
■[個別の頁からの質問に対する回答][商,分数関数の微分について/17.5.21]
下の方でいいので、答えを載せて欲しいです
=>[作者]:連絡ありがとう.一題でも間違ったら解説と答が出るようになっているのですが,この要望が来たということは全問正解で終わってしまった人だと考えられます.とはいえ,正解であっても答案を確かめたい人はあり得ますので,正解の場合でも解説が出る設定にしました. |