|
入試問題の学習の仕方(筆者の考え) ○基本(根)ができなければ,応用問題(枝)もできず入試問題(葉)は解けませんが,基本問題だけをやっていても入試問題が解けるようにはなりません. ○しかしまた,数学Aの整数問題という1つの単元に限っても,たとえば基本が10あるとして,これに対応する参考書の頻出問題はその10倍,入試問題はさらにその10倍というように膨大な数になるので,あらゆる入試問題を前もって練習しておくことはできません. 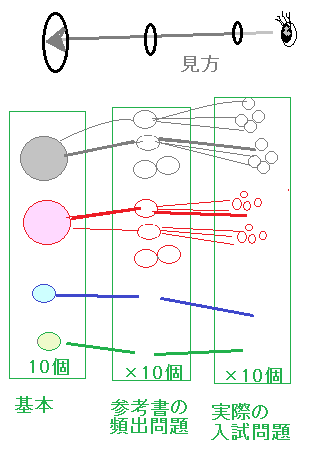 ○このように,膨大な数の入試問題から,それらを貫いている基本を「串刺しにする」ように見通していくと,膨大な量の暗記にはならず,基本の確認に絞ることができ,数学Aの整数問題では1桁程度の「やり方を身に付ければ」何とかできるようになります.
【要点】
1.入試問題を解きながら,基本のやり方を思い浮かべる. 2.入試問題(葉)の数は多くても,基本(根)の数は多くない.
【例題1】
(解説)a3−b3=65を満たす整数の組(a, b)をすべて求めよ. (京大2005年前期文系)
左辺を因数分解し,右辺を素因数分解すると (a−b)(a2+ab+b2)=5×13…(1) 可能な組み合わせは次の表の通り.
※方針が決まったら,体力勝負になってもやるしかない
(1)の場合,次の連立方程式を解くa2+ab+b2=65…(1.2) (1.1)よりa=b+1 これを(1.2)に代入
3b(b+3)=64
(b+1)2+(b+1)b+b2=65と変形して左辺は3の倍数,右辺は3の倍数でないと述べてもよい 3b2+3b−64=0 この方程式の判別式はD=9+4×3×64=777=3×7×37となって平方数でないからbの整数解はない. (2)の場合,次の連立方程式を解く a2+ab+b2=13…(2.2) (2.1)よりa=b+5 これを(2.2)に代入
a,bは正の整数とは書いてない
(b+5)2+(b+5)b+b2=13次のようなものも解になる 43−(−1)3=65 3b2+15b+12=0 b2+5b+4=0 (b+1)(b+4)=0 b=−1のときa=4 b=−4のときa=1 よって,(a,b)=(4,−1),(1,−4) (3)の場合,次の連立方程式を解く
3b(b+13)=−164
と変形して左辺は3の倍数,右辺は3の倍数でないと述べてる方が大きな数字なるのを避けることができる a2+ab+b2=5…(3.2) (3.1)よりa=b+13 これを(3.2)に代入 (b+13)2+(b+13)b+b2=5 3b2+39b+164=0 この方程式の判別式はD=392−4×3×164=−447<0となってbの整数解はない. (4)の場合,次の連立方程式を解く a2+ab+b2=1…(4.2) (4.1)よりa=b+65 これを(4.2)に代入 (b+65)2+(b+65)b+b2=1 3b2+195b+652−1=0 3b2+195b+64×66=0 b2+65b+64×22=0 この方程式の判別式はD=652−4×64×22=−1406<0となってbの整数解はない. (1)(2)(3)(4)から結局,(a,b)=(4,−1),(1,−4)…(答)
【押さえておきたいポイント】
○因数分解と素因数分解により各因数に分けて調べる ○整数でないことの証明には(判別式)が平方数でないことや(判別式)<0も使える
*** この解き方の印象 ***
方針が決まれば,後は理詰めの体力勝負になる. 正解できても,後に爽快感・充実感はあまり感じられない.・・・得点したければ突き進むしかないという感じ →右上に続く
|
※(3)(4)の判別式の計算は相当な難行苦行になる.これを避けるには,次のような方法も考えられるが,試験会場の現場対応でどちらが早いかは微妙.
M(=65)が与えられたとき のとき,a,bが実数になるためのkの値の範囲を求めておくと から,bが実数であるためには判別式が0以上でなければならない k>0のとき,次の関係を満たすことがbの実数条件になる(aから計算しても同じ) (3)では (4)では このようにk3−4Mの符号を調べると,酷な計算を逃れられる (図解) 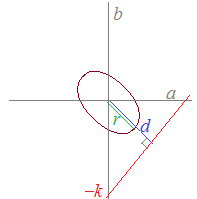 a−b=k
a−b=kすなわち b=a−k のグラフは右図の赤で示したように傾き45°の直線を表し,切片が−k (k>0)のとき,原点からの最短距離は もう一方の を 図の緑で示したように傾き45°の直線に垂直な傾き これら2つのグラフが交点(共有点)を持つには すなわち が条件となる. ※ kの値があんまり大きいとこれらのグラフは交わらない(共有点を持たない)ということです
【類題1】
参考答案を見るa3−b3=217を満たす整数の組(a, b)をすべて求めよ. (京大2005年前期理系)
左辺を因数分解し,右辺を素因数分解すると
(a−b)(a2+ab+b2)=7×31…(1) 可能な組み合わせは次の表の通り.
a2+ab+b2=217…(1.2) (1.1)よりa=b+1 これを(1.2)に代入 (b+1)2+(b+1)b+b2=217 3b2+3b−216=0 b2+b−72=0 (b+9)(b−8)=0 b=−9のときa=−8 b=8のときa=9 よって,(a,b)=(−8,−9),(9,8) (2)の場合,次の連立方程式を解く a2+ab+b2=31…(2.2) (2.1)よりa=b+7 これを(2.2)に代入 (b+7)2+(b+7)b+b2=31 3b2+21b+18=0 b2+7b+6=0 (b+1)(b+6)=0 b=−1のときa=6 b=−6のときa=1 よって,(a,b)=(6,−1),(1,−6) (3)の場合,次の連立方程式を解く a2+ab+b2=7…(3.2)
M(=217)が与えられたとき
のとき,a,bが実数になるためのkの値の範囲を求めておくと から,bが実数であるためには判別式が0以上でなければならない k>0のとき, 次の関係を満たすことがbの実数条件になる(aから計算しても同じ) 313>31×31>4×7×31となってbの整数解はない. (4)の場合,次の連立方程式を解く a2+ab+b2=1…(4.2) (3)と同様にk3, 4Mの大小を比較すると 2173>217×217>4×217 となってbの整数解はない. (1)(2)(3)(4)から結局,(a,b)=(−8,−9),(9,8),(6,−1),(1,−6)…(答) |