== ベクトルの差 ==
【考え方1】・・・「ベクトルの差」は「逆ベクトルの和」と考える方法
2つのベクトル , の差 −は、次の図のように、ベクトル にベクトル の逆ベクトル
−を加えたものと定義します。
[注意] −
と − は別のものです。(向きが逆になります。)
 [要点]
[要点]
「ベクトルの差は、逆ベクトルの和で定義する」
ベクトル  \( \vec{a} \) \( \vec{a} \)
にベクトル  \( \vec{b} \) \( \vec{b} \)の逆ベクトル
 \( -\vec{b} \) \( -\vec{b} \)を「接ぎ木」のようにつないで,
 \( \vec{a} \) \( \vec{a} \)の始点から
 \( -\vec{b} \) \( -\vec{b} \)の終点を結んだものを,ベクトルの差
 \( \vec{a}-\vec{b} \) \( \vec{a}-\vec{b} \)と決める.
【例1】
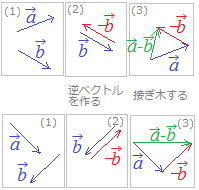
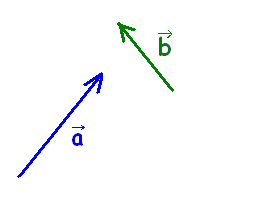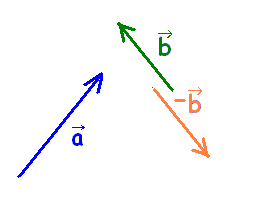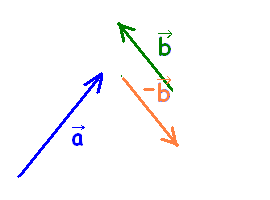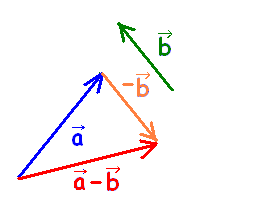
右上の図において(1)の問題に対して,  \( \vec{a}-\vec{b} \) \( \vec{a}-\vec{b} \)を作図するには,初めに(2)のように逆ベクトル  \( -\vec{b} \) \( -\vec{b} \)を作り,次に(3)のように接ぎ木するとよい.
右下の図も同様
※ベクトルは「大きさ」と「向き」だけで決まるので,『どこに描いてあるか』は関係ない.そこで,(2)で逆ベクトル  \( -\vec{b} \) \( -\vec{b} \)を作図してから(3)で接ぎ木するときに,  \( -\vec{b} \) \( -\vec{b} \)を自由に平行移動できる.
【考え方2】・・・2つのベクトルの始点がそろっている場合
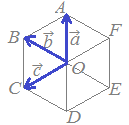
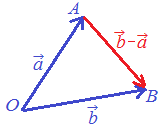 原点Oを始点とする2つのベクトル
原点Oを始点とする2つのベクトル \( \overset{\longrightarrow}{OA} \)を \( \overset{\longrightarrow}{OA} \)を
 \( \vec{a} \), \( \vec{a} \),
 \( \overset{\longrightarrow}{OB} \)を \( \overset{\longrightarrow}{OB} \)を
 \( \vec{b} \)で表す場合,2点A, Bを結ぶベクトル \( \vec{b} \)で表す場合,2点A, Bを結ぶベクトル
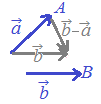
 \( \overset{\longrightarrow}{AB} \)は, \( \overset{\longrightarrow}{AB} \)は, \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \) \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \)
で表される.
(解説)
 \( \overset{\longrightarrow}{AB}=\overset{\longrightarrow}{AO}+\overset{\longrightarrow}{OB}=-\vec{a}+\vec{b} \) \( \overset{\longrightarrow}{AB}=\overset{\longrightarrow}{AO}+\overset{\longrightarrow}{OB}=-\vec{a}+\vec{b} \)
だから
 \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \) \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \)
になります.
【注意】
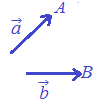
1.この関係は2つのベクトル  \( \vec{a},\vec{b} \) \( \vec{a},\vec{b} \)の始点がそろっている場合だけ成り立ち,右図のように始点がそろっていない場合には  \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \) \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \)とはなりません.
2.  \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \) \( \overset{\longrightarrow}{AB}=\vec{b}-\vec{a} \)です.  \( \overset{\longrightarrow}{AB}=\textcolor{red}{\vec{a}-\vec{b}} \) \( \overset{\longrightarrow}{AB}=\textcolor{red}{\vec{a}-\vec{b}} \)ではありません.
 危険な落とし穴 危険な落とし穴
「漫然と矢印の流れに目がついて行くためか」
 \( \overset{\longrightarrow}{AB}=\textcolor{red}{\vec{a}-\vec{b}} \) \( \overset{\longrightarrow}{AB}=\textcolor{red}{\vec{a}-\vec{b}} \)という間違いがビックリするほど多い!
覚え方としては
(終点)−(始点)
の形になると考えます.
【例2】
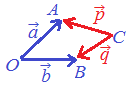
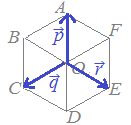
(1) 右図において2点 A, Bを結ぶベクトル  \( \overset{\longrightarrow}{AB} \) \( \overset{\longrightarrow}{AB} \)は,
 \( \vec{b}-\vec{a} \) \( \vec{b}-\vec{a} \)で表される.
(2) また2点 A, Bを結ぶベクトル  \( \overset{\longrightarrow}{AB} \) \( \overset{\longrightarrow}{AB} \)は,  \( \vec{q}-\vec{p} \) \( \vec{q}-\vec{p} \)と表すこともできる.
(2)は次のように示すことができます.
 \( \overset{\longrightarrow}{AB}=\overset{\longrightarrow}{AC}+\overset{\longrightarrow}{CB}=-\vec{p}+\vec{q} \) \( \overset{\longrightarrow}{AB}=\overset{\longrightarrow}{AC}+\overset{\longrightarrow}{CB}=-\vec{p}+\vec{q} \)
だから
 \( \overset{\longrightarrow}{AB}=\vec{q}-\vec{p} \) \( \overset{\longrightarrow}{AB}=\vec{q}-\vec{p} \)
※始点がそろっていれば,始点が原点以外の1点(C)であっても,(終点)−(始点)になります.
|

 右上の図において(1)の問題に対して,
右上の図において(1)の問題に対して, 原点Oを始点とする2つのベクトル
原点Oを始点とする2つのベクトル 【注意】
【注意】
 危険な落とし穴
危険な落とし穴 (1) 右図において2点A, Bを結ぶベクトル
(1) 右図において2点A, Bを結ぶベクトル