�y���4�z
�@���ʓ��ɎO�p�` ABC������D���̕��ʏ�ŁC�P�_ O���߂Ă����D���̖₢�ɓ�����D
(1)�@�O�p�` ABC�̓����ɓ_ P������Ƃ���D���̂Ƃ��C�R�̎O�p�` PBC, PCA, PAB�̖ʐς̔䂪 x:y:z�ł���Ȃ�C�_ P�̈ʒu�x�N�g��  \( \displaystyle \overrightarrow{\rm{OP}} \) \( \displaystyle \overrightarrow{\rm{OP}} \)�͎��̂悤�ɕ\����邱�Ƃ������D
 \( \displaystyle \overrightarrow{\rm{OP}}= \) \( \displaystyle \overrightarrow{\rm{OP}}= \) |  \( \displaystyle x\overrightarrow{\rm{OA}}+ y\overrightarrow{\rm{OB}}+ z\overrightarrow{\rm{OC}} \) \( \displaystyle x\overrightarrow{\rm{OA}}+ y\overrightarrow{\rm{OB}}+ z\overrightarrow{\rm{OC}} \) |
 \( \displaystyle x+y+z \) \( \displaystyle x+y+z \) |
(2) �O�p�` ABC�̂R�ӂ̒����� a=BC, b=CA, c=AB�Ƃ���D���̂Ƃ��O�p�` ABC�̓��S I�ɂ��āC���̈ʒu�x�N�g��  \( \displaystyle \overrightarrow{\rm{OI}} \) \( \displaystyle \overrightarrow{\rm{OI}} \)���C  \( \displaystyle \overrightarrow{\rm{OA}},\hspace{2px}\overrightarrow{\rm{OB}},\hspace{2px}\overrightarrow{\rm{OC}} \) \( \displaystyle \overrightarrow{\rm{OA}},\hspace{2px}\overrightarrow{\rm{OB}},\hspace{2px}\overrightarrow{\rm{OC}} \)��  \( \displaystyle a,\hspace{2px}b,\hspace{2px}c \) \( \displaystyle a,\hspace{2px}b,\hspace{2px}c \)��p���ĕ\���D
(3) �O�p�` ABC���s�p�O�p�`�ł���Ƃ��C���̊O�S Q�̈ʒu�x�N�g��  \( \displaystyle \overrightarrow{\rm{OQ}} \) \( \displaystyle \overrightarrow{\rm{OQ}} \)��,  \( \displaystyle \overrightarrow{\rm{OA}},\hspace{2px}\overrightarrow{\rm{OB}},\hspace{2px}\overrightarrow{\rm{OC}} \) \( \displaystyle \overrightarrow{\rm{OA}},\hspace{2px}\overrightarrow{\rm{OB}},\hspace{2px}\overrightarrow{\rm{OC}} \)�� ��=��CAB, ��=��ABC��p���ĕ\���D
�i2011�N�x�����̐����q�� ���w�����w�ȁj
�m������n
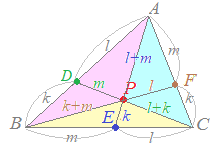
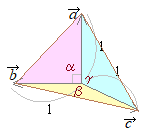
�@�E�}�̂悤�ȓ�����ł���Ƃ��C�ʐϔ� ��PAB:��PBC:��PCA=m:k:l�ɂȂ邱�Ƃ́C���̃y�[�W�ł����܂łɏq�ׂė����D
�@�t��������D���Ȃ킿�C ��PAB:��PBC:��PCA=m:k:l�̂Ƃ��C AD:DB=l:k, DP:PC=m:(l+k)�Ȃǂ����藧�D
�i�j
(1)
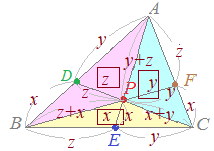
• ��PBC:��PCA�̖ʐϔ䂪 x:y�ł���Ƃ�
���PC�����ʂƌ���ƍ����i�ɔ�Ⴗ��ΕӁj�̔�́CBD:DA=x:y
• ��PCA:��PAB�̖ʐϔ䂪 y:z�ł���Ƃ�
���PB�����ʂƌ���ƍ����i�ɔ�Ⴗ��ΕӁj�̔�́CCE:EB=y:z��������
• ��ABC:��PCA�̖ʐϔ䂪 (x+y+z):x�ł��邩��
���BC�����ʂƌ���ƍ����i�ɔ�Ⴗ��ΕӁj�̔�́CEP:EA=x:(x+y+z)
���������āCEP:PA=x:(y+z)
�ȏォ��C BC�� z:y�ɓ�������_�� E�Ƃ���Ƃ��C EA�� x:(y+z)�ɓ�������_�� P�ɂȂ邩��
\frac{y\vec{OB}%2B z\vec{OC}}{y%2B z}}{x%2B (y%2B z)}) \( \displaystyle \overrightarrow{\rm{OP}}=\frac{x\overrightarrow{\rm{OA}}+ (y+ z)\dfrac{y\overrightarrow{\rm{OB}}+ z\overrightarrow{\rm{OC}}}{y+ z}}{x+ (y+ z)} \) \( \displaystyle \overrightarrow{\rm{OP}}=\frac{x\overrightarrow{\rm{OA}}+ (y+ z)\dfrac{y\overrightarrow{\rm{OB}}+ z\overrightarrow{\rm{OC}}}{y+ z}}{x+ (y+ z)} \)
 \( \displaystyle =\frac{x\overrightarrow{\rm{OA}}+ y\overrightarrow{\rm{OB}}+ z\overrightarrow{\rm{OC}}}{x+ y+ z} \)
�����B���� \( \displaystyle =\frac{x\overrightarrow{\rm{OA}}+ y\overrightarrow{\rm{OB}}+ z\overrightarrow{\rm{OC}}}{x+ y+ z} \)
�����B����
|
�m������n
(2)
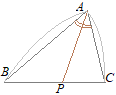
�y�p�̓����̐����z
�@�E�}�̂悤�ɁCAP����BAC�̓����ɂȂ��Ă���Ƃ��C
BP:PC=BA:CA
�����藧�D

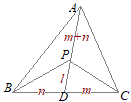
�@ ��ABC�̓��S�� I�Ƃ���Ƃ��C AI, BI, CI�͊e�X ��A, ��B, ��C�̓����ɂȂ邩��C AI, BI, CI�̉������e�X BC, CA, AB�ƌ����_�� D, E, F�Ƃ���� BD:DC=c:b, CE:EA=a:c, AF:FB=b:a
�@ ��IBC:��ICA:��IAB=a:b:c�ɂȂ邩��C(1)�̌��ʂ��g����
 \( \displaystyle \overrightarrow{\rm{OI}}=\frac{a\overrightarrow{\rm{OA}}+ b\overrightarrow{\rm{OB}}+ c\overrightarrow{\rm{OC}}}{a+ b+ c} \) \( \displaystyle \overrightarrow{\rm{OI}}=\frac{a\overrightarrow{\rm{OA}}+ b\overrightarrow{\rm{OB}}+ c\overrightarrow{\rm{OC}}}{a+ b+ c} \)
(3)

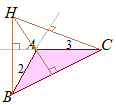
�@ ��ABC�̊O�S�� Q�Ƃ���Ƃ��C���w�Z�ŏK���悤�ɒ��S�p�͉~���p�̂Q�{������C ��BQC=2A, ��CQA=2B, ��AQB=2C�ɂȂ�D
�@ ��ABC�̊O�ډ~�̔��a�� R�Ƃ���Ƃ��C
��IBC:��ICA:��IAB
 \( \displaystyle =\frac{1}{2}R^2\sin 2A:\frac{1}{2}R^2\sin 2B:\frac{1}{2}R^2\sin 2C \) \( \displaystyle =\frac{1}{2}R^2\sin 2A:\frac{1}{2}R^2\sin 2B:\frac{1}{2}R^2\sin 2C \)
 \( \displaystyle =\sin 2A:\sin 2B:\sin 2C \) \( \displaystyle =\sin 2A:\sin 2B:\sin 2C \)
(1)�̌��ʂ��g����
\vec{OC}}{\sin 2\alpha%2B\sin 2\beta%2B\sin 2(\pi-\alpha-\beta)}) \( \displaystyle \overrightarrow{\rm{OQ}}=\frac{\sin 2\alpha\overrightarrow{\rm{OA}}+\sin 2\beta\overrightarrow{\rm{OB}}+\sin 2(\pi-\alpha-\beta)\overrightarrow{\rm{OC}}}{\sin 2\alpha+\sin 2\beta+\sin 2(\pi-\alpha-\beta)} \) \( \displaystyle \overrightarrow{\rm{OQ}}=\frac{\sin 2\alpha\overrightarrow{\rm{OA}}+\sin 2\beta\overrightarrow{\rm{OB}}+\sin 2(\pi-\alpha-\beta)\overrightarrow{\rm{OC}}}{\sin 2\alpha+\sin 2\beta+\sin 2(\pi-\alpha-\beta)} \)
\vec{OC}}{\sin 2\alpha%2B\sin 2\beta-\sin 2(\alpha%2B\beta)}) \( \displaystyle =\frac{\sin 2\alpha\overrightarrow{\rm{OA}}+\sin 2\beta\overrightarrow{\rm{OB}}-\sin 2(\alpha+\beta)\overrightarrow{\rm{OC}}}{\sin 2\alpha+\sin 2\beta-\sin 2(\alpha+\beta)} \)
�����B���� \( \displaystyle =\frac{\sin 2\alpha\overrightarrow{\rm{OA}}+\sin 2\beta\overrightarrow{\rm{OB}}-\sin 2(\alpha+\beta)\overrightarrow{\rm{OC}}}{\sin 2\alpha+\sin 2\beta-\sin 2(\alpha+\beta)} \)
�����B����
|
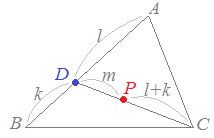 • AB��l:k�̔�ɓ�������_��D�Ƃ���Ƃ��CDC��m:(k+l)�̔�ɓ�������_��P�ł���D
• AB��l:k�̔�ɓ�������_��D�Ƃ���Ƃ��CDC��m:(k+l)�̔�ɓ�������_��P�ł���D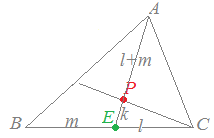 ���l�ɂ���
���l�ɂ���
 �@���w�Z�̐��w�Łu�����}�`�̐����v�Ƃ����̂��w�т܂��D
�@���w�Z�̐��w�Łu�����}�`�̐����v�Ƃ����̂��w�т܂��D
 �ƕό`����ƁuBC��
�ƕό`����ƁuBC�� �ƕό`�ł��邩��
�ƕό`�ł��邩�� �ƕό`�����
�ƕό`����� �i�j
�i�j �y�p�̓����̐����z
�y�p�̓����̐����z �@
�@ �@
�@ (2)
(2) �i�j
�i�j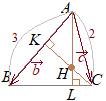 �i�j
�i�j