← PC用は別頁

== 高次方程式 ==

■解説
○　n 次の多項式 P(x) を用いて，P(x)=0 の形に書くことのできる方程式を n 次方程式という．
○　3 次以上の方程式を高次方程式という． ○　このページでは，「因数定理を用いて因数分解で解ける３次方程式」を扱う．

【 因数定理 】
　多項式 P(x) について P(a)=0 ならば， P(x) は x−a で割り切れる．（ x−a を因数にもつ．）
（参考）
  • ３次方程式，４次方程式には解の公式があるが，高校では扱わない．（カルダノの公式，フェラリの公式）
  • ５次以上の方程式には解の公式を作ることはできない．（ガロア）
    　これは「５次方程式は解けない」ということではない．「５次以上の方程式の解を『有限回の変形操作で』解くことはできない」ということで，具体的な数値で係数が与えられた５次，６次，...方程式でも『無限回の変形操作=無限級数を用いれば』解くことができる．
    ※気になる人は，wxMaxima（←リンク）を使って，５次，６次方程式を解いてみるとよい．
    方程式→高次方程式の解を求める→空欄を埋める
    【例】
    　x^5+1=0 → ５個の解が根号を用いて示される．
    　x^6-2*x^5+3=0 → ６個の解が各々小数点以下第15位まで示される．
  • 一般に n 次方程式には複素数の範囲で（重解も数えると） n 個の解が存在する（代数学の基本定理：ガウス）．
一般に，係数が実数である 3 次方程式の解は，
　（ア）実数，実数，実数
　（イ）実数，虚数，虚数
のいずれかになる．（これ以外の組合わせ［実数，実数，虚数］［虚数，虚数，虚数］はない．
　重解をもつ場合は，アに含まれる．
◎　以下で説明する３次方程式の解き方は，１つの実数解を因数定理で見つけ，次数を下げて２次方程式にし，残りは解の公式で解くというのが主な流れとなる．）

【 因数定理 II 】
　多項式 P(x) について P( )=0 ならば， P(x) は ax−b で割り切れる．（ ax−b を因数にもつ．）
（解説）
上の「II」は高校生が使いやすいように，かみ砕いて述べたもので，理論的には「因数定理」だけでよい．（その訳は以下に述べる．）

（因数定理←）
　「剰余の定理：多項式 P(x) を x−a で割った余りは P(a) に等しい．」を用いると，
P(a)=0 ⇔ 余りが 0 ⇔ 割り切れる
となるから，P(a)=0 ならば， P(x) は x−a で割り切れ，その逆も言える．

（因数定理ＩＩ←）
　因数定理や剰余の定理において，定数 a の値は，整数に限られず，分数でも小数でも無理数でも（さらに広げて虚数でも）よい．
P( )=0 ⇔ 余りが 0 ⇔ 割り切れる

となるから，P( )=0 ならば， P(x) は x− で割り切れ，その逆も言える．
　ところで，例えば
2x3−x2+2x−1=(x−)(2x2+2)
2x3−x2+2x−1=(2x−1)(x2+1)

のように，x− で割り切れことと，2x−1 で割り切れることは，同じことである．（どちらの式に２を振り分けるかの違いだけである．）
　そこで，x− で割り切れるということを整数係数で言えば，ax−b で割り切れることになるから，
P( )=0 ⇔ ax−b で割り切れる

　上の「因数定理II」の証明で納得できないときは，次の［別の証明］を見るとよい．
　 　まず，「剰余の定理」は次のように証明される：

「剰余の定理」の復習
　多項式 P(x) を１次式で割ったときの余りを求めるとき，１次式で割るのだから余りは定数項になる．そこで商を Q(x)，余りを R とおくと
P(x)=(x−a)Q(x)+R
と書ける．R を求めたいのであるが，この等式において Q(x) は単なる記号で実際の式の中身は分からないから，R を求めるためには，この Q(x) が消えるようにすれなよい．
　 Q(x) には x−a が掛けられているので，x−a がちょうど 0 になるような x の値を選べば，Q(x) がどんな式になるのかが分からなくても，消去できる．そこで x=a を代入すると，
P(a)=(a−a)Q(a)+R すなわち P(a)=R
になり，余り R が P(a) に等しいことが証明された．
［ax−b で割ったときの剰余の定理II］
　多項式 P(x) を１次式 ax−b で割ったときの余りを求めるとき，１次式で割るのだから余りは定数項になる．そこで商を Q(x)，余りを R とおくと
P(x)=(ax−b)Q(x)+R
と書ける．

　x= を代入すると，

P( )=(a·−b)Q( )+R

P( )=0·Q( )+R

P( )=R
ゆえに，余り R は P( ) に等しい．
［ ax−b で割ったときの因数定理 II ］別の証明
　上で述べた「剰余の定理II」により，P(x) を ax−b

で割ったとき， P( )=0 ⇔ ax−b で割り切れる．

例題1
　３次方程式 x3+x2+x−3=0 を解け．

答案
f(x)=x3+x2+x−3 とおくと
　f(1)=1+1+1−3=0 だから …(*1)
　f(x) は x−1 で割り切れる．
　割り算を行うと f(x)=(x−1)(x2+2x+3) …(*2)
(x−1)(x2+2x+3)=0 より x=1 ,−1±i …(*3)
【 この問題では 】
　x3+x2+x−3=(x−a)(x2+bx+c) ならば a は 3 の約数（符号は正負あり：±1，±3）
【 一般に 】
　x3+･･･ + p=(x−a)(x2+･･･+c) ならば a は p の約数（符号は正負あり）
　正負を考えて p の約数に順に当たっていけば「いずれ見つかる」
（舞台裏から）
(*1)　なぜ f(1) を思いつくのか？
　はっきり言って，「一発で当てる方法はない」．ある程度は「まぐれ当たり」
もし，x3+x2+x−3=(x−a)(x2+bx+c) の形に因数分解できる（係数は整数）とすれば，ac=3 になるはずなので，a は３の約数（正負の符号あり）．
⇒ a=1 ,−1, 3 ,−3 でやってみて f(a)=0 となるものを探す．
（答案は清書としてうまくいったものを見せますが，舞台裏では（運が悪ければ）３回も泣いている．）
(*2)　この式はどうやって出てくるのか？
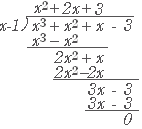次のように割り算をして，（割り切れるのは分かっている）商を書く．

　割り切れる場面では，次のように暗算でもできる．
　x3+x2+x−3=(x−1)(x2+bx+c) になるとすれば，定数項 −3 から，c=3
２次の係数(=1)から b−1=1 → b=2
(*3)　３次式から１次の因数を１つ見つけると残りは２次
残りは２次なので，２次方程式にすれば「解の公式」で直ちに解ける．

※　次の問題は，因数分解の結果が (2x−3)(x2+x+1) となる問題である．このような問題では，整数値 a をどんなに探しても，f(a)=0 にはならない．また，残り２つの解は虚数なのでこれも通常は思いつかない．

したがって，f( )=0 を見つけない限り，この問題の糸口はつかめない．

f( )=0 を見つける方法は？
例題2
　３次方程式 2x3−x2−x−3=0 を解け．

答案
f(x)=2x3−x2−x−3 とおくと

　f( )=2( )3−( )2−( )−3==0

だから
　f(x) は 2x−3 で割り切れる．
　割り算を行うと f(x)=(2x−3)(x2+x+1)

(2x−3)(x2+x+1)=0 より x= ,
（舞台裏から）

f( )=0 を見つける方法は？
もし， 2x3−x2−x −3=(ax −b)(cx2+dx+e) の形（ a , b , c , d , e は整数 ）に因数分解できるとすれば，
ac=2 , be=3
となるので，a は 2 の約数（±1，±2），b は 3 の約数（±1，±3）になる．

　したがって，f(±), f(±), f(±), f(±) の

８個の中に f( )=0 となるものがある．
　いずれ見つかるので「早いか遅いかの違いだけ」となる．
　
【 一般に 】
　px3+･･･ +q=(ax−b)(mx2+･･･+n) ならば
a は p の約数，b は q の約数として f(±)=0 となるものがある．
【　要約　】
　 f(x)=px3+･･･ +q　の因数分解　⇒　 f(±) を調べる．


※　整数や分数を用いて因数分解できる３次方程式はこの方法で対応できる．
※　次のような３次方程式は，ここで紹介した方法では解けない．x3−2.32 x2+x−=0

※「やり直す」で，別の係数の問題に変ります．
■問題１
　次の方程式を解け．
[ 0問 / 全8問中] [採点する] [やり直す] [次の問題]
　　
■問題２
　次の方程式を解け． 　　
[ 0問 / 全8問中] [採点する] [やり直す] [次の問題]

　　


...（携帯版）メニューに戻る

...メニューに戻る