|
【要点2】
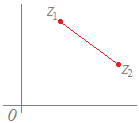
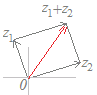
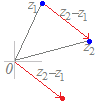
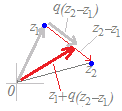
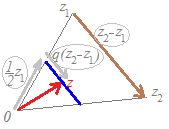
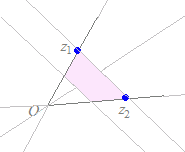
(解説)1直線上にない異なる3つの複素数z1 , z2 , z3が与えられていて,実数p, q, rが p+q+r=1, p≧0, q≧0, r≧0 の条件を満たしながら変化するとき, z=pz1+qz2+rz3 で示される点は,3点z1 , z2 , z3で作られる三角形の内部および周上になる. 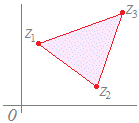 z=pz1+qz2+rz3 (p+q+r=1, p≧0, q≧0, r≧0) だから z=pz1+qz2+rz3 (p=1−q−r≧0, q≧0, r≧0) pを消去すると z=(1−q−r)z1+qz2+rz3 (q+r≦1, q≧0, r≧0) z=z1+q(z2−z1)+r(z3−z1) (q+r≦1, q≧0, r≧0) となるから,上の【例2】を参考にすると,まずz1まで進み,次にz2−z1,z3−z1を2辺とする三角形の内部および周上を指すことが分かる. 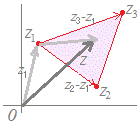 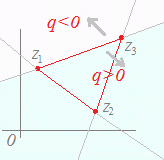 ※z=pz1+qz2+rz3
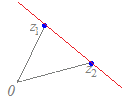
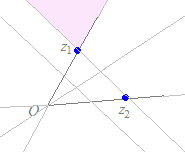
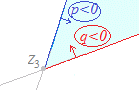
※z=pz1+qz2+rz3(p+q+r=1, q>0) (p+q+r=1, q<0) の場合は z=z1+q(z2−z1)+r(z3−z1) (q>0) (q<0) となるから,各々右図のような領域を表す. |
p+q+r=1は,何の役に立っているのか?
一般に,ある複素数zを,与えられた(直線上にはない)3個の複素数z1 , z2 , z3を使って,
z=pz1+qz2+rz3 のように表す方法は,ただ1通りには定まらず,何通りにでも表すことができる.(p,q,rを定めるための方程式と見たときは,不定解を持つ) すなわち z1=a+bi, z2=c+di, z3=e+fi, z=g+hi のとき pa+qc+re=g …(1) pb+qd+rf=h …(2) となる実数p,q,rは,未知数が3個であるのに対して,方程式が2個しかないため,ただ1通りには定まらない. 例えば,複素数0を3つの複素数1, i , −1で表す方法は 1×1+1×(−1)+0i=0 でも成り立ち 2×1+2×(−1)+0i=0 でも成り立つ. これに対して, p+q+r=1 …(3) という条件を追加しておくと,自由度が1だけ減って方程式が3個になるので,p,q,rはただ1通りに定まる. 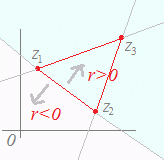 ※z=pz1+qz2+rz3
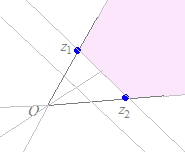
※z=pz1+qz2+rz3(p+q+r=1, r>0) (p+q+r=1, r<0) の場合は z=z1+q(z2−z1)+r(z3−z1) (r>0) (r<0) となるから,各々右図のような領域を表す. 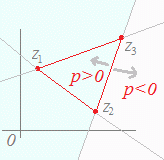 ※z=pz1+qz2+rz3
※z=pz1+qz2+rz3(p+q+r=1, p>0) (p+q+r=1, p<0) の場合は z=pz1+qz2+(1−p−q)z3 (r=1−p−q) z=z3+p(z1−z3)+q(z2−z3) (p>0) (p<0) と変形できるから,各々右図のような領域を表す. |
|
【例3】
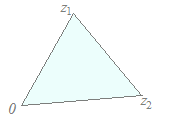
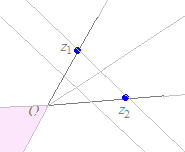
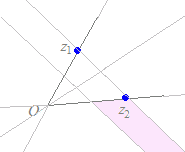
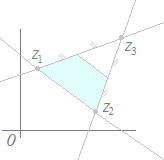
(解答)1直線上にない異なる3つの複素数z1 , z2 , z3が与えられていて,実数p, q, rが p+q+r=1, q>0, r<0 の条件を満たしながら変化するとき, z=pz1+qz2+rz3 で示される点は,,どのような図形を描くか? 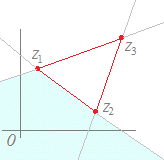 上記の解説で,q>0とr<0の共通部分を求めると,右図の水色の部分(境界は含まない)になる.
上記の解説で,q>0とr<0の共通部分を求めると,右図の水色の部分(境界は含まない)になる.
|
【例4】
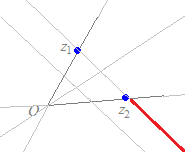
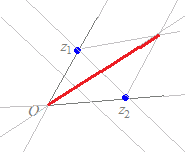
(解答)1直線上にない異なる3つの複素数z1 , z2 , z3が与えられていて,実数p, q, rが p+q+r=1, p=,q>0, r>0 の条件を満たしながら変化するとき, z=pz1+qz2+rz3 で示される点は,,どのような図形を描くか? 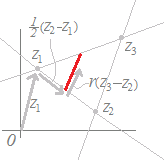 z=z1+q(z2−z1)+r(z3−z1)
z=z1+q(z2−z1)+r(z3−z1)q+r=,q>0, r>0 z=z1+(−r)(z2−z1)+r(z3−z1) 0<r< z=z1+(z2−z1)+r(z3−z2) 0<r< となるから,順次組み立てていくと,右図の赤線(端点を含まない)になる. |
|
【問題2】1直線上にない異なる3つの複素数z1 , z2 , z3に対して,
(1)解説
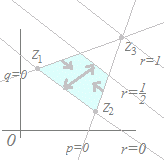
z=pz1+qz2+rz3 で定義される複素数が次の図形を描くとき,実数p, q, rが満たす条件として正しいものを右から選んでください. 領域については水色で示した部分,直線,半直線,線分については赤で示した部分とし,すべて境界線や端点を含まないものとします.
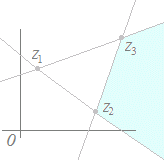 |
下図のようになります.
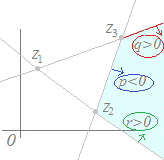 |
(2)解説
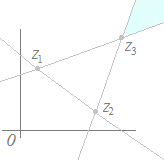 |
下図のようになります.
 |
(3)解説
 |
下図参照
 |
(4)解説
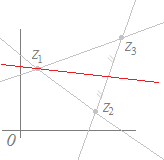 |
z1を通り,−z1に平行な直線は,
z=z1+t(−z1 )=(1−t)z1+z2+z3
ここで,z1, z2, z3の係数をp,q,rとおくと, p+q+r=1, q=r |
(5)解説
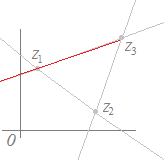 |
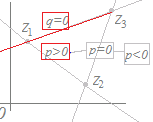 右図参照 右図参照(別解) z3から,z1−z3を同じ向きに定数倍してできる点だから, z=z3+t(z1−z3 )=tz1+0z2+(1−t)z3 (t>0) ここで,z1, z2, z3の係数をp,q,rとおくと, p+q+r=1, p>0, q=0 |
(6)解説
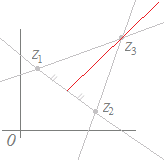 |
から,z3−を同じ向きに定数倍してできる点 と考えると, z=+t(z3− )=z1+z2+tz3 (t>0) ここで,z1, z2, z3の係数をp,q,rとおくと, p+q+r=1, p=q, r>0 |