|
現在地と前後の項目 2次関数のグラフ［標準形］/2次関数→頂点の座標/2次関数(標準形→頂点)/2次関数(標準形→グラフ)/2次関数(標準形→グラフ)2/2次関数(標準形→グラフ)3/2次関数(標準形→グラフ)4/平方完成の変形/平方完成2/平方完成3/頂点の座標/展開形→頂点の座標2/展開形→頂点の座標3/展開形→頂点の座標4/展開形→頂点の座標5/2次関数（展開形→頂点）/2次関数（展開形→グラフ5）/文字係数1/グラフの平行移動/放物線の移動/放物線の移動2/放物線の移動3/グラフと係数の符号/2次関数(３点→頂点)/２次関数の入試問題1/
このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒ ■（例題対比）２次関数のグラフ［標準形］ y=(x−p)2+q のグラフは y=x2 のグラフを x 軸の正の向きに p ，y 軸の正の向きに q だけ平行移動したもので，その頂点の座標は (p , q) である．
※ 右に（x 軸の正の向きに）p ，上に（y 軸の正の向きに）q だけ平行移動したときに
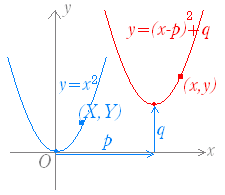
（解説） 右図のように y=x2 のグラフを x 軸の正の向きに p ，y 軸の正の向きに q だけ平行移動したとき，新しいグラフの方程式は，次のようにようにして求められる． 元のグラフ上の点を (X,Y) とおき，これを移動してできる新しいグラフ上の点を (x,y) とおく．このとき x,y の満たす関係式が求める方程式となる． (X,Y) は y=x2 のグラフ上の点だから Y=X2 …(1) が成り立つ． (X,Y) を右に p，上に q だけ平行移動したものが (x,y) だから x=X+p , y=Y+q …(2) が成り立つ． (2)から新座標を元の座標で表わすと， X=x−p , Y=y−q …(2)’ (2)’を(1)に代入して新座標だけの関係式にすると y−q=(x−p)2 …(3) ※このように，「右」「上」に平行移動すると， x も y も引き算になるが，「習慣に従って」y= ... の形に直すと（q を移項して） y=(x−p)2+q になる． ［例題1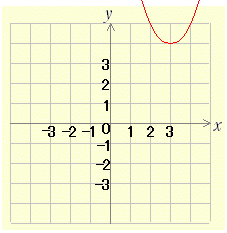］  y=(x−3)2+4 のグラフは，y=x2 のグラフを x 軸の正の向きに 3 ，y 軸の正の向きに 4 だけ平行移動したもので，頂点の座標は(3, 4)，グラフは右図のようになる． |
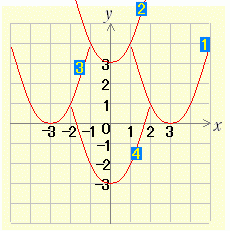
 →続き 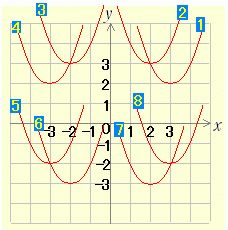 (3) y=(x−2)2−3 のグラフを右図の中から選び番号で答えよ．
 (4) y=x2+2 のグラフを右図の中から選び番号で答えよ．
|
|
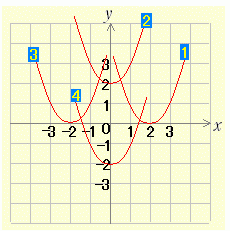
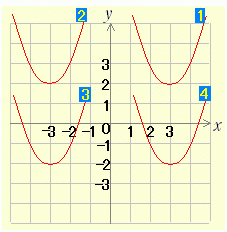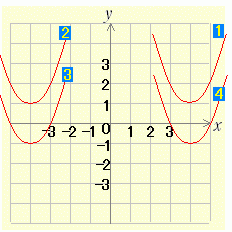［問題1］ 半角数字(１バイト文字)で解答すること(他の問題も同様)  (1) y=(x−3)2+2 のグラフを右図の中から選び番号で答えよ． (2) y=(x+4)2−1 のグラフを右図の中から選び番号で答えよ．右へ続く→ |
 (5) y=(x−3)2 のグラフを右図の中から選び番号で答えよ．
(6) y=(x+3)2 のグラフを右図の中から選び番号で答えよ．
|
|
y=a(x−p)2+q のグラフは y=ax2 のグラフを x 軸の正の向きに p ，y 軸の正の向きに q だけ平行移動したもので，その頂点の座標は (p , q) である．
※ x2 の係数 a で「形」が決まる． p ，q で「移動」が決まる．例 y=2(x−3)2+4 のグラフを書くときは，元の形として y=2x2 を考え，このグラフを x 軸の正の向きに 3 ，y 軸の正の向きに 4 だけ平行移動する． 例 y=−3(x+4)2+5 のグラフを書くときは，元の形として y=−3x2 を考え，このグラフを x 軸の正の向きに - 4 ，y 軸の正の向きに 5 だけ平行移動する． ［例題2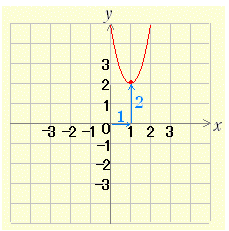］  y=3(x−1)2+2 のグラフは，y=3x2 のグラフを x 軸の正の向きに 1 ，y 軸の正の向きに 2 だけ平行移動したもので，頂点の座標は (1 , 2) ，グラフは右図のようになる． |
［問題2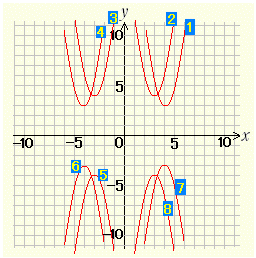］ (1)y=2(x+3)2+4 のグラフを右図の中から選び番号で答えよ． (2)y=−2(x−3)2−4 のグラフを右図の中から選び番号で答えよ． |
|
［例題3］ 次の空欄を埋めよ． （答案） ア=4，イ=3，ウ=2，エ=3，オ=2 |
［問題3］ 次の空欄を埋めよ． (1) (2) (3) |