.
■Excel：相関係数，回帰直線
◇このページで利用する関数等の一覧◇
  • グラフ--散布図
  • ツール--分析ツール
  • ｒ表
  • SLOPE(ｙの配列の範囲，ｘの配列の範囲)：傾き
  • INTERCEPT(ｙの配列の範囲，ｘの配列の範囲)：ｙ切片
  • CORREL(系列１の範囲，系列２の範囲)：相関係数
  • PEARSON(系列１の範囲，系列２の範囲)：相関係数
  • STEYX(系列１の範囲,系列２の範囲)：推定値の標準誤差
  • TREND(既知のｙ，既知のｘ，新しいｘ，１)：回帰直線上の推定値
  • FORECAST(新しいｘ,既知のｙ，既知のｘ)：回帰直線上の推定値
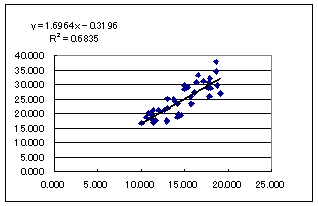
■操作方法の要約■
　Excelを用いて，右の表1のようなデータ（２列）から図１のような散布図を作成し，相関係数，回帰直線を求めるには

(1)
　散布図の作成方法は［こちら］

(2)
　図1の(2)　回帰直線　を表示するには：
散布図のマーカー（右図では青の点）の１つを右クリックし，「近似曲線の追加」→「線形近似」
(3)
　図1の(3)(4)　回帰直線，相関係数Rの２乗を表示するには：
●1
　グラフ中の「近似直線」を右クリック→「グラフに数式を表示する」「グラフにＲー2乗値を表示する」をチェック→ＯＫ
（これらの式はテキストボックスなので，適当な場所に移動して見やすくすることができる．）==>データが更新されれば自動的に追随する．（データ範囲が変われば，範囲指定の変更は必要）
●2
　回帰直線の方程式 y=ax+b のa,bだけを求めたいときは
=SLOPE(ｙの配列の範囲，ｘの配列の範囲)→a
=INTERCEPT(ｙの配列の範囲，ｘの配列の範囲)→b　（※引数の順序に注意）
(4)　相関係数を求め，無相関の検定をするには
(実際には相関がないものに回帰直線を求めてもだめなので相関係数を先に求める方がよい)
●1
　散布図を作成しなくても，「分析ツール」を利用すれば相関係数は求められる：「ツール」→「分析ツール」→「相関」→「ＯＫ」→入力元：入力範囲として表2の場合３列全体をドラッグ（範囲指定の際に，表２においてx,y,zというタイトルも含める場合，「先頭行をラベルとして使用」にチェック）→ＯＫ
　出力される表には，すべての組合せの相関係数が表示されるので，ｘ－ｘ組のように自分自身との相関係数は1となる．また，ｘ－ｙの相関係数とｙ－ｘの相関係数は異なるが，右の表３においてはｘ-ｙの相関係数が0.807と表示されている．(R=0.807→R2=0.6515)==>データが更新されても再度出力しないと結果は追随しない．
●2　correlation ：相関
　==>散布図なしで，データ更新時に相関係数が追随するようにするには（ただし，データ範囲が変われば，範囲指定は必要）
関数CORREL(系列１の範囲，系列２の範囲)
または
関数PEARSON(系列１の範囲，系列２の範囲)
を利用することができる．（直接入力または挿入→関数→統計）
返される値は表3のうちの１つの値（0.807など）
●3
　標本相関係数をｒとするとき母相関係数ρが0（無相関）でないための限界値は右のｒ表によって判断する．|r|がこの限界値以上ならば「相関あり」として回帰直線などを求める．
(5)
　図1の(5)のような推定値の標準誤差，信頼区間を求めるには
=STEYX(系列１の範囲,系列２の範囲)　==>　標準誤差Seとなる．

　図に示した灰色の線　（95%信頼区間の限界）　は回帰直線±1.96Seの線で，この線はExcelグラフには表示されない．
(6)
　図１の(6)のように与えられたｘ座標に対応する回帰直線のｙ座標を数値として求めるには
=TREND(既知のｙ，既知のｘ，新しいｘ，１)
または
=FORECAST(新しいｘ,既知のｙ，既知のｘ)
表１
x y
0.437 11.144
2.164 11.657
2.920 20.318
3.743 16.998
･･･ ･･･
　　 表2
x y z
0.437 11.144 23.857
2.164 11.658 23.911
2.921 20.318 24.116
3.743 16.998 24.229
･･･ ･･･ ･･･
図１
表3
　　 x y z
x 1 　 　　
y 0.807 1 　　
z 0.850 0.788 1
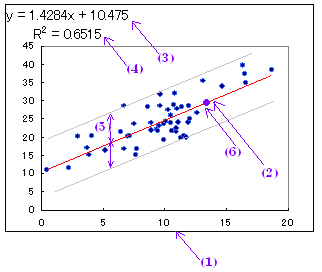
※　推定値の標準誤差Seは，Excelの組み込み関数
=STEYX(系列１の範囲,系列２の範囲)で求められるが，これは
ｙとｙの推定値ｙ’の誤差から計算される標準偏差
σ =
ではなく，
Se =
とする（ｎは点の個数=ｘ座標の個数）．（標本から母平均を求めるときの計算と同様に考えるが，今の場合ｘの平均とｙの平均が計算式にはいるので，自由度が2減る．）

両側検定用のｒ表
　 有意水準α（両側検定）
自由度(n-2) 0.1 0.05 0.02 0.01
10 0.497 0.576 0.658 0.708
11 0.476 0.553 0.634 0.684
12 0.458 0.532 0.612 0.661
13 0.441 0.514 0.592 0.641
14 0.426 0.497 0.574 0.623
15 0.412 0.482 0.558 0.606
16 0.400 0.468 0.543 0.590
17 0.389 0.456 0.529 0.575
18 0.378 0.444 0.516 0.561
19 0.369 0.433 0.503 0.549
20 0.360 0.423 0.492 0.537
21 0.352 0.413 0.482 0.526
22 0.344 0.404 0.472 0.515
23 0.337 0.396 0.462 0.505
24 0.330 0.388 0.453 0.496
25 0.323 0.381 0.445 0.487
26 0.317 0.374 0.437 0.479
27 0.311 0.367 0.430 0.471
28 0.306 0.361 0.423 0.463
29 0.301 0.355 0.416 0.456
30 0.296 0.349 0.409 0.449
40 0.257 0.304 0.358 0.393
50 0.231 0.273 0.322 0.354
60 0.211 0.250 0.295 0.325
70 0.195 0.232 0.274 0.302
80 0.183 0.217 0.257 0.283
90 0.173 0.205 0.242 0.267
100 0.164 0.195 0.230 0.254
110 0.156 0.186 0.220 0.242
120 0.150 0.178 0.210 0.232

■解説■
◇回帰直線◇
　中学校の頃には理科の実験結果をまとめるときに，次の図のように点が「上にも下にも半分ずつ来るように」「直線からなるべく離れないように」目分量で直線を引いていたが，これを数学的に求める．
　各点から直線 y = ax + b までの（ｙ方向の差）の合計
Σ｛ yk - (axk+b) ｝
は，上下で符号が逆になるから和は元々0となる．絶対値は変形しにくい．そこでΣ｛ yk - (axk+b) ｝2が最小となるようなａ，ｂを求める（最小２乗法）．

　（途中経過略：結果のみ示す．）
　ｘk の平均を m， ｙk の平均を n とおくと
a =
b = n - am

※　統計の書物では，数学と違って，定数を先に書いて
y = α + βx
の形で書かれることが多い．(例えば，株式相場で日経平均をｘ，ある銘柄の株価をｙで表わすとき，日経平均の増減に対するその銘柄の増減の割合はｘの係数βとなる．過去何ヶ月かの変動を見たときのβの値はヒストリカル･ベータと呼ばれる．)
　Excelグラフでは数学の表示が踏襲されているので，ここでは数学の書き方に従って y = ax + b の形で表示した．

※　ここで求めたa,bを用いて元いてy = ax + bの方程式にしたものが図１(3)でグラフに追加される回帰直線の方程式に一致する．（点検用に併用するとよい．）

※　回帰直線のグラフおよびその方程式は，相関が認められないような分布についても形式的に出てくる (直線の中で誤差の2乗和が一番小さいものを求めているだけだから)．そこで，これを使うかどうかは，次に述べる相関係数の検定をしてから判断することが重要．（右の図2のような場合，ｘ，ｙにはほとんど相関がなく，形式的に求まる回帰直線にも利用価値がない．）
　したがって，まず相関係数を求め，相関係数の検定を行って相関があると確かめた上で回帰直線を求める方がよい．		 ※何に回帰するのか･･･子の身長は親の身長と強い相関があるが，最終的に親の身長から予測される値よりも少し先祖返りするということで，回帰という名が付けられたらしい．（こんなイメージか？）

※　左に示したａ，ｂの計算をExcelで行うには次のように順次表を組み立てて行き，最後に和と商を求めればよい．
x y (x-m) y-n (x-m)2 (x-m)(y-n)
0.437 11.144 -9.191 -13.083 84.475 120.250
2.164 11.658 -7.464 -12.570 55.706 93.815
2.921 20.318 -6.707 -3.909 44.989 26.220
3.743 16.998 -5.885 -7.230 34.634 42.547
･･･ ･･･ ･･･ ･･･ ･･･ ･･･
上の図１の場合，a = 1.428，b = 10.475 となる．
※　Excelのグラフでは直線近似だけでなく，２次関数，･･･など曲線近似の結果も表示されるが，ここでは直線近似のみを扱う．

図2
◇相関係数◇

○　ｘが増えるとｙも増えるとき，ｘ，ｙは正の相関があるという．
ｘが増えるとｙは減るとき，ｘ，ｙは負の相関があるという．
直線的な関係に近いとき，強い相関があるといい，幅が広がるほど相関は弱くなる．

○　単に相関係数と言えば，通常，以下に述べるピアソンの積率相関係数のことを指す．

ｘk の平均を m， ｙk の平均を n とおくと
r =
　ア)　r　が１，-1に近いほど相関は強くなる．
　イ)　r　が0に近いほど相関は弱くなる．

○　相関係数の検定（母相関係数ρ=0の検定）
　標本相関係数をｒ，母相関係数をρとするとき，ρ=0ならば無相関となる．そこで，ρ=0という帰無仮説を立てて，これが棄却されるときに「相関がある」と考える．
　ｒの値に対して
が自由度n-2のｔ分布に従うことが知られており，これを用いて検定できるが，もっと簡単に，その結果がｒ表：「ｒの値→棄却域の値」としてまとめられているので，これを利用する．
　r表では，各自由度（標本の組の数-2），有意水準αに対して，この値よりも |r| が大きければρ=0が棄却され，相関があると判断できる．α=0.05でρ=0が棄却されれば，「相関がある」，α=0.01でρ=0が棄却されれば「強い相関がある」と考える．（ただし，両側検定用の値なので，片側検定に用いるときはαとして２倍の値を用いる．）		 ピアソンの積率相関係数：[概要]
i)　絶対温度で測れば強い相関が見られるが，摂氏温度で測れば相関がないというような，原点の取り方で相関が変わるのを防ぐために，x,yとも平均を原点にする．
ｘ’ = ｘk - m， y’ = yk - n
ii)　ｘ’y’＞0となる点が多ければ，正の相関
　ｘ’y’＜0となる点が多ければ，負の相関が見られる．
　ｘ’y’＞0，ｘ’y’＜0となる点が同程度ならほとんど相関がない．

==> Σｘ’y’すなわちΣ(ｘk - m)(yk - n)を候補にする．
iii)　cmの単位で測ると，ｍメートルの単位で測ったときよりも，100倍×100倍の相関が出てくるというようなスケールの取り方で相関が変わるのを防ぐため，各々の大きさで割る．
　==>　r =
■例と答■
例
　別添ファイル（ correl.xls ）Sheet1のデータについて，　(1) 散布図を作成し，　(2) 相関係数を求め，無相関の検定をし，(3) 回帰直線を表示し，　(4) 回帰直線の方程式を求め，　(5) 推定値の標準誤差，　(6) x=20のときのｙの予測値，　 (7) x=20のときのｙ予測値の95%信頼区間　を求めよ．
（解答）
(1) まず散布図を作成し，(3)近似曲線の追加：線形近似とする．

(4) 近似直線の右クリックで回帰直線の方程式，Ｒ-2乗を表示
もしくは
　回帰直線の方程式は
a =
b = n - am
で確かめることができる．
もしくは
　=SLOPE(B2:B51,A2:A51)　によりa = 1.428，=INTERCEPT(B2:B51,A2:A51)　により b = 10.48


(2) 相関係数は
　　=SQRT(R2の値)により r = 0.827
もしくは，
　　メニューから「ツール」→「分析ツール」→「相関」により r =0 .827
もしくは
　　=CORREL(A1:A41,B1:B41)　により r = 0.827
もしくは
　　=PEARSON(A1:A41,B1:B41)　により r = 0.827
もしくは
　r =
を表を組み立てて求める． r = 0.827
　
　ｒ表より，自由度38で有意水準α=0.05の場合， r = 約0.28，α=0.01の場合r=約0.36　だから，0.827は強い相関がある．
　
(5)　推定値の標準誤差は =STEYX(B2:B41,A2:A41)　により　Se = 3.128
もしくは
　y=1.6964x-0.3196　または　TREND($B$2:$B$41,$A$2:$A$41,A2,1)　で各々のｘに対するｙの推定値を求め（これをy’とおく），
Se =
(6) y=1.6964x-0.3196 にx=20　を代入して y’ = 33.609
もしくは
=TREND($B$2:$B$41,$A$2:$A$41,20,1)　で y’= 33.609
もしくは
　=FORCAST($B$2:$B$41,$A$2:$A$41,20,1)　で y’= 33.609

(7) 33.609±1.96Se = 33.609±6.131により　27.478≦y’≦39.740
■相関と因果関係■～♪作者の読書感想文
　「事例でわかる統計解析の基本」(*1)（柳谷晃著／日本能率協会マネジメントセンター）p.161には，夏の気温や湿度とビール売上高の相関が紹介されている．また，「やさしい統計学」(*2)（田畑吉雄著／現代数学社）p.123には各都市の街灯の数と性犯罪の発生件数の相関が紹介されている．この話を元に相関と因果関係について考察してみる．
　まず，右の図式1においては，相関関係，因果関係とも認められる．(*1)では気温よりもむしろ湿度との関係が強いことが示されているが，ここでは話を簡単にするために気温のみに絞る．
　気温が高くなっても，子どもはビールを飲まない．牛乳や清涼飲料水が売れる．そこで，夏の気温と牛乳，清涼飲料水の売れ行きも相関，因果関係ともありそうだ．クーラーを使うので，電力消費量も同様．（図式2）

　次に，各都市を比較すると，街灯の数と性犯罪の数には相関がある．しかし，街灯を減らしても性犯罪は減らない．(*2)		 (図式1)　相関：○，因果関係：○
　夏の気温・湿度→ビールの消費量


（図式2）

相関関係：①②③④どの組合わせにも有り
因果関係：①→②（または③または④）に有り


（図式3）　②③は相関：○，因果関係：×
　逆に，因果関係があるが，相関関係はない例を考えてみる．母馬：Ａが子馬：Ｂを産み，子馬：Ｂが競馬で優勝したとき
　自然的な因果関係としては，ある出来事Ａが起こらなければ，他の出来事Ｂは起こらなかったといえるとき，ＡはＢと因果関係があるとする．そこで，母馬：Ａが子馬：Ｂを産んだことは，Ｂが優勝したことと自然的な因果関係がある．
　次に，馬の世界では，母が強いと子どもも強いことが多いので，子馬：Ｂの成績と子馬：Ｃの成績にも相関がある．しかし，因果関係はない．		 （図式4）　①②の因果関係：○，②③の相関関係：○△
　①母馬：A　→　子馬：Ｂ　→　競馬の成績②
　　　　　　　　└→子馬：Ｃ　→　競馬の成績③
.
（まとめ）

　「あることが起こらなければ，他のあることが起こらない」といえるときは，これらの間には，自然的な因果関係がある．しかし，そのことが起こればかなりの確率で他のことが起こるといえる場合しか社会的な因果関係は認められない．

　右図式①④⑤のように因果関係がある事象（直系の子孫となる事象）には，相関が認められるものが多い．（因果関係があっても相関がないこともある--優秀な親の子どもが必ず優秀とは限らない．）右図式5の⑤⑥のように共通の親事象から発生しているもの同士にはどちら側を説明変数にしても相関が認められることがある．しかし，⑤⑥には因果関係はない．（それぞれの子どもが親に似ているだけ）

　社会現象は複雑に関連し合っているので原因・結果の関係は必ずしも明らかでないことが多い．むしろ，右の⑦⑧⑨のように関連があるのかどうか分からないことの方が多い．このとき，相関関係が認められれば様々な角度から因果関係を調べていくきっかけとなる．　		 （図式5）

相関と因果関係，例２つずつ：
（相関，因果関係が認められるもの）
ペルー沖の海水温の高低→世界的な異常気象
１日当りの喫煙本数×年数→肺ガンの発生率

（両論があり，よく分からないもの）2007.3現在
丸山ワクチン→?ガンの治療
ＦＭ電波の異常，地震雲→?地震の予知

（相関を調べてほしいという段階）2007.3現在
インフルエンザ治療薬の服用→?異常行動
携帯電話の電波帯域→?脳腫瘍の発生

（部分集合の取り方で相関の有無が分かれるもの）
入試の成績→入学後の成績
（限られた部分集合を合格させる学校：相関なし，ほぼ全員合格させる学校：相関あり）
(言い伝え)
「弘法さんと天神さんは仲が悪い．」･･･「弘法さん」とは弘法大師の縁日（毎月21日）のこと，「天神さん」とは菅原道真の縁日（毎月25日）のこと．表題の言い伝えは，21日が晴（雨）なら25日は雨（晴）になるということを表わしている．長年の経験から気づいた負の相関関係を表わしたものと考えられる．
　冬場の天候は三寒四温といわれ，４日後は天候が変わる確率が高いといえば因果関係についての今日的な説明になる．

（因果関係はないが，相関関係は考えられるもの）
「他人に風邪をうつせば自分は直る」という俗説．･･･上記図式3と同様に，①に「数日間の経過」があって②③に各々その結果として「自分について，日にち薬で風邪が直ってくる」ことと，「他人について，保菌・潜伏期間が経過して風邪の症状が出る」ことが平行して起こるという経験を持つ人が多いかもしれない．
確率統計のメニューに戻る 高校数学のメニューに戻る
■［個別の頁からの質問に対する回答］[相関係数，回帰直線について／16.12.8］
アンケート項目４，の手前、 『ｒ表より，自由度48で』というくだりですが、もしかしたら３８、ではないでしょうか。 公開されているデータのｎがｎ＝４０だからです。
＝＞［作者］：連絡ありがとう．訂正しました．