← PC用は別頁→ 印刷用PDF版は別頁

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック
◎内側の色を変えるには，次の色をクリック
◎標準文字色を変えるには，次の色をクリック
鼠 銀 黒 青 紺 茶 緑 桃


== 置き換えによる展開 ==

○　置き換えによる展開とは

　同じ式が２回以上登場するとき，これらに名前を付けて１文字で表わすと，「見やすく」「間違いにくく」なる．ここでは２回以上登場する式を１文字で置き換えて展開の計算を行うことを考える．
例１
(a+b+c)2 のように３つ以上からなる項の２乗は，教科書の基本公式にないからと言って，(a+b+c)(a+b+c) に直して「総当たり」で展開していると大変
　これを a+b=A と置き換えると，(A+c)2 になり展開公式が使えて，
(a+b+c)2
_____=(A+c)2
_____=A2+2Ac+c2
元に戻すと
_____=(a+b)2+2(a+b)c+c2
_____=a2+2ab+b2+2ac+2bc+c2 形を整えると
_____=a2+b2+c2+2ab+2bc+2ca

※　置き換えに用いた文字 A は自分が付けた名前なので（他の人は別の名前をつけてもよいので），
(a+b+c)2=A2+2Ac+c2
を答にしてはいけない．

※　慣れてくると，置き換える文字の代わりに　（　）を使って次のように変形することもできるが，「どれがよい」ということはない．「自分に分かりやすい＝間違いにくい」と思う方法でやればよい．
(a+b+c)2
_____=(a+b)2+2(a+b)c+c2
_____=a2+2ab+b2+2ac+2bc+c2
_____=a2+b2+c2+2ab+2bc+2ca
※　計算が多いので，１題解くだけなら「力まかせ・総当たり・単純計算主義」でバラバラにした方が速いと考える人がいるかもしれない．しかし，何題も解くときは，やはり置き換え方式が有利．さらに，バラバラにする方式では，展開の逆=因数分解（右辺を左辺に戻す）のときに見通しが立たなくなる． 　
「総当たりで」展開してもできないことはないが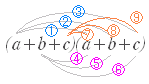
次のような問題が幾つも登場すると困ってしまう･･･
(a−b+c)2 , (a−b−c)2 , (x2+x+2)2 , (x2−2x+5)2 ···


　実は，次の展開はかなりよく登場するので「準公式」として覚えてしまうことが多い．
【準公式】　　(a+b+c)2=a2+b2+c2+2ab+2bc+2ca

　この立場に立つと，以下の問題は直ちに解決する．

・ (a−b+c)2=a2+(−b)2+c2+2·a·(−b)+2·(−b)·c+2ca
_________=a2+b2+c2−2ab−2bc+2ca
・ (a+b−c)2
上の変形を見ていると知恵がついてきて，直ちに分かるようになる（符号と係数を変えるだけ）
________=a2+b2+c2+2ab−2bc−2ca
・ (a−b−c)2=a2+b2+c2−2ab+2bc−2ca
【要約】
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
(a−b+c)2=a2+b2+c2−2ab−2bc+2ca　(←bが－)
(a+b−c)2=a2+b2+c2+2ab−2bc−2ca　(←cが－)
(a−b−c)2=a2+b2+c2−2ab+2bc−2ca　(←b, cが－)
　(−a+b+c)2は(a−b−c)2と同じ
　(−a−b+c)2は(a+b−c)2と同じ
　(−a−b−c)2は(a+b+c)2と同じ
※a2+b2+c2−2ab−2bc−2caとなるものはない！
（そのわけ）
−2ab → a, bは異符号
−2bc → b, cは異符号
を前提とすれば，a, cは同符号になる
　結果のまとめ方：上の例のように
a → b → c → (a)
のサイクルにして書くことが多い．それ以外はダメだいうことではないが，一定の規則で並べると「書く人も・読む人も」「見やすく・間違いにくい」．
　しりとりで一周させて
♪～「こぶた」→「たぬき」→「きつね」→「ねこ」
の順に並べるということ．

例２
　(x+1)(x+2)(x+3)(x+4) のように一見同じものがないように見える式でも（ x を A に置き換えても無駄 ） 工夫次第で同じ式が作れることがある．
　(x+1)(x+4)(x+2)(x+3) のように組み合わせると，
　(x2+5x+4)(x2+5x+6) になるので，x2+5x=A とおけば簡単に展開できる．
（２次と１次）の組を考える例
　　(x+1)(x+3)(x−5)(x−7) → x2−4x=A とおくと
(A−5)(A−21) になり A2−26A+105

（２次と定数項）の組を考える例
　　(x+1)(x+2)(x+3)(x+6) → x2+6=A とおくと
(A+7x)(A+5x) になり A2+12xA+35x2


■問題　次の式を展開せよ．
･･･　　♪♪浴びるほどやって得意ワザに入れる感じで♪♪

(1)　　(a−2b+3c)2
=a2+b2+c2−ab−bc+ca

(2)　　(x+y+1)(x+y−2)
=x2+y2+xy−x−y−

(3)　　(a−2b+3c)(a+2b+3c)
=a2−b2+c2+ac

(4)　　(x2+xy+y2)(x2−xy+y2)=x+xy+y


(5)　　(x−1)(x+1)(x+3)(x+5)
=x4+x3+x2−x−

(6)　　(x3−x2+x−1)(x3+x2−x+1)
=x6−x4+x3−x2+x−


［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません．下記のリンクを使ってメニューに戻ってください．
...（携帯版）メニューに戻る

...（PC版）メニューに戻る

■［個別の頁からの質問に対する回答］[置き換えによる展開について／18.8.19］
（4）はx^4-x^2×y^2+y^4ではないのですか？
＝＞［作者］：連絡ありがとう．そこに解説がありますので読んでください．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／18.4.24］
(X－1）(X+1）=
＝＞［作者］：連絡ありがとう．それがどうしたのですか？質問内容を言葉で言わないと，通じません．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／18.3.3］
とても分かりやすいものとなっています。 大変参考になりました。 今後もよろしくお願いします。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／18.1.25］
ここまでは一応、順調に来れました。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.12.01］
このページの問題を解いたのにも関わらずトップのメニューのところに印が付きません
＝＞［作者］：連絡ありがとう．なぜかそのページのPC版で記録用のページ番号が抜けていましたので訂正しました．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.8.23］
６番の問題、難しく感じました。二乗する、一つずつ掛け合わせいく事が、理解出来ました。
＝＞［作者］：連絡ありがとう．最後の問題なのでそれなりに骨のある問題になっていたかも
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.8.17］
自分なりのやり方ではなく、解答どうりの方法が出来ようになると、いいです。
＝＞［作者］：連絡ありがとう．そこそこは程度問題ですが（ものすごく遠回りの答案とか，体力仕事だけの単純計算主義はあまりよくないが），模範解答も１つの見本なので，自分なりのやり方でよいと思いますが．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.8.15］
６番の問題が難しいです。理解は出来ました！
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.8.15］
全て解答してから答えを出さないと、全て答えが出てしまう。
＝＞［作者］：連絡ありがとう．携帯版の方は１つずつ採点するようになっていますが，PC版の方はまだ直っていなかったようです．（お急ぎの場合は携帯版を見てください）
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.6.13］
（６）について質問があります。何度やっても－１以外符号が反対になってしまうのですが、解き方が間違っているのでしょうか？
＝＞［作者］：連絡ありがとう．この質問の仕方は間違っています．何度やっても･･ということよりも，どのようにやったのか，つまり自分の答案を書かないとどこが間違っているのかを回答するのは無理です．
【よくある間違い】
a2−(b−c)2=a2+(−b+c)2と考えている人は，符号が全部逆になります．
a2−(b−c)2=a2−(b2−2bc+c2)=a2−b2+2bc−c2
a2+(−b+c)2=a2+b2−2bc+c2
です．
各問題に解説がついているのでそれを読んでください．
■［個別の頁からの質問に対する回答］[置き換えによる展開について／17.2.20］
(5)に関しての質問です。 X3(Xの3乗)－X2(Xの2乗)＝A、X－1＝Bとおいたのですが、 (A－B)(－A－B)で計算すると答えが違ってきます。 この置き換えは間違いなのでしょうか？
＝＞［作者］：連絡ありがとう．質問が間違っています･･･(6)の問題でしょう．次に，その置き替えはできません．