|
→ スマホ用は別頁
== t検定 ==
【要約】
2群の平均に有意差があるかどうかを調べる検定は,伝統的には,次の3つに分けて行う
(1) データに対応があるとき ⇒ 対応のあるt検定
なお,最近では「データに対応のない場合には,等分散を仮定できるか否かに関わらずウェルチのt検定で行う」という立場も有力です.(2) データに対応がなく,2群間に等分散性が仮定できるとき ⇒ スチューデントのt検定 (3) データに対応がなく,2群間に等分散性が仮定できないとき ⇒ ウェルチのt検定 すなわち,
(1) 対応のあるt検定
の2つに分ける
(3) ウェルチのt検定 この教材では,対応がないときのt検定について,上記の学説の優劣を判断していません.読者に判断してもらうための材料を提供しているレベルですのでよろしく.(2群の要素数が僅差であるような場合を除けば,多くの場合にWelch検定の方が自由度がかなり小さくなるので,レポートを見れば,どちらのt検定を用いたのかは分かると言われています.)
|
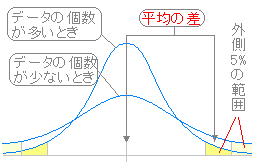
【平均の差の検定:要約】 ◎ 前提:以下において母集団は正規分布に従うとする. 幾つかのグループの「平均の差」が偶然的な誤差の範囲にあるものかどうかを判断したいとき,データの個数が少ないときは偶然的な誤差の範囲も大きくなるが,データの個数が多くなると平均の差が大きな値となることはめったにない. 同一の母集団からの標本と見なしたときに2つのグループの平均の差が両側5%の確率の範囲に入るようなことはめったになく,このような場合は平均に有意差があるとして異なる母集団から取り出された標本であったと見なせる. t検定 t検定は2つのグループの平均の差が偶然誤差の範囲内にあるかどうかを調べるものである.
データの個数と偶然の範囲
 |
|
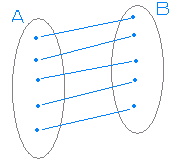
(1) データに対応があるときのt検定 「それぞれの被験者が2つのテストA,Bを受けたときの平均点の比較」のようにグル-プAのデータとグループBのデータに同一被験者のデータという対応があるとき,これら2つのテストの平均点の差に有意差があるかどうかは「対応があるときのt検定」を用いる. データに対応があるときは,単にデータの個数が等しいだけでなく,対応するデータ間の差を求めることができるので,それらの差の平均と分散から有意差を判断できる.
データに対応があるとき
|
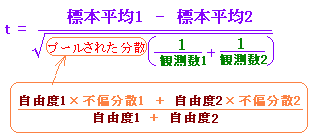
(2) データに対応がないときのt検定 A) 従来から行われてきた方法は,次のように2つのグループの分散が等しいか否かによって,t検定の種類を分けて行う.
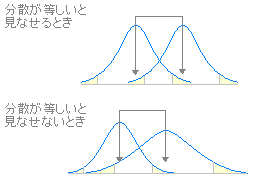
分散がほぼ等しいと見なせる場合と分散が等しいとは見なせない場合に応じて,各々「分散が等しいときのt検定」「分散が等しくないときのt検定」を適用する.
分散が等しいかどうかの判断はF検定によって行う.
データに対応がないとき
|
||||||||||
|
B) 最近有力となっている方法は,分散が等しいか否かに関わらずウェルチの検定で行うものです.
従来から行われてきた方法については,次のような問題点を指摘されることがあります.
ⅰ) 2つのグループの分散が「等しい場合」「等しいかどうか疑わしい場合」「等しくない場合」があるときに,従来の考え方でF検定によって「等しくない」とされるのは,等しいという帰無仮説が棄却される場合に限られるが,実際には,「ほとんどの場合は疑わしい」のに「等しいと見なせる場合の公式を当てはめる」ことになっていて,つじつまが合わない. ⅱ) F検定の上にt検定を重ねて用いると,誤差が膨らんでくる. そこで,2つのグループの分散が等しいか否かに関わらずウェルチの検定を1回で行うものです.
|
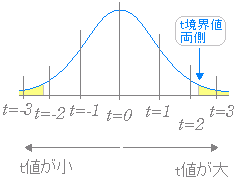
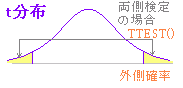
※t分布において「外側5%の範囲にあれば同一母集団からの標本ではなく,有意差があると考える」. 95%信頼区間の外側に来る確率を p とするとき,
※F分布において「確率が上側5%の範囲にあれば分散が等しくないと考える」.
※ 与えられた自由度に対するt値が95%の信頼区間の外にある=外側の確率が5%以下 → 平均値に有意差がある.
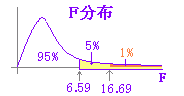
(有意水準5%がよく使われる.) 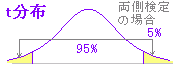 ※ 分母分子の自由度に対応するF値が95%の信頼区間の外にある=外側の確率が5%以下 → 分散に有意差がある. (有意水準5%がよく使われる.F分布表[5%点]は分母分子で決まる2つの自由度に対して上側確率が5%となるFの値を示している.) 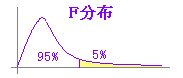 |
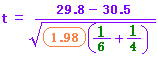 = -0.73
= -0.73


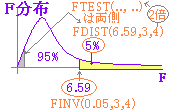
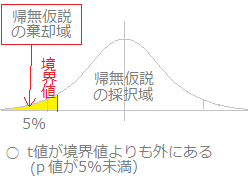 • Excelワークシート関数のTINV()は両側検定の場合のt値を返すので,この問題のように片側検定のt値を求めるには,確率を2倍しておく(両側で5%の図を片側で5%にする)
• Excelワークシート関数のTINV()は両側検定の場合のt値を返すので,この問題のように片側検定のt値を求めるには,確率を2倍しておく(両側で5%の図を片側で5%にする)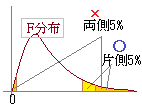 しかし,ほとんどのF検定で,分散に有意差があると見なすときは,一致する場合は含めないので,F検定は片側検定で行う.
しかし,ほとんどのF検定で,分散に有意差があると見なすときは,一致する場合は含めないので,F検定は片側検定で行う.