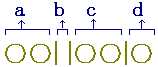重複組合せ
■重複組合せ《解説》
※順序が違えば別物として数えるのが「順列」，順序だけ違うものは同じものして数えるのが「組合せ」
【例】
異なる2つのものａ，ｂから重複を許して3つとる方法
重複組合せ
　
重複順列
{a,a,a}
{a,a,b}
{a,b,b}
{b,b,b}
計４通り
←→
←→
←→
←→
 (a,a,a)　　　　　　　1通り
(a,a,b),(a,b,a),(b,a,a)３通り
(a,b,b),(b,a,b),(b,b,a)３通り
(b,b,b)　　　　　１通り
計８通り
○ 重複組合せの記号
　異なるｎ個のものから重複を許してｒ個とってくる組合せの総数を
nHr
で表します.
（注意）
※異なるものが何個（ｎ）あって，それらから何個（ｒ）取ってくるのか，どちらが ｎ でどちらが ｒ かを「慎重に」見極めることが大切

≪表１≫
A3210
B0123
　例えば，２人の人A,Bに同質のお菓子3個を分ける方法の数を数えたいものとする．ただし，どちらかが１つももらわない場合や全部もらってしまう分け方も許されるものとする．
===> いずれも≪表１≫のように４通りになる．

≪表２≫
{A,A,A}
{A,A,B}
{A,B,B}
{B,B,B}

　これは，異なる２人の名前を重複を許して3回呼ぶ場合の数に等しい．（名前が呼ばれたらお菓子がもらえると考える）
===> ≪表２≫のように４通りになる．
※これらは
「異なる２つのものから重複を許して３個取って来る」場合の総数となっており，
「異なる３つのものから重複を許して２個取って来る」場合の総数
≪表３≫
A211000
B010210
C001012
≪表４≫
{A,A} , {A,B} , {A,C} , {B,B} , {B,C} , {C,C}

とは違う．

○ 重複組合せnHrの公式を作るには

1. 重複順列の総数から割り算で求めることはできない
　▼まず思いつくのは，順列と組合せの対応ですが
　順列　ｎＰｒ÷ｒ！　→　組合せｎＣｒ
　のように，順列をｒ！で割ると組合せになりますが，重複順列ｎΠｒと重複組合せｎＨｒの関係は単純ではありません.
　これは，上の例のように重複組合せの中身ごとに並べ方の総数が変わり，倍率が一定のｒ！にならないからです.
【例】
異なる2つのものａ，ｂから重複を許して3つとる方法
重複組合せ
　
重複順列
{a,a,a}
{a,a,b}
{a,b,b}
{b,b,b}
計４通り
←→
←→
←→
←→
 (a,a,a)　　　　　　　1通り
(a,a,b),(a,b,a),(b,a,a)３通り
(a,b,b),(b,a,b),(b,b,a)３通り
(b,b,b)　　　　　１通り
計８通り
　そこで，重複順列から逆算して重複組合せを求めるという方針を推し進めても公式は得られません.

2. 具体例で考える
【例】
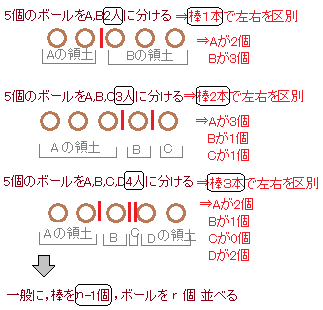
　４人の子供に重複を許して５個の同質のボールを分け与える方法

　４人の子供を区別するために，右図のように縦棒|を３個置きます．

　右図のｂのように，仕切り棒が隣り合う場合は0個を表すものとします．

　このようにすれば，○５個，｜３個同じものがあるときの順列の総数が求める数値となります.
例　ａ=2,b=0,c=2,d=1となる分け方

（縦棒の両側は各々ａ君，ｄ君のボールです.- - このように，両端を含む４か所を区別するときは，(植木算で！)仕切り棒は4-1＝３本です.）
→右上に続く
　《公式にする方法》
　上の答は＝56　ですが，しばしば登場するものに，毎回図を書くのは大変なので，通常ｎＣｒへの読み替え公式を利用します.

　５はボールの数（ｒ）です.３は子供の数（ｎ）-1です.
したがって，この結果は
と表すことができます.
　ところで，分母に登場する２つの数ｎ−１とｒの和が分子ｎ＋ｒ−１に等しいような式は，いつでもＣに直すことができます.
【例】

，
　そこで，＝n+r-1Ｃｒ　となります.

3. 公式ができた
《ＨをＣに直す公式》
ｎＨｒ＝n+r-1Cｒ

(-1は植木算になるから)

⇒　この公式を使って，Ｈが登場したら機械的にＣに直してから数字にする．
≪植木算：ｎ−１になる理由をしっかり覚えよう！≫

○ 例題と解答
【例1】
　次の値を求めなさい.　　4H5

　（答案）
4H5=4+5−1C5=8C5==56・・・（答）
※「５個の同質のボールを４人の子供に分ける方法（１つももらえない子供がいるいる場合も含む）」に対応
※「異なる４個のものから重複を許して５個とってくる組合せの総数」と書くと，上記とgiveとtakeが逆に見えますが，まったく同じです.
※「４人の子供の名前を５回呼ぶ方法としても同じ（重複を許してかつ１度も呼ばれない子供がいる場合も含む）」
【例2】
　次の値を求めなさい.　　5H3

　（答案）
5H3=5+3−1C3=7C3==35・・・（答）
※「５人の子供に３個の同質のお菓子を分ける方法（１つももらえない子供がいるいる場合，全部もらってしまう子供がいる場合も含む）」
※「３個の同質のお菓子を５人の子供に分ける方法（１つももらえない子供がいるいる場合，全部もらってしまう子供がいる場合も含む）」

（参考）
○ 重複組合せではｎよりもｒの方が大きいことがある
※順列の総数nPrや組合せの総数nCrでは，とってくるものの数rはn以下でなければなりませんが，重複順列や重複組合せでは，同じものを何回使ってもよいので，重複順列の総数nΠrや重複組合せの総数nHrにおいてはrがnよりも大きい場合があります．
≪ありえない≫
3P4
2C5
≪ありえる≫
3Π4=34=81
2H5=6C5=6


○ 重複組合せの記号には，なぜH を使うのか
　次数（掛けてある文字の数）が等しい多項式を「同次多項式」「斉次多項式」という（Homogeneous polynomial）．重複組合せは，同次多項式の異なる項の数として登場するので，このＨを記号にしたもの．

上の【例】では２つの文字で作られる３次式が何通りあるかを示しています．
(a+b)3を展開してできる同次式の総数は
=aaa+aab+aba+baa+abb+bab+bba+bbb
順序を区別すれば，項の数は「重複順列」
23=8通りになる
=a3+3a2b+3ab2+b3
文字の部分が同じものを同類項として整理すれば，文字の組合わせはa3 , a2b , ab2 ,b3で2H3=4種類になる

《問題》　左の値に等しいものを，右から選びなさい．
（ルール：左の式を一つクリックし，続けて答をクリックしたとき，合っていれば消えます．
･･･間違ったときは，ヒントを読む場合も読まない場合もやり直すボタンを押せば再開できます．




















■［個別の頁からの質問に対する回答］[重複組合せについて／17.8.19］
≪植木算：ｒ−１になる理由をしっかり覚えよう！≫ のところ、題と最終行のnとrが逆だと思います
＝＞［作者］：連絡ありがとう．おっと，この間違いはダメージが大きい，謝罪の記者会見級です．訂正しました．
■［個別の頁からの質問に対する回答］[重複組合せについて／17.5.14］
お世話になっています。 上において質問と回答のところに >問題を選択した時に、背景色が濃く、明暗比が悪いために見づらい の意見があったので私も確認してみました。私にも十分見えますが、選択した場合に背景色が白から青になるのでコントラストの関係で見えにくくなるということではないかと思います。 他の端末や色弱の人にどう見えるかについてはわかりません。 ※なんとなく気になったので意見を送信させていただきました。回答は不要です。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[重複組合せについて／17.5.4］
文系の自分でも良く理解できます 解説がとても分かり易いです。 ただ、重複順列 重複組み合わせの公式で、何故マイナス1なのか、文章からは、理解できません 理由を教えて頂ければうれしいです
＝＞［作者］：連絡ありがとう．質問・要望は重複順列の頁からですが，内容が重複組合せの頁に関してですので，重複組合せに関する質問として回答します．マイナス１になる理由は，先頭の例で絵を使って述べているように，植木算の考え方でｎ個のものを区別するにはｎ−１本の仕切り棒がいるからです．
■［個別の頁からの質問に対する回答］[重複組合せについて／17.4.22］
よくわからない
＝＞［作者］：連絡ありがとう．できれば助けてやりたいと考えていても，どこがどう分からないのかを述べないと，助けようがありません．
■［個別の頁からの質問に対する回答］[重複組合せについて／17.3.10］
例題が少ない
＝＞［作者］：連絡ありがとう．例題は理屈の部分で，重複組合せの総数は組合せの総数に読み替えて解くということさえ分かれば，後は重複組合せを組合せに直す練習をするのみです．問題は10題あります．サブメニューから文章題も選べます．
■［個別の頁からの質問に対する回答］[重複組合せについて／16.11.29］
問題を選択した時に、背景色が濃く、明暗比が悪いために見づらい
＝＞［作者］：連絡ありがとう．そんなことはありません．よく見えます--きっぱり