|
← PC用は別頁
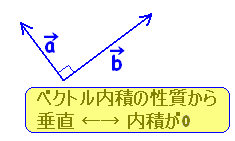
【ベクトルの平行条件】
(解説)2つのベクトル となるための必要十分条件は (
「存在すること」という表現が分かりにくいとき,「t(またはs)が求まればよい」と考えればよい。
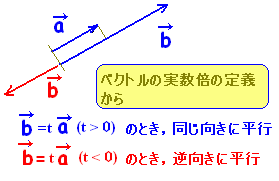
【例1】
(解答)より (x, −4)=t(−3, 6) 成分に分けると −4=6t…(2) (2)より これを(1)に代入するとx=2…(答)
【例2】
(解答)ベクトル 求めるベクトルを が条件になる. (1)から(x, y)=t(3, −4) → x=3t, y=−4t これを(2)に代入すると (1)によりt>0だから |