|
■[ケーリー・ハミルトンの定理2] ※ ケーリー・ハミルトンの定理は,使えない場面では使わないことが大切です。 [要点] ● ケーリー・ハミルトンの定理から <いえること> 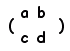 について, について,
p=a+d,q=ad−bcとおくと <いえないこと> |
<例:出てくる場面>
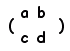 について, について,
A2-7A+6E=0のときa+d=7,ad−bc=6といえるか? → いえない。 |
|
■[ケーリー・ハミルトンの定理2] ※ ケーリー・ハミルトンの定理は,使えない場面では使わないことが大切です。 [要点] ● ケーリー・ハミルトンの定理から <いえること> 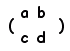 について, について,
p=a+d,q=ad−bcとおくと <いえないこと> |
<例:出てくる場面>
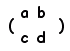 について, について,
A2-7A+6E=0のときa+d=7,ad−bc=6といえるか? → いえない。 |
| まず,次の関係に注意します。
「xA+yE=0」のときx,yの値は? (ア) A≠kEのとき (Aが単位行列の定数倍でないとき) となり矛盾するから, x=y=0 x=0,y=0でなくとも成立する。 (1,1成分をみれば十分) |
<上の例の場合>
A2-7A+6E=0・・・(1)与えられた条件
ケーリー・ハミルトンの定理から成立
(1)-(2)
(a+d−7)A+(6-ad+bc)E=0 (ア) A≠kEのとき (2k−7) k2-7k+6=0 k=1,6 各々A2-7A+6E=0は成立し, a+d=2,ad−bc=1・・答
及び,a+d=12,ad−bc=36・・答 |
|
例題1 A= 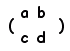 が A2-A-6E=0 を満たすとき a+d,ad−bc の値を求めなさい。 が A2-A-6E=0 を満たすとき a+d,ad−bc の値を求めなさい。
答案例 条件から,A2-A-6E=0・・・(1) ケーリー・ハミルトンの定理からA2-(a+d)A+(ad-bc)E=0・・・(2) (1)-(2) (a+d-1)A+(-6-ad+bc)E=0・・・(3) (ア) A≠kEのとき, (3)より,a+d=1,ad-bc=-6・・・答(イ) A=kEのとき, A= |
A= 条件から,A2+xA+yE=0・・・(1) ケーリー・ハミルトンの定理からA2-5A+2E=0・・・(2) (1)-(2) (x+5)A+(y−2)E=0 A≠kE だから・・・(記述式答案では,一言断ることが大切) x=−5,y=2・・・答 |
| 1 |
 |
| 2 |
 |