|
※ ケーリー・ハミルトンの定理は,使えない場面では使わないことが大切です。 [要点] ●A= 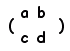 について,ケーリー・ハミルトンの定理から について,ケーリー・ハミルトンの定理から
<いえること>
p=a+d,q=ad−bcとおくと
<いえないこと>
a+d=p,ad−bc=q ×× |
|
<例(*):出てくる場面>
A= 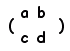 について, について,
A2-7A+6E=0 のとき a+d=7,ad−bc=6 といえるか? → いえない。 |
|
※高卒から大学初年度向けの「ベクトル,行列」について,このサイトには次の教材があります.
*** ベクトル *** ↓ ●ベクトル.行列の超基本 ●ベクトルの直交条件 ●1次独立,1次従属,基底,次元,核,階数 *** 行列 *** ↓ ●逆行列(1) ●逆行列(2) ↓ ●転置行列,対称行列,対角行列,三角行列 ●行列の階数 *** 行列式 *** ●行列式(1) ●行列式(2) ●行列式(3) *** 一次変換 *** ●行列と一次変換 ●点の像と原像 *** 固有値 *** ↓ ●固有値.固有ベクトルの定義 ↓ ●固有値と固有ベクトル(1) ●固有値と固有ベクトル(2) ●行列の対角化とは ●行列を対角化するには |
|
※ ケーリー・ハミルトンの定理は,使えない場面では使わないことが大切です。 [要点] ●A= 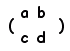 について,ケーリー・ハミルトンの定理から について,ケーリー・ハミルトンの定理から
<いえること>
p=a+d,q=ad−bcとおくと
<いえないこと>
a+d=p,ad−bc=q ×× |
|
<例(*):出てくる場面>
A= 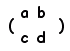 について, について,
A2-7A+6E=0 のとき a+d=7,ad−bc=6 といえるか? → いえない。 |
|
まず,次の関係に注意します。
「
(ア)
(証明)このとき,原式に 以上より,
(イ)
(証明)すなわち は \(x=0,y=0\) でなくとも成立する。
(1,1)成分をみれば
たとえば, |
| <上の例(*)の場合> 与えられた条件から A2−7A+6E=0…(1)
ケーリー・ハミルトンの定理からA2−(a+d)A+(ad−bc)E=0…(2)
以上の2つが成立することは言える.そこで (1)-(2) (a+d−7)A+(6-ad+bc)E=0
(ア) A≠kEのとき a+d=7,ad−bc=6・・答
(イ) A=kEのとき
A=
(2k−7)
(1,1)成分,(2,2)成分から
(2k−7)k+6-k2=0
A=k2-7k+6=0 k=1,6 各々 A2-7A+6E=0
は成立する.
a+d=2,ad−bc=1・・答
及び,a+d=12,ad−bc=36・・答
このようにして,A≠kEのときはa+d=7,ad−bc=6が成り立つが,
A=kEのとき,a+d=7,ad−bc=6以外の値になるので, A2-7A+6E=0 のとき a+d=7,ad−bc=6 とは限らない |
|
※A=kEの可能性がある問題は,結局,成分計算となる
例題1
A= 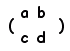 が A2-A-6E=0 を満たすとき a+d,ad−bc の値を求めなさい。 が A2-A-6E=0 を満たすとき a+d,ad−bc の値を求めなさい。
答案例 条件から,A2-A-6E=0・・・(1) ケーリー・ハミルトンの定理からA2-(a+d)A+(ad-bc)E=0・・・(2) (1)-(2) (a+d-1)A+(-6-ad+bc)E=0・・・(3) (ア) A≠kEのとき, (3)より,a+d=1,ad-bc=-6・・・答(イ) A=kEのとき, A= |
|
※A=kEの可能性がない問題は,一言断ればケーリー・ハミルトンだけで済む
例題2
答案例
A= 条件から,A2+xA+yE=0・・・(1) ケーリー・ハミルトンの定理からA2-5A+2E=0・・・(2) (1)-(2) (x+5)A+(y−2)E=0 A≠kE だから・・・(記述式答案では,一言断ることが大切) x=−5,y=2・・・答 |
|
[問題]
≪1≫
条件から,A2-4A+3E=0・・・(1) ケーリー・ハミルトンの定理からA2-(a+d)A+(ad-bc)E=0・・・(2) (1)-(2) (a+d-4)A+(3-ad+bc)E=0・・・(3) (ア) A≠kEのとき, (3)より,a+d=,ad-bc=・・・答
(イ) A=kEのとき,
A=
(2k-4) (1,2)成分,(2,1)成分は成立。 (1,1)成分,(2,2)成分から 2k2-4k+3-k2=0 k2-4k+3=0 k=3,1 k=3のとき,a+d=,ad-bc=・・答 k=1のとき,a+d=,ad-bc=・・答 |
|
≪2≫
|
|
|