|
○ はじめに 1次独立,1次従属は1つのベクトルがもっている性質ではなく,ベクトルの組がもっている性質である. 列ベクトルの組(もしくは行ベクトルの組)から成り立っている行列を考えると,1次独立・1次従属という性質は行列がもっている性質に対応する. ○1 簡単な例でイメージ作り (1) 例えば 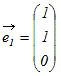 , ,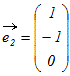 , ,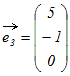 という3つのベクトルについては, という3つのベクトルについては,
=2+3 (2) しかし, 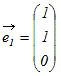 , ,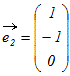 , ,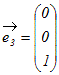 という3つのベクトルの場合,
ベクトルは,これらの1次結合 という3つのベクトルの場合,
ベクトルは,これらの1次結合
[←なぜなら]
このときベクトルは右図2のように2つのベクトル , で作られる平面上にない.k1+k2 の形に書けるためには
k1+k2=0
が成り立たなければならないが,これを満たすk1,k2は存在しない.
k1−k2=0 0 k1+0 k2=1 この頁では,ベクトルの組が与えられたときに「その中の少なくとも1つのベクトルが他のベクトルの1次結合で表される場合=1次従属」と「その中のどのベクトルも他のベクトルの1次結合では表せない場合=1次独立」を扱う. |
|
◇1次結合とは◇
k1+k2+ ··· +kn のように幾つかのベクトルの定数倍の和で表されるものをこれらのベクトルの1次結合という. 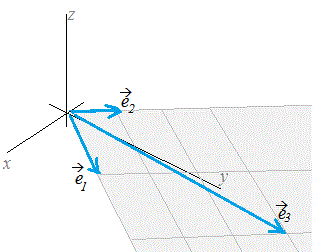 図1 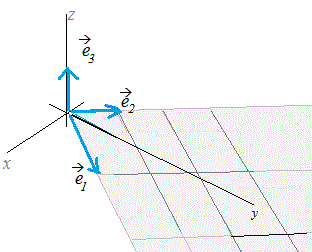 図2 |
|
○2 1次独立,1次従属の定義 ベクトルの組 , , ··· について
k1+k2+ ··· +kn=
ならば
k1=k2= ··· =kn=0
が成り立つとき,これらのベクトルの組 , , ··· , は1次独立であるという.1次独立でないとき1次従属であるという. k1=k2= ··· =kn=0のとき,k1+k2+ ··· +kn=は当然成立する.ここでは,「k1+k2+ ··· +kn=が成り立つのはk1=k2= ··· =kn=0の場合に限られる」ときに,そのようなベクトルの組を1次独立と定義するということである.
上では1次独立を定義して,そうではない場合を1次従属としていることになるが,1次従属の方から定義してそうでないものを1次独立としてもよい.この場合,
少なくとも1つのkp (1≦p≦n)について, kp≠0かつk1+k2+ ··· +kn=が成り立つときを1次従属と定義することになる. このとき,  |
|
◇「すべて」と「ある」に関するド・モルガンの法則◇
「すべてのxについてp(x)が成り立つ」の否定は「あるxについてp(x)が成り立たない」
「あるxについてp(x)が成り立つ」の否定は「すべてのxについてp(x)が成り立たない」 ⇔ 否定にするにはp(x)の部分を否定に変えるだけでなく,「すべて」と「ある」も入れ替える.
「ある」ベクトルについて
「すべての」ベクトルについて |
|
例1 次のベクトルの組が1次独立かどうか調べよ.
(解答)
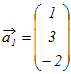 , ,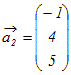 , ,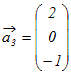
x+y+z= …(1) 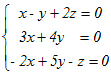 …(2) …(2)
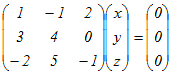 …(3) …(3)
ここで,(3)の係数行列をAとおくと,その行列式はdet(A)=39 (≠0)となり,逆行列が存在することになり, 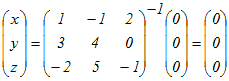
※ 後に述べる定理により,方程式の個数が未知数の個数よりも多いときは必ず1次従属となる. 方程式の個数が未知数の個数と等しいときは逆行列が0であるか否かで調べられる. 方程式の個数が未知数の個数よりも少ないときも形だけでは決められず中身を調べる必要がある.
例2 次のベクトルの組が1次独立かどうか調べよ.
(解答)
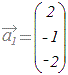 , ,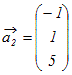 , ,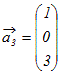
x+y+z= …(1) 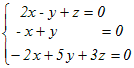 …(2) …(2)
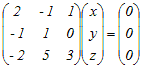 …(3) …(3)
ここで,(3)の係数行列をAとおくと,その行列式はdet(A)=0となり,逆行列が存在しない.例えばx=1, y=1, z=−1のとき(*1) 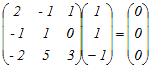
(*1)の求め方: ◇筆算で,いわゆる不定解として求めるとき◇
2x−y+z=0 …(1)
(2)よりy=(x) …(2’) …y , zをxで表す(xについては解かない)ことにして,解かないことを忘れないようにカッコに入れる−x+y=0 …(2) −2x+5y+3z=0 …(3) これを(1)(3)に代入
(x)+z=0 …(1’)
(1’)(3’)は同じ式だから(3’)は不要y=(x) …(2’) (3x)+3z=0 …(3’)
y=(x)
よって
z=(−x)
x=t
とするとx=y=z=0以外の解となる.y=t z=−t (t≠0) たとえば (x, y, z)=(1, 1, −1)はこれを満たす. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
◇Excelで,ソルバーを使って求めるとき◇ (1) 次の表のようにA1:C3に列ベクトルの組からなる行列を入力しておく. (2) E1:E3にx,y,zの仮の値を入力しておく. (3) G1:G3に行列の積 Aの結果を書き込んでおく. (4) ソルバーに依頼する作業は「 G1=G2=G3=0となるようにE1:E3の値を定めよ」ということであるが,ソルバーの目的セルは1つのセルしか指定できないので,次の関係式を利用して1つにする.
G1=G2=G3=0 ⇔ G12+G22+G32=0
(5) このままソルバーを走らせると,E1=E2=E3=0という自明解の方に向かって安易に流れてしまうので,これを防ぐための「制約条件」を指定する. 1) ほとんどの場合,ベクトルの大きさが1となるように指定すればよいが,この場合,下記の表のように小数で結果が出ることになる. 2) 数学の問題として解いていて「整数値で結果を出したい」ときは,制約条件としてE1:E3のうちの1つの値を1に指定するとそれらの比率が分かりやすい.(0:3:5のように第1成分が0になる場合もあるので,第1成分を1にすれば必ずできるとは限らない.)
【ソルバーを用いた不定方程式の解き方:まとめ】
(1) E1:E3には仮の値を適当に入力しておく. (2) G1に行列Aと列ベクトルE1:E3の積の計算式を書き込む. =MMULT(A1:C3,E1:E3) (3) (2)のままでは行列の積のうち1つの成分が書き込まれるだけなので,これをG1:G3に配列として書き込むために G1:G3を選択・反転させておいて,画面上にある数式バーをポイントして Ctrl+Shift+Enterとする. (4) G12+G22+G32=0によって,ソルバーの目的を設定するためにセルG5に =SUMSQ(G1:G3)と書きこむ. (5) E1:E3に整数値の解が得られるように,ソルバーの制約条件としてたとえばE1=1という条件を考えておく. (*) ソルバーを走らせる. Excel2002→ツール→ソルバー(Excek2007→データ→ソルバー) ・目的セル:G5,目標値:値0,変化させるセル:E1:E3,制約条件:E1=1 ⇒ 以上により,(1, 1, −1)の解が得られる. ※ 以上の方法でパラメータ(任意定数)1個を含む不定解が求められる.
例3 A1:D4に示される行列の4個の列ベクトルが1次独立かどうか調べよ.
(解答)
行列式が0となるから1次従属(Excel上のA1:D4までにデータがあるときは =MDETERM(A1:D4)により分かる) 証明としては上の答案だけでよいが,具体的に不定解の解ベクトルをF1:F4に示したいとき ・F1:F4の書式を「分数.3桁増加」に指定 ・ソルバーを走らせるときに制約条件としてF2=1を指定(試してみるとF1=0になるから) ⇒ E1:E4の結果が次のようになれば,
これより (x1, x2, x3, x4)=t(0, 3, 5, −7) (t≠0) 1つの例を示すには (x1, x2, x3, x4)=(0, 3, 5, −7) |
|
○ 以下においてn次元空間からn次元空間への1次変換のみ扱う.このとき1次変換を表す行列はn次正方行列となる.
○3 1次独立なベクトルの組による表し方の一意性
(証明)ベクトルの組 , , ··· が1次独立であるとき,あるベクトルをそれらの1次結合で表す方法はただ1通りに定まる. すなわち,
=s1+s2+ ··· +sn
=t1+t2+ ··· +tn
ならば s1=t1, s2=t2, ···, sn=tn が成り立つ.(※ 恒等式の係数比較法のときと同様に,対応する係数が等しいといえる.)
s1+s2+ ··· +sn=t1+t2+ ··· +tn
ならば
(s1−t1 )+(s2−t2 )+ ··· +(sn−tn )=
と変形できる.ここで, , , ··· は1次独立であるから,
s1−t1=0, s2−t2=0, ···, sn−tn=0
が成り立つ.よって, s1=t1, s2=t2, ···, sn=tn
|
|
※ n次元ベクトルをn個の1次独立なベクトルの組 , , ··· で表しているときは,次のように考えてもよい. これらのベクトルの組で作られる行列をAとおくと  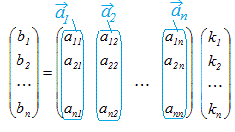
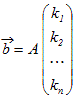
ベクトルの組 , , ··· が1次独立であるとき,行列Aには逆行列A−1が存在し,この式の両辺に左からA−1を掛けると 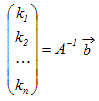
(※ の像がだから,逆変換が存在すればの原像がになる.) |
|
○4 基底と次元
○ ベクトルの組 , , ··· によって k1+k2+ ··· +kn ○ 空間Vを生成する1次独立なベクトルの組 , , ··· を空間Vの基底という. ○ 基底となるベクトルの組は一般に幾通りもあるが,そのうちn次元空間の基本ベクトルの組 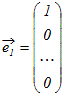 , , ,… , ,… , 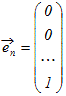
○ 1つの空間Vを生成する1次独立なベクトル(基底)の個数は,基底のとり方によらずに一定である.これを次元といい ※ n個の成分をもつベクトル 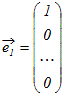 , , ,… , ,… , 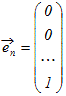
|
|
例 ○1で示したベクトル 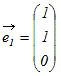 , ,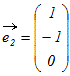 , ,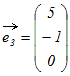 はxy平面を生成するが,これらのどのような1次結合もz成分が0でないベクトルを表すことはできない.これらのベクトルは1次従属で3次元空間の基底ではない. はxy平面を生成するが,これらのどのような1次結合もz成分が0でないベクトルを表すことはできない.これらのベクトルは1次従属で3次元空間の基底ではない.
 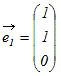 , ,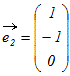 , ,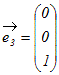 という3つのベクトルの1次結合はxyz空間のすべてのベクトルを表すことができる.これらのベクトルは1次独立で3次元空間の基底になっている. という3つのベクトルの1次結合はxyz空間のすべてのベクトルを表すことができる.これらのベクトルは1次独立で3次元空間の基底になっている.
 |
|
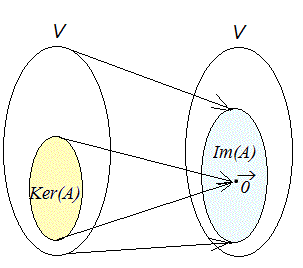
○5 像と核,行列の階数
(解説)n次正方行列Aで表される1次変換によってn次ベクトルがn次元ベクトルに移されるとき
(1) に移されるベクトル全体をAによる1次変換の核といい Ker(A) で表す.(kernelの略) (2) Aによる像(像の全体)を Im(A)で表す.(Imageの略) このとき
(3) dim(Im(A))(Aによる像の次元)をrank(A)で表し,行列(1次変換)Aの階数という.
【重要】
(4) dim(Ker(A))+rank(A)=n が成り立つ.
(*) det(A)≠0ならば(正則行列ならば)
dim(Ker(A))=0
が成り立つ.
rank(A)=n (1) の原像がkernel 記号で表せば,Ker(A)={ | A= }
Ker(A)は,加法と定数倍について閉じた1つの空間をなしている.
(2) 生成される空間(値域)全体がIm(A), ∈Ker(A) ならばA= , A=により
1) A(+ )=だから+∈Ker(A)
2) A(k )=k A=だからk∈Ker(A) 記号で表せば,Im(A)={ A | ∈V }
Im(A)は,加法と定数倍について閉じた1つの空間をなしている.
, ∈Im(A) ならばA= , A=となる , が存在し
1) +=A(+A )=A(+ )だから+∈Im(A)
2) k=k A=A(k )だからk∈Im(A) (3) 1次変換によって作られる空間の次元がrank(A)で,rank(A)は行列Aの列ベクトルのうちで1次独立な列ベクトル(または行ベクトル)の個数に対応している. (4) 1次変換によって作られる空間の次元は,元の空間の次元からに縮退する定義域の次元(kernelの次元)を引いたものに等しい. (*) 正則行列すなわち逆行列が存在するときは,det(A)≠0で,Ker(A)はだけからなる0次元の空間となり,行列Aの1次独立な列ベクトル(または行ベクトル)はn個ある. |
 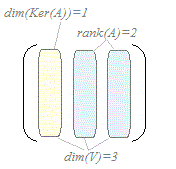 n次元空間Vの基底はn個ある.そのうちKer(A)の次元をrとし,その基底を , , ··· , とおく.残りの基底を , , ··· , とし,その次元をsとする.(ただし,r+s=n) このとき,A= , A= , ··· , A=で定義されるベクトル , , ··· , がIm(A)の基底となることを示せばよい.すなわち,これらがIm(A)を生成しかつ1次独立であることを示せばよい.
1) [← Im(A)を生成すること]
∈Im(A)ならば=Aとなるベクトルが存在する. Vの任意のベクトルはその基底 したがって, A=A(p1+p2+ ··· +pr+q1+q2+ ··· +qs ) =A(p1+p2+ ··· +pr )+A(q1+q2+ ··· +qs ) ここで , , ··· , はKer(A)の基底だから A(p1+p2+ ··· +pr )= が成り立ち A=A(q1+q2+ ··· +qs )=q1+q2+ ··· +qs となる. よって , , ··· , によって生成される.
2) [← 1次独立であること]
よって, すなわち ゆえに, |
|
例1
(解答)行列A= 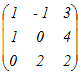 で表される1次変換について で表される1次変換について(1) Ker(A)を求めよ.(基底を1組示せ) (2) Im(A)を求めよ.(基底を1組示せ) (3) rank(A)を求めよ. (1) 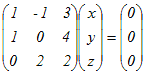 を解くと を解くと(x, y, z)=t(−4, −1, 1)となるから 基底(−4, −1, 1)によって生成される空間 …(答) (2) 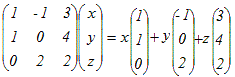
(3, 4, 2)=4(1, 1, 0)+(−1, 0, 2)となることに注意すると,(*)
(3) dim(Ker(A))=1だからrank(A)=3−1=2 …(答)
x(1, 1, 0)+y(−1, 0, 2)+z(3, 4, 2) =x(1, 1, 0)+y(−1, 0, 2)+z{ 4(1, 1, 0)+(−1, 0, 2) } =(x+4z)(1, 1, 0)+(y+z)(−1, 0, 2) x+4z=s , y+z=tとおくと =s(1, 1, 0)+t(−1, 0, 2) 2つの基底(1, 1, 0) , (−1, 0, 2)によって生成される空間 …(答) (*)からこの結果を直接述べてもよい.
例2
(解答)行列A= 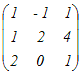 で表される1次変換について で表される1次変換について(1) Ker(A)を求めよ. (2) Im(A)を求めよ.(基底を1組示せ) (3) rank(A)を求めよ. det(A)=−9 ( ≠0 ) だから (1) Ker(A)={ } …(答) (自明解のみをもつ) (2) 基底 (1,1,2), (−1,2,0), (1,4,1)によって生成される空間(3次元空間全体)…(答) (3) rank(A)=dim(Im(A))=3 …(答) |
|
例3
(解答)○1 (1)で示した3つの列ベクトルからなる行列A= 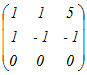 で表される1次変換について で表される1次変換について(1) Ker(A)を求めよ.(基底を1組示せ) (2) Im(A)を求めよ.(基底を1組示せ) (3) rank(A)を求めよ. (1)
x+y+5z=0
を変形してx, yを(z)で表すと((z)については解かないことにする)
x−y−z=0
x+y=(−5z)
x−y=(z)
x=(−2z)
したがって (x, y, z)=(−2z, −3z, z)=t(−2, −3, 1)y=(−3z) よって,基底(−2, −3, 1)によって生成される空間 …(答) (2)
x
基底(1,0,0), (0,1,0)によって生成される空間 …(答) +y +y +z +z =x  +y +y +z{ 2 +z{ 2 +3 +3 } }=(x+2z)  +(y+3z) +(y+3z) x+2z=s , y+3z=tとおくと s  +t +t さらに,s+t=p , s−t=qとおいて p 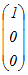 +q +q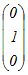 と書ける. と書ける.
(3) rank(A)=dim(Im(A))=2 …(答) |