|
○ 2次方程式の解と係数の関係
2次方程式 ax2+bx+c=0 ( a≠0 ) の2つの解を α,β とすると,
α+β=− αβ= が成り立つ. |
[ 証明を見る ] → (この定理は何の役に立つのか) 例1 3x2+5x+1=0 の2つの解を α,β とするとき,α+β,αβ の値を求めたいとき α,β= だから
α+β=+=−
が成り立つ.αβ=×== しかし,問題を見ただけでこの答は − , だと分かる. |
|
次の空欄を埋めよ.なお,答が負の分数になるときは,分子を負の数にして答えよ. |
|
| ■ 問題2 次の空欄を埋めよ. |
|
|
■ 問題3 次の空欄を埋めよ. |
|
|
○ 解の公式を用いた因数分解 2次方程式 ax2+bx+c=0 ( a≠0 ) の2つの解を α,β とすると,
※ 「2次方程式の解の公式」により,どんな2次方程式でも解を求めることができるので,さらにこの公式を用いれば,どんな2次式でも因数分解できる.ただし,「2次方程式の解の公式」からは,無理数解や虚数解が出る場合もあるので,「複素数の係数まで使えば,どんな2次式でも因数分解できる」という意味になる. 例題 次の式を複素数の範囲で因数分解せよ. x2+x+1=0 の解を求めると x= になるから,これらを α,β として因数分解の公式に代入すると x2+x+1=(x−)(x−) =(x+ )(x+) |
(証明について) 教科書においては通常,解と係数の関係を用いてこの因数分解公式が示される. このページの別添証明のように,この因数分解公式を用いて解と係数の関係を示すときは,循環論法にならないように気をつけて,因数分解公式を先に示すべきであるが,教材の並べ方については通常の教科書の順に従った.(つまり,別添証明で証明済みである.) ■因数分解に用いる係数の範囲■ 「 x4−4 を因数分解せよ.」というような問題では係数にどの範囲の数まで用いるかによって,次の(ア)(イ)(ウ)の3通りの因数分解が考えられる. (ア) x4−4=(x2−2)(x2+2) (イ) x4−4=(x−)(x+)(x2+2) (ウ) x4−4=(x−)(x+)(x−i)(x+i) (ア)のように,係数に有理数の範囲の数まで用いて因数分解することを「有理数の範囲で因数分解する」という.同様にして,(イ)のように係数に実数の範囲の数まで用いて因数分解することを「実数の範囲で因数分解する」といい,(ウ)のように係数に複素数の範囲の数まで用いて因数分解することを「複素数の範囲で因数分解する」という. ○ 複素数の範囲で因数分解すれば,整式は1次式の積に書ける. ○ 何も断りがないときは,有理数の範囲で因数分解すればよい. 例 通常は,「 x3−1 を因数分解せよ.」というような問題では, x3−1=(x−1)(x2+x+1) でよく, x3−1=(x−1)(x+ )(x+) までは求められない. ○ 有理数の範囲ですでに1次式に因数分解されているものは,実数の範囲に広げても結果は同じである.実数の範囲を複素数の範囲に広げるときも同様. |
|
■ 問題4 (1) x4−x2−2 を実数の範囲で因数分解したものを右から選べ. |
ア (x2+1)(x2−2) イ (x2+1)(x−)(x+) ウ (x−i)(x+i)(x−)(x+) |
|
(2) x4+2x3−3x2−2x+2 を有理数の範囲で因数分解したものを右から選べ.解説 f(x)=x4+2x3−3x2−2x+2とおくと,f(1)=0, f(−1)=0だから因数定理により(x−1)(x+1)=x2−1で割り切れる.
割り算を行うとf(x)=(x2−1)(x2+2x−2)となるが,x2+2x−2を因数分解すると無理係数になるから,そこで止める |
ア (x2+2x−2)(x2−1) イ (x2+2x−2)(x+1)(x−1) ウ (x+1+)(x+1−)(x+1)(x−1) |
| (3) x4−9 を複素数の範囲で因数分解したものを右から選べ. |
ア (x2+3)(x2−3) イ (x2+3)(x+)(x−) ウ (x+i)(x−i)(x+)(x−) |
|
○ 2数を解とする2次方程式の作成 2つの解 α,β が与えられているとき,これらが解となる1つの2次方程式は
|
例 α= , β= を解とする2次方程式を求めると α+β=1 , αβ= より, x2−x+=0 が1つの2次方程式であるが,両辺に9をかけて, 9x2−9x+2=0 とするのが普通である. 一般に,2次方程式の両辺を定数倍しても解は変らないから, a(x−α)(x−β)=0 としてもよい |
|
■ 問題5 |
|
| 例題 2x2+5x+1=0 の2つの解を α,β とするとき,2数 2α,2β を解とする2次方程式を求めよ. (答案)(定数倍を除いて決まる) 2x2+5x+1=0 の解と係数の関係から |
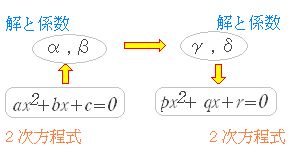 ※ 与えられた方程式についての「解と係数の関係」から,求める方程式の「解と係数の関係」を求める. |
| ■ 問題6 |