→ 携帯版
■[個別の頁からの質問に対する回答][微分係数,連続,微分可能 について/18.12.31]
図がめちゃくちゃ
=>[作者]: 連絡ありがとう.何の話をしているのかなと不思議に聞こえましたが,Chromeでは数学座標→物理座標の変換がSVGグラフィックスの仕様通りに働くが,Safariでは変換されずに,上下逆になるという事のようです.
■[個別の頁からの質問に対する回答][三角関数の値 について/18.12.26]
tan1°が0.0175と出たので計算してみたのですが、正解にならないのでtan1°=0.01745506492で計算してみると1/0.01745506492=57.2899616577。
1/0.0175=57.1428571429と比べると結構誤差が出てしまったのですが
=>[作者]: 連絡ありがとう.高校数学の三角関数表は,小数点以下4桁までの小数で表示することになっていますので,tna1°=0.0175です.正解にならなかったということについては,全角で入力したなど,別の原因が考えられます.なお,有効数字の桁数を変えれば,数字が変わるのは当然のことで,何桁使っても(仮に100万桁解答しても)真の値とは一致しません.三角関数表として示されている値を使って示さなけばダメです.(この話を言う必要があるのか?)
■[個別の頁からの質問に対する回答][条件付き確率 について/18.12.26]
センター対策に抜群でした!
このサイトを見つけることができて良かったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/18.12.25]
問題形式で面白かったです。不等式の性質の3番は、a>bではなく、a1<ではないでしょうか。(解説部分)
=>[作者]: 連絡ありがとう.質問の最後の部分に書き損じがありますが,話は分かりましたので訂正しました.
■[個別の頁からの質問に対する回答][センター試験問題 2次関数 について/18.12.23]
http://www.geisya.or.jp/~mwm48961/koukou/center_quadratic_fun1.htm
上記URLの【センター試験 2009年度:数学I・A(本試験) 第2問】において、ツ - ニの解説で、途中式に一部誤りがあります。
-正- (3a-9)ではなく、(3a-8)です。
(イ) -2≦a≦2のとき
...
9a2-27a+8=0
(3a-1)(3a-8)=0
-誤-
(イ) -2≦a≦2のとき
...
9a2-27a+8=0
(3a-1)(3a-9)=0
P.S.
高校数学を数年ぶりに解きなおしているのですが、当サイトの解説が非常に分かり易く助かっております。
これからも引き続き、サイト運営を続けていただければと存じます。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][指数方程式 について/18.12.17]
良いところはヒントがあること、悪いところは簡単なのでもっと応用が欲しい
=>[作者]: 連絡ありがとう.iPadでは左上にあるサブメニューが見えないかもしれませんので,メインのメニューを見て,指数方程式の次のページを選んでください.
■[個別の頁からの質問に対する回答][多項式・有理関数・無理関数の不定積分 について/18.12.17]
問題を解いたてクリックしたら、数問終わるまで正不が分からなかった…
=>[作者]: 連絡ありがとう.正誤いずれの場合も解説が出ますので,それを読めば,正誤は分かるはずです.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/18.12.15]
問題4の(4)の答えが違うのではないのでしょうか。私の間違いだったらすいません
=>[作者]: 連絡ありがとう.解説が出ますので読んでください.あなたはどう考えるのですか.
■[個別の頁からの質問に対する回答][1次不定方程式の整数解 について/18.12.14]
例2の527x-403y=31で、yの値が4となっていますが正解は-4です。途中で符号を間違えているかと。
P.S. いろいろな方法が載っているこのページは、数学と真剣に向き合う生徒にとってはとても助けになると思います。
=>[作者]: 連絡ありがとう.ゴール寸前でコケてしまったようです.実に,百里の道は九十九里が半ばのようです.訂正しました.
■[個別の頁からの質問に対する回答][位置ベクトルの応用 について/18.12.12]
全問正解したときに桜?の木が出るのが気持ちいいですね
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/18.12.11]
めちゃくちゃためになりました!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の計算 について/18.12.11]
とてもよかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数計算1 について/18.12.11]
確認問題がとても助かりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重積分--積分順序の変更 について/18.12.09]
とってもわかりやすかったです!!!!
基本的なことなので教科書では省かれていてわからなかったので本当に助かりました…
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][不定積分 について/18.12.07]
∫k(f(x)+g(x))のときはどうなりますか。
=>[作者]: 連絡ありがとう.
本当に分からないのですか?それとも数学の土台を疑っているのですか?
■[個別の頁からの質問に対する回答][指数法則 について/18.12.06]
少し複雑な問題も欲しいですが、授業より分かりやすいです。
=>[作者]: 連絡ありがとう.本当は左端にサブメニューがあって,前後の項目が選べるようになっているのですが,PC用のページを携帯で読んでおられるので,少し難しい問題のあるページへのリンクが見えていないようです.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値(区間や関数が変わる場合) について/18.12.05]
塾の宿題を解くのに役にたちました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/18.12.05]
対数関数の不定積分の例の(1)の答案途中
dtが一つ余分ではないですか?(3行目末)
=>[作者]: 連絡ありがとう.訂正しました- - 台本なしで,ぶっつけ本番の勧進帳風に書いていると,勢い余って間違うことがあるようです.
■[個別の頁からの質問に対する回答][相関係数,回帰直線 について/18.12.05]
難しいですね。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][合成関数 について/18.12.04]
合成する際、与えられた不等式の中も合成するのでしょうか?
ex) f(x)=x/(1-x) , x<1/2
⇒ x→f(x)だから、f(f(x))=x/(1-2x) , f(x)<1/2?
=>[作者]: 連絡ありがとう.定義域が定められている関数を合成するときに,合成関数の定義域は変化するのかという質問のようですが,その通りです.
例のように,
のとき,合成関数
とその定義域を求めよという問題でしたら,
定義域は,
■[個別の頁からの質問に対する回答][二項定理,多項定理 について/18.12.04]
最高
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/18.12.03]
ジョーカーが残るようにゲーム形式になっていたのがよかったです。
楽しめました!
=>[作者]: 連絡ありがとう.できる方の感想かもしれません
■[個別の頁からの質問に対する回答][対称式の変形 について/18.12.02]
難しかった~
=>[作者]: 連絡ありがとう.難しかったが最後までやり切ったということでしたら,よかったと思いますが
■[個別の頁からの質問に対する回答][累乗根 について/18.11.29]
問題文の答えを記入する欄に問題があるようです。
問題内に2か所答える欄がある場合、1個目は問題なく記入できますが2個目の欄には記入が不可能なようです。
=>[作者]: 連絡ありがとう.当教材の推奨ブラウザは:◎Chrome, ○Safari,▲IE,×Firefox,×Edgeの順です.
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/18.11.29]
例題3の頂点の座標は (3, -3)ではないですか。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][組合せ について/18.11.29]
余りわかりませんでした
=>[作者]: 連絡ありがとう.少数意見かも?
愛知県[ コノハズクさん/18.11.28]
次の微分方程式の解き方で同次系を用いて解くことはわかるのですが、計算過程が分かりません。※補足としてu=1/y^2として計算します。
y'+y/x=xy^3
=>[作者]: 連絡ありがとう.同次系(形)→ベルヌーイ形.まず
このページ を見てください.次に,そのページの内容に沿って,以下のように変形します.
の両辺を
で割る
とおくと
これを代入して,
の微分方程式にすると「次の線形微分方程式」になる
右辺を0とした同次方程式の1つの解は
だから,非同次方程式の解は
■[個別の頁からの質問に対する回答][数列の極限(∞/∞型) について/18.11.28]
テスト前でよく分からなかったのでとても助かりました!
ありがとうございます( ¨̮ )
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/18.11.28]
自分が高校生の時に指導要領になかったものなので一から勉強しています。
練習問題もあり基礎から理解していけるので活用させていただいています。
ありがとうございます。
=>[作者]: 連絡ありがとう.複素数平面や行列は,指導要領に出たり入ったりで,習う方も教える方も苦労が多いようです.
■[個別の頁からの質問に対する回答][集合の要素 について/18.11.27]
参考書よりも理解しやすくありがたいです。
活用させていただいています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/18.11.26]
ありがとうございます
=>[作者]: 連絡ありがとう.
大阪府[まやまやさん/18.11.26]
男子4人、女子4人の合計8人を横一列に並ばせるとき、次の問いに答えよ
女子が2人ずつ隣り合う(4人が隣り合う場合は除く)ような並び方は何通りあるか。
6P6x(4C2x2x2)-5P5x4P4
どうしてこれだと誤答になるのか理解できません。
教えて下さい
=>[作者]: 連絡ありがとう.問題を単純化すると,かゆい場所を拡大して見せられます:「男子1人,女子4人の計5人を一列に並ばせるとき,女子が2人ずつ隣り合う(4人が隣り合う場合は除く)ような並び方は何通りあるか」
あなたの考え方では,
になりますが,この
という箇所が違います.女組A,男,女組Bと3つのものを並べる方法
のそれぞれについて,女2組の分け方
,女組Aの中での並べ方:×2,女組Bの中での並べ方:×2とすると,例えば女組A(a,b),男,女組B(c,d)となる場合と女組B(a,b),男,女組A(c,d)となる場合を重複して数えていることになります.実際には,(女a,女b)男(女c,女d)のように,女子2人-男子-女子2人となる並び方は
通りです.
解き方1) 男子の並べ方
×女子2組の入る空席2by2のとり方
×女組Aの入り方
×女組Bの入り方
=1×1×12×2=24
解き方2) 女組の入る空席2by2は同じものとすると,女組,女組,男の並べ方
×女の入り方4!−女4人組,男の並び方
=72−48=24
この方法を真似して元の問題を解くには,
解き方1) 男子4人の並べ方:4!,その各々について,両端を含む隙間5個のうち空席2by2(同じもの)を選ぶ方法は
,その各々について女子を並べる方法は4!
解き方2) 女組2by2,男4の6個のもののうち女組は同じものとする.これらの並べ方
,その各々について女子の並べ方は4!----これらのうち,女子が4人とも隣り合っている並び方5!×4!
後の計算は自分で考えてください.
■[個別の頁からの質問に対する回答][極座標 について/18.11.25]
練習問題もあり、わかりやすかった。
直交座標があるのになぜ極座標が生まれたのかを知りたかった。
=>[作者]: 連絡ありがとう.一様な重力場における自由落下(地上でのボールの運動)のような現象を記述するには,直交座標が便利ですが,太陽の周りの惑星の運動や原子核の周りの電子の運動のような現象を記述するには,円や楕円を念頭に置いた極座標(球座標)の方が便利でしょう.
■[個別の頁からの質問に対する回答][常用対数 について/18.11.23]
覚えるべきところがとても分かりやすく書いてあるので何を覚えればいいのかがすぐに分かって理解することが出来ました。類題や入試問題も付いていて凄く助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作19・・・定数係数2階常微分方程式 について/18.11.23]
MaximaについてはいろいろHPにあるが、やり方ばかりを描いているものが多く分かりにくかった。一方このサイトは解こうとする例が初めに一般的な表記で書かれ、入力と出力が書かれているだけでなく、筆算やMaximaの出力との違い・理由、注意点などが大変丁寧に書かれていて、分かりやすかった。最後までやる気が途切れることなくできました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/18.11.22]
(6)なのですが、問題が (x3-x2+x-1)(x3+x2-x+1) で
+xと-x1、-1と+1で符号が違うのに x2-x+1= Aとなる理由を教えてください
=>[作者]: 連絡ありがとう.解説に書いてある通りです.(採点しないと解説は出ません)
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/18.11.20]
要点2.異なる2つの虚数解を持つときの(解説)部分について、
虚数表示から実数表示にするためにy3とy4を考えていますが、y3とy4がなぜ解として成立するのでしょうか。
y1とy2の線形結合であれば虚数で割ろうが問題ないのでしょうか。
=>[作者]: 連絡ありがとう.その通りです.そのページの先頭に書いていますように,2階微分方程式の2つの1次独立な解を
とするとき,それらの1次結合
は,
が実数であっても,虚数であっても
は,
になるから0になります.つまり,解になります.
また,虚数で「割る」ということにこだわる必要はないでしょう.
のような割り算になっていても,割り算は逆数のかけ算だから
となって,一次結合の一種です.
■[個別の頁からの質問に対する回答][行列の積の定義 について/18.11.20]
問題1-2で、問題は「左からかけることができる」になっていますが解説は「右からかけることができるのは」となっています。この解説は問題に対して正しいですか?
=>[作者]: 連絡ありがとう.おっとと,1のメッセージを2が使い回しでコピペしていたので,同じものになっていました.訂正しました.
■[個別の頁からの質問に対する回答][群数列 について/18.11.20]
いつも勉強させて頂いています。
問題1の(2)で初項n^2-2n+2,公差1,項数2n-1の等差数列の和を出すために公式に当てはめても
正解とされている「(2n-1)(n^2-n+1)」とはならないと思いましたのでご連絡差し上げました。
此方の思い違いであれば申し訳無いのですが一度ご確認下さい。宜しくお願いします。
=>[作者]: 連絡ありがとう.まず公式を確認しますと,初項
,公差
,項数
の等差数列の和は
だから,初項
,公差
,項数
の等差数列の和は
となります
■[個別の頁からの質問に対する回答][負の指数 について/18.11.20]
マイナスのマイナス乗は
どうなるんですか。
=>[作者]: 連絡ありがとう.簡単な例で具体的に考えると,分かり易くなります.
のとき,
だから,たとえば
など丁寧に計算したら何でもないことです.
■[個別の頁からの質問に対する回答][ベクトルの定義,大きさ,向き について/18.11.20]
大変参考になりました😂
またお願いします🤲
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの平行条件,垂直条件 について/18.11.19]
例2は25t^2ではなく5t^2ではありませんか?
=>[作者]: 連絡ありがとう.両辺を2乗しているので,左辺は根号の中になります.
■[個別の頁からの質問に対する回答][展開公式1 について/18.11.19]
a(x+1)(x-1)
この展開を教えてくれますか?
=>[作者]: 連絡ありがとう.ax2 −a です.中学生ですか?
■[個別の頁からの質問に対する回答][重複順列 について/18.11.19]
さるのくだりが分かりません。助けて
=>[作者]: 連絡ありがとう.「六つ菓子五猿」は「むつかしござる」なので,自分が納得できる図を描くとよいでしょう**菓子から猿に矢印が向かっている図がよいでしょう
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/18.11.18]
よく利用させてもらっています。少し気になった点がありました。見るのにはあまり困りませんが、三角関数の積分公式の(4)に所々cosxがcotxになっています。直していただくとより見やすくなると思います!
=>[作者]: 連絡ありがとう.下端の感想と回答の欄にも書きましたが,その質問は時々ありますので,本文に注釈を書きました.
■[個別の頁からの質問に対する回答][n進数の演算 について/18.11.17]
高校一年生で、何が何だかわからなかったけど、先生よりわかりやすくて助かりました!ほんとにありがとうございます😻😻😻
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組合せ(文章題) について/18.11.16]
ヒントが必要ならば出せるようにしていただけたらもっと良くなると思います
常に出てると見てしまうので…
=>[作者]: 連絡ありがとう.教材で想定している使い方をしておられないように思えます.この教材は紙に印刷された問題集とは違います.選択肢をクリックすれば,採点結果と解説が出ます.対話型のプログラムです.これに対して,画面をただ見ているだけでは,何も出ません.そこのところを分かってもらえているかどうか
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/18.11.15]
公式を対応させる問題は、とてもありがたいです。
ピッタリ正解すると消えるのは、とても嬉しい。
ありそうで他にはない工夫です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][
点Aの周りの回転問1(5)の解説
1+i=(cos45°+i sin45°)だから
AC=AB×√2
∠CAB=45°
なぜこうなるか分かりません。教えてください。
=>[作者]: 連絡ありがとう.それは,【三角形の形状】という要点に書いたことそのものだから,そこをよく読めば分かります.
■?県[?さん][18.11.13]
2次関数のグラフと係数の符号について
全ての図が上下逆さまになっていませんか?
=>[作者]: 連絡ありがとう.
このページ の右上「凸とは,どこを見るのか?」を読んでください.
■[個別の頁からの質問に対する回答][負の指数 について/18.11.13]
良い
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/18.11.13]
字が小さくて読みにくい
=>[作者]: 連絡ありがとう.PV用のページを携帯で読んでいるから字が小さいのです.先頭に「→携帯用は別頁」と書いているので,それをタップしてください.(携帯を自動で判定して,自動で転送するプログラムにしていたこともありますが,そのようにすると「戻る」キーが使えなくなるので,各自の手動に戻しましたので悪しからず)
■[個別の頁からの質問に対する回答][2次関数のグラフと係数の符号 について/18.11.13]
私のPCでは以下のページのグラフが表示されないのですが、何が原因か判りますでしょうか?
=>[作者]: 連絡ありがとう.SVGグラフィックスに対応していないブラウザではグラフは表示されません.Chrome, Safariについては作動確認済みです.
■[個別の頁からの質問に対する回答][不定積分の漸化式 について/18.11.12]
とてもわかりやすい解答ありがとうございます。わからなかった問題を理解することができました。これからも活用しますヾ(@⌒ー⌒@)ノ
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数のグラフ について/18.11.12]
とても分かりやすい問題です!0の、答えの時、打って回答してますが❌なってしまいます
=>[作者]: 連絡ありがとう.解答が0であることと白紙答案とは違うので,0は0と答えなければなりません.
■[個別の頁からの質問に対する回答][ 2次関数のグラフと係数の符号 について/18.11.12]
問題の上に凸と下に凸は逆ではないんでしょうか
=>[作者]: 連絡ありがとう.どの問題の話かが書かれていませんが,凸という言葉の意味を「開いている」という意味に誤解していませんか.
左図のようなタンコブは下に凸ではなく,上に凸と言うことは,納得してもらえますか
■[個別の頁からの質問に対する回答][重複組合せ について/18.11.11]
今の高校生はこんなの習ってるんですかね?
資格取得のために数学を20年ぶりに勉強しています。
テキストでは意味不明でしたが、このページでよくわかりました。
ありがとうございます。
分らんことは簡単にネットで調べられる。ええ時代になったもんやなー。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][隣り合う並び方・隣り合わない並び方 について/18.11.09]
解説 例3の 端またはすきまに男子3人を並べる方法は5・4・3通り のところのイメージが分かりません、、、。3人の男子よりも空席のほうが多いのに、なぜP(順列)の考え方なのでしょうか?これは、空席の方を男子3人に割り当てるというイメージなのですか?
=>[作者]: 連絡ありがとう.左図のイメージで積の原則にそって確実に押さえるとよいでしょう.空席が5つあって,男Aの座り方は5通り,その各々について男Bの座り方は4通り,その各々について男Cの座り方が3通りだから5×4×3です.空席の方が男の子よりも多いので,男の子が座らない空席もあります.
「空席の方を男子3人に割り当てる」と軽く考えると混乱することがありますが,十分な練習をしてからなら
番号札のもらい方 のページを見てください.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/18.11.09]
客の満足度は順序尺度ではありませんか。
=>[作者]: 連絡ありがとう.客の満足度(非常によい:4,よい:3,悪い:2,非常に悪い:1)と「目盛が等間隔になっていると仮定」されている場合は間隔尺度に入れてよいでしょう.分析にあたって,このようなアンケート結果は順序尺度(非常によい>よい>悪い>非常に悪い)の大小の区別しかないと判断する分析者もあり得ますが,そうすると平均,分散,因子分析などほとんどの統計的手法が使えなくなります.アンケート結果を間隔尺度と「見なす」分析者は多いと思いますが,順序尺度なのか間隔尺度なのか,白黒をはっきりさせようぜという問題として考えるよりも,便宜的に間隔尺度と見なせば,このような結果が得られますといった報告書になっていると読むのでしょう.
■[個別の頁からの質問に対する回答][逆行列 について/18.11.08]
逆行列を求める例2でdet(A)を求める式の導出がわからなかったです。
=>[作者]: 連絡ありがとう.大学の方の教材は取りつきにくいので,
高校の方の逆行列 を先にやってください.
■[個別の頁からの質問に対する回答][平方完成(基本) について/18.11.08]
やり方や解説の書き方が読んだ時にわかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][
中間項を消す工夫の問題2の(2)の解説をもっと詳しく説明して頂きたいのですが宜しいですか?
=>[作者]: 連絡ありがとう.そこに解説が書いてありますが,分数計算は目で見ただけでは分かりにくいので,計算用紙を使って納得した方がよいでしょう.
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/18.11.08]
Edgeでは 解答後の色分けが 次回に引き継がれませんので、Chromeを使ってます。
=>[作者]: 連絡ありがとう.管理人は点検作業をChromeでやっています.ほとんどの読者はSafariかChromeのようです.
■[個別の頁からの質問に対する回答][展開公式 について/18.11.07]
大変面白い教材ですね。繰り返しチャレンジできるし、熱中すると時間を忘れてしまいます。50歳を越えた今 集中力の衰えと確認の怠りから凡ミスの連発ですが、若かりし日の思い出を振り返りながら楽しんでいます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][順列,組合せ(章末問題) について/18.11.05]
問題6 H の計算ミスがあります。
=>[作者]: 連絡ありがとう.HINTの欄の途中経過の入力ミスのことかな
■[個別の頁からの質問に対する回答][置き換えによる展開 について/18.11.04]
この手の問題はケアレスミスしないことですね。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][曲線で囲まれた図形の面積 について/18.11.04]
20/3ですか?
=>[作者]: 連絡ありがとう.何が?
■[個別の頁からの質問に対する回答][ベクトルの内積 について/18.11.03]
誤りですが、■Excelを用いた内積の計算のところで、
「※ ベクトルの成分が表5のように2つとも縦型に書かれているときは,内積を書き込みたいセルに =SUMPRODUCT(A1:A5,B1:B5) とすればよい.」とありますが、内容は表6のことを指しているようです。
=>[作者]: 連絡ありがとう.文章中の表の番号がズレていましたので訂正しました.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/18.11.03]
誤りですが、表1のなしの単価が120となっていますが、ベクトル成分では→a=(130, 150, 80, 150)と
150となっています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][ベクトルの大きさ(長さ) について/18.11.02]
問題3において、正解と共に(1/2,1/2)も同じ単位ベクトルだと思ってしまいました。一次方程式の「傾き」に方向を加えたものとは違うのでしょうか?
=>[作者]: 。一次方程式の「傾き」に方向を加えたもの,とはどういう意味なのか分かりませんが,(1/2,1/2)は単位ベクトルではないです
■[個別の頁からの質問に対する回答][重回帰分析(2) について/18.11.02]
説明通りやらせていただきましたが、結果がどうも違うようです。
エクセルでもRでも以下の結果が出力されましたが(最初の例、ほかの例も違います)、
どこで間違えたのでしょうか?
Coefficients
Intercept 7950000
女 -1150000
高校 1200000
大学 50000
20代 -8100000
30代 -5875000
40代 -3000000
=>[作者]: 連絡ありがとう.確かにおかしいです.管理人のExcelに,あるアドインソフトを組み込んでから「範囲指定」にエラーが起こり易くなっているのを,不注意にそのまま使ったようです.訂正します.
■[個別の頁からの質問に対する回答][変数分離形.微分方程式の解き方 について/18.11.01] 分離定数でL(L*1)の意味はなんですか
=>[作者]: そのページには分離定数という言葉もなく,L(L*1)という記号もありません.そもそも,何の話をしておられるのですか?
■[個別の頁からの質問に対する回答][積分定数の決定 について/18.10.30]
初学者(例えば私)にとって、与えられたf'(x)からf(x)を積分で求める時に、定数が一意でなく、さらに初期条件によってそれは一意に定まることは、グラフから知覚的に理解に苦しいと思います。
それよりかは微分が積分の逆演算ことに立ち返って
(具体的な関数, 例えば)f'(x)=2xを与えてあげて, 微分するとこうなる関数として
f(x)=x²+1, f(x)=x²+3,...
と列挙すればいいと思います。なぜなら微分の方が馴染みがあるからです。
そしてここから、f(x)を一意に決定するには当然、一意に定まらないf(x)に関する条件が必要であることもわかります。
=>[作者]: 連絡ありがとう.熱い思いを述べておられるようですが,教材に書いてあることを繰り返しておられるだけに見えます.
■[個別の頁からの質問に対する回答][展開公式 について/18.10.29]
つい最近、本サイトを知りました。色々楽しめそうです。よろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ 因数分解(応用問題) について/18.10.29]
お世話になります。
コツコツやらせていただいています、ありがとうございます。
例3-2がわからないと言う方が投稿されていましたね・・
実は私も同じく悩んだのですが、一生懸命計算をしたり、展開したりして、
先生の・・(x-y)3+(y-z)3+(z-x)3-3(x-y)(y-z)(z-x)
=(x-y+y-z+z-x)(…)=0
を利用すると・・の部分、結構頭がパニクッているとわかりにくくなるのです。
結局、カッコの中がなぜ0になるかと言う所だと思うのです。
冷静に考えれば公式の(a+b+c)の部分なのですね、説明はaの部分bの部分cの部分、それぞれカッコでくくってやるとパニクッた頭にもわかりやすいかもしれません。
先生は頭もいいし、慣れているから公式じゃん、これ以上どう説明するんだョ・・と思われるでしょうが、計算でパニクッて深入りした頭には「わからん」・・となるのだと思います。
私も同じ疑問を持ったもので・・時間を置いて、公式を見直してあまりにも簡単な事で拍子抜けしました。
頭のいい人がうらやましいですナァ
失礼します・・
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/18.10.26]
ずっと疑問だった事がわかりました!
ありがとうございます!
=>[作者]: 連絡ありがとう.Excelの指数表示のことかな?
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/18.10.25]
実際にといて、問題に答えれるのでとても良かったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率変数の変換 について/18.10.25]
簡単な穴埋め問題2,3個のさいころを同時に投げたとき,分散は26.3(2.92の9倍)ではないでしょうか?
=>[作者]: 連絡ありがとう.要約(6)の公式において
の場合を考えると
:和の分散は,各々の分散の和になる.これを使って【例1】を解いています.
さいころを3個投げるときは,独立変数が3個の場合になるから
となります.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.10.25]
問題2(3)の解説の「3次方程式の解と係数の関係を使う場合は:」以下の部分についての質問です。
当該解説の「(**1)(**2)(**3)より x4=a(x3+y3+z3)-b(x2+y2+z2)+c(x+y+z)」は、
正しくは、「(**1)(**2)(**3)より x4+y4+z4=a(x3+y3+z3)-b(x2+y2+z2)+c(x+y+z)」ではないでしょうか?
(**1)(**2)(**3)の左辺と右辺をそれぞれ足すと、この式が導かれて、
さらに右辺に問題2(1)(2)の結果を代入すると、答えが導けるという解釈なのですが、合っていますか?
=>[作者]: 連絡ありがとう.式が一部抜けていましたので,訂正しました.あなたの解釈で合っています.
■[個別の頁からの質問に対する回答][F検定→t検定・・・平均値の差の検定 について/18.10.22]
具体例を分かりますく、して欲しい。基礎知識がなくてもわかるような伝え方をして欲しい。もう少し
噛み砕いて噛み砕いて話して欲しいかも。
=>[作者]: 連絡ありがとう.もともと取りつきにくい項目なので,1ページ見ただけで分かるのは無理です.Excelを使って「体で覚える」までやるのがよいでしょう.
■[個別の頁からの質問に対する回答][関数の極限 について/18.10.22]
とても分かりやすかった。
大変記憶に留めやすいんだ!ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][多項式・有理関数・無理関数の不定積分 について/18.10.20]
一番下の問題の第5問目、解説の途中式で、x^3/2とありますが、x^-3/2ではないでしょうか・・・?
=>[作者]: 連絡ありがとう.考えられる原因1:あなたは数学Ⅱの段階で,累乗根と有理指数の対応関係を間違って覚えていませんか?
は
ではなく,
です→
このページ で復習してください
考えられる原因2:それでもなおかつ,x^-3/2はどこからも出てきません.微分と積分を間違えていませんか.
は ではなく, です
■[個別の頁からの質問に対する回答][多項式・有理関数・無理関数の不定積分 について/18.10.20]
一番下の問題の第5問目、解説の途中式で、x^3/2とありますが、x^-3/2ではないでしょうか・・・?
=>[作者]: 連絡ありがとう.考えられる原因1:あなたは数学Ⅱの段階で,累乗根と有理指数の対応関係を間違って覚えていませんか?
は
ではなく,
です→
このページ で復習してください
考えられる原因2:それでもなおかつ,x^-3/2はどこからも出てきません.微分と積分を間違えていませんか.
は ではなく, です
■[個別の頁からの質問に対する回答][連立不等式の表す領域 について/18.10.20]
いい問題
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/18.10.18]
問題2.5の問題なのですが
2勝3敗のあとAが勝った場合
または3勝2敗のあとAが負けた場合、もう一度試合が続きませんか?
なので、その試合に勝つか負けるかの計算も必要になるように思うのですが、分からないので教えてください。
=>[作者]: 連絡ありがとう.確率の問題は,数学の要素だけでなく,日常用語の解釈の仕方にも関係します.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.10.18]
(2)のⅱの部分分数分解の導き方を教えて下さい。分子を(ax+b)と(ax+b)^2に分けられるのが不思議です。
=>[作者]: 連絡ありがとう.まず,積極的に何もしなくても勝手に都合のよい答えが出てくるのではなく,
「だったらいいな, If I could have danced」「この形にならないかな」と意欲することが重要です.もしこの形に変形できたら
になって,そこに書いてある(*1)(*2)に持ち込めるからです.
ところで,係数比較をすれば分かるように,
のとき,
から
を求めることはつねにできます.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/18.10.18]
積和の公式の(A)と(B)の違いはなんですか?
=>[作者]: 連絡ありがとう.(B)なんか不要という意見でしたら,筆者は全く同感です.内容的には(B)は(A)と同じことの繰り返しになっていますので要りません,だから管理人も書きたくないのです.しかし,これは「こっち側のチーム」の仲間内の会話なのです.
■[個別の頁からの質問に対する回答][内分点・外分点の図示 について/18.10.17]
練習問題がありがたかっです!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/18.10.17]
回答ありますか?
=>[作者]: 連絡ありがとう.回答→解答.選択肢をクリックすれば採点結果と解説が出ます.
■[個別の頁からの質問に対する回答][逆行列とは について/18.10.17]
行列の解がマイナスになるときを教えて
=>[作者]: 連絡ありがとう.日頃全然勉強していない大学生からの質問として受け取りました.行列の解という用語はなく,それがマイナスになるというのも通常意味を持たない言葉です.もうこうなってしまったら,言葉の意味を勝手に推定して,解答可能な質問に勝手に答えるしかありません.
「行列式の値がマイナスになるときは,逆行列をどのように求めたらいいですか」
例えば,行列
の行列式は
です.そこで,行列
の逆行列を求めるには,
とします.(ただ単に,各成分を負の数で割るだけです)
■[個別の頁からの質問に対する回答][階差数列 について/18.10.16]
めちゃくちゃ分かりやすいわ😉
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組分け について/18.10.14]
本当に分かりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組分け について/18.10.14]
とても分かりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二項定理,多項定理 について/18.10.14]
よかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/18.10.13]
説明がわかりやすいとともに、練習問題が用意されていたので、理解を深めることができました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][関数の極限1 について/18.10.13]
中間試験の勉強の役に立ちました、ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][位置ベクトルの応用 について/18.10.11]
とてもわかりやすく、問題もついていて、テスト前の再確認には最適だと思いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトル成分の計算 について/18.10.11]
《3》の2番目の問題の答えは(1, 7)ではなく、(1, 5)です
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][面積 について/18.10.10]
計算式もヒントと同様にワンクリックすると表示されるようにしてほしい。
=>[作者]: 連絡ありがとう.その問題は,計算式を答える問題だから,計算式を表示してしまうと,生徒のやる仕事がなくなってしまいます
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/18.10.9]
いつもお世話になっています。誤字がありましたので訂正します。
問題5の3行目、「=2(sinθ·cos30°+sinθcos45°)」となっていますが
「=2(sinθ·cos30°+cosθ·sin30°)」だと思います。ご確認下さい。
=>[作者]: 連絡ありがとう.訂正しました.
■千葉[しらせさん/18.10.9]
場を間違えた質問をしてしまいすみませんでした、またそれにも関わらず親切に教えて頂き本当にありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/18.10.9]
ちょっとした復習に役立出てます
とても助かります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次方程式の解と係数の関係 について/18.10.9]
お世話になっています!
問題の解答にαβγの値はいらないと思いました。
=>[作者]: 連絡ありがとう.ん?だから書いてない.どこか他のサイトの話をしているのですか
■千葉[しらせさん/18.10.9]
はじめまして、ここに質問して良いのかわからなかったので違っていたらすみません。今エクセル数学3ブルー版を解いていてよくわからない点があります。例題136のx=(π/2)-tと置換して、I=∮[0→(π/2)] sinx/(sinx+cosx) dxの値を求めよ。という問題で置換積分の流れ自体はわかるんですが途中のI=∮[0→π/2]cost/(sint+cost) dt =∮[0→π/2]cosx/(sinx+cosx) dxという風にtからそのまま文字をxに変更できる理由が全然わかりません同じような疑問で例題138等式∮[1→2x] f(t)dt=e^x +aを満たす関数f(x)と定数aの値を求めよ。という問題でも2x=uと置いて∮[1→u] f(t)dt=e^(u/2) +a両辺をxで微分しf(u)=(1/2)e^u/2からf(x)=(1/2)e^(x/2)という風にuからxに文字を変更できる理由がわかりません。これはどういう理屈でこうなるんでしょうか?
=>[作者]: 連絡ありがとう.出版物に対する質問は,その出版社にすべきなので,ここに質問してもどうにもなりません.また,∫記号の代わりに周回積分の記号∮を使っておられますが,全然違う意味になりますので要注意です.
ところで,不定積分は結果が関数になるので積分変数に依存します
しかし,定積分は値を代入して引き算をするので,積分変数に依存しません
だから,積分可能な関数である限り,つねに
が成り立ちます.
このページ を参照のこと
次に,明治時代に欧米の学問を導入するときに,functionを何と訳するかと考えたときに,箱に物を入れる入れ物として,函館の函(中国語のファン)を使って函数と訳したと言われている.戦後,旧字体の整理でそれが関数と書かれるようになった.要するに,関数の実体は数字を入れる箱なので,中身に何をいれるかは「そいつは,おいらの自由だ!」
という話は,高校数学Ⅰ以来,何百回と見ているはずです.数学Ⅲになってから,今さらその質問が出たら,今までどうやって数学をやってきたのか,不思議
■[個別の頁からの質問に対する回答][指数法則 について/18.10.7]
タイトル見にくい
=>[作者]: 連絡ありがとう.画面のサイズが1280×1024なので,かなり左にくるということかな
■[個別の頁からの質問に対する回答][指数法則 について/18.10.6]
2^(n +2)-2^(n +1)はどうして2^(n +1)になるのですか?
=>[作者]: 連絡ありがとう.一言文句を言おうと思ったが,その感情を押し殺した.あと10年もしたら,自分はいなくてこの若者が生きているのだから,この頼りない若者らに未来を託するしかないのだから
■熊本県[田中太郎さん/18.10.5]
突然の質問失礼します。
剰余の定理のページの質問です。割る数と余りだけが開示されている条件で、割る数のなかに 解の公式を用いてでしかxの値が求められない式があった場合、答えが二つ出てきます。何がいけないのでしょう。
「例」
P(x)=(x+1)(x^2-x+1)Q(x)+2x^2+13x
よろしくお願いします。
=>[作者]: 連絡ありがとう.何か訴えているという気持ちは伝わってきますが,何を求める問題なのか書かないと,答えようがありません.仕方がないので,問題を勝手に推定して,その問題に対して答えることにします.
[問題] 整式
を
で割ると
余り,
で割ると
余るとき,
を
で割った余りを求めよ.
[解答]
とおく(割る式が3次式だから余りは高々2次式になる).
だから
…(1)
を
で割ると,右辺の第1項は割り切れるから,余りは第2項を割ったものから出る.(**)
したがって,
…(2),
…(3)
(1)(2)(3)より
となるから,求める余りは
…(答)
あなたが行き詰っているのは,たぶん(**)で示した箇所です.
には虚数解しかないから,剰余の定理を使うために何を代入したらよいのか?という箇所です.上記のように,剰余の定理を使うことなく,「割り算実行」で押し切るところがミソです.
以上が普通の答案ですが,数学Ⅱの虚数を習った後なら,次のような天真爛漫,天衣無縫の答案もあり得ます.
…(1)は同じ
次に,
の1つの解を
とおくと(ただし
は虚数),
が成り立つから
ところで,虚数
について,実数係数の等式
が成り立つとき,
が成り立つ(***)ので,
…(2),
…(3)
以下,上記と同様にして(1)(2)(3)から解けます.
この答案は,剰余の定理に虚数
を代入して
を計算するところが「そんなことしてもいいのか?」と抵抗感がありますが,教科書の剰余の定理をよく読むと,「実数しか代入できない」などと書いてないから,虚数でもよいことになります.
※(***)は背理法で証明でき,
ならば
となって
が虚数という仮定に反することから言えます.そのとき,
から
も言えます.
■[個別の頁からの質問に対する回答][内分点・外分点 1 について/18.10.4]
問題の答えと解説をお願いいたします
=>[作者]: 連絡ありがとう.解説は上に書いています.世の中には,図でしか示せないものもあります.(不立文字て誰の言葉だったかな)
■[個別の頁からの質問に対する回答][3点が同一直線上にあるための条件 について/18.10.4]
僕たちの学校には、物理の教員がいません。
ですが、物理をやらなくてはいけません。
=>[作者]: 連絡ありがとう.冗談で言ってみただけということでしょう!?江戸取と張り合いながら,医学部12名合格とか言えば,物理の授業はやっているが「専任教員」を募集中なので,放課後に質問に行けないという話かな?
■[個別の頁からの質問に対する回答][和の法則 について/18.10.3]
中学生ですこれはいちいち表を作らないといけないのですか
=>[作者]: 連絡ありがとう.問題1,4,5,6に表を使わない解答例を示しているので,その質問はあり得ないでしょう.
■[個別の頁からの質問に対する回答][無理数の独立 について/18.10.3]
余談の部分の件、直していただきありがとうございました。
=>[作者]: 連絡ありがとう.お礼を述べなければならないのは,こちらの方です.
■[個別の頁からの質問に対する回答][番号札のもらい方 について/18.10.2]
組み合わせの番号札のもらい方《6》で、赤玉の並べる方法を考慮して5!をかけないのですか?
根本的に私が間違ってしまっていたらすみません。
お時間あるときに解説よろしくお願いします
=>[作者]: 連絡ありがとう.このページで「赤玉4個,白玉3個」というとき,各々同質で区別ができないものを扱っています.つまり,この問題は同じものがあるときの順列の総数の問題です.
○あなたの弱点⇒とにかく計算しようとしていますが,その計算のもとになっている根拠を確かめていません.
○順列,組合せの問題で「考え方」が正しいかどうかを確かめるには⇒数字を少なくし,単純化して具体例で調べるとよい.
例えば「赤玉2個,白玉2個を1列に並べるとき,白玉が隣り合わない(赤玉は隣り合ってもよい)並べ方は?」
[正しい考え方]
赤玉を並べておき,その両側を含む3つの隙間に白玉を並べる:● (2)● (3)3 C2 =3…(答)● 〇● ,〇● ● 〇,● 〇● 〇の3通りが答えになる)
[あなたの間違った考え方]
(1)● (2)● (3)● (3)● (2)● (1)● (3)● (3)● (1)● (1)● (2)● (2)● (1)
■[個別の頁からの質問に対する回答][無理数の独立 について/18.10.2]
余談の例の式 d√2→b√2ですか?
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/18.9.30]
すみません💦ω17+1/ω17-1=ってなんになりますか?
分数になると分からなくなる、
=>[作者]: 連絡ありがとう.当教材にある問題については,質問に答えますが,各自の宿題などについては原則として回答していません.
そこで,尋ねられた問題に答えずに,尋ねられていない問題に答えて,各自の答は各自で考えてもらうことがあります.
の値を求めたい場合
そのページの用語で[特急券]を使うと,
次に,そのページの用語で[急行券]を使うと
より
■[個別の頁からの質問に対する回答][変数分離形.微分方程式の解き方 について/18.9.28]
(5)においてC=0のときはy=0となって,この場合も元の微分方程式を満たす.(特異解と呼ばれる)
例1にそう書いてありますが、C=0と置くとy=0の解は得られるので、y=0は一般解に含まれ、特異解ではないのでは?
*拝見させていただきましたが、実にわかりやすく詳説してあり、学習者にとってすばらしいサイトだと思います。
=>[作者]: 連絡ありがとう.なるほど.一応,一般解はC≠0が条件なので,C=0の場合は含まれませんが,他の変形方法で,この場合も含める方法があるようです.包絡線の方程式とか,特異解とは何かという定義に突入すると高校の範囲を超えてしまいますので,このページで触れる必要なしということで,そのかっこを削除しました.
■[個別の頁からの質問に対する回答][点の存在範囲 について/18.9.27]
とてもわかりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/18.9.27]
(1)
(2)
(3)
上記の説明読ませて頂きました。私の宿題の問題でこちらに書いてあるのではないので申し訳ないのですが、
「白玉4個、黒玉3個、赤玉1個を円形に並べる方法は35通りある。また、これらの玉に紐を通し、輪を作ると何通りできるか。」
という問題があまり理解出来ません。答えは19通りになるのですが.....。もし宜しければ教えてください!お願いします。
=>[作者]: 連絡ありがとう.各自の宿題の答えについては,原則として回答しないことにしていますが,答も書いてあるので境界線はあいまいでもよいかと.そこで,尋ねられた問題に答えずに,尋ねられていない問題に勝手に答えて,本当の答案は自分で考えてもらうことにします.
まず,同じものがあるときの「円順列」については≪10≫の解説を読んでください.次に,「じゅず順列」については赤1個,白3個,黒2個の場合に勝手に簡単な問題に書き換えて,これに答えてみます.「円順列」の総数は
通り.[A]上の図(1)(2)のように左右非対称なものは「円順列」では別々に数えるが,「じゅず順列」としては,裏返したら重なるから,同じものとみなす.[B]これに対して上の図(3)のように左右対称なものは,「円順列」の段階でも初めから1通りしか数えていない.そこで,「円順列」の総数
通りのうち[B]の型のものはそのまま数えて,[A]の型のものは半分だけ数えるとよい.([B]の個数は絵を描いて1つずつ調べる).[B]は2通りだから,[A]は8通り.したがって,
通り…(答)
あなたの質問した問題では,「円順列」の総数が
通り,[B]が3通りだから,[A]が35−3=32,これらを使って上記のように計算すると19になります.
(これは基本問題ではなく,ほぼほぼ応用問題)
■[個別の頁からの質問に対する回答][関数の極限1 について/18.9.26]
大学卒業にあたり,数学3の極限分野の知識が必要になった.そこで使わせていただいたが,非常に要点を得てまとめられていたので,復習に役立った.統一の取れたサイト構成でしたので,今後も利用していきたい.
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階差数列 について/18.9.24]
最高によき
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][立体の体積 について/18.9.24]
例4)の解答の1)のV1=の式の、x^1-1はx^2-1ではないでしょうか?0-(1-x^2)から求めていると思うので
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][整数の入試問題1 について/18.9.23]
[例題1]で(3)(4)の判別式を避ける方法の四角の中の上から10行目
(b+k)^2+(b+k)+b^2=M/kとなっていますが、
(b+k)^2+(b+k)b+b^2=M/kだと思います。
=>[作者]: 連絡ありがとう.訂正しました.(ここまで読んでいる人がいるんだ!と,感心)
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/18.9.23]
素朴な疑問なんですが、この変数変換って、離散的な関数に対しては同じようなことってできないんですかね?重和分するときの自由度って連続なときよりも低いんですかね?どう思われますか?
=>[作者]: 連絡ありがとう.この教材は,大学初年度レベルの内容を取り扱ったものです.和分,差分というのは昔からある分野なので,何か確立された公式的なものがあるはずです.見つからない項目については,自分で作っていくことになります.
■[個別の頁からの質問に対する回答][部分積分 について/18.9.22]
logの不定積分で昨日質問したものです。不明点が正しく伝わっていなかったのでもう一度部分積分で疑問に思ったことを書かせていただきます。この項では同じ番号の例題が上の方と下の方にあるので、上下で区別して質問を書いていきます。
上の方の例3,4では、下の方の例1のようには微分する側が0にならないのに、下の方の例2のように部分積分の繰り返しをしなくていいのはなぜなんでしょうか?
=>[作者]: 連絡ありがとう.下の方の例1では部分積分の公式
において,右辺第2項が既知の関数ではなくて求めたい未知関数自体であるのに対して,上の例3,4では既知の(計算可能な)関数だからです.
【参考】
中学校1年生が,次の問題を解く場合
(1)
の場合
が計算可能だから
と答えるでしょう.
(2)
の場合
右辺の
は既知の数ではないから,方程式を立てなおして,
にして解くでしょう.
■[個別の頁からの質問に対する回答][対数方程式 について/18.9.22]
logが1つだけの時の例もあったら助かります
=>[作者]: 連絡ありがとう.理屈の上では,ご要望のことは
対数の定義 のページで,
の形を
に直すだけのことで,教科書的には,その問題もあり得ます.
【例】
教える方からは不要と考えていましたが,学ぶ方からは必要と思う可能性がありますので,検討の余地あり.
■[個別の頁からの質問に対する回答][展開公式 について/18.9.22]
いつも参考にさせていただいています。
採点する、やり直すの二つの欄がグレーになっていて開けないので、答えを教えていただけないでしょうか。
=>[作者]: 連絡ありがとう.確かに,プログラミングの世界では,選択できないものをグレーで表示する習慣はありますが,この教材でのそのボタンの色は「次の問題」という選択を忘れられないために目立つ色にし,「採点する」「やり直す」の方を地味な色に設定しただけのものですので,クリックしていただくと作動します.(採点すると答えは出ます)
■[個別の頁からの質問に対する回答][logxに関する不定積分 について/18.9.21]
(*5.10)の解説の下の方にある、文言、したがって~の、1行上の式の右辺の1/aは1/a^2ではないでしょうか?
=>[作者]: 連絡ありがとう.その箇所のaの部分は,確かにおかしいですが,あなたの計算もおかしいです.訂正しました.
■[個別の頁からの質問に対する回答][部分積分 について/18.9.21]
高卒の項の不定積分で、∫(logx)^2 dxが問題としてあったのですが、これをこの項の部分積分の繰り返しのところの表をつかった解き方でといたのですが、答えのx(logx)^2-2x+Cにたどり着けませんでした。微分する側を(logx)^2にしたのですが、微分する側が0にならないため困っています。表を使った解き方で解いてはくれないでしょうか?(表の途中式が知りたいです)
=>[作者]: 連絡ありがとう.
このページ の下の方を見てください.
■[個別の頁からの質問に対する回答][2次関数のグラフと係数の符号 について/18.9.21]
2つの式の符号から決めるってどういう事ですか?
(二次関数のグラフと係数の符号の問題についてです)
=>[作者]: 連絡ありがとう.解説に書いてあることを,そのままオーム返しのように聞くのはよい質問ではない.
■[個別の頁からの質問に対する回答][連立方程式の解き方 について/18.9.19]
連立方程式の分数が分からない
=>[作者]: 連絡ありがとう.中学生が高卒向けの連立方程式のページを読んでも分からない.分数係数の連立方程式は
中学生向けのページ にあります.
■[個別の頁からの質問に対する回答][三角関数の定義 について/18.9.19]
簡単でした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][双曲線関数 について/18.9.19]
冒頭にオイラーの公式がのっていますがそこのところで質問です。e^(-ix)=cosx-isinxとなっていて、e^(-ix)の指数マイナスがありますが、マイナス乗すると数は無理数になるではないですか。
それで、私は、e オイラーの公式e^(ix)=cosx+isinxをマイナス乗したら、e^(-ix)=(e^(ix))^-=√(cosx+isinx)になるのかなと思ったんですが、この変形はダメなんでしょうか?
=>[作者]: 連絡ありがとう.マイナス乗と無理数とは何の関係もありません.逆数(分母と分子が逆)になります.だから,あなたの変形はダメです.
この変形を使うのなら
しかし,その教材では途中経過なしで一瞬で変形していることから分かるように,そのような遠回りの変形はしていません.次のようにやっています.
という公式の
に
を代入すると
[∵
]
■[個別の頁からの質問に対する回答][三角不等式 について/18.9.18]
いつも大変勉強させていただいております。
例題の解答で
π12<θ<π4, 13π12<θ<15π12…(答)
となっており約分されておりませんでしたのでお伝えします。敢えてなのかなとも思いましたが。
=>[作者]: 連絡ありがとう.約分しておきました.
■[個別の頁からの質問に対する回答][マクローリン展開 について/18.9.18]
さきほどこの項で質問したものです。前回の質問の回答で疑問に思ったことを下にかきたいと思います。
質問1 前回の質問の回答で、多項式のような関数は何回でも微分可能で、角のあるグラフなどは連続であっても微分可能ではないとのことですが、多項式のような関数、角のあるグラフとはたとえばどのようなものなんでしょうか?
質問2 この項のマクローリン展開の説明で、x=0の近傍でn回微分可能であれば、という文言がありますが、ようするに、関数f(x)をn回微分して出てきた第n次導関数全てに、x=0が代入できるとき、ということでしょうか?
=>[作者]: 連絡ありがとう.多項式が分からなければ話ができない.角のある関数はそこに書いた例[1]
■[個別の頁からの質問に対する回答][マクローリン展開 について/18.9.18]
マクローリン展開の説明のところで、関数f(x)が、x=0の近傍でn回微分可能であれば~という文言がありますが、x=0の近傍でn回微分可能である、というのはどういう事なのでしょうか?関数f(x)にx=0を代入したものが、n回微分可能ということなんでしょうか?
=>[作者]: 連絡ありがとう.「関数f(x)にx=0を代入したものが、n回微分可能ということ」ではない.代入したものは定数なので,何階微分してもすべて0になります.(n) (x)が定義されている場合だということ.そうでなければf(n) (0)が存在しないことになり,意味を持たない.2 (x≧0), f(x)=0 (x<0)はx=0で1回微分可であるが,2回微分可能ではない.3 (x≧0), f(x)=0 (x<0)はx=0で2回微分可であるが,3回微分可能ではない.n+1 (x≧0), f(x)=0 (x<0)はx=0でn回微分可であるが,n+1回微分可能ではない.
■[個別の頁からの質問に対する回答][行列式の性質とクラメールの公式 について/18.9.16]
この項で2つわからないところがありましたので申し訳ないですが質問をさせていただきます
質問1
この項のはじめにのところの、未知数が2この連立1次方程式の場合のところで、x,yの解がx=(pd-bq)/(ad-bc)、y=(aq-pc)/(ad-bc)
となっていますが
この項の1つ前の項の、未知数がn個で逆行列を用いて解く方法の項の例1のように、逆行列をかけてx,yをもとめると
x=dp-bq,y=aq-cpになりました
どうやったら、x,yの解がx=(pd-bq)/(ad-bc)、y=(aq-pc)/(ad-bc)になるんでしょうか?
質問2
この項の中下部にある、クラメールの公式と青点線でかこまれたところの、下にある、クラメールの公式の証明の上の方に、1列目を(**)の左辺にかきかえると、という文言がありますが、なぜ1列目を(**)の左辺にかきかえられるのでしょうか?
=>[作者]: 連絡ありがとう.質問1:あなたは,逆行列の計算を間違っています.
の各成分を行列式ad-bcで割らなければならないので,分母にad-bcが付きます.
質問2:行列式は方程式とは違います.関数や多項式のように値を持った式です.たとえば,f(x)=ax+bのときにxの代わりにpを代入するとf(p)=ap+bになりますが,この場面で「なぜ代入できるのか」という質問は,pは定義域にあるのかという質問になり,あなたの質問とは全然違う話になります.
そもそも,そこの証明は,元の行列式をDとし,1列目を(**)の左辺に入れ換えたときの行列式をD’とすると,D’=xDになると書いているのです.(D’=Dだと書いているのではない.)だから,x=D’/D ←これを証明しています.
■[個別の頁からの質問に対する回答][2次不等式 について/18.9.15]
よくある間違いNo.1の例のb²-4acのbが-bになっていると思います。
(2が(-2)になっていると思います)
=>[作者]: 連絡ありがとう.訂正しました
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.9.15]
三度目の送信失礼します。
(3)-2の問題は、絶対値でなくカッコでいいのではないでしょうか(正になりそうです)。
最後の問題は、一応高校範囲の逸脱だと明記した方が良いかもしれません。tanが出てこないと思い、手が止まってしまいました。ただ明記したら用いる前提になってしまって考える練習にならないのかもしれませんので、微妙なところでしょうか。細かい感想になってすみません。
=>[作者]: 連絡ありがとう.tan −1 xx2 +1 のように直ちに正であることが分かる式では| |を省略しても戸惑いはありませんが,判別式を使わなければ分からないような場合には,その説明をさらに追加しなければならず,猫の額のような名刺サイズの中に書くのは?| |で間違っているわけではない.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.9.15]
連投すみません。
(*B1)の形になるときはいつでも(*B2)の形にできる.(比較してみるとCの値が少し違うだけだと分かる.)
の部分は、B2のBとCを入れ替えた方がわかりやすいのではないかと思いました。
Cの値が少し違うだけ、というのがB1とB2のどちらのCとみるかで混乱しそうだからです。
=>[作者]: 連絡ありがとう.名前の付け方だけのことなので,全体の論旨を理解できればよいと考えられます.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.9.15]
分数関数(有理関数)の不定積分
=>[作者]: 連絡ありがとう.-0→-1
■[個別の頁からの質問に対する回答][ 行列のn乗 について/18.9.14]
逆行列の説明より前に逆行列が来ている気がします…!
=>[作者]: 連絡ありがとう.?.逆行列の説明を読めばよい.
■[個別の頁からの質問に対する回答][行列の階数 について/18.9.12]
公益社団法人の上から7番目の問題の解説で質問です。3列目から2列目のa倍を引くとありますが、aが0の可能性があるときに文字の掛け算をしてもいいんでしょうか?
=>[作者]: 連絡ありがとう.掛けることは何も問題がありません.割ることに問題があるだけです.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/18.9.12]
非常に丁寧に解説されており理解しやすい内容になっています。
今後もさらに高度な内容を判りやすく提供お願いいたします。
69歳の数学好きです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の階数 について/18.9.12]
公益社団法人の、上から4つめの問題で、解説下部の連立方程式で、2-a=0ではなく2b-a=0ではないでしょうか。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][展開公式 について/18.9.11]
iPadのSafariで利用させて頂いてますが、採点する、やり直すが機能していないです。ど、どうしましょう…
=>[作者]: 連絡ありがとう.Windowsのsafari,iPhoneのsafariで問題なくて,iPadのsafariで動かない?
■[個別の頁からの質問に対する回答][転置行列,対称行列,対角行列,三角行列 について/18.9.10]
対角行列の性質のところの、対角成分が0でないときは~の文章の日本語がおかしいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][信頼性係数の計算 について/18.9.10]
統計は初心者なので、とても難しくとらえていますが、そんな私にもわかりやすい内容でした。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/18.9.9]
凄い!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/18.9.9]
先程この項で質問した者です。まだいくつか疑問に思ったことがあるので申し訳ありませんが質問させていただきますm(__)m
質問1 5.像と核の例1の(3)で、なぜ、dim(ker(A))=1なんでしょうか?
私の考えとして、4.基底と次元のところの次元の定義から基底の個数を次元としていますから、(1)の(x.y.z)=t(-4.-1.1)は基底の集合だと私は思うので、基底の個数はt、tは実数のことでしょうから実数が次元となるのだと思いました(何次元かを聞かれて実数次元なんていう答えが間違いなのはわかります)
質問2 5.像と核の例1の行列Aは、det(A)=16≠0から逆行列が存在するのに、なぜ、(1)で(x.y.z)がx=y=z=0以外の解、t(-4.-1.1)、があるのでしょうか?例2では例2のAの行列が逆行列を持っているのでx=y=z=0ですが。
質問3 5.像と核の例3の(3)で、逆行列が存在しないのに、5.像と核の青線でくくられた定義が書かれているところの米印の定理?を使っていますが、いいのでしょうか?
=>[作者]: 連絡ありがとう.質問1:t(-4.-1.1)は1次元です.質問2:det(A)=0です.質問3:(*)は使っていません.【重要】(4)です.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/18.9.9]
5.像と核の(4)の解説で、1次変換によってつくられる空間の次元は~のあとに1次変換によってつくられる空間の次元についての説明がありますが、原像と一次変換による像とで次元は変わらないのではないでしょうか?変換の意味からして。
=>[作者]: 連絡ありがとう.書いてあるつもりですが,それではわからんということかな?
dim(Ker(A))+rank(A)=n だからdim(Ker(A))=1のときは原像が3次元でも像は2次元に,dim(Ker(A))=2のときは原像が3次元でも像は1次元になります.
【例1】
の場合,原像が3次元でも,Ker(A)が1次元だから像は2次元になります.
【例2】
の場合,原像が3次元でも,Ker(A)が2次元だから像は1次元になります.
■[個別の頁からの質問に対する回答][因数定理による因数分解 について/18.9.7]
問題2の(2)で、正解と思われる(2X+3)(X^2-X+1)を選ぶとXになります。なお解説は間違ってません。
=>[作者]: 連絡ありがとう.最近アップしたばかりのページですが,突っ込みどころ満載のボケネタを混ぜたわけではない.紛らわしい選択肢を作っているうちに,管理人が罠にかかったということです.やはり,点検は他人が一番のようで,訂正しました.
■[個別の頁からの質問に対する回答][ 逆行列 について/18.9.5]
質問1 AA_~=Aの行列式としていますが、余因子行列とは、のところで、なぜ、A_~Aの順でかけているんでしょうか?
質問2 例2のdet(A)は余因子展開して求めているように見えないのですが、どうやって求めたんでしょうか?
=>[作者]: 連絡ありがとう.
だから,右から掛けても左から掛けても等しいです.
質問2について:9行にわたって余因子を求めています.それを行列に組んだものが余因子行列 - - 余因子展開は行列式の計算≠余因子行列
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/18.9.5]
いつも参考になってます!
=>[作者]: 連絡ありがとう.「いつも参考になってます!」とは微妙な表現かな.主語は何かと一瞬詰まるが,すれすれセーフかな.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/18.9.5]
簡単だったので、もう少し難しい問題お願いします。
=>[作者]: 連絡ありがとう.メニューを見て,その次のページに進んでください
■[個別の頁からの質問に対する回答][行列式 について/18.9.5]
行列と行列式の定義について詳しくわかりやすく教えてほしいです。このサイトの数Cのところで行列は扱ってますが、行列とはなにかについては扱ってなかったです。また、行列と行列式が違うことを今日初めて知り、いろいろ勘違いが生じたので、ベクトル行列超基本の項に行列と行列式は違いますと書いておいてほしいです
=>[作者]: 連絡ありがとう.そのページの先頭に,要約があります.行列とベクトルなどの定義は
ベクトル,行列の超基本 にあります.(何もかも1つのページに書いてなければならないと考えても無理です)
■[個別の頁からの質問に対する回答][不定積分の置換積分 について/18.9.4]
全然分からなかったので、ヒントをお願いします。
=>[作者]: 連絡ありがとう.十分たくさんのヒントが書いてあります.
■[個別の頁からの質問に対する回答][展開公式1 について/18.9.4]
(4) (x+1)(x2−2x+1) この問題 すごい 公式がちがちだったのでまんまと間違えました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/18.9.4]
ありがとう😊
助かりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][Σ記号の変形 について/18.9.2]
ヒントを見てもなかなかできませんでした。もうちょっと詳しくお願いします。
=>[作者]: 連絡ありがとう.最近は「教師無限責任論=分からなくなったら先生が悪いと言えば正義になる」が主流ですが,生徒数が多かった時代には「生徒無限責任論=ちゃんと勉強したんかい」が主流でした.ところで,ある項目を学習するには,それに対するレディネス(=準備)が必要だということはご理解いただけますか.下位目標を満たさずに上位目標を目指しても身に着きません.サイドメニューから,前に学ばなければならない項目を先にやってから,そのページをやってください.
■[個別の頁からの質問に対する回答][点の像と原像 について/18.9.2]
この項の確認問題で、問題の行列の成分に、マイナスが入るとマイナスのあとに続く数字が見えなくなってしまいます。
=>[作者]: 連絡ありがとう.iPad上のSafariでの見え方はチェックできません.Windows上のChromeやSafariではご指摘の現象はありません.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.9.2]
問題4.1の(2)の解説の、答えとなる行列の、2行1列目の成分で、マイナスが分母と分子の間の線のところの左横に来ていますが、正しくは分子の2^(n+1)の左横に来るべきだと思います
=>[作者]: 連絡ありがとう.ズバリ書き損じがありました.よく見ると(1)の段階ですでに…訂正しました.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.9.2]
例題1.2に登場するΣの上端は、nではなくn-1だと思ったのですが、どうなんでしょうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/18.9.1]
ひとつ、間違えてるやつがありましたがほらはわざとなのでしょうか?
=>[作者]: 連絡ありがとう.わざと「ぼけた芸をした」わけではなく,カードを配るプログラムで6分の1の確率で,右欄に間違ったカードが配られていました.訂正しました.
■[個別の頁からの質問に対する回答][展開公式1 について/18.8.31]
分かりやすく、いつも利用しています。全国的な大まかな学習の順番をならべてくれると助かります
=>[作者]: 連絡ありがとう.
メニューの目次 が,ほぼ教科書の目次の順です.教科書の目次は会社によって順序が変わるところがある.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/18.8.29]
問題2(4)
(2a+2c)(2c)=4b(a+c) …(誤)ではなく
(2b) (正)
=>[作者]: 連絡ありがとう.解答の1つ前のcがbだということで訂正しました
■[個別の頁からの質問に対する回答][2次不等式(文字係数) について/18.8.29]
【問題3】の(2)ですが、x^2の係数がaであることから、a<0の場合、上に凸のグラフになると思います。
そのため、例えばa=-1のとき、解なしとされていますが、不等式のaに-1を代入するとx<-1, -1<xになるなど、下記3つの解答が違っていませんか?
a<-1
a=-1
-1<a<0
また、上記の認識が正しい場合、【問題3】の(3)の下記3つの解答も違っているということになると思います。
a<-1
a=-1
-1<a<1
=>[作者]: 連絡ありがとう.aが負の場合について,訂正します.
■[個別の頁からの質問に対する回答][確率の乗法定理 について/18.8.29]
数学Aの「原因の確率」のページがあると良いです。
毎度毎度質問、それも直接ゲイシャ様のページの問題と関係ないものですみませんが、できたら教えていただけませんか。教科書に問題と解答例が載っていますが納得できません。
例題、ある製品を製造する工場A,BがありAの製品には3%、Bの製品には4%の不良品が含まれている。Aの製品とBの製品を4:5の割合で混ぜた大量の製品の中から1個を取り出すとき、次の確率を求めよ。
(1)それが不良品である確率
(2)不良品であったときに、それがAの製品である確率
解答例(1)は理解できたのでざっくりとだけ書きます。
不良品はAの製品の場合と、Bの製品の場合があり、それらの事象は互いに排反であるから
((4/9)×(3/100))+((5/9)×(4/100))=8/225
やっかいなのは解答例(2)です。まず教科書の解答例を書きます。
取り出した1個がAの製品であるという事象をA、Bの製品であるという事象をB、不良品であるという事象をEとする。求める確率は、条件付き確率P_E(A)であるから、P_E(A)=(P(A∩B))/(P(E))=((4/9)×(3/100))÷(8/225)=3/8
この解答例(2)ではベン図でいうとこの部分集合Eを全事象として、そのなかでAである確率を計算しています。
個人的には問題文があいまあだと感じています。どちらかというと問題文のにある混ぜた全ての製品の中から1個を取り出したときにそれが不良品かつ工場Aの製品である確率を問われているように読めます。
私の考えはおかしく、教科書の問題文も解答例も完全なものなのでしょうか?
よろしくお願いいたします。
=>[作者]: 連絡ありがとう.そのページの先頭にある図と解説,特に※の部分を読んでください.また,原因の確率については
このページ の例3を読んでください.なお,あなたの間違いは,分母のとり方について,定義よりも自分の信条を優先させている点にあります.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/18.8.28]
∮xsinx/(cosx)^3はどうやって解くのでしょうか。
また、置換でも解けるのでしょうか。よろしくお願いします。
=>[作者]: 連絡ありがとう.質問を正確に書いてください.∮は複素積分で留数定理やストークスの定理のときに出てくる周回積分の記号です.また積分変数は?
文句を言っても始まらないので,適当に解釈して勝手に答えてしまいます.はじめに,
このページ を見てください.
そこで次の公式をメモします.
次に
部分積分の公式に当てはめる
##高校生にはこんな問題はできません!
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/18.8.26]
x三乗ーx二乗ー10xー8 を因数分解がわかりません
=>[作者]: 連絡ありがとう.数学Ⅰの教材から質問しておられますが,その問題は数学Ⅰの問題ではなく,数学Ⅱの剰余定理,因数定理を使う問題です.
このページ
とおいて,
となるaの値を探す.
aは−8の約数になるから,a=±1,±2,±4,±8のうちで合うものを探します.(因数分解は,あてもんです.まぐれ当たりがほとんどです.とはいえすぐ見つかります.a=−1)x+1で割り切れるから割り算をすると,残りは2次式だから見ただけで分かります.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.8.25]
質問です。
問題2の(1)の計算式、計算式1で、行列の恒等式における文字の比較をすていますが、左辺と右辺のどの行列のどの成分同士を比較したら、b=c,2a=3bとなるんでしょうか?
=>[作者]: 連絡ありがとう.あなたの勉強の仕方には弱点があるようです.すなわち,自分で鉛筆を動かさずに全部を尋ねているようです.1つでも計算すれば分かるはずのことを尋ねています.それとも行列の積の項目をまだ学習していないのなら,そちらを先にやるべきです.
■[個別の頁からの質問に対する回答][Sn→an関係式 について/18.8.24]
Sn+1-Snはありですか
=>[作者]: 連絡ありがとう.仲間うちで使うほどの省略語では,質問の意味が正確に伝わりません.
も使えますか,という質問なら,使うことは出ます.
ですかという,という質問なら,違います.
そこに書いてある8両連結の列車を見ると分かるように
です.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.8.22]
2つほど疑問に思ったことがあるので質問させてください
質問1 (1)の解説の、次にP^(-1)APの形の行列については~のあとの、同様にして~の隣に続く式で、左辺から中辺へ式変形するさいの途中式を教えてほしいです。
質問2 a,b,cという異なる3つの行列があって、(a×b×c)^n=(a^n×b^n×c^n)という恒等式は成り立つのでしょうか?
ちょうどこの行列のn乗を学習しているさい疑問に思いました
=>[作者]: 連絡ありがとう.質問1について:その質問はあり得ない.少しでも書いてみれば分かります.
質問2について:一般には行列の積について交換法則は成り立たないから
したがって
一般に
ただし,対角行列など特別なものについては,交換法則が成り立つ
特に
■[個別の頁からの質問に対する回答][行列のn乗 について/18.8.22]
福岡大理工2005年の入試問題のところで、S^-1は、どうやって計算したのでしょうか?
この項までに行列のマイナス乗はふれられてないと思うので、途中式を教えてほしいです
=>[作者]: 連絡ありがとう.行列のマイナス乗が一般的に定義されているわけではないことに注意しましょう.当面,正方行列Aに対して,その逆行列A
−1 という特別なものだけを考えます.
このページ を先に読んでください.
■[個別の頁からの質問に対する回答][零因子 について/18.8.21]
零因子の作り方のところにある文字の行列式で、(a,b)を(a,ka)とおくのは大丈夫ですが、(p,r)を(-kr,r)とおくのはなぜなんでしょうか?(a,ka)のように、y座標のとこよに、x座標に傾きをかけた値がくるのではないでしょうか?
=>[作者]: 連絡ありがとう.
だから
とおいてもよいが,分数を避けて
とおいても同じことになります.普通の感覚なら分数は煩わしいので,分数を避けて整数係数にします.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/18.8.20]
和積と積和の問題をやりすぎると頭がこんがらがってきました...。
=>[作者]: 連絡ありがとう.歌を歌うように,スラスラと答えようとしていませんか?そのやり方だと月日がたてば忘れます.この教材の管理人は高校で○○年教えましたが,その公式は覚えていません→「公式がある」と覚えるのです.実際に必要になったら,加法定理から作るのです.(1分もかからない)
■[個別の頁からの質問に対する回答][零因子 について/18.8.20]
今日、零因子のところで質問したものです。y軸に平行な直線は,傾きを用いたy=kxの直線の方程式によって表すことはできないということを忘れていました(というか恥ずかしながら初耳です)失礼しました
あの、零因子のところの式の例外の場合というのは、図を書いてみるのも手なんでしょうか?(というより、他に手はあるのでしょうか?)
=>[作者]: 連絡ありがとう.「これには例外がある」ということを覚えるのです.
■[個別の頁からの質問に対する回答][
例と答1の(4)の(ア)で
Σ(k+3)となってますがΣ(2k+3)の間違いではないですか?
=>[作者]: 連絡ありがとう.訂正しました.そのほか,Σの上につく末項の位置がずれていましたので直しました.
■[個別の頁からの質問に対する回答][零因子 について/18.8.20]
零因子の作り方のところで、昨日の質問の回答で、上の式と下の式は対応していないとのことですが、上の式は一般的な零因子の式ですよね。それが、下の具体的な零因子の式と対応してないのはおかしくないですか?
=>[作者]: 連絡ありがとう.一般の場合と具体的な場合の関係ではありません.一般の場合と例外の場合の関係です.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/18.8.20]
このサイトいい復習になりました。ありがとう。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][恒等式 について/18.8.20]
(1)の定理の証明でxに0と1を代入して証明していますがこれだけでは「←」が示されたとは言えないと思います。全ての実数についてこの定理が成り立つような証明をしてもらいたいです
=>[作者]: 連絡ありがとう.「←」は,明らかだから明らかと書いているのです.証明は不要です.(0+0が0になることを証明する必要はない.)
■[個別の頁からの質問に対する回答][零因子 について/18.8.19]
零因子の作り方のところで質問です。
質問1 なぜ、(a.b) (c.d)の傾きをkとすると、これらは(a.ka)、(c.kc)とおくことができるんでしょうか?
質問2 1番したの行列の左零因子で、aが0で、kaが1となっています。行列に対応?する図ではy軸上を上に向かってすすむベクトルとなってますが、このベクトルの傾きは、1/0から定義できないですよね?ですが、この場合、aが0で、kaが1となっていますから0にkをかけたら1になるということになります。でも、0になにをかけても0ですよね。
ここで、この場合のkの値は何になるのでしょうか?
=>[作者]: 連絡ありがとう.質問1について:点(a,b)が傾きkの直線y=kx上に4あるときは,b=kaが成り立つから,(a, ka)とおけます.(c,d)についても同様です.
質問2について:上の図に上の式が対応しており,下の図に下の式が対応しており,上の式と下の式は対応していません.具体的に下の式について言うと
y軸に平行なベクトル
とx軸に平行なベクトル
は垂直だよね→
から
y軸に平行なベクトル
とx軸に平行なベクトル
は垂直だよね→
まで,下の図に描かれた4種類の垂直を確かめているだけです.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/18.8.19]
(4)はx^4-x^2×y^2+y^4ではないのですか?
=>[作者]: 連絡ありがとう.そこに解説がありますので読んでください.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/18.8.19]
公式に当てはめたものは計算していいのですか??
=>[作者]: 連絡ありがとう.まず当てはめて,次に計算します.そのページでは第1段階の当てはめが確実にできるように練習していますが,それができれば式を簡単にすることはすぐできるはずです.
■[個別の頁からの質問に対する回答][2進数の演算 について/18.8.18]
めちゃくちゃわかりやすかったです、参考になります
=>[作者]: 連絡ありがとう.言葉とイラストだけで知的なモヤモヤを解消するには,どこから切り込んで,どのように展開すれば分かり易いか,読者は何分まで持ちこたえられるか?この問題をほとんど毎日考えています.
■[個別の頁からの質問に対する回答][2次曲線の極方程式と媒介変数表示 について/18.8.17]
5.焦点を極とするときの二次曲線の極方程式の、''極とする''とはどういう意味なんでしょうか?
=>[作者]: 連絡ありがとう.ある点を極とすれば,その点のrは0になります.(x,y)座標の言い方で言えば,その点が原点になります.
■[個別の頁からの質問に対する回答][2次曲線の極方程式と媒介変数表示 について/18.8.17]
問題5の(4)の最大値の計算で、3/2+〈(5√5)/2〉(cos(2θ-α))を3/2+〈(5√5)/2〉(sin(2θ-α))として計算していませんか?
θ=π/4+α/2のとき最大値は3/2だと思うのですが
=>[作者]: 連絡ありがとう.重要なところを突いていますが,結論は微妙に違います.解答の結論は変わらず,途中経過の一部を訂正しました.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/18.8.17]
ひょんなことからチェビシェフの多項式のことを調べるはめになり、cos関数の加法定理ってなんだっけか、とググってたらこのサイトに出会いました。
高校生の頃にこのようなページがあれば良かったなぁ、と思いました。
まぁ、40年以上前のことなのであり得ませんが(^^;
これからも分かり易い解説、宜しくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面の入試問題3 について/18.8.15]
問題2.1(福岡教育大2016年の問題)の(2)ですが、答えは0なのに、0をクリックすると×になり、-1をクリックすると〇になります。
ミスではないでしょうか。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][複素数平面の入試問題 について/18.8.14]
例題3.2で、z≠βは示されていますが、(zの共役複素数をz_、βの共役複素数をβ_として)z_≠β_は示されていません。複素数=複素数だったら互いに共役複素数をとっても=関係が成立するみたいな定理があるんでしょうか?
=>[作者]: 連絡ありがとう.
真であるものがすべて定理であるわけではない.汎用性があって重宝するものしか定理とは呼ばない.だから,個別の式を変形しただけの結果は,目で確かめるだけでよい.
のとき
ならば,
または
だから
と
は等しくない.
■[個別の頁からの質問に対する回答][複素数平面の入試問題 について/18.8.13]
例題1.2と問題1の(2)で質問です。
どちらの問題とも因数分解の形にできていないですけれど、何を目標に式変形をしていけばいいのでしょうか?また、その目標を達成するためにどのように式変形をしていけばいいかも教えて欲しいです
=>[作者]: 連絡ありがとう.複素数平面で,中心がα,半径がrの円の方程式は
だから
すなわち
の形を目指して変形します.
■[個別の頁からの質問に対する回答][間接的に求める について/18.8.13]
例題2の解説(ア)の(1)、途中計算式2行目で、【log(sinx+cosx)】(積分区間0からπ/2)となっていますが、途中計算式1行目の右辺の与関数の分子がマイナス分母を微分したものとなっていますから、途中計算式2行目は、-【log(sinx+cosx)】(積分区間0からπ/2)ではないでしょうか?(logの前にはマイナスがつくのではということです)
=>[作者]: 連絡ありがとう.符号を訂正しました.
■[個別の頁からの質問に対する回答][重要な極限値(1) について/18.8.13]
ありがとう
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/18.8.11]
たすき掛け因数分解1の問題4 2問/5問についての確認です。
解答は(3x-5y+1)(5x-4y+1)ですが、(-3x+5y-1)(-5x+4y-1)も正解ではないでしょうか?
=>[作者]: 連絡ありがとう.問題,途中経過,解答はプログラムで生成していますので,第何問がどういう問題になるのかは,見ている人によって違います.さて,問題文に灰色で書いていますように,「x の項を前に書くこと.先頭の符号を負にしないこと」という条件を外してしまうと,同じ答案が何通りも書けることになります.(3x-5y+1)(5x-4y+1)と(-3x+5y-1)(-5x+4y-1)は同じものですが,採点の都合で(5y-3x-1)(4y-5x-1)や(-3x+5y-1)(-5x+4y-1)でなく,(3x-5y+1)(5x-4y+1)のように書いてくださいということです.[かっこ内の順序の入れ替え,符号の入れ替え,かっこの前後の入れ替えで144通りの書き方ができますが,x の項を前に書くこと.先頭の符号を負にしないことで2通りになります]
■[個別の頁からの質問に対する回答][if 分岐 について/18.8.11]
本頁中の記述に『それ以外はせ真=true』とありますが、『せ真』の意味が分かりません
=>[作者]: 連絡ありがとう.漢字変換のミスが,そのままになっていましたので,訂正しました
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積2 について/18.8.9]
問題1のオは、左斜めの向きで変化するのでは。t=0のときの座標が(0.3)t=1のときの座標が(1.0)ですから
=>[作者]: 連絡ありがとう.(0,3)→(1, 0)で右下がりなので,元の教材で正しいです.(6)のy2の部分に相当
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.8.8]
問題3の(2)の解説部分について 本文では(x+y)2+(y+z)2+(z+x)2=(-z)2+(-x)2+(-y)2とありますが(x+y)2+(y+z)2+(z+x)2=x2+y2+z2ではないでしょうか。(符合がマイナスになっている。)私の指摘が間違っているようでしたら、なぜそれが間違いなのかの解説もいただけると助かります。
=>[作者]: 連絡ありがとう.あなたの指摘は間違っています.その原因は問題を読んでいないからです.2 =(−z)2 =z2 .以下同様マイナスがあってもなくても2乗すれば正です.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積 について/18.8.8]
問題5の定義域は、1≦x≦3ではなく、-1≦x≦-3では。そのため、答えも異なるので問題の訂正が必要かと
=>[作者]: 連絡ありがとう.-1≦x≦-3ということはありません(-1が-3よりも小さい[以下]ということはない).左図のようになりますので,元の答案で正しいです.2次不等式の解き方があなたの弱点ですので簡単に復習しておくとよいでしょう.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積 について/18.8.7]
例1のS=の式で、-(-√2^2-x^2なのに、-(√2^2-x^2になっています
=>[作者]: 連絡ありがとう.元のままだと消えてなくなりますので,訂正しました.
■[個別の頁からの質問に対する回答][組分け について/18.8.6]
手持ちの教科書に次のように例題とその回答が載っていますが、どうも納得できません。
例題:7人を次のようにする方法は、何通りあるか。
(1)部屋A,B,Cに2人ずつ入れ、部屋Dに1人入れる。
教科書記載の解答:7C2×5C2×3C2=630通り
私の思う解答:630×3×2=3780通り
教科書記載の解答は、ただ2人、2人、2人、1人にわけただけであり、本来は3つの2人組をABC3つの部屋に振り分ける順列3P3をかける必要があると考えています。
(2)2人、2人、2人、1人の4組に分ける。
教科書記載の解答:(1)でABCの区別をなくすと、同じものが3!通りずつできるから、求める方法の総数は630/(3!)=105通り
私の思う解答:7C2×5C2×3C2=630通り
私の考えはおかしいですか?
お手数ですが、ご協力いただけませんでしょうか。
よろしくお願いします。
[追伸]教科書の組分けの例題が分からずに先ほど質問しましたが、自力で分かりました。お手数おかけしました。
=>[作者]: 連絡ありがとう.分かったのでもうよいということですが,順列・組合せ・確率の問題で解き方・考え方が正しいかどうかを確かめる方法を,長年考えてきました…他の問題なら,グラフを描くなど別の根拠を示すことができますが,順列・組合せ・確率の問題に対して,何が示せるのか?
あなたの疑問に対しては「問題を単純化しても成り立つかどうか調べる」という方法があると思います.つまり,3人を部屋A,B,Cに1人ずつ入れる方法は
(通り)
これに対して,3人を1人ずつ3組に分ける方法は
(通り)
このように,そのページの先頭にある「■部屋に名前(区別)がある場合--これが基本」と書いたように
は部屋に区別がある場合に対応しています.
■山形県[マンサン/18.8.6]
この「高校数学の基本問題」を利用させていただき感謝、感謝です。
そして、ご報告ですが、遂に「高校数学」+「大学基礎程度」までを完全履修(…完全写記)することができました。時間的には2年弱かかりました。(…途中確認の為におさらいで「中学数学」をざっと済ませました。) その間で「漸化式」「三角関数の不定積分」など難関で挫折しそうになりましたが、何とか頑張り通しました。学習を進めているうちに、高校数学の量が多いのに驚きました。私の若い時もこんなにあったのだと、今更ながら、驚きです。他の科目もありますしね。
いつの日か「高校数学」をやり直したいと思っていたのは、大学を卒業してからの事です。私が大学入学の年に、あの有名な「学園紛争」があり、1年教養課程での数学等が半端になってしまったからです。その大学数学を学ぶためには、その前の高校数学を理解しておく必要があり、そのために、時間のできたとき、いずれ数学をやり直そうと考えてきました。そして、本講座にめぐりあい、始めたというわけです。パソコン・インターネットがこんなにも普及した時代でなければ、叶わぬことだったでしょうね。お蔭様で、高校数学全体を理解することができ、又、全体的に理解しやすく書かれていた内容でしたので、助かりましたし、終了してみて最後まで頑張り通して本当に良かったと今感じております。只々感謝感謝です。
付け加えますと、この後は、「微分・積分」「線型代数」の一段上を学びたいと考えております。何か良いサイトがありましたらご紹介ください。どこまでやれるかわかりませんが、…頑張ります。皆様も頑張ってくださいね、蔭ながら応援しております…2018.8.6
=>[作者]: 連絡ありがとう.サイトはわかりませんが,教科書として出版されたものが無難だと思います.
■山形県[マンサン/18.8.6]
いつもこの数学講座を利用させていただき感謝しております。
これが修正依頼メールの最後になると思います。「高卒から大学基礎程度」中の行列式関連の「*連立方程式…掃出し法」中の【具体例による解説】3×3の場合について…
中央yの係数操作で
[1] A) 2行2列成分が0でなければ,2行目をその成分で割る
図5の右側から出発したとき,図6のようになります
とありますが、これは
➩図4の右側から出発したとき,図5のようになります
そして
[2] ……図4の右側から出発したとき,図4のようになります
とありますが、これは
➩図5の右側から出発したとき,図6のようになります
が良いのではないでしょうか
…以上ですが宜しくご検証ください。2018.8.6
=>[作者]: 連絡ありがとう.縦方向に長くなって点検が大変ですが,訂正しました.
■[個別の頁からの質問に対する回答][三角関数の定積分(絶対値付き) について/18.8.6]
問題1の解説で、積分されていないです。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][領域における最大最小 について/18.8.5]
いつも参考にしています。
以下 ご教授下さい
[解答] x≧0 , y≧0 , x+2y≦8 , 3x+y≦9 の領域は図の通り.
また,x+y=k すなわち y= - x+k とおくと,図の赤で示した直線になる.
傾きについては - 3<-1< - 1/3 が成り立つから,k が最大となるのは,(0 , 4) や (3 , 0)ではなく交点 (2 , 3) になることに注意する
☆質問)傾きー1/3はどこから出てくるのですか
x+2y=k すなわち y= - 12x+k2 とおく
2x+y=8 , x+3y=9 の交点は,(3 , 2)
図の四角形の領域(内部及び周上)において k の値は,切片 k2 が最大となるときに最大となる.
- 3< - 1/2< - 1/3 だから,交点 (3 , 2) において最大値をとる.最大値は 7
☆質問)傾き-3はどこから出てくるのですか?
=>[作者]: 連絡ありがとう.どの問題のことなのかを書かないと,推定で答えることになります.
■[個別の頁からの質問に対する回答][指数法則 について/18.8.3]
非常にわかりやすいです。もっと複雑な問題が欲しい気もします。
=>[作者]: 連絡ありがとう.そのページは基本の入り口です.ページの先頭にメニューがありますので,続きを見てください.
■[個別の頁からの質問に対する回答][ベクトル内積(成分) について/18.8.2]
丁寧な説明をありがとうございます。
(参考)で、「ところで基本ベクトル→eと→bの内積については」になっています。皆さん自然に読み直すと思いますが。
=>[作者]: 連絡ありがとう.訂正しました.
■山形県[マンサン/18.8.1]
いつもこの数学講座を利用させていただき感謝しております。
今回の投稿は、すべきかどうかで悩みましたが、このサイトを利用している方々が多いし、私のように苦労してほしくないので、連絡すべきと考え、投稿しました。
「高卒から大学基礎程度」中の行列式関連の「連立方程式(クラメールの公式)」という課題で、最後の出題されている「問題5」についての「誤り」についてです。
この問題に着手したとき、付属の答で、暗算で答えを出しておけば、苦労せずに済んだのですが、素直に始めてみたものの、どうしても答えが合わず、何度やっても係数行列式が「12」にならない…計算中に良く「+・-」のミスをすることが多い私ですが、何度やってもxの答が出ない…仕方なく、問題の答を問題で検算したところ、どの答えも当てはまらない…しかし、どこに問題があるのか、と考えていたら、すぐにその原因が分かりました…「問題5」自体が間違っているのです…これが結論です…多分先生方を含めて、このサイトを学習している方々なら直ぐにわかるでしょうから、正解はここでは書きません…ヒントは問題中のyの係数3つのうちの一つの「+・―」が反対です。それを修正すると、係数行列の答が「12」になり、連立方程式の答もきちんと合致します。
先の課題の「行列式(数値計算)」の最後にある「自由研究」の「4次の行列計算」ソフトがありますから、ご確認ください。どうぞ宜しくお願い致します。乱筆・乱文御免なさい。…こんな風に書くと、「年寄」だというのがバレバレですね。…
=>[作者]: 連絡ありがとう.元のままだと (-1,-6,-1,2)が解になるので,選択肢に合うように問題の方を書き換えました.
■[個別の頁からの質問に対する回答][N進数の小数 について/18.7.31]
【例8】の(解説)の小数点第二位の8は1の間違いではないですか?
=>[作者]: 連絡ありがとう.小数第1位と第2位を読み間違えたようです.途中経過が違うだけでなく,解答も違っていましたので訂正しました.(ボロボロ答案)
■[個別の頁からの質問に対する回答][対数計算1 について/18.7.30]
すごくわかりやすかったです
ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率のセンター試験問題 について/18.7.29]
一番最初のトランプの確率の(2)の解説がわからないです。
=>[作者]: 連絡ありがとう.その図を見て何か感じ取らないと…
順列/順列で考えるときは:カードのとり方の総数は,N=20×19×18通り.そのうちで,色も番号も違うカードをとる方法は,図のように1つ目のカードのとり方は黄色の20通り(とりあえず●のカードだったとする).1つ目のカードと色も番号も違うカードは,水色の12通り.(とりあえず次の●のカードだったとする).3つ目に前の2つと色も番号も違うカードをとる方法は,灰色で示した6通り.以上により
この計算は
になっていますが,(同時にこだわって)組合せ/組合せで考えるときは:
にするということです.
■[個別の頁からの質問に対する回答][ベクトルの平行条件,垂直条件 について/18.7.29]
例2は25t^2ではなく5t^2ではありませんか?
=>[作者]: 連絡ありがとう.
だから
です.1段階省略がありますが,瞬間の暗算ということです.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/18.7.28]
問題1ー5のkは何故はずれるんですか?ωの6k乗は1の2k乗になるんじゃないですか?
=>[作者]: 連絡ありがとう.「特急券」は使いましたか?ω3 =1 だからω3k =(13 )k =1k =1, ω6k =(13 )2k =12k =1 だよね.他に何か言う必要ありますか?
■[個別の頁からの質問に対する回答][ 三角関数のグラフ について/18.7.28]
解答ください
=>[作者]: 連絡ありがとう.解答を選択して,HELPを押せば,解答は出ます.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.7.28]
基本の形の(2)(iii)の(*)で、(b)を(a)に代入するととありますが、…(a)が抜けているので、…(a)がさす場所に、…(a)をつけてほしいです。
=>[作者]: 連絡ありがとう.加筆修正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式3 について/18.7.27]
「その考え方に至った経緯は書かなくて良い」
って、テストに書かなくてもいいかもしれませんが、ここには書いてください。突然言われても
=>[作者]: 連絡ありがとう.やってみれば分かり,やってみないと分からない,ということが世の中にはあるのです.
■[個別の頁からの質問に対する回答][三角測量 について/18.7.27]
素晴らしい教材をありがとうございます。感謝しております。
細かいことなのですが、[問題2]-(3)の三角形に直角記号が抜けております。失礼いたしました。
=>[作者]: 連絡ありがとう.加筆修正しました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/18.7.26]
dx^2/dt^2=-a^2xとなっているときに解がx=Ccos(at+δ)と表されることについても書いてほしい
=>[作者]: 連絡ありがとう.【要点】2の場合で
すなわち
に対応する2次方程式は
解は
次に数学Ⅱの三角関数の合成公式により
と変形します
■[個別の頁からの質問に対する回答][分数関数の不定積分 について/18.7.26]
コメント失礼しますm(__)m
一番したの問題のところの(4)の答えの選択肢が教材だと、1/(x+1)+log|x/(x+1)+C (選択肢一番右の行の上から2列目)となっていますが、正しくは、-1/(x+1)+log|x/(x+1)+Cではないでしょうか?
私の計算ミスでしたらすいません。
=>[作者]: 連絡ありがとう.
です
■[個別の頁からの質問に対する回答][増減.極値.凹凸.変曲点.漸近線.グラフ について/18.7.25]
コメント失礼しますm(__)m
変曲点の説明が、この項と数3微分の項をみてもこの教材ではまだ載ってなかったのでよければ載せてほしいです。また、変曲点を求めるために、2階微分をすると思うのですが、2階微分(n階微分についてもできたら)の説明も載せて欲しいです。
=>[作者]: 連絡ありがとう.変曲点や第2次導関数を単独に取り上げたページはまだ作っていなったようですので,検討します.項目数が多くなってくると,どこに何が書いているかは言えますが,どこに何が「書いてない」のかは簡単には言えないので,言われてから考えることになります.
■[個別の頁からの質問に対する回答][逆行列の求め方 について/18.7.25]
余因子行列のところで対角成分の計算はA ~Aではなく~A Aではないでしょうか?
=>[作者]: 連絡ありがとう.
が成り立つので,どちらでやってもよい.
■[個別の頁からの質問に対する回答][ベクトル内積(成分) について/18.7.24]
a→とb→の内積は公式より|a||b| cosθではないんですか?a→とb→の内積を求めるとき上の式だとa→・b→=a→×b→のようになっているのですが正しいのですか?
=>[作者]: 連絡ありがとう.
はそこに書いた通りです.それを質問してどうなる?「上の式だと」とはどの式のことですか?外積とは違うと書いてありますが,しっかり読みましたか?
■[個別の頁からの質問に対する回答][ ベクトルの和 について/18.7.24]
a→+b→=z→とした場合、|z→|= |a→|+|b→|なのですか?例えば、a→=2→、b→=3→の場合、2→+3→=5→なのですか?一般的にいうと|z→|つまり|a→+b→|=|a→|+|b→|は成り立ちますか?
=>[作者]: 連絡ありがとう.教材の内容と質問の内容が食い違っています.
このページ の危険な落とし穴というところを読んでください.
結論から言えば,全然違います.また質問にも使ってはいけない記号を使っていますので要注意です.
など,全然勉強していない生徒の答案になっています.書くのなら,
などと書くべきです.
a→+b→=z→とした場合、|z→|= |a→|+|b→|なのですか?は
とした場合,
なのですかということで,質問としては成り立っています.ただし,
このページ の危険な落とし穴に書いたように,一般には
です.もっとはっきり言えば,
は三角形の2辺の長さの和で,
は三角形の他の1辺の長さだから,
です.(
との違いに注意)
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.7.24]
コメント失礼しますm(__)m
この形の不定積分はのところで逆関数の微分を用いるととあるのですが、これは高校範囲なのでしょうか?この教材の数3の関数のところと微分のところではなかったです。
また、この形の不定積分はのところと特急券のところで、置換積分という文言がありますが、この段階では未習なので、公式を覚えて導出は後回しでもいいんでしょうか?それとも、置換積分のところを先に学習したほうがいいんでしょうか?
加えてこの形の不定積分のところでは逆三角関数の微分がありますが、公式を覚える前にこれを学習して公式を導出できた方がいいんでしょうか?
=>[作者]: 連絡ありがとう.(1)「この形の不定積分は逆三角関数が登場するので高校では扱わない.ただし,定積分は「定数」になるので高校数学で扱う.」と書いてある通りです.(2)「置換積分」の件:どちらが先でも構いませんが,できるようにすべきです.(3)「逆三角関数の微分」について:この教材を読んでいるのは,高校生だけではありません.高校生が卒業単位認定のために必要か,高校生が大学入試のために必要か,卒業生が復習しているときに必要か,は立場によって違います.高校の卒業単位認定のためだけに限定すれば必要ないということは初めに示しています.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.7.24]
コメント失礼しますm(__)m
↓この頁では既習事項と考えている問題
のこめじるし
の(イ)の
合成関数微分法の途中式が違っています
dy/dx= dt/dx・dy/dtではなく、dy/dt・dt/dxです。
訂正お願いします
=>[作者]: 連絡ありがとう.質問・指摘の趣旨が不明です.dy/dx= dt/dx・dy/dt と dy/dx=dy/dt・dt/dx は同じものです.
■[個別の頁からの質問に対する回答][循環小数の計算 について/18.7.23]
コメント失礼しますm(__)m
無限等比級数については、この教材で、この項で初でてきた言葉なので、それについての説明がほしいです。あと、無限等比級数和の公式も載せて欲しいです。有名な公式ですし、ちょっと検索すれば出てきますけど載せて欲しいです。
=>[作者]: 連絡ありがとう.確かに級数の内容が薄いので,加筆しなければならないようです.
級数と言えば,言葉のマジックにかからないように気を付けないといけない部分があります.
数列:a1 , a2 , a3 , …, an a1 +a2 +a3 +…+an
であるのに対して
無限級数:a1 +a2 +a3 +…+an +…
数日中に教材を作ります.
■[個別の頁からの質問に対する回答][Excelを用いた度数分布表の作成[1] について/18.7.23]
人によりますが、私には金魚はいいですね。
=>[作者]: 連絡ありがとう.多少なりとも気持ちに余裕のある人の感想だと思う.動くものがあると全く勉強が手につかないという傾向の人が何%いて,その場合は上端の「水槽を消す」を押してもらうという想定になっています.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/18.7.21]
ω^2もωと同様にω~2+ω+1が成り立つという証明と共約複素数にも触れたほうがいいかなと思った
=>[作者]: 連絡ありがとう.証明も共約複素数のことも書いてありますが,明示的に示してないということかな?
■[個別の頁からの質問に対する回答][一般角の定義 について/18.7.21]
数学好きの僕にはたまらないwebだよ‼
本当にありがとう‼( ≧∀≦)ノ
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][媒介変数表示 について/18.7.21]
コメント失礼しますm(__)m
ここに書かれている曲線は全て、各々の図形的な意味を理解して、各々の曲線を表す方程式を覚えないといけないのでしょうか?
=>[作者]: 連絡ありがとう.義務教育(中学生)向けに出題する公立高校入試では「全ての教科書に出ている内容しか出題してはいけない」が,高校生向けに出題する大学入試では「1社でも教科書に書いてあれば出題してよい」と言われたことがある.どの程度守られる暗黙のルールかよくわかりませんが,一応の目安にはなる.ところで,K社の教科書には,サイクロイド,アステロイド,カージオイド,ハイポトロコイド,リサージュ,正葉曲線,アルキメデスの螺線,ハイポサイクロイドなどほとんど網羅されています.では,どうなるのか.
■[個別の頁からの質問に対する回答][階差数列 について/18.7.20]
Σの中が二次関数の場合の公式は存在するでしょうか。
=>[作者]: 連絡ありがとう.
自然数の累乗の和 のページに書いています.
だから
あとは,必要に応じて因数分解などして使いやすい形にします.
■[個別の頁からの質問に対する回答][指数法則 について/18.7.19]
授業聞いてもわからなくて、必死に調べてたどり着いたのがこのサイトでした。すごくわかりやすくて、解説もバッチグーです!
=>[作者]: 連絡ありがとう.点検のついでにコメント欄もすっきりさせておきました.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/18.7.18]
3分の2の6分の1乗を(2の6分の1乗×3の-6分の1乗)にするような例題もあってもいいかも。自分はこのサイトをみていたらひらめくことができましたが分数を分解することに気づかない人もいるはず
=>[作者]: 連絡ありがとう.すべての材料を横に並べるのは,管理人おすすめの方法と一致します:なんでもかんでも
に直す.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/18.7.17]
コメント失礼しますm(__)m
lim x→0 (e^x + x )^1/x という問題をネットで見つけたのですが解けなくて困っています;_;
よければ解いていただけないでしょうか?
=>[作者]: 連絡ありがとう.よそ様の問題には干渉しないようにしています(
wxMaxima に問題を書き込めば答えが出ます:e
2 )
■[個別の頁からの質問に対する回答][2文字のたすき掛け因数分解 について/18.7.17]
多くの良問を有難うごいます。
1点だけ感想を:正解に対する「ごちになります」、不正解に対する「・・・ワ~大変だ」がいまひとつピンときませんでした。
=>[作者]: 連絡ありがとう.正解か不正解かが分かれば最小限の働きをしているものと….
■[個別の頁からの質問に対する回答][放物線 について/18.7.16]
コメント失礼しますm(__)m
放物線の標準形のところで、要点1要点2ともに、焦点が頂点になっています。ので、頂点を焦点に訂正お願いしますm(__)m
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][根号計算の入試問題 について/18.7.16]
[4]二重根号の【要点3】の a>0,b>0,a>bのとき の(例)の一行目の右辺√2の符号は-でないでしょうか?
=>[作者]: 連絡ありがとう.間違わなくてもいい所で間違っていますが,別にわざとではない.管理人にも,それなりの事情があるかもしれん.訂正しました.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/18.7.16]
コメント失礼しますm(__)m
この分野で3日くらいつまづいていて困っています。この指数対数関数の微分の分野って、ここまで登場した極限値のまとめのところの極限値の導出をできるようにして、問題を解くときはこのような極限値の形に帰着できるようにしていくものなんでしょうか?
なかなか問題が解けるようにならないので、どう勉強していけばいいか教えて欲しいですm(__)m
=>[作者]: 連絡ありがとう.極限値にまで遡っている問題(3.のような問題)が出たら,定義に戻って極限値を求めます.普通の場合(4.のような問題)は,
により機械的に処理します
■[個別の頁からの質問に対する回答][点の存在範囲 について/18.7.15]
s+t=1,s≧0の条件ときの点Pの存在範囲があると分かりやすい。
=>[作者]: 連絡ありがとう.見た目の通りで,s+t=1は直線AB,s≧0はOBの上(以上)だから,直線ABのBよりもA側の半直線
■[個別の頁からの質問に対する回答][2直線の交点(3通り) について/18.7.15]
【要点3:直線の交点をベクトルや複素数で求める方法】
において、OCベクトルを2/5aベクトルと書かれてますが、3/5aベクトルの間違いかと思われます。
ご確認おねがいします。
=>[作者]: 連絡ありがとう.いかん,いかん,得意の計算間違いでしたので,訂正しました.(こんな調子で,ん十年勤まったとは,どんなゆるい職場?)
■[個別の頁からの質問に対する回答][余弦定理 について/18.7.14]
いつもお世話になっております。【問題3】の(2)ですが正弦定理のみで解けますか?
=>[作者]: 連絡ありがとう.無前提に「正弦定理のみで解けますか?」と尋ねられれば,解けますと答えますが,「数学Ⅰの正弦定理のみで解けますか?」と尋ねられれば,無理ですと答えます.たぶん,BからCを求めるために数学Ⅱの加法定理(*)が必要になります.そのような迂遠なことをしなくても,余弦定理で一発解決なので,余弦定理の方がよいでしょう.
次の作戦盤に沿って,順に求めます.( )内は既知
により
次に
だから
…(*)
により
したがって
加法定理
と三角関数の相互関係
を使うと… ←(*)
■[個別の頁からの質問に対する回答][関数の連続,極限関数 について/18.7.13]
コメント失礼します(m(__)m
いくつか改善してほしいところと誤植が見られるところがあるので下に書かさせていただきます。
1つめ、問題(1)のガウス記号を含む関数の極限のところで、数2の微分のこのサイトの教材で、多項式の極限値は関数値と等しいと書いてあったのですが、ガウス記号はこの問題でいうと→3の3をただ代入するわけにはいかないですよね。不定形や発散したり収束したりする関数の極限はこのサイトで扱われていましたが、ガウス記号の関数?は今回が初登場でしたので、説明をくわえてほしいです。
2つめ、(2)の問題で、f(x)={5-1/x (x≠0のとき)とありますが、この-1/xの文字が小さくて、指数を表しているのか、ただ単に項を表しているのかわからないです。レイアウトがちょっと変なので確認して修正して欲しいです。
3つめ、(3)の計算1の2段目の式変形の中辺で、x^nでくくっているはずなのに、くくっているx^nが抜けています。修正してほしいです。
4つめ、(4)の計算1の2行目の計算、lim n→∞ 〔x^(2n+1)+1〕/x^2n-x=1/-xで、nが∞近づいて?いるからか、nに関係ない右辺の1/-xの-xが余ってますが、近づいていく文字に関係ない変数は、極限値をとったときに余るよみたいなことをどこかしらに書いて欲しいです。私の理解不足なのかもしれませんが、ちょっと混乱しました。
=>[作者]: 連絡ありがとう.(1)切り上げ,切り捨て,四捨五入などの階段状関数は多項式ではありませんから,極限値と関数値が一致するとは限りません.(2)少し上げました.(3)分母分子の両方にあるので約分しています.(4)
において極限を考えるのはnの関係式だけです.
■[個別の頁からの質問に対する回答][展開公式1 について/18.7.13]
65才になり約50年ぶりに高校数学に(再)挑戦してみました。実に分かりやすく楽しめました。有難うございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の方程式 について/18.7.13]
わかりやすい解説もついていて、途中式も丁寧に書かれてるので理解しやすかった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角形の重心,内心,外心,垂心(ベクトル,三角関数) について/18.7.12]
勉強になりました。ありがとうございます。
角の2等分線の説明のでは、AB=b AC=c ですが、内心の解説では、AB=c, AC=bとなっており、読んでいて躊躇しました。
また、内心の解説で、BP:PC=AB:AC=b:c と記述があります。図からは、 BP:PC=AB:AC=c:b となります。後者が正しいと思いますがいかがでしょうか。
角の2等分線の説明の記号は、ABCを使わず、UVRとか別な記号を使うといいかもです。
=>[作者]: 連絡ありがとう.図の方を直しました.
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/18.7.11]
なかなかよかったぞ
=>[作者]: 連絡ありがとう.この内容は,他では読めないかも
■[個別の頁からの質問に対する回答][分数関数の不定積分 について/18.7.11]
ウェブ上で問題を解くことができるところはいいと思う
が、採点をするを押してもイラストが表示されるだけで回答は表示されない
回答まで表示していただきたい
=>[作者]: 連絡ありがとう.計算1,計算2で詳細な途中経過が表示されますが,…さらに解答も表示できるようにしました.(ぶつぶつ)
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/18.7.11]
とてもいい!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][直線のベクトル方程式 について/18.7.11]
問題2の解答に青字で「BE:EC=14:5」と記載がありますが、問題分に「BCを6:5に内分する点をE」と記載されているのでBE:ECは6:5ではないですか?
=>[作者]: 連絡ありがとう.前の問題の解答を引きずってきたのかどうか,よく分かりませんが,余計なことが書いてありましたので削除しました.
■[個別の頁からの質問に対する回答][展開公式 について/18.7.09]
数学の記録が付きません。どうしたら良いでしょうか。
=>[作者]: 連絡ありがとう.機種によって,そういう問題があることは認識していますが,リアルタイムで動かしながらデータ形式を変更する(ホットスワップもどきに)と何が起こるか分からないので,延び延びになっています.
■[個別の頁からの質問に対する回答][2文字のたすき掛け因数分解 について/18.7.09]
このページの一番最初の設問は、式の後半が-6(2y-1)(y-3)と-6が前に出て、考えさせられる良問ですね。このパターンの練習問題が数問増えると嬉しいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][変数分離形.微分方程式の解き方 について/18.7.08]
一つ一つの式の途中式、解説が書いてあり、非常に分かりやすいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][放物線 について/18.7.08]
X^2=4yの焦点の求め方が分かりません。
=>[作者]: 連絡ありがとう.教材を書いた当時は,前から読むと公式そのものだから省略できると考えたようで,確かに直接的には書いてないようです.何らかのまとめ的なものを加筆します.
ご質問の点については
(1) 公式に当てはめる場合:
で縦横が逆だから
焦点の座標は
(2) (1)の内容を確かめるには,焦点の座標を
,準線の方程式を
,動点の座標を
とすると,
だから
が成り立つ.
■[個別の頁からの質問に対する回答][2次関数のグラフ について/18.7.07]
悪いところありません。このサイトのおかげで理解度が増しました
感謝します
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][隣り合う並び方・隣り合わない並び方 について/18.7.06]
選択式よりも文字で入力する式にしたほうがいいと思います。
=>[作者]: 連絡ありがとう.パソコンを使ったいわゆるCAIの時代には,そのような考え方が多かったが,あなたのようにスマホで学習している人がほとんどになったため,現在この教材の管理人はそのようには考えません.調査結果と考察を
PDFファイル:486KB にまとめています.要望事項に関する内容は「4. 第二方向:学習者の入力方式はどんなものがよいか」に書いています.
■[個別の頁からの質問に対する回答][三角比の相互関係 について/18.7.06]
例題2の答えは、±2ルート2では?
=>[作者]: 連絡ありがとう.例1のように,
において
のとき,Aは第1象限,第2象限の2つの可能性がありますが,例2のように,
において
のときは,第1象限
だけになります.この違いは重要ですので覚えておくようにしましょう.
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/18.7.04]
難しい
=>[作者]: 連絡ありがとう.まだ習っていない人や一応習った(一応読んだ)が演習はこれが1回目という場合には,難しいのが普通です.公式に当てはめるだけの問題なので,時間をかけてやればできるようになるはずで,2回目以降(復習など)で「難しい」と言う感想はあり得ません.
■[個別の頁からの質問に対する回答][数学的帰納法とは について/18.7.04]
非常に詳しく書かれていてすごいテキストだと感じました。
質問ですが、例1において
【※ n=1 のとき,左辺は 1+3+5+ … +1 にはならない.この式は 1 から順に 2n - 1 まで足すことを分かりやすく初めの2,3項を例として示したものなので, n=1 のときは +3+5 は付かない.(当然!!)】
とあり、言いたいことはわかりますが、もやもやします。
列挙の形で記述するときは右側の項2n-1=f(n)のnが左側の項5=f(3)の3以上である、という「列挙の基本」(列挙の原理?)があると習いました。
例えば、階差数列の一般項を求めるとき∑(k:1~n-1)b(k)でシグマ部分に列挙の原理が成り立つからn=1のときは分けて考えるという習い方をしたので
列挙やシグマをみるとこの原理には注意するようにしています。
例題では、実際解くときは揚げ足とりっぽいので自分でもそんなことはしないと思いますが、
i)でn=1,2,3まで示して
ii)でn=k(k≧3)のとき
としないと気持ち悪いです。
入試問題でも同じような書き方を見たことがありますが、(「a1a2+a2a3+……ana(n+1)=」のような問題)
厳密な書き方とかにあまりこだわらないほうが精神衛生上良いでしょうか?
=>[作者]: 連絡ありがとう.どこの教科書でも,このような場合は書いている人も読んでいる人も,表されている内容が分かっているものとして記述しています.だから,「ii)でn=k(k≧4 )のとき」などと分ける必要はありません.私の教材で(当然!!)という注意書きを書いたのは,式や図が表している「内容」を思い浮かべることができずに,式や図「そのもの」の外形的特徴にこだわっていく傾向の生徒が実際にいるからそのように書いたまでです.
■[個別の頁からの質問に対する回答][sin(π+θ)など について/18.7.03]
cos(θ-3π/2)は-cos(3π/2+θ)よりsinθになると思うのですが・・
=>[作者]: 連絡ありがとう.
三角関数の性質 にありますように,
は偶関数,すなわち
が成り立ちます.(
とは異なり,
になっても,符号は変化しません.間違いやすいものです).
したがって,
です.
の図で示しています.
この場所で,
だから,第1象限の図に直すと
です.
■[個別の頁からの質問に対する回答][三角関数の性質 について/18.7.03]
問題2/5でcos(θ-270)をcos(270-θ)に変形させていますが-cos(270-θ)ではないでしょうか?
ご確認よろしくお願いします。
=>[作者]: 連絡ありがとう.先頭の解説(8)にありますように,
は偶関数,すなわち
が成り立ちます.(
とは異なり,
になっても,符号は変化しません.間違いやすいものです).
したがって,
です.
■[個別の頁からの質問に対する回答][対数の定義 について/18.7.02]
わかりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数 について/18.7.01]
コメント失礼しますm(__)m 数3をこのサイトで学習していて思ったのですが、私は最初複素数平面から始め、その後微分法のところをやろうと思ったのですが、数3微分ではこの学習サイトの''関数''のところをやってからだなと思い関数のところを学習していたのですが、逆関数のところでlogとeが出てくる関数があって、eをやってからじゃないといけないなと思い、調べたところ微分法の範囲にあることを知り、ちょうど関数の学習をある程度終えていたので順調に学習が進んでいたのですが、媒介変数表示の微分まで来て媒介変数のところをとばしていたので、媒介変数のところを(サイクロイドのところ)までやってまた微分のところに戻ったのですが、三角関数の微分がどうやら必要ぽくってこれからやろうと思ったところなのですが、長々となってしまい申し訳ないのですが、このように、どの順番で学習を進めていけばいいのかわからなくて困ってます。どの順番で学習していくのがよいのでしょうか?
=>[作者]: 連絡ありがとう.主要な(基本の)内容は,教科書の目次の順に学ぶようになっています:①2次曲線,媒介変数と極座標;②複素数平面;③数列の極限,関数の極限;④微分;⑤積分.[教科書会社によって①②を逆にする場合があります]
ただし,「融合的な内容」,例えば指数の対数乗
を考えると,指数関数と対数関数のどちらを先にやってもできないように見えますが,一巡基本を押さえてから,振り返るようにします.高い山に登るときは,まっすぐに上る一本道があるのではなく,4000M地点から5000M地点を往復して,高地順応しながら荷物を上げるように,行ったり来たりするということです.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.6.30]
問題3の③解説について
x3+y3+z3=3xyz+(x+y+z)(x2+y2+z2-xy-yz-zx)
から
x3+y3+z3=3xyz=3(a-b)(b-c)(c-a)
までの過程がわかりませんでした
x3+y3+z3=3xyz
となる解説をお願いします。
=>[作者]: 連絡ありがとう.問題にx=a−b, y=b−c, z=c−aと書いてあるのだから,x+y+z=0です
■[個別の頁からの質問に対する回答][因数分解(応用問題) について/18.6.29]
問題3の(2)の細かい解説が欲しかったです。
例題と+、-、が違ったりするので解説がもうちょっとあると、とても助かります。
=>[作者]: 連絡ありがとう.解説はあります.他に何を言えばよいのか?
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/18.6.29]
大問2の答えが偏ってるのが気になりました。
=>[作者]: 連絡ありがとう.例えば,どの選択肢も同じ頻度で登場するという場合,それはそれで一定の規則に縛られていることになります.このように宝くじのあたり番号で同じ番号が続いてはいけないというルールはないのです.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/18.6.29]
分かりやすくていいと思います
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.6.28]
[4] 行列の対角化を意識して解く方法のPがあらかじめ提示されてましたがPを求める方法が知りたいです
=>[作者]: 連絡ありがとう.その内容は完全に高校数学の範囲を外れますので,
このページ を見てください.
■[個別の頁からの質問に対する回答][空間における平面の方程式 について/18.6.28]
問題2の解説において、分母のルートの中身が2^2+2^2+(-1)^2かと思います。
=>[作者]: 連絡ありがとう.問題2には分母もルートもないので,問題3のことのようです.訂正しました.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/18.6.28]
公式(4)の中に出てくるーcotとは-cosのことでしょうか?
=>[作者]: 連絡ありがとう.今の高校の教科書では sinθ,cosθ,tanθまでは書かれていますが,それらの逆数 cosecθ,secθ,cotθは書かれていないのが普通です.(学習指導要領からの逸脱と言われないように,言ってはならないと自己検閲してしまう)他方で,高専や大学では,そんなことは分かっていて当然という対応もあり,隙間が埋まらないことがあるようです.接続がスムーズに行くように,両方から手を差し伸べる方がよいように思いますが.
【ポイント】読むときは「3文字目の逆数」と覚えます.自分が書く必要はなく,今まで通りに書けばよい.
自分が書くときは,
などと書けば十分です.
■山形県[マンサン/18.6.27]
いつもこの数学講座を利用させていただき感謝しております。
現在「1階線形微分方程式」を学習中で、そのうちの問題5を、何気なく解き、回答合せをしたら正解でしたので、良かったと思ったのですが、良く見ると定数変化法ではなく、同次形微分方程式として解いていたことに気付き、おかしいと感じたので、問合せいたしました。
問題5は、(y2+x)y'=y の線形微分方程式で、これを変形して、y'=y/(y2+x)、そして、ひっくり返して
x'=(y2+x)/y=y+x/y
とここまでは同じですが、x/yをみてx/y=uとおいて、同次形微分方程式で
dx/dy=y+u=u+y(du/dy)
y(du/dy)=y
du/dy=1
これを解いて
u=y+C
元のxに戻して
x/y=y+C ➩x=y2+Cy …答
➩そのまま解いていったら正解となりましたが、この解き方は正しいのでしょうか?
ご解析・ご指導宜しくお願い致します。 2018.6.27
=>[作者]: 連絡ありがとう.それでよいと思いますが,記述式の答案は読みやすさも重要です.y+u=u+y(du/dy),y(du/dy)=yとつないでいく変形は読みやすくないので,次のように記述する方がよいかと考えられます.
とおくと
問題を変形すると
したがって
(以下は同様)
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.6.27]
問題3(3)の解説の
x3+y3+z3=3xyz+(x+y+z)(x2+y2+z2-xy-yz-zx)
x3+y3+z3=3xyz
なぜこうなるのか解りません。
=>[作者]: 連絡ありがとう.問題を読まないと解けません:x=a−b, y=b−c, z=c−a だからx+y+z=0です.
■[個別の頁からの質問に対する回答][組合せ について/18.6.26]
とてもわかりやすくて問題もスラスラ解けました!これからも使わせてもらいます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][絶対値付の不等式 について/18.6.25]
絶対値が二つ以上連なった形の不等式の解き方を載せてくださるとありがたいです
=>[作者]: 連絡ありがとう.
このページ で幾つか取り上げています.
■[個別の頁からの質問に対する回答][(各駅停車)二重根号 について/18.6.25]
スマホ版でもパソコン版でも、第三頁に進むと問題の文字列や回答欄の配置が崩れていて、問題が読めないです。
=>[作者]: 連絡ありがとう.かなり前(8年以上)に作ったプログラムで,現存するブラウザと合わないようですので削除しました.全く同じ内容で,出題形式が異なる二重根号のページがありますので,そちらを見てください.
■[個別の頁からの質問に対する回答][対偶証明法と背理法 について/18.6.25]
お世話になります。背理法を使って数について考えていますが、行き詰まってしまいました。知恵をお借りできませんでしょうか?
任意の有理数をY、任意の無理数をMとする。Y÷Mが有理数なのか無理数なのか、両方ありえるのか考える。
Y÷M=Y/Mであり、これが有理数だと仮定すると、互いに素な自然数a.bを用いてa/bと表せるので、
(Y/M)=(a/b)
両辺にMaをかけると、Yb=Maとなり、左辺は有理数、右辺は無理数なので矛盾する。したがって、Y÷M=有理数という仮定は誤りで、Y÷M=無理数となる。
ところで、Y=0のとき、Y÷M=0となり、有理数となってしまう。
と、こんな具合に無理数なのか、有理数なのかわかりません。
私の解き方、どこがおかしいのかわかりませんか?
よろしくお願いいたします。
=>[作者]: 連絡ありがとう.
「両辺にMaをかけると、Yb=Maとなり」の部分はおかしいですが,ほぼ合っています.ただし,主張の内容をはっきりしなければなりません.
ア)
のとき
の両辺に
を掛けると
左辺は有理数で右辺は無理数だから矛盾.よって元の式は無理数.
イ)
のとき
は有理数.
したがって,有理数になる場合と無理数になる場合がある.
問題が,「任意の有理数をY、任意の無理数をMとするとき,Y÷Mは無理数になる」という命題ならば,イ)が反例となって偽
問題が,「任意の有理数をY、任意の無理数をMとするとき,Y÷Mは有理数になる」という命題ならば,ア)により偽
■[個別の頁からの質問に対する回答][積和の公式.和積の公式の練習問題 について/18.6.24]
とてもいい練習になりました!ありがとうございます😊
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対偶証明法と背理法 について/18.6.23]
証明問題では、背理法とか対偶法といった証明のテクニックだけでは点がとれません。例えば無理数は整数/整数で表せないとか、無理数÷有理数は無理数みたいな、予備知識が必要です。そこで、大学入試の証明問題に必要でよく問われる予備知識をまとめたノートを作り始めたのですが、なかなか必要な予備知識をまとめたサイトが見当たりません。ゲイシャ様のページでそれら予備知識をまとめたページがあるとうれしいです。
=>[作者]: 連絡ありがとう.「幾つか」は可能ですが「全部」は無理でしょう.
■[個別の頁からの質問に対する回答][不定積分の置換積分 について/18.6.23]
少し読みづらい
=>[作者]: 連絡ありがとう.漠然と書くのでなく,もっと具体的に指摘してもらう方が,他の人のためにもなるでしょう.たとえば,スマホの機種ごとに利用可能なフォントが違うので,積分記号の表示,被積分関数との間隔がPC版と異なる形で表示されることがあります.
■[個別の頁からの質問に対する回答][二重根号 について/18.6.23]
根号と数字がずれて問題として解くことはできません
=>[作者]: 連絡ありがとう.あなたが使ったというPC版Internet Explorerで点検しましたが,全く問題なく表示されます.利用環境(パソコン,OS,ブラウザなど)についての情報がないとこれ以上の調査は無理です.なお,何ページ目の何番がズレているという形で具体的に指摘する必要があります -- 全部ずれているということはありません.全部ずれていないということもないでしょう.現実にあるものは真っ白でもなく,真っ黒でもないはずです.
■[個別の頁からの質問に対する回答][分数不等式の解き方 について/18.6.22]
コメント失礼しますm(__)m
下の4つの問題の最初の第1番目の問題で誤りがあります。解答の2行目から3行目にかけて、分子の4x+1が4x+2になっています。
=>[作者]: 連絡ありがとう.訂正しました.
■山形県[マンサン/18.6.21]
いつもこの数学講座を利用させていただき感謝しております。
現在「重積分;変数変換ヤコビアン」を学習中なのですが、そこで出てきます所の面積要素dS=dxdyについて、気になることを思い出して、急にお尋ねしたく、このようにメールさせていただきました。
それは、遡ること、「簡単な重積分の計算」の説明中…「立体の体積dVは、面積要素ds=dxdyに高さz=f(x, y)を掛けて得られる体積要素dV=f(x, y)ds=f(x, y)dxdy の総和」とあり、この点については理解できますが、その付属の説明図中「図で示した壁の面積S(y)を求めて」又、「図で示した壁の面積S(x)を求めて」という記述は、面積要素は底面積dSであるのに何故「壁の面積S(x),S(y)」になるのか、ということです…これが当時私が理解できなかったことです。…正しくは、
…xを固定して、それぞれのdxについて、高さf(x,y)を掛けて 変数yで積分した結果、積分要素f(x,y)dxの総和が、図の壁のS(x)である…
というのが、正しい記述なのではないでしょうか。
これは、次の章の「重積分…積分領域が変数に依存する場合」の説明図を見て、漸く上述の理解に辿り着くことができました。又、そこでの説明中、「面積要素ds=dxdyに高さz=f(x, y)を掛けて得られる体積要素dV=f(x, y)ds=f(x, y)dxdyの総和」という説明はdxdyの両者共の式ですから、これはこれで正しいし、理解できることは重ねて申し上げます。
まとめて申し上げますと、壁の面積S(x)、S(y)ではなく別の文字、例えばW(x),W(y)とした方が宜しいのではないでしょうか?
…以上ですが、宜しくご検討お願いいたします。2018.6.21
=>[作者]: 連絡ありがとう.元の記述で問題ないと考えます.使用する文字は書く側の好みや読む側の読みやすさの選べばよいと考えられます.
■山形県[マンサン/18.6.20]
お蔭様で、順調に数学学習が進んでいます。
さて、「高卒から大学数学基礎程度」に於いて、「重積分…積分順序の変更」の問1のhelp中、茶色文字の重積分計算で、…初めの重積分1行目のx2ydy積分が1/3xy3になっています。➩1/2x2y2…それからその次の重積分x2ydx積分が1/2x2y2になっています➩1/3x3yが正しいので?…思考が回転してしまいました。…宜しくご確認お願いします。間違いでしたら、御免なさい。2018.6.20
=>[作者]: 連絡ありがとう.確かにおかしい.計算の部分が前の例題の引き写しになっていましたので訂正しました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/18.6.19]
ネットならではの工夫された問題形式で楽しかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][共通部分と和集合 について/18.6.18]
高校になってから数学が難しくなり、困っていたのですが
解りやすい解説で理解することができました!ありがとうございます。
=>[作者]: 連絡ありがとう.
■愛知[りんさん][18.6.17]
いつもお世話になっております。時々PC、時々iPadからやってますがiPadからだと履歴(色つき)がつかないのが少し困っています。何か方法はないでしょうか?
=>[作者]: 連絡ありがとう.どうもそのようで,プログラムを直さなければならないのですが,もっと複雑な問題がEU圏で起こっていて(2018年5月25日施行の「一般データ保護規則」)対応方法をゆっくり考えないといけないようです---数としては少ないのですが,EU圏に留学中の学生や社会人が調べ事の途中でこの教材を見ることがたまにあります.そのときに履歴が残る仕組みになっていると違法とされるか否か,それが問題のようです.
■[個別の頁からの質問に対する回答][1次不定方程式の整数解 について/18.6.16]
【問題2】
1次方程式7x+8y=11
を満たす整数x, yの一般解を求めてください.
の問題で、x=-3,y=4を代入した結果、回答がx=-8n-3,y=7n+4になりました。これも正解でいいのでしょうか?
=>[作者]: 連絡ありがとう.解答,解説の本文でなく,傍論の参考の部分で定数項の符号が逆になっていましたので,訂正しました.
■[個別の頁からの質問に対する回答][組分け について/18.6.15]
≪9≫の問題、6c2=15 4c2=6 2c2=1 女子3人を別々に分けるので×3
部屋の区別がないので3!で割るのではないのでしょうか?
15×6=90
90×3÷3!=270÷(3×2)=45
で45となるのでは?
=>[作者]: 連絡ありがとう.「女子3人を別々に分けるので×3」というのが違います.×3!です.だから,あなたの考え方に沿って計算すると,90×3!÷3!=90になります.
■[個別の頁からの質問に対する回答][組合せ(文章題) について/18.6.15]
わかりやすく解説が乗っていてとても助かりました。
ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][整数の入試問題1 について/18.6.15]
n2+n+1=±1…(1)
または
n3−n+1=±1…(2)
プラス・マイナスですよねぇ
=>[作者]: 連絡ありがとう.この質問の仕方は全然ダメです.どの問題か書かずに,「幾つかのページで...」などと書いてある質問と同様,「1日かけて全部見直してもらおうか!」というけんか腰の態度になっています.管理人は,具体的に提起された問題を,具体的に解決することを考えており,文学的に奥行きのある表現を好んでいるわけではありません.
■[個別の頁からの質問に対する回答][順列 について/18.6.15]
数学初心者でもなんとか付いていけるくらい説明が易しく理解しやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/18.6.14]
こういうサイトを作っていただきありがとうございます。
=>[作者]: 連絡ありがとう.教科書レベルの基本にニーズがあるという意味に理解しました.
■[個別の頁からの質問に対する回答][ベクトルの和、差、実数倍 について/18.6.13]
全体的に問題多くして頂けたら嬉しいです
=>[作者]: 連絡ありがとう.そのページが体験入門的なもので,それができるようになったら,サブメニューにある「ベクトルの図形への応用」に進むことを想定しています.
■[個別の頁からの質問に対する回答][分数関数 について/18.6.13]
とてもわかりやすく素晴らしい学習サイト、ありがとうございます。いつも活用しております。誤字だと思われる点のご報告です。
漸近線の方程式(3)の以下の部分
“例えば,y=q が漸近線であるとき,x のどのような値に対しても y=q となるることはない.”
【なるる】とありますが、【なる】かと思われますが、いかがでしょうか。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][面積 について/18.6.13]
3つの関数が混じった定積分の例も上げてほしいです……
よろしくお願いします🙏💦
=>[作者]: 連絡ありがとう.具体的に何が要望なのかが分かりません.幾つかの区間に分ける問題のことなのか?
■[個別の頁からの質問に対する回答][(複素数で表される)軌跡の方程式 について/18.6.13]
コメント失礼しますm(__)m
定点からの距離が一定である点の軌跡のところの、赤字、z=x+yi, α~a+biとして,|z-α|=rを(x, y)座標で表すと,
√(x-a)2+(y-b)2=r
(x-a)2+(y-b)2=r2
となって,数学IIで習う円の方程式と一致する.
しかし,複素数で示された問題を常に(x, y)座標に直して考えていると能率が悪いので,特に行き詰ったときだけ(x, y)座標に直すようにし,複素数の問題は複素数のままで答えるようにするのがよい.
の冒頭、α~a+bi は、 α=a+biなのではないでしょうか?
=>[作者]: 連絡ありがとう.Shiftきーを押しながら,1つ隣のキーを押したようですので,訂正しました.
■[個別の頁からの質問に対する回答][行列の積 について/18.6.12]
昭和の初期に生まれた84歳の老人です。ふとしたことから行列、ベクトルに興味をもち、これまた偶然にこのサイトに出会いました。(もちろん高校時代に行列やベクトルなど教科書にありませんでした。)説明が非常にわかりやすく、よく理解できました。ありがとうございました。最後のページの行列の積の問題をやり全問正解だったとき自分で拍手をしてしまいました。これからも時間があったら少しずつ勉強してみようと思っております。よろしくお願いいたします。
=>[作者]: 連絡ありがとう.この教材の管理人が行列を習ったのは今からほぼ半世紀前です.50歩100歩かも.
■[個別の頁からの質問に対する回答][円の方程式 について/18.6.12]
問題1(3)の解答解説が(2)のものになっています
=>[作者]: 連絡ありがとう.訂正しました
■[個別の頁からの質問に対する回答][数列の極限 について/18.6.7]
解説が分かりやすく、無限数列の極限値 を基礎にして微分、積分の学習に、望みます。
=>[作者]: 連絡ありがとう.望むと臨むの使い分けは難しいですが,管理人に何かを望んでいるわけではないと理解しました.
■[個別の頁からの質問に対する回答][cosxに関する不定積分 について/18.6.6]
前回のご回答、ありがとうございました。
さて、改めまして、「やはり符号がおかしい」所があります。
【理由】置換積分の場合、sin3xの場合*1.10と、cos3xの場合*2.10 は、初めの被積分関数f(t)の符号が-・+の違いがあるのに、どうして、結論のI(x)は+1/4、-1、-1、と同じ並びになるのでしょうか。これについては、*2.8の最後のI式で絶対値記号が外されたとき、符号が反対になるのでしょうか? *1.8では、符号が反対になっていませんのでとても違和感があります。…絶対値の外し方について、良く理解できていないところがある私ですので、この指摘が間違っていましたら御免なさい。どうぞ宜しくお願い致します。2018.6.6
=>[作者]: 連絡ありがとう.被積分関数の符号が逆だから,積分の結果が逆になります.絶対値記号のはずし方は sin xのページに書きました.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/18.6.6]
地球上の2点の緯度・経度を与えて、その2点間の距離を求めたいのですが。
簡易な方法と正確な方法を教えて頂けると助かります。
=>[作者]: 連絡ありがとう.球面三角法というキーワードで検索すると公式が出てきます.
このページ など.結果を確かめるには
このペ-ジ など
■[個別の頁からの質問に対する回答][逆関数 について/18.6.6]
曖昧になりやすい部分を取り上げ、分かりやすく解説されている部分が良かった。大変参考になりなった。グラフを用いているのも良い。難しい内容をあえて避けてあるのかもしれないが、一対一の関数になるのは『「狭義」増加関数』とすると混乱がなく良いと思った。
=>[作者]: 連絡ありがとう.ア)狭義の増加関数:a<b → f(a)<f(b) ,広義の増加関数:a<b → f(a)≦f(b) という分け方をする場合もあります(矢野健太郎.公式集)が,イ)増加関数:a<b → f(a)≦f(b) ,強増加関数:a<b → f(a)< ≠ =. f(b) という分け方(新数学事典)もあります.高校の教科書や入試の答案では,ウ)増加関数:a<b → f(a)<f(b) ,非減少関数:a<b → f(a)≦f(b) という分け方をよく見かけます.
■[個別の頁からの質問に対する回答][回転と拡大 について/18.6.5]
コメント失礼しますm(__)m
単位円上の複素数→偏角の差になるというところで間違っているところがあります。
分母はcos^2θ+sin^2θ=1になるから~より2つ上の式の分母が、cos^2θ-isin^2θとなっていますが、正しくはcos^2θ-i^2sin^2θです。
=>[作者]: 連絡ありがとう.2乗が抜けているということで訂正しました.
■[個別の頁からの質問に対する回答][陰関数の導関数 について/18.6.5]
陰関数の微分が全然わからなくて困っていたので助かりました!!一番わかりやすかったです。問題演習がちょっとついてるのもポイント高いです。明日のテストもなんとかなりそうです!ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][累乗根 について/18.6.4]
問題に全角数字で入力すると不正解になるので、改善したほうがいいと思います。
=>[作者]: 連絡ありがとう.注意の文章を入れました.なお,google音声入力でも問題なく入力できます.
■山形県[まんさん][18.6.04]
*高卒から大学数学基礎程度の*sinxに関する不定積分、(*1.10)の解説に於いて、
最後の結論式
1/4{log(1+cosx/1-cosx)} ═1/(1-cosx) ═1/(1+cosx) +C
は
1/4{log(1+cosx/1-cosx)} +1/(1-cosx) +1/(1+cosx) +C
が正しいのではないでしょうか?…
私の間違いかどうか、知りたいので、ご確認お願いします。2018.6.4
=>[作者]: 連絡ありがとう.筆者の解答は符号が逆で,あなたの解答は前半の符号が逆のようです.元の教材の部分分数分解以下の省略が冷たい雰囲気なので,その部分を加筆します.
■[個別の頁からの質問に対する回答][必要条件と十分条件--不等式の問題 について/18.6.4]
実数aについて、a-2>0は、a>0であるための何条件ですか?詳しくお願いします…
=>[作者]: 連絡ありがとう.a-2>0→a>2>0が成り立つ.次にa>0であってもa>2が成り立つとは限らない.(例えばa=1)
以上から,
の矢印が成り立っている方を見て,十分条件.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/18.6.3]
解き方を書いてあるのが助かりました。
大学ではこんな風に教えてくれないので。
こんなにわかりやすい説明がインターネット上にあるのなら大学の適当で一方的な授業はあてにしない方がよさそう。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/18.6.3]
コメント失礼しますm(__)m
極形式のところでz=r(cosθ+isinθ)となりますが、この教材の極形式のところをみたとき()のなかが、(cosθ+i.sinθ)のもうに見えてしまいました。iとsinθの間をあいているのはiが虚数というのを見落としていそうな人のためかと思われますが、私みたいにスペースが空いていると座標のように勘違いしてしまう人もいるのでレイアウトをちょっと変えてほしいです。スペースを無くしてiは虚数と注意書きを書いていただければいいんじゃないかなと思います。あと、複素数平面上の座標って極座標というのですよね?それも明記したほうがいいと思います。もうちょっと教材を進めれば出てくるのだと思うのですが、数3はこの複素数平面の分野から始めたので最初に明記してほしいですm(__)m
=>[作者]: 連絡ありがとう.表記のほとんどは世界共通の約束なので,ローカルルールを作って違うことをすることはできません.
次に,複素数平面上の点は,(1) 実部+虚部 i で書く場合,(2) 実部+虚部 i をr(cos θ+i sinθ)の形に変形して使う極形式の場合がありますが,(*3)極座標とは違います.
【例】(1)
は,複素数平面上の点を 実部+虚部 i の形で表したもの. (2)
は,複素数平面上の点を極形式で表したもの,(*3)
は,2次元の実平面での極座標
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/18.6.2]
やっと弧度法がなぜ360°を2πにする定義なのかわかりました。θ=l/rでもlが2πrで計算できるが定義からrが割られるので2πが360°(円周の長さ)になるんですね?
=>[作者]: 連絡ありがとう.理屈を納得しやすい内的なロジックは,人ごとに異なることがあるようなので,横やりを入れにくいですが,「θ=l/rでも」というのはどういうことなのか,よくわかりません.「r=1のときは,L=2πになるので,L/r=2πになる」というロジックならわかるのですが.
■[個別の頁からの質問に対する回答][底の変換公式 について/18.6.2]
底の変換公式1の問3-(2)は㏒(3)7=bではなく㏒(2)7=bだと思います
でないと計算が合いません
=>[作者]: 連絡ありがとう.昨日訂正しましたが,ブラウザのキャッシュにまだ古いデータが残っているようですので,リロードしてください.PCでは多分これで更新されますが,携帯で更新されない場合は,その携帯の使用法にしたがってキャッシュを消してください.
■[個別の頁からの質問に対する回答][簡単な重積分の計算 について/18.6.2]
解答に解説があり、助かりました。
問も適切だと思います。
読んだだけでは、理解が不十分でした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][底の変換公式 について/18.6.2]
logの計算が苦手なので、とても勉強になりました。
問題3の⑵は選択肢の中に正しい答えがないかと、、解説をみたところ、全ての底を2にしていますが、問題ではbの底は3になっているので、問題が間違いか解答が間違いかだと思います。
=>[作者]: 連絡ありがとう.確かに入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][空間における平面の方程式 について/18.6.1]
コメント失礼しますm(__)m
例1の解説のところに 『3次元空間(自由度3)において,1つの制限(1次方程式)を入れると平面(自由度2)になります.
これに対して,直線(自由度1)は,2平面の交線(2つの平面の共通部分)として,2つの制限(連立1次方程式)を入れたものとして表されます』とあります。『』の、これに対しての次の文にある『直線』がなんなのか疑問に思いました。私が先生に質問したところ、これは2つの平面の方程式を連立してえられた直線の方程式と説明してくれました。また、『』内のこれに対して~の前で、3次元空間に1次方程式をいれるととありますが、これこでいう1次方程式とはax+by+cz+d=0の形の1次方程式で、空間における直線の方程式ではないですよね?この2点を詳しく明記して欲しいです。私の考えが間違っていたらごめんなさいm(__)m
=>[作者]: 連絡ありがとう.そのページの先頭にサブメニューがあります.直線→平面→平面と直線の順に読んでください.
■[個別の頁からの質問に対する回答][定積分の部分積分法 について/18.6.1]
(1)のcosxは-cおsxでは、。
=>[作者]: 連絡ありがとう.(sin x)’=cos x, (cos x)’=−sin x だから (−cos x)’=sin x
■[個別の頁からの質問に対する回答][1次独立,1次従属 について/18.5.31]
コンマは読みづらいから辞めてほしい
=>[作者]: 連絡ありがとう.?? 数学の文書で,コンマ以外の区切り文字が使われているものがあるのか?
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/18.5.28]
3が邪魔
=>[作者]: 連絡ありがとう.??それがないと sin kx, cos kxなどの練習にならない
■[個別の頁からの質問に対する回答][内分点,外分点の位置ベクトル について/18.5.28]
位置ベクトルの応用3の練習問題の最後の一問、
線分‘BA‘を2:3に内分する点
とありますがABの間違いではありませんか?
=>[作者]: 連絡ありがとう.ABがと言うのと,BAがと言うのでは,比率が逆順になることを意図した問題でしたが,結果に反映していなかったので直しました.
■[個別の頁からの質問に対する回答][順路の問題 について/18.5.26]
解答が正解だった場合でも解説が見られるようにして欲しいです。
=>[作者]: 連絡ありがとう.PC番の方はそうなっていましたが,携帯版の方がまだのようでしたので,そろえました.
■[個別の頁からの質問に対する回答][基本的な三角比の値(図あり) について/18.5.26]
楽しい!もっと勉強していれば良かったです
=>[作者]: 連絡ありがとう.お互いさまです.もっと勉強していれば…筆者は,もう幕が下りそうなのですが.
■[個別の頁からの質問に対する回答][根号の計算 について/18.5.26]
勉強のやり直しにピッタリです。懐かしいし、解けると楽しいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][連立不等式 について/18.5.26]
練習問題をもっと増やしてほしい
=>[作者]: 連絡ありがとう.5題ありますが,「もっと」とは,10題,50題のレベルの話でしょうか
■[個別の頁からの質問に対する回答][総和記号Σ について/18.5.25]
問題6(3)の正答の選択肢①では、sum 3*2^k, k=3 to n-2とあります。計算すると、3*2^3+3*2^4+...3*2^(n-2)、元の式の3+3^2+...3^(2n-2)とは違います。
=>[作者]: 連絡ありがとう.確かに違う,困ったもんです.訂正しました.
■[個別の頁からの質問に対する回答][展開公式1 について/18.5.24]
だいぶ忘れてしまっていた。な、4つしか正解していないだと。そうだよなぁ。14年前に習ったものだもの。ただの暇つぶしですよ。教材としては最高に良い出来だと思います。
by もうじき三十路の孤独なおじさん
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][双曲線 について/18.5.23]
今、中学2年ですが、とても簡単でわかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/18.5.22]
因数分解のたすきがけの練習がしたかったので、できてよかったです。もっと練習問題が欲しいです。
=>[作者]: 連絡ありがとう.そのページの左側にサブメニューがあります.その中に
◎たすき掛け因数分解1 など問題が限りなく出てくるものがありますので,それをやってください.
■[個別の頁からの質問に対する回答][2次関数のグラフ について/18.5.21]
とてもわかり易かった。それと解説を読んですぐにやり直せるシステムもとてもいいと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][部分集合,集合の包含関係 について/18.5.20]
とても分かりやすい説明で助かっています。ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角方程式(2次) について/18.5.20]
問題8の解説の中の(別解)の中で、「そこで両辺を cos^2 θ=0 で割る」とあるが、「cos^2 θ≠0 で割る」ではないでしょうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][条件付き確率 について/18.5.19]
≪問題4≫
ある家庭に2人の子どもがいて、玄関で1人を呼んだら女子が出てきたとき、もう1人も女子である確率を求めよ. (男女の出生比率はここでは1:1とします.)
この問題で
「玄関で一人を呼んだら女の子だった」という情報から、姉が来たのか妹が来たのかが分からないため「少なくとも一人は女の子」だと思い、問題3のように解いてしまいました。
解答を見たのですが、
玄関から出てきたという事柄は、生まれたというのと同じように考えることができます。
の部分がよく分かりません。
何故、この解き方で間違えてしまったのか、教えてください。よろしくお願いします。
自分なりに考えた結果を下に記します。
解答が1/2になるには
玄関に出たのが第一子なのか第二子なのか分かっている時
→「一人目が女の子」という事象をA「子供が二人とも女の子」という事象をBとすると
p(A)=1/2
p(AかつB)=1/4より
p(B | A)={1/2}/{1/4}であるから 答え1/2
=>[作者]: 連絡ありがとう.生まれたと同じに考えるときは,初めに出てくるのは第1子でしょう.第2子が先に出てきた場合は,出生を類推できないので,玄関でインターホンを押している場面を考えるしかないでしょう.なお,計算はよろしいが最後の分母と分子が逆です.{1/4}/{1/2}=1/2
■[個別の頁からの質問に対する回答][内接円の半径 について/18.5.19]
扇形に内接する円の半径求めて
分かりづらい
=>[作者]: 連絡ありがとう.扇形の角度を0<θ≦πとし半径をRとして,内接円の半径rをRとθで表すことはできます.あなた自身が解かなければならない宿題かもしれなので,考え方のみ伝え,答は書きません.
をrについて解きます.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/18.5.19]
助かりましたー
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2進数の演算 について/18.5.19]
二進数の割り算の筆算が、授業でも、テキストをみても、動画を見ても、まったく分からず困っていましたが、やっと理解できました。本当にありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2直線の垂直条件 について/18.5.18]
見づらい
=>[作者]: 連絡ありがとう. W=375,H=812のiPhoneで見ておられるようですが,こちらは同じレベルの画面サイズのAndroidで快適に見えます.だから,画面の問題ではないようなので,長い段落に切れ目を入れて,息継ぎがしやすいように,すこし変形しました.
■[個別の頁からの質問に対する回答][ド・モルガンの法則 について/18.5.18]
間違えた際の、ここがポイントっていうのが、次の問題文にかぶってしまい、読みずらいので、改善お願いします
=>[作者]: 連絡ありがとう.了解です.問題3,4,5のメッセージ欄の幅を広げました.
■[個別の頁からの質問に対する回答][極座標 について/18.5.17]
1の点設定を画面上でするのが難しいので点選択が望ましいと思います。
=>[作者]: 連絡ありがとう.日本製Androidで点検していますが,ズームインすれば簡単にできます.
■[個別の頁からの質問に対する回答][指数法則 について/18.5.16]
高一です。分かるところもあったのですが、書き方などが教科書のように難しいので、もう少しわかりやすく、かみくだいて説明して欲しいです。
=>[作者]: 連絡ありがとう.もっと前の
負の指数の導入 のところから読んだらどうでしょうか.
■[個別の頁からの質問に対する回答][内分点・外分点 について/18.5.16]
外分点3(2)
何度やっても正解が出ません
ー3xー2+1x5
1ー3
11
ー2
ではないのでしょうか
=>[作者]: 連絡ありがとう.それであっていますが,あなたはそのようには入力していないようです.例えば分母に1--3などと入力していませんか.なお,この教材は作ってから10年以上経過しており,内容や見え方に不十分さがありますので,今日更新した
このページ を見てください.
■[個別の頁からの質問に対する回答][ 因数分解(応用問題) について/18.5.15]
例の3の2の説明を詳しく
=>[作者]: 連絡ありがとう.教える側は,これで十分詳しく,他に何が言えるのか?と考えますが,受け取る側がまだ足りないと思うとすれば,そのギャップを埋めるには何が必要なのか.長い目で見て考え中.
■[個別の頁からの質問に対する回答][負の指数 について/18.5.14]
今さら聞けない数学の部分を、このように反復問題を含めて
勉強できるサイトには、正直、感謝しかないです。
有難うございます。
40代文系エンジニア
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内分点・外分点の座標 について/18.5.14]
テスト勉強になりました!ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.5.13]
的確かつ簡潔で、知りたいことが見事に解決しました。素晴らしいです。
元ネタや、参考文献はあるのですか。
=>[作者]: 連絡ありがとう.参考文献というものはありません.高校で教えていたときに出会った内容をまとめて,補強したものです.
■[個別の頁からの質問に対する回答][整数の累乗と整除 について/18.5.12]
初投稿失礼しますm(__)m
東京女子大2005年の例題の問題と解答が一致していない気がします。
チェックテスト風の問題の(7)(8)の問題が一緒です。
また、教材改善として(6)の愛知教育大の問題の2項定理による証明で(k+1)^n-kn-1から(k+1)^n-kn+(k^2-1)を導く理由を書いてほしいです。(k+1)^n-kn-1と3^n-2n+3と数字を比較して、同じ式の形ではないので違う式の形を考えるのはいいですが、(k+1)^n-kn+(k^2-1)がなぜ3^n-2n+3と対応するのかというのがこの教材だけではわかりませんでした。例えば4と8という数字があって、前者に4を足して後者の数字になっても、両者は4でわれますね。これと似たようなことをやっているのだと思いましたが、(k+1)^n-kn+(k^2-1)という式をなぜ(k+1)^n-kn-1から導出する必要がありそれも(k+1)^n-kn+(k^2-1)だけを考えるという発想にはなかなか至りませんでしたので、そのあたりの発想の仕方というのも書いてくれたら嬉しいです。
=>[作者]: 連絡ありがとう.1番目の質問:何もおかしくありません.これで一致しています.2番目の質問:(7)の問題を書き間違っていましたので訂正しました.3番目の質問:k=2で成り立ちます.
■[個別の頁からの質問に対する回答][複素数の計算 について/18.5.12]
とても分かりやすかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][共通部分と和集合 について/18.5.11]
空集合についての解説が欲しい
=>[作者]: 連絡ありがとう.確かにその部分が薄いようですので,考えておきます.
■[個別の頁からの質問に対する回答][定積分で定義される関数 について/18.5.9]
定積分で定義される関数項の問題②(1)ですが、
答えはf(x)=2x-4ではないのですか?
=>[作者]: 連絡ありがとう.本当に,完全に間違っている!作業中にモグモグタイムでも取ってしまったのか?訂正しました.
■[個別の頁からの質問に対する回答][条件付き確率 について/18.5.8]
モニターや設定によって違うかも知れませんが、ジャンケンの絵が薄い黄色なので見えにくいです。
できれば違う色の方が見やすいかと思います
=>[作者]: 連絡ありがとう.少しは濃くしましたが,ブラウザにキャッシュデータがあると,反映しないようです.
■[個別の頁からの質問に対する回答][展開公式1 について/18.5.3]
(Xの三乗➖Yの三乗)(Xの三乗➕Yの三乗)
の簡単な因数分解の仕方・正しい因数分解の仕方を教えてください
=>[作者]: 連絡ありがとう.因数分解のことは
因数分解のページ を見てください.
■[個別の頁からの質問に対する回答][2直線の交点を通る直線の方程式 について/18.5.3]
間違っていたらごめんなさい。
「2直線の交点を通る直線の方程式」のところで「要点と注意点」の項で直線(2)はこの形式では表せない.とありますが
k=(d-a)/d
の時は(2)の方程式になりませんか?
=>[作者]: 連絡ありがとう.それは無理です…xの係数は合いますが,yの係数や定数項が合いません.
少し下の,簡単な例でイメージ作り1,2に述べていますように,lim k→ ∞ または lim k→−∞ の極限において,直線(2)に限りなく近づきますが,有限確定の値で直線(2)に一致することはありません.
正確さを度外視してイメージだけで言えば,直線 (1)+k×(2) は,(1)と(2)をk:1に内分(または外分)する直線なので,k=±∞の場合に(2)に近付きます.
例えばx+2y+3=0…(1), 4x+5y+6=0…(2)に対して,x+2y+3+k(4x+5y+6)=0…(3) を考えるとき,(3)は (1+4k)x+(2+5k)y+(3+6k)=0と書けるから,k=10のときは41x+52y+63x=0 すなわち 4.1x+5.2y+6.3=0となって,(2)に近付きます.さらにk=100とすると,401x+502y+603=0すなわち 4.01x+5.02y+6.03=0となって,一層(2)に近付き(1)の影響は薄くなります.ついに,k→∞とすると限りなく(2)に近付くということです.
■[個別の頁からの質問に対する回答][対数計算 について/18.5.3]
どのページも説明がわかりやすく、大変参考になります。
[係数があるとき]の例3の第1式の右辺第2項の
底が4となっていますが、正しくは3ではないでしょうか。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][指数計算 について/18.5.2]
2*(-5^2)は、-50となる理由?
=>[作者]: 連絡ありがとう.中学校1年生の4月に習う内容ですので,
そちら を見てください.
■[個別の頁からの質問に対する回答][不等式の証明1 について/18.5.2]
こんにちは すごくわかりやすかったです
問題集のページを作ってもらえませんか?
=>[作者]: 連絡ありがとう.要望の意味が通じません.これが問題集です.印刷用のPDFファイルがほしいという要望でしたら,多くのページは先頭部分にリンク先が表示されています.それがないページでも,PCからは印刷の出力先をファイルにすれば各自でできます.(iPadの操作方法はこちらからは分かりません)
■[個別の頁からの質問に対する回答][内分点の内分点 について/18.5.2]
【内分点の内分点】の、「複素数平面上に3点A(z1 ), B(z2 ), C(z3 )があるとき、
z=(pz1+ qz2+ rz3)/(p + q + r)とすると、」となっています。
図2では、三角形の辺に、pとqとrが2個ずつ記載されていますが、
どちらのp、q、rのことでしょうか?
=>[作者]: 連絡ありがとう.p,q,rは長さそのものではなく比率なので,青同士,赤同士,緑同士が比率を表すように色分けしたつもりです.青のp,q,rは正確に言えば,ps,qs,rs,赤のp,q,rはpt,qt,rt,緑のp,q,rはpu,qu,ruと書くべきですが,そのように書くと図がコテコテして分かりにくくなるので,色分けによって比率の組を表しています.
したがって,複素数平面上に3点
があるとき,
とおくと,赤字の対応では,BF:AF=p:q,青地の対応では,CD:BD=q:r,緑字の対応では,CE:AE=p:rなどと読んでください.次に,やや小ぶりの文字について,中央の黒丸をXとすると,赤はFX:CX=r:(q+p)などと読みます.以下同様です.(どこから突っ込まれてもよいように正確に書くか,見やすく分かり易い方を選ぶか,難しい判断ですが,市販の出版物なら前者にすべきでしょう)
■[個別の頁からの質問に対する回答][2次不等式(絶対値付き) について/18.5.2]
2次不等式(絶対値付)問題2の(2)の解説なのですが、
ア)の最後のところのしたがってのところは、x≦-2、7≦xじゃないのですか?
=>[作者]: 連絡ありがとう.図が正しく,ご指摘の通りです.
■[個別の頁からの質問に対する回答][三角形の辺の長さ(三角測量) について/18.5.1]
問題2の(1)(2)の解答間違ってませんか?
=>[作者]: 連絡ありがとう.確かにおかしいので訂正しました.
■[個別の頁からの質問に対する回答][複素数の1次結合が表す図形 について/18.5.1]
●「【問題2】1直線上にない異なる3つの複素数z1 , z2 , z3に対して,z=pz1+qz2+rz3
で定義される複素数が次の図形を描くとき,実数p, q, rが満たす条件として正しいものを
右から選んでください.」
の(2)の解答「p+q+r=1 p<0, q<0 」についてですが、
「r>0」は必要ないのでしょうか?
●同様に「【問題2】(5)の解答「p+q+r=1, p>0, q=0」も「r<1」は必要ないのでしょうか?
=>[作者]: 連絡ありがとう.前半:p+q+r=1 p<0, q<0のとき,r=1−p−q>1が当然成り立つので,r>0は書かなくても成り立ちます.
■[個別の頁からの質問に対する回答][ベクトルの直交条件 について/18.4.30]
解答どこ見ればいいか分からん
=>[作者]: 連絡ありがとう.先頭に「※正しい番号をクリックしてください.」と書いてありますように,すべてのページが,読者との対話的応答プログラムになっていますので,選択肢をクリックすれば解説が出ますが,何も答えなければ解説は出ません.
■[個別の頁からの質問に対する回答][二重根号 について/18.4.30]
「二重根号は,現在高校の教科書では扱われていない」ということに驚きました。また、それにも関わらずこのようにわかりやすく詳しい解説・問題を掲載してくださっていることに感謝します。ぜひ無くなさないでいただきたいです。
=>[作者]: 連絡ありがとう.この教材を作ったころ(ゆとりの時代)には,学習指導要領で「二重根号をはずす計算は扱わないものとする」とされ,どんな事情があっても例外は許されないという意味の「~ものとする」で強く否定されていましたが,2018年現在の教科書では,発展学習として参考程度に触れられていることがあります.
■[個別の頁からの質問に対する回答][補集合 について/18.4.27]
たびたび申し訳ありません。《問題3》の(4)の解説を拝見しても3行目の①②③④⑤⑦⑧となるには∩ではなく⋃ではないかと思われるのですがいかがでしょうか。
=>[作者]: 連絡ありがとう.問題を特定できました.確かにそうなりますが,∪が並んでいる問題はあまり良い問題にならず,当初作成したときの意図と変わってしまうので,暫定版を見てもらってから,書き換えるかもしれません.
■[個別の頁からの質問に対する回答][補集合 について/18.4.27]
(4)の∩は⋃ではありませんか?
=>[作者]: 連絡ありがとう.(4)は問題1,2,3の3個あり,どの(4)か不明です.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/18.4.25]
わかりやすい
=>[作者]: 連絡ありがとう.
■福岡県[おやじさん]18.4.25]
いつも勉強させていただいています。
数列のSnAn関係式のところの問題3のイの解答なのですが、
解説が2^2-2^n-1=2^n-1になるのがわかりません。
教えていただけないでしょうか??
=>[作者]: 連絡ありがとう.2→n訂正しました.ついでに,省略されていた式を追加しました.
■[個別の頁からの質問に対する回答][対称式の変形 について/18.4.25]
いつも勉強させて頂いております。本当にありがとうございます。
基本3 の(3.3)において、.....(a+b+c)^2 -2abc(a+b+C)....となっておりますところの
(a+b+c)^2 が、(ab+bc+ca)^2 ではないかと思いご連絡致しました。
ご確認頂ければと存じます。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/18.4.25]
解約分されて分数ではなくなりました。これを一般化しましょう。2次方程式ar42br + c = 0(a * 0)が69-ac 2.0を満たすとき、この解の公式を導いてください。
=>[作者]: 何の話をしているのか,全く通じません.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/18.4.24]
(X-1)(X+1)=
=>[作者]: 連絡ありがとう.それがどうしたのですか?質問内容を言葉で言わないと,通じません.
■[個別の頁からの質問に対する回答][不等式の証明 について/18.4.24]
[2] 正負の数との積
【例題2.1】
において、
c<dで0<bだから
bc<dc
この条件ではこの不等式が成り立たない気がするのですが、読解力が無いだけでしょうか?
次の文で、
ゆえに
ac<bd
となっているので余計に違和感を覚えました…
間違いなら、修正お願いします。
=>[作者]: 連絡ありがとう.単純な入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/18.4.22]
3個ぐらいまとまりがあるやつを教えて欲しかった
=>[作者]: 連絡ありがとう.入学年度によって,中学校では未知数の入っている不等式を全く習わなかった人もあり,他方では中学校で中学校でそこそこ習っている場合には,こんな問題は「やさし過ぎる」ように見えます.
■[個別の頁からの質問に対する回答][三角関数のグラフ について/18.4.21]
48歳の男性です。高校生の時、苦手になってしまった三角関数がこのページで分かることができ、とてもうれしかった。面白かった。これを掲載していただきましたこと、本当にありがとうございます。
=>[作者]: 連絡ありがとう.そのグラフは管理人なりに自慢の作で,毎回プログラムで描いています(我田引水,自画自賛,一人自慢の褒めて無しともいう)
■[個別の頁からの質問に対する回答][ 展開公式 について/18.4.20]
とってもわかりやすかったし、しっかり勉強できました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][基本的な三角比の値(図あり) について/18.4.20]
図形の性質は無いのですか?
=>[作者]: 連絡ありがとう.三角比と図形という単元を見てください.
■[個別の頁からの質問に対する回答][内分点・外分点 について/18.4.20]
とても分かりやすかったです。ありがとうございます。^^
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/18.4.19]
練習問題がついていて、とても分かり易かったです。
ありがとうございました。
テスト頑張ります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/18.4.19]
助かります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/18.4.18]
例題の
= 3log|x+2|−4log|x+4|+C …(答)が、
= 3log|x+2|−2log|x+4|+C にならないわけを教えてください。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.(いい訳:管理人はワープロで教材を作っているのでなく,テキストエディタで <span class="itl16">= 3<span class="sct">log</span>|x+2|−2<span class="sct">log</span>|x+4|+C</span> …(答)などと直接入力しているので,後でブラウザで点検はしますが,管理人が書いている画面と読者が見る画面は同じでないため,結構大変なのです)
■[個別の頁からの質問に対する回答][因数分解(応用問題) について/18.4.17]
○2-□2の形に持ち込む”の所の問題4、(2)の解説を読んだ時に、なぜ原式の一番最初が(x2-y2-4)2+8(x2-y2)-8(x2+y2)になるのか分かりませんでした。
=>[作者]: 連絡ありがとう.
だから
,したがって
になりますが,一方向の変形と捉えにくいようですので,その隙間を加筆します.
■[個別の頁からの質問に対する回答][3次関数の最大値・最小値 について/18.4.16]
最後の問題の解説の1<a≦2のとき,
x=-1で最大値2をとる
x=1で最小値-2をとるとありますがそのとき-aは-2≦a<-1
なのでx=2で最大値2 x=-2で最小値-2をとるとはならないのですか?
=>[作者]: 連絡ありがとう.-2≦-a<-1で1<a≦2というのはその通りですが,その範囲でHELPに示したようなグラフになるのだから,「x=-1で最大値2をとる.x=1で最小値-2をとる」ことになります.はなしがややこしければ,たとえばa=1のときに絞って考えるなど単純化すると迷いが少なくなるでしょう.
■沖縄県沖縄市[マンサン][18.4.16]
〇まとめのcheckテスト…三角・指数・対数関数の計算…問題5の「指数関数の大小比較」で、読んでいるうちに脳がくるっと回ってしまうので、じっくり調べましたら、図解下10行目と12行目が反対ですね…多分…イ…..<..…ア と ア…..<..…ウ の行を交換するときちんと話がまとまるみたい。悩んだけど、皆さん理解に苦しんでいるだろうと思い…私も苦しんだから…送信しました。間違っていたら、ソリー!
=>[作者]: 連絡ありがとう.確かに理由と式が逆なので訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作18・・・1階常微分方程式 について/18.4.16]
ode2(1-'diff(z,x,1)=1/z^2,z,x);
logcontract(%);
subst([z=x-y],%);
(%*2)-2*(x-y);
lhs(%)=expand(rhs(%));
subst([2*%c=C],%);
exp(lhs(%))=exp(rhs(%));
こんな具合にMaximaのみでの処理の勉強に手ごろな講座でした。有難う誤差いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作18・・・1階常微分方程式 について/18.4.15]
ベルヌーイ形の2番目ですが、解の分子が2y^2-6xとなっていますが2y^3-6xなのではないでしょうか。
変形もy^3=Cx^(3/2)+3xまでしかできませんでした。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作14・・・三角関数の積分(2) について/18.4.15]
フレネル積分でsin(x^2)およびcos(x^2)の積分範囲は[-inf,inf]なのではないでしょうか。
sin(x)/(3sin(z)+4cos(x))の筆算の最終行の
I=3pi/2-4(log(3)-2log(2)の部分は重複していますし不要ではないでしょうか。
=>[作者]: 連絡ありがとう.各々訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作14・・・三角関数の積分(2) について/18.4.15]
Maxima ver 5.37.3.5以降では
fx:'integrate(1/(sin(x)+cos(x)),x,0,%pi/2)=integrate(1/(sin(x)+cos(x)),x,0,%pi/2);
fx1:rat(fx),algebraic:true;
fx:'integrate(sin(x)/(3*sin(x)+4*cos(x)),x,0,%pi/2)
=integrate(sin(x)/(3*sin(x)+4*cos(x)),x,0,%pi/2);
fx1:rat(fx),algebraic:true;
fx2:logcontract(fx1);
で正常に処理されました。
=>[作者]: 連絡ありがとう.筆者も新しいものに更新しなくては・・・
■[個別の頁からの質問に対する回答][補集合 について/18.4.15]
問題も例題も最高でした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][最大角,最小角 について/18.4.15]
(*1)A2≧β,B1≧αだからA2+B1≧α+β=180°
となり矛盾
(*2)A2+B1≧90°+90°=180°となり矛盾
1)2)よりA≦B
この3行目のB1はB2の誤りではないかと思われます。入試問題を解く際に参考にさせていただきました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作14・・・三角関数の積分(2) について/18.4.15]
2番目の例でsin(x)/(3sin(x)+4cos(x))のMaximaの入力式が
sin(x)/(4\sin(x)+5cos(x))になっています。
=>[作者]: 連絡ありがとう.タイプミスですので訂正しました
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/18.4.14]
関数4.34×165520850^-0.0313
=>[作者]: それは関数ではない.このページとも何の関係もない.質問があるなら言葉で言わないと通じません.2.4
■[個別の頁からの質問に対する回答][maximaの初歩的な操作13・・・三角関数の積分 について/18.4.14]
1/sin^n(x)および1/cos^n(x)の漸化式の分子がcos(a)およびsin(a)となっています。cos(x),sin(x)ではないでしょうか。
また、1/cos^n(x)の漸化式でmが使われていますがnなのではないでしょうか。
=>[作者]: 連絡ありがとう.タイプミスですので訂正しました
■[個別の頁からの質問に対する回答][maximaの初歩的な操作17・・・関数のフーリエ級数展開 について/18.4.13]
|sin x|に関して次の式であるはずの式のcos(nx)はcos(2nx)なのではないでしょうか?
(4)の式も変形しないとグラフが例示されているようにはなりませんが....
4/pi(1/2-(cos2x/(2^2-1)+cos3x/(4^2-1)+...))ではないでしょうか?
=>[作者]: 連絡ありがとう.詳しく点検してくれてありがとう.訂正しました.
■[個別の頁からの質問に対する回答][直線の像,領域の像 について/18.4.13]
数学C 行列の応用…【1次変換の線形性】で、図形の1次変換の(A)直線は直線に移される、の解説、11行目A(a)には´が付くのではありませんか、そうでないと、なんだか意味不明…下の14.16.17行目のaにはついているようだが、…もう少し…すべて指摘するには、時間が掛かり過ぎるので、手抜きしています。
=>[作者]: 連絡ありがとう.ベクトルの表示方式が古いInternet Explorerの時代に作ったものだったので,今日のブラウザに合うように変更しました.見やすくなったと思います.(EdgeとFirefoxは事情があって点検できません)
■[個別の頁からの質問に対する回答][グラフの平行移動 について/18.4.13]
代入の説明は理解できるのですが
両軸とも正の場合に、
なぜxは戻してyは上げるのですか?
=>[作者]: 連絡ありがとう.1ページを使って,そのことを説明しているのに,説明が終わってから,そのことを質問しているのでは,そのページの説明を読んでいないということになりませんか?
本来,
と書くべきところを,「習慣に従ってyについて解いた形に直すと」
になるというだけのことです.(移項しただけ)
■[個別の頁からの質問に対する回答][maximaの初歩的な操作7 について/18.4.13]
指数関数の最初の入力部に無理関数が混入しています。
=>[作者]: 連絡ありがとう.コピペで作業場所を作ってから,さあ作業を始めようとして,忘れたようです.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作7 について/18.4.12]
部数関数の2番目(x+3)/((x-1)(x+2))の結果ですが、第2・3項の分子が1になっていますがx+3となるのではないでしょうか?
=>[作者]: 連絡ありがとう.分数関数・・・訂正しました.
■[個別の頁からの質問に対する回答][
問題2の解説と回答の結果が異なります
=>[作者]: 連絡ありがとう.問題2の何番がどう違うのですか?
■[個別の頁からの質問に対する回答][maximaの初歩的な操作6・・・行列計算,固有値,固有ベクトル について/18.4.12]
行列式を求める部分の入力部ですが、determinant(A)がdeteminant(A)とrが欠落しているようです。
=>[作者]: 連絡ありがとう.管理人は,老眼の近眼の乱視なので,ゴシック体の rn とm の区別が難しかったようです.2文字組で1文字と入れ替わるのは珍しい.(ビックリするほどよく似ている.ほとんど区別がつかない)
■[個別の頁からの質問に対する回答][maximaの初歩的な操作11・・・漸化式の一般項 について/18.4.12]
IIでAnを求めている部分で-10+5*22^nの指数ですが2^(n+1)なのではないでしょうか?
結果を求める場合にはキャンセルされるので影響しませんが。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作12 について/18.4.11]
その他の級数和の3番目はpi^6/945ですがこれは1/k^6の間違いではないでしょうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作5 について/18.4.11]
積分の項でg(x)が未定義です。f(x)の間違いではないでしょうか。(3)の被積分関数がf(x)を微分したものになっています。ミスプリントかと思われますが。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作3 について/18.4.11]
[]の件ですがlinsolveは行列から解を求めているため、1組のリストとして結果を出力するのに対し、solveは解の組をリストとして出力していることの差ではないかと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/18.4.11]
問3でたくさん計算ミスをしたことで、今後は慎重に計算しよう!と思えました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列のn乗 について/18.4.10]
P-1AP計算で答案では右からの行列計算ですが、左からの行列計算でも良いのですよね…結果は同じ様ですが…。問題4.1で最後の答でCnの場合-2のn+1乗+2✖5のn乗/3ではありませんか?…-が抜けていると思いますが…、宜しくご指導ください。
=>[作者]: 連絡ありがとう.Cnの場合というのが何を意味するのか伝わってきませんが,2,1成分の符号に間違いがありましたので訂正しました.
■[個別の頁からの質問に対する回答][円の方程式 について/18.4.10]
工具顕微鏡や3次元測定器など各工場で一般的にかつ便利に使用してます。そもそも円の直径や座標が簡単に算出できる元はこの円の方程式があるからだと思い、基本に立ち返って勉強しました。たいへん参考になりました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数学的帰納法とは について/18.4.7]
数学的帰納法の証明2で、私なりに解釈した次のような解答した場合、数学的帰納法の証明方法として妥当でしょうか? ご教示ください。
【解答】
1)4角形の場合において、対角線の数は2であり、与式(1)の性質をみたす。
2=4(4-3)/2
2)一般的にK角形においても与式(1)が成り立つと仮定した上で、
すなわち k角形の対角線の数=k(k-3)/2とした上で、
k+1角形に対角線の増加規則=「(k-2)+1」(初項のk-2は頂点に隣り合う頂点間では対角線が引けいないことを、第2項の+1は頂点が一つ増えることによってそれまで辺であったものが新たに対角線へと変わることを表す)を適用すると、
k+1角形の対角線の数=仮定+増加規則
=(k(k-3)/2)+(k-2)+1
これを整理すると
=(k(k-3))+2(k-1)/2
=(K^2-k-2)/2
=(k+1)(k-2)/2
=(k+1)((K+1)-3)/2
となり、n=k+1の場合においても与式(1)の性質をみたす。
よって、1)2)により、n=4以上の全てのn角形において対角線の数は与式(1)の性質を常にみたす。
=>[作者]: 連絡ありがとう.それでよいのですが,教材に書いてある解答とほぼ同じに見えますが・・・
■[個別の頁からの質問に対する回答][数学的帰納法とは について/18.4.7]
[数学的帰納法による証明の例2]の解説で
図のように対角線が 1+(k-2)=k-1 本増えるからの、 「1+(k-2)」の部分がよくわかりません。
例えば、四角形 五角形、六角形、七角形の対角線の数を、2,5,9,14の数列とみなしてその等差が3,4,5と一ずつ増えているので、これをK角形のkとの関係から「k-1」という上記解説の右辺は、凸n角形の対角線の数で保存される規則というのはわかるのですが、左辺の1+(k-2)という式は、どのような性質を言い表したものなのでしょうか?
=>[作者]: 連絡ありがとう.図に青線で示していますように,第k+1番の頂点から2,3,4,...,k−1までのk−2本の対角線が新たに増える他に,k角形のときは対角線でなく辺であった1番-k番の線が新たに対角線に入るから1+(k−2)です.
■[個別の頁からの質問に対する回答][場合分けのまとめ方 について/18.4.6]
問題3で自分の頭の中でAとBでカードを交換する操作のように勘違いしてしまって同じカードが戻ってくる可能性について見落とした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/18.4.4]
途中途中に問題があって有り難かったです。
=>[作者]: 連絡ありがとう.はじめは問題を小出しにすると理解しやすいようですので,最近はそううスタイルにしています.
■[個別の頁からの質問に対する回答][3点が同一直線上にあるための条件 について/18.4.3]
最後の問題のQの位置ベクトルがなぜ3分のになるのかわかりません。
=>[作者]: 連絡ありがとう.2点
を結ぶ線分
をm:nに外分する点
の位置ベクトル
は
(これは公式)
したがって,4:1に外分する点の位置ベクトルは
■[個別の頁からの質問に対する回答][空間における平面と直線 について/18.4.2]
三角形を含む平面を考えるとき、頂点の一点を通って、その平面に垂直な直線は、どの考え方を利用すればまとめることができるでしょうか?参考書などで勉強しているのですが、平行な直線を扱ったものばかりで、垂直な直線の問題がなく、困っています。ご教授願います。
=>[作者]: 連絡ありがとう.
その1つ前のページ に3点を通る平面の方程式の求め方が書いてあります.普通の解き方は,【例5】3点O(0, 0, 0), A(3, 1, 2), B(1, 5, 3)のように係数を求めるだけで解きますが,法線ベクトルを求めて解く場合は
Oを通り
と
の両方に垂直なベクトル
を求めることから始めます.
未知数が3個で方程式」が2個だから不定解になります.そこで
については「解かない」ことに決めて,右辺に持って行きます.
…(1)
の方程式として解くと,
以上により,
(
は任意の実数)
点O(0, 0, 0)を通り
に垂直な平面の方程式は
…(答)
■[個別の頁からの質問に対する回答][展開の順序 について/18.4.1]
問題1について
{ (x−1)(x+1) }3={x2−1}3
の場合
x2・x2・x2はx6ではなくx8になりませんか?
よって
=x6−3x4+3x2−1ではなく
=x8-3x4+3x2-1ではないでしょうか
間違っていたらすみません。
=>[作者]: 連絡ありがとう.指数法則を正確に覚えてもらう必要があります.
ではなく,
です.だから,
ではなく,
です.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.4.1]
僕は問題を他の少し時間がかかる方法でできたのですが、解説のようなやり方でできるようにならないとだめですか?
=>[作者]: 連絡ありがとう.解き方は自由です.別解を何通りも書けるようになると力が着きます.
■[個別の頁からの質問に対する回答][2次-2次連立方程式の解き方 について/18.3.31]
問題4②で、2x²+xy+y²は、2x²+xy+2y²の間違いではないかと思われます。
=>[作者]: 連絡ありがとう.問題が転記ミスということで訂正しました.
■[個別の頁からの質問に対する回答][展開の順序 について/18.3.30]
はじめまして、私の勘違いでしたら大変恐縮なのですが、問1の(1)の回答部分で-3Xの3乗とあるのですが、-3Xの4乗の間違いではないでしょうか?
もし、3乗で合っているのなら、公式を含めた詳しい解説を乗せていただきたいです。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積3 について/18.3.30]
問題2の6/5について、ご回答ありがとうございました。まさにご指摘の通りで、π/3で、3/5でした。大変ご迷惑かけました。有難うございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積3 について/18.3.30]
いつも勉強させていただいて感謝しております。問題2で、答…私計算のでは、6/5、になりますが、どこに間違いがあるか、わかりません。どうか教えて下さい。宜しくお願い致します。
=>[作者]: 連絡ありがとう.途中の行間が詰まり過ぎている箇所や分数の形が崩れている部分は直しました.後は,HELPで表示される式を見てもらうしかないと思いますが.π/3→π/4のところが要注意
■[個別の頁からの質問に対する回答][組分け について/18.3.29]
私は、60を過ぎた老人です。必要あって、数学の勉強を始めて、貴殿のサイトにたどり着きました。大変親切な記述は、半ば腐敗した老人の脳にも、大変わかりやすいです。是非このサイトをさらに発展させて、若い人たちの学習の助けになるように、頑張ってください。最後に、御努力ご苦労様です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][余弦定理 について/18.3.28]
今晩は
余弦定理、【問題2】(4)
△ABCにおいて,a=√2 B=2 C=1+√3のとき,Bを求めてください.
解説に誤植がありました。
二番目の式の分子が、
2+4+√3-4になっていますが、2+4+2√3-4が正しいと思います。
2018.03.28 平 凡太郎
=>[作者]: 連絡ありがとう.先日書き換えたときに点検不十分だったようです.
■[個別の頁からの質問に対する回答][順列 について/18.3.28]
感想というか質問というか...
最後の問題があまりよくわかりません
=>[作者]: 連絡ありがとう.HELPは読んだのですか?それ以上に詳しい解説はどこにもないと思いますが.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/18.3.27]
答えが、(2x+5y-4)(5x-9y+3)となっていたのですが、
(-5x+9y-3)(-2x-5y+4)と答えてしまいました。
展開してみたら、数字の順番が違うだけで、出てくる数字自体は同じだったのですが、これも間違いになるのでしょうか?
もし、間違いなのだったらこのようなミスを防ぐにはどうすればよいですか?
=>[作者]: 連絡ありがとう.はじめの要約に書いていますが,「式を入替えても式の順序が変るだけだから,上下を入替える必要はない.」「また,係数の符号を全部換えても同じものになるから両方調べる必要はなく,x の係数が正のものを調べたらよい.」
(-5x+9y-3)(-2x-5y+4)は(2x+5y-4)(5x-9y+3)と順序と符号を入れ換えただけのものなので,数式としては等しいです.ただ,授業では符号を全部入れ換えたものは好ましいとは考えません.例えば,
を因数分解しなさいと言う問題について,
を正解としますが,
,
,
,
,
,など変形すれば様々な式ができますが,これらは標準的な書き方だとは考えません.(定期テストなら考慮しますが,問題も解答もコンピュータ合成にしていますので,要約に示した以外の書き方は画面上では不正解としています)
■[個別の頁からの質問に対する回答][複素数の計算 について/18.3.26]
もっっっっっのすごくわかりやすくて、教科書よりも全っっっ然役に立ちました。ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][cosxに関する不定積分 について/18.3.26]
cosxに関する不定積分問題5について、計算の答えが選択肢に見当たりません。おそらく、選択肢3の符号が誤っているのだと思います。(2.20)の解説#7においても、最後で置換されたtをtan(x/2)に戻す時に-をつけ忘れています…
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][数学的帰納法(不等式の証明) について/18.3.25]
たとえば12と打ちたいとして、まず十の位の「1」を入力すると「誤答」と判断されるのはよくないと思う
=>[作者]: 連絡ありがとう.選択肢を1つ選ぶのですから,2つ選ぶことはできません.
■[個別の頁からの質問に対する回答][余弦定理 について/18.3.25]
いつも数学の勉強で,お世話になっております。
余弦定理 問題1の(4)
△ABCにおいて,a=1+√3,c=2のとき,bを求めてください.
解説では、(1+)と3√3で違っています。
2018.03.25 HN 平 凡太郎(たいら ぼんたろう)
=>[作者]: 連絡ありがとう.書きかけの原稿のままになっていましたので訂正しました.
■[個別の頁からの質問に対する回答][sinxに関する不定積分 について/18.3.24]
問題10は正しくは選択肢3になるはずの解答が、選択肢4になっています。
解説#8の計算は合っているので、問題10の第4式第2項の計算で符号を誤ったと思われます。
=>[作者]: 連絡ありがとう.訂正しました.ついでに置換積分の補足も追加しました.
■[個別の頁からの質問に対する回答][不定積分(まとめ2・・・三角関数) について/18.3.24]
「三角関数の不定積分」で「V.12」の最後の「看板」…「あー、ため息、コテコテニ濃い」は疲れて来ていたときに面白い言葉に出会い、気持ちが楽になりました。有難う。この章をまとめた先生方も大変だ、ということが分かりました。私たちも大変ですが、本当に「Phylosophy愛智の道」ですね。そして、この章で解かれている公式を見つけた人は誰だろうな?、と思ってしまいます。本当に目から鱗が落ちて、もう落ちる鱗がない感じ。…問題6の解で、2/3I2で、2/3I1ではありませんか?
=>[作者]: 連絡ありがとう.肝心なところを間違えていましたので訂正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式 について/18.3.22]
(8)の2の解答の3:1内分する点は9/4ではないのですか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/18.3.21]
足し算も書いてほしい
=>[作者]: 連絡ありがとう.質問の意味が不明です.指数の和になる場合については,そのページに初めから書いてあります.
.これに対して,本体の足し算
のような計算?足したらよいのでは.
■[個別の頁からの質問に対する回答][根号の計算 について/18.3.21]
2 3
---- - ---- こういうけいさんのときかたを
1√+6 1-√6 おしえてください!
=>[作者]: 連絡ありがとう.そのページの先頭に現在地の表示があるので,2つ進んだところの
分母の有理化 というページを見てください
■[個別の頁からの質問に対する回答][行列の積 について/18.3.21]
行 列 行 列 と頭の中で念仏の様に唱えながら解きました
行は漢字に横の線があるから横 列は縦の漢字があるから縦とも覚えてみました
=>[作者]: 連絡ありがとう.各自の内的なロジックで身に着いていくのだと思う.
■[個別の頁からの質問に対する回答][分数型の方程式 について/18.3.20]
誤植と思われます。
(b) a/x=c/d のように未知数が左辺の分母にある場合
両辺の分母にあるx,dを2つとも払うために,両辺にをxb掛けると
〇 xbではなくてxdでは…
2018.03.20 平 凡太郎
=>[作者]: 連絡ありがとう.訂正しました.年配の方の署名かも
■[個別の頁からの質問に対する回答][三角不等式 について/18.3.15]
例題1の(最後までたどり着けない答案)の図の
青色グラフy=cos(2θ+プラスπ/3)と
表記されていますが
y=cos(2θ-マイナスπ3)ではないでしょうか。
青色グラフはy=cos(2θ-π3)のようです。
=>[作者]: 連絡ありがとう.Google Chart APIのタイトルを訂正しました.
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/18.3.15]
基本的な問題だったので、楽しくできた。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][一般項の記号 について/18.3.15]
まちがってもユニークなイラストではげまされるのがいい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][同じものがあるときの順列 について/18.3.15]
非常にわかりずらい
=>[作者]: 連絡ありがとう.中学生なのか,高校生なのか,社会人なのか,順列を習ったことがあるのかないのかなど,読者の属性を書かないと何を言おうとしているのか通じません.中学生や,順列を習っていない人が,たまたまiPhoneからググって出てきた画面を見たのなら,分かるはずはないとも言えます.
■[個別の頁からの質問に対する回答][母平均,母比率の推定 について/18.3.10]
①標本比率 r = t / n についての質問です。
t は、”あたりあるいはある事象の起こる個数、件数” n は標本数 として、t が二項分布B(n,p) (pは起こる確率)に従うとして、正規分布N(np,np(1-p)) に従うことを使って、
r は正規分布N(p,p(1-p)/n)に近似することが示されますが、この正規分布N(np,np(1-p)) を近似するもとになる二項分布はどのようになりますか?
B(n,p/n) B(n^2,p/n^2) どちらもしっくりあいません。
問題を解くにはあまり考えなくてもよいことですが気になっておりよろしくお願いします。
②もうひとつ、母集団と標本との関係で、標本の”あたり”個数(ある事象の起こる回数、個数)の分散は
np(1-p) (pをあたりの確率として)であり、一方 標本の平均の分散は 母分散σ^2/n ですが、この母分散σ^2 を個数の分散であるnp(1-p)と置き換えることは間違い(意味がない)ですか?またそれはなぜですか?母分散がわからないときに標本分散(標本が与えられればもとまるので)で代用するということですが...
以上 よろしくお願いします。
=>[作者]: 連絡ありがとう.nが十分大きいときに二項分布は正規分布で近似できるのですから,n=1にしたら無理でしょう.②は[高校数学C]と書いてある灰色文字の部分が高校での取り扱いの限界です.それ以上は大学の統計教科書になります.
■[個別の頁からの質問に対する回答][漸近線の方程式 について/18.3.10]
数Ⅲ導関数-漸近線の方程式2 [例3-2]で、問題の関数 y=(x3+1)/(x2+1) では、x=1→y=1となり、漸近線y=x と交わることになりますが、どこがおかしいのでしょうか、教えてください。間違っていたら、御免なさい 2018.3.10
=>[作者]: 連絡ありがとう.なるほど,教える側は交点と漸近線を混同しないように,実際に交わるのが交点で,「限りなく近づいていくが交わらないのが漸近線」という部分を強調しますが,実は漸近線と元の曲線は交わっても構いません.
図1は
のグラフで,その例と同様に
のとき曲線と漸近線が1回交わり,無限のかなたで下から近づいて漸近線となります.このように漸近線と元の曲線が交わることは何も問題がありません.
区別するには「有限確定の範囲で交われば交点」「限りなく近づけば(交わっても,交わらなくても)漸近線」と考えるとよいでしょう.(実際に,授業を行う場合には,このような回りくどい話をすれば理解率は著しく低下するので,「交わらなくても漸近線」とバシっと決めるでしょう)
図2は
のグラフで,曲線は何度も漸近線
に交わりながら漸近線に近付いていきます.また,図3は
のグラフで,曲線は何度も漸近線
に交わりながら漸近線に近付いていきます.
さて,根本問題を述べます.そもそも「限りなく近づく」というときの近付き方は,「小さい方から次第に」「大きい方から次第に」という一方向に限られるわけではありません.行ったり来たりしながらでも,
が成り立つならば,直線
は曲線
の漸近線になります.図2では
だから
の直線が漸近線です.(有限の値で何回交わっていてもこの定義は影響を受けません.実は無限に行ってもまだ交わっていますが,それも関係なしです.)図3では
だから
の直線が漸近線です.(有限の値で何回交わっていてもこの定義は影響を受けません.実は無限に行ってもまだ交わっていますが,それも関係なしです.)
たぶん,あなたの疑問は「行ったり来たりの極限値」というものを許容していなかったことにあると考えられます.
さよなら代わりの一撃:
■[個別の頁からの質問に対する回答][指数法則 について/18.3.10]
答えはどこにあるんですか?
=>[作者]: 連絡ありがとう.選択肢をクリックすれば,採点結果と解説が出ます.見ているだけでは出ません.
■[個別の頁からの質問に対する回答][複素数平面の図形問題(三角形の形状問題) について/18.3.9]
問題4(2)の答えの選択肢と回答が違っています。
=>[作者]: 連絡ありがとう.1つ前の問題の選択肢を引きずっていたようですので,訂正しました.
■[個別の頁からの質問に対する回答][恒等式 について/18.3.6]
ワークにこのような問題が乗っていて、↑の例題を見ても解き方がよく分かりません。お手数ですが、解答いただけると嬉しいです。
「 x^2=ax(x-1)+bx(x+1)+c(x-1)(x+1) が x についての恒等式となるような、定数 a、b、c を求めよ。 」
というものです。
よろしくお願いします。
=>[作者]: 連絡ありがとう.PC版では,下に解説がありますのでそれを読んでください.
問題を解いてしまうとあなたのやるべき問題がなくなってしまいますので,類似問題で答えます .
2x2 +4=ax(x−1)+bx(x+1)+c(x−1)(x+1)
が恒等式となるように,定数
a, b, c の値を定めよ.
(定数比較法による答案)
右辺を展開して係数を比較する
2x2 +4=(a+b+c)x2 +(−a+b)x−c
2=a+b+c
0=−a+b
4=−c
この連立方程式を解くと,
a=3, b=3, c=−4
- - -
(代入法による答案)
どんな
x についても成り立つならば,
x=0, 1, −1 のときにも成り立つ.(この値は,右辺の係数が2つずつ消える都合の良い形をしているから,それに合わせて選んだもの)
x=0 を代入すると
4=−c
x=1 を代入すると
6=2b
x=−1 を代入すると
6=2a
したがって,
a=3, b=3, c=−4 が必要条件になる.
しかし,2次式が異なる3つの値に等しいなら,恒等式であるから,十分条件も満たす.よってこれが解答.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数 について/18.3.6]
非常にわかりやすかった。テスト前に見て良かった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/18.3.5]
わかりやすかったです(≧▽≦)
テスト勉強に利用させて頂きました!(^^)!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][(複素数で表される)軌跡の方程式 について/18.3.5]
複素数の垂直二等分線の式がダブり?
(x+1)2+y2=(x+1)2+y2
=>[作者]: 連絡ありがとう.転記ミスですので訂正しました.
■[個別の頁からの質問に対する回答][繁分数式 について/18.3.4]
とてもわかりやすいです
助かりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][不定積分 について/18.3.3]
∫x4乗を積分したら5分の1x5乗じゃないでしょうか
=>[作者]: 連絡ありがとう.その通りですが,その質問がなぜ出てくるのかが,通じません.
1つ考えられるのは,そのページの問題は,固定問題でなく,読むたびに問題と解答の順序が変わるプログラムになっているところが,作者の気付かない1つのパターンで問題と解答が対応していないということですか?かなり調べましたが,正しい組合せしか登場しないようです.
もう1つの方は,高校の先生が聞いたら,腰を抜かすような話ですが,積分定数を別として
は
と同じものだということに気付いていないということですか?
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/18.3.3]
例題10で、赤紙、青紙、黄紙をビーズだと考えて糸を通して輪を作るとすると、どのような計算方法になりますか?
=>[作者]: 連絡ありがとう.同じものが含まれているような場合の円順列,じゅず順列の計算は,実際上は「根性物語」が計算方法だと思います.
左図のトリニトロトルエンの異性体が何通りあるかという問題と同じです(自然界ではNO
2 がCH
3 に対して,2,4,6の位置にあるものしかできないらしいが,理屈上は何通りあるかと考えた場合).CH
3 を上端に固定して,Hを並べていくとよいでしょう.この問題のように同じものがある場合には,左右対称なものは裏返しても同じなので,1つと数えるようにします.
根性で順に絵を描いていくと6通り.[円順列10通りから削っていく場合は,円順列が左右非対称なもの4通りは裏返したら重なるから-4.円順列が左右対称なもの2通りはそのまま2通り⇒結局6通り]
■[個別の頁からの質問に対する回答][群数列 について/18.3.3]
問題1のウの答えが間違いではないですか?
=>[作者]: 連絡ありがとう.では,あなたが正しいと思う答は?
■[個別の頁からの質問に対する回答][置き換えによる展開 について/18.3.3]
とても分かりやすいものとなっています。
大変参考になりました。
今後もよろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/18.3.3]
cotとはなんですか?
=>[作者]: 連絡ありがとう.一番最初に書いていますように,
のことを
で表します.
だから,
になります.
なお,
というものはないのと同様に,
というものはありません.
のように角度があっての記号です.
■[個別の頁からの質問に対する回答][集合 について/18.3.2]
解説はわかりやすいです。問題の選択肢に番号や記号を付けて頂けると選びやすいです。
=>[作者]: 連絡ありがとう.一長一短です.解答欄に転記するような場合は,記号がある方がよいが,この教材のように選択肢自体が解答用のボタンになっている場合は,その必要はないでしょう.また,番号の数字を答の数字と読み間違う場合があります.
■[個別の頁からの質問に対する回答][度数分布表,相対度数分布表 について/18.3.2]
初心者にもわかりやすく役立ちました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][楕円の方程式 について/18.3.2]
おもしろい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数計算1 について/18.3.1]
解説の横にそれと似たような問題があって助かります!
私の学校は県で二番目の進学校なのであまり演習をしてくれません。
だから、このサイトは本当にありがたいです。
これからもよろしくお願いします!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列 について/18.2.28]
即答問題があるのは、簡単でもOUTPUTすることで頭に定着しやすくなるので良いと思いました。
採点でサクラが咲くのは楽しく効果的で良いと思いましたが、文字でも表示してもらえると更に良いと思いました。
=>[作者]: 連絡ありがとう.携帯版の方が,対応が親切なので,携帯版に合わせました
■[個別の頁からの質問に対する回答][分母の有理化 について/18.2.26]
【問題1】と【問題2】に挟まれている解説文中、青囲みⅡ(1)式の、「5√3/6」という表示は誤記か何かではないでしょうか。
=>[作者]: 連絡ありがとう.転記ミスでしたので訂正しました.
■[個別の頁からの質問に対する回答][整数の累乗と整除 について/18.2.26]
(1)
すべての自然数nについて,24n-32nは7で割り切れる
の解説で
詳しく書けば,xn-an=(x-a)(xn-1+xn-2+...+x2+x+1)
とありますが
x^n-a^n=(x-a)(x^n-1+x^n-2a+...+xa^n-2+a^n-1)
の方がいいのではないでしょうか。
初学者なので間違った指摘でしたら申し訳ないです。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式2 について/18.2.26]
zが虚軸上を通るものも解説してほしい
=>[作者]: 連絡ありがとう.そだねー(テレビの見過ぎでした).余裕があれば検討します.
■[個別の頁からの質問に対する回答][正弦定理 について/18.2.26]
いみわからん
=>[作者]: 連絡ありがとう.ゲームをやろうと思えばできた時間に,このサイトを探し当てたのだから,あなたには何とか理解しようという「思い」があったはずです.まったく歯が立たない場合には,簡単な問題(その次のページ)で,解き方を真似するとよいでしょう.ロンドンでは小学生でも英語を話すのは,とにかく大人の真似をするからではないか.
■[個別の頁からの質問に対する回答][回転移動の1次変換 について/18.2.26]
「説明方法が幾つかありますが,一長一短ですので,各自の思考パターンに合うもので納得しましょう。」
すべて掲載していただいてありがとうございます。私は、基本ベクトルがイメージしやすかったです。加法定理との関係も疑問に思っていたことが説明してあり、すごく参考になりました。また、問題がついていることで、理解があっているかどうかの確認もでき、大変助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][グラフの平行移動 について/18.2.25]
三角関数のグラフの挿入誤ってますよ
=>[作者]: 連絡ありがとう.図版の番号が1つずれていたようです.
■[個別の頁からの質問に対する回答][点の像と原像 について/18.2.24]
問2の解説の一行目が(3 8 5 5)となっておりますが、(3 8 2 5)では無いでしょうか?
=>[作者]: 連絡ありがとう.問題に合わせて,解説の方を訂正しました.(文字数などの関係か?行列の表示が崩れやすく,注意力が落ちていました)
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/18.2.23]
x4乗+3x2乗+4の因数分解が、分かりません。
=>[作者]: 連絡ありがとう.
その次のページ の(4)の項目に,そのものずばりの問題と解答があります.
■[個別の頁からの質問に対する回答][楕円の方程式 について/18.2.22]
ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数法則 について/18.2.22]
上記の負の指数の定義の解説中、
「指数法則という「演算」の都合に合わせて「負の指数」が定義されています。」
とあるのですが、これは歴史的にみてどのような事情や欲求があって、そのように定義されたのでしょうか?
文系頭の私が朧げに聞いたところでは、そもそも「数える」という行為と「計算する(演算する」という行為は全くの別物で、前者は「対象の量の大小を比較する」欲求と。後者は「対象を操作する」という欲求によるところが大きいたと聞いた覚えがあるのですが…。
実際のところはどのような事情があり、また「数える」という行為と「計算する」という行為には本質的にどのような違いがあるのか、できましたらご教示ください。
=>[作者]: 連絡ありがとう.○○とはといった大げさな議論をしても,身に着かないことが多いです.もし,実際に身に着けて,学習や仕事に役立てようと考えておられるのなら,簡単な操作を「真似する」ことから始めてください.その必要がなければ,amazonなどに数学史の参考書が結構たくさん出ていますので,そちらを読まれるとよいでしょう.
■[個別の頁からの質問に対する回答][同次形 微分方程式 について/18.2.21]
どの問題も良いレベルでありがたいです。
参考にさせていただき、ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/18.2.21]
0の指数の定義の解説について。
最初の解説では、「指数が1ずつ減少すると式の値は底aの値だけ割ったものになります.」とありますが、文脈を補則して読み込んでしまうと、「底aの値で指数回だけ割る」というように読めてしまわないでしょうか? つまり0回割るんだから解はa^1だなと読めてしまわないでしょうか?
下段の別解説、0の指数はa^m/a^nと分数表記して通分して1になるから、0の指数の場合は1という解説の方が、私には分りやすかったです。
=>[作者]: 連絡ありがとう.図で説明していますので,文章だけで「引く数」と「引いた結果」を混同する可能性は少ないでしょう.
■[個別の頁からの質問に対する回答][数列の極限 について/18.2.20]
病欠によりほとんど学校行けてなかったのでとても助かり庵下。
=>[作者]: 連絡ありがとう.「ほとんど」というのは大変ですが,どう言えば元気玉を送れるのか,それが問題です.(1/3規定とか,1/5規定とか,ここからアウトみたいなのに引っかかないように,たまには皆の顔を見に行かないと・・・)
■[個別の頁からの質問に対する回答][指数法則 について/18.2.20]
指数法則に関して質問させていただきました。
ページの内容に直接的には関係ない質問を連投してしまい、確認などお手数をおかけしてしまい、すみませんでした。
お忙しい中すばやい対応、ありがとうございました。
=>[作者]: 連絡ありがとう.いや,この間違いを見つけてくれたのは,すごいと思います.(複素関数論はきれいなので,とても気に入っていましたが,高校の教員になってから全然使う場面がなくて,いわゆる竹光状態で申し訳ないことです)
■[個別の頁からの質問に対する回答][指数法則 について/18.2.20]
前回指数法則に関して質問させていただきました、ご返答ありがとうございます。
(攻撃的と思えわれましたらすみません、長く文章を書くのが苦手なもので。)
ネット上には指数法則が成立しない例というものも紹介されているところもあります。通常の複素解析の教科書ではnが自然数ならe^(nz)=(e^x)^zとありますが、e^(mn)=(e^m)^nが一般の複素数m,nで成り立つという記述は見たことがありません。私の勉強不足のせいかもしれませんが、もし証明や参考文献がありましたら教えてください。
=>[作者]: 連絡ありがとう.指数が複素数であることは問題ないですが,その教材のレベルでe^(mn)=(e^m)^nが一般の複素数m,nで成り立つと主張する必要はなく,その根拠もないので,その個所を削除しました.(複素関数の微積が自由にできるはずなのに,指数法則の幾つかを使っていないとは,目から鱗です.複素関数論といえば50年も前の参考書で,カビが・・・)
■[個別の頁からの質問に対する回答][指数法則 について/18.2.20]
『数学Bを習う人は最終的にm , nが複素数の場合でもよいことが分かります。』の部分の根拠が分かりません、出典など教えていただけないでしょうか。(指数法則(3)に関してです。)
=>[作者]: 連絡ありがとう.この教材は,20年近く書き足したものなので,どの時代に書いたものなのかよくわかりませんが(書き直すとファイルのyyyy.mm.ddが変わる),この数十年間の学習指導要領の改訂でオイラーの定理が入ったことはないようですので,訂正しました.なお,あなたの書き方は丁寧ですが,戦闘モードの匂いが付いているのが幾分気になるところです.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.2.19]
【問題2】 (2)ですが、解説がx3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)の公式をつかっていましたが、x3+y3+z3=3xyz+(x+y+z)(x2+y2+z2-xy-yz-zx)から
x3+y3+z3=3xyz+(x+y+z)((x+y+z)2-3(xy+yz+zx))になる理由がわかりません。教えて下さい。
=>[作者]: 連絡ありがとう.
このページ に出ていますように,
(a+b+c)2 =a2 +b2 +c2 +2ab+2bc+2ca
は,公式並みによく使われるものなので,いつでも使えるようにしておくとよいでしょう.
そうすると
a2 +b2 +c2 −ab−bc−ca
=a2 +b2 +c2 +2ab+2bc+2ca−3(ab+bc+ca)
=(a+b+c)2 −3(ab+bc+ca)
になります
■[個別の頁からの質問に対する回答][pならばqの真偽 について/18.2.19]
pならばqの真偽について理解できず長年苦しんでいましたが、このサイトのお陰でついに理解できました。
有難うございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][期待値 について/18.2.18]
期待値とは確率の平均値のこと!という説明がわかりやすかった。ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][(各駅停車)二重根号 について/18.2.18]
(各駅停車)2重根号なのですが…。
問題がぐちゃぐちゃになり、よくわからないです。
改善をお願いします。
=>[作者]: 連絡ありがとう.Android上のChromeで見ておられるようですが,こちらからは問題なく表示されます.ただ,この形式(下位目標が達成されな変えれば上位目標の問題が表示されない形式)でストレスを感じる人があるらしいので,その1つ前の項目にほぼ同じ内容で「二重根号」という選択形式の問題を作っています.つまり,改善済みです.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/18.2.17]
問題3の⑴の解説の二行目二乗されてないのですが…
=>[作者]: 連絡ありがとう.2を付けました.
■[個別の頁からの質問に対する回答][二項定理,多項定理 について/18.2.17]
(x+y)^5(3x-y)^2の展開式におけるx^4y^3の係数を求める問題の解説が知りたかったです😢
=>[作者]: 連絡ありがとう.宿題の問題かどうかわからないので,尋ねられた問題に答えずに他の問題に答えます.
の展開式における
の係数を求めたいとき
の展開式の各項は
この項が
を表すのは,
のとき
1)
のとき,
2)
のとき,
3)
のとき,
これらを加えて5
■[個別の頁からの質問に対する回答][複素数平面の図形問題 について/18.2.16]
【例題2.2】
(解答)
β2=(β-α)2+2βα+α2
γ2=(γ-α)2+2γα+α2
を代入すると
の部分の符号が間違っていませんか
=>[作者]: 連絡ありがとう.黒字になってからの最初の符号が違っていましたので,訂正しました.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/18.2.15]
問題2ですが、{(a +b +c)(b +c -a)}{(c +a -b)(a +b -c)}この組み合わせがベストだと予め分かる理由は何でしょうか
=>[作者]: 連絡ありがとう.問題2には4題ありますが,そういうことは書いてありません.問題1(2)には書いてありますが,質問の意味が通じません.問題がそうなっていたらその問題を解くのは当然で,ベストもなにもありません.全くこの惑星の住人は,言っていることがわからん.
■[個別の頁からの質問に対する回答][3次方程式の解と係数の関係 について/18.2.15]
カラフルで見やすくかつ証明まで詳しく解説されているので、素晴らしいと思います。
悪い点はこれといって見当たりませんね。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/18.2.15]
分かりやすくよかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次の不定方程式 について/18.2.15]
いつも分かりやすい解説をありがとうございます。お世話になっております。
問題5の答えについてですが、
m=0の時のyの値は9ではないでしょうか。
=>[作者]: 連絡ありがとう.入力ミスですのでで訂正しました.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/18.2.14]
こんにちは。三次方程式の解法について質問させてください。
三次の変数aを消す為に両辺をaで割るというのは何となくわかるのですが、
その後に立法完成させるべくX=x-b/3 or X=x+b/3を代入して、X^3+pX+q=0の式を導くというのは、なぜそのような操作ができるのでしょうか? 一部のサイトでは平行移動といって幾何的にグラフ移動の説明をするものもありますが、あくまでも代数的な操作理由が知りたいです。
また代入すべき変数Xは、元の三次式の係数に関係なく、とにかくX=x-b/3 or X=x+b/3を代入してかまわないのでしょうか?
=>[作者]: 連絡ありがとう.
のとき
とおくと
となって
の項が消せるところに目を付けたのがカルダノ公式です.
とおくというのは各自の自由ですが,結果が生きて使えるという保証はないでしょう.X=x+b/3では2次の項は消えません.
※この教材ではカルダノ公式は扱っていませんが,実際には
となってからの変換の方がミラクルで,思いついた人が偉いとしか言いようがないでしょう.なぜ思い付くのかなどと考えても無駄でしょう - - 相手は数学史に残る偉人なのだから,後の人は真似をすることから始めるのが無難
■[個別の頁からの質問に対する回答][群数列 について/18.2.14]
問題1の(2)ウの途中式をお願いします。
どうしても分母の2を消せなくて分からないです。
=>[作者]: 連絡ありがとう.ヒントの文章に沿って,答案を作ると,第n群は,初項[n
2 -2n+2],公差1,項数2n-1の等差数列だから,その和は
※その問題の下に灰色で書いてある公式に正しく代入すればできます.
■[個別の頁からの質問に対する回答][極限値,不定形の極限 について/18.2.14]
見やすいしわかりやすくてよかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重積分...積分領域が変数に依存する場合 について/18.2.14]
問6はなぜ、はじめにxで積分してるのですか?
=>[作者]: 連絡ありがとう.解説に,はじめにxで積分する理由が書いてあるのに,さらになぜと問うには,その解説がおかしいということを示さなければなりません.
■[個別の頁からの質問に対する回答][データの代表値(平均値,中央値,最頻値) について/18.2.14]
下記の部分に誤植があります。255=>25
その3番目255と4番目27の平均をとって,26を中央値とします.
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][部分分数分解 について/18.2.13]
なぜKの式を通常の部分分数分解のように
A/k+B/(K+1)+C/(K+2)
と置いて計算するとKの規則性が分からず答えが導き出せないことがあるんですか?
=>[作者]: 連絡ありがとう.一般論だけでは分かりにくいので,そのページにある具体的な問題で説明します.
を求めたいときに
と変形しても,その先の展望が持てません.なぜなら,そのページの初めから書いていますように,部分分数に分解することは目的ではありません.すなわち,ある与えられた式
が何らかの式
を使って,
という形で「差」の式で書くことができる場合に,
という形で(中間項が消えて)和が求まります.
この
を求めることが当面の目的です.
ところで,本文にも書いていますように,与えられた式
を
という形で「差」の式で書くことができるとき,一般に
は
の積分と同様に1次だけ次数の高い式になります.今の例で言えば,
は分母が3次式で分子が1次式だから,全体で-2次です.この式を
という差で表現できるのは
を-1次:分母が2次で分子が1次とした場合です.だから
とおいて
の係数を比較すると
となって,和が求められる形になるのです.
見かけ上「部分分数に分解したことになる」から部分分数分解というだけです.
■[個別の頁からの質問に対する回答][不等式と領域 について/18.2.13]
とてもわかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ 因数分解(応用問題) について/18.2.12]
中3です。とても使いやすいサイトでテスト勉強に助かります。自分のみたい項目を見つけるのが大変なので、トップページで検索できたりすると嬉しいです。
=>[作者]: 連絡ありがとう.過去には,サイト内検索を設置したこともありますが,あまり利用されないようでしたのでやめました.代わりに,前後の項目を示すサブメニューを設置しています.
■[個別の頁からの質問に対する回答][極限値,不定形の極限 について/18.2.12]
極限値の問題(4)の解が∞となる理由を教えてください。
=>[作者]: 連絡ありがとう.アクセス数の多い携帯版を先にメンテしていますが,PC版はまだでした.携帯でPCは読めませんが,PCで携帯版は読めます.そちらに解説があります.PC版は可及的速やかに(←お役所かい!)携帯版に合わせます.
■[個別の頁からの質問に対する回答][総和記号 について/18.2.11]
すごく勉強になります。例7の注意書きの、したがっての後、Σ=1+1+1.....=nがわかりません。nは終わりではないのですか?言葉足らずで、すみません。気になってしまって。理解力が足らず、すみません。
=>[作者]: 連絡ありがとう.第1項が1,第2項が1,第3項が1,第4項が1,…第n項が1,これら(n個を)加えると1+1+1+…+1=nになります
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/18.2.10]
積和の公式の問題集が無かったので助かりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][楕円 について/18.2.10]
離心率や二次曲線の統一的な見方も解説してほしいです。
=>[作者]: 連絡ありがとう.統一的とまでは行きませんが,離心率や準線の話題は
このページ にあります.二言三言追加して,直交座標での離心率と極座標での離心率をつないでおきます.(数日かかります)
■[個別の頁からの質問に対する回答][一般項の記号に慣れる について/18.2.9]
非常に、見やすくわかりやすい。復習に役立ちます。
=>[作者]: 連絡ありがとう.
■鹿児島県[いろいろな因数分解について][18.2.8]
問3の問題の解説で□²-○²に置き換えるという所が分からないのですが
=>[作者]: 連絡ありがとう.
このページ の解説を読んでください.
■[個別の頁からの質問に対する回答][条件付き確率 について/18.2.8]
例えば
当たりくじ2本を含むn本のくじがある
nは3以上の整数としてこのくじをA、B、C
の3人が引くとき、各人が当たる確率を求めよ
ただし、引いたくじは元に戻さない
という時はどうすればいいですか?
=>[作者]: 連絡ありがとう.
2人の場合は,その次のページ にそのものずばりの解説があります.一般に,引く順序に関係なく,p=2/nになると言えますが,3人の場合の証明は少し長くなります - - 特に,当たりくじが2つしかないときに,前の2人が当たってから3人目のCが引く場面を考えると「Cは損じゃないか!」と言いたくなる心理的な部分と,「引く順序に関係ない」という客観的な事実が計算上どのように示されるかという観点から見ると,興味が持てるかもしれません.
結論から言えば,前の人(AやB)が外れる場合に後の人Cが当たる確率は高くなって「埋め合わせ」される(次の計算でp
4 が大きい)と考えれば,心理的な納得が得られるでしょう.
A=○,B=○,(C=○) ⇒前2人が○なら,3つ目の○はないから,この確率はp
1 =0
A=○,B=×,C=○ ⇒
A=×,B=○,C=○ ⇒
A=×,B=×,C=○ ⇒
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/18.2.8]
確率を絡めた問題も欲しかった
解説は非常に分かり易い
=>[作者]: 連絡ありがとう.前から順に学んだ場合,順列・組合せを習っている段階では,確率はまだ習っていない取り扱いになります.あなたのような要望が出るのは,数学Ⅰを全部終了した人の場合ですが,その場合は,確率のページを見てください.ただし,標本空間と事象(分母と分子)が円順列という問題は,少ないようです.
■[個別の頁からの質問に対する回答][複素数平面の入試問題3 について/18.2.8]
2-2(4)の解答について確認をお願いします。
=>[作者]: 連絡ありがとう.百里の道は九十九里が半ばと言われ,九十九里になると判で押したように疲れが出るのは歳のせいか.訂正しました.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/18.2.8]
2番は待遇のよいものを調べるだけで十分てわは?待遇のよいものの中に平家以外がいるかでは?源氏は調べなくて良いのてわは?
=>[作者]: 連絡ありがとう.日本語を勉強中ですか?掲示板用語では通じません.
■[個別の頁からの質問に対する回答][空間における平面の方程式 について/18.2.8]
慶應商学部2017年Ⅲのベクトルの解説をしてほしいです。
=>[作者]: 連絡ありがとう.個別の問題には対応できませんが,
その次のページ を読めばわかります.
■[個別の頁からの質問に対する回答][等比数列の和 について/18.2.7]
公式は導出からお願いしたいです
=>[作者]: 連絡ありがとう.その教材を作った2000年頃には授業の中で使うことを想定していましたので,まさか教科書をもっていない生徒がいるとは考えていませんでしたが,その後の世の中の移り変わり(熱狂は失望に変わった:e-ラーニング)により,最近は基本事項の解説もいれています.数列の和の公式がまだだったということですが,Σ記号の解説のページに書き込むことはありません.(前のことを全部書いていると,後ろの方のページは膨大なものになる)
■[個別の頁からの質問に対する回答][集合 について/18.2.7]
個別質問[部分集合,集合の包含関係について/18.2.6]をさせていただいたものです。ご親切なご指導ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][平方完成 について/18.2.6]
とても分かりやすいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][部分集合,集合の包含関係 について/18.2.6]
こんにちわ。部分集合と真部分集合の違いについてわからないところがあるので教えてください。
A={x|xは素数全体の集合}
B={x|xは奇数全体の集合}
として、
A-B={2}であり、A-B⊆A。
すなわちA-Bの差集合は、Aの部分集合である。
という記述を見かけたのですが、なぜA-Bの差集合がAの真部分集合ではなく、部分集合なのかがよくわかりません。
大変恐縮ですが、ご教示いただければと思い質問させていただきます。
=>[作者]: 連絡ありがとう.初めに記号を整理しておきます.そのページの下端に(注意)という形で表で示してありますように,部分集合と真部分集合を表す記号は,昭和30年代,40年代と現代とでは異なっています.かつては,不等号の ≦,<と対応して,部分集合を
で,真部分集合を
で表す方式がメジャーでしたが,現在の高校では部分集合を
で,真部分集合を
で表す方式がメジャーです.
さて,A-B={2}で,今日の書き方では
です.さらにもっと限定して,
も言えますが,この2つは背反関係ではありません.真部分集合であれば部分集合なので,特に等しくないということを強調する必要がなければ,単に部分集合で示す方が簡単なのです.
他の例:N={1,2,3,...}は自然数全体の集合,E={2,4,6,...}は正の偶数全体の集合とするとき,EはNの部分集合でもあり,真部分集合でもあります.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/18.2.4]
すっかり式と導出方法を忘れていたので助かりました。ありがとうございますm(_ _)m
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の方程式 について/18.2.4]
体調不良などで授業を受けられなかったときに、教科書だけでは理解できないので利用させていただいております。解説、まとめられた公式とそこに至る証明、練習問題等あらゆる面で非常に助かっております。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数方程式 について/18.2.4]
全体的に色がありすぎて見にくい
=>[作者]: 連絡ありがとう.見解の相違です.
■[個別の頁からの質問に対する回答][2直線の平行条件・垂直条件 について/18.2.2]
ウェブでいろんなサイトを見ましたが一番わかりやすかったです、
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2直線の平行条件・垂直条件 について/18.2.2]
平行条件の例題2 CD→CAじゃないですか??
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][三角関数の定義 について/18.2.2]
5年ぶりに解きました。
学生時代の時よりも文章の意味が分かるようになり、少し嬉しくももう戻らない時間を感じ、ちょっと悲しい複雑な気持ちを感じています。
気が向いたらまた来ます、ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][隣り合う並び方・隣り合わない並び方 について/18.1.31]
隣り合う並び方の問9の解説が分かりにくいです
=>[作者]: 連絡ありがとう.その問題は「むずかしい」と書いてありますように,そこそこ難しいです.少し解説を追加します.
■[個別の頁からの質問に対する回答][対数不等式 について/18.1.31]
真数条件などの見落としやすい場所の解説は丁寧でわかりやすかった、できれば、対数が定数に挟まれた不等式の解説も行ってほしい。
=>[作者]: 連絡ありがとう.
ならば
だから
です.
また,
ならば
,
だから
です.
■[個別の頁からの質問に対する回答][極座標 について/18.1.31]
私は文系で、極座標のイメージがずっとつかなかったのですが、このサイトの問題を解いていくうちに、マスターできました!図に点を打っていくような方法は簡単で楽しかったです!
ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/18.1.30]
大学で統計をかじった程度の入門レベルの人間ですが、必要に迫られ調べているうちにこのページにたどり着きました。しっかり解説してくださって、ありがとうございます。とても助かりました。
一方で、少し分かると、さらにどんどん分からないことが出てきます。
例えば、t検定の際に、なぜ事前に等分散かどうか調べる必要があるのでしょうか?前提が変わると何か計算方法が変わったりするのでしょうか?また、F検定で「等分散でない」ということが有意となった場合は、その時点でもう2つの集団には「差がある」と言えるようになるのでしょうか?
F分布とt分布とはどう違うのでしょうか?
2つの集団の平均値の差の検定をExcelで分散分析とt検定の両方で行ってみると、ほぼ同様の結果でしたが、微妙にP値が異なりました。これはなぜでしょうか?2つの集団の平均値の差の検定の場合は、分散分析とt検定のどちらの方が「より良い」・「より適切」とかあるのでしょうか?
やっぱり難しいですね・・・。
=>[作者]: 連絡ありがとう.「t検定の際に、事前に等分散かどうか調べる必要」はあります.等分散と見なせる場合とそうでない場合とでは,t検定の公式が違うからです.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/18.1.30]
参考にさせていただきました
数学の問題は数をこなさないとすらすら解けるようにならないですかね?
=>[作者]: 連絡ありがとう.「数をこなさないと」という部分については,そうだと思う部分と,数だけではないと思う部分があります.自分の内的ロジックとして使えるかどうかが身に着くかどうかの違いかな.
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/18.1.30]
二重積分の応用の例題も作ってもらえると助かります。しかし、テストでは非常に助かりました。
=>[作者]: 連絡ありがとう.一歩踏み出せば,果てしなき応用の世界が広がっているようですが・・・
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/18.1.29]
練習問題が付いていて実践的に用いることができました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/18.1.29]
1〜nの番号がついたn個の玉から3つ重複ありで選ぶ方法は?
=>[作者]: 連絡ありがとう.そのまんま,n H3 でしょう!
■[個別の頁からの質問に対する回答][楕円 について/18.1.29]
最近楕円の方程式について学んだ学生です。
ここにある問題には何の文句も無いのですが、一つ疑問があります。
楕円の焦点の座標がそれぞれ
F(c,d),F’(-c,-d)
(c≠0,d≠0)
……この場合はどうなるのでしょうか。それとも、こういった場合は考慮しないのでしょうか。
=>[作者]: 連絡ありがとう.長軸と短軸がx軸,y軸に平行である場合が教科書で扱う基本です.(A)今の教育課程では,行列,一次変換,回転移動がないので,軸が回転している楕円は基本ではないでしょう.(B)楕円と直線の合成で考える場合は,数学Ⅲの応用としてあり得ます.
例えば,円
の方程式は無理関数を2つ使えば
と書くことができます.(図1)そこで,
すなわち
すなわち
すなわち
のグラフは左図2のようになりますが,一般にこのように長軸,短軸がx軸,y軸に平行でなく,それらから回転されている場合は,方程式にxyの項が含まれます.
楕円の焦点の座標がそれぞれF(c,d),F’(-c,-d)(c≠0,d≠0)にある場合は,(短軸の長さが指定されていませんが,標準形で
であったとすれば)
標準形の楕円の方程式
に
だけ「かさ上げ」すると
すなわち
すなわち
となって,この式を展開すると
の形の方程式になります.(なお
のグラフを原点の周りに角θだけ回転したとき,
の方程式を求める問題は,昔は大学入試に出ましたが,最近はあまり見ません)
■[個別の頁からの質問に対する回答][漸化式と一般項(階差形) について/18.1.29]
(10)の初項は4ではないのでしょうか?
=>[作者]: 連絡ありがとう.テンキーを使っていて,1つズレたようですので,訂正しました.
■[個別の頁からの質問に対する回答][底の変換公式 について/18.1.28]
log4低の2ってなんですか
=>[作者]: 連絡ありがとう.このページを読んでその内容について質問しておられるのなら歓迎しますが,あなたはそうではありません.宿題か何かの答えを探すためにgoogleの検索で出たこのページを「読まずに」=「30秒間画面を流しただけ」で答えを聞いています.
そもそもlog4低の2という言い方は変わっています.その問題を出した人に聞いた方がよいです.対数で使うのは低学力の低ではなく,海底の底,基底の底です.
log4低の2が
を表しているのか
を表しているのかによって,話が変わってきます.サブメニューでもっと先頭にある
対数の定義 のページを読んだ方がよいでしょう.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/18.1.28]
わかりやすくていいです。
宿題が分からなくて困っていましたが、これを見たらほとんどわかったのでとても助かりました
=>[作者]: 連絡ありがとう.この内容は結構大事です.
■[個別の頁からの質問に対する回答][軌跡の方程式2 について/18.1.28]
円の反転は直線、直線の反転は円ということなのでしょうか?
=>[作者]: 連絡ありがとう.結論を先に言えば,そんなことはありません.原像が0≦r≦1にある図形ならば,その像は1≦r<∞の範囲に来ますが,原像が他の範囲にあればそうはなりません.例えば,原像が原点を中心とする半径1の円である場合,その反転も原点を中心とする半径1の円になります.
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/18.1.27]
数2三角関数 性質で問題3から 見たことのない計算式が出てきて ヒントもなし、どこを参考にしていいのか分かりません
=>[作者]: 連絡ありがとう.解説がヒントです.見たこともない計算式とは,心外です.そのページの先頭から図あり式ありで解説している内容を踏まえて計算することになります.(あなたの読み方を見てみると[なぜわかるのかは,詳しく言えない],問題3あたりまで余り読まずに進んでいます.時々,先頭部分んまで振り返っていますが,それは一瞬で5回です.初めの方に重要な解説があるので,その部分を飛ばしてしまうと,理解できません.)
■[個別の頁からの質問に対する回答][3次関数のグラフ について/18.1.27]
とてもわかりやすいと思います!一次・二次関数グラフと合わせると個人的に面白い図になるので、それも載せていただけるとありがたいです(個人的なお願いで申し訳ございません)
小4 名無しより
=>[作者]: 連絡ありがとう.3次関数と1次関数の共有点の問題は,移項すれば3次関数の問題になり,3次関数と2次関数の共有点の問題も,移項すれば3次関数の問題になるので,関係としては同じになります.図としては一応別ですが.
■[個別の頁からの質問に対する回答][無理関数(2次式の平方根)の定積分 について/18.1.27]
お世話になっております。
修正箇所がいくつかありましたのでお時間がある時で結構ですのでご確認いただければと思います。
最初に、いちばん上の解説部分の右下の被積分関数が"2x/√(a^2-x^2)"の問題についてなのですが、下から2行目の右辺について、分母の√xは√tの誤記だと思われます。
それと、∫の前のマイナスか積分変数の分母の-2xのマイナスはどちらか一方が不要と思われます。
次に【問題1】の解説の最後2行なのですが9/2になるべきところが9になっているのと、π/4+π/4となるべきところがπ/4-π/4になっています。
あと【問題3】の解説の下から3行目ですが√tは1/√tだと思います
そして【例5】の(解答)の中ほどあたり、定積分の下端と上端が0→1になってますが1→2だと思います
最後に、このページ内に問題の解答解説箇所も含めて4か所”被積分j関数”と記されている部分があるので検索や置換にてご修正ください。
私が間違ってるところがあったらすみません。
=>[作者]: 連絡ありがとう.全てご指摘の通りですので,訂正しました.(こんなにたくさん間違えて,作者しっかりしないと!)
■静岡[ヘンリーさん][18.1.26]
なぜaベクトルが(x,y)の時それに垂直なベクトルの成分が(ーy,-x)になるんですか?
=>[作者]: 連絡ありがとう.そういう事実はありませんし,この教材にもそのような記述はありません.
■[個別の頁からの質問に対する回答][展開の順序 について/18.1.26]
公式に当てはめコツコツ解けば必ず答えが出る問題である。
煩雑な数式なので、ケアレスミスに気をつけなければいけないと思う。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/18.1.25]
ここまでは一応、順調に来れました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/18.1.24]
画面を大きく表示したい時、CTRL+で大きくすると左右のスクロールが効かなくなります。
=>[作者]: 連絡ありがとう.ん?逆ではないでしょうか.横幅1366ドットの画面で見ている場合,通常の倍率なら教材の横ドット数がそれよりも小さいので,横スクロールバーが表示されないが,Ctrl+ を数回行うと,画面一杯以上に表示されるので,左右スクロールができるようになります.
■[個別の頁からの質問に対する回答][ベクトルの定義 について/18.1.24]
"しかし,ADとCBは「長さ」が同じですが「向きが逆」なので"の後についている数式の画像が間違っている。
=>[作者]: 連絡ありがとう.演説を力み過ぎて,手が滑ってしまったらしい.訂正しました.
■[個別の頁からの質問に対する回答][合成関数 について/18.1.24]
スマートフォンでも気軽に問題を解けるので、授業確認に重宝しています。もう少し、高度な問題(黄チャート)も含めて頂けると、尚良いと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/18.1.24]
練習問題が複数問あったが、多過ぎず少な過ぎずちょうど良かったと思う。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ ベクトルの大きさ(長さ) について/18.1.23]
ベクトルの絶対値について質問です。
絶対値のついたベクトルを、ベクトルでは『大きさ』といいますが、『距離』や『長さ』という言葉ではニュアンスが変わってしまうのでしょうか。
(大きさ=距離=長さ、という風に考えていいのでしょうか。)
勉強不足ですみません。
教えていただけると嬉しいです。
=>[作者]: 連絡ありがとう.ニュアンスということでは変わるかもしれませんが,ベクトルの定義とか他の分野との共通性を重視すると「大きさ」と言うのが無難かもしれませんし,高校生が習う2次元,3次元のベクトルとの関連性を考えれば距離や長さと言っても何ら問題ない場合がほとんどです.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/18.1.22]
面白かった!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/18.1.22]
良い勉強になりました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の積 について/18.1.22]
わかりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/18.1.22]
56歳です。ボケ防止のために(ややボケが入っていますが)始めました。
今回はクリアできましたが、以後壁にぶち当たることが多々出てくると思います。よろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/18.1.21]
例は最初に見せて後から問題を溶かせたら良いと思う
あと、字が小さいから見にくい
=>[作者]: 連絡ありがとう.スパンの長い解説とまとめの問題だけでよいという考え方は,昭和の時代のやり方かな.形成的評価を重視する現代のやり方は,スパンの短い解説と小問の繰り返しから成り立つものと理解しています.Ctrl+(+)
■[個別の頁からの質問に対する回答][対数方程式 について/18.1.19]
とてもよかったです(^^♪
問題を解きながら学べてとてもいいです!
また来ようと思います!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/18.1.18]
問題1の(4)の答えは上記以外であっているのですが、上記以外と答えると×と出ています
=>[作者]: 連絡ありがとう.今年になってから書き換えたものですが,点検が甘かったようで訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作9・・・無理関数の不定積分 について/18.1.18]
ソレノイドの作る磁場を計算する際に用いた積分公式について知りたいです。
=>[作者]: 連絡ありがとう.その式を書かないと話が通じません.三角関数の方は簡単です.無理関数で分数になる方ですか.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/18.1.17]
分かりやすかったです!ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][直線のベクトル方程式 について/18.1.17]
問題2で、DE:DB=5:8で正解ですか? 宜しくお願いします
=>[作者]: 連絡ありがとう.おっと,解答が問題に答ていませんでしたので追加しました.しかし,あなたの質問は変です.この問題では,縦横の尺度は決められていないので,同一直線上にないDE:DBのような比率は定まりません.AD:DBなら定まりますので,それを追加しました.
■[個別の頁からの質問に対する回答][区分求積法の入試問題 について/18.1.17]
一番最後の問題6の答案ア)の後半なのですが、x[k]=k/2nなのでx[0]=0/2n=0,x[2n]=2n/2n=1が正しくてその下の∫の範囲も0→1が正確なのかなと思いました。必要でしたらご修正ください。区分求積法の多様な出題パターンを知れて勉強になりました。白紙の解答用紙が来ても解答書けるようにがんばります・・
=>[作者]: 連絡ありがとう.入力ミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/18.1.17]
アンケートから失礼致します。非常にわかりやすい文章ありがとうございます。質問なのですが、y"+ay=bの場合は、bを一旦無視して、上に記載されているように解き、y= c1cos ax+c2sin axのようになりました。その後bの特解はどのように解けばよろしいでしょうか?教えていただきましたら、嬉しい限りです。よろしくお願いします。
=>[作者]: 連絡ありがとう.右辺が0のものを同次形といい,右辺が0でないものを非同次形といいます.先頭のサブメニューで,現在地を「定数係数の2階線形微分方程式(同次)」と表示していますが,その次に「定数係数2階線形(非同次)」という項目がありますので,そのページを見てください.
■[個別の頁からの質問に対する回答][2次関数の最大値,最小値 について/18.1.16]
いつも数学の勉強に利用させてもらっています。
独学なのでとても助かっています。
ところで、僕の勘違いかもしれませんが、もしかして、
問題6 (1) ア) 「a<0」は、「t<0」ではないでしょうか?
=>[作者]: 連絡ありがとう.入力ミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][展開公式1 について/18.1.16]
とてもわかりやすく見やすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次方程式の解と係数の関係 について/18.1.16]
証明
=>[作者]: 連絡ありがとう.質問がある場合は,それなりに言葉で書くべきです.証明は「証明を見る」というリンクをたどれば書いてあります.
■[個別の頁からの質問に対する回答][ベクトルの和 について/18.1.16]
ベクトルの定数倍のところの図の→a+→bが始点+始点になっているので間違えいるとおもいます
=>[作者]: 連絡ありがとう.そのページはベクトルの和を扱っています.ベクトルの定数倍の質問ならベクトルの定数倍のページで質問すべきですが,どうやら質問者の書いている「定数倍」という言葉は,意味がないようです.
おそらく,その前のベクトルの定義のページを十分読んでおられないと考えられます.すなわち「2つのベクトルは,「大きさ」と「向き」さえ等しければ「等しい」といい,”どこに描いてあるか”は問題にしない.」
そこで,「ベクトルの和を考えときは,終点に始点を接ぎ木して和を作ります」が,問題の図で終点に始点が接ぎ木してあるとは限らず,自分で移動させて作るのです.
問題が図1のように書いてある場合に,それは問題が間違っているのではなく,問題を解く人が図2のように書き換えて答えを出すのです.
「ベクトルは,どこに描いてあっても構わないから移動させてよい」ということを理解するには,それなりに知的能力を必要としますが,これがクリアできなければ,ベクトルの和差などは理解できません.
■[個別の頁からの質問に対する回答][展開公式1 について/18.1.15]
学校の授業が嫌になったので、ここに来ました。正直に言うと、授業よりわかりやすい。
これからテスト勉強とかここでしよう。
=>[作者]: 連絡ありがとう.授業や教科書は必要最小限のことが詰まっていて,能率がよいので大事にする方がよい.こちらの教材も使えるところは使ってください.
■[個別の頁からの質問に対する回答][指数法則 について/18.1.14]
4^a=-4 は、なんですか?
=>[作者]: 連絡ありがとう.このページの内容と関係のない質問です.指数方程式の質問なら,指数方程式のページで方程式の解を尋ねるべきです.
高校生でない方が尋ねておられるのなら,複素関数で留数定理かオイラーの定理の辺りを調べるとよいでしょう.
■[個別の頁からの質問に対する回答][組分け について/18.1.14]
下に問いがあるのはいいと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/18.1.12]
問題解きました。結びつけるだけは簡単すぎます。
=>[作者]: 連絡ありがとう.公式が分かるようになるのが第1段階で,それができるようになったら,サブメニューで練習問題に進むようになっています.この手順を踏まずに,はじめから練習問題や応用問題に入ると身に着かないことが多いようです.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/18.1.12]
とても役に立ちました!
ほんとにこういうのがあると助かります!
無料でこのサイトを見れるのは、ありがたいです。これからも、よろしくお願いします。
しかし、円順列とじゅず順列の問題の15番だけ解説が表示されません。
=>[作者]: 連絡ありがとう.点検してみましたが,iPhone, Androidのいずれでも正常に表示されました.- - ただし,数年前にGoogleから個別にご指導を受けたことがあり,「リンクの間隔が狭過ぎる!」という趣旨だったので,スマホ用ページでは,できるだけ選択肢や解説などの作動ボタンを離して設置するように改良している(年月がかかる)途上です.どうしても誤作動する場合は,ズームインしてから選択してください.
■[個別の頁からの質問に対する回答][指数法則 について/18.1.10]
とても分かりやすいです!ありがとうございます!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][Excelを用いた判別分析 について/18.1.10]
はじめまして。マハラノビスの距離の処理について質問があります。
(8)のMMULT(こちらのExcelの例のマハラノビスシートでいうとMMULT(J3:L3,(G3:I3)))の計算がctrl+hift+enterを押しながら計算してもエラーになるのですが、もしほかに注意点などがあれば教えてください。また、(8)に、SA-1の範囲に$を付けるのを忘れないとありますが、(7)で行った計算式に$をつけ忘れないようにという解釈で間違っていないでしょうか?返答お待ちしております。
=>[作者]: 連絡ありがとう.Excelのバージョンやセキュリティレベルの設定によって,エラーの出方は様々になると考えられますので,個別に回答するのは無理です.画面上の記述と下端の例と答別添ファイル(hanbetu2.xls)で確かめてください.特に,Ctrl+Shift+Enterが入力されている場合には,数式バーの式に{ }の記号が入っています.それがなければうまく押せていません.
■[個別の頁からの質問に対する回答][指数関数のグラフ について/18.1.10]
良い所
・スマホでも見やすいレイアウト
・曲線や数字が色分けされてわかりやすい
改善の要望
・次の問題文を、iPhoneで見ると数字が重なって見えます
問題1-3、問題2-5
=>[作者]: 連絡ありがとう.PC版のSafariやAndroid版のChromeで点検しても,要望の内容がなかなか理解できませんでしたが,今,解読できました.
画面の横幅が320ドットくらいのiPhoneで見ると,各々最後の選択肢が改行されて左下に来るということらしいので,その選択肢のレイアウトを変更しました.
■[個別の頁からの質問に対する回答][ベクトルの実数倍 について/18.1.10]
問題の第2問目の答えの絵の始点がずれている気がします…
=>[作者]: 連絡ありがとう.その点に興味を持ってもらうのは,よいことです.一瞬,興味を持ってもらって,それは関係ないことだと分かってもらうように,わざとずらしています.ページ上端にあるサブメニューで,
ベクトルの定義 の一番最初に話として,「【要点】2つのベクトルは,「大きさ」と「向き」さえ等しければ「等しい」といい,”どこに描いてあるか”は問題にしない.」と書いています.その意味を考えてください.例えば平行四辺形
ABCD において
が成り立つという場合,一方は
A から出ていて,他方は
D から出ており,描かれている場所がずれているのに「2つのベクトルは等しい」というのは,「どこに描いているかは問題にせず,大きさと向きが等しければよい」からです.
■[個別の頁からの質問に対する回答][曲線で囲まれた図形の面積 について/18.1.10]
このサイトにはふさわしくない、rentaとかいう気持ち悪いまんがの広告出すのはどうかと思います。
=>[作者]: 連絡ありがとう.幾つかの避けたいジャンル(アダルト,カルト,出会い系,サラ金など)の広告はブロックしていますが,一般の広告でどのような広告が出るかは,多くの場合,読者自身の検索傾向によるものと考えられます.すなわち,この数日間,数週間,あなた自身がそのiPhoneからGoogleでゲームやコミック関係の検索をした場合,その人の興味・関心,はっきり言えば購買傾向としてその分野の広告を出していれば,当たりやすいということが個人ごとに把握されていて,その結果としてそういうジャンルの広告が出るようです.つまり,予備校の広告のようにこのページの内容関連で登場するものだけでなく,その情報機器を使っているユーザごとの関心に応じて表示されるものがあるので,広告の内容を決めているのは,1人ずつのユーザです.筆者は広告を指定したりはできません.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/18.1.9]
(x^2-3x)(x^2-3x-2)、左のかっこの中身がまだ因数分解できますがこのままで大丈夫ですか?
=>[作者]: 連絡ありがとう.筆者は言葉を慎重に選んでいて「因数分解し(切り)なさい」とも「展開し(切り)なさい」とも書いていません.「等しいものを選びなさい」と書いていますので,何も問題はありません.すなわち,中間生成物と中間生成物の対応でも可能で,あなたが気付いていない問題と選択肢の組は何個もあります.
■[個別の頁からの質問に対する回答][集合 について/18.1.8]
とても良い問題でためになりました!
=>[作者]: 連絡ありがとう.読者の評価が高いのはどんな問題なのか,感想が送られて来たらそのページを見て,勘を養うようにしています.
■[個別の頁からの質問に対する回答][決定係数 について/18.1.8]
決定係数に目安などはありますか
現在数値解析を行っていますが、決定係数がどのくらいの値まで向上すればいいのか目安などありましたら教えてください
=>[作者]: 連絡ありがとう.そのページ内に書いていますように「回帰式がよく当てはまっていると言えるためには,決定係数が幾らあればよいのか一概にはいえない.」参考書などでは「0.7とか0.8とか全変動の7割,8割程度の説明ができればよく当てはまっていると考えることが多い.」などとされています.
■[個別の頁からの質問に対する回答][空間における平面と直線 について/18.1.7]
問題2の方程式のところがyのところがtになっていました。
とてもわかりやすいです。
=>[作者]: 連絡ありがとう.t→y 訂正しました.
■[個別の頁からの質問に対する回答][重積分...積分領域が変数に依存する場合 について/18.1.7]
とても詳しく書いて頂き独習者にはありがたいサイトと感謝しています。
積分領域が変数に依存する場合のページの例2の解答は16/15になりました。お時間がある時に確認して頂けたら、と思います。
よろしくお願い致します。
=>[作者]: 連絡ありがとう.1つ前の式の符号が間違いで,結果は正しいことになります.
■[個別の頁からの質問に対する回答][根号計算 について/18.1.6]
問題1(3)√54が9√6になっていますが、3倍になっているのは何故でしょう。3がどこから来たのかわかりません。
=>[作者]: 連絡ありがとう.問題の方に3を付け忘れていましたので,訂正しました.
■[個別の頁からの質問に対する回答][期待値 について/18.1.6]
このサイトの字から伝わるイメージをもっと易しいものにしたらもっとよくなるとおもいます。字体やカラーを変えられてはいかがでしょう。
=>[作者]: googleから来て1ページ見ただけで,サイト全体の議論を?
■[個別の頁からの質問に対する回答][展開公式1 について/18.1.6]
わかりやすい、そして問題も引っ掛けとかあっていい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/18.1.5]
誤記のご確認をお願いします。
対数関数の不定積分[例]の(3)について、f=logx、f'=1/x、g=2/3x√x、g'=√xが正確なのかなと思いました
あと公式がfg'=fg-fg'になってますが正しくはfg'=fg-f'gかと思います
あと対数関数の不定積分の<<問題>>の(2)の解説について、f=logx、f'=1/x、g=(x^2)/2、g'=xかなと思いました
あと順番が前後しますが指数関数の不定積分[例]の(4)と<<問題>>(4)の解説もfとgが入れ替わっているような
必要でしたら修正をお願い致します。
=>[作者]: 連絡ありがとう.公式の説明で'の位置が逆になっている箇所は訂正しました.他については,どの文字に当てはめるのかは単なる好みの問題で,正誤の問題ではないと考えます.∫f·g 'dx=f·g−∫f '·gdx ∫f '·gdx=f·g−∫f·g 'dx
■[個別の頁からの質問に対する回答][部分分数分解 について/18.1.5]
例題4が、どうして分母が4になるのかが分かりません
=>[作者]: 連絡ありがとう.元の式がk(k+1)(k+2) という3次式で,これを4次式の差で表すために,「試しに」k(k+1)(k+2)(k+3)−(k−1)k(k+1)(k+2) k(k+1)(k+2){(k+3)−(k−1)}=4·k(k+1)(k+2) …(**)
■[個別の頁からの質問に対する回答][sin xに関する不定積分 について/18.1.2]
段組みが2つになっていて、左側を読み終わったとき、一番上までスクロールして右へ行かなければならないので、1段にしてほしいです。
=>[作者]: 連絡ありがとう.段組みしないことはできませんが,折り返しのスパンを短くすることはできます.なお,携帯版は1段ですが縦長です.
■千葉県[代々木さん/18.1.1]
説明がとてもわかりやすかったです
模擬試験で間違えていたところも合うようになりました
ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/17.12.31]
問題も載っており、とても分かりやすかったです。ありがとうございました。しかし、間違った時しかHELPの解説が読めないのが少し残念です。
=>[作者]: 連絡ありがとう.正解の場合でも解説が出るように,設定を変更しました.
■[個別の頁からの質問に対する回答][2次不等式(解き方まとめ) について/17.12.30]
問題2の(3)で出てくる解説の図が間違っていると思います。
解答通りなら、共有点が2つあるべきなのに、解説の図は共有点が無く、この場合の正解は全ての実数になってしまいます。
=>[作者]: 連絡ありがとう.サ-バの容量を節約するために画像の使い回しをしていて,違う番号の画像を貼り付けていたようですので,訂正しました.
■[個別の頁からの質問に対する回答][内分点・外分点 1 について/17.12.30]
ありがとうございます。
子供に教えるために検索しました。外分点の「一方の足は必ずPを踏んでいる」なんて、すごくいい表現ですね。
勉強になりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.12.30]
とても分かりやすくて良かったです
式=((a+1)x−a)((2a+1)x+(a−1))
=(ax+x−a)(2ax+x+a−1)
これとても参考になりました。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの定義,大きさ,向き について/17.12.30]
例(2)で「ベクトル●●●●●の大きさ(長さ)が3であるとき」とありますが(●●●●●の所には「ベクトルaの絶対値=ルート2」の式が入っている)、ここはベクトルaの絶対値だけでないと、文章としておかしいと思います。
=>[作者]: 連絡ありがとう.違う図が貼り付けてありましたので訂正しました.
■[個別の頁からの質問に対する回答][指数不等式 について/17.12.30]
わかりやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次不等式 (絶対値付き) について/17.12.30]
(3) |x2-1| <= |x-1| の答えが -2<=x<=0,x=1 (解説の通り)で間違いになっております。 =>[作者]: 連絡ありがとう.いずれも訂正しました.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.12.30]
1番の回答の説明が2番の回答の説明と同じになっていますよ
=>[作者]: 連絡ありがとう.PC版の方でコピーミスがあったようですので訂正しました.
■[個別の頁からの質問に対する回答][センター試験問題 2次関数 について/17.12.29]
2013年以降のは載せないのですか
=>[作者]: 連絡ありがとう.そのページを作ったときに,まだ2013年になっていなかったということですが,時間的に余裕ができたら考えます.
■[個別の頁からの質問に対する回答][余弦定理 について/17.12.29]
三辺の長さが解って角度を出したいと思ったのですがこの式をそのまま自分の思い描いている式と答えを出すにはだいぶ時間がかかると思いますが少しだけ理解できたのかもしれません ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数 について/17.12.26]
たいへん勉強になっております。さて(4)について解答は -cost/sint なのではないでしょうか?
tに条件がないので、t=π/2の時、tantは定義されません。
よろしくおねがいします。
=>[作者]: 連絡ありがとう.高校によって(学科によって)は,
cot tを習わないことがあるため,
を避けて
としたものですが,そうすると確かに北極と南極の接線は表せません.
ただそれは,tに条件がないからということではないです.他にも,赤道上でも接線はありませんが,一般に分数関数,無理関数を条件を示さずに使うときは「その式が定義される範囲で使う」ことになっています.だから,この形で書くと赤道上でも北極,南極でも接線は考えていないことになり,あなたの流儀で書くと,赤道上は助からないが北極と南極は助けられるということになります.
このような除外点を個別に検討すると,すべての問題についてtの値の範囲を書かなければならないという解釈になりますが,この教材では初歩的に媒介変数表示から微分する練習として,「関数なり導関数が意味を持つ範囲で成り立てばよい」という普通の解釈でやっています.
■[個別の頁からの質問に対する回答][陰関数の導関数 について/17.12.26]
問題に正解した時に右側に出てくる絵が少し分かり辛いかもしれません。文字で正誤を表示していただけると尚良いと思われます。他はとても分かりやすいです。
=>[作者]: 連絡ありがとう.文字も入れることはできます.
■[個別の頁からの質問に対する回答][定積分(多項式,分数関数,無理関数) について/17.12.23]
分母の有理化を行う問題の解答欄、分子が8-√2となっています。
=>[作者]: 連絡ありがとう.計算間違いがありましたので,訂正しました.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数 について/17.12.23]
例3dy/dxがdx/dxになっています
=>[作者]: 連絡ありがとう.訂正しました.
■?[?][17.12.18]
チェバの定理とメネラウスの定理はどのページに記載されていますか?
=>[作者]: 連絡ありがとう.高校数学Aの平面幾何の単元は,今のところ扱っていません.教材のまとまりから考えると,中学3年生の相似図形の応用あたりに押し込んでもよいかなと思いますが,まだ作っていません.そのうち考えます.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/17.12.18]
誤植だと思います。
問3 2次関数y=−(x−t)2+1の区間0≦x≦1における最大値と最小値を求めてください.
で
○最大値
ア<tのとき,x=イで最大値ウをとる
の符号が
ア>tのとき、
としなければなりません。
=>[作者]: 連絡ありがとう.不等号の向きが逆ということで,訂正しました.
■[個別の頁からの質問に対する回答][度数分布表から平均値,分散,標準偏差を求める について/17.12.18]
教科書に、グラフの相関関係が正か負かまたは無いかの見分け方は、傾向によると書かれていたのですが、『傾向』に、対する具体的な表記が、されていないため、どのように見分けたらいいのか戸惑います。具体的な定義もしくは完全な見分け方があったら教えてください。
=>[作者]: 連絡ありがとう.この教材と質問がどう関係しているのか通じません.
何の教科書の何の項目のことなのか分からない状況では,広く浅く多くの人に関係しそうなことを推定して答えることになります.
統計の話で,回帰直線の傾きのことを聞いておられるのなら,相関係数を求めて正か負を見れば分かることですが,奇妙に思うのは,その個所を習っておられないのなら,この質問はあり得ないし,習っておられる場合には,なぜその質問があるのか不思議です??
相関係数
■[個別の頁からの質問に対する回答][Σ記号の変形 について/17.12.16]
(5)がわかりません。3k-2ではないのでしょうか?
=>[作者]: 連絡ありがとう.1週間前に同じ質問に回答したばかりです.
は間違いです.
でなければなりません.
入力方式にする以上,空欄がかっこに囲まれているように見えるのが読者に酷ですが,これは防ぎようがありません.選択問題にするのなら,上記2つの選択肢を含む選択肢から選べることになりますが・・・
■[個別の頁からの質問に対する回答][積の微分 について/17.12.16]
こんにちは。
良かった所:積の微分について知りたいと思っていろいろ探しました。ほとんどのサイトや動画は公式の覚え方しか示していなかったのに、このページでは、公式の証明ものっていたので面白かったです。証明まで紹介しているところは、他には一か所しかみつからなかったです。
その他:公式の導き出し方がひじょうにかっこいいと感じました。いったい誰がさいしょに思いついたのですか。
=>[作者]: 連絡ありがとう.1650年代にニュートンやライプニッツが微分積分学を始めた頃には,既に積の微分法の公式はあったと思う.
■京都府[ワンワンガンプさん/17.12.13]
こんな丁寧なサイトを運営いただき感謝申し上げます。かけだし技術者ですが、高校数学に立ち返って学習したいとき、このサイトを発見して感激です。これからもよろしくお願いいたします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/17.12.13]
複素数の範囲での解説もお願いします。
xの4乗-1の因数分解です
=>[作者]: 連絡ありがとう.複素数の範囲での因数分解は
数学Ⅱ で扱っています.
なお,
このページ の解説に沿ってwxMaximaをインストールし,画面上で空打ちをして入力欄を作ってから
gfactor(factor(x^4-1)); SHIFT+Enter
とすると,次のように因数分解の結果が出ます.
(x-1)*(x+1)*(x-%i)*(x+%i)
wxMaxima上では虚数単位は %i で表されています.
※このレベルなら暗算でできますが,筆者が計算間違いしそうな問題は,wxMaximaを検算に使っています.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.12.13]
4x<8
=>[作者]: 連絡ありがとう.その問題が解けないので解いてほしいということのようですが,このページを読んだ人はそのような質問はしないはずです.あなたはこの頁をほとんど読んでいません.だから分からないのです.
■[個別の頁からの質問に対する回答][放物線の移動 について/17.12.12]
誤植があります。
【例】
(1) 元のグラフの方程式:y=3(x−1)2+2
y=4の直線に関して線対称移動
(t=2q−nで求めてもよいが,算数的に1→4:+3だから4+3=7としてもよい)
新しいグラフの方程式:y=−3(x−1)2+7
は…
算数的に2→4:+2だから4+2=6としてもよい)
新しいグラフの方程式:y=−3(x−1)2+6
…です。
=>[作者]: 連絡ありがとう.場所が分かりにくいですが,【y=qの直線に関する対称移動:要点】の下半分がコピペの後,書き換えができていない部分があるということで了解しました.ただし,y=qの直線に…です。
■[個別の頁からの質問に対する回答][逆行列の求め方 について/17.12.12]
わかりにくい
=>[作者]: 連絡ありがとう.そういう人がいてもおかしくはない.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/17.12.11]
ひとつだけ暗記し、後は思い出して計算する、同感です。
符号の変化に注意(+→-,-→+)
と解説していらっしゃいますが、たとえば
sin(-a)=-sin(a), cos(-a)=cos(a)
sin(a+π/2)=cos(a), cos(a+π/2)=-sin(a)
が分かればsin(a+b)からcos(a+b)が出ます。
符号を暗記するより、sinとcosの位相ズレを知る方が
将来的に有望な気がします。
=>[作者]: 連絡ありがとう.位相のズレで考える方が将来的に有望というのはその通りですが,この教材は高校2年生の初めの頃に習うものですので,位相で説明すると9割以上の生徒は学習を放棄ことが手に取るように予測できます.だから,この場面では言いたくても言うと混乱するのです.
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/17.12.11]
理科であれば巨大な数字を10の累乗で表すと記載されているのですが問題だと10の2乗まで細かく乗っているのですがその場合はどうしてその様になるのですか?
=>[作者]: 連絡ありがとう.どの問題に対して何を質問しているのか通じません.「問題だと10の2乗まで細かく乗っているのですが」と質問されていますが,そのような事実はありません.
ここから先は,推測で答えるしかありませんが,まず「有効数字2桁のものと有効数字2桁のものを掛けたときは、四捨五入して有効数字2桁にします。」「割り算の場合も、有効数字の少ない方の桁数まで求めます。」と書いていますように,有効数字2桁の小数,例えば3.1と有効数字3桁の数字,例えば 2.72,有効数字4桁の数字,例えば1.414の次のような積や商はいずれも有効数字2桁(一番精度の低いもの)になります.
その理由は「有効数字の桁数が異なる場合の取り扱い」という項目に書いていますが,怪しい数字?が1つでも絡んでいる桁は怪しいとみなすと,「有効数字の桁数が最も小さいものに合わせる」と覚えます.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/17.12.10]
最高
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][Σ記号の変形 について/17.12.10]
こんにちは。(5)の解答、helpと異なっているのでは?
=>[作者]: 連絡ありがとう.この質問は以前にもあったように思う.もし,あなたが 3k-2 が正解になるはずだとお考えなら,それは違います.
このページ を読んで,かっこが必要な理由を考えてください.
■[個別の頁からの質問に対する回答][2次関数のグラフと係数の符号 について/17.12.10]
bの符号が読んだのですが一向にわかりません。何故頂点のx座標が関係してくるのですか?
=>[作者]: 連絡ありがとう.あなたが今日読んだのはそのページだけです.基本問題をやらずに,いきなり応用問題をやって「分かりません」という場合に,自分のやり方の間違いに気付かないといけません.先頭にあるサブメニューでもっと前の基本の項目から読むのです.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/17.12.09]
問題数を増やして欲しいです!
=>[作者]: 連絡ありがとう.1つのページに問題を詰め込んであるよりも,必要に応じて様々な問題ができるように,いくつかのページに分けてあります.先頭のサブメニューから,前のまたは後ろのページを選んで,前後の教材を見てください.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/17.12.09]
非常にわかりやすい
練習問題があるのは高評価
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][漸近線の方程式 について/17.12.08]
素晴らしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次関数のグラフ について/17.12.08]
うーん、難しいですね。
=>[作者]: 連絡ありがとう.いや,このページに書いた勘が働かないと,問題を解くときに見当をつけにくいのです.
■[個別の頁からの質問に対する回答][展開の順序 について/17.12.07]
同じような式が消える理由は、計算しても残らないから、1つにまとめるのですね?
=>[作者]: 連絡ありがとう.どういうことを言おうとしておられるのか通じません.
■[個別の頁からの質問に対する回答][三角関数の2倍角公式,半角公式 について/17.12.06]
先生から、出された特別問題一般に、実数の角度において(180√(2-2cosΘ))÷θ<πである事を示せという問題が解けません。教えてください。
=>[作者]: 連絡ありがとう.子供の宿題に答えを教えるようでは,日本の未来が危ないな~.そんな甘いことはしない.
■[個別の頁からの質問に対する回答][2次関数のセンター試験問題 について/17.12.06]
今日は。いつも参考にして頂いています。2011年度の0≦x≦bにおける2次関数①の最小値が-1/4であるときの問題の途中の式が2b2+2b-1=0から
(2b-1)(b+1)=0になっているのですが因数分解の式が間違っているのではと思います。
宜しくお願いします。
=>[作者]: 連絡ありがとう.確かに,その部分おかしいので直しました.
■[個別の頁からの質問に対する回答][部分集合,集合の包含関係 について/17.12.06]
重ね重ね質問すみません。私は11月7日に、集合の範囲で、一度質問させて頂いた高校生です。貴方の回答は、とても参考になりました。ありがとうございます。まず全体集合の補集合が空集合に、なる証明方法がわかりましたので載せておきます。 U=A∪Ā 両辺を補集合にするとドモルガンの法則より Ū=Ā∩A Ā∩A=∅(AとA以外の共通部分は、ないため) より、∅=Ūである。と、ここまでは、分かったのですが。この式にU=∅を、代入すると、(空集合が全体集合の時) ∅=∅の補集合となり、明らかに矛盾しているように思えます。これはどうしてですか?簡単に、かつわかり易く回答して頂けたら、幸いです。
=>[作者]: 連絡ありがとう.
あなたの考えでは,一般に
が成り立つはずがない(特に
が成り立つはずがない)と決めておられますが,次の関係が成り立ちます.
すなわち,
と
が等しくなるならば,
になり,逆に
ならば
と
が等しくなります.
前回の質問と今回の質問に共通して,あなたの思考は集合という概念に終始している傾向があります.そもそも,集合は「もの」の集まりなので,難しくなったら具体物である「もの」をもってきて考えるとよいでしょう.
このページ (集合の要素を用いた証明)を読むと少しは分かるようになるかもしれません.
前回も書きましたが,空集合は要素が何もない集合です.すなわち,
.言葉で言えば,そんな「もの」はないということを空集合で表しています.
(余計混乱するかもしれないが,興味や関心は深まりそうな参考)
集合の要素を用いた証明では,
とは,
が成り立つことと定義されます.
例えば,「犬ならば動物である」が真であるのは,犬の集合の任意の要素
(これが具体的な1匹の犬)をもってきたら,必ず動物の集合の要素になっているからです.
ところで,集合の公式として,任意の集合
に対して
という公式があります.これを集合の要素,すなわち「もの」で考えると,次の関係式が成り立ちます.
そもそも,要素が何もない集合が空集合なので,この式の仮定の部分
は間違っています(偽)ですが,式全体は真になります.それは,「仮定が間違っていれば,どんなことでも証明できる」ということを表しています.筆者が気に入っている逸話:あるとき論理学者バートランドラッセルが「仮定が間違っていれば,どんなことでも証明できる」といったら,新聞記者が「それでは,あなたがローマ法王であることを証明してください」と言った.ラッセルは少しも慌てずに,次のように答えた.
「もし,2が1に等しいなら」(これが間違った仮定)「2人の人,ローマ法王とラッセルは1人の人になる」.以上によって証明された.
■[個別の頁からの質問に対する回答][無理関数(2次式の平方根)の定積分 について/17.12.06]
上記の、
すなわち,x=sinθとおくことにより,
_ _______
√1-x2=√1-sin2θ=±cosθ(符号は選ぶ)の、
「符号を選ぶ」は、
±cosθ ≧0となるように選ぶのであっていますか?
=>[作者]: 連絡ありがとう.定積分なので,置換した後のcosθの符号をどちらに合わせばよいかは,区間を見て考えます.
たとえば,そのページの例1で
の区間を使って置換積分を行う場合は,
cos θ≦0になるので,
とします.
■[個別の頁からの質問に対する回答][数学的帰納法(不等式の証明) について/17.12.06]
問題欄において、[?]を押した後に選択肢を押しても反応しないので確認をお願い致します。ブラウザはChromeです。
あとこの他に数Iの[ 三角比と図形 ]の「三辺→角」と「筆算だけで解く問題」の両ページにおいて、
1問正答した後に2問目が選択できなくなるのでご確認をお願い致します。この数Iの両ページはページ内にアンケート送信欄が無いのでこちらでまとめて報告させていただきました。
=>[作者]: 連絡ありがとう.いずれのページも携帯用ページは訂正済みでしたがPC用を訂正するのを忘れていたようです.訂正しました.また2つのページについて送信欄を付けました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.12.05]
1次不等式の分数がある計算について教えて欲しいです
=>[作者]: 連絡ありがとう.解説は少し書いてあり,他の取り扱いは1次方程式と同様(不等号の向きとか等号の有無はある)ので,教える側から見れば大した違いはないように思いますが,習う側から見れば,構えなければならないくらいの違いがあるということでしたら,幾つか追加は可能です.数日かかります.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/17.12.05]
すごく分かりやすく、テストでも良い点をとることができました。ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の値(270゜~360゜) について/17.12.04]
第4象限の角、公式(6)では
cosθ(270°+θ)=sinθ
と、符号がプラスになっていますが、その下の例では
cos345°=cos(270゜+75゜)=-sin75゜
と、符号がマイナスになっています。この場合どちらが正しいのでしょうか?
=>[作者]: 連絡ありがとう.よく見つけてくれました.公式の方があっていて,cos345°とtan345°の方の符号が入れ替わっていましたので訂正しました.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/17.12.04]
全然わかんないちんぷんかんぷん
=>[作者]: 連絡ありがとう.基本問題を先にやってから,応用問題に進みましょう.
■[個別の頁からの質問に対する回答][内分点・外分点 について/17.12.04]
わかりやすいし、問題もあって嬉しい!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数法則 について/17.12.03]
本当にわかりやすかったありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/17.12.03]
すごくいいとは思うのですが、どれを選んだかわかるようにしていただけるとなお助かると感じました。
=>[作者]: 連絡ありがとう.その方が分かり易いと思うことで,直せるものは直すという考え方で,直しました.
■[個別の頁からの質問に対する回答][2次不等式 について/17.12.03]
x(2ーx)>0なども入れて欲しい!
=>[作者]: 連絡ありがとう.基本が分かるようになったら,
まとめのページ もやってください
■[個別の頁からの質問に対する回答][分母の有理化 について/17.12.02]
(7)の回答の選択肢、左から2つ目の分子が誤植?
=>[作者]: 連絡ありがとう.%2Bと書くべきところを%3Bと書いていたようですので,訂正しました.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.12.01]
このページの問題を解いたのにも関わらずトップのメニューのところに印が付きません
=>[作者]: 連絡ありがとう.なぜかそのページのPC版で記録用のページ番号が抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][不定積分(多項式2) について/17.12.01]
高校の期末考査出るところを勉強したい
=>[作者]: 連絡ありがとう.学校にもよりますが,定期試験では習ったところ(1つの章くらいの範囲)が出ます--つまり,あまり変な問題は出なくて,習った範囲は幅広く全部出ます.画面左側のサブメニューをたどって浅く広くやるとよいでしょう.--抜けている箇所を作らないことが重要です.
■[個別の頁からの質問に対する回答][漸化式と一般項(等比形) について/17.11.29]
「例と答2」の(9)参考(B)の解説でS-S/2ではなく、2S-Sではないでしょうか。前式では答が合わず、泣けてきます。2S-S=Sで計算すると、この答になります。よろしく教えてください。
=>[作者]: 連絡ありがとう.S-S/2でも2S-Sでもできますが,公式どうり言えばS-S/2のつもりですが,変形ミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][不定積分(まとめ1) について/17.11.29]
Ⅲ7(2)でe^(x^-2)はe^(-x^2)では?
=>[作者]: 連絡ありがとう.訂正しました
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/17.11.29]
単なるミスプリでしょうが、例8の解答のxが+に見えます。
=>[作者]: 連絡ありがとう.+は1つですので訂正しました
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/17.11.29]
素晴らしい講義です!半世紀にわたる疑問が解消しつつあります。こんな授業を高校生時代に受けることができていたら、人生がもっと違っていたかもしれません。有難うございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の方程式 について/17.11.27]
中学生です。今ちょうど2乗に比例の式をやっている3年生ですが、高校見学に行った際、数学の授業でグラフに円が書いてあって『何これ面白そう』と思い“円 グラフ 式”と検索し調べていました。他のサイトはどこも高校生向けというか、難しく中学生の私にはわかりませんでした。
しかしここのサイトは中学生でもできるように基本的な平方完成の仕方やルートの計算などこれでもか!とくらいにわかりやすく、円についてよく分かることが出来ました。
作られた問題は全て満点でとても気持ちが良かったです。
高校の数学もそんなに難しくないですね!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次の不定方程式 について/17.11.27]
問題4の答え違ってませんか?
=>[作者]: 連絡ありがとう.解答としては違っていませんが,細かな訂正が幾つかありました.
■[個別の頁からの質問に対する回答][rn の極限 について/17.11.27]
よかっあ!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/17.11.26]
分かりやすく理解できました。ありがとうございます。
[Ⅶ][Ⅸ]の見分けるのを早く出来るのには練習しかないでしょうか?コツがあれば教えて頂きたいです。
=>[作者]: 連絡ありがとう.[Ⅶ]と[Ⅸ]は全く違うものです.ゆっくり見れば分かります.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.11.26]
なんとなく大体理解することができました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分の部分積分法 について/17.11.26]
採点後のマークが大変分かり難いため、〇と×等のようなシンプルな画像に差し替えるべきだと思う。
=>[作者]: 連絡ありがとう.珍しい意見です.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/17.11.26]
定期テスト対策にちょうどいいです。ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの定義 について/17.11.26]
説明文が分かりやすく、間違えた後の解説もあるのでとてもやりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/17.11.24]
問の正誤がすぐわかるので便利です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][剰余の定理 について/17.11.24]
例5についてですが、P(1)のときに矛盾が発生しませんか?
=>[作者]: 連絡ありがとう.鋭い指摘です.P(x)=(x−a)(x−b)Q’(x)+Ax+B P(x)=(x−b)(x−c)Q”(x)+Cx+D A,B,C,D は自由度4で気楽に決めるわけにはいかない(自由度3しかない)ということで訂正しました.
■[個別の頁からの質問に対する回答][複素数の和差積 について/17.11.23]
神経衰弱の要領で楽しく学習できました。このサイトはわかりやすくて本当に助かっています。本当にありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.11.23]
とてもわかりやすかったです!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][合成関数 について/17.11.23]
とてもわかりやすかったです!ありがとう。当年60歳!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/17.11.22]
理解できました!!!
助かりました!!!
本当に分かりやすかったです!
これからも活用させて下さい😁
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/17.11.22]
楽しく解かせて頂いています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.11.21]
問題《5》についてですが、先生の並ぶ順番が回ることを除いて1通りなのはなぜですか?
=>[作者]:
連絡ありがとう.上のA,B,C,・・・,の並び方は円順列としては同じものです.「向かい合う」という指定があれば2人のT(先生)の相互関係は回ることを除いて1通りに決まります.
■[個別の頁からの質問に対する回答][定積分 について/17.11.21]
上記問題1(5)の解答、はじめの 21分の1は6分の64の間違いだと思われます。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][不定積分(数学II.多項式) について/17.11.21]
上記 (多項式の積分は、「展開してから」公式(2)を利用して行う)のところ、2分の3x ではなく、2分の3xの二乗だと思われます。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][複素数平面の図形問題 について/17.11.20]
ここの【問題5】の(1)と(2)の解説の一部がわかりません。
(1)の解説OA:ABはOA:OBの記述ミスなのでしょうけど
OA:OBの比率がわかったからと言ってABとの比率は決定しないわけで
その説明で何故角OABが直角だとわかるのかが理解出来ません。
(2)の解説も右図のようにとありますがどうしてそんなことがわかるのかも理解出来ません?
(1)は
(β-α)/α=bi より AB/OA=bi で角OABが直角とわかる
(2)は点CをOCの中点がBとなるような点として仮定した場合
(2β-α)/α=(1/2)bi より AC/OA=(1/2)bi で 角OACが直角とわかるので
OCが直径で中心Bの円上の点がAとなりOB=ABとなる
こうやって理解することなら出来るけど
=>[作者]: 連絡ありがとう.各自の理解しやすいロジックで解いてもらったらよいでしょう.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積3 について/17.11.20]
独学の僕でもわかる解説の丁寧さと多すぎず少なすぎずといった問題数。このサイトに出会えて良かったです。今夜は興奮して寝れそうにないです。筆者さんに感謝
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積2 について/17.11.20]
分かりやすいです。今日からお世話になります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.11.20]
一つ一つの問題に解説がついていてよかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.11.20]
この頁の問題は、不等式を等式と考えて解き、X=答えになったあと不等式に変えれば簡単に解けますね。
=>[作者]: 連絡ありがとう.そうとも言える側面もありますが,それだけではないという側面もあります.不等号がどちら向きか,等号付きかどうかはていねいに扱わないと失敗することがあります.
■[個別の頁からの質問に対する回答][展開公式 について/17.11.20]
中学二年生初見でも理解できました。作者さんすごいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][次数の方程式 について/17.11.19]
4題ある、穴埋め問題の最初の問題の最終的な答えはf(x)=x^2+4x だけでなくf(x)=-4 もあると思うのですが、どうでしょうか。
=>[作者]: 連絡ありがとう.なるほど,その場合が抜けているようですので,書き加えました.
■[個別の頁からの質問に対する回答][
問7のcosβの答えは-√15/13ではないでしょうか
=>[作者]: 連絡ありがとう.132 =169で122 =144,169−144=25です.質問者はその計算を間違えていませんか.
■[個別の頁からの質問に対する回答][順列,組合せ(章末問題) について/17.11.18]
公務員試験直前問題にとても役立ちました。なかなか苦手な問題ばかりを練習問題を探すのが難しく、とても力になりました。問5aaabbc の6文字のうち4文字を使ってできる順列の総数を求めよ.
の途中の解説があれば嬉しかったです。でもとても良い問題ばかりで助かりました。
=>[作者]: 連絡ありがとう.途中の解説はHELPにあります.
■[個別の頁からの質問に対する回答][ 行列式 について/17.11.16]
【行列式の性質III】(1)の記述についてですが、「~行列式はk倍になる.」ではなく、「~行列式は1/k倍になる.」ではないでしょうか?
=>[作者]: 連絡ありがとう.
を文章にすれば,「(1) 行列の1つの行(または1つの列)を定数k倍すると行列式はk倍になる.」です.
※行列式は単なる1つの値です(ここのところが重要).だから,行列式
の値は,行列式
の値と等しいと読まなければなりません.
を
に変形すると,行列の1行目の成分が1/kになっていると読むと,その等号が表す意味とは異なります.
■[個別の頁からの質問に対する回答][y=sin(θ-α)のグラフ について/17.11.16]
解説をした後に実話際に数問解かせてもらえるのがとてもいいと思いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次不等式 について/17.11.15]
問3の(2)の解説
正しくは(イ)-1+√6<x<2だと思います
確認お願いします。
=>[作者]: 連絡ありがとう.解説を解答に合わせました.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/17.11.15]
わかりやすい!!
問題付きで助かります。これからも頼りにしています!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数方程式 について/17.11.14]
真数条件より、x>0。という表記が教科書や参考書によって書いてあったり無かったりする。全ての場合で真数は正だから、とりあえず書いておけば原点はされないだろうか。
=>[作者]: 連絡ありがとう.答案全体の構成方法として,(1)原式と必要かつ十分に(つねに後戻りできるスタイルで)変形していく方法 (2)とりあえず必要条件を満たすものから捜査範囲を絞って行き,しかる後に,最後に十分性を満たさないものをはねるという方法があり得ます.
■[個別の頁からの質問に対する回答][数学的帰納法(不等式の証明) について/17.11.13]
採点されません…クリックしても反応有りません…残念です
=>[作者]: 連絡ありがとう.あなたの使っているChromeで点検しましたが,問題なく作動しています.おそらく質問者は,問題を選ばずに答を選んでいると考えられます.- - 画面上に書いてありますように,「※初めに [ ? ] で示される空欄を1つ選び,続いてその空欄に入る値を右の選択肢から1つ選べ.」です.問題を選ばなければ答は決まりません.
■[個別の頁からの質問に対する回答][重複組合せ について/17.11.13]
大学生になって重複組み合わせが気になってこのページにたどり着きました。具体例で考えるのがとても分かりやすかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][グラフの平行移動 について/17.11.11]
すいません。ドラマで出た以下の情報だけでこの問題を解いていただけないでしょうか?丁寧に小学生にわかるように よろしくお願いします
4xー3・2^+2≦0
3・2^の2の横の^マークは2の右肩にxがついている(2をx乗している)と言う意味です。この情報しかありません
=>[作者]: 連絡ありがとう.この教材と全然関係ない問題で,また指数関数は小学生だけでなく中学生でも分かるようにはできません.問題が正確に再現されていません.答だけならコンピュータに書き込めば出てきます.x≦0.8868684983, 1≦x
■[個別の頁からの質問に対する回答][3次方程式の解と係数の関係 について/17.11.11]
わかりやすくまとめていただきありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][最大公約数,最小公倍数,ユークリッドの互除法 について/17.11.11]
とても分かりやすいです。参考になりました、ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][相関分析 について/17.11.09]
質的×質的、量的×質的もスピアマンで可能でしょうか。ぜひご教示お願い致します。
=>[作者]: 連絡ありがとう.質問が省略しすぎということもありますが,管理人はその部分はあまり得意ではないので,答えられません.
■[個別の頁からの質問に対する回答][部分集合,集合の包含関係 について/17.11.09]
私は、高校一年生なのですが、集合の範囲でどうしても納得できない所が、有ります。全体集合の補集合が何故空集合なのかが分かりません。空集合は、あらゆる集合の、部分集合になっているので、当然、全体集合の部分集合にも、空集合は、含まれる(要素になる)筈です。この様に考えると、もし、全体集合の補集合が空集合ならば、全体集合の要素が、全体集合以外のものという意味になり、明らかにおかしいように思えます。何故この様になるのかを、出来る限りくわしくわかり易く解説を、して頂きたいです。
=>[作者]: 連絡ありがとう.いきなり無が空しいことを言ったというような超越的な話に入らずに,もっと普通のおとぎ話から始めます.
鳥軍団
と獣軍団
がけんかをしているときに,コウモリ軍団
が両方に入っています.
…(1)
鳥軍団
が完全に勝ってしまって(
)獣軍団
がいなくなってしまった(
)場合でも,コウモリ軍団
は両方に入っています.
実は,コウモリ軍団には,兵隊が1人もいなかったのです.
一般に(1)のように,任意の集合
とその補集合
のどちらにも入っているものはありません.
何もないことを空集合があるという.
…(1)
■[個別の頁からの質問に対する回答][行列のn乗 について/17.11.09]
岩手大引用の問題の(2)の答えで-2*4^n+1ではなく-2*4^n+2ではないでしょうか?
=>[作者]: 連絡ありがとう.その1つ前のP−1 も含めて訂正しました.
■[個別の頁からの質問に対する回答][負の指数 について/17.11.08]
すっかり数学から離れて十数年になりますが、復習というより、再勉強で利用させていただいております。理解しやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/17.11.08]
問題4(3)の解説で
x3+y3+z3-3xyz=(a+b+c){4(a2+b2+c2)-4(ab+bc+ca)}
=4(a+b+c)(a2+b2+c2ab+bc+ca)
=4(a3+b3+c3-3abc)
2行目が
=4(a+b+c)((a2+b2+c2-(ab+bc+ca))
かと思います
=>[作者]: 連絡ありがとう.下から2行目でコピペに失敗しているようですので訂正しました.
■東京都[猫さん/17.11.07]
http://www.geisya.or.jp/~mwm48961/kou3/sin004.htm
のTan(θーπ)のヒントで、赤い点の位置が違うと思ったのですが、どうですか?あのヒントだと答えは-Tanになると思います。 もしヒントがあっていれば、解説をお願いします。
また、わからないところで、sin(-θ-2π)のヒントがなぜ0にならないのですか?
最後に要望で、90-θや90+θの公式を具体的に、細かく解説して載せていただければ幸いです。
=>[作者]: 連絡ありがとう.赤い点の位置は確かにおかしいので訂正しました.
「sin(-θ-2π)のヒントがなぜ0にならないのですか?」は質問の意味が通じません.そのヒントでは,-θ-2πの位置が赤丸で示されているはずです.0になることはないでしょう.
「90-θや90+θの公式」の公式は
このページ にあります.
■[個別の頁からの質問に対する回答][点と傾き→直線の方程式 について/17.11.07]
数学Ⅱ 【点と直線】の『点と傾き→直線と方程式』の問題で、最後まで残った解答が【点(2,3)を通り傾きが-4の直線】と【y-3=2(x-4)】でした。答えの組み合わせがどこかで食い違っているようです。確認お願いします。
=>[作者]: 連絡ありがとう.6分の1の確率で,同じカードを2回配っていたようですので,訂正しました.
■[個別の頁からの質問に対する回答][動径の表わす一般角 について/17.11.07]
問題の図の線で、どちらがOXでOPなのかがわからなかった。
=>[作者]: 連絡ありがとう.質問者が本当に分からないことはないでしょう.「穿った見方をすれば,理論上」OXが毎回角度を変えて斜めになっている可能性があると言っているのだと思いますが,解説文,解説図,他の教科書などでもOXを右横向けに書くのは当然のことで,OXに斜めに書くことはないでしょう.
■[個別の頁からの質問に対する回答][群数列 について/17.11.07]
問題2のア が、どうしてK+1で正解なのか考えても分かりません。
=>[作者]: 連絡ありがとう.第1群に属する分数の分母と分子の和が2で,第2群に属する分数の分母と分子の和が3で,第3群に属する分数の分母と分子の和が4,...だから,第k群に属する分数の分母と分子の和は k+1 です.
■[個別の頁からの質問に対する回答][定積分の置換積分 について/17.11.06]
例4で、2)t:-π→π/2でもよい。とありますが、この場合計算は一致しないのでは?
一般的に置換するときは増減のない1to1対応でなければ計算は合わないような気がします。間違っていたらごめんなさい。。
=>[作者]: 連絡ありがとう.変数変換が1対1でないときにどうなるのかということについて,ゆっくり考えてみるのはよいことだと思います.そこの部分は踏み込んで書いていませんので,納得してもらえなかったかもしれません.
一般には単調増加な(または単調減少な)区間たとえば左図の
c≦x≦d を使って行うというのが基本です.しかし,何らかの都合で左図のように,yがxの値に応じて増減する区間を使って変数変換を行った場合,増減のある区間で行った定積分の計算は,「正と負がちょうど相殺しあって」0になるので,結果に影響しないということです.
■[個別の頁からの質問に対する回答][リッカチ形の微分方程式 について/17.11.06]
お世話さまです
直していただきありがとうございます。
v=u-1とおくと
dvdx=-u^2dudx
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][リッカチ形の微分方程式 について/17.11.05]
お世話様です。大変参考に成りました。ある一つ特殊解y1について、y=y1+uとおくような、工夫しているようですが、なぜこのようなことがおもいつくのですかね。
尚、印刷版の方の左上の方の、文字が文字化けしているようです。私のパソコンのせいでしょうか?
ㅪㅅ㇫ㅆ形 微勃挹稉弑
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][リッカチ形の微分方程式 について/17.11.05]
お世話様です
v=u-1とおくと
の後の微分のところに
イコールが消えているようです。
ご確認をお願いいたします。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/17.11.05]
分かりやすいのですが、文章の問題から表を自分で作らないといけないときもあるので、文章だけで、表を自分で作るような例文も欲しいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.11.02]
高校に入ってから数学が全然理解できなかったけれどこの問題などで理解できました。
ありがとうございます。
=>[作者]: 連絡ありがとう.1次不等式の解き方については,中学校の教科書から消えたり戻ったりしたので,高校の先生から言えば,できて当然と思う場合と全く習っていないと思う場合の態度の使い分けが大変です.一応どちらの場合でも対応できるように,全く習っていない場合を想定した教材として作りました.
■[個別の頁からの質問に対する回答][曲線で囲まれた図形の面積 について/17.11.01]
いつもありがたく利用させていただいております。問題2の計算間違い防止ルート探索(5)で検算の(x-1)^4の積分は良いのですが、3(x-1)^3の積分が違う様に思いますが確認をお願いします。
=>[作者]: 連絡ありがとう.おかしい箇所がありましたので訂正しました.
■[個別の頁からの質問に対する回答][三角比の相互関係 について/17.10.31]
第一象限や第二象限がよくわかりません。どのような時にどんな象限がきまり、それに対する答えがどうなっていくのかを教えていただきたいです
=>[作者]: 連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.
象限という用語を使わないと,反比例のグラフが「どこ」と「どこ」にあるというようなことが言えなくなって不便だと思うのですが,そういう場所を表す用語はないらしい.
象限という用語は,高校数学Ⅰで初登場のようです.左図のように,
x, y とも正の場所を「第1象限」といい,以下反時計回り(左回りに)第2象限,第3象限,第4象限とします.ただし,座標軸上はどの象限にも入れません.
三角関数との関係で言えば,象限ということを意識しないと,符号の決め方が分からなくなるはずです.
例えば,
において
x, y は象限に応じて決まる符号が付いていて(符号付の実数),
r だけは半径(長さ,符号なしの実数)なので常に正です.
だから,第1象限では
第2象限では
のように各象限に応じて三角関数の符号が決まります.[まずこれが重要]
逆に,三角関数の符号が決まれば,象限が決まる場合と決めきれない場合があります.
例えば,
という条件だけでは,第3象限と第4象限の可能性があってどちらと決められませんが,さらに,
という条件もついていると,第3象限に決まります.
■[個別の頁からの質問に対する回答][定積分 について/17.10.30]
多項式の積や累乗の定積分
の(i)の例の途中式∫2,1が[ ]3,1になってます。
間違っていたらすみません、、
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][2次不等式(絶対値付き) について/17.10.29]
はじめまして、コメント入れさせていただきます。
勉強のために使わせていただいております、ありがとうございます。
さて、問題2の(3)についてなのですが、
回答と解説が違っていました。
=>[作者]: 連絡ありがとう.解説にそろえました.
■[個別の頁からの質問に対する回答][定積分:基本計算 について/17.10.29]
いいと思う
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/17.10.29]
≪ここがポイント≫の文章が次の問題にかぶっていて見にくい部分があります。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][ 円の方程式 について/17.10.29]
ありがとう
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.10.28]
問題4の1回目の答えは(3x-2y-8)(6x+y-4)ではないのですか?
=>[作者]: 連絡ありがとう.その頁では,プログラムによって問題,解説,解答を作っていますので,あなたが見ている問題と管理人や他の読者が見ている問題は違うものです.だから,問題4の1回目の問題という決まった問題はありません.あなたがもう1回その頁を見た場合にも全然違う問題になっているはずです.そんな訳で,質問や意見をいただくためには,問題のコピーとあなたが解答だと思う式を送っていただかないと,正しいとも間違っているとも言えないのです.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.10.28]
とてもわかりやすくて、楽しく覚えられました!
ずっと分からなくて困っていたので助かりました!
明日の模試もがんばれます!!
=>[作者]: 連絡ありがとう.模試,頑張ってください.
■[個別の頁からの質問に対する回答][確率のセンター試験問題 について/17.10.27]
基本問題だったので楽しく出来ました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][グラフの平行移動 について/17.10.27]
Yの正方向の移動は「右」ではなく、「上」のほうがいいと思いますが。
=>[作者]: 連絡ありがとう.何かの都合で機械的に変換したようです.訂正しました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.10.27]
要点より解が異なる実数解をもつときそれを、A,Bとしたときy=C1epx+C2eqx の式に代入するのはA<Bの場合pにはA、qにはBですか?
=>[作者]: 連絡ありがとう.
は任意定数倍の和なので,どちらが前でも順序に影響されません.
例えば,例1の場合,
が解だから
…(1)
…(2)
のどちらでもよい.(
の役割が入れ代わるだけです)
■[個別の頁からの質問に対する回答][対数不等式 について/17.10.27]
とてもわかりやすくて助かりました
問題を解くところに関して、正解したところでも途中式が確認できるようにしていただけたらなと思います
=>[作者]: 連絡ありがとう.了解.「間違っていれば解説ボタンを表示する」→「間違っていなくても解説ボタンを表示する」というロジックに変更しました.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/17.10.25]
よかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][微分方程式...変数変換による解き方 について/17.10.25]
こちらの計算ミスでしたら申し訳ありません。「(III)の例」の一般解が「y=x*(C*e^(2x))/(C*e^(2x)-2)」となっていますが、「y=x*(C*e^(2x)+1)/(C*e^(2x)-1)」ではないでしょうか。ご確認いただけると助かります。
=>[作者]: 連絡ありがとう.ご指摘の論旨の方が正しいようですので訂正します.変数が3個あって,分かりにくい部分も直しました.
■[個別の頁からの質問に対する回答][F検定→t検定 について/17.10.24]
SD法からの因子分析で因子わけしたあとにこのF検定とt検定を用いて使うことができました。正直細かくはわからなかったんですけど、何に手をつければよいかわからなかったので大変参考になりました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][位置ベクトルの応用 について/17.10.24]
内容がとても簡潔でとても分かりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2進数の演算 について/17.10.24]
実生活で2進数を使うことはなかなかありませんが、この頁で、2進数の使い勝手の良さや計算のしやすさが実感できました。唯、10進数を変換するのが面倒に感じます…
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][漸化式と一般項(等比形) について/17.10.24]
例(9)の別解Bについてですが、Sの初項は2分の1ではなく、2の2乗分の1だと思います。それで解くと解答と同じになりました。1/2Sがbnになるのがどうしても理解できず気づきました。確認、よろしくお願いします。
=>[作者]: 連絡ありがとう.確かにおかしいので訂正しました.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/17.10.24]
問題が全てとけたら成績優秀などの文字が出てくるのは嬉しいですね^ ^
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/17.10.24]
問題3の(1)の解説の一行目がミスってます!!
=>[作者]: 連絡ありがとう.分数を表示する関数のかっこが閉じていなかったので,分数が表示されていなかったようです:Frac_102('A+B','2','',4,4,1,'',''; → Frac_102('A+B','2','',4,4,1,'','') ; 訂正しました.
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間 について/17.10.24]
分かりやすい解説で、やっと問題4まできました。ところが、問題4にあるgooleの広告が問題文に重なって意味が分からないので削除しようとするのですが、消えません。他の広告は、暫くすると台紙自体がきえるのですが、問題4に限っては、台紙のようなものが残って本文が見えません。仕方なくyahooで問題を確認した次第です。先生にお願いするのもどうかと思ったのですが、この欄を使わせていただきました。
=>[作者]: 連絡ありがとう.ChromeとSafariで表の形が歪んでいましたので訂正しました.(これら2つのブラウザでは,半角アルファベットの単語が長くなった場合に,改行せずに表の形が変わってしまうようです…今回トラブルのもとになった半角文字は =NORMDIST(61,60,4/8,TRUE)−NORMDIST(59,60,4/8,TRUE)) で,通常はハイフネーションで2行に分かれるか,丸ごと次の行に写るはずのものが,これを全部1行に入れるために表の形が変わるらしいです.
■[個別の頁からの質問に対する回答][数学I における三角比の定義(復習) について/17.10.24]
第11問の答えは2分の√3だと思うのですが、解答では、2分の1と書いてあります。
確認をお願いします。
=>[作者]: 連絡ありがとう.
です.解説図もそうなっています.質問者は120°と間違っていませんか.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数 について/17.10.24]
「媒介変数表示のときの微分」のページの例2の問題で問題文にはdx/dxを求めなさいとなっているんですが、答えにはdy/dx=~となっています。自分は微分をやり始めたばっかりなんで勘違いしているだけかもしれませんがおかしいと思いました。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][ペル方程式 について/17.10.23]
双曲線の方程式 このページが出ません
=>[作者]: 連絡ありがとう.PC用のページでリンク先のディレクトリ階層が1段ずれていましたので訂正しました.
■[個別の頁からの質問に対する回答][行列の対角化とは について/17.10.23]
内容は良いと思いますが、正直読みづらいです。2段組のレイアウトはやめたほうが良いと思いました。
=>[作者]: 連絡ありがとう.読みやすさというのは好みの問題で,正しいものというものはありませんが,通説に沿って1行文字数を35~40文字以内にしています.それよりも長いのは,英文のように改行が多いと単語のハイフネーションが煩わしい場合やその訳文では見かけますが,逆に学会誌で段組みでないものは見たことがありません.
■[個別の頁からの質問に対する回答][累乗根 について/17.10.21]
左の「現在地」の欄がとても使いやすくなってうれしいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][小数を分数に直す練習 について/17.10.21]
わかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理など公式一覧 について/17.10.20]
素晴らしいです、高校の式より分かります
=>[作者]: 連絡ありがとう.連絡を受けるとその頁を見るようにしていますが,1箇所間違いを見つけましたので訂正しました- - 自慢するような話ではない!
■[個別の頁からの質問に対する回答][放物線の頂点の座標 について/17.10.20]
私は中学生ですが、数検の勉強に役立ちました。しかし、問題の解答スペースで既に-記号がついているものがあり、符号の間違えに気づかなくなってしまう可能性がありました。なので、そこを改善して欲しいです。
=>[作者]: 連絡ありがとう.その頁は一連の練習の中で初めの頁です.その頁ができるようになったら次の頁をやるのです.サブメニューで同5まであります.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/17.10.19]
三人でじゃんけんをる時最初の2回があいこで3回目に2人が勝つ確率
=>[作者]: 連絡ありがとう.自分自身の言葉がないと,質問しているのか意見を言っているのか分かりません.すなわち,その問題が間違っていると言っているのか,その問題(よそから持ってきた問題=宿題など)が分からないと言っているのか?
ほぼ同じ問題は
確率の乗法定理のページ (問題6)で解説しています.
■[個別の頁からの質問に対する回答][指数法則 について/17.10.19]
なんにもわからん
=>[作者]: 連絡ありがとう.YAHOO!から検索で直接にその頁に入られて,3分ほど見ただけで,前のページに書いてあることを読んでおられないようです.サブメニューで負の指数の定義を30分くらいやってからそのページに戻るとよいでしょう.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/17.10.19]
問題が実際に出来るところが良いです!
1発で解決出来ました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][直角三角形の辺の長さ について/17.10.19]
「三角形の辺の長さ」がnot found になっています! なんとかしてください!
=>[作者]: 連絡ありがとう.PC用に作った教材のレイアウトを縦長に直すのが無理なので,携帯用の教材がまだないためエラーになっていました.文字が小さくて見にくい場合は,iPhoneを横に持ってください.
■[個別の頁からの質問に対する回答][群数列 について/17.10.18]
例題
次の群数列の第100項を求めなさい。の答え間違ってませんか?
=>[作者]: 連絡ありがとう.答は間違ってませんが,こういう質問があるということは,今の解説では分かりにくいということらしいので,解説の仕方を少し変えました.
■[個別の頁からの質問に対する回答][累乗根 について/17.10.18]
問一に誤りあり
=>[作者]: 連絡ありがとう.誤りありではなくて,途中経過にあやしいものがあるということでは?
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/17.10.18]
暗算で解けるのが一番良いのですか?
=>[作者]: 連絡ありがとう.質問の意味が通じません.そろばんの足し算,掛け算のように,機械的な操作でできることを,イメージの中で行うことを暗算というとすれば,高校数学の中で暗算で行えることは,よく使う公式を覚えていて,それに数値を代入して答を出すような場合が考えられます.しかし,この頁に登場するような問題は,一時的な記憶に置いておいてそれらを足したり引いたりしなければならないので,暗算は無理でしょう.
■[個別の頁からの質問に対する回答][2進数の演算 について/17.10.18]
分かりやすい
助かりました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/17.10.17]
P値の理解の仕方として、確率なので1(100%)を超えることはない。
P値は有意差が無いと言える確率ということでしょうか?
=>[作者]: 連絡ありがとう.有意差の有無は何らかの基準を設定して,その基準よりも外れていると「みなす」かどうかということなので,ワンクッション置いた2次的な判断・評価です.これに対してP値は,同一母集団から抽出された標本なのに偶然誤差で生じる確率を求めたもので,P値が小さいと「そのような極端なことが起こることはめったにない」ことになります.・・・「有意差がない確率」というロジックはあまり聞きません.先に確率と判断の境目を求めて,その後に判断しなければなりません・・・管理人の理解では,まず,「同一母集団から抽出された標本」という仮説を設定してそれが成り立つ確率をPで表し,P値が小さ過ぎたら,仮説が棄却されるというロジックだと考えています.
■[個別の頁からの質問に対する回答][2次不等式 ==(解き方まとめ) について/17.10.17]
問題2(2)の答えをクリックすると×が出てしっまてします。修正よろしくお願いします。
とても分かりやすかったです!
=>[作者]: 連絡ありがとう.申し訳ない,解説と採点のつじつまが合っていませんでしたので訂正しました.
■[個別の頁からの質問に対する回答][因数分解(応用問題) について/17.10.16]
問4の(2)の(x²-y²-4)²-16y²この式を展開すると-2x²y²という数字が出てきて答えが合いません
=>[作者]: 連絡ありがとう.何と何が合わないのですか?−2x2 y2 という項は出て来るので,整合性はあります.
■[個別の頁からの質問に対する回答][展開の順序 について/17.10.15]
(x-1)(x+2)(x+3)(x-6)は、Xの数を揃えるのではないのですね?
=>[作者]: 連絡ありがとう.xの係数をそろえるのではありませんが,そこに解説があるのでそれを読んでください.
■[個別の頁からの質問に対する回答][積の法則 について/17.10.14]
このようなタイプの問題集は面白いと思うのでこれからも続けて欲しいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆三角関数 について/17.10.14]
平成21年度技術士第一次試験問題の解説が間違っているので報告します。
1 < (√3)/2 < √3 だから
と書かれていますが、実際には tanγ = (√3)/2 ≒ 0.866 < 1 です。
ゆえに、tanγ が tan(π/6) = 1/(√3) ≒ 0.577 よりも大きいことを示す必要があります。
=>[作者]: 連絡ありがとう.ていねいに読んでくれてありがとう.管理人の注意力がそこら辺で途切れていたようです.訂正しました.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/17.10.14]
例題で右図とあるのですが、その図が解説の下にあり見難かったです。
その他は解きやすく、勉強がスムーズにできました。ありがとうございました。
=>[作者]: 連絡ありがとう.PC用の教材を携帯用の教材に作り替えたときに,左右に並んでいた文章および図を上下に並べ替えましたので,右という言葉が残ってしまったようです.この頁は直しましたが,他の頁で同様の食い違いがまだ残っている可能性は大です.お気づきの場合はまたお知らせください.
■[個別の頁からの質問に対する回答][一般項の記号 について/17.10.13]
面白すぎぶっちゃけこれやってれば学校の授業なんて受けなくていや
=>[作者]: 連絡ありがとう.いやいや授業は大切です - - おごれる平氏久しからずともいうので謙虚に攻めよう.
■[個別の頁からの質問に対する回答][同じものがあるときの順列 について/17.10.13]
携帯版で、答えを選択すると発信の画面になり、選択できないものものがあります。
=>[作者]: 連絡ありがとう.携帯で確かめましたが,iPhone, Androidいずれもエラーはありませんでした.なお,「…ものがあります」という書き方では,管理人側から読むと全部調べてくださいという意味になりますので要注意です.
■[個別の頁からの質問に対する回答][順列 について/17.10.12]
順列の式はnPr, 組合せの式はnCrで、PとCはそれぞれpermutationとcombinationの頭文字と説明されていますが、nとrはなぜ選ばれるのでしょうか? nは natural numberではないかと推測するのですが、そう断言しているものを見たことはありません。rの方は推測さえできないのですが、もしかすると、remnantかも知れないと思い始めています。本によって、またサイトによってはnPk, nCkとなっていますが、kとなると候補がまるでおもいあたりません。ご教授頂けたら幸いです。中高で英語教師をしているものです。
=>[作者]: 連絡ありがとう.まず,式としては前後関係から必要となったアルファベット小文字は何でも使えるでしょう.単に公式を説明するような場合は,26文字のうち2文字が自由に使えるときにどの文字を使うかというのは,ほとんど習慣によると思います.
FORTRAN77で整数を表す変数はI~Nでなければならない,他の文字はこの制限を受けないとされていたように,整数を表す変数は i~n が好まれます.ただし,特に必要がなければ,i,l,oは避けたいです.iは分野によっては虚数単位や電流と混同しやすい,lは数字の1と混同しやすい,0は0と混同しやすい.これらの事情から手書きでコーディングするときは,oにはオーバーラインを付けるなどの工夫が普通に行われていたようです.しかし,必要があれば使います.次の例は行列A,Bの積ABのi行k列成分を表す公式です.
次にrのことですが,確かに母数をnで,抽出される方をrで表すことは多いようですが,組合せの公式は次の形で書かれることもあります.この公式では整数はi~nの文字で書くという習慣に合うようです.
等差数列の一般項
の
(difference)や等比数列の一般項
の
(ratio)は英語がそのまま残っています.関数では f が好まれ,素数では p が好まれるのも同様でしょう.
※以上を要約すると,公式をどの文字で書かなければならないという決まりはないでしょう.ただし,学習者は類似の書物も読むのだから,文化的伝承となっている習慣に沿って書く方が混乱が少なく読みやすいので,特定の文字で表すことが好まれるのだと思います.質問者は英語的に解決したいようですが,管理人の考えでは読みやすさと好みの観点を重視した解釈にしています.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/17.10.12]
こんにちは。測量士補の国家試験合格した者です。こちらのサイトを参考書としてラジアンを理解できて本当に助けていただきました。高校の時ちゃんと習っておけばよかったと今さら後悔しきりです。
現役高校生の若者たちよ!三角関数とラジアンはちゃんとやっておいたほうがいいぞ笑
現役ドローンパイロット(UAV測量が生業で空撮は趣味の48歳)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][極座標 について/17.10.12]
例3、Cの直交座標は(-2,2√3)ではないでしょうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][接線の方程式 について/17.10.11]
全ての単元で丁寧なご指導ありがとうございます。極線の方程式(1)の解説の式で分母のaとbが逆ではないでしょうか?
=>[作者]: 連絡ありがとう.確かに間違いですので訂正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式1 について/17.10.10]
授業でもついて行けなくて困っていましたがこちらの方がすごくわかりやすかったです!1人で解けて嬉しかったです!ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の計算 について/17.10.10]
学校の先生がわかりにくすぎるため、活用させてもらってます
本当にありがとうございます
助かります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/17.10.9]
大学1年です。教授の講義を聞いてもわからなかったのですがこのサイトを見ると1度で理解できました。非常に助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][微分係数 について/17.10.9]
社会人でCG関係の勉強しております
直線方程式と楕円の合成で、傾いた楕円の長径と短径を出すときに
微分をせざるをえなかったのですが
微分のパターンを丸暗記していただけだったので行き詰ってしまったのですが
不定形極限値、導関数の定義の基本的な概念とやり方、微分係数
がよく解り、無事導関数を導くことができました。ありがとうございます
これのおかげで、パース上の正円と楕円が卵型にならないと、自分を納得させることができそうです
予備校で「東大で出題されることの多いパターン」ばかりを教わっていたのは、一体なんだったんだ?と痛感しました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][因数分解の入試問題 について/17.10.8]
昔、受験生だった主婦です。受験数学はすっかり忘れていましたが、頭の体操にと、このページを使っています。前ページの解説が分かりやすいのでこちらのページの問題もすらすら解けますね。脳に適度な負荷をかけている感じで楽しいです。有難うございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][順路の問題 について/17.10.7]
とても分かりやすくていいですね
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の計算(まとめ) について/17.10.7]
参考になります!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の積 ABの定義 について/17.10.7]
すごく参考になります!ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の乗法の性質 について/17.10.6]
難しいですけれど、面白いです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][不定積分の置換積分 について/17.10.5]
まとまっていて、簡単な練習問題で演習しながら理解できたのでとても役に立った。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][整数の入試問題1 について/17.10.5]
例題3のc<b+a<a+a<c+cの変形がおかしいと思います。b<aは成り立たないと思うのです。余弦定理b^2=c^2+a^2-acから、a<cのときb<cを示し、b+a<c+cとするのが正解と考えます。類題3.1についても同様の主張をします。
=>[作者]: 連絡ありがとう.全体構想に気を取られてしまって細部の詰めに甘い箇所があったということで訂正しました.
■[個別の頁からの質問に対する回答][分散分析・・・3つ以上の母集団の平均の差の検定 について/17.10.4]
◇繰り返しのない二元配置法◇
○ 定義に従って表を組み立てるとき:(実務は分析ツールがお薦め)
・・・
(4) (誤差)=(元の値)-(行の効果)-(列の効果) の表を右下に作る.
・・・
これは(誤差)=(元の値)-(全体の平均)-(行の効果)-(列の効果) の間違いではないですか?
=>[作者]: 連絡ありがとう.その文章には間違いがありましたので訂正しました…かなり以前から公開している教材ですが,今まで質問がなかったのは,実際の式の説明がその文章と関係なかったからかもしれません.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/17.10.4]
問題2、4についてですが、「6Cr が最大となるrを求めるとあります」がなぜ最大を求めるのですか?
教えてください。よろしくお願いします。
=>[作者]: 連絡ありがとう.変わった質問だなという印象です.「...どの位置にある確率が最も高いか.」という問題なので,確率が最大となるrの値を求めるのです.
■[個別の頁からの質問に対する回答][放物線 について/17.10.3]
いつも参考にさせていただいております。ありがとうございます。放物線の方程式、2の焦点の働きと軌跡の説明のグラフ上のHの座標が(-p,0)になっていますが正しくはH(-p,y)ではないでしょうか?恐れ入りますが確認をお願いします。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/17.10.3]
■2次関数の最大値・最小値(区間や関数が変わる場合)
回答クリックできません涙
直してほしいです(/_;)
=>[作者]: 連絡ありがとう.他のブラウザでは正常に表示できますが,Internet Explorerだけ作動がおかしいようです.そもそも図1とか図2も表示されていません.
■[個別の頁からの質問に対する回答][ 2次不等式(いろいろな問題) について/17.10.1]
問4 (2) の問題文に2x^2-(3a-2)x+a(a-1)>0 とありますが、解答にある(2x-a)(x-a+1)<0に因数分解するには2x^2-(3a+2)x+a(a-1)>0が正しいと思います
後、(2x-a)(x-a+1)<0の符号の向きは>0だと思います
追記:今朝の迅速な対応ありがとうございます。謝罪などは必要なく、こちらもサイトを利用させて頂いてる分、ご協力させていただこうと思ってますのでよろしくお願いします。
=>[作者]: 連絡ありがとう.前半の因数分解は,元の解説で正しいです.不等号の向きは訂正しました.
■[個別の頁からの質問に対する回答][2次不等式 ==(文字係数) について/17.9.30]
スマホ版の数1-二次不等式-文字係数の問題4 (1)ですが問題文に出てくる
二次不等式(x2-(k+1)x+k(k+1)≧0)と解答で使用してる二次方程式(x2-kx+k(k-1)=0)が違うので答えが間違ってると思います
=>[作者]: 連絡ありがとう.2,3日前に作成した問題で,点検ミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][不等式と領域 について/17.9.30]
考査前、わからなくて調べてたらここのサイトにたどり着きました。
解けない問題も解けるようになったので、ものすごく助かりました!
ありがとうございます!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][集合の表し方(オイラー図) について/17.9.30]
問題5(1)の解説
X=φかつY=φではなく
X=φかつZ=φではないでしょうか
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][内分点,外分点の位置ベクトル について/17.9.29]
線分BAを2:3に内分する点の問題の答えと解説が一致していません
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][一般の行列のn乗 について/17.9.29]
計算機と A^n の関係が分かりません。
=>[作者]: 連絡ありがとう.単に何でも分かりませんと言えばよいわけではありません.たとえば,あなたには電卓で13×13×13= と入力したらなぜ答が表示されるのかは分かるのですか.(作者には分かりませんが)
・・・もっと具体的にどのレベルで何を答えてほしいのかが分かるように質問すべきです.
その行列のべき乗プログラムの中身を教えてほしいということでしたら,次のような単純なものです(ブラウザでソースを表示すれば見えます).再帰は使わずに単なるループで求めています.
初めに入力された行列の成分を各々a11, a12, a21, a22とし,b11, b12, b21, b22はこれと同じものとしてスタートします.
1回の掛け算で得られた結果を一時c11, c12, c21, c22に保管しておいて,b11, b12, b21, b22に戻します.これを入力された回数 nnn だけ繰り返します.
for(var kaisuu = 0; kaisuu < nnn-1; kaisuu++)
{c11 = (b11 * a11 + b12 * a21);
c12 = (b11 * a12 + b12 * a22);
c21 = (b21 * a11 + b22 * a21);
c22 = (b21 * a12 + b22 * a22);
b11 = c11;
b12 = c12;
b21 = c21;
b22 = c22;
}
ループが止まったら,最終的に得られたb11, b12, b21, b22を表示します.
■[個別の頁からの質問に対する回答][補集合 について/17.9.28]
例題が何問か出されていて良かった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][決定係数 について/17.9.28]
自由度調整済決定係数について
nの範囲が n≧ p+1 となっていますが、(A')式において n-p-1=n-(p+1) が存在します。
n= p+1の時、これは成立しませんので、
nの範囲は n> p+1 ではないでしょうか。
=>[作者]: 連絡ありがとう.そうなんですが,「n≧ p+1 のとき,重回帰分析を行うことができる.」「ただし,n=p+1 のとき問題有り」「自由度調整済決定係数は(A')で定義される」と書いてあるのです.「自由度調整済決定係数はn≧ p+1 のとき定義される」とは書いてないのです.
■[個別の頁からの質問に対する回答][三角関数のグラフ について/17.9.28]
高校数学の復習に利用させていただいております。
三角関数の周期の練習問題において、y=cos3θのグラフがおかしいように見えるのですが、いかがでしょうか。選択肢のグラフはy=cos3/2θのグラフに見えます。
=>[作者]: 連絡ありがとう.確かにおかしいので直しました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.9.27]
一般解にはどうして三角関数が登場するのですか。
=>[作者]: 連絡ありがとう.まさにその説明が書いてあるのに「どうして」と尋ねるということは,オイラーの公式とかド・モアブルの定理が分からないのでその部分を読み飛ばしているということじゃないのか?
■[個別の頁からの質問に対する回答][行列の乗法の性質 について/17.9.27]
3の【要約】の⑴の右側の、上から6行目あたりの
零行列のところの1つ目のイコ-ルのあとの零ベクトルと(a b c d)
の行列の積が読みにくいです。
説明がわかりにくくてすみません。
=>[作者]: 連絡ありがとう.そのエラーがなぜ発生するのかよくわかりませんが,作成時は正常に表示されていて,その後何も変更していなくてもgoogleの都合か何かでエラーになる箇所があり,書き換えました.- - なぜか,今は正常でも後日に形が変わる可能性は否定しきれませんが.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.9.27]
一般解にはどうして三角関数が登場するのですか。
=>[作者]: 連絡ありがとう.まさにその説明が書いてあるのに「どうして」と尋ねるということは,オイラーの公式とかド・モアブルの定理が分からないのでその部分を読み飛ばしているということじゃないのか?
■[個別の頁からの質問に対する回答][行列の乗法の性質 について/17.9.27]
3の【要約】の⑴の右側の、上から6行目あたりの
零行列のところの1つ目のイコ-ルのあとの零ベクトルと(a b c d)
の行列の積が読みにくいです。
説明がわかりにくくてすみません。
=>[作者]: 連絡ありがとう.そのエラーがなぜ発生するのかよくわかりませんが,作成時は正常に表示されていて,その後何も変更していなくてもgoogleの都合か何かでエラーになる箇所があり,書き換えました.- - なぜか,今は正常でも後日に形が変わる可能性は否定しきれませんが.
■[個別の頁からの質問に対する回答][行列式 について/17.9.27]
問題7の回答の最初の|3 2 2|は|1 3 2|の間違いでは?
=>[作者]: 連絡ありがとう.最初の部分が入力ミスで,訂正しました.その後は生きているようです.
■栃木県[takaさん/17.9.26]
こんにちは、takaです。部分的にやっています。内積と行列についてです。5頁くらい終了したのですが、ちゃんと合計されているのか分かりません。
=>[作者]: 連絡ありがとう.確かに送信されたデータは空でした
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/17.9.26]
答えが分かってても答えれない
=>[作者]: 連絡ありがとう.iPadでの操作性の問題?
■[個別の頁からの質問に対する回答][行列の積 について/17.9.26]
私は、行列について初心者でしたが、
分かりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][累乗根 について/17.9.25]
僕は中学生なんですが文が少し難しく理解できない場所がとこどことあった
=>[作者]: 連絡ありがとう.それは高校向け教材なので,扱い方が違います.中学生なら中学生向けの基本を固める方がよいでしょう.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/17.9.24]
aベクトル✕aベクトルの内積のcosθはθ=0度の1ですがaベクトル✕2aベクトルの内積のcosθのθは0度なんですか?
=>[作者]: 連絡ありがとう.
は
を同じ向きに2倍に引き伸ばしたものだから,当然それらのなす角は0°です.
蛇足ですが,ベクトルの内積に掛け算の記号×を使ってはいけません- - -それはベクトルの外積という別のものを表します.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.9.24]
いつもこのサイトに大変お世話になっております。
大変わかりやすい解説を有難うございます。
もしお時間がありましたら、「■ 高卒~大学の数学基礎程度 ■」の微分方程式の項目からも
このページに飛べるようにしていただけると大変有難いです。
■定数係数の2階線形微分方程式(非同次) のページも同様にお願いしたいです。
お手数をおかけしてしまい、申し訳ありません。
よろしくお願い致します。
=>[作者]: 連絡ありがとう.内容的には高卒程度なのですが,初めに教材を作ったときに,高卒程度という分類がなかったので,とりあえず高校に入れておいたようです.高卒程度は後から足していってできたもの.そんな訳で了解しました.
■[個別の頁からの質問に対する回答][行列の相等,和,差,実数倍 について/17.9.24]
わかり易かったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列 について/17.9.24]
成分と成分の間の空白は
全角ですか、それとも半角ですか。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組分け について/17.9.24]
組み分けで6人を三つの組に分けるのに、特定の3人が同じ所に入る場合を求めよという問題で、特定の3人を選ぶ式がないのはなぜでしょうか?
⚠︎問題はここにあったものではありません
=>[作者]: 連絡ありがとう.この質問は,主に順列・組合せで使われる「特定の」という用語の使い方が鍵になると考えられます.
6人の人を3組に分けるとき,特定の3人(源さん,平さん,徳川さん)は同じ組に入る・・・他の3人(豊臣さん,織田さん,足利さん)については特に制限はない・・・という問題を考えてみると,特定の3人は「選ぶまでもなく決まっています」.だから選ぶ必要はないのです.
特定のという用語の使い方が,まだ十分わからないということでしたらもう1題.
「5人の候補者から3人を選ぶとき,特定の人Aさんは必ず選ばれ,特定の人Bさんは必ず外れるように選ぶ方法は何通りあるか」
はじめから,Aさんを当選させておき,Bさんを落選させておく.残り3人の候補者から2人選んでAさんに合流させたらよいから
3 C
2 =3通り(バイキング料理で5種類のメニューから3つ選んで食べる場合に,好き嫌いがあってAは必ず食べたいが,Bは食べたくないとき,メニューの選び方は何通りあるかという問題なら学習意欲がわいてくるかもしれません)
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値(区間や関数が変わる場合) について/17.9.24]
山口です。こんにちは。例題2の『○最大値のア)tが0以下の場合、
区間の左端で最小値になります』の
最小値は最大値ではないでしょうか。
間違っていたら、できたら、説明してください。
お願いします。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][内分点の内分点 について/17.9.23]
図1のpとqが逆ではないでしょうか?
=>[作者]: 連絡ありがとう.本来の図ではなく,計算の仕方を解説した図になていましたので訂正しました.
■[個別の頁からの質問に対する回答][複素数の内分点,外分点 について/17.9.23]
七十近くになって学び直し中です。丁寧な解説で、何とか続けられております。有難うございます。例2が中点ではなく、2:1の内分点になっているのではないでしょうか?
=>[作者]: 連絡ありがとう.作業の途中でコーヒーでも飲んでしまったのか,例1をコピーして場所を作っただけで後の作業を忘れてしまったようです.訂正しました.
■[個別の頁からの質問に対する回答][合成関数 について/17.9.23]
有難うございました。少し解ったような気がします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][双曲線関数 について/17.9.23]
sinhx=coshx?
=>[作者]: 連絡ありがとう.質問があるのなら言葉で書いてください.これらが等しくなることはありません.
■[個別の頁からの質問に対する回答][漸化式と一般項(階差形) について/17.9.22]
http://www.geisya.or.jp/~mwm48961/electro/recurr_series1_m.htm
から
同(等比形)
などのページがつながっておりません
スマフォからみてるのでソースまでは見てませんが
相対リンクが./mobile/ページhtmlになってるようです
=>[作者]: 連絡ありがとう.そのページは古い方のリンクで現在表示できないはずになっているのですが,どこかに古いルートが生きているのかもしれませんので調べます.なお,正しくは
階差型 ,
等比型 です.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/17.9.22]
よく理解できました 有難う御座います
標準基底e1=(1) e2=(0)
(0) (1)
とするとこの基底で線形写像fに対応する行列(1.-1)
(2.4)
fを基底(1) (1)
(2) (1)
によって表すとき対応する行列に求めよ
上記の解答をお願いします
よろしくお願いします
=>[作者]: 連絡ありがとう.質問を解読するのが難しいのと同様に,プレーンテキストで書かれたメールで行列を表すことはできませんので,web上で回答します.
そもそも質問内容が十分伝わりませんが,「標準基底で表された点
が一次変換
によって点
に移されるとき
この移動を
,
を基底とする座標で表したときの一次変換の行列を求めよ」という問題だとします.
すなわち,「
であって,
,
,
であるとき,
を
で表せ」という問題ならば
これにより,行列の積
を気長に計算すればよいことになります.
■[個別の頁からの質問に対する回答][集合の要素を用いた証明 について/17.9.22]
問題2の(2)の解説と正答が食い違っています。解説と考え方は正しいようですので、正答の判断のみを修正いただきたく存じます。
=>[作者]: 連絡ありがとう.確かにおかしいので訂正しました.
■宮崎県[アスナさん/17.9.19]
双曲線の問題です
9x2乗-4y2乗=1の場合
どう解けば宜しいのでしょうか?
=>[作者]: 連絡ありがとう.問題を示しておられないので質問の言葉通りに答えるのは無理ですが,高校生の質問としてありそうな心情を推察して答えてみます.
は
と変形できるので
として公式に当てはめて,それぞれの問題を解けばよい.
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/17.9.19]
有効数字の割り算バージョン入れて欲しいです
=>[作者]: 連絡ありがとう.解説も問題も入っています.
■[個別の頁からの質問に対する回答][微分方程式:変数変換による解き方 について/17.9.18]
【問題4】の答えは(2x-y-7)(y+3x)=C ではなく、(x-2y+7)(y+3x)=C になります。検証をお願いします。
=>[作者]: 連絡ありがとう.解答欄の選択肢で各々y,xが入れ替わっていましたので訂正しました.
■[個別の頁からの質問に対する回答][微分方程式:変数変換による解き方 について/17.9.15]
【問題4】の回答の5行目の「右辺の分母分子をXで割って,z=Y/Xとおくと」の次の式ですが、
右辺の分子は、6-5x ではなくて 6-5z だと思います。 答えが合わないのですが。
=>[作者]: 連絡ありがとう.問題4のHELPの途中経過にタイプミスがあるということで訂正しました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.9.15]
文章問題の解き方を教えてください(文章問題)
文化祭のパンフレットをつくることになった。印刷代は100冊までは23500円、100冊を超えた分については1冊あたり200円
印刷の予算額35000円の時、何冊まで印刷できるか求めなさい。(答えが157です)どうすれば答えにたどり着きますか?
=>[作者]: 連絡ありがとう.この質問は,この頁の教材と遠い関係があるといえばあるようにも見えますが,内容的には小学生の問題です.例外的に答えた方がよいような汲むべき事情があるか考えると,答が書いてあるから宿題の答えだけ教えてほしいのとは違うらしいですが,逆に答えを聞いてもなぜそれが答なのか分からないと述べているのだから,解き方を教えてもなぜそうなるのか分からない可能性があります.また,学年・年齢を書かないと未知数を使って解くのか使わずに解くのかも決まりません.
■[個別の頁からの質問に対する回答][双曲線 について/17.9.13]
高校時代には、習ったことがない『双曲線の方程式』を、解りやすい説明文で、微に入り、細に入り教えて頂き、更に、練習問題があるので、大層、ためになりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][検定 について/17.9.13]
疑問点の解決ができるので有りがたく思っております。ついては次の点についてよろしくお願いします。
例4の(考え方)分散がA池の分散は3の二乗となっていますが、右欄ではσ1の二乗/n1となっています。「3」は標本平均の分散ですから、A池全体の魚の分散はσ1はだと思いました。そこで、σ1二乗/n1=3*3
から、σ1の二乗=3*3×n1=900と途中を自分なりに補ってみたのですが、考え方として正しいでしょうか。よろしくお願いします。
=>[作者]: 連絡ありがとう.右欄に公式が書いてあって
右欄の公式に具体的な数字を代入したものが左欄だから,右欄と左欄の見かけが違うのは当然です.
■[個別の頁からの質問に対する回答][2次不等式 について/17.9.13]
問題くれ
=>[作者]: 連絡ありがとう.言葉づかいがやや横着なことは別として,何を言おうとしているのか通じません.
■[個別の頁からの質問に対する回答][組合せ について/17.9.11]
赤玉3個、白玉3個入った袋(赤玉、白玉はそれぞれ区別がつかない)から2個取り出す組み合わせについて質問したいです。組み合わせの定義から6C2だと思う一方、この6C2の意味が6P2という順列を重複分の2!で割っていると考えると赤玉3個と白玉3個をそれぞれ区別して考えていることになると思うのですが、どうして赤玉、白玉を区別して考えていいのでしょうか。もしくは、根本的に考え方が間違っていたら訂正してもらいたいです。お願いします。
=>[作者]: 連絡ありがとう.まず初めに組合せの公式の前提を確かめておきますと
(相)異なるn個のものから,(相)異なるr個のものを取り出して作れる組合せの総数はn Cr
ところで,場合の数(順列,組合せなど)と確率を続けて習うときに,場合の数では「ものに区別がない場合」も登場しますが,高校の確率では通常「ものが区別できる場合」しか扱いません.
ここから先は,学習指導要領や教科書・参考書にはっきりと書いたものがなくて筆者独自の考えですが,これは扱っているものの性質によります.すなわち,巨視的な(人の目に見えるレベルの大きさの)ものは「どんなによく似ていても」区別できるものとして計算しなければなりません.・・・日本の造幣局が作った10円硬貨の新品が3個あるような場合でも,確率の計算をするときは必ず別物として数えなければなりません(そうしないと現実と合わない).これに対して,ミクロの世界では,光の粒子を数えるときに全く同じものがあるとして成り立つ確率があります.
このように実際の世界では,ものが区別できるかどうかはそのものの性質によります.数学では初めに約束を決めておいてから,どちらの場合も取り扱いますが,その結果は初めの約束によって変わることになります.
さて,元の問題に戻りますと,赤玉3個、白玉3個入った袋(赤玉、白玉はそれぞれ区別がつかない)から2個取り出す組み合わせは,赤赤,赤白,白白の3通りでしょう.(組合せだから白赤は別に数え上げないでしょう).…(2)
・・・はじめに(赤玉、白玉はそれぞれ区別がつかない)と書いてあるからです.
間違ってはいけないのは,確率の問題をやっているときにはこの計算は使えないということです.すなわち,大きさ形重さが全く同じで区別のつかない赤玉3個、白玉3個から2個取り出すとき,赤玉2個が出る確率は
でしょう.間違っても
と答えてはいけません.なぜなら,高校の数学に登場するのは,人の目に見える程度の大きさのものだからです.
■[個別の頁からの質問に対する回答][条件付き確率 について/17.9.11]
図で描いてあるので条件付き確率が視覚的にわかりました。ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/17.9.11]
例題5の増減表まちがっとる
=>[作者]: 連絡ありがとう.増減表の y' の符号が逆ということで訂正しました.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/17.9.11]
【例題3】にて増減表の
X=-1をy1に代入した値ですが0でなく-7となりますが
x>0の意図で0とされているのでしょうか
増減表上では-7としないのでしょうか
=>[作者]: 連絡ありがとう.難しい話は何もないです.単純な入力ミスですので,訂正しました.
■[個別の頁からの質問に対する回答][広義積分 について/17.9.10]
最後の問題が、少し説明が難しく感じました。なぜタンジェントを使うかを最初に説明して頂けるともっとわかりやすく感じると思います。
=>[作者]: 連絡ありがとう.言い過ぎると嫌われますが,このページは高卒レベルの演習問題なので,高校の基本は黙って使っています.例えば,
このページ や
このページ に登場する置換積分で,成功体験を基にして(そんな話があったなという感じ)以後に登場したら真似するという考え方でよいでしょう.
■[個別の頁からの質問に対する回答][双曲線 について/17.9.9]
とても、解りやすい説明文かつ例題は、素人の私でも理解することができました。現役の頃、難しくて解けなかった双曲線の方程式が、解決しました。感謝いたします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/17.9.9]
ご報告ですが,【例題1】(オ)a>1のとき1個→(オ)a>2のとき1個に訂正必要と思われます.
=>[作者]: 連絡ありがとう.入力ミスですので訂正します.
■[個別の頁からの質問に対する回答][条件付き確率 について/17.9.9]
条件付き確率の問題4ですが、問題3と同様に考えるのであれば答えは1/3ではないでしょうか。
=>[作者]: 連絡ありがとう.そこに解説が書いてあって図も付いています.問題4は問題3と同様ではありません.
この問題について,アメリカの研究者の話として,いくら説明しても遂に分からない人が何割かは残るらしいということを数学雑誌で読んだことがあります.
どう違うのか,図を見てゆっくり考えてください.
■[個別の頁からの質問に対する回答][不定積分 について/17.9.8]
感想です。
多項式の積分の復習が、すっと頭に入ってきました。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][変数分離形.微分方程式の解き方 について/17.9.8]
良いところ
> 慎重な方は,なぜ積分記号を付けたり外したりできるのかと疑問に思うかもしれませんが
まさにここで悩んでいたので、このページの解説がとても勉強になりました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ 漸化式と一般項(等比形) について/17.9.8]
PC版のメニューページで数Bの「漸化式と一般項(等比形)」と「3項間漸化式と一般項」をクリックしてもモバイル版のページが表示されてしまいます。
=>[作者]: 連絡ありがとう.最近は,初めに携帯版の教材を作って,次に横幅を変えたものをPC版にするという流れにしていますが,まだPC版ができていないのでとりあえず携帯版が見えているということです.なるべくはやくPC版も作ります.(対応しました)
■[個別の頁からの質問に対する回答][累乗根 について/17.9.6]
とてもわかりやすく、役に立っています。
もう少し問題量を増やしてくださるとうれしいです。
=>[作者]: 連絡ありがとう.目次をたどってその次のページを読むとよいでしょう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.9.5]
14と15の問題の解き方がわかりません
=>[作者]: 連絡ありがとう.質問者の状況が分かりませんので,答えられないです.つまり,13番までは分かったが14,15が分からないのか,13番までも分からないのか.HELPで解説が出ることに気付かないのか,解説を見てもまだ分からないのか.順列を学習してから円順列を学んでいるのか,それともネットでたまたま出たページを見ているのか.
■[個別の頁からの質問に対する回答][必要条件と十分条件--不等式の問題 について/17.9.2]
問1はなぜ必要条件なのですか?
=>[作者]: 連絡ありがとう.必要条件という言葉の使い方については,
その前の頁 を見てください.
そうするとHELPに書いてあるように,x>2 → x>1 が成り立って,x>1 → x>2 が成り立たないのだから,x>1 は x>2 (であるため)の必要条件になり,x>2 は x>1 (であるため)の十分条件になります.
■[個別の頁からの質問に対する回答][微分方程式...変数変換による解き方 について/17.9.2]
教えてください。「(III)の例」の、”y1=xが1つの特別解になる”というところがわかりません。
もし、問題の式「xy'-y+y2=x3」の右辺がx2 (xの2乗)であれば、y1=xが特別解になるのはわかるのですが。
=>[作者]: 連絡ありがとう.確かにおかしいので訂正しました.
■[個別の頁からの質問に対する回答][4次方程式 について/17.8.30]
(A)[3] 相反方程式の【例 A.3.1】の(解答)の3行目、x+1/xであるはずのところがx+2/xになっています
あと、【問題 A.3.1】の解答選択肢の1つ目(正答)が-3±2√2iとなっていますがiが不要です
=>[作者]: 連絡ありがとう.点検が甘くなっていたようですが訂正しました
■[個別の頁からの質問に対する回答][補集合 について/17.8.29]
答えわかりません
=>[作者]: 連絡ありがとう.当面,お急ぎの場合は(
携帯版 には回答があります
■[個別の頁からの質問に対する回答][内分点・外分点 1 について/17.8.29]
全くわかりません
=>[作者]: 連絡ありがとう.手がかり不足のため「そーか―」としか答えようがないです.
■[個別の頁からの質問に対する回答][2次不等式 について/17.8.29]
文字があまり
=>[作者]: 連絡ありがとう.15年余り経過すると,そもそも高校向けの教材がなかった時代には許された字体も直さなければならないようになって・・・今直しています.
■[個別の頁からの質問に対する回答][解と係数の関係 について/17.8.28]
ページの一番上にスクリプトの一部(数百文字)が表示されてしまっていますよ~
PC版のページでブラウザはchromeです
=>[作者]: 連絡ありがとう.何かの拍子に,かっこ(<)が1つ飛んでしまったため,プログラムとなるべきものがそのまま表示されたようです.訂正しました.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.27]
どうしても解けない問題は、順番に展開していくと、時間は掛かりますが、正解になりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.27]
昨夜、解くことが困難で苦戦していた問題の答えが一致しました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.27]
答えと解答が合わない!基礎計算能力が足りないのか、ここまでの公式が理解出来ていないのか?もう一度、解いています。夜中遅く勉強すると、善くないですかね?
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.26]
計算間違いをなくしたい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][双曲線の方程式 について/17.8.27]
中学校で習う直角双曲線xy=aは、一般的双曲線x2/a2-y2/b2=1の特殊解として導くことはできるのでしょうか?教えて下さい。
=>[作者]: 連絡ありがとう.
…(A)の
に特定の値を与えると,
…(B)の形になるかという問いでしたら,そうではないということになります.
これに対して,
のグラフを適当に回転すれば
になるかという問いでしたら,そうですということになります.
そもそも,中学校で習う直角双曲線
は「2つの漸近線が直角(
)」かつ「焦点が座標軸から45°回転した場所にある」ものです.これに対して,高校で習う双曲線の標準形では「2つの漸近線(
)は様々な角度になる」かつ「焦点は座標軸上にある」ものです.そこで,
…(A)のうちで,直角双曲線のもの(
)で,かつ,原点から図の緑で示した点までの距離を
とすると標準形での方程式は
すなわち
…(1)
このグラフ(旧グラフ)上の点の座標を
,原点の周りに45°回転してできるグラフ(新グラフ)上の点の座標を
とおくと
すなわち
この変換式を(1)に代入して旧座標を消去すると新座標の関係式
…(B)になります.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.24]
解答してから目次の欄に戻り、もう一度、解答する欄に戻ると、解答欄の順序の入れ換えがある。
=>[作者]: 連絡ありがとう.問題を解いている途中に解答欄の順序が入れ替わるようでしたらエラーですが,全部解き終わってからもう一度やり直すときに「問題文」も「解答欄」も入れ替わるのは,そういう仕様です.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.24]
1問目、正解でした!数字が大きくなって、大丈夫かなぁと思いました。
=>[作者]: 連絡ありがとう.確かにあまり大きな係数が登場すると心配になりますが,見直してもそうなら押し通すしかないです.
■[個別の頁からの質問に対する回答][展開の順序 について/17.8.24]
式と答え、合わせて消していくのが、面白い。
=>[作者]: 連絡ありがとう.割とできる方の人の感想かもしれません.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/17.8.24]
簡単よー
=>[作者]: 連絡ありがとう.簡単でも基本なので必ずできるようにしてください
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.8.23]
6番の問題、難しく感じました。二乗する、一つずつ掛け合わせいく事が、理解出来ました。
=>[作者]: 連絡ありがとう.最後の問題なのでそれなりに骨のある問題になっていたかも
■[個別の頁からの質問に対する回答][確率の加法定理,余事象の確率 について/17.8.23]
(5) 赤玉3個,白玉3個,黄玉2個の計8個の玉が袋に入っている.この中から同時に3個取り出すとき,出た玉の色が2色となる確率を求めよ.
の余事象を使った問題の解き方は理解できました。そこでより身につけるため余事象を使わずに問題をとこうとしたのですが、うまく答えと同じになりません。
私の考えている方法は、まず、赤、白、黄の中から二色となる組み合わせ、(赤、白)、(赤、黄)、(白、黄)となり、一つを例に赤と白の組み合わせでは、赤が二個、白が一個、または、赤一個、白二個といった感じで、3C1 * 3C2 + 3C1 * 3C2 = 18と言った具合で残りの2つの組み合わせを計算しそれぞれを足したやつを8C3で割る形を取っています。すると答えは3/4となってしまいます。
自分なりにこれが思いつく全てでようやく解けたと思いましが、どうやら違うようです。考え方や抜け落ちてる部分を指摘していただくことで結構ですのでよろしくお願いします。
=>[作者]: 連絡ありがとう.何もおかしいところはありません.分数計算をていねいにやればできます.
赤2白1+赤1白2
赤2黄1+赤1黄2
黄1白2+黄2白1
これらの和は
■[個別の頁からの質問に対する回答][確率の加法定理,余事象の確率 について/17.8.23]
(2)
3で割り切れるのは {3n|34≦n≦66} の33通り
5で割り切れるのは {5n|20≦n≦39} の20通り
15で割り切れるのは {15n|7≦n≦13} の7通り
33+20-7 / 100=46 / 100=23/50 …(答
の答えが間違っていると思うので報告します。
5で割り切れる数の説明はあっていると思いますが、3で割り切れる{3n|34≦n≦66}は{3n|33≦n≦66}になると思います。あと15で割り切れる{15n|7≦n≦13}は{15n|6≦n≦13}になると思います。
どちらも通り数の記載は正しいですが、上記の指摘したところは間違っていると思います。
私もあまり自身がないのでできれば返信をお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.8.22]
準備1の1と2から、「y=c1y1+c2y2が解になる」という命題の十分性は理解しましたが、必要性が分かりません。つまり、ある解として方程式を満たすことは分かっても、なぜそれが一般解にもなるのか、他に解は無いのかが分かりません。
=>[作者]: 連絡ありがとう.確かにそのページには,解の一意性が書いてありませんが,それは次のような考えによります.
Web教材では,読者はいつ何時でも学習を放棄して逃げる準備ができていると考えられます(戻るボタンを押すだけで放棄完了).そうすると,このページのような入門的な内容を扱っている場合に,無駄なく厳密に・正確に記述しても理解の助けにはなりません.(どちらかと言えば,伝統的な数学の教科書の無駄なく厳密に・正確に書かれた記述で分からなかったから,Web上で調べている人がほとんどです.)
あなたの知りたいことは,ほとんどの入門書に書かれていますが,その要点は次の通りです.
一般に,xのある値に対するyとy’が与えられた2階常微分方程式の解はただ1つ存在します.(解の存在と一意性の定理)
そこで,x=pのとき,y=q, y'=rという初期条件を満たす2階の常微分方程式の解 yが存在したとすると,そのページに書かれた2つの特別解 y
1 ,y
2 を用いて,y=C
1 y
1 +C
2 y
2 となる定数 C
1 ,C
2 が定まることを述べます.
ここで,y
1 ,y
2 は一次独立な2つの解です.
だから
すなわち,
このとき,連立方程式
は係数行列の行列式が0でないから,C
1 ,C
2 がただ1通りに定まり,これにより,どんな解 y も
の形に書けることになります.
(一般にはロンスキアンを使って示されます)
■[個別の頁からの質問に対する回答][組分け について/17.8.22]
「
□例
部屋に区別がある次の6通りの入り方は,組分けとしては同じものです.
とある
」
のところなのですが、何回読んでも理解できずにいたので他のサイトをみて勉強してみると、上記の文章は間違っているのではないかと思ったので報告します。私が間違っていたらごめんなさい。
どこがおかしいかと思ったかというと、部屋に区別がない場合はそりゃ重複してるやつを消す必要があるので3!で割るとわかりますが、部屋に区別があれば割る必要はないですよね?
=>[作者]: 連絡ありがとう.組分けと聞いただけで何か割り算をして求めなければならないと思い込んでいませんか.順列,組合せなどは教科書にも登場する使い方の定まった用語ですが,ここでいう組分けは世間でいう組に分ける方法ぐらいの用語です.そこで,普通に読めば
A{1,2,3} B{4,5,6}, C{7,8,9}
のように部屋に入れば,1,2,3はいつも同じ組にいて,4,5,6も同じ組,7,8,9も同じ組で部屋が変わっただけだということが分かるはずです.
何も計算はいりません.{1,2,3} ,{4,5,6}, {7,8,9}はそれぞれ仲良しグループでいつも同じ部屋に入っているな~つまり同じ組になっているな~部屋は変わっても組分けは同じじゃないか~と読めるのです.
たぶんあなたの場合,何か計算しなければならないと難しく考え過ぎているため,平凡な普通の話が入っていないのです.
■[個別の頁からの質問に対する回答][指数法則 について/17.8.19]
問題形式になっているのがいいです
間違えたときも、それに沿って解説をして貰えるのが非常に親切だしわかりやすくて助かります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分母の有理化 について/17.8.19]
とても楽しかったです。有難う御座います。また数Bやってみたいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/17.8.19]
≪植木算:r-1になる理由をしっかり覚えよう!≫
のところ、題と最終行のnとrが逆だと思います
=>[作者]: 連絡ありがとう.おっと,この間違いはダメージが大きい,謝罪の記者会見級です.訂正しました.
■[個別の頁からの質問に対する回答][定積分の置換積分 について/17.8.18]
例3がわかりやすくて、非常によかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/17.8.17]
わかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/17.8.17]
とても理解しやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2進数の演算 について/17.8.17]
10-1は、
1
1
-1
として下の位に展開するのはどうでしょう?
=>[作者]: 連絡ありがとう.10=1+1なので,10-1=(1+1)-1=1という意味でしたら,その通りです.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.8.17]
自分なりのやり方ではなく、解答どうりの方法が出来ようになると、いいです。
=>[作者]: 連絡ありがとう.そこそこは程度問題ですが(ものすごく遠回りの答案とか,体力仕事だけの単純計算主義はあまりよくないが),模範解答も1つの見本なので,自分なりのやり方でよいと思いますが.
■[個別の頁からの質問に対する回答][定積分:基本計算 について/17.8.16]
分かりやすいです
中身が何乗になってるときの公式(説明下手ですみません)とか他の公式も一緒に教えてほしいです泣
=>[作者]: 連絡ありがとう.質問と回答とが正確に対応しているかどうか分かりませんが,この教材は数学Ⅱの定積分の教材です.
参考書や授業の中では,確かに1次式のn乗の積分を扱う場合もあるようですが,その証明には置換積分(または合成関数の微分法)を必要としますので,数学Ⅱで教えるのは無理があるようです.したがって,数学Ⅱで扱っている場合は,ただ単に頭ごなしに「覚えとけ!」と言っているだけで良心的な教え方には見えないので私の場合は数学Ⅲで教えるようにしています.
■[個別の頁からの質問に対する回答][1階線形 微分方程式 について/17.8.16]
特に気にすることではないと思いましたが、微分方程式の1回線形微分方程式のページにおいて、例題3の解答の積の微分によりx&apos=…… となっています。
もしかすると私のスマートフォンが原因かもしれませんが、一応アンケートに書かせていただきました。
=>[作者]: 連絡ありがとう.訂正しました.
' と書くべきところを &apos と書いていたようです.(セミコロンが1つ足りない)
■[個別の頁からの質問に対する回答][ 展開公式 について/17.8.16]
詳しくて練習もついてる。たいへん助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][検定 について/17.8.15]
こんにちは。例と答え⑴でz = (85-100)/7.071 =-2.12<-1.96となっていますが、この7.071で割るところに疑問があります。どうして他の問題ではσ/√nで割っているのに、今回はσで割っているのでしょうか? 拙い質問ですがお答えいただけると幸いです。宜しくお願い致します。
=>[作者]: 連絡ありがとう.
1階の試行で事象Aの起こる確率がpのとき,この独立な試行をn回繰り返すときにできる確率分布は二項分布と呼ばれ
で表されます.二項分布はnが十分大きな値であるとき,期待値
,標準偏差
の正規分布とみなすことができます.したがって,二項分布
については
…(A)
が標準正規分布になると考えます.
これとは別の話として,母平均m,母標準偏差σが既知である母集団から大きさnの標本を抽出したときの標本平均は
…(B)
の標準正規分布をなします.
(1)の問題は(A)で解きます.もっと気の利いた説明ができるとよいのですが,確かにそのページの解説は分かりにくいので,機会があれば直さないといけないようです.
■[個別の頁からの質問に対する回答][展開公式1 について/17.8.15]
公式が目の前にあると、計算しやすい!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/17.8.15]
公式を自分で導き出せるようになった!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/17.8.15]
回答が事前に書いてあり、自分の回答に自信のない時、回答の導き方が思い出せる!
=>[作者]: 連絡ありがとう.数学のことでなく漢字のことですが,問題の答えは解答,返事は回答と書くのが普通です.
■[個別の頁からの質問に対する回答][逆関数 について/17.8.15]
いいっすね
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.8.15]
6番の問題が難しいです。理解は出来ました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.8.15]
全て解答してから答えを出さないと、全て答えが出てしまう。
=>[作者]: 連絡ありがとう.携帯版の方は1つずつ採点するようになっていますが,PC版の方はまだ直っていなかったようです.(お急ぎの場合は携帯版を見てください)
■[個別の頁からの質問に対する回答][三角不等式 について/17.8.15]
例1の答えの書き方はあれで合っているのでしょうか?前のページでは違う書き方がしてあったのですが。
=>[作者]: 連絡ありがとう.おっと,120°と180°が逆になっていましたので訂正しました(冷汗)
■[個別の頁からの質問に対する回答][組分け について/17.8.14]
徐々に難しくなっていて、問題の構成が非常に良いです。
唯一欠点を挙げるとしたら、文字の字体が読みにくいことかと思います。
できるだけ、左端をそろえたほうが読みやすいかと思います。
=>[作者]: 連絡ありがとう.字体という話と左端に揃えるという話のどちらに重点を置いて読めばよいのか?
■[個別の頁からの質問に対する回答][2次関数の頂点 について/17.8.13]
解答を求める際に、頂点の向き(∔.-)も併せて解答させてはどうでしょうか。
=>[作者]: 連絡ありがとう.一度に2つのことをさせると,採点の仕方を具体化するときに複雑になります・・・頂点が正しくて凹凸が違う場合,凹凸が正しくて頂点が違う場合,頂点も凹凸も違う場合,・・・その情報を回答者に返しても複雑過ぎてうれしくない可能性が大です.
■[個別の頁からの質問に対する回答][1階線形 微分方程式 について/17.8.13]
以前参考書で読んだのは、
exp(∫P(x)dx) ※不定積分でCを出さない
を両辺にかける事で
左辺=exp(∫P(x)dx) *y'+exp(∫P(x)dx) *y=(exp(∫P(x)dx) *y)'
右辺=exp(∫P(x)dx) *Q(x)
となるので、両辺をxで積分して最後に両辺にexp(-∫P(x)dx)を掛ければyが出てきます。
これでやっていることは茶色字で書かれている公式と中身は同じですが、
暗記事項はexp(∫P(x)dx)を両辺に掛けることだけで良く、
0からの導出は厳しいですが結果的に正しいことを示すのは容易で
変形の検算も比較的容易なのでオススメです。ご参考までに。
まぁ結局の所慣れた方法で計算するのが一番な気はしますけども…
=>[作者]: 連絡ありがとう.なるほど,そのやり方でできます・・・ただし,あなたの式では左辺第2項に P(x) が抜けているようです.
■[個別の頁からの質問に対する回答][定積分:基本計算 について/17.8.11]
変数文字の種類である程度想定できるので、問題としては同じ文字を使った方が良い感じがした。
久々に(40年ぶりに)定積分を説いてみた。意外と面白い。
=>[作者]: 連絡ありがとう.ある程度分かっている人の感想のようですが,この小項目は「区間の両端が定数であるとき,積分変数と被積分関数が同じ文字であれば,定積分の値は内部変数の種類に依存しない」ということを学ぶための教材なので,異なる変数で練習しないとそもそも練習にならないのです.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/17.8.9]
問題5(1)の解説で「先頭5と末尾-24」とありますが、末尾の24という数字はどこから来ているのでしょうか?
=>[作者]: 連絡ありがとう.確かに変です.
今となっては,なぜ間違ったのか,正確には分かりませんが,コメントをプログラムで書いていた時に,うっかり書くと小学生でも間違わない次のような間違いが起こることがあります.
訂正しました.
■[個別の頁からの質問に対する回答][ベクトル内積(成分) について/17.8.8]
内積の定義を導く方法の最後の答えが間違ってます!
=>[作者]: 連絡ありがとう.確かに!ただの計算間違いと違って,こんな大事な公式を写し間違ってどうする.筆者も気合を入れないと!
■[個別の頁からの質問に対する回答][共通部分と和集合 について/17.8.8]
確かに仰るとおり、日常で「または」という語を使う場合に数学的な意味とは異なる場合の方が多いのは確かですが、日常会話でも数学的な使い方と同様になる場合は沢山あり、しかもそういった例は数学的な「または」とイメージ的にも似通っている場合が多いので、そのような例を用いて数学的な使い方の正確なイメージを伝える方が学習者にはより有益ではないかと感じました。
たとえば、「ある中学のサッカー部(という全体集合)では、6月の練習試合に小学生時の経験者(という集合)『または』2年生以上(という集合)が出場できる(出場可能者 = 経験者 ∪ 2年生以上)」といった場合であれば、集合における「または」とほぼ同じ意味を表すことになり、数学的な集合のイメージと重ねて理解がしやすいと思います。
コーヒーと紅茶を例に出すなら、「彼はコーヒーまたは紅茶を飲みましたか?」という質問に対して、Yesと言える状況は彼が何を飲んだときか、と考えると、彼がコーヒーのみ飲んだ場合、紅茶のみを飲んだ場合、あるいはその両方を飲んだ場合、いずれもYesと答えられます。彼がどちらも飲んでいない場合のみ、答えはNoとなりますね。
そのような例と合わせて、「セットにコーヒーまたは紅茶がつく」のような意味の異なる例を合わせて紹介することで、「数学的な『または』とは、○または○の『どちらか一方にでも当てはまる』ことを意味する」と結論づけておけば、より理解を促すことが出来るのではと思います。
=>[作者]: 連絡ありがとう.詳しく書いてもらいましたが,教材に書かれていることのように思えますが・・・
■長崎県/めぐたんさん[17.8.7]
最後の問題が分かりやすかったです。
=>[作者]: 連絡ありがとう.ただし,どの頁の話なのか書いてもらわないと分かりません.
■[個別の頁からの質問に対する回答][複素数の計算 について/17.8.7]
とても分かりやすかったです。
とても参考になりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][陰関数の導関数 について/17.8.7]
問3の解説の2行目の式で、yの微分になってしまっているところがあります。
問題3の解説の二行目-3(d/dy(x)y + x d/dy(y))は-3(d/dx(x)y + x d/dx(y)) では?
・解説の中で出てきた答えが選択肢の中にないのはなぜ?
どれが正しいのかがわからず混乱しています。改善よろしくお願いします。
=>[作者]: 連絡ありがとう.前半について,訂正しました.
後半について,そのような質問はあり得ないと考えていますが,一応確認のために加筆しました.(一勝一敗になる)
は,自明の理なので解説は不要だと思いますが.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/17.8.7]
(5)←
非常に参考になりました。
ひとつ訂正箇所があるのですが、三角関数の不定積分の(5)で
tanx=sinxcosx
d/dx( f(x)g(x))=f’(x)g(x)-f(x)g’(x)/g(x)2
【だから d/dx(tanx)=cosxcosx-sinx(-cosx)/cos2x=1/cos2x】
とありますが
【だから d/dx(tanx)=cosxcosx-sinx(-sinx)/cos2x=1/cos2x】
ではないでしょうか。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][指数法則 について/17.8.5]
問4の(5)は分母の指数が等号と重なって読めないです。
=>[作者]: 連絡ありがとう.Safariで見た場合でも,読めないというのはやや誇張がありますが,重なっているとはいえるので訂正しました.
■[個別の頁からの質問に対する回答][階乗 について/17.8.3]
何も知らない中学生でしたが、五分くらいで階乗についての簡単な理解が可能でした
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][Σ記号の変形 について/17.8.3]
(5)の答えは3k-2だと思ったのですが、採点しても不正解になってしまいます。ヒントを見ても3k-2だと思うのですが、私の考え方が違うのでしょうか?
=>[作者]: 連絡ありがとう.いい線まで行っていて,内容も合っていますが,表現が完全ではないのです.
和の記号Σの一番最初の頁に書いています基本:
この頁 の第3段落『Σ記号は積でつながっている範囲まで作用する.作用する範囲を明確にするために「かっこ」が使える. 』に注意しなければなりません.
とすると,Σ記号の内部変数が3kまでしか届かないので
を表してしまい,元の式と等しくなりません.等しいものに直すためには,かっこを使って
と書かなければなりません.
■[個別の頁からの質問に対する回答][(各駅停車)正規分布 について/17.8.2]
分かりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][不等式と領域 について/17.8.2]
わかりやすい説明でした 連絡ありがとう.
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][連立方程式 について/17.8.2]
先頭の問題ですが、回答方法が正しいのであれば、問題式2行目はX-λY+Z=0ですね?
問題が正しければ、不定解になり③以外はすべて成立します。
=>[作者]: 連絡ありがとう.確かにyは入力漏れですので訂正しました.
質問・意見の後半の「問題が正しければ、不定解になり」は変でしょう.
例えば,問題が正しくて,[5] λ=1の場合
は不定解にはならず,x=1,y=−1,z=0という解になります.(自明解ではなく,不定解でもなく,普通の解になる)
とりえず,問題は訂正しましたので,その議論は不要になります.
■[個別の頁からの質問に対する回答][対応のある場合のt検定 について/17.8.2] 対応のあるt検定について教えてください。
preとpostで変化があったのかを分析するとした場合についてお伺いします。
preが正規分布していて、postが正規分布していなかった場合は、対応のあるt検定をせずとも「変化があり」と結論付けて良いのでしょうか。
対応があるにもかかわらず分布が変わっているということは、変化があったということとニアリーイコールだと思います。
=>[作者]: 連絡ありがとう.どちらかと言えば,筆者があまり得意としていない分野なので,たぶんというレベルの話として・・・そもそもt検定は母集団が正規分布をなすことを前提としているので,実験群か統制群(比較群)のいずれか一方が正規分布をなしていなければ,そもそもt検定による有意差検定はできないのではないか.順序相関など正規分布を前提としない分析方法がよいと思いますが・・・
■[個別の頁からの質問に対する回答][展開公式 について/17.7.31]
問題3-第3問-(3)で、指数の分配法則が多項式でも成り立つのか、ちょっと考えてしまいました。成り立つのですね。直観ではスッと入ってきませんが…。
=>[作者]: 連絡ありがとう.指数法則
は成り立ちます.
「指数の分配法則が多項式でも成り立つ」とはどういうことを表しているのか?いまいち要領を得ませんでした.
■?[?さん/17.7.31]
http://www.geisya.or.jp/~mwm48961/statistics/siguma2.htm
の第2問目、100になっていますが、10の間違いでしょうか?
=>[作者]: 連絡ありがとう.他の解説との整合性を考えると10が正しいようですので訂正しました.
■[個別の頁からの質問に対する回答][展開の順序 について/17.7.31]
一題選択、解答後。次の問題に進もうと、左欄より次の式を選択しようにも選択できません。つまり先に進めません。ブラウザはchromeです。
=>[作者]: 連絡ありがとう.古いプログラムの消し忘れでエラーになって止まったようです.訂正しました.
■[個別の頁からの質問に対する回答][ド・モルガンの法則 について/17.7.27]
問題2 の (3)
ここがポイント≫ まずA∩B={2,3}を求めてから,次にこれとC={3,4,6,7}の和集合を求めます
次の行のA∩Bの上のバ-はいらないと思いますが。
=>[作者]: 連絡ありがとう.ほんとだ,いらないので訂正しました.Web画面上でバーを表示するプログラムをいじくったりしているうちに間違ったようです.改行位置も見にくいので少し修正しました.
■[個別の頁からの質問に対する回答][行列と連立方程式 について/17.7.27]
例題が間違ってると思う。
=>[作者]: 連絡ありがとう.?? 例題が間違っているということはないでしょう.例えば,例題の解答が間違っているとか,例題の問題の符号が間違っているというような場合はあり得ますが・・・ところで,あなたは不定解や不能解が出る連立方程式は,問題が間違っていると考えていませんか.
■[個別の頁からの質問に対する回答][平方完成(基本) について/17.7.27]
問題の数字が文章と重なって表示されるために判読できず、解けない場合がある。
=>[作者]: 連絡ありがとう.あなたは質問や意見の書き方を間違っています.その頁ではなく,他の何千頁もある教材の内のどこかの頁で,あるブラウザで見た時に文字が重なって見えるが,どの頁かどのブラウザかは明らかにできないと述べていることになります.これは,まともに対応してほしいという感想ではありません.
■[個別の頁からの質問に対する回答][因数分解(応用問題) について/17.7.27]
問題4の(2)は、-16y^2となっていますが、-16x^2ではないでしょうか。
=>[作者]: 連絡ありがとう.話がややこしいのですが,解説の通り読めば後はご指摘のように見えますが,解説の1行目が間違っていました(訂正しました)ので,後は正しくなります.
■[個別の頁からの質問に対する回答][放物線の頂点の座標 について/17.7.26]
いつも利用させてもらってます。
問題の答えがあればな、と思いました。
どうなってこうなる!というのではなく、ただ答えがあればな、と。
=>[作者]: 連絡ありがとう.この教材を作ったときは,解答は採点すれば分かるので,公式に数字を当てはめたら答が出るというような問題では特に解答を表示する必要はないと考えていましたが,最近は筆者も少しはまーるくなって,解答もある方が便利がよいかもなと考えるようになりましたので,解答を付けた頁を増やしています.まもなく付けます.
■[個別の頁からの質問に対する回答][複素数の計算 について/17.7.26]
複素数の定義 5-3iは複素数ではないのか。虚数となっている。
=>[作者]:連絡ありがとう.「複素数の定義」の右にある図で示されるように,複素数は実数と虚数から成り立っています.だから,虚数は複素数であり,実数は複素数です.・・・虚数と複素数とは「あれかこれか」の関係ではなく,西日本と日本のように一方が他方を含んでいる関係です.もちろん,実数と複素数も東日本と日本のように一方が他方を含んでいる関係です・・・(率直に言えば,この質問は想定外の質問です)
とありますが、実数と虚数は背反関係にあるため「複素数の定義」の右の図のような包含図は誤りではないでしょうか。
=>[作者]: 連絡ありがとう.なるほど,そういう見方をする人がいるのかと感心しています.
集合をオイラー図で描くとき「境界線の外と中,境界線をまたいだら背反関係になっていることを表す」「ただし,四角の中に丸がある場合や,丸の中に丸がある場合は内側にある丸は部分集合であることを示す(=背反関係ではない)」という約束で絵を描きます.
左の図では,虚数と実数は背反関係であることを表し,虚数が実数の部分集合であるという意味ではなく,実数が複素数と一致するという意味でもありません.
左図1のように描くと,あなたの見方とは近いかもしれません・・・左図1のうちで純虚数の丸を取り除いた図が東京図書の数学Ⅱの教科書に出ています.
虚数と純虚数の関係は,どの図でも混乱なく理解できますので,以下において実数と虚数の関係が分かりやすいかどうかを考えてみます.
あなたの見方では元の図では虚数が実数の部分集合と見えることになり,教科書(図1)では実数が虚数の部分集合と見えることになって,いずれも具合が悪いように見えますが,上の解説から分かるようにそれは間違いです.
図3は論理的には正しいのですが,実数でも虚数でもない場所(本来空集合となるべき箇所)ができてしまって,初心者がそこに目を向けると混乱が起こることになります.
要約すると,元の図,図1,図2,図3のいずれも問題なく同じ内容を表しているのですが,集合図の約束(境界線による背反関係の表示,内側の境界線による部分集合の表示)をゆっくり論理的に考えなければ理解できないということでは,図示による視覚化の長所が薄まってしまいますので,おそらく,図2(ベン図とオイラー図の折衷方式)が最も自然に理解できるのかもしれません.図を入れ換えるかどうかはしばらく様子を見ます.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.7.23]
x2乗+22x乗+96のように
大きい数字の時のコツを教えてくれたら嬉しかったです!
=>[作者]: 連絡ありがとう.たすき掛け因数分解の頁から質問しておられますが,その問題は
中学3年生の問題 です.すなわち
96=25 ×3=16×6 22=16+6 966 で和が22 となる2数を見つけると16, 6 になるからx2 +22x+96=(x+16)(x+6) とします.
コツといっても,中学で習う通りで,積を先に考えます.
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/17.7.22]
3変数はどのようにすればよいのでしょうか
=>[作者]: 連絡ありがとう.省略し過ぎで意味がつかみにくいですが,3変数の場合のヤコビアンはどうなりますかという質問でしたら
(の絶対値)を使うことになります.
■[個別の頁からの質問に対する回答][Σ等比数列 について/17.7.22]
等比数列の和の公式について質問させてください。
先生のページでは、項比rから-1するという形になっていますが、
別の書籍等では、1から項比rをマイナスするという形になっているものもあります。
この違いは何に起因するのでしょうか?
ご教示ください。
=>[作者]: 連絡ありがとう.
と
とは等しいので,どちらで表してもかまいません.(分母と分子の両方に -1を掛ける[全体には1を掛けることになる]と分数としては等しい)
あえて言えば,生徒が自然に感じる(したがって,計算間違いしにくい)方を使うようにしているだけでしょう.
数学ⅡBの段階では有限数列しか登場しないから,和の公式からさらに変形する場合でも符号を間違わないように最高次の係数を正にして
が好まれるでしょう.これに対して,数学Ⅲでは無限等比級数の和も扱うので
のとき
を使って
とする方が自然に見えます.
でももちろん「正しい」のですが,こちらを好む人は少ないでしょう.
■[個別の頁からの質問に対する回答][自然数の累乗の和 について/17.7.21]
II.8について,$p$が3以上の奇数のときには$S_p$は$S_3=S_1^2$で割り切ることができることは,
例えばHans Rademacher著,Topics in Analytic Number Theory, Springer-Verlag の
p.1~p.8に証明があります.
=>[作者]: 連絡ありがとう.ていねいに読んでくれてありがとう.整数問題は詳細に研究されているので,証明があるかもと感じていましたが,実際に証明した人がいたというのは,やはりという感じです.
■[個別の頁からの質問に対する回答][Σ等比数列 について/17.7.21]
Σ式を変形して一般解を導出する方法何とか理解しました。まずは、Σの変数を1に直すと同時に項数も変形してから、一般項の指数部分をk-1の形に直して、初項部分と項比を求めるのですね。
その後にΣの一般式に、初項、公比、Σ式の項数を項比の指数部分に代入してΣ和のい一般解を求めるのですね。私は早とちりして一般項の指数部分をΣ式の一般式の項比の指数部分に代入してしまい、指数の次数があわなくなってしまいだいぶ間違えました。もう一度ぐらい練習すれば、与えられたΣ式を変形してΣ和の一般解が求めることでできそうです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][部分積分 について/17.7.21]
問題2の(2)の答えは 1/4(2x^2+1)sin2x+1/2x cos2xだと思いますが?
=>[作者]: 連絡ありがとう.ていねいに読んでくれてありがとう.各々の選択肢で第2項にxが抜けているということで訂正しました.(ただ,あなたの答案も符号が逆になっています)
■[個別の頁からの質問に対する回答][一般項の記号に慣れる について/17.7.21]
(5)の解法についてお尋ねします。
与えられた数列の差から別異の数列{4,6,8,10}を出してから、この数列の一般項ak=a1+d(k-1)を求めると、ak=4+2(k-1)=2k+2となります。
この一般項から元の数列の一般項:an=n(n+1)を導出するにはどうしたらよいのでしょうか?
作問のように、一般式が例示されていれば計算によって一般式の正答をあてることができますが、
一般式が明示されていない場合、数列だけから一般式を導出できません。
ご教示ください。
=>[作者]: 連絡ありがとう.ご質問の方法は,一般には「
階差数列 」の項目で取り扱っていますのでその項目を見てください.
ただし,この頁はそのような計算問題以前の,はるかに単純な「一般項の記号に慣れよう」という絵本のような入門コースです.計算しようと思わずに,鉛筆を置いて薄眼で「ながめる」と次のようになっていることが分かるのです.(3D画像AHA体験という感じで)
(2=)1·2 , (6=)2·3,(12=)3·4 , (20=)4·5 , (30=)5·6 ,...
したがって,
an =n(n+1) になります.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/17.7.21]
逆関数のも知りたいです
=>[作者]: 連絡ありがとう.逆関数の定義,逆関数の微分法は各々目次を見てもらえばありますが,この頁の文脈の中で「逆関数のも」と言えば逆関数の不定積分法になりますが,あまり聞きません・・・例えば,逆三角関数は高校数学には登場しないので,不定積分が逆三角関数になるような問題は高校数学には登場しません.これに対して定積分は定数なので逆三角関数の定積分なら一応高校数学で扱うことができます.
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/17.7.20]
途中式も丁寧に挟まれており、旧変数←新変数の形など、単純に見えるが案外間違えていたり抜けてしまう過程などが明記されているので、最後まで立ち止まる事なく理解に徹することが出来ました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][連立不等式 について/17.7.16]
正解の数字を入力しても誤りの表示が出る
=>[作者]: 連絡ありがとう.全角数字で入力していませんか?(Chromeで入力している場合,全角数字は自動的に半角数字には変換されません.入力する人自身が半角入力モードにしなければなりません.)
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.7.16]
わかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組合せ について/17.7.16]
正解後に次の選択肢を選択できません。ブラウザはChromeです。
前項の「組合せ」のページのコメント欄に同様の問題が発生してたらしき記述があるので同じバグかもしれません。
=>[作者]: 連絡ありがとう.未定義のオブジェクトを参照していたためエラーになっていました.訂正しました.
■[個別の頁からの質問に対する回答][組合せ について/17.7.16]
正解後に次の選択肢を選択できません。ブラウザはChromeです。
前項の「組合せ」のページのコメント欄に同様の問題が発生してたらしき記述があるので同じバグかもしれません。
=>[作者]: 連絡ありがとう.未定義のオブジェクトを参照していたためエラーになっていました.訂正しました.
■[個別の頁からの質問に対する回答][簡単な重積分の計算 について/17.7.14]
簡単な問題もあってよく理解できました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][点の存在範囲 について/17.7.13]
ベクトル方程式の点の存在範囲について、s+tの範囲が指定されているものだけでなく ☆≦s≦★、○≦t≦◇などsとtの範囲が無関係に変化するものも紹介して欲しいです
=>[作者]: 連絡ありがとう.
質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,
当教材で扱っている内容よりもはるかに簡単なのでこの頁では取り上げませんでした.
例えば,
となる位置ベクトル
の表す範囲は,左図のようになります.
■[個別の頁からの質問に対する回答][根号の計算 について/17.7.12]
問題を実際に解くことができるから良いです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組分け について/17.7.12]
『数学A 組分け』の頁の【例2】の末文「※部屋に区別がある場合÷2!と覚えてしまってもよい.」とありますが、「部屋に区別がない場合」の誤記ではないでしょうか?
ご確認願います
=>[作者]: 連絡ありがとう.(部屋に区別がない場合)=(部屋に区別がある場合)÷n! (nは同じ人数となる部屋の数)なので誤記ではありません.
■[個別の頁からの質問に対する回答][3次関数(文字係数と極値) について/17.7.12]
こんにちは、いつも勉強の参考にさせてもらっています。
3次関数(文字係数と極値)の問題3について、答えは3番を押すと〇となるのに、
HELPを開くと2番が答えとなっています。
環境はPCです。対応宜しくお願いします。
=>[作者]: 連絡ありがとう.解答(採点)は正しくて,HELPの中に書いてある記号[2]が間違っていましたので訂正しました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/17.7.10]
定数係数の2階非同次微分方程式について、y" +2y' +y = (e^(-x))*ln(x) のような、右辺にln(x)を含む方程式についてはどのようなアプローチをするべきでしょうか。
ln(x)については、解いている感じだとln(x)に対してx^2を乗じた A*(x^2)*ln(x) を特殊解としておくとうまくいっている気がします。しかしln(x)を含む方程式はロンスキアンを用いる解法が良いという話も聞きます。
=>[作者]: 連絡ありがとう.右辺に対数関数がある場合も,ロンスキアンも当教材で想定している範囲を超えています.
別頁 に解説していますようにwxMaximaをインストールして,wxMaximaを起動し,画面上で空打ちすると入力画面になります.そこで
ode2('diff(y,x,2)+2*'diff(y,x,1)+y=%e^(-1*x)*log(x),y,x); (←diff の前にカンマを忘れないように!)
のように入力すると
が得られます.これは
を表しています.
■[個別の頁からの質問に対する回答][楕円の方程式 について/17.7.8]
すでに大学を出て○○年なのですが、計算をする必要があって復習のために使わせてもらいました。
計算力が劣化しているのに愕然としました。
自分で計算しないと、わかっているかどうかわからないので、練習問題が役に立ちました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][極限値,不定形の極限 について/17.7.8]
nについて何も但し書きがなく、lim n→∞ cos(nπ/2) の極限を調べよ。
解答:n=1,2,3,4・・・とすれば、0,-1,0,1・・・だから振動する。とありますが
nは自然数とは限らないんで、こういう書き方はまずくないのですか?
=>[作者]: 連絡ありがとう.
(1) この頁を全部見ましたがそういう内容はどこにも書いてありません.どこか他のサイトや他の参考書に書かれていた記述について,当サイトの管理人に苦情を述べておられるのでしたら「江戸の敵を長崎で」の類で,こちらは事情がよく分かりませんので答えにくいです.
(2) 内容的には,引用されている文章を見る限る「あなたの全面敗北」「教材の全面勝利」です.
すなわち,実数か整数か分からない
について
が収束する場合には「どのような近づき方をしても特定の値に近づく」と言えなければなければなりませんが,「ある近づきかたをすれば,どこまで行っても異なる値を取る」と言えれば,その否定になります.
(2.1) 解答:n=1,2,3,4・・・とすれば、0,-1,0,1・・・だから振動する。
でもよろしいが
(2.2) n=1,3,5・・・とすれば、1,-1,1・・・だから振動する。としても証明になります.
(2.3) nの実数値にこだわれば,
とすれば,どこまで行っても
となりますが,このような答案を好む受験生も採点官もめったにいないでしょう.
(2.1)(2.2)の答案の方が歓迎されるでしょう.
(要するに,ある近づき方をしたときに,特定の値に収束せず,振動する例を示せば十分なので,なるべく単純な例を示せばよいことになります)
このように,「収束しないことの証明は収束しない近づきかたの例を1つ示せばよい」ことになります.
(3) 思いが強くて正義感が強い場合に,その思いを検証する別の心的過程も持ち合わせていないと,SNSなどで炎上の加害者になりやすいと言われています.お互いに気を付けたいものです.
■[個別の頁からの質問に対する回答][t分布 について/17.7.7]
信頼関数が0.90の場合どうすればよいでしょうか
=>[作者]: 連絡ありがとう.信頼度95%の信頼区間という言い方はしますが,信頼関数という用語は聞いたことがありません.
*p<0.05 となるt値を求めるには=TINV(0.05, 自由度)**p<0.01 となるt値を求めるには=TINV(0.01, 自由度)† p<0.1
教材の本文に書いてあることを質問するのは,よくない
■[個別の頁からの質問に対する回答][集合の表し方(オイラー図) について/17.7.7]
集合とオイラー図の理解が進みました。ありがとうございました。
PC版頁の問題2の(2)についてですが、解説文の中で"1≦m≦4"とすべきところが"1≦m≦3"になっていたり"mを1以上3以下の自然数とするとm=1,2,3,4になり"という誤記があったり、選択肢はxになっている箇所の解説がnになっていたり複数の誤記があるようです
=>[作者]: 連絡ありがとう.確かに,疲労がたまって,誤記があったようです.
■[個別の頁からの質問に対する回答][重回帰分析(2) について/17.7.6]
とても詳しく、わかりやすくて助かります!
重相関分析で問題になる多重共線性のページも読んでみたいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.7.6]
ヒントを開くとほぼ答えが出てたのでもうすこし答えを厳しくして欲しいです。
=>[作者]: 連絡ありがとう.様々なレベルの読者がいて,ヒントだけでなく解答そのものが欲しいという要望の方が多いです.この頁では,ヒントを開くとほぼ答えが分かるというのですから,それでヒントとしてよい働きになっていると思います.
■[個別の頁からの質問に対する回答][組分け について/17.7.5]
9番 3!でわるだろ!
=>[作者]: 連絡ありがとう.解答を見てもなぜそれが答なのか分からないということですか?・・・屋上屋を重ねて,文章題における人=ペルソナの取り扱いについて,さらに一言述べると.解答に書いてありますように,人は必ず区別します.だから,どの女子と同じ組かということは重要な区別になり,入れ換えると別の組になります.入れ換えることはできません.・・・なお,「わるだろ!」は表現としてよくない.
■[個別の頁からの質問に対する回答][3次関数の最大値・最小値 について/17.7.5]
全問題に共通して言える事ですが、定義域や極値をとるxの値を2次元表示する解法を採用されると格段に学生の理解がすすむのではないでしょうか? a-x 平面にですが、
=>[作者]: 連絡ありがとう.得られた結果の整理方法のことを述べておられるのかな?
■兵庫県[Boyuさん/17.7.5]
恐らく技術的な問題だとは思いますが...
画面を全画面表示にせずに半分ほどのウィンドウで閲覧すると
高校数学の各科目のサイドメニューが隠れてしまいます
スクロールしたくても出来ません...
PC:Windwos 7 HP SP1 64ビットオペレーション
Chrome:Ver 59.0.3071.115 (64ビット版)
IE:Ver 11.0.6300.18697 (製品 Ver 11.0.43)
スクリーンショット: - - -
ついでに[回転と拡大について/17.7.3]について
現高校生としての感覚ですが、
例えばこのページの[→ 携帯版]
上記スクリーンショットの[→ 携帯版は別頁]
高校数学トップの((m))←[数Ⅰ.携帯版メニュー] etc
"携帯"と"スマートフォン"は別物と感じています
それと"頁"を"ページ"と読める人は少ないかと思います
(少なくとも私は先ほど調べて初めて知りました)
そして スマートフォン から見た時、
この表記はかなり小さく、目立ちにくいです
Androidスクリーンショット:- - -
(画像自体は大きいですが、実際は6cm x 10cm程しかありません)
あるサイトでは スマートフォン でアクセスした場合"のみ"
スマートフォン版で表示する と言う"デカデカとした"表示が
"一番上に"来るようになっていました
あくまで参考程度ですが、考慮してくれたら幸いです
=>[作者]: 連絡ありがとう.現在対応できることがありません.利用できる範囲で利用してください.
■[個別の頁からの質問に対する回答][回転と拡大 について/17.7.3]
見にくいし図がよくわかんなーい
=>[作者]: 連絡ありがとう.携帯用は別頁と書いてあるのに,360×640の画面の小さなAndroidで,わざわざPC用の教材を見ておられるのだから,見にくいのは当然のことではないでしょうか.・・・携帯の場合に自動転送するプログラムは,検索順に影響し過ぎるので現在止めています.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/17.7.3]
【例-右辺が指数関数のもの2】
y''-4y'-5y=e5x
の1つの特殊解を求めてください.
のAは1/4でないでしょうか?
ごかくにんいただけると幸いです。
=>[作者]: 連絡ありがとう.教材の途中経過に一部余計な係数が付いていましたが,結果については間違いはありませんでした.A=1/6
■[個別の頁からの質問に対する回答][三角関数の導関数 について/17.7.2]
拝見していて疑問がありました。
最後の問題の中で、
y=1/(1-tanx)を求める時、
y=1/(1-u)とおいて、
dy/du=1/(1-u)^2とされてるところで、
dy/duは分子が-1ではないでしょうか。
y=1/(1-u)=(1-u)^-1なので。
=>[作者]: 連絡ありがとう.間違いはないのですが,誤解を招きやすい表現がありましたので(←おい!)詳しく説明しました.
■[個別の頁からの質問に対する回答][2次関数の最大値,最小値 について/17.7.1]
わかりやすく、とても参考になっています。
条件式が比例形になっている場合 の最初の解説の比例形で式が x/2=y/3=y/4 と不可能な式となっていました。y/4はz/4の間違えではないでしょうか。
=>[作者]: 連絡ありがとう.y→z書き換えました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.7.1]
一次不等式が苦手だったので分かって良かったです ありがとうございます
でも 例題をあと一問でもいいので載せてくれるともっと分かりやすいと思いました
=>[作者]: 連絡ありがとう.このサイトの読者層は,現役が3分の1,卒業生が3分の1,社会人が3分の1くらいの割合となっています.現役世代から見れば,1次不等式の解き方は中学校でも習っているので,くどくどと分かり切ったことを言われたくないと受け止めるでしょうし,30代以上の人も同じでしょう.1次不等式を中学校で習わず高校で2,3時間習ったというのは20代の方かもしれません.
■[個別の頁からの質問に対する回答][広義積分 について/17.6.29]
【数学】Ⅲ-10
=log 1-log12=0-(1-log2)=log2 ではなく、
=log 1-log12=0-(log1-log2)=log2 ですね。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][分母の有理化 について/17.6.29]
最近お世話になっています!
「分母の有利化」問題2の(5)について。
私が計算したところ答えが4+2√15となったのですが、こちらの答えは4+√15でした。
私の計算が間違えているのならかまいませんが、もしこちらの答えが間違いでしたら訂正お願いいたします。
=>[作者]: 連絡ありがとう.「分母の有利化」→「分母の有理化」
解説が付いていますので読んでください.たぶん,解説を読んでなお疑問をお持ちのようですので,約分についてのよくある思い込みをしておられるかもしれません.
この頁 を見てください.
■[個別の頁からの質問に対する回答][番号札のもらい方 について/17.6.28]
今日、初めてこのサイトを使いましたがとても気に入りました。
さくさくゲーム感覚で問題を解いていけるのはとても楽しいです。
希望としてはチャレンジ問題のような発展問題が最後に1問ほどあると良かったと思います。
=>[作者]: 連絡ありがとう.サブメニューの章末問題などをやってみるとよいでしょう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/17.6.28]
良いと思います。
=>[作者]: 連絡ありがとう.
■兵庫県[emmataroさん/17.6.28]
確認問題で簡単に定着を確認できたのでよかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/17.6.27]
問題3は正負の記号も解答させる問題形式が良いと思います。
=>[作者]: 連絡ありがとう.理屈の上ではそうですが,実際に次のような解答欄にすると明らかに違和感があり,数学で許される形式にはならないでしょう.
(x−2)(x2 +2x+4)=x3
※後ろから掛ける式を答える形になっています
■[個別の頁からの質問に対する回答][ベクトルの平行条件,垂直条件 について/17.6.27]
正解はいいものの、途中式は欲しいですね。
=>[作者]: 連絡ありがとう.ヒントというボタンを押したときに表示されるものを途中式というのではないのか?他にどんな途中式があるのか?
■[個別の頁からの質問に対する回答][判別式 について/17.6.26]
前略 いつも楽しく老化防止に問題演習をさせていただいています。ありがとうございます。
ブラウザの不具合かもしれませんが、最初の■問題1の[採点する][やり直す][次の問題]のうち、[採点する][やり直す]がずれて隠れてしまい、[次の問題]のタブを2回ずつ押して先に進みましたのでご報告します。草々(17.6.26)
=>[作者]: 連絡ありがとう.頁を更新したときにボタンが飛んでしまったようです.
■[個別の頁からの質問に対する回答][定積分 について/17.6.25]
問題(3)の(2)、(3)、(4)かいとうらんがありません。
=>[作者]: 連絡ありがとう.PC版の方でHELPと解答の境目がずれたようですので,訂正しました.
■[個別の頁からの質問に対する回答][順路 について/17.6.24]
順路の図が見やすくて解説も丁寧でわかりやすいです。助かっています。これからも学習の傾向に応じたよくわかる問題をたくさんお願いします(^^)
=>[作者]: 連絡ありがとう.連絡を受けたらその頁を読み直すようにいますが,「同じものがあるときの順列」と「組合せ」が等しいことについて,前の頁を読んでいない・覚えていない場合があると戸惑うかもしれないので,その解説を再掲しておきました.
■[個別の頁からの質問に対する回答][相加平均.相乗平均.調和平均 について/17.6.23]
a>bのときa>(a+b/2)などの普通に不等式の証明をする問題と、a>0のときa+(1/a)≧2などの相加・相乗平均を利用する問題の解き方の区別(どういう時に相加・相乗平均を使うのか)が分かりません。見分け方はありますか?
=>[作者]: 連絡ありがとう.
授業や教科書レベルの問題で練習している場合に,相加相乗の関係を利用できるのは「登場する文字が正(または0以上)」の場合です.正負の符号が分からない問題について相加相乗の関係を適用することはできません.
【例】
のとき
…(1)
しかし,「登場する文字が正(または0以上)」の場合でもすべて相加相乗の関係で解けるとは限りません.
【例】
のとき
…(2)
見かけだけでは「あれかこれか」の区別ができるとは限りませんが,普通の証明になる場合も相加相乗の関係を使う場合も,「大小比較は差の符号で判断する」(
大小比較の原則 )という一段上の原則にまとめることができます.大小比較の原則に戻って証明すると,次のようになります.
(1)←
(2)
※相加相乗の関係は,証明済みの結果から出発できるので早くできるというだけのことです.だから無理に見分ける必要はないとも言えます.
■[個別の頁からの質問に対する回答][2次関数の最大値,最小値 について/17.6.22]
問題5の(2)が、問題文では0≦x≦5となっているのに、解答では1≦x≦5になっています。
=>[作者]: 連絡ありがとう.問題文の入力ミスとして訂正しました.
■[個別の頁からの質問に対する回答][根号の計算 について/17.6.21]
中学校レベルの質問ですが、例えば2.5√5など√の前に小数がつくのは大丈夫ですか?よろしくお願いします。
=>[作者]: 連絡ありがとう.係数が小数になる根号はあまり見かけないようですが
の形で表される数について,
のいずれも「何でもあり」です.
係数が小数(分数)の場合の例:
根号内が小数の場合の例:
係数も根号の場合の例:
根号内が負の数の場合は,高校で習う虚数になります:
■[個別の頁からの質問に対する回答][階差数列 について/17.6.21]
わかりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.6.20]
特性方程式の重解になる場合の一般解の形と、xの関数を掛けたものものが解の一つになると言う点がどうしても理解できません。こうなる的に覚えて過ごしてきました。何か補足説明を頂けたら幸いです。
=>[作者]: 連絡ありがとう.そこに書いてあります.
■東京都[TKさん/17.6.19]
純循環小数と、混循環小数について、それぞれの数を分数に直した時に何か規則性はありますか?
=>[作者]: 連絡ありがとう.市販の公式集に出ていますが,次のようになるので規則性はあると言えるでしょう.
【純循環小数】小数第1位から循環節が始まり,循環節の長さがn桁であるとき
の場合
両辺に10000を掛けて頭出しをすると
(小数点以下が同じになって,引けば消えるところがミソ)
(約分できるときは約分してまとめる.以下同様)
一般に,循環節の長さがn桁の純循環小数
の場合
のように,分子がn桁の循環節になり,分母が9をn個並べた数字になります.
【混循環小数】小数第1位からm桁まで循環しない部分があって,その下に循環節の長さn桁の循環部分が続くとき(循環しない先頭部分には整数があってもかまわないがここでは整数部分のない例で示す)
の場合
両辺に10000000を掛けて頭出しをすると
両辺に1000を掛けて頭出しをすると
一般に,小数第1位からm桁まで循環しない部分
があって,その下に循環節の長さn桁の循環部分
が続くとき
の場合
になります.
※これらの計算自体は,無限等比級数の和について詳しく理解していなくても,「頭出しして引くだけでできる」ので,昭和30年代の田舎の公立中学校で普通に習った覚えがある.(教科書には載っていなかったかも)
■[個別の頁からの質問に対する回答][軌跡の方程式1 について/17.6.19]
半世紀ぶりの数学の学び直し、脳内の霧が晴れていくような気持がしています。本当に有難いサイトです。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率の基本 について/17.6.18]
基本の問題が網羅されており、非常にためになると思った。解説もわかりやすく、わからなかった問題も解けるようになった。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の方程式 について/17.6.18]
中心(-1、-1)半径2の解答欄に選択肢がありません。
=>[作者]: 連絡ありがとう.解説ボタンを押してよく読んでください.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/17.6.18]
問題1の(3)解答欄がありません。
=>[作者]: 連絡ありがとう.西暦2000年にはまだChromeはありませんでしたが,2017年現在ではそれなりのシェアになっています.そのChromeで見た場合,入力欄が他のブラウザと全然違う表示なるということはそこそこ知られていますが,教材の数が数千頁と多いため,苦情が来たものから順に訂正するするしか仕方ないようです.世の中にある多くのWeb頁でこういうことはあるかもしれません.
■[個別の頁からの質問に対する回答][導関数の定義 について/17.6.17]
計算過程全部見せてください
=>[作者]: 連絡ありがとう.要望の意味が通じません.計算というボタンをクリックすれば途中経過が表示されることに気づいていないのか,Androidでは計算が表示されないと言っているのか?また,その頁はPC用です・・・携帯用は別の頁です.
■[個別の頁からの質問に対する回答][行列式 について/17.6.16]
例の(3)の2回目の行列式の変形の時に最後の3を1番前に出してある行列式のところで1とあるのですが、-2が正しいと思います
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/17.6.15]
例5は(cos3x/12)-(3sinx/4)+Cでもあってますか?
=>[作者]: 連絡ありがとう.三倍角公式を逆に解いて,被積分関数を三角関数の1次式に直すのは「あり」です.ただ,結果は少し違うようです.
■[個別の頁からの質問に対する回答][二項定理,多項定理 について/17.6.15]
大変参考になりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数式の和・差 について/17.6.15]
いつも参考にさせて頂いてます。
よくある間違い1の間違い答案のところで分子の(x+3)と分母の(x+2)を約分しています。
=>[作者]: 連絡ありがとう.Web画面上で分数式を表示して,取り消し線に色を付けるという術に集中していたため,数学の話が飛んでいたようです.
■[個別の頁からの質問に対する回答][等比数列の和 について/17.6.14]
素晴らしい よく理解できた 練習問題のなんいとまをもう少しあげてもいいと思う
=>[作者]: 連絡ありがとう.さらに進んだものは
この頁 など
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/17.6.14]
最初に因数分解をすれば良いということが分かれた
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/17.6.14]
ありがとうございました。
小テスト前に利用させて頂きました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.6.13]
(6)について質問があります。何度やっても-1以外符号が反対になってしまうのですが、解き方が間違っているのでしょうか?
=>[作者]: 連絡ありがとう.この質問の仕方は間違っています.何度やっても・・ということよりも,どのようにやったのか,つまり自分の答案を書かないとどこが間違っているのかを回答するのは無理です.
【よくある間違い】a2 −(b−c)2 =a2 +(−b+c)2 と考えている人は,符号が全部逆になります.a2 −(b−c)2 =a2 −(b2 −2bc+c2 )=a2 −b2 +2bc−c2 a2 +(−b+c)2 =a2 +b2 −2bc+c2
各問題に解説がついているのでそれを読んでください.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.6.10]
青いカード3枚と赤いカード6枚を円形に並べる問題で、書いてある通りに9!/3!6!=84として、
その後9で割ろうとしても割り切れません。どうして10番の問題ではその解法を使えるのですか?
=>[作者]: 連絡ありがとう.円順列については,公式が成り立つ場合だけを説明するのが普通で,公式が成り立たない場合に踏み込んでいくと複雑過ぎて初心者が混乱してしまうことが多いので,触れずに置いておいて応用問題に回すようにしています.すなわち
「n個の異なるものを」「全部使って」できる円順列の総数は (n−1)!
という公式において,「同じものがある場合」「一部分だけを使う場合」は公式の前提を満たしていないので,簡単には求められません.戦国時代の混とん状態になり,積の法則・和の法則や樹形図・辞書式配列のような原始的な取り扱いに帰って1つずつ数えざるを得ません.
【例1】5個の異なるものから4個とってできる円順列の総数は?5 C4 =5(4−1)!=3!=6 通り.結局,30 通り(3−1)!=2!=2 通り.しかし,青玉は区別できないのだから,各々の円順列において青玉を交換した倍率(2倍)だけ数え過ぎているので,2で割ると1 通り.2 通り.4 C2 =6
さて,質問の本題に戻ると,教材の10番の問題では赤が1枚になっていて,これを固定すると残りのものは単に同じものがあるときの順列になるので解けるのです.これに対して,青玉3個,赤玉6個があって同じ色の球が区別できないとき,例えば頂上に位置に置く青玉を固定しようにもどの玉の話なのか決まりませんので,3個の青玉の配置を考えます.(1) 青玉3個が(3個連続で)互いに隣り合っている場合→1通り.赤玉は残りの場所に自動的に入る.(2) 青玉2個が互いに隣り合い,もう1つの青玉が左回りに数えて2個目,3個目,4個目,..,6個目にある場合→4通り.赤玉は残りの場所に自動的に入る.(3) どの青玉も隣り合わない場合→根性で数えていくことになります.
このように,同じものがあるときの円順列の総数はとても複雑になります.1個しかない玉があれば,それを固定すると単に同じものがあるときの順列になって,簡単になります.
※通常,教科書でもキラキラ輝く明るい道筋だけ(異なるものを全部使う円順列の総数)を扱っており,1つでも前提が外れると(同じものがある場合,一部分を使う場合,何回でも使える場合)暗闇の中でもがくような話になってしまうので,あまり触れていません.しかし,この前提を確認することは重要だということをどこかに書いておきます.
■岐阜[Vin Dieselさん/17.6.11]
選んでいくのがよかった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分の置換積分 について/17.6.11]
証明のF(g(t)+Cに注意するとのところとその上の式の ↑の)が足りない気がします
=>[作者]: 連絡ありがとう.かっこが抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式1 について/17.6.10]
例題1の解答で2点 AP 間の距離は AP=√(x+1)2+(y-3)2 とありましだか、それはどうしてですか??詳しくお願いします!!よろしくお願いします!
=>[作者]: 連絡ありがとう.回答の文章を考えるときに,いつも思うのは,この人は何歳ぐらいの人で,この分野の内容をどれくらいやった人なのだろうかが不明の場合に,どこまで答えるのかということです.もし,高校生になっていない人が,たまたま検索でヒットした頁に質問しているのなら,それなりに事前学習をしてもらわないと言えないこともあります.
その頁の右半分に書いてありますように,2点
間の距離は
です.
したがって,2点
間の距離は
です.
これが「なぜ?」ということでしたら,中学校3年の
この教材 を初めに読んでいただく必要があります.
■[個別の頁からの質問に対する回答][2次不等式 について/17.6.9]
ちょうどいい難易度と、分かりやすい解説でとても迅速に理解できました、ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分の置換積分 について/17.6.9]
いつも参考にさせて頂いております。証明に「(左辺)=F(b)−F(b)」とありますが、(左辺)=F(b)−F(a)」の誤植だと思います。参考になれば幸いです。読者Nより。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][絶対値付の不等式 について/17.6.8]
解説に別解があるといいと思います!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/17.6.8]
分数の場合のやり方ものせて欲しいです。
=>[作者]: 連絡ありがとう.当サイトは中学生から高齢者まで読者層が広いので,分数の場合という言葉が何を表しているのか絞り切れません.例えば,係数が分数になっている場合という意味でしたら,問題1の第4問,問題3の第3問にありますが,展開するだけですから取り扱いとしては同じです.中学生向けのように,分数の係数になると間違いやすいから,特別な頁を作って専用の解説を・・・ということは,高校の教材としては考えにくいです.また,例えば分数式の場合という意味でしたら,分数式の頁が別にありますのでそちらを見てください.
■[個別の頁からの質問に対する回答][共通部分と和集合 について/17.6.7]
解説がとても分かりやすく、よく理解できました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分の置換積分 について/17.6.6]
例4で∫dx/√(4-x^2)dx
と書かれているがdx多くね?
=>[作者]: 連絡ありがとう.dxが多かったので訂正しました.
■[個別の頁からの質問に対する回答][実数係数方程式の虚数解 について/17.6.6]
最後の解法の解説を探していたのですごく助かりました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/17.6.5]
やりやすかったです。参考にさせてもらいます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][底の変換公式 について/17.6.5]
とても解いていて楽しかったのですが、どうしてもわからない時に答えを確認したくても正解するまで答えがわからないシステムが少し時間がかかって大変です。
=>[作者]: 連絡ありがとう.前半については解答を付けました.
■[個別の頁からの質問に対する回答][分数不等式の解き方 について/17.6.4]
例えば,分子2 分母x-1 < x の場合はどうなりますか
=>[作者]: 連絡ありがとう.以下,質問が
であるものとして回答します.
(A)の場合分けして分母を払う方法では,次のような答案になります.
1)
x>1 のとき
2<x(x−1) x2 −x−2>0 (x−2)(x+1)>0 x<−1, x>2 x>1 の場合だから,x>2
2)
x<1 のとき(
x=1 のときという場合分けは不要であることに注意.分母が0になるから,成り立つはずがないから)
2>x(x−1) x2 −x−2≷0 (x−2)(x+1)<0 −1<x<2 x<1 の場合だから,−1<x<1
以上をまとめると,
−1<x<1, x>2 …(答)
(B)の通分だけで行う方法では,次のような答案になります.
両辺に
を掛けると
左図より,
−1<x<1, x>2 …(答)
(C)のグラフを描く方法では,次のような答案になります.
方程式に書き換えて交点のx座標を求めておく.
左図より,y=xの方が上にあるのは,
−1<x<1, x>2 …(答)
■[個別の頁からの質問に対する回答][1次不定方程式の整数解 について/17.6.4]
整数x, yの一般解を求めてください.というのは整数解全てを求めなさいという言い方もできるのでしょうか?
=>[作者]: 連絡ありがとう.世間一般の言い方として,それら2つはほとんど同じ意味につかわれていると考えてもよいのですが,この頁では「解が無限個あって書き並べることができない場合に,一般解を求めよ」と述べ,「解が有限個になって書き並べることができる場合に,すべて求めよ」と述べています.
■[個別の頁からの質問に対する回答][行列と連立方程式 について/17.6.2]
付録中の代入式の中で、かっこが斜めっているのは解せん。
=>[作者]: 連絡ありがとう.筆者はどちらでもよいと思いますが,とりあえず直立にしました.
■[個別の頁からの質問に対する回答][微分係数 について/17.6.2]
問題2 (4)式の最後の方で、2bh+h^2+h / h となりますがその次で、分子全体をhで括ったらだめなんでしょうか?
=>[作者]: 連絡ありがとう.それでよいです.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.6.2]
どちらか、もしくは両方に「-」がつく場合{(5)(4)など}どっちにつくかがもう分かってしまっているので解く側が、符号がどうなるのかを考えれるように工夫してほしいです。
=>[作者]: 連絡ありがとう.その頁は入門的なもので,そこそこ手がかりがあるようになっています.
この頁 の方がご要望の形にあっているかもしれません.
■[個別の頁からの質問に対する回答][零因子 について/17.6.1]
採点できませんでした。
=>[作者]: 連絡ありがとう.2000年ごろに当時全盛期だったIEでエラーが起こらないようにテストしたものですが,現存するブラウザ(Chromeも含む)では文法が合わなくなっているようですので,訂正しました.・・・このプログラム,変化の速い業界で10年以上持ちこたえたようなのでご容赦を.
■[個別の頁からの質問に対する回答][剰余の定理 について/17.5.30]
割る式が2次式と4次式で 問題に聞かれるのが3次式の余りという応用の解き方だけ知りたかったです。(3次式は因数分解できないもので、
割っている2次式と4次式とは何の因数も持たないパターン です。)
=>[作者]: 連絡ありがとう.想像力豊かで物事を深く考える方のようですが,詰めが甘いのが弱点かもしれません.すなわち,アンダーラインをひいた箇所が,問題文を無にしており,そんな問題はありえないのです.・・・仮にそのような問題を出題したとすると,余りが定まらないのです.
【簡単な例】x で割ると1 余り,x+1 で割ると割り切れる多項式を,x+2 で割ったときの余りを求めよ」という問題があったとすると,仮定として与えられているx, x+1 と求めるべきx+2 が独立(割っている式と何の因数も持たないパターン )になっているので,答は定まらず,どんな余りでもありえます.f(x)=x+1 とすると,x で割ると1 余り,x+1 で割ると割り切れる.この式をx+2 で割ったときの余りは−1 f(x)=(x+1)2 とすると,x で割ると1 余り,x+1 で割ると割り切れる.この式をx+2 で割ったときの余りは1 f(x)=(x+1)(2x+1) とすると,x で割ると1 余り,x+1 で割ると割り切れる.この式をx+2 で割ったときの余りは3
そもそも,条件で示される2つの式
x, x+1 と余りを求めたい式
x+2 に
何の因数も持たないパターン では,答は定まらないのです.だからそういう問題はないのです.
※3次式が有理係数では因数分解できないが,無理係数,複素係数で因数分解でき,それらの因数が各々与えられた2次式,4次式の因数となっている問題なら解けます.
※
この頁 とか
この頁 の問題をやる方がためになるでしょう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/17.5.30]
通信制高校で学んでいる76歳の男性(老人)です。
60年近く学問と遠ざかっていて数学Ⅱは難解ですが、解の公式の解説を見てよく理解でき又、
虚数単位の計算もあり、助かりました。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数関数 について/17.5.30]
分数関数の問題4は絶対値があって、どう場合分けしたらhelp通りのグラフになるか分かりません。宜しくお願いします。
=>[作者]: 連絡ありがとう.問題4の(2)は場合分けした答案がついているので,(1)の話として答えます.
のグラフはそこに書いてあるグラフになるので,そのうちの負の部分の符号を変えるということです.(実際には,
のとき負になるから符号が変わります.)
※xの値に応じて(木を見て)場合分けしようと考えているのは理解できますが,
(森)を一目見れば直ちに分かります.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/17.5.30]
問題2で分数の指数を伴った単項式の割り算が入るとき、割り算を先に掛け算に変換するという解法はないのでしょうか? ヒントでは係数ごとに指数法則で指数の加法法則でまとめるときにマイナスを掛けてから加法していますが、マイナスを掛けるというのもなぜそうするのか今一つ呑み込めません。
また、各単項式を2と3などの素数の積の形にした後に素数単位ごとに指数の加法法則が成り立つのも今ひとつよくわかりません。剰余算の記号が式に入っているからそう思ってしまうのかもしれませんが、剰余記号を省略して長い一つの単項式と理解すればよいのでしょうか?
=>[作者]: 連絡ありがとう.質問が長いので区切って答えましょう.
(1)「割り算を先に掛け算に変換するという解法はないのでしょうか?」⇒一番初めの解説にありますように,
ですので,これは
と同じことです.つまり,割り算を掛け算に変換しています.
(2) 「マイナスを掛けるというのもなぜそうするのか今一つ」⇒負の指数の定義
この頁 や
この頁 の内容を先に読んでください.
(3) 「剰余算の記号が式に入っているから」⇒割り算の余りは使っていないので,この文章はおかしい.
(4) 「長い一つの単項式と理解すれば」⇒当然そうなっています.
(5) 「各単項式を2と3などの素数の積の形にした後に素数単位ごとに指数の加法法則が成り立つのも今ひとつよくわかりません」⇒たとえば,
のような場合,6と2に分けて(3まで分解せずに)済ませることもできますが,ほとんどの問題は素因数分解で行うのが最短・最良の解き方ですから,慣れるまで練習した方がよいでしょう.
※質問者がどういう現状で,何を尋ねているのか分かりにくいですが,推定で言えば「マイナスの指数がよく分からないから,使いたくない.逃げたい」という心理があると推定すれば,これらすべての質問がなぜ出てくるのかを説明できるようです.「マイナスの指数から逃げることはできません」ので上記2つの頁の「負の指数の定義」を読むことから始めてください.
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間 について/17.5.30]
標本サイズN=300、ある意見が40%、信頼度95%、という条件で信頼区間を求めるとしたら、どれに当てはまりますか?
=>[作者]: 連絡ありがとう.ある意見が40%とは何を表しているのか,何の分布についての母平均の信頼区間を求めようとしているのか,どれに当てはまりますかというためには選択肢を示さないと議論が成り立たない,標準偏差が不明のままで?・・・もっと質問内容を正確に表現してみる必要があります.そうすれば,尋ねるまでもなく自分で解けることがあります.
■[個別の頁からの質問に対する回答][期待値 について/17.5.29]
期待値の問題(3)についてhelpの赤1、白1はなぜ6/10なのでしょうか。
=>[作者]: 連絡ありがとう.計算の根拠はhelpに示した通りですが,6/10をなぜ3/5にしないのかという質問でしたら,約分してから通分するのなら何も触らない方が間違いが少ないからです.
■[個別の頁からの質問に対する回答][複素数平面の入試問題3 について/17.5.29]
丁寧な作り、びっくりします。
=>[作者]: 連絡ありがとう.連絡をもらうとその頁を見るようにしていますが,ブラウザ(IEなど)によっては空欄の枠が表示されない場合があるようですので,ついでに訂正しておきました.
■[個別の頁からの質問に対する回答][展開公式1 について/17.5.29]
とてもわかりやすく、4択で問題数も少ないので気軽にとりくむことができました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■?[?さん/17.5.28]
方べきの定理などの問題はありますか?
見つけられなくって…
=>[作者]: 連絡ありがとう.数学Aでは,3つの内容「場合の数と確率」「整数の性質」「平面幾何」のうち2つ(2単位)を学校が選んで学ぶことが多く,平面幾何を選ぶ学校は少ないと考えられますので,当サイトでも扱っていません.
■[個別の頁からの質問に対する回答][連立不等式 について/17.5.28]
とても理解しやすいです。ひとつだけもうすこし解説を加えていただけると助かります。上の例題の−1<2x+1<x+4ですが -1<x+4を連立不等式の片方にするのはなぜいけないのか、の解説を加えていただけないでしょうか。
=>[作者]: 連絡ありがとう.いけない訳ではないが,無駄になるということですが,言い始めるとコテコテしそうな感じです.
A<B<C ←→
A<B…(1)A<C…(3)
(3)は間違いではないので,書いてもかまわない.ただ(1)(2)から(3)が作れるから,無駄になっています.
そうではなくて,(1)(3)だけにすると
B≧C の場合も許すことになり,(2)(3)だけにすると
A≧B の場合も許すことになるので,元の問題と同じではない.
高校生でこのことが分からない人に,上記のように説明をしても,分かるようにはならないでしょう.
■[個別の頁からの質問に対する回答][絶対値 について/17.5.27]
《問題》
(5) 次の方程式をきなさい
イ)は
2(x-1)-2x=6
と書いてありますが、
本当は
-2(x-1)-2x=6
ではないでしょうか。
=>[作者]: 連絡ありがとう.まず初めに|1−x| は|x−1| に等しいです.だから,イ)の場合,2|1−x|−2x=6 を2|x−1|−2x=6 と考えて絶対値をはずすと,左側の答案のように,2(x−1)−2x=6 2|1−x|−2x=6 の絶対値をそのままはずせば,−2(1−x)−2x=6
■[個別の頁からの質問に対する回答][根号の計算 について/17.5.27]
windows10で完璧です。
ありがとうございます。
=>[作者]: 連絡ありがとう.Windows10でIEなら正常に読めるという連絡だと理解しました.
■[個別の頁からの質問に対する回答][組合せ について/17.5.26]
果物の図がかなりわかりやすい。
このサイト見たからks分からないがいつもより数学の点数高かった
=>[作者]: 連絡ありがとう.連絡をもらったらその頁を見るようにしていますが,ふと見ると,プログラムミスで正解した後に次の選択ができなくなっていましたので訂正しました.
■[個別の頁からの質問に対する回答][絶対値 について/17.5.25]
間違えたときに答えを表示するようにしてほしいです。
なぜか、ここは答えが出ないので少し使いにくいです。
=>[作者]: 連絡ありがとう.教材を作ったときは「ここまでお膳立てしてある場合に,答えが必要な生徒がいるとは思わなかった」というのが本音です.しかし,今考えてみるとWeb教材では,読者は中学生から老人まで,海外在住で日本語の教科書が入手できない人まで幅広いので,確認のために解答が必要な場合もあるようですので,そのうち解答を付けます.(付けました)
■[個別の頁からの質問に対する回答][定積分の基本 について/17.5.25]
図3の下の紫色の囲みの式について、
F(b-a) という風に代入すると楽になると学校で教わったのですが、そうするとF(b)-F(a) で計算するときと答えが合わなくなります。
F(b-a)は間違いですか?
=>[作者]: 連絡ありがとう.一般に「F(b-a) という風に代入すると楽になると学校で教わった」ことはないでしょう.ノートの写し間違いでしょう.f(x) が定数になっているような特別な場合,すなわちf(x)=k → F(x)=kx → F(b)−F(a)=kb−ka=F(b−a) となるような場合だけです.
■[個別の頁からの質問に対する回答][ベクトルの和 について/17.5.25]
第3問の問題ですが答えは、横軸X,縦軸Yとするならば座標(X,Y)にとして
始点座標(0,2)終点座標(2,2)ではないのでしょうか?
始点座標(2,0)終点座標(4,0)の回答絵を押すと正解のようですが、もしそうだとするなら どのように理解すればよいのか教えてください。
=>[作者]: 連絡ありがとう.ベクトルは「大きさ」と「向き」をもつ量として定義され,「大きさ」と「向き」さえ等しければベクトルとして等しいといいます.
このことから注意すべきこととして,ベクトルにとっては「どこに書いてあるか」「始点がどこにあるか」はどうでもよいということになります.
ご質問の(1) 始点座標(0,2)終点座標(2,2)というベクトルは「x軸の正の向き」に「大きさ2」です.
ご質問の(2) 始点座標(2,0)終点座標(4,0)というベクトルは「x軸の正の向き」に「大きさ2」です.
これら2つのベクトルは「大きさ」と「向き」が等しいので全く同じベクトルです.左の図において
,
※問題の趣旨としては,回答者がまず(1)の形でベクトルを作図するはずなので,それと「大きさ」と「向き」が等しいもの(2)が見つけられるか?という設定になっています.
※ベクトルに関する一連の教材の中で,ベクトルは「大きさ」と「向き」をもつ量として定義される,すなわち「どこに書いてあるか」「始点がどこにあるか」はどうでもよいという辺りの練習問題が足りませんでしたので,そのうち追加します.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.5.25]
問題がとても良い
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分の基本 について/17.5.24]
いつも使わせて頂いてます。ありがとうございます。
問題(4)でdxが重複しています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/17.5.23]
分かり易いI解説で助かっています。ありがとうございます。「πと並んで有名な無理数」の「π」ですが、GoogleChromeで見ると「n」に見えてしまいます。よく見ると「π」なのですが、一見すると[n」に見えます。ご報告まで。
=>[作者]: 連絡ありがとう.確かにGoogle Chromeで見るとゴシック体で表示されるようですので変更しました.
■[個別の頁からの質問に対する回答][展開公式1 について/17.5.23]
気にいった所 : 解説がわかりやすく表示してある。
わかりにくい問題 : なし
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の計算(まとめ) について/17.5.23]
感で解けます(ヒラキ)
=>[作者]: 連絡ありがとう.勘ぐるの勘の方がこの文脈で使う漢字としてはいい感じです.ヒラキとは?人名?
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.5.22]
たーのしー!ティーカップのイラストいいっすね!流石俺でもに数学の課題にまで緑マーカー引いてもう一回とかは流石に気が引けるのでこういうの増えるといいなぁと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/17.5.22]
括弧があると、括弧が必要なのか、答えを区切るだけなのか、それがわかりません。
括弧が必要ではない式は、四角や、括弧でも種類を変えた方がいいと思います
=>[作者]: 連絡ありがとう.かっこは必要です.幾つかの教科書を引用して例を示してみましょう.
東京図書.数学Ⅰ:4x2 +xy2 −2x+y+5 をx について整理すると4x2 +(y2 −2)x+( y+5) x2 +3xy+4y+2x−5 をx について降べきの順に整理するとx2 +(3y+2)x+( 4y−5)
上記の答案において,どのかっこも省略できず,書かなければ不正解です.定数項の
( ) だけは省略しても正解の許容範囲となる場合がありますが,不正解とする先生もいます.
かっこは一重のとき ( ),二重のとき { (...) },三重のとき [ { (...) } ] のように入れ子にする順序が決まっているので,自分流に変えてはいけません.
■[個別の頁からの質問に対する回答][不等式と領域 について/17.5.21]
まあよかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][商,分数関数の微分 について/17.5.21]
下の方でいいので、答えを載せて欲しいです
=>[作者]: 連絡ありがとう.一題でも間違ったら解説と答が出るようになっているのですが,この要望が来たということは全問正解で終わってしまった人だと考えられます.とはいえ,正解であっても答案を確かめたい人はあり得ますので,正解の場合でも解説が出る設定にしました.
■[個別の頁からの質問に対する回答][n進数の演算 について/17.5.21]
例3の解説(3)のところ2進数になってます。流れを汲めば躓くことはないですが一応
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][絶対値付の不等式 について/17.5.20]
ありがとうございます!!!ようやく理解出来ました♪
もう少し(B)に似た問題が欲しいかなと思いました。
=>[作者]: 連絡ありがとう.絶対値のはずし方については
この頁 ,
この頁 ,
この頁 を見てください.
■[個別の頁からの質問に対する回答][Σ記号の変形 について/17.5.19]
(5)と(6)がわかりません。
どうやってとけばいいんですか。
=>[作者]: 連絡ありがとう.画面にHELPがありますが,それを見ても分からないのですか.本当に見ていますか?an =3n−1 ならばak =3k−1 です.an =n(n+1) ならばak =k(k+1) です.k に変える」ということが分かっていないのではないでしょうか.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/17.5.18]
a,bの文字が大きくて見づらいです
=>[作者]: 連絡ありがとう.その頁は毎週3000人以上の人が見る人気の頁で,悪い評価は少ないです.文字が小さくて見づらいという意見は他の頁では時々ありますが,文字が大きくて見づらいとは?・・・作業時間に余裕ができたら考えます.
■[個別の頁からの質問に対する回答][補集合 について/17.5.18]
例題が最高すぎる
=>[作者]: 連絡ありがとう.急には意味が分かりませんでしたが,ゆっくり考えて褒めてもらっていると解釈しました.
■[個別の頁からの質問に対する回答][部分分数分解 について/17.5.18]
部分分数分解の問題コーナー(分子に(3k+2)がある問題)で解答に原式が1次/3次だから2次/3次の差にすると書いてありますが、計算過程を見ると1次/2次の差になっていると思います。1次上げるために分母を1次下げ、差にしたと解釈してよいのでしょうか。
=>[作者]: 連絡ありがとう.ご指摘の通りでしたので訂正しました.
■[個別の頁からの質問に対する回答][行列式の性質とクラメールの公式 について/17.5.18]
クラメールの公式の問題1で下の式が間違っている
3x+5=7ではなく、3x+5y=7では?
=>[作者]: 連絡ありがとう.問題文でyが抜けているということで,訂正しました.
■[個別の頁からの質問に対する回答][最大公約数,最小公倍数 について/17.5.17]
特に問題ないと思います、でも今の教科書にあまりあっていない気がします
=>[作者]: 連絡ありがとう.最大公約数,最小公倍数については,小学校で1回習って,中学校ではもう習わず,高校1年生前半ではまだ習っていないはずなので,「今の教科書にあまりあっていない」というのは正常な感覚だと思います.・・・教科書ではこの項目は冷遇されているようです.
■[個別の頁からの質問に対する回答][連立不等式 について/17.5.17]
貢の数が全然増えないのはなぜでしょうか?なので進み具合を報告できません
=>[作者]: 連絡ありがとう.iPadでは(記録方式が違うためか)記録されないという報告が以前からあります.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/17.5.17]
大学生ですが、高校の内容で分からないところがあったときに見ています。ネットの情報なのでスマホさえあればいつでも解説と例題を見ることができ重宝しています。更に大学範囲や例題が増えるととても嬉しいです。これからもよろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/17.5.17]
分かりやすいと思います
非常にためになります。
=>[作者]: 連絡ありがとう.複素数平面の単元は,教育課程の改訂の度に出たり入ったりで,現役大学生でも習っていない場合があるかもしれません.採用試験の担当者が,教育課程についてどこまで正確に調べているのか分かりませんが,「分からない者は採用しない」とすべて受験者責任にしてしまうと楽だろうな,さもなければ新人教育の経費をどうするのかな,などと他人ごとながら現場の対応が気になる今日この頃です.
■[個別の頁からの質問に対する回答][内分点・外分点の座標 について/17.5.16]
いい頭の運動になりましたありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][樹形図、辞書式配列 について/17.5.16]
見やすい!
わかりやすい!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][隣り合う並び方・隣り合わない並び方 について/17.5.16]
答えが分かりにくい
=>[作者]: 連絡ありがとう.学校で対面授業を行っているときは,やり取りが繋がっていくので「答まで言わすなよ」「自分で考える余地を残しておくように」とよく言う.しかし,Web教材では,分からなくなったら投げて終了という場合もあるかもしれません.現役の生徒が問題練習として解いている場合を除けば,答えを聞いてもなぜそれが答なのか分からないという場合もあってもおかしくない・・・解説が出るようにしました.
■[個別の頁からの質問に対する回答][2進数の演算 について/17.5.15]
何を言っているか全然わかりませんでした
=>[作者]: 連絡ありがとう.分からないことを分かるようにするにはどうすればよいか,という前向きの姿勢で臨むことが大切です.「分からないことが書いてありましたので数学を投げました」でよいのでしたらそれまでです.
前向きに言えば,二進数の「演算」以前の,中学校で習う
二進数 の「表記」からやり直すと解決するかもしれません.
このまま放置すると,さらにもっと破滅的な議論「そもそも能力的に問題が・・・」という風な話も出てきそうな文脈になっています.
■[個別の頁からの質問に対する回答][一般角の定義 について/17.5.14]
いつも数学で分からないところが分かりやすく書かれていてとても助かっています。これからもよろしくお願いします(_ _)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.5.14]
説明がとても見やすかったです。質問はここに書いてもいいのでしょうか?
=>[作者]: 連絡ありがとう.質問はその欄に書いてもらうといいです.
■[個別の頁からの質問に対する回答][重複組合せ について/17.5.14]
お世話になっています。
上において質問と回答のところに
>問題を選択した時に、背景色が濃く、明暗比が悪いために見づらい
の意見があったので私も確認してみました。私にも十分見えますが、選択した場合に背景色が白から青になるのでコントラストの関係で見えにくくなるということではないかと思います。
他の端末や色弱の人にどう見えるかについてはわかりません。
※なんとなく気になったので意見を送信させていただきました。回答は不要です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ド・モルガンの法則 について/17.5.14]
問題とは関係ないのですが、
スマホで縦スクロールだけで見れるようにしていただけるとうれしいです
=>[作者]: 連絡ありがとう.その頁の先頭に「→ 携帯版は別頁」というリンクがあり,それをたどれば携帯版に行くようになっていますが,その表示が分かりにくいということでしょうか?もう少しその表示を大きくする?
■[個別の頁からの質問に対する回答][不等式と領域 について/17.5.11]
わかりやすい説明、とても助かりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3点が同一直線上にあるための条件 について/17.5.10]
解答ページを作って欲しい
=>[作者]: 連絡ありがとう.なるほど解答が分からない場合がありますので,解答を付けます.ただしその頁内に付けます.
■[個別の頁からの質問に対する回答][複素数の対称式,値の代入 について/17.5.10]
間違いの指摘です
白い四角の二つ目のところで割り算の説明をしていますが
「この変形は,次の割り算の結果を「割り算の原理」:A÷:B=Q...R ⇔ A=BR+Rによって,掛け算と足し算で書き直したものです.」のところで
A=BR+RではなくA=BQ+Rの間違いだと思います
=>[作者]: 連絡ありがとう.入力ミスでしたので訂正しました.
■[個別の頁からの質問に対する回答][平方完成(基本) について/17.5.10]
問題5(1)の判定が間違っています。
=>[作者]: 連絡ありがとう.この教材は昨日書き換えたばかりで,さっそく見てくれた人がいたとは感謝です.
■[個別の頁からの質問に対する回答][複素数の計算 について/17.5.10]
「√{2×(-1)}=√2√-1」と「次の変形規則が自由に使えるのは,a>0, b>0の場合であり,それ以外の場合は必ずしも成り立つとは限りません√a√b=√ab」が少し気になりました
自由に使ってないのかもわかりませんが、a,bの少なくとも一方が正であれば良いような気がします
「√{2×(-1)}=√2√-1」が成り立つ根拠となるものはどこを見たら良いでしょうか
分数の方を計算してみると分母が鬼門なので、少なくともb>0であれば掛け算も分数も良さそうです
=>[作者]: 連絡ありがとう.注意深く読んでもらっているということがよくわかります.
ご質問の場合については,その通り少なくとも一方が正なら成り立ちます.東京図書の教科書には,
(1) a>0, b>0 (2) a>0, b<0 (3) a<0, b>0 (4) a<0, b<0 の各場合について
(A)
(B)
のどれが成り立つか一覧表を作りなさい.という問題が出ています.その問題は深く考えさせる良問だと思う.
私の教材で「次の変形規則が自由に使えるのは,a>0, b>0の場合であり,それ以外の場合は必ずしも成り立つとは限りません.」とは,成り立つ場合と成り立たない場合があるということです.いわゆる部分否定です.とりあえずにっこり笑って「安全に変形できる」のは,「両方とも正の場合」ということで,それ以外は正誤様々です.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.5.9]
1階微分方程式の場合、例えばy'-y=xのようなものは解が1つしかないので重解と考え、y=e^px(C1+C2x)と考えるのですか。
=>[作者]: 連絡ありがとう.その頁は2階微分方程式の頁です.1階微分方程式と2階微分方程式とでは解き方が違いますので,
1階微分方程式の頁 を見てください.その頁の【例題1】にほぼ同じ(係数が2になっているだけ)問題がありますので見てください.なお,あなたの問題の解は
y=−x−1+Cex になります.(1階微分方程式の一般解の任意定数は1つです).
その教材は,分類の都合で高校数学の応用のような箇所に置いてありますが,もしあなたが高校生なら1階線形微分方程式も2階微分方程式も範囲外です.
■[個別の頁からの質問に対する回答][対数の計算 について/17.5.9]
途中でlog/logやlog×logは当てはまらないと出て来ますがその場合の計算方法も載せて欲しい。
=>[作者]: 連絡ありがとう.そこに書いていますように「この式の変形は、後で出てくる底の変換が考えられる程度」です.すなわち,
…(1)や
…(2)の形になっていたら,それを変形する公式はないということです.
ただし,そこに書いていますように「
底の変換の頁 」を見てもらうと(2)は
に変形することはできます.・・・この質問は少々ずれています.「後に出てくる底の変換が考えられる」と書いてあるのだから,後に出てくる底の変換の頁を見るのが普通です.
もう1点,どんな式でも変形できる公式があるに違いないと思い込んでいませんか?上記の(1)のような式は,もっと複雑にすることはできますが,これ以上簡単にする公式はありません.ないからないと書いているのです.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/17.5.9]
ベクトルの内積の定義が誤っています。
――>a=(x1 , y1 , z1 , … ) , ――>b=(x2 , y2 , z2 , … ) のとき,
誤: ――>a· ――>b=x1x2+y1y2+x3y3+…
正: ――>a· ――>b=x1x2+y1y2+z1z2+…
=>[作者]: 連絡ありがとう.訂正しました.添え字が重なりがちなので,ついでに直しておきました.
■[個別の頁からの質問に対する回答][関数の極限 について/17.5.9]
不定形の極限のところが分かりやすくとても良いと思う
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/17.5.8]
定数係数の2階非同次微分方程式について、y"+y=tanx のときは特殊解の候補をどのように置けばいいのでしょうか?
=>[作者]: 連絡ありがとう.右辺がtan xの場合は,この頁で想定している初歩的な解き方の範囲外です.すなわち,特殊解を求める簡単な方法がありませんので,そのアプローチでは無理でしょう.
解くためには,一般解を求めてから「定数変化法」を試みることになるでしょう.
同次方程式の一般解は
なので,定数変化法により,非同次方程式の解を
とおいて微分方程式に代入して,関数
の満たすべき微分方程式に直してこれを解きます.ただし,そのままでは余りに無限定で解けませんので
…(1)
という条件を勝手に追加します.このようにすると,(1)がうまく働いて,
の関数と第2次導関数を含まない
だけの連立方程式になります.
…(2)
(1)(2)より
…(3)
…(4)
などとなって,理屈の上では解けますが,(3)(4)の計算も結構大変です.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/17.5.8]
解けなどという文面ではなく、求めてくださいと書いてあるので嬉しい。本当に嬉しい。
=>[作者]: 連絡ありがとう.自分の担当している生徒や受験生に対しては,教えるものと学ぶものという上限関係がはっきりしているので,伝統的な数学本のスタイルで「解け」といってもおかしくないのですが,Web上の一時的な関わりではそれほど明確な上下関係はないので,敬語もありかなという感じです.ただし,教材作成に18年近くかかっていますので昔風に「解け」という文章も残っています.
■[個別の頁からの質問に対する回答][連立不等式 について/17.5.7]
すごくわかりやすく、為になりました。
ありがとうございます!(v^-゜)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/17.5.4]
(2直線の垂直条件)の式(C)において
m1*m1 = -1
になっています。
正しくは
m1*m2 = -1
だと思います。
修正を検討してくださるとうれしいです。
ありがとうございます。
=>[作者]: 連絡ありがとう.タイプミスですので訂正しました.
■[個別の頁からの質問に対する回答][重複組合せ について/17.5.4]
文系の自分でも良く理解できます
解説がとても分かり易いです。
ただ、重複順列 重複組み合わせの公式で、何故マイナス1なのか、文章からは、理解できません
理由を教えて頂ければうれしいです
=>[作者]: 連絡ありがとう.質問・要望は重複順列の頁からですが,内容が重複組合せの頁に関してですので,重複組合せに関する質問として回答します.マイナス1になる理由は,先頭の例で絵を使って述べているように,植木算の考え方でn個のものを区別するにはn-1本の仕切り棒がいるからです.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/17.5.3]
問題2 平家の人でなければ~ならないは読みようによっては平家の人だけが良い待遇を受けるとも読めます。
論理的には裏でおかしいとは思いますが、日本語としてはそう読めてしまう気がしました。
答えがあったので一応納得はしています。
=>[作者]: 連絡ありがとう.「平家でなければよい待遇を受けられない」ということを表にすると
よい待遇 悪い待遇
平家 ○(A) ○(B)
平家でない ×(C) ○(D)
「日本語としてそう読めてしまう」のは,数学の論理としてはまずいです.上の表において「平家でなければよい待遇を受けられない」が禁止しているのは,「平家でないもので,かつ,待遇のよいもの」がいることだけです.したがって,裏:「平家ならば待遇がよい」とは言えません.「平家でなければよい待遇を受けられない」という場合,(B)のように平家の中で(主流派でないまたは下級の武士などで)待遇が悪い者がいる可能性があります.
「平家でないもので,かつ,待遇のよいもの」はいないと言っているだけなので,日本語的に裏を認めてしまうと数学論理になりません.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/17.5.3]
命題という規則があっての論理になる。規則がなければ真も偽も考えようがない。ここがミソなのかなと感じました。
バカバカしいことですが、さきほどベン図を使っているて[集合のまたは]の感覚とは全く別物なのだなと思いました。
確認したいことだけここだけでいいのですが、Cパターンの場合、4月1日=7月1日が日曜日であるならば、7月1日は日曜日というところでいいのでしょうか。
運転手じゃないけど免許あるからは離れてますが。
=>[作者]: 連絡ありがとう.質問の意味が分かりにくいですが,「4月1日が日曜日ならば7月1日は日曜日」「4月1日が日曜日でなければ7月1日は日曜日でない」.だからCパターンは起こりません.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式 について/17.5.3]
三次の時も同様とあるのですが二次の時と同じでいいということですか
=>[作者]: 連絡ありがとう.もちろん3階微分方程式ということではなく,「右辺が」3次のときも同様にできるという意味です.(「同様に」とは,3次の式で試すということで,2次の式と「同じ」ではない)
■[個別の頁からの質問に対する回答][pならばqの真偽 について/17.5.2]
PならばQのベン図がよかった。
Pかつ─Qの図を命題のまま引用してしまっていたので。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/17.4.30]
問1 キ及びコは、2だと思います。(1で○になる理由が解りません)
=>[作者]: 連絡ありがとう.プログラムの点検ミスがありましたので訂正しました.(同じ問題でPC用は正常で携帯用だけ違っていたようです)
■[個別の頁からの質問に対する回答][和の記号Σ について/17.4.30]
とてもわかりやすい解説で、いつも楽しく勉強させていただいてます✨
上から4番目の(K-1)²は(K-2)²ではないですか?
=>[作者]: 連絡ありがとう.その頁は何度でもやり直せるように,読み出すたびに問題順が入れ替わるようになっています.だから,あなたに上から4番目に見えている問題は,他の人には上から4番目ではなく,あなたが再度見たときにも上から4番目にはならないはずです.だから,上から4番目という言葉では,どの問題なのか指定できていません.
参考までに
です.この問題に弱い人はΣ(式)の(式)の形に左右され過ぎており,その(式)に初項と末項を代入する作業を行っていない可能性があります.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式 について/17.4.29]
公式一覧表的なものを作って欲しいです。
=>[作者]: 連絡ありがとう.演習用だけでなく,調べ事や確認用として使うことがあるように思いますので,鋭意努力する予定です.
■[個別の頁からの質問に対する回答][定積分 について/17.4.29]
いつも楽しく拝見しています。
間違いと思われる箇所を見ましたのでご連絡させて頂きます。
当該箇所は、PCでfirefoxより見ていたところ、定積分のページで、
”○多項式の積や累乗の定積分”の要点Ⅲの証明について、最後の式の-符号が抜けています。
下記該当箇所のコピペです。
(III)は,(II)の結果を用いて次のように証明できる.
β∫α(ax2+bx+c)dx=aβ∫α(x-α)(x-β)dx
=aβ∫α(x-α)(x-α+α-β)dx
=aβ∫α{(x-α)2+(α-β)(x-α)dx
=┌│└ a
(x-α)3
3+a(α-β)
(x-α)2
2 β┐│┘α
=a
(β-α)3
3+a(α-β)
(β-α)2
2-0=a
(β-α)3
3-a
(β-α)3
2
=
a(β-α)3
6
=>[作者]: 連絡ありがとう.符号が1つ抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][余弦定理 について/17.4.27]
レイアウトが段組みなのか、図が隣にあるだけなのか、わかりづらいときがある。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.4.26]
大学の授業でわからなかった内容がとてもわかりやすく書かれていたので、とても助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件--不等式の問題 について/17.4.25]
問題1を正解した後、問題2の「必要でも十分でもない」を選ぶと問題1の画像が間違いに変わります。
HELPを見るかぎり間違ってなさそうですが…
=>[作者]: 連絡ありがとう.プログラムのミスで,確かに問題1を正解した後に問題2で「必要でも十分でもない」を選んだ場合に誤作動するようですので,訂正しました.(指摘の仕方が的確なので直ちに直せました)
■[個別の頁からの質問に対する回答][1次不定方程式の整数解 について/17.4.25]
問題5の解説について
10行目が間違っているように思います。y=71m+9 では?
解答には直接影響しないとは思いますが。
=>[作者]: 連絡ありがとう.確かに怪しい計算になっていましたので,訂正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式3 (媒介変数表示) について/17.4.24]
こんにちは!
とてもわかりやすい解説ありがとうございます!!
線分の中点の軌跡がわからないので教えていただきたいです!!
点Qが直線y=x+2上を動く時、点A(1.5)と点Qを結ぶ線分AQの中点Pの軌跡を求めよ。
という問題です!!AQの中点はPだというところまでの証明(?)は出来たのですが、その後のPは条件を満たすというところまでは解けずに困っています…
よろしくお願いします!
=>[作者]: 連絡ありがとう.その前の頁
軌跡の方程式(動点2個) を見てください.答を教えるよりも自分で解けるようになる方がよいでしょう.
■[個別の頁からの質問に対する回答][補集合 について/17.4.23]
とっても参考になりました。
これからもこのように問題形式になっているととても良いかと思います。後、もう少し問題を増やしたらいいと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/17.4.23]
x4乗-16の答えがわかりません。
教えてください!
=>[作者]: 連絡ありがとう.まず,x4 −16 の答という言い方はおかしいです.x4 −16 の因数分解というべきです.x4 −16=(x2 −4)(x2 +4)=(x−2)(x+2)(x2 +4) x2 +4 の部分をこれ以上因数分解すると虚数係数となるので,通常(実係数,さらに有理係数を前提とする)はこれ以上因数分解しない.
■[個別の頁からの質問に対する回答][数列の漸化式と極限 について/17.4.23]
問題1.2(1)解説下から5行目(D)-(C)は(C)-(D)と思われる
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][二項定理,多項定理 について/17.4.23]
全然わからない。
=>[作者]: 連絡ありがとう.できれば助けてやりたいと考えていても,どこがどう分からないのかを述べないと,助けようがありません.
■[個別の頁からの質問に対する回答][空間における平面の方程式 について/17.4.22]
非常にためになった。僕が持っている教科書や参考書クリアー数学には2問しか載っていない、しかもこのサイトにあるような定理、法則が詳しく載ったページはどこにもない。解答を見ても、数式が羅列しているだけです。どうしても具体的な解法が知りたかったのでこの解説文は非常に役立ちました。ある本を読むと京都大学の理系クラスで3変数の1次方程式が3次元空間の平面を表すことを知っていた学生が皆無だったそうです。正直に言ってかなり危ない事じゃないかと思いました。僕もこの本を読むまで全く素通りしていたのです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/17.4.22]
よくわからない
=>[作者]: 連絡ありがとう.できれば助けてやりたいと考えていても,どこがどう分からないのかを述べないと,助けようがありません.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.4.22]
ぜんぜんわかんない
=>[作者]: 連絡ありがとう.できれば助けてやりたいと考えていても,どこがどう分からないのかを述べないと,助けようがありません.
■[個別の頁からの質問に対する回答][相加平均.相乗平均.調和平均 について/17.4.21]
下記の欄の数式に誤りがあると考えます。
”■相加平均.相乗平均.調和平均 ”
↓
”【相加平均≧相乗平均の関係】(3文字以上の場合)”
↓
”(C)”
↓
”対数関数は上に凸だから”の2行目左辺に”log(...)”が無いと考えます。
PS,資料がとても分かりやすく感謝しています。
=>[作者]: 連絡ありがとう.ご指摘の通り,抜けていましたので訂正しました.(読んでくれている人がいるようなので,凸関数の重心について補足説明も追加する予定)
■[個別の頁からの質問に対する回答][数学的帰納法とは について/17.4.19]
数学的帰納法による証明の例2で⑴でn=4が成り立つことを証明したのに⑵でn=k(k≧4)と4を含む仮定をしたのでしょうか?
=>[作者]: 連絡ありがとう.注意深く読んでおられるのは伝わってきますが,数学的帰納法の原理について完全には理解してもらえなかったようです.
2段階の証明:(Ⅰ)n=4のとき・・・ (Ⅱ)n≧4のとき・・・
の記述において,(Ⅱ)が(Ⅰ)の範囲を含んでいなければ,将棋倒しの論理が働かないのです.
(Ⅰ)n=4のとき・・・ (Ⅱ)n≧5のとき・・・となっていれば,(Ⅰ)によりn=4のとき成立することはいえますが,(Ⅱ)でn≧5のとき・・・の証明にしてしまうと,n=5のとき成り立つことは示されず仮定されただけになります.だからn=5,6,7,...のときはすべて砂上の楼閣になります.
実は,例1でも(Ⅱ)はn≧1のときですが,すべての自然数について述べているのだから,n≧1は当然のことだから省略されています.
【この頁】 の例題はすべて(Ⅱ)の段階で上記の点に注意して書かなければなりません.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.4.19]
ありがとうございます!参考になりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/17.4.19]
タンジェントの練習がない
=>[作者]: 連絡ありがとう.その頁は sinθ,cosθ関連の基本練習までを扱っています.tanθはその次の頁に(少し)あります.
■[個別の頁からの質問に対する回答][はさみうち論法 について/17.4.19]
例題の、実際の答案による解説のところで、辺々掛けた後の変形が分かりません。
他の項はどこに行ってしまったのですか?
=>[作者]: 連絡ありがとう.中間項は両辺にあるので,約分と同様の仕組みで消えます.
初めの例では
辺々かけると
両辺にあるものを約分すると
■埼玉県[kunkunさん/17.4.19]
次数の方程式の例2について
いつも利用させて頂いております。
他の方も質問されておりましたが、f(x)が2次以上と1次以下で場合分けする根拠がどうしても理解できていません。
例1と状況は変わらないように思うのですが。
宜しくお願い致します。
=>[作者]: 連絡ありがとう.n=0 すなわち定数項の場合,f(x)=a, f '(x)=0 になります.したがって,左辺2f(x) は実際には2a になり,その最高次の項が2ax0 =2a というのは成り立ちます.しかし,右辺xf '(x)+2x+6 は実際には2x+6 になり,最高次の項が0ax0 =0 というのは成り立ちません.n=1 すなわち1次式の場合,f(x)=ax+b, f '(x)=a になります.したがって,左辺2f(x) は実際には2ax+2b になり,その最高次の項が2ax1 =2a というのは成り立ちます.しかし,右辺xf '(x)+2x+6 は実際にはax+2x+6 になり,最高次の項が1ax1 =ax というのは成り立ちません.xf '(x) が1次式以下になる場合には,右辺xf '(x)+2x+6 の最高次の項がnaxn とは言えないことになります.(2x だけが最高次の項になる場合と,2x も最高次の項に合流する場合があるので,分けずに議論できないということです.)
■[個別の頁からの質問に対する回答][行列と1次変換 について/17.4.17]
すごく分かりやすかったです
ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/17.4.17]
テスト内容がこのページでまなんだことを繰り返し確認できるものだったこと
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/17.4.16]
問題3の(3)、(x+2)(x2-2x+4)ついてなのですが、xの係数は2ではないですか?
公式はどうして使えるのでしょうか
=>[作者]: 連絡ありがとう.よく似た質問が時々あります.次の点に注意して下さい.
公式Ⅷ (a +b )(a 2 −a b +b 2 )=a 3 +b 3 において,「a b 2 のときはこの公式は使えない」(a +b )(a 2 −2 a b +b 2 ) はa 3 +b 3 a=x , b=2 としたものなので,(x +2 )(x 2 −2 x +2 2 )=x 3 +2 3 となっているのです.係数 が2 b 2
■[個別の頁からの質問に対する回答][恒等式 について/17.4.14]
例題2の係数比較している部分が違うような
=>[作者]: 連絡ありがとう.確かに途中経過に怪しい式がありましたので訂正しました.
■[個別の頁からの質問に対する回答][2進数の演算 について/17.4.13]
シンプルなページですが解けるようになりました、ありがとうございます
=>[作者]: 連絡ありがとう.
■東京都[シータさん/17.4.12]
y=x^2-4x-5とその二次関数に接する直線m,n m:y=1 n:y=-8x+1があり、xの大きい方から順に接点A,B・直線mとnの交点をCとしたときに、三角形ABCの面積と、<CBAを求めたいと思っています。
積分を使って面積を求めるのはわかりますが、このような三角形の場合、どのようにして求めればいいのかわかりません。
よろしくお願いします。
=>[作者]: この問題はこのサイトに出題している問題ではなく,あなた自身で解かなければならない宿題か何かの問題のようですので,本来は回答しないことにしています.
■[個別の頁からの質問に対する回答][共通部分と和集合 について/17.4.11]
段階を追って問題を解けるので、わかりやすかったです。最後の問題を間違えましたが、説明で理解することができました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][恒等式 について/17.4.11]
例題3で、x=0、1、2を代入するのは式を見てdがある、(x-1)がある、(x-2)があるからでしょう
か? それは恒等式となるための条件Ⅱで解説してあるならば、その説明は判りにくいです。
=>[作者]: 連絡ありがとう.未知数がa,b,c,d の4個あるので,異なる4個の値を代入して4個の連立方程式を作らなければなりません.x=3,4,5,6 などとするのも自由ですが,やってみるとx=0,1,2 以外では煩雑になるという勘が働くはずです.条件Ⅱは必要な方程式の「個数」について述べており,あなたが判ろうとしているかもしれない「x に代入する値」のことはそもそも書いてありません.
■[個別の頁からの質問に対する回答][2次関数のグラフ について/17.4.10]
-の入っている答えがあっていても罰にされてしまいます
=>[作者]: 連絡ありがとう.「罰→×」.どの問題の話をしているのか述べないと話が通じません.
■[個別の頁からの質問に対する回答][ド・モアブルの定理 について/17.4.10]
ド・モアブルの定理のイでcos0+i sin0=1のθが抜けてるため等号が成り立たなくなっています
=>[作者]: 連絡ありがとう.確かに読みにくいかもしれませんが,どんな値θ に対しても,0θ=0 が成り立つ.これは「抜けている」のではなく「消える」のです.(中学校の常識:0a=0 を思い出してみよう!)
■[個別の頁からの質問に対する回答][ax +a-x の値 について/17.4.10]
このままでも面白いけど、sinh coshの話があると、より面白くなると思いました。
=>[作者]: 連絡ありがとう.高卒向け
双曲線関数の頁 を見てください.
■[個別の頁からの質問に対する回答][1次変換 について/17.4.9]
とても良い!
=>[作者]: 連絡ありがとう.この教材は,実際には体験・入門レベルの内容ですが,この教材でよい評価が得られる理由として,教育課程の改訂とか科目選択の都合で,そもそも習っていない方が読んでいる場合があるのかなと真剣に考えています.
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/17.4.9]
問題1の(1)の解説部分について
本文では
(a+b+c)2+(b+c−a)2+(c+a−b)2+(a+b−c)2
=(a+(b+c))2+(a−(b+c))2+(a−(b−c)2+(a+(b−c))2
とありますが
(a+b+c)2+(b+c−a)2+(c+a−b)2+(a+b−c)2
=(a+(b+c))2-(a−(b+c))2+(a−(b−c)2+(a+(b−c))2
ではないでしょうか。(1回目の因数分解をした後の式で、2つめの()で括られている部分の符号が違う)
私の指摘が間違っているようでしたら、なぜそれが間違いなのかの解説もいただけると助かります。
=>[作者]: 連絡ありがとう.まず,かっこの中の符号が変わっても2乗の結果は変わらないことに注意しましょう.
(b−a)2 =b2 −2ab+a2 =(a−b)2 (b+c−a)2 ={a−(b+c)}2
もし,マイナスの符号を前に出して考えるのなら
(b−a)2 ={− (a−b)}2 =(−1)2 (a−b)2 =(a−b)2 (b+c−a)2 =[− {a−(b+c)}]2 =(−1)2 {a−(b+c)}2 ={a−(b+c)}2
ところが,あなたの変形では
(b+c−a)2 =− {a−(b+c)}2
としているので,マイナスが2乗されておらず,符号が逆になっています.これは元の簡単な例で言えば
(b−a)2 =b2 −2ab+a2 −(a−b)2 =−(a2 −2ab+b2 )
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.4.9]
2x²-4x-6因数分解
=>[作者]: 連絡ありがとう.通常,この問題はたすき掛けの因数分解の問題とは考えない.すなわち,2 でくくると中学校で習う問題になる.2x2 −4x−6=2(x2 −2x−3)
■[個別の頁からの質問に対する回答][ 行列と1次変換 について/17.4.8]
図で示してくれているので、とてもわかりやすかったです。
今使っている教科書には図がなく、式だけなので面白くなく、意味がわからずこまっていました。
ここの説明はとても、役に立つ内容でありがたいです。
=>[作者]: 連絡ありがとう.人にはいろいろなチャンネルがあって,通常,文章や式で論理的に示している解説以外に,イラスト・動画なども効果的な扉であり得ると考えています.ただし,音は自粛しています.
研究[PDF:486KB] 5.1表6
■[個別の頁からの質問に対する回答][条件付き確率 について/17.4.8]
n(A∩B)とは何なのかの説明がありませんよ。
=>[作者]: 連絡ありがとう.
必要なことを学習してから その頁を読んでください.
■[個別の頁からの質問に対する回答][確率の基本 について/17.4.8]
確率は樹形図をつかって組み合わせが何通りあるかを求めたり、公式に当てはめて確率を求めることなどを学びました。
統計学は習ったことがありません。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内分点・外分点 3 について/17.4.7]
とても勉強になりました。子供が今年室蘭工業大学に合格するまで一緒に数学を勉強して来ましたが、この勉強サイトで、あいまいな理解しかしていなかった箇所がはっきり理解できました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][マクローリン展開 について/17.4.7]
2問目の解説の、log(1+x)のマクローリン展開のn!の部分は誤植ではないでしょうか?
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][総和記号 について/17.4.6]
問題1の終わりの値が全て4なのに、答えが一つだけ三つの数になっています
またその影響で、問題1の上から1番目の答えと4番目の問題の答えが同じはずなのに違う判定になっています
=>[作者]: 連絡ありがとう.あなたは初めの値を見ていないようです.頁の先頭にある例3をよく見てください.
であるが
です.
次に,一般項の違いですが
■[個別の頁からの質問に対する回答][展開公式の応用問題 について/17.4.6]
わかりにくい・・・。
=>[作者]: 連絡ありがとう.応用問題から始めるのでなく,基本問題から始めるとよい.
■[個別の頁からの質問に対する回答][展開公式1 について/17.4.6]
1番最後の問題。なぜXの係数が-2だと公式が使えないのかわかない!!その他使えないときの例はありますか??
=>[作者]: 連絡ありがとう.公式に合わなければ公式が使えないのは当然だと思いますが.
(a+b)(a2 −ab+b2 )=a3 +b3 :公式→公式に合う(x+1)(x2 −x+12 )=x3 +13 →公式に合わない(x+2)(x2 −x+12 ) :展開してみないと分からない →公式に合わない(x+1)(x2 +12 ) :展開してみないと分からない →公式に合わない(x+1)(x2 −2x+12 ) :展開してみないと分からない →公式に合わない(x+1)(x2 −3x+12 ) :展開してみないと分からない (a−b)(a2 +ab+b2 )=a3 −b3 :公式→公式に合う(x−1)(x2 +x+12 )=x3 −13 →公式に合わない(x−1)(x2 +12 ) :展開してみないと分からない →公式に合わない(x−1)(x2 +2x+12 ) :展開してみないと分からない →公式に合わない(x−1)(x2 +3x+12 ) :展開してみないと分からない →公式に合わない(x−1)(x2 +4x+12 ) :展開してみないと分からない
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/17.4.6]
とってもわかりやすいです😊✨高校の宿題でまだ習っていないところが出てきて焦っていたところでした😅最後にある練習問題もちょうどいい難易度で、良かったです!習っていない人ように最初からヒントを出せるようにしてくれるとありがたいです。これからも使わせていただきます!!
=>[作者]: 連絡ありがとう.習っていないなと思ったら前の項目が見られるように,はじめにサブメニューが付いていますのでそれを見てください.
■[個別の頁からの質問に対する回答][相加平均.相乗平均 について/17.4.5]
相加相乗平均でa>0.b>0を言っているならば
a+b≧2(ab)^1/2 >0 の最後の>0は本当に必要ですか?
チャートなどの問題集や参考書にも記述が省かれていると思うのですが。
=>[作者]: 連絡ありがとう.単発でそれで終了なら構わない場合もありますが,さらに組み合わせて使う場合には,言わなければならない場合があります.
などとは言えません.(
のような場合がある)
は言えます.このように大きいもの2個の積と小さいもの2個の積とを「安全に比較できるのは」全部正の数の場合です.(負の数が混じっていると怪しくなる)
そこで
などとは言えませんが
は言えます.
■[個別の頁からの質問に対する回答][展開公式(解説) について/17.4.5]
苦手撲滅完了!?(笑)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/17.4.5]
こんにちは。お世話になっております。問題3の右図の軸が問題の点(HELPで確認)とずれて表示されるようです。私のシステムの問題でしょうか。確認をお願いします。
=>[作者]: 連絡ありがとう.確かにEdgeで見ると点がやや下にずれるようです.今忙しいので今夜訂正します.
■[個別の頁からの質問に対する回答][たすき掛け因数分解(2文字) について/17.4.5]
わかりやすいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][正弦定理 について/17.4.4]
具体的にどこが重要かが丁寧にのっていて中学生にも、易しいです。有難うございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][一般角の定義 について/17.4.4]
いきなり、動径を動く半径と定義していますが、もともと動径は極座標を前提にしているものと思います。三角関数の表現のための「動径」であれば、単位円周上を動く点Pが点(1,0)を出発して回転するというイメージをはっきりさせてからのほうがわかりやすいのではないでしょうか。
=>[作者]: 連絡ありがとう.あなたの考えは分かりましたが,極座標を習っていなくても動径は扱います.また単位円とは限りません.
■[個別の頁からの質問に対する回答][微分方程式:変数変換による解き方 について/17.4.4]
例Ⅳ2の解答にz&aposと表示されていますが、z'の誤りではないかと思われます。
=>[作者]: 連絡ありがとう.ブラウザ用の文字符号でセミコロンが1つ抜けていましたので訂正しました(&apos → ')
■[個別の頁からの質問に対する回答][数学的帰納法とは について/17.4.4]
私が高校生のときは、
数学的帰納法は、例1のほうですが、
『⑵の両辺に』は、習った覚えがないので
絶対的に、必要ではないと思うのですが、
私の思い込みかもしれません。すみません。
年老ると、忘れてしまいますよね。
よろしくお願いします。
=>[作者]: 連絡ありがとう.どういう話なのかよく分かりません.
■[個別の頁からの質問に対する回答][2直線を表わす方程式 について/17.4.3]
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13172550918
どの解答が優れていますか。
よろしくお願いいたします。
=>[作者]: 連絡ありがとう.このサイトは,数学そのものではなく数学教育を扱っていますので,相手のある話です.つまり,無駄なく正確な答案であればよいわけではなく,無駄が多くても相手に理解できる方がよい.そうすると,学力・気力などの準備状況がどうであるかによって,いうべきことが変わります.書く場所が少なければ,最も人数が多いと思われる相手方を想定してそれに合うように書くのがよく,書く場所に制限がなければ全部書いて好きなものを選んでもらえばよいことになります.
■[個別の頁からの質問に対する回答][2直線を表わす方程式 について/17.4.3]
たしかに,解法のテクニックとしてはとてもわかりやすいが,
①,式Aは二次曲線(楕円)なのに,どうして直線2本になるのですか?ときかれたら,どう答えたらよいのか。
「続く」の後半では,
②,D式をxについて解き,その根号内が平方数でなくてはならないということの説明不足。
を感じました。
=>[作者]: 連絡ありがとう.「①は楕円なのに」という思い込みが間違っています.直線になる実例が目の前に示してあるのに,それは言えないでしょう.なお,一般的には
ax2 +bxy+cy2 +dx+ey+f=0
は
a>0, c>0 …(*1)のとき楕円,
a>0, c<0 …(*2)のとき双曲線になるのではないかという予測を持つのは悪くはないが,正確なことは調べてみないと分からないという立場に立たないといけません.
例えば(x−1)2 +4(y−3)2 =1 を展開してみると(*1)の形になり,楕円になります.(x−1)2 −4(y−3)2 =1 を展開してみると(*2)の形になり,双曲線になります.(x−1)2 −4(y−3)2 =0 すなわち(x−1)=±2(y−3) は2直線になります.このように二直線になる場合があるのです.
②について.教えるものと学ぶものの二者からなる場面において,学習の成果が上がらないときに教え方が悪いか,学ぶ者が悪いかは昔からある水掛け論でしょう.普通の生徒は成績が下がってきたら勉強して成績を上げようとしますが,瀬戸際作戦で乗り切る生徒もたまにいます.すなわち「PTAの会議などで,○○の先生は教え方が悪いので生徒の成績が下がってきた」と親が騒ぎ立てると成績が良くなるらしい.このように現実は,声の大きい方の勝ちになりがちですが,説明不足か理解不足かはどっちもどっち,○○喧嘩は犬も食わんともいう.
■[個別の頁からの質問に対する回答][基本的な三角比(図あり) について/17.4.3]
なるほど!分かりました
こんなにいろいろ作ってお疲れ様です
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の計算 について/17.4.3]
√の外し方教えてください
=>[作者]: 連絡ありがとう.「√の外し方」と言えば中学校の話になりますが,対数計算とのかかわりで言えば,あなたが今やらなければならないのは対数関数の真数部分を累乗根から分数指数(有理指数)に直す変形です…(*1).(急がばまわれ:
この頁 とか
この頁 を先に読まなければなりません)
もう一つは,蚤の三段跳びの変形です…(*2).
すなわち
とか
のような式を簡単にするには,対数計算の前に累乗根を分数指数(有理指数)に変形できなければなりません.
具合的には,(*1)により
のように分数(有理数)の指数に直すこと.
次に「蚤の三段跳びの変形」(*2)
を使って
のように変形します.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.4.2]
ゆえに,2x2+7xy+3y2 - x+2y - 1=(2x+y+1)(x+3y - 1)
これがよくわからないです
=>[作者]: 連絡ありがとう.たすき掛けの因数分解について,答を聞いても答えの読み方が分からないといった感想が見られるので,解説中に鍵となることばを繰り返し入れることにしました.
■[個別の頁からの質問に対する回答][たすき掛け因数分解(2文字) について/17.4.1]
穴埋めだと真面目に計算しなくても答えがわかってしまいます
=>[作者]: 連絡ありがとう.大きく見下した発言ですが,油断していると単なる穴埋め問題のセンター試験問題でも満点はとれないのではないでしょうか.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/17.3.31]
いつもありがとうございます。
問題3の答え「4√a」と対になる問いに関して、いくら解こうとしても4√aになりません。ヒントを開けてみたところ、√3√a2乗bの解き方に誤りがあるような気がしていますが、いかがでしょうか?
=>[作者]: 連絡ありがとう.点検しましたが,特に間違いはありませんでした.
累乗根の形で書く場合に,書いている人と読んでいる人が違う解釈をするかもしれないと思うものとして,次のような例があります.
と
の違い.
と
の違い.
以上は,通俗的に言えば,「肩」と「手のひら」が近くにある,「body」と「肩」が近くにあるための混同で,これらが紛らわしいときは横のスペースを適当に広げて書くと防ぐことはできます.
どちらかと言えば,あなたの疑問はその部分ではなく,次の「指数法則」が十分使えていないためではないでしょうか.
■[個別の頁からの質問に対する回答][循環小数の計算 について/17.3.30]
ある数に属するすべての位の数は確定しません。言い換えると、ある数のすべての位は集合を作りません。(ある数の小数点以下のすべての位は集合を作ります。)
循環する数字の9に対する比ではいけないでしょうか?
=>[作者]: 連絡ありがとう.そもそも誰が何を言っているのかが伝わりません.この文章は筆者の言葉ではありません.また,どこかの書物なりWeb記事なりにこのような文章が書いてあるはずがありません.とすると,あなたがそう思うということですか?
■[個別の頁からの質問に対する回答][3次関数のグラフ について/17.3.30]
難しい読み物(2)実数解が2つある場合(x+2)(-2)でⅹが抜けています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][重積分...積分領域が変数に依存する場合 について/17.3.30]
積分順序を一通りではなく二通り書いてくれたらありがたいです。
=>[作者]: 連絡ありがとう.積分順序の変更は1つの大きなテーマになりますので,その次の頁に書いてあります.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.3.29]
問題2なんですけど、他のつなぎ方だけでも4通りくらいあるような気がするんですけど。輪の中心に向いて手を繋ぐとか、外を向いてとか、手をクロスさせてとか…
=>[作者]: 連絡ありがとう.順列,組合せ,確率の問題のように日常生活で登場する一場面を題材とした数学の問題では,問題の定式化において数学と同レベルの厳密さで記述するのは難しいようです.実際には,その日常生活でおいて前提とされている暗黙の文脈が前提となるようです.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.3.29]
何を言っているのかがわかりにくいです「例1からわからない」
=>[作者]: 連絡ありがとう.いきなりその頁だけを見ているようですが,順列・組合せの基本が理解できていないのかもしれません.投げるのもあなたの自由,食らいつくのもあなたの自由です.
■[個別の頁からの質問に対する回答][補集合 について/17.3.28]
わかりやすくて復習程度にでもためになりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.3.27]
わかりやすかったです。ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/17.3.26]
すごく分かりやすくて、勉強中に使わせていただいています
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の計算(まとめ) について/17.3.25]
今春から大学生になりますが、
高校3年間ちょくちょくわからない場面で使わせていただきました。
本当に助かりました。
大学の予習にもぼちぼち使わせていただきます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/17.3.25]
質問と答えの方法に工夫を感じます。これから利用させていただこうと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/17.3.25]
いい教材を作っていただきありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][累乗根 について/17.3.24]
とても分かりやす方です
この単元の問題数増やしたり、一問一答形式にしてくれたらもっとうれしいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][sinθ+cosθ について/17.3.23]
(5)の3乗公式が間違っていると思います
=>[作者]: 連絡ありがとう.HELPの中の途中経過の符号が違うということで訂正しました.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/17.3.22]
8x3乗-27の答えを教えて下さい
=>[作者]: 連絡ありがとう.(1) まず初めに「8x3乗-27の答え」というものはないことに注意してください.「8x3乗-27=0の答え」はありますし「8x3乗-27の因数分解」はあります.文字式の場合と方程式の場合では使われる用語が違います.(2) 次に,
8x3 −27 の因数分解は[I] [II]の例 という箇所に窓枠で囲って書いてあります.書いてあることに気が付かなかった場合は,見たら解決です.書いてあっても,それが因数分解の答えだとは思えない場合は少々込み入った話になります.
の部分をどうしても1次式の積にしたい場合は解の公式を使って虚数の係数で因数分解しますが,通常「因数分解しなさい」という場合は無理数や虚数の係数を使わずに,整数や分数の範囲で因数分解します.
因数分解しなさいという場合:
はそのままでよい
複素数の範囲で因数分解しなさいという場合:
■[個別の頁からの質問に対する回答][対数の計算 について/17.3.22]
累乗根の問題で分母をアとウ、分子をイとエとするとわかりやすいと思います
=>[作者]: 連絡ありがとう.例えば「3分の2」の場合,3を先に読むじゃないかという話のようですが,センター試験問題などマークシート方式の問題で分母と分子を空欄にする場合は,分子から分母への順に名前を付けていくのが普通です.単なる習慣の違いで間違う生徒が出ないように,広く用いられる流儀に合わしています.なお,英語,コンピュータでは分子を先に読むようです:「3分の2」の場合,two thirds; 2 over 3; 2 by 3; fraction{2}{3}
■[個別の頁からの質問に対する回答][広義積分 について/17.3.22]
H23のⅢ-7の問題は広義積分なのですか?∞が入ってないのですが、、、
私の勘違いでしたら無視して下さい。
=>[作者]: 連絡ありがとう.その頁の先頭にまとめていますように,積分区間が有界でない場合
のような場合だけでなく,積分区間が有界でも被積分関数が有界でない場合
のような場合も広義積分に含めて考えます.(
なので,関数f(0)が定義されていない)
■[個別の頁からの質問に対する回答][重積分 について/17.3.22]
H24のⅢ-10の問題いいですね。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/17.3.22]
X4乗-6X2乗➕1の因数分解
=>[作者]: 連絡ありがとう.サブメニューをたどって,因数分解の応用問題を見てください.x4 −6x2 +1=(x2 +1)2 −(??)2 と変形できるか,それともx4 −6x2 +1=(x2 −1)2 −(??)2 と変形できるかを両方試してから判断します.
■[個別の頁からの質問に対する回答][行列 用語と記号 について/17.3.21]
上記問題の解答で、3問目、4問目は間違いとされました。同じ回答を半角で打ち込んだところ正解となりました。半角で回答せよとかコメントが欲しかったです。
=>[作者]: 連絡ありがとう.あなたが使っておられるブラウザは,漢字変換モードをプログラムから切り替えるコマンドをサポートしていません.(その教材を作成した当時はまだ存在していませんでした.)今日では小中学校で全角文字(2バイト文字)は数字ではないと習うはずなので,半角数字で書かなければならないという注意書きは書いている場合と書いていない場合があります.全角数字でも正解とすると便利ではあるが教育的には疑問が残り,全角数字を誤答にすると教育的配慮はできていても不便になり一長一短ですが,ここでは両方とも正解とする方式に変更しました.
■[個別の頁からの質問に対する回答][確率変数と確率分布 について/17.3.20]
広告の位置がじゃまで、例2が見にくいのですが、消すor動かすっていうことってできますか?
因みにx印のない広告です
=>[作者]: 連絡ありがとう.確かにChromeで見たときだけ,~くじの賞金を扱う問題~の前までが,他のブラウザと全く違う表示になるようです.原因は解明できませんでしたが,応急処置をしておきました.リロードしてもらえば直っているはずです.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.3.19]
最後の問題12番では、3の倍数でない数の2乗が3の倍数であることを反例として挙げればいいのですよね。
ならば√3はどうなのですか?
=>[作者]: 連絡ありがとう.この質問については
以前にも お答えしています.問題文に「整数nについて」と書いてあるのだから,整数の中で考えます.
■[個別の頁からの質問に対する回答][余弦定理 について/17.3.18]
最後の「(参考)」内の「右図のようにa , c , Aが与えられたとき」は「右図のようにb , c , Aが与えられたとき」として「a」が2つある場合とした方が理に適っているのでは?もしくは図のaとcの位置が逆である。
=>[作者]: 連絡ありがとう.図と文章のつじつまが合っていませんでしたので訂正しました.
■[個別の頁からの質問に対する回答][期待値 について/17.3.18]
訂正です。確率/期待値/問5 のhelpについて
『…100硬貨が裏、100円硬貨のうち1枚が表、1枚が裏→10円となる確率は…』とありますが、
正しくは、『…100硬貨が裏、【10】円硬貨のうち1枚が表、1枚が裏→10円となる確率は…』ではないでしょうか?
いつもお世話になっています。ありがとうございます。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][展開公式1 について/17.3.17]
公式を使える問題なのか使えない問題なのかがよく分かりません
=>[作者]: 連絡ありがとう.係数も含めて同じ形になっているかどうかで判断します.その頁は公式が使える問題と使えない問題を見分ける練習にもなっていますので「分からない」というのは勉強不十分ということです.
■[個別の頁からの質問に対する回答][累乗根 について/17.3.17]
計算問題は、一対一ではなくて、残るような設定でないと簡単ではないでしょうか。
=>[作者]: 連絡ありがとう.その頁は簡単な問題を扱っているから簡単なのです.それができるようになったら次の頁に進むのです.
■[個別の頁からの質問に対する回答][展開公式1 について/17.3.17]
[VIII][IX]の例の説明で,二段目の数式のが(見たらすぐ答え。特別な計算はいらない)理由がわからない。abの係数は2なので気長にばらばらにする必要があるのではないか.
=>[作者]: 連絡ありがとう.{(2x) −1}{(2x) 2 +(2x) +1} の係数は全部1になっています(ただし最初のかっこ内の定数は−1です).
■[個別の頁からの質問に対する回答][??? について/17.3.17]
これの意味が分かりませんでした。
この係数 1 , 3 , 3 , 1 は右のような「パスカルの数三角形」で求められる
=>[作者]: 連絡ありがとう.あなたはWeb上の教材ではなく,自分のPCにダウンロードして別の名前を付けたものを使っており,ディレクトリ名とファイル名が変更されています.作者が回答するためには,ディレクトリ名とファイル名が手がかりですが,あなたの使い方ではどの教材の話をしているのか分かりません.元の教材から質問してください.
■[個別の頁からの質問に対する回答][複素数平面の図形問題(三角形の形状問題) について/17.3.16]
問題5(2)の答えの選択肢が解説と相違しています。解説のOB=ABではなくOA=ABを選択しないと丸がつきません(T-T)
=>[作者]: 連絡ありがとう.選択肢の番号を訂正しました.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/17.3.14]
教科書を学校に忘れて演習問題を解けずに困っていたのですが、これを見ながらだと演習問題を解くことができました!
要点だけをまとめていて、とっても見やすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][不定積分(まとめ2・・・三角関数) について/17.3.13]
間違っていたらすいませんが、問題4の中の∫1/(1-cox)dxの回答は、-(1+cosx)/sinx ではないですか?これが正解なら右の回答欄に付け加えた方が良いと思います。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][展開公式 について/17.3.11]
とてもわかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/17.3.10]
気にいった所 : 平方完成を途中を跳ばすことなく、愚直に進めているところ。途中を省くと必ず計算間違いをすると教えてくれたこと。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/17.3.10]
例題が少ない
=>[作者]: 連絡ありがとう.例題は理屈の部分で,重複組合せの総数は組合せの総数に読み替えて解くということさえ分かれば,後は重複組合せを組合せに直す練習をするのみです.問題は10題あります.サブメニューから文章題も選べます.
■[個別の頁からの質問に対する回答][不定積分(まとめ1) について/17.3.9]
**III.8**の(2)∫1/(e^nx+e^-nx)dx=∫1/(t+t^-1)dt/ntは、∫1/(e^nx-e^-nx)dx=∫1/(t-t^-1)dt/ntではないですか? また、問題6の3行目の問題は、∫dx/(e^x+e^-x)は、問題を∫dx/(e^x-e^-x)とするか、又は回答にarctan(e^x)+Cを加えたほうが良いと思いますがあってますか?なお、貴サイトの教材は非常に良くできていて、私の若い時にこのような手段があったらもっと数学が理解できた違いないとつくづく思っており、もう少ししたら孫にこれで勉強するよう勧めようと思っています。
=>[作者]: 連絡ありがとう.符号を訂正しました.
■[個別の頁からの質問に対する回答][展開公式1 について/17.3.8]
最後はずるいw
=>[作者]: 連絡ありがとう.この間違いは結構多いので,注意を促すためにあえて出題しています.
■[個別の頁からの質問に対する回答][分数式の和・差 について/17.3.8]
問題2の(5)の解説で、
=x2(c-b+a-c+b-a)+x{(c+b)(c-b)+(a+c)(a-c)+(b+a)(b-a)}+bc(c-b)+ac(a-c)+ab(b-a)
の
+x{(c+b)(c-b)+…
は、どうして、
-x{(c+b)(c-b)+…
こうならないんでしょうか?
=>[作者]: 連絡ありがとう.どうやら1次の符号が逆のようですので訂正しました.
■[個別の頁からの質問に対する回答][展開公式 について/17.3.7]
左に表示される「大きな区分」や「現在地と前後の項目」が見切れていて左三分の一ほどが表示されていない。
=>[作者]: 連絡ありがとう.画面の横方向1366ピクセルのFirefoxで見ておられるので,普通なら十分画面に入っているはずです.文字サイズやズーム画面の拡大率を標準(100%にリセット)にして試してください.
■[個別の頁からの質問に対する回答][数学的帰納法とは(小話) について/17.3.7]
内容としては非常にわかりやすく、テスト前はいつも参考にさせていただいているのですが、左から右に読むレイアウトがみづらいので改善していただけるとありがたいです
=>[作者]: 連絡ありがとう.各々の頁で「携帯版」を選んでいただくと縦1列のレイアウトになった教材を見られます.
■[個別の頁からの質問に対する回答][(例題対比)2次関数のグラフ[標準形] について/17.3.7]
すごく分かりやすい文章でした。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][部分分数分解 について/17.3.7]
この説明で、<f(k)-f(k+1)を使ったΣ>の全容がわかりました。素晴らしい解説です!感謝です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][関数の極限1 について/17.3.7]
三角関数の極限を載せてほしい
=>[作者]: 連絡ありがとう.三角関数の極限の頁を見てください.
こちら
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/17.3.7]
はじめの方の解説や問題はすごく良かったのですが、問題の解説がなくて、分からなかった時に困ってしまいました…。自力で、サイトの最初の方から読み直して解決したのですが、問題の解説はやはりあった方が良いと思われます。
=>[作者]: 連絡ありがとう.「最初の方から読み直して解決」するように意図したものです.読み直したときにあいまいな知識がはっきりしてくるので,それが身に付く読み方です.・・・一般に直線的に読み進むのでなく,行ったり来たりしながら読む方が身に付くと言えます.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/17.3.6]
分かり易かったです。ですが、答えを詳しく出して頂けると幸いです。
=>[作者]: 連絡ありがとう.HELPボタンを押すと詳しい途中経過がでますのでそれを読んでください.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/17.3.3]
問題の答えってあってますか?
=>[作者]: 連絡ありがとう.合っています.なお,この質問の仕方はよくありません.「この問題の答えについて自分はこうだと思うが,答はこうなっているので間違いではないか」という形で具体的に指摘しないと,「全部見直してくれ」と言っているのと同じことになります.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/17.3.3]
むずかしい。
=>[作者]: 連絡ありがとう.それ以前の内容がどれくらい身に付いているかによってハードルが超えられるかどうかに関係すると思います.
■[個別の頁からの質問に対する回答][行列の積 ABの定義 について/17.3.3]
行列に関してほぼ知識なしの状態でこのページにたどり着きましたが、ちゃんと理解できました。すごく分かりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の定義 について/17.3.2]
これはよいです。 約30年振りにdBの計算で対数を学ぶことになり、このサイトを発見しました。
基本の覚え方と実例、それに練習問題。そして記号を使った問題では選択する作業がひっかけを誘発する感もあり、時間制限があったら、あせって間違うかもしれませんでした。 脳がいい汗かきました。 ありがとうございます。
=>[作者]: 連絡ありがとう.対数は高校の教育課程につねに入っていましたので,私の方も忘れることはありませんでしたが,ものによっては複素数平面のように教育課程から出たり入ったりの上に,開講講座数が少なくて,めったに担当させてもらえないものもあり,元教員でも忘れていることがあります.30年ぶりならまだまだ最近の話で,こちらは50数年ぶりですが気楽にやっています.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式 について/17.3.2]
1+tanα^2=1/cosα^2
も有名ですので加えてみてはいかがでしょう
=>[作者]: 連絡ありがとう.親切心で言っておられるということは分かるのですが,この頁は数学Ⅱの加法定理や倍角公式の話題を扱っています.あなたが述べている話は
数学Ⅰの三角比の相互関係 の頁で扱っています.
■[個別の頁からの質問に対する回答][積の法則 について/17.3.1]
ノート型ではヘルプの文章が表示部と入力部を開ける角度により見えなくなります
=>[作者]: 連絡ありがとう.要望の内容が理解できませんが,とりあえずモニター画面の反射で見えにくいという話をしておられると解釈して,文字色を濃くしておきました.
■東京都[ゲホゲホさん/17.3.1]
先生、お忙しい所、ご解説をありがとうございました。
ある意味、グラフ化してある程度解の位置を特定してからでないと、やはり求められないのですね。
何か自動化する良い方法が無いか、こちらで考えてみたいと思います。取り急ぎ、御礼を申し上げます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][文字を含む不等式 について/17.2.27]
いつも勉強させていただいております。
(Ⅱ)の例題のXの係数に負(マイナス)が抜けているのではないでしょうか。
=>[作者]: 連絡ありがとう.(Ⅱ)の例題とはどれのことなのか,見当たりませんが?
ひょっとして,「
a<0 のとき
ax<b ならば
などの変形のことを述べておられるのでしたら,それはあなたの勉強不十分です.1つの文字
a で負の数が表せるのです.
他の例で言えば,
a<0 のとき
a2 >0 などはよく出てきます.
■[個別の頁からの質問に対する回答][重回帰分析 について/17.2.27]
最小二乗法でいいので1カテゴリ変数2水準の場合の一般論、1連続変数1カテゴリ変数2水準の一般論等を具体的に計算してもらえるとかなりわかりやすくなると思います
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数列 について/17.2.27]
正解を、表示していただければ、嬉しいです。
=>[作者]: 連絡ありがとう.この問題は導入用のパズルのようなものです.ヒント以上のことは・・・どちらかと言えば,友人間で類似問題を出し合って脳の活性化を図る材料にするくらいのものだと思いますが・・・
■東京都[ゲホゲホさん/17.2.27]
学生ではございませんが、エクセルで作業をしている所でつまづき、検索で先生のサイトに行き着きました。
ソルバーの使い方なのですが、「(2) 次の方程式の実数解を1つ見つけよ.
sinx + sin2x + sin3x = cosx cos2x cos3x」と言う問題を出していらっしゃいますが、ここで示される様な解が複数ある場合、どの様に条件を指定したら全て拾い出せるのか、解答例をご教示頂くことは出来ますでしょうか。
お忙しい時に、先生のサイトの本質的な目的ではありません質問を致しまして、大変申し訳ありません。ご検討を宜しくお願い致します。
=>[作者]: 連絡ありがとう.エクセルのソルバーの場合,(少し大きいまたは少し小さい)近くの解に向かって行くので,初期値の与え方にって異なる解が出ます.ご質問の問題は周期2πの周期関数なので,0~6.28まで調べると,その外側では限りなく繰り返されます.0~6.28までに6個の解があるということは,次のようにして分かります.
(1) ワークシートでA列1行目に0と記入 (2) A1:A629の範囲を選択して反転表示にする (3)編集.フィル.連続データの作成;増分0.01
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.2.26]
採点するを押すと右の欄にキャラクターが表示されるがこれが正解か不正解かわからない。
全角で数字を入力すると値が正しくても不正解になる。
=>[作者]: 連絡ありがとう.全問不正解なら区別はつきませんが1つでも正解があればわかるはずです.半角文字で入力してください.
■[個別の頁からの質問に対する回答][全微分方程式 について/17.2.26]
初めまして、ミスタイプがあると思われるのでご連絡申し上げます。ご確認をお願い致します。
以下のところで、
○ 変数分離形の微分方程式としても解釈できる問題を,変数分離形として解く場合と,全微分方程式として解く場合とでは,別々に積分するかまとめて積分するかの違いがあります.
○ 変数分離形の微分方程式を変数分離形として解く場合には
dy/dx=f(x)g(x) →dy/dx=f(x)g(y) と思われます。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][分数関数 について/17.2.26]
(x-5)/(x-2)=3x+k というkが定数の式があり、この式の実数解の個数を求めるにはどうすればよいでしょうか?
分数関数と3x+kが一点で交わるようにするkを求める方法がわからず、解けません。
よろしくお願いします。
=>[作者]: 連絡ありがとう.x−5=(x−2)(3x+k), (x≠2) として2次方程式の判別式で判断するとよいでしょう.3x2 +(k−7)x+(5−2k)=0 D=(k−7)2 −12(5−2k) =…… =(k+11)(k−1) k<−11, k>1 → ... イ)k=−11, 1 → ... ウ)−11<k<1 → ... x=2 となることはない
■[個別の頁からの質問に対する回答][集合の要素を用いた証明 について/17.2.26]
問題1の(1)正解は3∉Aのはずですが、それをクリックしてもXマークが出てしまうようです。
=>[作者]: 連絡ありがとう.そうでないことはない・・・と言っているうちにややこしくなっていたようです.訂正しました.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/17.2.24]
練習問題の解説欲しいです
=>[作者]: 連絡ありがとう.あなたの学習の記録を見てみると,解説の箇所を読んだ形跡がありません.もしかして,問題を解いていないのではないでしょうか・・・解答をクリックすれば,画面上で採点でき,解説が出るようになっています.PDFなどで作られた読むだけの教材とは違い,応答型になっています.解答しなければ解説は出ません.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/17.2.24]
数学はさっぱり駄目な文系大卒の32歳です。
現在業務の都合から電験三種の勉強をしていますが、電験用の基礎数学の参考書ですら理解に苦しみ、ネットを徘徊しているときに出会いました。
非常にわかりやすく解説して頂き、何とか参考書を読み解くことができるようになりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内分点・外分点 1 について/17.2.24]
もっと問題を増やして欲しいです。
お願いします。
=>[作者]: 連絡ありがとう.その頁は1つの思い違いを解消するためのワンポイント・レッスンですので,少し読んだら次の頁の本来の高校の問題をやってください.
■[個別の頁からの質問に対する回答][(各駅停車)対数計算 について/17.2.24]
12まで正解したのに進行状態の12が達成サインになりません。
=>[作者]: 連絡ありがとう.苦労して山の頂上まで来たのに山頂の標識がなくなっていたというような場合,どっと疲れが出て不満が残る感じで申し訳ないです.このプログラムを作ったのは私ですが,かなり以前に作ったもので,複雑すぎて点検が難しいのでご勘弁を!
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/17.2.23]
わかりやすかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次変換 について/17.2.22]
東工大受験3日前に良い勉強できました。回転座標の問題や明らかに行列式をモチーフにした問題が出たら是非複素平面といった回りくどい方法を取らずにバッチリ一次変換を使って行きたいと思います
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分 について/17.2.22]
めちゃくちゃありがたいです!
すごく助かってます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][多項式の除法(割り算) について/17.2.22]
いいでしょ。完璧
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][同じものがあるときの順列 について/17.2.21]
凄くわかりやすいです!調べたらすぐ出てきてすぐ解決しました!大助かりです!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間 について/17.2.21]
問題1の解説で、なぜ解説のような式が成り立つのかということがわかりまかせん。解説をお願いできますか。
=>[作者]: 連絡ありがとう.
という式を変形して,
という形にしてzの範囲を求めています(この変形は上の不等式を「芋づる形」「連なり形」ではなく切り離して2つにして,1つずつ変形すればできます.教材の記述は少々不親切かもしれません)
■[個別の頁からの質問に対する回答][対数の定義 について/17.2.21]
とても分かりやすかったです。あと、何故、この対数を使うのか、対数を使うと、どういうメリットがあるのか、説明して頂けると、興味がわくと思います。
=>[作者]: 連絡ありがとう.歴史的には,ケプラーなどの天文学者が惑星の運動を研究するときに,膨大な数の掛け算や割り算を行う必要があって,そのせいで寿命が縮んだと言われており,より計算量が少なくて済む足し算や引き算に書き換える方法がどうして欲しかったと言われている.
だから,歴史的には
,
のように分ける計算がありがたかった.
しかし,今日では膨大な桁数の掛け算や割り算でもコンピュータを使えば一瞬にできるので,そのありがたさは分からない.ここから先は,各自がどんな作業を主にやっているかによって変わる.ア)微積をよく使う人にとっては,分数関数の積分を表すために対数関数は絶対必要になります.
イ)指数関数的に変化する現象を扱う場合には,元の変数の対数をとると,より扱いやすい1次関数にできる.
ただ,こうした興味ある話題に触れるには,それなりに対数関数に慣れて足腰を鍛えておかないと,余計混乱するかもしれず,どこまで踏み込むとよいのか迷うところがあって,今のところ書いていません.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/17.2.21]
わかりやすいです。
問題があるのがすばらしいです。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次変換 について/17.2.21]
とてもわかりやすいです。参考になりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/17.2.20]
わかりやすかったです!
最後にテスト形式でチェックできるのは助かります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/17.2.20]
(5)に関しての質問です。
X3(Xの3乗)-X2(Xの2乗)=A、X-1=Bとおいたのですが、
(A-B)(-A-B)で計算すると答えが違ってきます。
この置き換えは間違いなのでしょうか?
=>[作者]: 連絡ありがとう.質問が間違っています・・・(6)の問題でしょう.次に,その置き替えはできません.
■[個別の頁からの質問に対する回答][決定係数とは について/17.2.20]
回帰分析をGA(Genetic Algorithm)のパラメータ最適化に使用することを検討しています。
Excellを使用してGAの各Generationの回帰分析を行ってみたのですが、Excellの回帰分析結果レポート
の用語説明をWEBで検索中にこのサイトに遭遇しました。
説明は丁寧で分かりやすいく素晴らしいです。
強いて難を言うのであれば、
1.Excelの表中(以下)の用語(重相関、重決定、補正)
と本文の用語(重相関係数、決定係数、自由度調整済決定係数)の対応が初めの部分にまとめて説明
してあると、私としては効率的でした。
2.決定係数、自由度超セ済決定係数の値の目標値を幾つにすれば良いのか目安がほしいです。
=>[作者]: 連絡ありがとう.目安は「決定係数 R2とは」の最後の方に灰色で書いています.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/17.2.19]
全然分からない
=>[作者]: 具体的な手掛かりが何も書いてないので,「そーか分からないのか」としか言いようがない.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/17.2.19]
角度はラジアン(π)を使って表して欲しい
=>[作者]: 連絡ありがとう.角度の単位をラジアンにしなければならないのは,三角関数の微積分を行うときです.それ以外では両方とも使います.
■[個別の頁からの質問に対する回答][部分集合,集合の包含関係 について/17.2.18]
問題についての質問です
(2) A={2n | 0≦n≦5 , n は整数} , B={n | n は32の約数} のとき, A ? B
という問題で答えは=となっていますが、32の約数には1も含まれると思うので正答は なし ではないのですか?
それと、部分集合と真部分集合の違いがよく分からないので詳しく説明して欲しいです。
よろしくお願いします。
=>[作者]: 連絡ありがとう.「32の約数には1も含まれる」のでA=Bなのです.
「AがBの部分集合:A⊂Bであって,かつ,A≠B」のとき,したがって「A⊂Bであって,かつ,Bの中にAでないものが実際に存在するとき」AはBの真部分集合になります.このことは,※ (注意)のところに書いています.
ところで,あなたが分からないのは部分集合と真部分集合の関係ではなく指数関数,特に
20 だと考えられます.
この頁 (数学Ⅱの内容)に解説していますが,
20 =1 です.したがって,
A= {
2n | 0≦n≦5 , n は整数}のとき,
A= {
1,2,4,8,16,32 }になります.
■[個別の頁からの質問に対する回答][連続整数の積 について/17.2.18]
6で割りきれることの証明の(1)の3Kの代入がおかしかない?
=>[作者]: 連絡ありがとう.確かにn(n+1)(n+2)の話になっていましたので訂正しました.
■[個別の頁からの質問に対する回答][軌跡の方程式 について/17.2.18]
私は学生時代部活ばかりしていて、高度な数学知識はありません。中学時代の数学ですら数学として理解してない場合が多い。算数のそろばん時代に戻りたい。
=>[作者]: 連絡ありがとう.言っても始まらないことを考えるのは前向きな考えではないので,できることを探しましょう.
■[個別の頁からの質問に対する回答][決定係数とは について/17.2.16]
まだざっと見ただけですが、とりあえず知りたい部分に関しては、要点を得てわかりやすいと思った。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][媒介変数表示で表された関数の導関数 について/17.2.15]
微分積分法の復習に大変お世話になっております。
媒介変数表示の微分[問題](5)ですが、与式のうちy=a(cost-tsint)が、回答解説と違っているようです。
解説内のy'から察するに正しい式は
x=a(cost+tsint)
y=a(sint-tcost)
ではないでしょうか。
更新をお休みになっておられたら恐縮です。
ご確認いただけたら幸いです。
=>[作者]: 連絡ありがとう.問題文の方がタイプミスでしたので訂正しました.
■東京都[銭湯犬さん/17.2.13]
早速のご回答ありがとうございました。要約を読み落としており失礼しました。
「先頭のxの係数がなるべく小さな正の数になるように答えるのが常識」ということはよくわかりましたが、同じものを入力して×になるというのは、初学者に対しては少々不親切なような気も致します。
特にこの場合、後半の(-2y+9)と(-5y+2)の項自体に-1を掛けているというのは、初学者(や復習者)は見落としがちなところではないかと愚考いたします。
=>[作者]: 連絡ありがとう.問題も解答もプログラムで作られているので,誰が見ても同じ問題になっている訳ではありません.だから,後半の・・・と言われてもこちらではどんな問題が出ているのか確かめられません.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/17.2.14]
接点がわからない時の、接線の求め方が知りたいです
=>[作者]: 連絡ありがとう.サブメニューでその次の項目を見てください.
■[個別の頁からの質問に対する回答][Excel:重回帰分析(2) について/17.2.14]
Rコマンダーがうまく動かず、困っております。
=>[作者]: 連絡ありがとう.質問内容が漠然としていて答えようがありません.
■[個別の頁からの質問に対する回答][部分積分 について/17.2.13]
とっても分かりやすくて良かったです!
参考になりました!ありがとうございました!
=>[作者]: 連絡ありがとう.
■東京都[銭湯犬さん/17.2.13]
お世話になります。
http://www.geisya.or.jp/~mwm48961/kou3/tasuki1.htm
問題4の2回目ですが、回答は
(-4x+2y-9)(-3x+5y-2)
だと間違いなのでしょうか。
(他の問いでも、x項と数値項のプラマイを入れ替えらえそうな気がします)。
=>[作者]: 連絡ありがとう.初めに要約に書いていますように「係数の符号を全部換えても同じものになるから両方調べる必要はなく,x の係数が正のものを調べたらよい.」というのはそういう意味です.
のように符号や定数倍を調整して変形したものが等しいのは当然のことです.これも答えです,これも答えですといちいち言ったりしません.先頭のxの係数がなるべく小さな正の数になるように答えるのが常識だということです.
■[個別の頁からの質問に対する回答][対数計算1 について/17.2.12]
制御工学の問題で出てきた,20 log K = G (Gはゲイン[dB])のときのゲイン定数 K の求め方を知りたくて検索しており拝見させていただきましたが,残念ながらこのサイトでは分かりませんでした.デシベルが絡む計算はややこしく,いつも忘れてしまいます(-_-;)
=>[作者]: 連絡ありがとう.それぞれの専門分野ごとの約束事があれば別として,高校数学での取り扱いは,その頁の先頭に書いてあります「対数の定義」を見てもらえばできます.
だと思いますが.
■[個別の頁からの質問に対する回答][三角関数の値 について/17.2.12]
sin(π+θ)など"の項で、tan(θ-π/2)の問題について、図が3π/2の外接円との交点にマークを
示しているので間違いと思いますが如何でしょうか。
=>[作者]: 連絡ありがとう.sin(π+θ)の話をしておられるのか,tan(θ-π/2)の話をしておられるのか通じません.3π/2の外接円とは何のことなのか,Firefoxで表示がおかしいということでもないようで,全く話が通じません.
■[個別の頁からの質問に対する回答][絶対値記号2つの外し方 について/17.2.11]
第5問1≦xのときx2+8x-13=0とありますがx2+9x-13=0ではないでしょうか。
=>[作者]: 連絡ありがとう.2(3x+1)+3(x−1)=−x2 +x+12 においてxの係数は左辺の9だけでなく右辺の1もあるので,これを移項すると8になります.
■東京都[あいうえおさん/17.2.11]
数学Iの数と式の分母の有理化の解説のIIの中にルート2が一つありますがルート3ではないでしょうか。
=>[作者]: 連絡ありがとう.キーボード上で隣のキーに触れたみたいです.訂正しました.
■[個別の頁からの質問に対する回答][sinx,cosxに関する不定積分 について/17.2.10]
このページ含めインテグラルのあるページについて、インテグラルと式の間にかなりスパンがあり、左側の文字に被って見えなくなっているところがあります。
=>[作者]: 連絡ありがとう.Chromeで読んでおられるようですが,ブラウザごとバージョンごとに見え方に違いがありますが,目立つところは直しておきます.なおインテグラルと式の間のスパンは積分区間の下端と上端を書き込むために少しは必要です.問題はさじ加減です.
■[個別の頁からの質問に対する回答][定積分 について/17.2.10]
問題があるのはとてもいいけど問題が変わるようにしてほしい!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][因数分解(応用問題) について/17.2.10]
問題3の(3)は(x+y+z)3-(y+z−x)3-(z+x−y)3-(x+y−z)3ではないでしょうか。
=>[作者]: 連絡ありがとう.最近アップしたもので,点検が甘く問題文の方に転記ミスがあったようです.
■[個別の頁からの質問に対する回答][ ベクトルの和 について/17.2.9]
還暦を過ぎ、学び直しています。
とても良く理解でき、解った自分に感激しています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][関数の極限1 について/17.2.9]
復習になりました
ありがとうございます☺
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][領域における最大最小 について/17.2.9]
例題2の傾きの範囲は
-3<k<-1/2
ではないでしょうか?
=>[作者]: 連絡ありがとう.少し記述に問題がありましたので訂正しました.
■[個別の頁からの質問に対する回答][Excel:相関係数,回帰直線 について/17.2.8]
相関関係と因果関係の項は今一つわかりませんでした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/17.2.8]
いま有斐閣の「統計学」2008年版を独習して、どうにもわからなくなって本サイトにお助けいただいているところです。大学生用の教科書だとはいえ、どうしてこれほどわかりにくいのかと困っていたところ助かりました。やはり、手で計算すると分かりやすくなると実感しています。EXCEL2013では少し関数が違うので、フォローしていただけるとなおうれしいです。
=>[作者]: 連絡ありがとう.関数が違うということはないと思いますが,画面上端のメニュー構成は変わっています.
■[個別の頁からの質問に対する回答][逆行列とは について/17.2.8]
EXCELの操作が大変わかりにくいです。説明だけではなく、動画をつけるとよいです。私は操作を理解するのに、マイクロソフトのサポートも使い、半日かかり、そのあと、反復練習して(キーを三つ押すのがむつかしいこともある)やっとできるようになりました、
=>[作者]: 連絡ありがとう.こちらの返信の方が後なので,解決したようでよかったです.
■[個別の頁からの質問に対する回答][逆行列とは について/17.2.8]
何回やってもうまくエクセルで表示されません(EXCEL2013)。私の理解が悪いのでしょうか。途方にくれています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2直線の交点を通る直線の方程式 について/17.2.8]
例題1の直線 x-2y-7=0 , 2x+y+1=0 の交点においては,(1)式は 0+0k=0 、、のところの意味が分かりません。どういうことなのでしょうか。他は分かりやすく理解できました!
=>[作者]: 連絡ありがとう.2直線 x-2y-7=0 , 2x+y+1=0 の交点の座標(x,y)は x-2y-7=0 も 2x+y+1=0 も両方を満たすので
■[個別の頁からの質問に対する回答][行列の積 について/17.2.8]
windows8.1、IEの環境ですが、4(2)と(3)の数字が上下消えていて読めなくなっておりました(他は問題ありませんでした。こちらの機種(NECのタブレットPC)のせいかもしれませんが、念のため報告します。
=>[作者]: 連絡ありがとう.原因となる箇所は特定できるのですが,区切り文字のスペースを入れるとエラーになる場合と,区切り文字のスペースを入れないとエラーになる場合があって,やってみないと分からないという感じです.(2)はスペースあり:エラー,なし:正常,(5)はなし:エラー,あり:正常とちょうど逆にすると直りました.
■[個別の頁からの質問に対する回答][F検定→t検定 について/17.2.7]
どうして、大学のテキストは同じ内容があれほど難解に記述するのか、と痛感するばかりです。このページを読むことでようやくテキストの大意がつかめました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数式の和・差 について/17.2.7]
チャート式で、この単元に部分分数分解があるので、このページでも解説をしてほしいです。分子が定数のタイプです。
=>[作者]: 連絡ありがとう.チャート式はとてもメジャーな参考書ですが,その構成に合わせて記述するというのは著作権的にグレーに近づいてきます.当教材では,実際に部分分数分解が必要となる項目
数列の和 ,
不定積分 で解説しています.
■[個別の頁からの質問に対する回答][指数法則 について/17.2.7]
悪い所は一切ないと思います。非常にわかりやすいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.2.6] 最後の問題で、√3をnに代入すると
n²が3になり 3の倍数になるのですが、nは√3となり3の倍数ではなくなるとですが、この考え方は間違っているのでしょうか?
=>[作者]: 連絡ありがとう.問題文に整数nについてと書いてあるので,整数で考えます.「整数nについて」が1行上にあって見落としてしまうという話が前にもありましたので,改行しました.
■[個別の頁からの質問に対する回答][3点が同一直線上にあるための条件 について/17.2.6]
3点が一直線上にあるようにxの値を求める問題で、学校の宿題で3点が(2,x),(x,0),(-2,6)というように二箇所にxが入っている問題が出たのですが、その場合は解き方はこの頁に載っていたものとは変わるのでしょうか?教えていただけると嬉しいです。
=>[作者]: 連絡ありがとう.同じ考え方で解けます.なお,問題の写し間違いのせいか,このままでは解けません(虚数解になります.)
他に,直線の方程式で考える場合は
この頁 (ただし,未知数をxのままで計算すると直線の方程式のxと混ざってしまうのでtに変えるなど工夫を要す)
■[個別の頁からの質問に対する回答][検定 について/17.2.5]
大変わかりやすく、助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定・・・平均値の差の検定 について/17.2.5]
わかりません
=>[作者]: 連絡ありがとう.何も手掛かりが書いてないので答えようがありません.
■[個別の頁からの質問に対する回答][行列 について/17.2.5]
大変分かり易くて理解できました。
私は60の手習いで、行列式を学習し始めました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/17.2.5]
問題4の(2)や例(4)など、掛けているのかそれとも指数なのか分かりにくいにので、スペースをもっと開けるか掛け算のマークを入れて欲しいです
=>[作者]: 連絡ありがとう.ご指摘の点については了解できません.掛け算のマークを書き込む箇所はありません.
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間(問題練習 について/17.2.4]
例題4の最後のμの平均の範囲158.3じゃなくて168.3です
=>[作者]: 連絡ありがとう.途中計算に入力ミスがあったのは事実です.少々ややこしいですが,168.3が間違いで158.3が正しいです.
■[個別の頁からの質問に対する回答][4次方程式 について/17.2.4]
(B)(例1)のⅩ3乗+4Ⅹ2乗+5Ⅹ+6÷Ⅹ+3の途中式が一部間違っています
=>[作者]: 連絡ありがとう.2乗が抜けていたので訂正しました.
■[個別の頁からの質問に対する回答][複素数平面 について/17.2.3]
z=2-6iを(1/6)πだけ回転させた複素数を出すにはどうすればいいですか?
極形式に直してから回転させるというステップはわかるのですが、2と6なので三角比が使えず極形式に直せません。
よろしくお願いします。
=>[作者]: 連絡ありがとう.複素数の回転については
この頁 に解説があります.
極形式に直さなくても(1/6)πだけ回転させるには,単にcos(π/6)+i sin(π/6)を掛けたらよいので,(2-6i)(cos(π/6)+i sin(π/6))=(3+√3)+(1/3√3)i
■[個別の頁からの質問に対する回答][1次不定方程式の整数解 について/17.2.3]
問題6の解答解説が間違っていませんか。
上から10行目は
y=94m+14
になります。
406ではなく406/29のはずです。
したがって問題の解答の方も、
-29m+1>0
94m+14>0
を共に満たすmが0のみですから、与式を満たす整数解は1つということになると思います。
ちなみに、同じく10行目の、-84という部分がありますが、これは-94の間違いでしょう。
検証して下さい。
=>[作者]: 連絡ありがとう.長い答案になると最後の方で疲れが出てしまうようで,訂正しました.
■[個別の頁からの質問に対する回答][合成関数 について/17.2.2]
解説、とても分かりやすいです。
(g゜f)(x) = g(f(x))というのはわかったのですが、((f゜g)゜h)(x) や(g゜(f゜h))(x)、(h゜g゜f)(x)といった場合はどのように考えればよろしいでしょうか?
解き方というよりも、このページの右上にあるようなイメージをつかみたいです。
よろしくお願いします。
=>[作者]: 連絡ありがとう.
(f は
x→h(x)→g(h(x))→f(g(h(x))) のように右から順に作用していきます.
g は
x→h(x)→f(h(x))→g(f(h(x))) の順,
(h は
x→f(x)→g(f(x))→h(g(f(x))) の順です.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.2.2]
とても分かりやすかったです!苦手を克服できました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][判別式 について/17.1.31]
素晴らしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角形を解くとは について/17.1.31]
三角形のB角の式 Cos B=b^+c^-b^/2ac
となっていますが Cos B=a^+c^-b^/2ac
ではないでしょうか?
=>[作者]: 連絡ありがとう.メールソフトが故障していたため,約1か月半の間連絡の文章が行先不明になっていましたが,フォルダの検査で生き返りました.入力ミスを訂正しました.(2017.3.6)
■[個別の頁からの質問に対する回答][三角比の相互関係 について/17.1.31]
公式2の証明、仮定の部分でsinA=y/xになっていますが、y/rの間違いではないでしょうか?
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/17.1.29]
非常にわかりやすくて助かりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][簡単な重積分の計算 について/17.1.29]
よく解りました(理解できました)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/17.1.29]
π-aなど文字の場合もやった方が良いと思います。
=>[作者]: 連絡ありがとう.この頁は基本練習ばかりなので言われる意味はわかりますが,言葉尻を突っ込むと,πは定数aはθと同種の文字なので,文字の場合の練習はやっていることになっています.
■[個別の頁からの質問に対する回答][集合の表し方(オイラー図) について/17.1.29]
問題2の(2)で正しい答え(上から二番目)を選択しても×となるが、解説には上から二番目が正解と書いてある。
=>[作者]: 連絡ありがとう.昨日アップしたばかりで,トラブルは初期に起こるのお決まりのコースのようで.訂正しました.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/17.1.28]
宮廷志望理系
1ヶ月切ってはじめて和積覚えました
=>[作者]: 連絡ありがとう.旧帝大志望理系と読むのかな
■[個別の頁からの質問に対する回答][2円の交点を通る円・直線の方程式 について/17.1.28]
2円の交点を通る円・直線の方程式の
[解説]
○ 2つの円
x2+y2+ax+by+c=0 …(1)
x2+y2+dx+ey+f=0 …(2)
が2点で交わるとき,方程式
x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0…(A)
は,定数 k の値にかかわらず2交点を通る円を表す.
ここ、2交点を通る円ではなく、図形ではないですか?
k=-1のとき直線になるので。
=>[作者]: 国語表現の好みの話をしておられるのなら対応しません.「ただし,k=−1 のときは,2交点を通る直線を表す」と書いてあるのですから何も問題はありません.
これを「(A)は三角形を表すか,四角形を表すか,ただ2点を結んだ曲がった曲線を表すかまったくわかりません.アッハッハー,とにかく図形を表します.」と書けば,この文章は読者に対してほとんど情報を与えません.そんな文章なら書く必要がありません.
これに対して,日本国憲法第四十五条「衆議院議員の任期は、四年とする。但し、衆議院解散の場合には、その期間満了前に終了する。」のように原則を書き,例外を示すと明快になりますが
衆議院議員の任期は、そんなもの決まっていません,アハッハー
衆議院が四年以内に解散されなかった場合は四年とする。
と書く方が好まれるとは限りません.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/17.1.28]
素敵なページですね!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2進数の演算 について/17.1.27]
引き算以外なら、解けるようになりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/17.1.27]
いつも参考にさせて頂いております。
例3の回答(2)の3行目、
(x+2y)(1,1,0)・・・・略
ですが、(x+2z)(1,1,0)ではないでしょうか。
私が勘違いしているだけかもしれませんが、ご確認のほどよろしくお願いいたします。
=>[作者]: 連絡ありがとう.入力ミスでしたので訂正しました.
■[個別の頁からの質問に対する回答][不定積分(多項式2) について/17.1.26]
問題の∫(3x+4)dxを選択すると∫(3x-4)dxに変わってしまいます
=>[作者]: 連絡ありがとう.反転画像を作る作業で,圧縮比の加減で縦線が消えた?のが原因かな.直しました.
■[個別の頁からの質問に対する回答][微分係数 について/17.1.24]
わかりやすいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/17.1.24]
とってもわかりやすい。
本当に素晴らしい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内分点・外分点 について/17.1.24]
わかりずらいです。ちなみにぼくは一年間数学をやっていないため忘れた可能性があります!!!!
=>[作者]: 連絡ありがとう.易しい問題から初めて勘を取り戻さないと
■[個別の頁からの質問に対する回答][検定 について/17.1.24]
例3の右側の解説についてです。
「左の問題では,z = (59-61)/0.1=-2.0 < -1.96となって帰無仮説は棄却される」となっていますが、(59-61)/0.1=-20となるように思われます。
=>[作者]: 連絡ありがとう.訂正しましたが−20<−1.96は成り立ちます.(もっと微妙な問題にしないと離れすぎだろ!と突っ込みどころ満載になってしまった)
■[個別の頁からの質問に対する回答][検定 について/17.1.24]
例題(2)は出荷基準がある値以下であるのに、どうして片側検定でないのでしょうか?
=>[作者]: 連絡ありがとう.まず両側検定にするか片側検定にするかはデータから自動的に決まるのではなく,分析者が何に関心があるかによって決まるということを押さえておきましょう.ある値から離れていたら困る場合は両側検定に,ある値よりも小さければ困るが大きいのは構わないという場合は片側検定と考えましょう.
さて,標準偏差1(g)以下と,言葉としては「以下」と言っていますが
の「範囲内にある」というのが帰無仮説なので,その両側に外れたら棄却域になります.だから両側検定で調べようと考えたわけです.
■[個別の頁からの質問に対する回答][1次不等式 について/17.1.23]
わかりやすかったです
テスト勉強に役にたちました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次不等式 について/17.1.23]
よかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][面積の求め方 について/17.1.23]
わかりにくいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][平方根の計算・・・センター試験問題 について/17.1.23]
【センター試験 2010年度:数学I・A(本試験) 第1問[1]】の回答クの0~3の式の中の1の式に誤りがあります。分母の5が√5になっています。√を消してください。
=>[作者]: 連絡ありがとう.転記ミスですので訂正しました.
■[個別の頁からの質問に対する回答][合成関数 について/17.1.22]
とてもわかりやすかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組合せ(文章題) について/17.1.22]
わかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/17.1.22]
非常にわかりにくい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][多項式,分数関数,無理関数の不定積分 について/17.1.22]
見やすい!
あらゆる場合を網羅していて、分かりやすく復習ができた
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重積分.変数変換.ヤコビアン について/17.1.22]
問4のxに誤り.
x=1/3(2u+v)
=>[作者]: 連絡ありがとう.その間違いを引きずってさらに2,3個の式がおかしかったので,併せて訂正しました.
■[個別の頁からの質問に対する回答][関数の極限 について/17.1.21]
いつも分かりやすい説明で、よく利用させてもらっています。
このページで、いくつかの問題を解く際に、答え欄をクリックしても反応しないために解答できなかった問題が3つほどありました。私はMac OSを使っていて、Safariを重荷利用していますが、たまに他のサイトを利用する際にSafariでは動かなくても、Google chlome では動く場合があり、こちらのページもGoogle Chlomeでも試してみましたが、やはり動きませんでした。(厳密に言うと、即答問題の上列左から2番目と4番目をクリックできないことと、問題1の(6)に答えを入力できないことです。)あまり支障をきたすわけではないのですが、気になったのでコメントしました^^
でも、基本的にどのトピックも分かりやすい説明で、とても助かっています。ありがとうございます。
=>[作者]: 連絡ありがとう.ブラウザによってはチェックボックスや入力欄が左の関数の陰に入ってしまって下敷きになっていたようですので訂正しました.
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/17.1.20]
例がとてもわかりやすく、完璧な解説で、初学者にとっても嬉しい限りでした。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][決定係数 R2とは について/17.1.20]
※についてですが独立な時に総和の関係が成立しないのは引数が独立な場合だけではないですか?
一つのデータ点y_iに関して残差偏差σ^i_eと回帰偏差σ^i_Rの和が総偏差になっていなさいという関係がn個あって全部足しなさい:Σ_i (y_i-\bar{y}) = Σ_i(σ^i_e+σ^i_R)が元の等式ですよね?
σ^i_eとσ^i_Rは元々i番目のデータ点に対して全偏差を回帰直線の値で分割して作った値なので独立ではないですよね?両辺二乗したときの引数がiとjのコンビネーションの場合には消えますが。
もしくはこの系のパラメータの拘束条件から自動的に消えるのでしょうか?
=>[作者]: 連絡ありがとう.特に難しい話しはしていないつもりです.
独立←→無相関←→垂直 のとき
n次元ベクトル
が垂直となることを使って
と書いてあるのです.
■[個別の頁からの質問に対する回答][多項式の除法(割り算) について/17.1.18]
多項式の除法 の問3において、一部下線がずれております。
=>[作者]: 連絡ありがとう.15年くらい昔に作ったプログラムで現在のMSIEとEdgeに合わなくなっていましたので訂正しました.(応急処置の継ぎはぎで持たしてあります)
■[個別の頁からの質問に対する回答][2進数の演算 について/17.1.17]
二進数の演算の例2の問題が1101×1011に対して、解き方A.Bの問題が1101×1010についての解き方になっています。
あと、例2の解き方A(3)の最後にでてくる答え0が一つたりなかったです。
最後に、質問なんですが…
回答Aの(3)にでてくる22=っとなっている22は何処からきた22なのでしょうか?
頑張って考えてるのですがわかりません。
あと、ほんとーのほんとーに最後に。
凄く分かりやすく大変ためになっています。
こんなサイトを作ってくださりありがとうございます。
=>[作者]: 連絡ありがとう.例2の解き方Aはいろいろと違っていました.というか,上の例1のコピペをしてから作業を始めようとして,コーヒーか何かを飲んでいるうちにその行を見失ったという辺りが真相かも
■[個別の頁からの質問に対する回答][確率の加法定理,余事象の確率 について/17.1.17]
問題2の(5)のイ)の(答)の中で、3色となるときの分子の最後は、3C2ではなく2C1だと思います。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][n進数の演算 について/17.1.17]
a=d(n) ,b=e(n),c=f(n)とする。10進数で a×b=cのとき,d(n)×e(n)==f(n)は成り立つのか?
=>[作者]: 連絡ありがとう.a(10) =d(n) ,b(10) =e(n) ,c(10) =f(n) と書いてあるのだから,a(10) ×b(10) =c(10) のとき,d(n) ×e(n) =f(n) が成り立つのは当然でしょう.
■[個別の頁からの質問に対する回答][展開公式 について/17.1.16]
全て素晴らしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/17.1.16]
いやー時代が変わりましたね。素晴らしいの一言です。私は第2世代ベビーブームの薬剤師です。
人生をやり直した気持ちでやってみました。今後もっともっと素晴らしいサイトを構築してくださいませ。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の定義 について/17.1.16]
対数が少しわかった。嬉しい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][群数列 について/17.1.16]
答えください
=>[作者]: 連絡ありがとう.2択の問題で間違いなら他方が正解で,3択の問題で間違いなら残りのどちらかが正解なのだから,押せばわかります.
■[個別の頁からの質問に対する回答][補集合 について/17.1.15]
問題もあってわかりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆行列の求め方 について/17.1.15]
大変にわかりやすい解説だと思います。成分の余因子をひとつずつ求めて、余因子行列の転置行列を求めるところなど、とても良いと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数のグラフ[標準形] について/17.1.15]
他のサイトよりも遥かに解説が丁寧で(わかっている前提だと見なさず省略しないorその問題を解く上での、前の範囲の予備知識を解説しているページにすぐ飛べるようになっている)、かつ例題を解いていけば何がわかっていないかを即座に確認できて非常に便利でした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/17.1.14]
自分は受験生なのに勉強する意思が弱いのですが、パソコンを使って簡単にできて、すごくわかりやすく勉強しやすいです。本当に感謝の気持ちでいっぱいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.1.15]
11 間違っています
反例としてルート3
ルート3^2は奇数ですが、ルート自体に奇数偶数の定義付けがされていませんので
答えは十分条件です
(追伸) 整数nでしたか…
見落としてました。申し訳ない
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/17.1.13]
(5)のλ=ー3のときの3列目の3行目がー6ではなくてー3だと思います。あとは(6)が分かりにくく感じました(;'∀')
=>[作者]: 連絡ありがとう.(5)は訂正しました.
■[個別の頁からの質問に対する回答][行列の積 について/17.1.12]
(5)の式を示す画像が正しく表示されておりません。修正していただけると嬉しいです。
=>[作者]: 連絡ありがとう.このエラーが時々起こることは認識していましたが,今原因が特定できました(たぶん).直っています.
■[個別の頁からの質問に対する回答][軌跡の方程式2 について/17.1.11]
問題3のヘルプの下から2行目
「(s , t)=(3 , 0) のとき (x , y)=(2 , 0)」は間違っていて、正しくは
「(s , t)=(6 , 0) のとき (x , y)=(2 , 0)」ではありませんか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][恒等式 について/17.1.11]
「次の問題」のボタンに「忘れずに!」の吹き出しが重なっていて押しにくいので、もう少しずらしてほしいです。
=>[作者]: 連絡ありがとう.昔はなかったブラウザのEdgeが昨年あたりから増えてきて,上下方法のずれ方がFirefoxと同じになるようです.対応しました.(この問題は「忘れずに!」の吹き出しがあるどの頁でも起こりますが,頁数が多過ぎて前もって訂正できませんので,要望が出た頁を直すようにします)
■[個別の頁からの質問に対する回答][三角形を解くとは について/17.1.11]
2辺とその間の角(2角きょう辺ともいう)
→2辺とその間の角(2辺きょう角ともいう)
ではないでしょうか?
=>[作者]: 連絡ありがとう.小見出しがあやしいコピペになっていて,数か所引きずっていたようですので訂正しました.
■[個別の頁からの質問に対する回答][次数の方程式 について/17.1.11]
f(x)が定数の場合(例2ではn<=1のとき)を場合分けする説明があればありがたいです。
問題と例1ではn>=1,例2ではn>=2でやっていますが,これらをn>=0としてまとめて扱うことはなぜできないのでしょうか。
=>[作者]: 連絡ありがとう.次の点に注意してください.
n次式を微分したらn-1次式になるとは限らない・・・1つだけ例外があるのです.つまり無警戒に
としたら間違いとなる数nが1つあるのです.左の式はn=0ならかろうじて成り立つように見えますが
にはなりません.右の式でいえば
とはなりません.
簡単なことですが,定数を微分すると0になります.(
)したがって,上記の式でnが0になる可能性があれば微分の形が変わるので,場合分けが必要となるのです.
■[個別の頁からの質問に対する回答][同次形 微分方程式 について/17.1.10]
問題6
右辺 = -u - 2u^2
=>[作者]: 連絡ありがとう.解説の中で係数の2が抜けているところがあるというご指摘だと理解しました.訂正しました.
■[個別の頁からの質問に対する回答][二重根号 について/17.1.10]
解答の正解不正解を問わず、次の問題に進めるようにして欲しいです。
=>[作者]: 連絡ありがとう.その問題は,前の問題ができなければ次の問題に進めないように作ってあるものです.ほかの頁の問題をやってください.
■[個別の頁からの質問に対する回答][たすき掛け因数分解(2文字) について/17.1.10]
(ax+b)(cx+d)=acx2+(ad+bc)x+bdで、bとdが、両方マイナスになっている問題があることの、説明が欲しい。
=>[作者]: 連絡ありがとう.どうも言葉がうまく通じませんが(ax+b)(cx+d)=acx2 +(ad+bc)x+bd と(ax−b)(cx−d)=acx2 −(ad+bc)x+bd は同じものじゃないのかという質問なら「同じではない」「1次の係数の符号が違う」2x2 +7x+3=(2x+1)(x+3) であるが2x2 −7x+3=(2x−1)(x−3) になります.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/17.1.10]
助かりました(`_`)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.1.10]
この辺が数1aでの不安要素だったのですが、とても分かりますいし、問題形式で理解度も深まったので安心してセンター試験に臨めそうです。助かりました。
=>[作者]: 連絡ありがとう.受験生は大変ですが頑張ってください.
■[個別の頁からの質問に対する回答][多項式の除法 について/17.1.9]
問1-4の余りを間違えてもendと出ますが宜しいのでしょうか?
=>[作者]: 連絡ありがとう.チェックしましたがそのようなことは起こりません.例外的に,まず余りまで正解にして,後から誤答に書き換えてもendになったままということでしたら興味の方向が違うように思いますが・・・.
■[個別の頁からの質問に対する回答][連続整数の積 について/17.1.9]
面白かった
=>[作者]: 連絡ありがとう.この教材は公開してから1年経過していないかも
■[個別の頁からの質問に対する回答][ケーリー・ハミルトンの定理 について/17.1.9]
問題2のA³-5A²+7A は、A³-5A²+7Eの間違いだと思います。(でないと答えが違う)
=>[作者]: 連絡ありがとう.問題と解答にはエラーはないが,解説図に数か所ボロボロのところがありましたので訂正しました.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/17.1.8]
勉強に活用しています
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルのなす角 について/17.1.8]
図形など図があればもっといいと思う
=>[作者]: 連絡ありがとう.現在筆者は次のように整理しています.
(1) 高校数学で習うベクトルには,図形で表される「矢印ベクトル」と成分で表示される「成分ベクトル」とがあります.ベクトルのなす角というのは図形的な意味ですが,実際には成分計算だけでできることに慣れるというのが第1の目標です.
(2) 3次元,4次元,5次元・・・今日では中学生でも多次元のデータを扱っていますが,そう言わないだけです.
生徒名 x(国語) y(数学) z(英語) a 2 3 2 b 5 2 3 c 3 1 4 d 3 5 2 e ・・・ ・・・ ・・・ f 4 4 5
左の表で生徒ごとの3教科の得点傾向が似ているかどうかを判断するには,行ベクトル
などの個人ごとの「3次元ベクトルのなす角」が小さいかどうかで見るのが1つの方法です.また,教科ごとの得点傾向が似ているかどうかを判断するには,列ごとに見たベクトル
などの「6次元ベクトルのなす角」が小さいかどうかになります(左の表で6次元というのは縦に6個の数字が並んでいるから:6人だから).
このようにして,実生活で扱うデータのほとんどは多次元ベクトルに対応しており,図を使わずに大きな数値の表だけを見て「ベクトルのなす角」という夢を見る能力が必要となります.(
この頁 参照)
(3) ご質問の頁は2次元ベクトルを扱っていますので,図を描こうと思えば描けますが,図があっても問題が解けるわけではありません.次のような意味合いで,1つや2つは図があってもよいとは思います.
3.1) 答が2つあって迷うような場合とか,方程式で求めた値に対して実際には図が描けないような場合に,図で検証することができる.
3.2) 文字ばかりの教材では暑苦しいが,ワンポイントの図があればリラックスでき,結果的に学習が進む.
■[個別の頁からの質問に対する回答][対数計算 について/17.1.8]
この前は、解説ありがとうございました!
この前と同じような問題ですが…途中までわかったのですが、その先がわかりません。教えてください!
log2(1/9)×log3(1/8)
=(-log2 9 )×(-log3 8)
この先の計算方法を教えてください!
底の公式にしても前の問題のようにできないのでどうすれば良いのかわかりません…
=>[作者]: 連絡ありがとう.今度は底の変換公式の練習になります.
…(底の変換公式)
(ここでcは>0, ≠1なら何でもよいので都合の良いものを選ぶ)
において,(ア)全部の底を10にそろえる場合は
こので「ノミの三段跳び」に持ち込む:
とすると,次のように約分できて
(イ)全部の底を2にそろえる場合は
(ウ)底を3にそろえてもできる
■東京都[p-npさん/17.1.7]
x^2+y^2=1上に(a,b)で接している接線Lと、x軸・y軸で囲まれた面積Sが最小になるaの値の求め方がわかりません。
Lの方程式を求めて、xとy切片の切片を掛けて・・と考えたのですがうまくできませんでした。
=>[作者]: 連絡ありがとう.
点(a,b)が座標軸上にあると囲まれた図形ができないので,a,b>0とする.このとき接線の方程式は
…(1)
ただし,(a,b)は円周上の点だから
…(2)
が成り立つ.(1)とx軸との交点(のx座標)はy=0を代入すると得られて
(1)とy軸との交点(のy座標)はx=0を代入すると得られて
直角三角形になるから
…(3)
(2)の条件の下で(3)の最小値を求めるのであるが,変数が2つもあるのは煩わしいので,(2)式を書き換えて1つの変数で表す.
とおく
このとき
(←2倍角公式)
のとき
は
のとき最大値1をとる.
したがって,Sは
のとき,最小値1をとる.
※三角関数の2倍角公式や媒介変数表示を習っていない場合は
正の数a,bについての相加平均≧相乗平均の関係
(等号成立は
のとき)
を使って
(等号成立は
のとき)
としてもよい.
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/17.1.7]
すごくわかりやすく、勉強が楽しいです!ありがとうございます!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][回転と拡大 について/17.1.5]
問題2-3は1-iではないでしょうか?
=>[作者]: 連絡ありがとう.画面上のHelpを見てください.
■[個別の頁からの質問に対する回答][N進法の小数 について/17.1.5]
例8の8進法で表された小数について、7.08とありますが、8進法なのに8があるのは変なのではないですか?7.1ではないですか?違ったらごめんなさい
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました。
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/17.1.5]
むずかしかった
=>[作者]: 連絡ありがとう.1次不等式は教育課程の改訂ごとに中学校と高校の間を行ったり来たりしたので,中学校でほとんど習っていない場合があるかもしれません.
■[個別の頁からの質問に対する回答][軌跡の方程式 について/17.1.5]
とても分かりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/17.1.5]
そもそもページが見づらい
=>[作者]: 連絡ありがとう.ここら辺が一杯々かな
■[個別の頁からの質問に対する回答][絶対値付き関数の積分 について/17.1.5]
短時間でこなせるように、難易度の低い問題から中程度の問題に遷移する形で、問題数を増やしてほしい。
=>[作者]: 連絡ありがとう.サブメニューが易しいものから難しいものへの順に並んでいますので,活用してください.
■[個別の頁からの質問に対する回答][正弦定理 について/17.1.4]
>[個別の頁からの質問に対する回答][正弦定理について/16.12.28]
「例3の解答は3/√3ではないのですか」への回答ありがとうございました。
分母の有理化ですね。忘れてました。またよろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/17.1.4]
シンプルかつわかりやすくて苦手分野のところは助かります。活用していきたい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][位置ベクトルの応用 について/17.1.4]
解答して合っていると消える、というのが、やる気を出しやすいと思います。
昔習ったベクトルの復習をしたくて、このページにたどりつきましたが、
とてもわかりやすかったです。
=>[作者]: 連絡ありがとう.
■北海道[キズナさん/17.1.3]
0≦Θ<2πの範囲でsinΘ<-√3/2の値を求める問題がわからないです。教えてください
=>[作者]: 連絡ありがとう.
この頁 に類似問題がありますので見てください.
質問がラジアンを使って書かれているので,数Ⅰでなく数Ⅱの範囲でしょう.
左図のように
となる角度が
で
の値がこれよりも小さくなるのはy座標が下になる所なので,黄色で示した範囲になります.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/17.1.3]
整数nについてをもっと見やすく目立たせたほうがいいと思います。
=>[作者]: 連絡ありがとう.改行してあり結構目立っていると思いますが・・・この「整数について」という前提を読まなくても,意味が変わる問題は含まれていません.例えば第9問で「nが3の倍数であることは,nが6の倍数であるための( )条件 」という問題では,nが3の倍数であることはとなっているので,普通に読めばnが小数,分数,無理数,虚数である場合はどうなるのかとは考えません特に注意書きがなくても,nが3の倍数であるなら整数と考えのが普通です.
■[個別の頁からの質問に対する回答][絶対値 について/17.1.1]
問題4、2000年度東北薬大の問題ですが、ヒモの長さで表されても分かりません。
=>[作者]: 連絡ありがとう.その説明方法では分かりませんという形で前提を覆してしまう場合は,自分で他の方法を考えるしかなくなります.前提を覆してはいけません.(絶対値は符号のない数なのでひもの長さで考えることができるのです)
■[個別の頁からの質問に対する回答][底の変換公式 について/16.12.31]
log2 1/5 ×log5 1/4など分数のある場合の計算方法も教えて欲しい
=>[作者]: 連絡ありがとう.
のような変形は底の変換公式とは関係なく,
それ以前に 登場する対数の変形です.
この公式
の特別な場合として
もしくは,この公式
の特別な場合として
と考えます.
これらの前処理を行ってから,次に底の変換公式を使うことになります.
■[個別の頁からの質問に対する回答][順列 について/16.12.30]
分かりやすい!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.12.30]
わかりづらい
=>[作者]: 連絡ありがとう.そういう感想もあり得るかも.相性がよくなかったということで・・・
■[個別の頁からの質問に対する回答][正弦定理 について/16.12.28]
例3の解答は3/√3ではないのですか。
=>[作者]: 連絡ありがとう.途中計算に省略がありますが
になります.(
と
を約分したら,分子に
が残るということで・・・)
■[個別の頁からの質問に対する回答][展開公式 について/16.12.27]
41のおっさんです。小さい頃から母親から罵られまくって高校に入って全く自暴自棄になって、勉強しなかったのですが、今落ち着いて見直すととても面白いです。欲を言えば、誘惑になる広告が非表示だといいですね。これからも使わせてもらいます。素晴らしいサイトをつくってくれてありがとう。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆裏対偶 について/16.12.25]
この命題などに関する問題があればよかったと思います。
=>[作者]: 連絡ありがとう.簡単な問題は問1,問2にあります.もっともよく使う対偶証明と背理法の問題はその次の頁にあります.
■[個別の頁からの質問に対する回答][t分布 について/16.12.24]
t分布が、よく理解できていないので、いきなりt分布の応用問題の解き方を教えていただいても、理解できた感じがしません。 お手数ですが、正規分布やt分布関数の導入の仕方を、分かりやすく解説頂けないでしょうか?
=>[作者]: 連絡ありがとう.メニューから正規分布,t分布と順に読んでください
■[個別の頁からの質問に対する回答][漸近線の方程式 について/16.12.24]
わかりやすい説明で概要を掴めますがいざ実践してみるとなかなかできないものです。
なので簡単な問題がその後に付属して実戦形式で行えるのは良かったと思います。
それによって理解が深まった気がします。
=>[作者]: 連絡ありがとう.筆者の苦労が込められているという点からいえば
増減.極値.凹凸.変曲点.漸近線.グラフ の方もお勧めしたいところです.
■[個別の頁からの質問に対する回答][確率の基本 について/16.12.23]
a b c d e の5人がじゃんけんを1回するとき
a b c の3人が勝つ確率を教えて下さい
=>[作者]: 連絡ありがとう.
5人の手の出し方は
通り
そのうちで,a,b,cが1回で勝つのは
abcの手 deの手 パー(紙) グー(石) チョキ(ハサミ) パー(紙) グー(石) チョキ(ハサミ)
の3通りだから,
■[個別の頁からの質問に対する回答][ベクトルの実数倍 について/16.12.23]
図をペイント式ではなくラスタ式にした方が良い。少し矢印が見にくい
=>[作者]: 連絡ありがとう.Webページに表示可能な jpg,gif,png いずれの方式でも無理です.
■[個別の頁からの質問に対する回答][繁分数式 について/16.12.23]
良かったと思います
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数2階線形非同次微分方程式 について/16.12.23]
2階線形非同次微分方程式のページの問題5の解答が間違っていると思われますので,確認をお願いします.
=>[作者]: 連絡ありがとう.あなたが考える解答をお知らせください.
■[個別の頁からの質問に対する回答][2点を通る直線の方程式 について/16.12.22]
xの軸に垂直な直線を引くための方法がわかりません。
=>[作者]: 連絡ありがとう.この教材は高校数学Ⅱの教材で「2点を通る直線の方程式」を扱ったものです.あなたが,どのような立場の人で,どのレベルの回答を求めているのか述べていただかないと,答えるのは難しいです.
■広島[CHARGE MAZDA 787Bさん/16.12.21]
極大×極小<0 が分かりません
=>[作者]: 連絡ありがとう.何の話をしているのか通じません.どの頁を見ているのか書いてありません…アクセスログからあなたが見た頁を調べても,その話はありません.おそらく,教科書とか参考書に書いてある別の話を尋ねているのだと思います.
高校生が出遭う初歩的な問題で極大×極小<0が出てくるのは,「3次方程式が3つの異なる実数解を持つ条件」などです.
3次の係数が正負いずれであっても,3次関数がx軸と異なる3点で交わる条件を求めるには,上の(A)(B)の図のように極大×極小<0となります.
だから問題に応じて極大値と極小値を求めて(おそらく文字係数)それらの積がマイナスになることを条件にします.
ただし,理屈上はこれでよいが,このようにして求めると次数が高くなって解きにくいので,実際には(A)(B)いずれも極大値>0かつ極小値<0を条件にする方が解きやすくなります.…問題も見ないで言えるのはここまでです.(##)
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/16.12.21]
解を求めるプログラムで分数や小数の2次方程式が解けない
=>[作者]: 連絡ありがとう.正負の整数を入力して[解を求める]と書いてあるのだから,正負の整数になるようにするのです.
読者がカチンと来るか,当然だと思うかは分かりませんが,その頁は高校生向けの頁で,分数や小数係数なら分母を払うとか10倍,100倍,...すれば簡単に整数係数になります.
【分数の例1】
の場合
両辺に6を掛ける
【分数の例2】
の場合
両辺に12を掛ける
【小数の例1】
の場合
両辺に10を掛ける
【小数の例2】
の場合
両辺に100を掛ける
■[個別の頁からの質問に対する回答][展開公式1 について/16.12.21]
問題3の(4)、公式から外れたものを出題しているのがとても良いと思いました
=>[作者]: 連絡ありがとう.何でも公式にあてはまると考えられると,とんでもない答案ができてしまうので,注意を促すために入れました.
■[個別の頁からの質問に対する回答][双曲線関数 について/16.12.21]
第1ページ右側に x=sinθ,y=cosθとありますが、x,yが逆ではないでしょうか?
同様にその下も x=sinhθ,y=coshθとあるのもx,yが逆になっていると思われます。
=>[作者]: 連絡ありがとう.逆でしたので訂正しました.
■[個別の頁からの質問に対する回答][直交行列 について/16.12.20]
よかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][相関分析 について/16.12.20]
大変わかりやすい説明でした。
最後のクラメールの計算についてわからない点があります。手元の教科書ではクロス表の縦計、横計に1つでも「0」がある場合、独立係数は計算できません、とあります。これはそれぞれ表14で言うと「ア」や「A」と答えた人の合計値を差し示し、「B2:E5」の黄色の範囲にある個別の回答者数は「0」であっても構わないということでしょうか?また2×2のクロス集計ではよくイエーツの補正が紹介されていますが、それ以上のクロス表については記載が見つかりません。このような場合補正方法はないのでしょうか?それともマス数が多く数値が十分あるため、補正しなくとも相関性について十分な吟味をすることができる、という考えがなされているのでしょうか?このような細かい疑問点についても書かれていると個人的に大変うれしいです。
=>[作者]: 連絡ありがとう.縦または横の合計が0の場合,期待度数の計算で分母が0になるのでできないと思います.しかし個別の度数が0であることは問題ありません.
■[個別の頁からの質問に対する回答][剰余の定理 について/16.12.19]
重解のときの解き方も載せて欲しい。
=>[作者]: 連絡ありがとう.
この頁 の下の方を見てください.
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/16.12.19]
1/tanx=cosx?
=>[作者]: 連絡ありがとう.
(ア)基本公式そのものを質問しているものとして答えます.
が成り立ちますか?という質問だとします.結論から言えば,成り立ちません.
その頁の(6)にある
の右辺はコタンジェントです.
でお互いに分母と分子を入れ換えたもので,
の方は授業では習う場合も習わない場合もあります.
(イ)これとは異なり,ある特定の角で1/tanx=cosxが成り立つことはありますか?という質問である場合
となる場合は
になり,
となる角度では初めの式の
が定義されませんので,結局この式が成り立つ角度はないということになります.
■ibaraki[ichiさん/16.12.19]
三平方の定理を使い
x^2=(2+sqr3)^2+1^2
xを求めようとしていますが、ルートの中にルートがあり先に進めません。
答えは sqr6+sqr2 です。
=>[作者]: 連絡ありがとう.
二重根号の外し方 のことですから,質問者が当然高校生以上だと想定して答えます.
の右辺を展開してから整理します
二重根号の内側の係数は必ず2にします
積が12,和が8となる2数は6と2だから
■[個別の頁からの質問に対する回答][期待値 について/16.12.18]
式の導出が詳しくて分かりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の方程式 について/16.12.18]
国家試験の勉強で活用しましたが、大変懐かしく、解りやすく勉強させて頂きました。有難うございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][センター試験問題 三角比2012 について/16.12.18]
最後の問題の解説、点Gは△ABCではなく△FBCの重心ではないでしょうか
=>[作者]: 連絡ありがとう.訂正しました.また,(1)以下の文章で根号の表示がずれていましたので直しました.
■[個別の頁からの質問に対する回答][展開公式 について/16.12.17]
合っていたら記号を『×→○』にしてほしい。
=>[作者]: 連絡ありがとう.SafariかChromeで全角数字で入力していませんか?今の生徒は小学校以来コンピュータを使う授業を経験しているので,漢字の一種の全角文字(2バイト文字)と半角英数字(1バイト文字)の違いは分かっているはずです.数値計算は半角数字で行います.…(A)
■[個別の頁からの質問に対する回答][絶対値 について/16.12.16]
絶対値が三つの関数の解き方とそのグラフの書き方とそのグラフの最大値と最小値の解き方が無いので、作った方がいい。
=>[作者]: 連絡ありがとう.まず基本が分かるようになることが第1の目標です.■4の問題のように絶対値が3つある問題を幾つか示す場合もありますが,一層踏み込んだ問題については,基本がわかった後の各自の研究課題とするのがよいと考えます.
■[個別の頁からの質問に対する回答][対数の計算 について/16.12.16]
こんにちは。Windows 8.1 + IE11から閲覧すると、「変数は分けるのではなく集める方が多い」という項に、広告がかかってしまって、文章の右端が読めません。全選択してメモ帳貼り付けすれば読めるのでそこまで支障はないですが、気になったのでフィードバックします。
当方社会人ですがたまに数学計算が必要になり、このような Web サイトは大変ありがたいです。今後ともよろしくお願いいたします。
=>[作者]: 連絡ありがとう.tableが2重になってたため,paddingの幅を読み間違っていたようです.訂正しました.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルをエクセルのソルバーで求めるには について/16.12.15]
固有値ベクトルを求めることができません。
=>[作者]: 連絡ありがとう.
(A) 筆算で求めるには
この頁
(B) R(インストール方法は
この頁 )で求めるには
この頁
(C) wxMaxima(インストール方法は
この頁 )で求めるには
この頁
自分のやりやすい方法で行ってください.
■[個別の頁からの質問に対する回答][3点が一直線上にあるための条件 について/16.12.14]
分かりやすく、重宝しています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの和 について/16.12.14]
全く理解できませんでした()
=>[作者]: 連絡ありがとう.それ以上やさしい教材は準備していません.
■[個別の頁からの質問に対する回答][数学的帰納法(等式の証明) について/16.12.14]
例題5の
1·2+2·3+3·4+···+k(k+1)=13 k(k+1)(k+2) …(B)
(B)の両辺に (k+1)(k+2) を加えると
1·2+2·3+3·4+···+k(k+1)
左辺に加えられてますか?
1·2+2·3+3·4+···+k(k+1)+(k+1)(k+2)ではないかと。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][媒介変数表示 について/16.12.12]
媒介変数表示の例2の345度の時に表示する点が間違えているかもしれません
とてもわかりやすかったです、復習に使わせていただきました
=>[作者]: 連絡ありがとう.ブラウザによっては表中の座標のマイナスの符号が上下にずれるものがありましたので訂正しました.また,ブラウザによっては点が縦方向に微妙に下にずれる場合がありましたので訂正しました.
■[個別の頁からの質問に対する回答][条件付き確率 について/16.12.12]
とてもわかりやすくてよかったです。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/16.12.11]
(cosα)^3*sinα
=>[作者]: 連絡ありがとう.質問なら文章で書いてください.その式をどうしてほしいのですか?
参考までに,
wxMaxima で (cos(a))^3*sin(a)と書き込んで,メニューから三角関数の整理を選ぶと
と表示されるようですが・・・
■[個別の頁からの質問に対する回答][剰余の定理 について/16.12.11]
例題の解説の後についている要点で納得することがあったので凄く助かりました!
問題も典型問題が多いし、ページも見やすいです。
難易度の高い問題も1.2題つけてもらえたら嬉しいです。大学の過去問レベルのもの等々……
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.12.11]
8番の問題を間違えました。
解説の[十要は重要である]のやり方が役に立ちました!
問題か沢山ないサイトが多いので、ここでは助かりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3直線が1点で交わるための条件 について/16.12.11]
求める定数がaとbの二つある場合が書いてないので、そこがあるといいと思います
=>[作者]: 連絡ありがとう.未知数がx,y,a,bのように4個ある場合を,3直線が1点で交わる条件から解くと,条件不足のため不定解になります.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/16.12.9]
分かりやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][剰余の定理 について/16.12.9]
例題8の解答の中間式で係数2が抜けてます。
=>[作者]: 連絡ありがとう.最近加筆した部分なので,入力ミスがまだ他の読者にバレていなかったようです.訂正しました.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/16.12.8]
非常に分かりやすく、やりがいのあるwebです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/16.12.8]
問8?
=>[作者]: 連絡ありがとう.問8がどうかしましたか?選択肢のうちのいずれかを選んでもらうとhelpが出ますので,それを読んでください.
■[個別の頁からの質問に対する回答][相関係数,回帰直線 について/16.12.8]
アンケート項目4,の手前、
『r表より,自由度48で』というくだりですが、もしかしたら38、ではないでしょうか。
公開されているデータのnがn=40だからです。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][繰り返しのある対応のない二元配置の分散分析 について/16.12.8]
混合計画で交互作用があった場合は、どのような分析をすればよいのか教えていただけると助かります。
=>[作者]: 連絡ありがとう.この教材は体験・入門的なもので,さらに踏み込んだ内容や質疑は想定していません・・・筆者も責任の持てる解答を示せません.
■[個別の頁からの質問に対する回答][逆関数 について/16.12.8]
基本のチェックの2問目で解答の配置が悪いと思います。
√2xを選んだつもりで(3)を選んだのに…
=>[作者]: 連絡ありがとう.謎の暗号のような感想を解読するのにとても時間がかかりました.読者が「基本のチェックの2問目で解答の配置が悪いと思います。」と述べていることから「Edgeというブラウザを使ったら,ほかのブラウザと全く異なる配置になることがある」という意味だと分かって,ようやく訂正できました.⇒ブラウザなどの情報も書いてください.
■[個別の頁からの質問に対する回答][マクローリン展開 について/16.12.7]
ためになりました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/16.12.7]
正解をしているのに×がつきます
=>[作者]: 連絡ありがとう.何番の問題に何と答えたのか述べないと,話が通じません.
■[個別の頁からの質問に対する回答][点Aの周りの回転 について/16.12.7]
点αの周りの回転、最後の+αを知らないで覚えてました
どうりで合わないわけだ
ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][期待値,標準偏差 について/16.12.6]
右の例4の度数分布表において,10個のデータの平均 mと標準偏差 σ(X) を求めると,(右欄に途中計算が書けるようにしておく)
m=(5+30+100+70+45)/5 = 25
とありますが、分母は10ではないでしょうか。
=>[作者]: 連絡ありがとう.訂正しました・・・その後の計算結果には影響しません.
■[個別の頁からの質問に対する回答][Excelを使った一元配置の分散分析 について/16.12.6]
見づらいです。
=>[作者]: 連絡ありがとう.モニター画面の32ビットで点検したものなので24ビットで見ると色調が薄くなり過ぎるようですので,灰色を茶色に変更しました.
■[個別の頁からの質問に対する回答][複素数の対称式,値の代入 について/16.12.6]
問題1~3でyが抜けています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][最大公約数,最小公倍数 について/16.12.5]
不定方程式をのせてほしいです
=>[作者]: 連絡ありがとう.今は別のことで手がいっぱいですが,そのうち不定方程式の頁を作らなければならないと考えています.
■[個別の頁からの質問に対する回答][内分点・外分点 について/16.12.5]
高校の授業で1時間かけてもわからなかった外分の意味や解き方を、このページが10分で完璧にしてくれました!ありがとござます!例題も理解できるようになりました(●´ω`●)
=>[作者]: 連絡ありがとう.昔,生徒の手元を見ていると,外分の意味を間違っている人が多かったので,この教材を作りました.
■[個別の頁からの質問に対する回答][総和記号Σ(シグマ)に慣れよう について/16.12.5]
<Σに慣れよう1>の問3の、<一番下の問題=Σ(j+1)の2乗>ですが、答えの4の2乗は必要ないのでは?
もし必要だとすればそれはなぜでしょうか?
=>[作者]: 連絡ありがとう.
(j+1)2 にj=0 を代入すると12 (j+1)2 にj=1 を代入すると22 (j+1)2 にj=2 を代入すると32 (j+1)2 にj=3 を代入すると42
要するに,
3+1 が
4 になるからです.あなたの理解は,まだ十分ではないかも・・・
■[個別の頁からの質問に対する回答][規則を見つける問題 について/16.12.4]
問9のヒントの、<2段目の差>とは?
2段目はどこにあるのですか?
=>[作者]: 連絡ありがとう.分かりにくそうなので,1段目,2段目の数列も表示しました.
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/16.12.4]
どこの教師よりも教科書よりも分かりやすかったです!
三角関数(性質?)分からなかったので調べてたら
このとんでもないわかりやすい図と説明が出てきて
なんか泣きそうになりました笑
本当感激です!
これから頼らせて貰います!
出会えて良かった、、、、、。!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][微分係数 について/16.12.4]
例2 答案A f&rsquoになっています
=>[作者]: 連絡ありがとう.セミコロンが1つ抜けていましたので追加しました.
■[個別の頁からの質問に対する回答][決定係数とは について/16.12.4]
すごいですね。もっと統計を勉強したらまた来ます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][等式の証明 について/16.12.3]
もっと詳しく教えてほしい。そして、違った不等式などもだしてほしい。
=>[作者]: 連絡ありがとう.不等式の証明については,先頭にあるサブメニューから不等式の項を選択してください.
■静岡[なしさん/16.12.3]
いつも参考にさせてもらっています。
二次曲線の極線の解説のところで、楕円の(解説)の部分でx0がx1になってる間違いがあると思います。
=>[作者]: 連絡ありがとう.解説の文章としては整合的になっていますが,図の解説と考えると合わないので訂正しました.
■[個別の頁からの質問に対する回答][順列,組合せ(章末問題) について/16.12.2]
前回に引き続き、あまり大きなことではないのですが、、、、、公式の要約の重複順列で、記号がHではなくΠが使われているのは何か深いわけがあるのでしょうか?僕が根本的にダメな間違いをしていましたら、おゆるしください・•・m(_ _)m
=>[作者]: 連絡ありがとう.その頁は章末のまとめの問題なので,詳しい話は前にある個別の頁を見てください.
深いわけというほどのことでもないのですが,異なるn個のものから重複を許してr個のものをとってくる組合せの総数を
n Hr で表し,異なるn個のものから重複を許してr個のものをとってくる順列の総数を
n Πr で表します.
(例えば)(a+b)2 を展開するとaa+ab+ba+bb となりますが,ab とba のように「書いてある文字の順序を区別する」と順列と見ていることになり,これが異なる2つのものa, b から重複を許して2つとってくる順列の総数2 Π2 =22 =4(a+b)2 を展開したときに,ab とba を書かれた順序を区別せずに同類項としてまとめるとaa+2ab+bb すなわちa2 +2ab+b2 となって,項の数は3個と数えることになります.これが異なる2つのものa, b から重複を許して2つとってくる組合せの総数2 H2 =3(a+b)3 を展開するとaaa+aab+aba+abb+baa+bab+bba+bbb となりますが,aab, aba, baa のように「書いてある文字の順序を区別する」と順列と見ていることになり,これが異なる2つのものa, b から重複を許して3つとってくる順列の総数2 Π3 =23 =8(a+b)2 を展開したときに,aab, aba, baa などを書かれた順序を区別せずに同類項としてまとめるとa3 +3a2 b+3ab2 +b3 となって,項の数は4個と数えることになります.これが異なる2つのものa, b から重複を許して2つとってくる組合せの総数2 H3 =4
※関係があるようなないような話として,ギリシヤ文字のΣは和を表すときに使い,Πは積を表すときに使う.Hはアルファベットで,その意味は重複組合せの頁に書いてあります.
⇒ギリシャ文字のΣはアルファベットのS...
S um(和)に対応
⇒ギリシャ文字のΠはアルファベットのP...
P roduct(積)に対応
■[個別の頁からの質問に対する回答][条件付き確率 について/16.12.2]
わかりやすかった!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積の法則 について/16.11.30]
とてもささいな点ですが、、、、、例3のエの塗り方は(アイウエで使った色以外)ではなく、(アイウで使った色以外)だと思いました。最終的な答えはあっていたので書くまでもないかと思いましたが、とりあえず書くことにいたしました。
=>[作者]: 連絡ありがとう.確かに筆の勢い(キーボードの勢い)が余って,エを選ぶときにエ以外などとあり得ない話になっていましたので訂正しました.
■[個別の頁からの質問に対する回答][重複組合せ について/16.11.29]
問題を選択した時に、背景色が濃く、明暗比が悪いために見づらい
=>[作者]: 連絡ありがとう.そんなことはありません.よく見えます--きっぱり
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/16.11.29]
有効数字について調べていたが、まったくわからない。説明が意味不明。
=>[作者]: 連絡ありがとう.通俗的に言えば,波長が合わなかったとかご縁がなかったということかな
■[個別の頁からの質問に対する回答][面積の求め方 について/16.11.28]
この積分の面積の分野でしたが、このページを見た途端に学校での授業での謎(お前は何を言っているんだ状態)や、教科書の謎(製作者の頭の中身にはウジでも沸いているんかレベルの欠陥教科書「東京書籍:数3」)が氷解しました。
考え方としては、まさにインテグラル橋を渡り、数値a,bの川に挟まれたメソポタミアの上を通る積分範囲を決める(わかっている数値によるxyグラフでの高さを決める)ことと、その橋の幅(xyグラフにおける横)をdx,dyなどの積分で求めるという内容でしたか。
※ただし、ここでのxyグラフは代名詞のみであり十字のグラフを指すものとする
意味不明な文章かもしれませんが、理解力のある先生が解読し、説明力のある先生が説明したならば文系を選択なさったこれから先の生徒さん、1998年生まれの私の後輩たちにも理解してもらえるかもしれません。
まぁ、もう既に似たような説明をされているようでしたら、自力でそこに辿り着いた身の程知らずの子供が埼玉に一匹(?)いたことを胸に留めてくだされば、この感想文(?)を書く時間に意味を見出せるというものです。
積分の面積の求め方を知らない私にすれば、底を合わせる、という考え方が最初にきて、その上で縦横の数値~、の行の方が嬉しいです。建築でもでも建物の基盤を固めてから建築、と言いますしね(謎)
長くなりましたが、稚拙な文をここまでお読み頂き、誠にありがとうございました。
そして、テスト前日にテスト範囲が全く(今までもそうで、IQは最低値110で最低平均120overあるのに学校の授業が理解できた試しがありませんでしたが(笑))わからない私を助けてくださり感謝の念でいっぱいです。大変失礼致しました。(失礼にも程がありますよね…)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/16.11.28]
むりなものがあります
=>[作者]: 連絡ありがとう.主語を省略すると反対の意味になる場合があります.すなわち「あなたには無理なものがある」ということでしたら「もっと頑張りましょう」になりますが,「そもそも解けない問題がある」ということでしたら「問題が間違っています」という意味になります.
■[個別の頁からの質問に対する回答][n進数の演算 について/16.11.27]
素晴らしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][割り算について成り立つ等式 について/16.11.27]
とても分かりやすかったのでこれからも使わせて頂きます!!ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数列の漸化式と極限 について/16.11.27]
問題1.1(2)解説の特性方程式で求めた値が違うと思われる
=>[作者]: 連絡ありがとう.解説の途中経過で符号が逆になっていましたので訂正しました.結果は変更なしです.
■[個別の頁からの質問に対する回答][対偶証明法と背理法 について/16.11.26]
1対偶証明法の問題1で[ア]の選択肢 両方とも1より小さい、 少なくとも1つは1以下、 少なくとも1つは1より小さいの3つを選んでもエラーになり、404:File Not Found となって結果が表示されません。ゲイシャさんの管理者に問い合わせるようにとのことでしたので、ここに書かせていただきました。僕はiPadでSafariを使ってこのページを開いています。(使っている検索エンジンはGoogleです。)肝心な正解の選択肢でさえ開けませんので(とはいえとても難しい問題というわけではありませんが、、、)どうかご点検をお願いいたします。
補足:なぜか唯一 両方とも1以下 の選択肢だけは反応してバツになります。[イ]の方は問題ありませんでした。
=>[作者]: 連絡ありがとう.「あ〝~ 」ビックリ仰天のプログラムミスでしたので,訂正しました.
■[個別の頁からの質問に対する回答][母平均,母比率の推定 について/16.11.25]
例題が充実していて理解が深まった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][回帰直線,回帰係数 について/16.11.24]
お世話になります。
データが「観測結果」の取り扱いとして大変わかりやすいと思うのですが、一つ質問があります。
データが「点群」の場合はいかがでしょうか?
具体的には、一直線上にあるはずのものが千鳥足になっている場合、このページの手法でも「あるはずの直線」を求められるでしょうか?
(座標系が任意であっても同一の直線が得られるか?ということになります)
「回帰直線とは?」のあたりに補足として記載があれば最適と思います。
=>[作者]: 連絡ありがとう.興味を持っていただいたということはありがたいことですが,質問内容をもっと絞ってください.
すなわち,質的に異なる内容が1つの質問として尋ねられていますので,整合的な回答を示すことができません.
(1) データが「点群」の場合は・・・通常の統計データは点群だと思いますので,この用語は何も限定しておらず,特に何も語っていません.
(2) 一直線上にあるはずのものが千鳥足になっている場合・・・通常の統計データは,千鳥足になっています.はじめから同一直線上にあれば,回帰直線は不要で数学で解けます.
(3) 座標系が任意であっても同一の直線が得られるか・・・「一般に,xからyを予測する式を裏返してもyからxを予測する式にはならない.」と文章で示してあります.
文章で回答すると以上のような味もそっけもないものになりますが,左図において図1の赤線はxからyを予測する直線で,図2の青線はyからxを予測する直線です.通常の場合これらは一致しません.
■[個別の頁からの質問に対する回答][指数法則 について/16.11.24]
わかりやすかったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次方程式の解と係数の関係 について/16.11.23]
色つきでわかりやすいです
ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][補集合 について/16.11.22]
例題つけるの素晴らしい!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/16.11.20]
いい問題がありましたね。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率変数と確率分布 について/16.11.19]
いつも丁寧な解説と図を載せて下さり感謝しています。硬貨の表の枚数の問題のところで、異なる5枚の硬貨A、B、C、D、Eのうち、表を向く硬貨2枚を選ぶ方法が5C2=2!3!/5!になる理由が分かりませんでした。確かに解説にある通り最後の答えは10通りになりましたが、間にある階乗の式が自分の計算では何度やっても2×6/120=12/120=1/10になり、どうしても10にならなくてどのような意味があるのかが理解できませんでした。僕の計算が間違っているのか、誤植なのか教えてください。ちなみに自分は5×4/2×1になると思いました。中3で数検2級の2次が合格できるようにこのサイトを利用しています。本当に助かっています。
=>[作者]: 連絡ありがとう.分母と分子が逆になっていましたので訂正しました.
■[個別の頁からの質問に対する回答][点Aの周りの回転 について/16.11.18]
様々な解説をお読みさせて頂きました。
とても分かりやすく、いい解説でした。
ここからは要望です。
カリキュラム上この順番なのかも知れませんが、出来れば「回転と拡大」のページの後に入れた方が理解が楽かも知れません。
お願いします。
=>[作者]: 連絡ありがとう.やや応用問題ということで,深い考えもなく後ろの方に配置していましたが,内容のまとまりという点からはご指摘の通りですので訂正しました.
■[個別の頁からの質問に対する回答][展開公式 について/16.11.16]
全体的に、フォントの色が淡かったり、線が細かったりして少々読みづらい
=>[作者]: 連絡ありがとう.文字色は少し濃くしました.Chromeで線が細く見えるとはどういうことなのか分かりません.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/16.11.15]
独学で学ぶのに役立つので、嬉しい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/16.11.15]
左と右から選んで消していく問題について、誤タップから選択を消す方法がないので、再度タップすると選択中の赤枠が消えるなどあると使いやすい。
=>[作者]: 連絡ありがとう.問題の選び直し(=いわゆる迷い箸のようなもの)については考えておきます.
■[個別の頁からの質問に対する回答][分散,標準偏差 について/16.11.14]
初めてメールさせて頂きます。
詳細にご説明頂いております、本統計学の頁には大変お世話になっております。有難うございます。
一つ質問があります。分散を求める場合には偏差平方和を自由度で除すと思っていましたが、本ページの最初の部分に記載されている分散ではNで除されています。これは確率変数を扱っているからでしょうか。ご回答頂ければ幸甚に存じます。
=>[作者]: 連絡ありがとう.その頁は高校生向けの教材なので,推測統計には触れていません.
すなわち,その頁で述べている
は,与えられたN個の標本の分散です…(1)
これに対して,あなたが言っておられるのは
で,与えられたN個の標本から推測される母集団の分散です.…(2)
今日ではコンピュータを使って何万個のデータでも簡単に処理できるので,全数検査も可能です.全数検査では分散は(1)式になります.[記述統計]
これに対して,与えられたN個のデータが巨大な母集団から抽出された標本であるときに,元の母集団の分散は(2)式になります.[推測統計]
これらの違いや相互関係については
この頁 に書いています.
なお,Excelでは(1)に対応する標本分散は VARP() で求めることができ,(2)に対応する母集団分散は VAR() で求めることができます.
[追伸]
■[個別の頁からの質問に対する回答][媒介変数表示 について/16.11.14]
とてもわかりやすかったです!
ありがとうございます
役に立ちました!
大学の過去問などから引用した問題なども掲載してもらえるとありがたいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重要な極限値 について/16.11.14]
大学の授業が全然理解できなかったので調べてこのページに来ました。
読むだけ読んで、わかった気になって、実際はわかっていないということが多いため、
問題を解いて理解できたか確かめられる機能とても良いと思いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][不定積分の部分積分法 について/16.11.13]
(4)の別解の最終形が間違っていると思います。
(logx)^3/xではなく、(logx)^3/3ではないですか。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/16.11.13]
絶対値をのせてほしいです
=>[作者]: 連絡ありがとう.教育課程の改訂のときに不等式の解き方が高校に移り,超基本から扱うようになったので,絶対値付きはちょっとした応用になります.機会があれば検討します.
■[個別の頁からの質問に対する回答][2次関数のセンター試験問題 について/16.11.13]
二次関数の2012年のセンター試験問題のキクケの答えの符号、逆ではないでしょうか?
=>[作者]: 連絡ありがとう.点検しましたが間違いはありませんでした.
■[個別の頁からの質問に対する回答][基本的な三角比の値(図あり) について/16.11.13]
もっと問題を増やしてほしいです。
=>[作者]: 連絡ありがとう.三角比の入門で取り扱う角度は全部で3個で三角関数の種類が3種類なので,合計9個ですべての問題を網羅しています.だからその項目ではそれ以上問題を増やすことはできません.
■[個別の頁からの質問に対する回答][正弦定理(解説) について/16.11.12]
ものすごく分かりやすいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数列,関数の極限 について/16.11.11]
平成23年度の問題についてなんですが、lim[x→∞]なのにnの関数になっていました。
一つ一つの解説が丁寧で分かりやすかったです。これからも使わせていただきたいと思います。
=>[作者]: 連絡ありがとう.転記ミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][2次不等式 について/16.11.11]
練習問題が付いているのが、素晴らしいですね。理解が深まります。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの成分 について/16.11.10]
配色が見にくかったです。
他は参考になりました。ありがとうございます!
=>[作者]: 連絡ありがとう.配色を少し変更しました.
■[個別の頁からの質問に対する回答][2次関数の平行移動 について/16.11.9]
今日の基礎力判定試験の範囲ってわかりますか?
=>[作者]: 連絡ありがとう.?? 冗談を言っているのですか?どこかの予備校か学習塾の試験範囲のことなら,それをやっているところに尋ねないと・・・通りがかりのおじさんに尋ねてどうする.
■[個別の頁からの質問に対する回答][決定係数とは について/16.11.9]
全くわからない
=>[作者]: 連絡ありがとう.初めに書いてありますように,回帰分析,重回帰分析の内容を先に読んでください.
■[個別の頁からの質問に対する回答][平方根の計算・・・センター試験問題 について/16.11.9]
2011年の数1数Aのコからの解説をもっと詳しくしてほしいです。よろしくお願いします。
=>[作者]: 連絡ありがとう.そこそこ解説が書いてあるつもりですが,画面構成の都合上,あまり多くの式が書けないので・・・(なお2011年の問題は2つあります.どちらなのか?)
■[個別の頁からの質問に対する回答][空間における直線の方程式 について/16.11.9]
(1’)のグラフはy軸に垂直な(y軸を串刺しにしたような)~の説明でY-Y0/aはZ-Z0/bではないでしょうか?67歳です。放射線被曝の影響評価を理解するために、高校数学を学び直しています。丁寧な解説と直近の問題があるので、とても理解しやすく役立っています。ありがとうございます。なんとか微積・統計確率まで行きたいと思いますので、よろしくお願いいたします。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][1次不等式の解き方 について/16.11.9]
最後の4項に分けている問題は、最初に式を出して、ボタンを押すと残りの式と答えが出る方式がいいと思います!
式の書きかた、そして途中式の書き方がわかるからです!
=>[作者]: 連絡ありがとう.そのような構成も考えられますが,全体としては簡単な問題から複雑な問題へ順に並んでいるので,その問題に達したときには,そこそこできるようになっていると想定しています.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/16.11.9]
2次方程式(1)について教科書では
b二乗ー4ac≧0 の時とありましたがどういう意味かわかりません
=>[作者]: 連絡ありがとう.高校の数学Ⅱの教科書では,複素数を習ってから2次方程式の解の公式を習うので,解の公式について
b2 −4ac≧0 という制限は必要なく,
b2 −4ac<0 の場合でも成り立ちます.だから,数学Ⅱの教科書には解の公式が
b2 −4ac≧0 の場合だけ成り立つとは書いてありません.
実際には,解の公式の説明が終わってから,判別式
D=b2 −4ac の説明をするときに,
(1) D=b2 −4ac>0 のとき異なる2つの実数解を持つD=b2 −4ac=0 のとき異なる実数の重解を持つD=b2 −4ac<0 のとき異なる2つの虚数解を持つ
と書いてあるはずです.さらに,これらのうちで(1)でも(2)でも実数解になるからこれらをまとめて書くと
b2 −4ac≧0 となります.
■[個別の頁からの質問に対する回答][重回帰分析(2) について/16.11.8]
○ 予測値の計算方法
ツール→分析ツール→回帰分析 はわかりますが ここまでしていただいたのなら Y値 X値をどの範囲で指定するのか まで載せていただけないのでしょうか・・・。
=>[作者]: 連絡ありがとう.分析ツールを用いた出力結果は,元の表になく,各自で設定して出力された結果を使います.○予測値の計算方法と書いているような表が出力されたら,その右側に1列作って,縦に101100などと入力して,=SUMPRODUCT(係数の列, 右の列)とすると1回で計算できます.
■[個別の頁からの質問に対する回答][行列の対角化とは について/16.11.8]
Pの求め方がわからない
=>[作者]: 連絡ありがとう.その頁は対角化とはなにかということを説明した頁です.次に
行列を対角化するには という頁を読んでください.
■[個別の頁からの質問に対する回答][3次関数(文字係数と極値) について/16.11.8]
例題1の(イ)の増減表の中で,x=aのとき極大値をとるというのは誤りではないでしょうか.
=>[作者]: 連絡ありがとう.ポカミスにしてはやや大きめのミスでした.訂正しました.
■[個別の頁からの質問に対する回答][連続型確率分布 について/16.11.8]
「問題7」の場合、期待値が図形的にどんな意味をもつのか、について説明があればありがたいのですが。
=>[作者]: 連絡ありがとう.
期待値は「式」で定義されていますので,図形的にうまく対応するものが示せるとは限らないようです.たとえば
は縦の長さ
は面積
のように対応しますが
は何に対応するのか言いにくいです.
※言葉で言えば「重心」を表し,次の図A,Bのように左右対称な確率密度関数の場合には,期待値(平均値)は対称軸になり確率密度曲線で作られる図形の面積の二等分線になります.しかし,C,Dのように左右対称でない場合は,重心を表す縦線は面積の二等分線にならず,Cではやや左寄り,Dではやや右寄りになります.(てこの原理で考えると,遠くて軽い物は近くて重いものと釣り合う.C:S<T,D:S>T)
だから一般の場合には面積の二等分線とは言えないのですが,面積の二等分線を引けば重心とそこそこ近い線になります.目分量で考えるだけなら面積の二等分線あたりに縦線を書いておけば感じはつかめます.
■[個別の頁からの質問に対する回答][総和記号Σ について/16.11.7]
例12のkが3の時の計算が抜けてる気がします
間違ってたらゴメンナサイ…
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][三角方程式 について/16.11.7]
例題3は誤答ですか?
=>[作者]: 連絡ありがとう.間違いですので訂正しました.
■[個別の頁からの質問に対する回答][行列の対角化とは について/16.11.6]
対角行列でない行列Aを対角行列にすることはできない.対角化とは,P-1APを対角行列にすることをいう.
対角行列しか対角行列に出来ないというのはどういう意味でしょうか?
=>[作者]: 連絡ありがとう.これはよく考えてみると当然のことを,読者の気を引くように刺激的な表現にしたものです.
「対角行列でない行列」
A は,対角行列でないのだから,対角行列に等しいはずはありませんし,変形して対角行列にできるはずはありません.
が対角行列でないときに,
などと変形できるはずはありません.そんな変形は正しい変形ではありません・・・なぜなら,
A は,対角行列でないのだから,
の形に書けるはずはないということです.
対角化とは,与えられた行列
A に対して,うまく行列
P を見つけて
のように対角行列のサンドイッチにすること
もしくは,(同じことを別の書き方で示すと)
のように
A のサンドイッチが対角行列になるように変形することです.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/16.11.6]
数式に使われている色が全体的に淡いのでもう少し濃くしてもらいたい
=>[作者]: 連絡ありがとう.少し濃くしました.
■[個別の頁からの質問に対する回答][空間における直線の方程式 について/16.11.5]
例題4の解答欄図のP0の座標数値が(1,2,0)になっています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][指数が対数のもの について/16.11.4]
一番難しい例題1のところが見ても読んでもさっぱりわからない。どれだけ紙に書いて計算しようとしても意味がわからず筆が一切動かない
=>[作者]: 連絡ありがとう.その頁は指数も対数もどちらも理解していないとできません.頁の先頭にあるサブメニューをたどって,基本の定義を理解してから読み直すとよいでしょう.・・・教材の順序から推定すれば,おそらく対数の定義がまだ十分身に付いていない可能性があります.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.11.4]
素晴らしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][フリ-ソフトmaximaの初歩的な操作1 について/16.11.4]
maxima1.htm 内の解説で
2^¥frac{3}{2} = (¥sqrt{2})^¥frac{3}{2} = 2¥sqrt{2}
とされているところがありますが、
2^¥frac{3}{2} = (¥sqrt{2})^3 = 2¥sqrt{2}
の入力ミスかと思います。
本筋とはあまり関係ないのですが、、、
=>[作者]: 連絡ありがとう.訂正しました
■?[ゆみらさん/16.11.3]
半角の公式を用いてsin^2(2α)を求めたいのですが、どうやって求めたらよいかわかりません。
=>[作者]: 連絡ありがとう.
半角公式というのは,2倍角公式を逆向きに読んだだけのもので
…(1)
または
…(2)
の形で使います.(1)の式を使うとすると,
に
を代入して
このように特に難しい問題ではありません.(2)からスタートすると,何が
なのだろう?と一瞬たじろぐかもしれませんが,(1)と(2)は見かけは違うが内容的には同じことを表しています.
■[個別の頁からの質問に対する回答][不等式と領域 について/16.11.3]
例の(1)の2はy<x+2じゃないんですか?
=>[作者]: 連絡ありがとう.元の問題の符号が逆でしたので訂正しました.
■[個別の頁からの質問に対する回答][導関数の定義 について/16.11.1]
問題2の(1)の解答欄のx2乗が次の行に行ってしまっていて分かりにくかったです。
それ以外はとてもわかりやすかったです。
=>[作者]: 連絡ありがとう.たしかにiPhoneで見ると次の行にわたってしまうようですので訂正しました.
■[個別の頁からの質問に対する回答][正弦定理 について/16.10.31]
かなり分かりやすい説明で驚いています。この講座の正式な名前を教えて下さい。
=>[作者]: 連絡ありがとう.正式というほどの格式のあるものかどうか,単に「高校数学の基本問題」という名前でやっています.
■[個別の頁からの質問に対する回答][不定積分(展開) について/16.10.29]
「なお発展学習として,1次式の累乗になってる関数の積分については... 」この部分の公式の右は1/aが足りなさそう。
=>[作者]: 連絡ありがとう.訂正しました.ついでに文字色も濃くしました.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/16.10.29]
被積分関数の左端とインテグラルが被って表示されることがある
=>[作者]: 連絡ありがとう.Mac上のSafariでということのようですが,Windows上のSafariでは問題ないので,「ことがあります」のようにあいまいな言い方でなく,「何番目の式のどの関数」というように具体的に述べてもらわないと対応できません.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/16.10.27]
分かりやすくて助かりました。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][極方程式 について/16.10.27]
例8計算ミスしていませんか?
=>[作者]: 連絡ありがとう.符号が逆になっていましたので訂正しました.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/16.10.26]
原点 O.Aの場合は?
=>[作者]: 連絡ありがとう.この公式は
中学校で習う内容 の復習になっています。確かに普通の教科書では2点AB間の距離の公式と並べて2点OA間の距離の公式も書いてありますが,・・・必要ですか?
■[個別の頁からの質問に対する回答][ベクトルの大きさ について/16.10.24]
とてもためになりました
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値(区間や関数が変わる場合) について/16.10.24]
問1t>0のとき,2次関数y=−x2+2xの区間0≦x≦tにおける最大値と最小値を求めてください
最小値の変域が違う気がします・・・。ほかのページの問題でも、変域が違う問題がありました・・・。
=>[作者]: 連絡ありがとう.その頁内でつじつまの合わない箇所は訂正しました.
■[個別の頁からの質問に対する回答][共通部分と和集合 について/16.10.23]
とても役に立ちました!Thank U!
もうすぐ数検準2級を受けるのでとても参考になりました。最後に問題があるのがいいと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数方程式 について/16.10.22]
最後の問題8番の、2の2x乗-2のx+1乗-8についての質問です。ヒントでは2のx乗をtとすると、tの2乗-2t-8になるとあります。しかし、tの2乗+4t-8になるような気がして、そこで行き詰ってしまったのですが、いかがでしょうか。
=>[作者]: 連絡ありがとう.あなたの場合は,指数法則が十分身に付いていないという弱点があるようですので,
この頁 で復習するとよいでしょう.なお,指数法則や対数の計算規則は,1つの問題の中で何回も多重的に登場しますので,(水や空気に親しむように)反復練習が必要です.
元の問題:
amn =(am )n だから2x =t とおくと22x =(2x )2 =t2 am+n =am an だから2x+1 =2x 21 すなわち2x+1 =2t
−2x+1 は
(−2)2 2x →4t にはなりません
■[個別の頁からの質問に対する回答][展開公式 について/16.10.22]
展開公式2 問題3の第3問で【採点する】をクリックできません。
=>[作者]: 連絡ありがとう.IEまたはEdgeをお使いのようですが,いずれでも問題なく採点できます.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.10.22]
Xやaの二乗の組み合わせが複数通りある場合はどの組み合わせが正しいか最初からわからないようにしてほしい
=>[作者]: 連絡ありがとう.その頁では6番目以降がそうなっています.初めのサブメニューにありますように,その頁は一番最初の初歩的な練習なので,難しい問題は後にいくらでもあります.
■[個別の頁からの質問に対する回答][行列の階数 について/16.10.21]
問題を解く時のヒントなどをもっと入れた上が良いと思います!
=>[作者]: 連絡ありがとう.問題に解答すれば,詳しいhelpが出ます.
■[個別の頁からの質問に対する回答][不定積分の置換積分 について/16.10.21]
もう少しレベルの高い実践的な問題を1問置くといいと思った
=>[作者]: 連絡ありがとう.言われる意味は分かりました.なお,頁の初めにあるサブメニューで
同(2) を行ってもらうことができます.
■[個別の頁からの質問に対する回答][2次関数のグラフと係数の符号 について/16.10.20]
素晴らしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの大きさ について/16.10.17]
座標上の点をクリックして回答する場合に、点が勝手にずれて不正解になってしまいます。
=>[作者]: 連絡ありがとう.この頁には座標軸はありません.質問や意見のある頁を示さないと話が通じません.
■[個別の頁からの質問に対する回答][2次不等式 について/16.10.16]
解説がとてもよくわかります
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率の基本 について/16.10.15]
問題2以降の【採点する】が押せません
=>[作者]: 連絡ありがとう.Edgeは表示が遅い場合があるようで,その頁のすべての要素が表示されるまで反応しないのかもしれません.こちらで確認したところ,問題ありませんでした.
■[個別の頁からの質問に対する回答][放物線の方程式 について/16.10.14]
とても良いです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布(χ2分布) について/16.10.13]
とてもわかりやすいですが、
途中式をいれていただけるとありがたいです。
=>[作者]: 連絡ありがとう.後半の「途中式」については,書けるものは書いているつもりですが,Excelがどんな処理をしているのかというようなことは全く書きえないことです・・・どの式とどの式の間という具合にもっと具体的に質問してください.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/16.10.13]
本文の15行目にあるsin15°=sin(45°-30°)ですが、
45°ではなく40°になっています
修正お願いします
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][逆関数 について/16.10.13]
テスト前にこのページを見ていたのですが、大変わかりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベルヌーイ形 微分方程式 について/16.10.12]
詳細な式変形があるので、自分の間違いにすぐ気が付きます。大変に参考になっています。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数の計算 について/16.10.11]
複素数の定義 5−3iは複素数ではないのか。虚数となっている。
=>[作者]: 連絡ありがとう.「複素数の定義」の右にある図で示されるように,複素数は実数と虚数から成り立っています.だから,虚数は複素数であり,実数は複素数です.・・・虚数と複素数とは「あれかこれか」の関係ではなく,西日本と日本のように一方が他方を含んでいる関係です.もちろん,実数と複素数も東日本と日本のように一方が他方を含んでいる関係です・・・(率直に言えば,この質問は想定外の質問です)
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/16.10.10]
ありがとうございます
わかりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率の基本 について/16.10.9]
一部の説明で灰色になっている箇所がありますが、見落としがちになったりしてしまうので、黒などの分かりやすい色で書いてあるとよりよくなると思います。
=>[作者]: 連絡ありがとう.そこそこ対応できたと思います.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/16.10.9]
例2の解答の8行目の
sin2β=1-sin2β=1-14=34
は1-cos2βの間違いではないでしょうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][等式の証明 について/16.10.9]
いつも参考にさせていただいています。
数ⅡB、式と証明、等式と証明、条件付き証明の例題2の答案3行目
(左辺)=(k^2a^2+k^2y^2+k^2z^2)は
(左辺)=(k^2x^2+k^2y^2+k^2z^2)ではないでしょうか
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][不等式と領域 について/16.10.8]
答えが間違っている
=>[作者]: 連絡ありがとう.どの答えがどう間違っているのかを連絡しないと,話が通じません
■[個別の頁からの質問に対する回答][群数列 について/16.10.8]
100項を求める時の nが14の時が91で15の時が105だと思います
=>[作者]: 連絡ありがとう.n-1に目が行っていたようで訂正しました(解答は変更なし)
■[個別の頁からの質問に対する回答][y=sin(θ−α)のグラフ について/16.10.6]
グラフの表の角度をπを使って分数でも表してほしいです。
=>[作者]: 連絡ありがとう.その頁の先頭にあるサブメニューで
次の項目 ,
さらに次の頁 が弧度法の表示になっています
■[個別の頁からの質問に対する回答][1の3乗根ω について/16.10.6]
三つ目の例の所なのですが、
割り切れて、あまりは0、つまり答えは0になるのでは
ないでしょうか?
疑問に思ったので送らせていただきました
ご説明とてもわかりやすかったです
=>[作者]: 連絡ありがとう.元の式が間違っていて」解説になっていませんでしたので訂正しました・・・○眼の□眼の△視なので文字の大きさによっては,3と5と6が同じに見えていたようです.
■[個別の頁からの質問に対する回答][判別分析 について/16.10.5]
変数3の数値が最も高いと書いてありますが、変数1の方が数値が高いと思います。
=>[作者]: 連絡ありがとう.数値ではなく係数です.・・・「ここで行った例では,説明変数3の係数が最も大きく,説明変数3が群の判別に重要な役割を果たしていることが分かる.」→左の欄(2)にあります.
■[個別の頁からの質問に対する回答][不等式と領域 について/16.10.4]
分からなかった所がわかりました。ありがとうございます。
分数の場合のやり方も載せて欲しいです。
=>[作者]: 連絡ありがとう.分数の場合というのは「何が分数の場合」なのか話が通じません.係数が分数の場合なら特に説明するまでもないように思えますが,関数が分数の場合(分数関数になる場合)は境界線の描き方を数学Ⅱのこの教材の段階ではまだ習っていないと思う.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/16.10.4]
問題の答え選択肢と答え合わせの方式、helpの出し方がすごくいいです。工夫されてますね。結構画期的です!感動 この方法いいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.10.4]
苦手な範囲をわかりやすく解説付きで載っており回答も4択から選ぶだけなので手間をかけずにで来ました。今後も活用するかもしれませんがその時はよろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.10.4]
特になし。素晴らしい解説ですね。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/16.10.2]
こんにちは。22歳の大学2年生です。
久しぶりに数学の力が必要になったのでどこかで復習できるところはないかと思っていたところこちらのサイトに出会いました。
大変わかりやすくまとめられており、またそれが文章としても頭にすっと入ってきやすい形でまとめられていて、学生の頃勉強したことがみるみる蘇りました。ありがとうごさまいます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][同一直線上にあるための条件 について/16.10.2]
読みやすさ
理解しやすさ
利用しやすさ
三拍子揃っていて素晴らしい、公式もただ書いてあるだけでなく証明を1からまとめてあり、思い出せた、ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][n進法の演算 について/16.10.2]
例1の問題が間違っています
=>[作者]: 連絡ありがとう.答が間違っているという話はよくありますが,問題が間違っているとは変わった話だな~と,ふと見ると,おお!!なるほど間違っています.訂正しました.
■[個別の頁からの質問に対する回答][部分分数分解 について/16.10.1]
前か後ろの項との差で表される数列の和は中間の項が消えるというのは面白かったです。
でも、例3で1/√(k+1)+√(k)=√(k+1)-√(k)に変形できるのかがわかりませんでした。同様に例4でk(k+1)(k+2)={k(k+1)(k+2)(k+3)/4}-(k-1)k(k+1)(k+2)/4になるのかがわかりませんでした。変形後の式からは自力で答えにたどり着けるのですが、どうすればこの式通りになるのか教えてください。
それともう1つ、【以上の要約】の1つ目の黒丸の文章で「簡単」が「間単」になっていました。ご訂正をお願いします。いつもありがとうございます。
=>[作者]: 連絡ありがとう.公開型のweb教材では,それが高校生向けの教材であっても,ある検索語句の上位に表示されれば中学生や70歳の方が読まれる場合があります.そのような場合に,必要な前提知識(レディネス)が欠如している場合を想定しなければなりませんが,どこまでの欠如が想定内でとこからの欠如が想定外とみなすのかは,難しい判断です.
■[個別の頁からの質問に対する回答][剰余の定理 について/16.9.30]
3次式で割ったやつがないです
=>[作者]: 連絡ありがとう.3次式で割ったときの余りの求め方を述べても4次式で割ったときの,5次式で割ったときの余りは・・・となってイタチごっこになります.ここでは,何次式で割った問題が出ても「一般して対応できるだけの力が付くように」順を追って解説しているつもりですが,特に3次式で割った余りに即答しなければならないのでゆっくり考えている時間がないというような事情がありますか.
■[個別の頁からの質問に対する回答][根号の計算 について/16.9.28]
重なっていること。 記号が
読みずらい。解答の時に記号と記号が重なっていること。
=>[作者]: 連絡ありがとう.あなたが使っておられるFirefoxで点検しましたが,解答欄と記号が重なるということはありえません.ただし,Firefoxでだけ他のブラウザと異なる作動になる箇所があって,解説と解説が重なることはあったようです.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/16.9.27]
解説をもう少しわかりやすくしないと理解できない人もいると思います。
この分野が苦手な友人に勧めたらわからないと言われてしまいました。
=>[作者]: 連絡ありがとう.この頁で扱っているテーマは逆三角関数の微分法なので,三角関数が分からない場合はその頁に戻り,三角関数の微分法が分からない場合はその頁に戻り,逆三角関数が分からない場合はその頁に戻らなければならないと考えますが,いずれも分からないままにこの頁をやるのは無理です.公開型web教材でそこまで,ことさらに事実を強調して,読者の気分を害しても誰に何のメリットがあるのか疑問あり.
■[個別の頁からの質問に対する回答][対数の計算 について/16.9.27]
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.9.26]
勉強したい単元を集中してでき、とても良いです。
携帯で勉強できるのは、汽車の中など机がないところや立っている時でもできるため、とても便利で、少しの隙間時間でも解くことができとても良いです。
解説が出た時に次の問題とかぶって読みにくいことと、間違えた時に正答が出ないことが改善ポイントかなと思いました。
苦手だった単元がわかるようになり、とても嬉しいです。今後も利用しようと思います。
=>[作者]: 連絡ありがとう.筆者の機器では解説と次の問題がかぶるということはありませんが,いろんな機器がありますので,オバーフローしたときに対応できるようにしました.
■[個別の頁からの質問に対する回答][対数不等式 について/16.9.26]
センターの過去問で対数不等式の真数に定数aが含まてれいる問題があり、解けず悩んでいます。解説があると有難いです。因みに以下のような問題でした。
aを定数とする。
不等式 log2(x-a)+log2(x-3)+log1/2(4-4a)<0・・・(*)
が成り立つようなxの値の範囲を求めよう。
以下誘導形式の穴埋め問題でした。
どうかよろしくお願いします。
=>[作者]: 連絡ありがとう.問題が間違っているので,(問題を写し間違っているので)解けないのです.(第1項の符号に注意)
真数条件から
…(*)
第3項を底の変換公式を用いて底を2に揃える
とりあえず,
と
の間と見ておく
(*)から
の大小関係に応じて共通部分を答えにする.
1)
のとき
の順に並ぶから
2)
のとき
の順に並ぶから
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.9.26]
ヒントが、とても分かりやすくて良かったです。有難う御座いました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次不等式 について/16.9.26]
問の2,4の符号がおかしい気がします
=>[作者]: 連絡ありがとう.あなたの考えを書かないと答えようがありません.
■広島[えびすさん/16.9.25]
正弦定理(解説)「(角度が大きいと辺も大きい) 右図のような三角形を描いてみると、3つの角度の中でAが一番大きいとき」の右図の直角三角形と説明内容が、いまいち理解できません、
=>[作者]: 連絡ありがとう.Aが大きい図になっていないということで,文字を入れ換えました.
■?[ごーちゃんさん/16.9.25]
大変わかりやすくて助かっています。
ご指摘になりますが、数Ⅰ・A 、集合・命題・証明、受験向き:集合・条件の問題9のヒントの「捜査の範囲を絞ります」以降の「必要条件」「十分条件」が逆ではないでしょうか。確認よろしくお願いします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][総和記号 Σ(シグマ)に慣れよう について/16.9.25]
問題1の4番目の答えが待ちがってます
=>[作者]: 連絡ありがとう.
は
に
を代入したときの式の値を足したものになりますので
になります.
あなたはどう考えたのか,自分の答えも書きましょう.(それを書いていないので誠実さがダウンして見えます.待ちがって→間違って,よく使う漢字がこんな文脈からばれやすいので投稿のまえにチェックすべし[筆者もな])
■[個別の頁からの質問に対する回答][ベクトル内積 について/16.9.24]
エーベクトル➕ビーベクトル=エービーベクトル
になるんですか???
=>[作者]: 連絡ありがとう.質問の意味が通じません.
この頁は,成分で表されたべクトルの内積の求め方を扱っています.もしベクトルの和差のことを聞いておられるのなら,先頭のサブメニューに従ってベクトルの和差の頁を見てください.
のとき,
ですかと尋ねておられるのなら,高校では大文字1文字は点を表すときに用いるので,左辺のような記号は使いません.
のとき,
ですかと尋ねておられるのなら,ベクトルの和と内積は別のものです.
のとき,
ですかと尋ねておられるのなら,そうではありません.
のとき,
になります.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/16.9.22]
エクセルの使用例までわかりやすく解説されているので、実用的だと感じました(過去に見た参考文献の中には、指定するセルがわかりづらいものもありました)。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.9.22]
とても考え方や解説など、とても解りやすく、また例題もあるため身に付けやすく助かりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][同次形微分方程式 について/16.9.22]
詳しい解説をありがとうございます。
自分の計算ミス・不注意なミスが良くわかります。とても勉強になります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][点の存在範囲 について/16.9.21]
イメージが掴めました。ありがとうございますヽ(´ー`)ノ
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][総和記号Σ について/16.9.20]
一問一問問題を解いていけるのが良い。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][変数分離形 微分方程式 について/16.9.20]
数検1級 微分方程式がわからいなので、こちらにたどり着きました。 丁寧な説明でとってもよくわかりました。ありがとうございます。
もうすぐ定年オヤジでした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/16.9.19]
■問題3
次の式を展開せよ.
[ 第3問 / 全3問中]
この時に、[採点する]のところがクリックしても反応がほとんど無く、回答がなかなか出来ませんでした。連打すると稀に反応してくれます。
このページの他の問題に関しては、この症状は出ませんでした。当方、osはwindows10 ブラウザはMicrosoft edgeです。
=>[作者]: 連絡ありがとう.edgeで点検しましたが,特に不具合は見当たりませんでした.
■[個別の頁からの質問に対する回答][絶対値 について/16.9.18]
自分で解く問題について、helpを付けてほしいです。特に
・・・グラフを利用する方法・・・
以下の問題についてお願いします。
=>[作者]: 連絡ありがとう.そこに書いてあるグラフがそれなりのヒントですが,全部まで書いてしまうかどうか考え中です.
■[個別の頁からの質問に対する回答][数学的帰納法 について/16.9.18]
将棋、k、k+1、もちろん文章も非常に良くできていると思います。他のサイトも検索しましたがトータルで一番解り易いです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数のグラフ について/16.9.18]
y=cos2(x-π/2)のグラフとy=cos(2x-π/2)のグラフの違いがわかりません。教えてください。
=>[作者]: 連絡ありがとう.11番目の問題の解説にありますように
のグラフは
のグラフをx軸の正の向きに
だけ平行移動したものです.このように変数xの代わりに何を使っているかによって判断するのが基本です.
そこで,
のグラフは
に書き換えて判断します.つまり,
のグラフをx軸の正の向きに
だけ平行移動したものです.
※
のグラフをx軸の正の向きにp,y軸の正の向きにqだけ平行移動してできるグラフの方程式は,次のようにして考えます.
元のグラフ上の点の座標を
,移動してできる新しいグラフ上の点の座標を
とおくと
…(1)
…(2)
…(3)
(2)(3)から
これらを(1)に代入して旧座標を消去すると新座標だけの方程式ができる.
すなわち
習慣に従って
で書くと
…(*)
このように(*)の形の方程式(グラフ)が元の方程式(グラフ)(1)をx,yの向きにどれだけ移動したかを調べるためには,xの代わりに何が,yの代わりに何が代入されているかを調べなければならないので
…(**)
の形では判断できず,(*)の形で判断しなければならないということです.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/16.9.17]
非常に分かりやすかったです。勉強になりました。ありがとう。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][データの代表値 について/16.9.15]
エクセルを使わなくてもできるようなデータの数が少ない例題を用意しておいて欲しかった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/16.9.15]
かなり良い
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列と一次変換 について/16.9.15]
行列の各列の意味がよく分かりました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][主成分分析 について/16.9.15]
主成分分析、実際の作業(エ)、3節目の「相関係数行列の固有ベクトルを求める」の説明の「図のC19に =MMULT(B14:D16,B19:B21)」の関数のパラメーター2つ目の引用が2乗の式を引用しているが、係数そのものの「A19:A21」ではないか?
=>[作者]: 連絡ありがとう.Excelを使って行列の積を求める方法は
この頁 の下の方にある(■参考■) Excel を用いた逆行列の計算にあります.・・・ワークシート上で「配列」を作る方法です
■[個別の頁からの質問に対する回答][三角比の相互関係 について/16.9.13]
説明が難しすぎてよくわかりませんでした。
苦手な人にもわかりやすい説明を希望します。
=>[作者]: 連絡ありがとう.YAHOO! から「三角比 相互関係」で検索するとその頁が検索上位に来ますが,頁の先頭に注意書きで書いていますように「前提となっている内容が分からない」という場合にはサブメニューのもっと前の頁から見てください.
■[個別の頁からの質問に対する回答][内分点,外分点の位置ベクトル について/16.9.12]
中点についてよくわかりません
=>[作者]: 連絡ありがとう.初めの方に「特に」の続きに書いている説明そのままの問題です.
■[個別の頁からの質問に対する回答][2点を結ぶベクトル(有向線分)の演算 について/16.9.11]
すごくわかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.9.11]
ずっとわからなかったけれどわかるようになりました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][底の変換公式 について/16.9.8]
英数が読みずらい
=>[作者]: 連絡ありがとう.公平に言えば,この頁のブロック字体のフォントはきれいとは言えませんが,読み間違うことはないでしょう.人によっては,
こちら の方が見やすいかもしれません.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式の練習問題 について/16.9.8]
三角関数の和積の公式の練習問題を増やしてくだされ(°_°)
=>[作者]: 連絡ありがとう.積和,和積で3つある教材の内で1つの頁を見ておられるようですが,他に2つありますのでそちらも見てください.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/16.9.7]
独立試行の確率・反復試行の確率の問題で、
ここに掲載されている問題以外でもっと難しいのは
ありませんか?
=>[作者]: 連絡ありがとう.もう少し難しいのは
センター試験問題(過去問) にありますが,さらにとなると各大学の2次試験問題を検索で調べられるとよいでしょう.ただし,ただ難しい問題をやっていればそれだけ偉くなったなどと考えてはいけません.どれだけ身に付いたかも重要です.さらに,根本問題として「数学では知識を関連付けて考える」ことが重要で,1点だけ深い知識があってもあまり力にはなりませんので,広い範囲をやる中で個別にも深めていくというスタイルで臨むとよいと考えられます.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/16.9.8]
全体的にはわかりやすかったです。ベン図は良いですが、文章の並びが多少、左右分かりにくかったです。また、p⇨q の真偽について、前原昭二先生の『記号論理学入門』に挑戦しています。
=>[作者]: 連絡ありがとう.ほとんどの頁は携帯版も作っていますが,その頁はまだPC版だけだったようです.数日中に携帯版も作ります.
■[個別の頁からの質問に対する回答][不等式の証明2 について/16.9.7]
下部 問8(1)の候補は空欄外の「+(6y)^2+3」まで入っており不自然に感じます。
全体的なステップはとても分かりやすく参考になりました。
しかし計算部分の大半が記されており、このページの問題の勉強には向かないように感じました。
=>[作者]: 連絡ありがとう.問8(1)の問題と選択肢は整合的になっていませんでしたので,訂正しました.
■[個別の頁からの質問に対する回答][一般角 について/16.9.6]
ipad mini を使用して問題を解いていたら問題画像がバグって出ました。一応確認お願いします。
=>[作者]: 連絡ありがとう.管理人はiPad miniを持っていませんので,その環境での点検はできませんが,Windows上のsafariとiPhoneでは問題なく作動します.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.9.4]
解説がはみ出てしまいます。
=>[作者]: 連絡ありがとう.筆者の方では,Mac上のFirefoxの作動確認はできません.Windows上のFirefoxでは問題ありません.
■[個別の頁からの質問に対する回答][展開公式1 について/16.9.2]
中学生です
わかりやすくて
楽しかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][回転移動の1次変換 について/16.9.1]
解り易くて、よいと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/16.9.1]
TTESTorT.TEST関数についてもう少し解説が欲しいです。
=>[作者]: 連絡ありがとう.メニューから別の教材を見ていただくとよいかと思います.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/16.8.31]
大変素晴らしい、ありがとうございます。
他のページへのジャンプがいっぱいあれば、なおよいと思います。
=>[作者]: 連絡ありがとう.PC版の方は画面が大きいので「メニューに戻る」などが自由に選べると思いますが,携帯版の方は移動が大変なので現在書き換え中です.
■[個別の頁からの質問に対する回答][無理関数 について/16.8.31]
問題2の y=√x-2+3 の答えが不服
=>[作者]: 連絡ありがとう.詳細が分かりませんので,今までに出会った高校生に多かった傾向からの予断と偏見から答えますが,
のグラフについて,y方向(上に)
だけ移動するということを間違う人はめったにませんが,x方向(右に)
だけ(左に
だけ)移動すると考える間違いは結構多くあります.もう一度「無理関数のグラフの平行移動」(1)の解説を読んでください.
yだけ見た目のままでxは見た目と逆に動くのは「不公平だ##」という#正義感#は悪魔の誘惑です.例えば,
は(根号内が0以上でなければならないので)
x<2 のとき定義されず,
x≧2 の場所にだけグラフがあります.
■東京都[元素太郎さん/16.8.31]
どこに送れば良いのか迷いましたが、数Ⅱしかここではやっていなかったので・・・今年の8月中に指数関数と対数関数、微分、積分のそれぞれ項目の一部の頁をしっかりとやり、問題も一頁分全ての問題を解いたりしたのですが、自分の最近完了した頁数が全く更新されず数Ⅱで1頁だけしかやっていないという記録になっています。どうすればやったとカウントされるのでしょうか?万が一学習の記録が壊れていた場合どうすればいいのでしょうか?いつも勉強の助けになり感謝しています。
=>[作者]: 連絡ありがとう.
トップメニュ- の下端に赤字で学習の記録をリセットするボタンを作っていますので,それを押してください.
■[個別の頁からの質問に対する回答][定積分で定義される関数 について/16.8.30]
いつもお世話になっております。定数をkとおいて関数f(x)を求める問題の事で教えて頂けますか?例題を取り上げて申しますと、「関数f(x)を求めなさい」ときかれたら、その時点で ∫(上端2)(下端0)f(t)dtは定数だと決めても大丈夫なのでしょうか?どのような場合に定数と決めても良いのかはっきりとした見分け方があるのかどうか教えて下さい。基本的なことですみません。
=>[作者]: 連絡ありがとう.結論から言いますと,「上端と下端が定数であるような定積分はつねに定数になります」.
関数
F(x) の微分が
f(x) になるとき
すなわち,
のとき
(1) 不定積分は関数です.(積分変数に依存します.)
【例】
◎(2) 上端と下端が定数であるような定積分はつねに定数になります.
【例】
(3) 積分区間の上端が変数であるような定積分は不定積分と同様に関数になります.
(この場合は話が混乱しないように積分変数と上端に使う変数を変える方がよい)
【例】
(4) 積分区間の下端が変数であるような定積分は上記の関数と符号が逆になります.
(この場合は話が混乱しないように積分変数と上端に使う変数を変える方がよい)
【例】
※(2)(3)(4)において,定数a, b を代入したものF(a), F(b) は定数です.これがポイントです.
■[個別の頁からの質問に対する回答][数学的帰納法とは について/16.8.30]
とてもわかりやすくて為になります。
数学的帰納法だけでなく、一般的な帰納法などの説明があるところも有り難いですm(*_ _)m
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/16.8.30]
気にいった所 : 例1の運転免許の解説が非常に分かりやすかったです=>[作者]: 連絡ありがとう.問題6の方はhelpにも書いていますように,ある日でも可能です.問題7の(2)は,読者がこれを昨日,明日,先月あるいは来月読んでいたらどうなるのだろうと考え出すと迷うかもしれませんので,今のあなたに絞るよう加筆しました.(実際には真→真の組合せしか出ないようになっていますので真になります).(3)も同様にして,偽→偽の組合せしか出ないようにプログラムされていますが,迷わないように加筆しました.
■[個別の頁からの質問に対する回答][三角関数の値(270゜~360゜) について/16.8.29]
And not nor 論理回路 ぶれっくboard pic nic の組み込み用 C言語 コンパイル アセンブラ に利用してます。助かりました。
=>[作者]: 連絡ありがとう.前半はそちらの専門分野のようで筆者には分かりませんが,後半はなつかいし話です.アセンブラの方は真っ暗な画面の中で死ぬほど書かないと1つの仕事にならないとか,前方参照禁止とか苦労が多いなという記憶があります.20年ぐらい前のゲームはアセンブリ言語で開発していたようでプログラマは大変だとかいう噂でした.
■[個別の頁からの質問に対する回答][累乗根 について/16.8.29]
aのn乗根だとx^n=aを満たす数という風になり、a^(1/n)とならないと思います(1の4乗根は1,-1,i,-iの4つ)
たしかn乗根aという方がよりそちらに近い気がします
=>[作者]: 連絡ありがとう.確かに,初めの方は記号を紹介する上であいまいな用語になっていますが,数学Ⅱのこの段階でド・モアブルの定理を持ち出しても読者が分からなくなるばかりです.
「n乗根a」と言い換えればという話は,教科書や参考書でメジャーな使われ方ではないだけでなく,
のような記号や「n乗根a」のような用語が,多価関数を表すか1価関数を表すかは,この記号,用語が使われている文脈によって変わります.
←多価関数として使っている場合には,こういう意味になることがあります.
「※以降」に述べていますように「このページでは,以下においてa>0のみ扱います。」として,累乗根の内の第1象限にある部分だけを扱っています.
■[個別の頁からの質問に対する回答][三角比の相互関係 について/16.8.28]
今学習しているところ、効率よく学習をする上でのポイントをしっかり書いてあって、分かりやすく説明しているのでとてもいいと思います。
問題も○×がすぐわかり、解説もしてくれるので、とてもいいです。
これからも利用させていただきます。
=>[作者]: 連絡ありがとう.問題をやり,必要に応じて解説に立ち返る学習方法は,このサイトの一番良い利用方法だと考えています.
■神奈川県[?さん/16.8.26]
剰余定理について勉強しています。
大変参考になりました。
高校数学のウェブサイトであることは後から知りました。
大変素晴らしいウェブサイトだと思います。
今後も利用させていただきます。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.8.25]
問9について。
"すべてのCについて"○○となることは、△△であるための~。
というのはあるCのときに○○が△△になれば、他のCのときに関係が成立しなくても、○○→△△という関係になると解釈してよろしいのでしょうか?
=>[作者]: 連絡ありがとう.言葉通りに答えると,「そうではありません」.この問題の解き方として,「すべてのCについて○○が成り立つ」に対して「あるCについて○○が成り立つ」は必要条件です.
他の例1:「どんな実数c についても(c+a)2 ≧b 」が成り立つとき,「特定の都合の良いc=−a を持ってきても(c+a)2 ≧b 」が成り立つはずだから「0≧b 」が成り立つはずです.だから「0≧b 」は必要条件です.0≧b 」ならば,「どんな実数c についても(c+a)2 ≧b 」が成り立つかどうかは,別途調べてみなければなりません.c についても(c+a)2 ≧0≧b 」が成り立つことが言えるので,結局「どんな実数c についても(c+a)2 ≧b 」に対して「0≧b 」は必要十分条件であることが証明できたことになります.
他の例2:「どんな集合
C についても
(A∪C)⊂(B∪C) 」が成り立つとき,「特定の都合の良い
C=φ (空集合)を持ってきても
(A∪C)⊂(B∪C) 」が成り立つはずだから「
A⊂B 」が成り立つはずです.だから「
A⊂B 」は必要条件です.
しかし,「
A⊂B 」ならば,「どんな集合
C についても
(A∪C)⊂(B∪C) 」が成り立つかどうかは,別途調べてみなければなりません.
そこで,十分性について検討してみると,問題9のヒント図のような一般的な集合図を描き
A⊂B となるようにすると
A のうちで
B の外側にある2か所がないことになり,「どんな集合
C についても
(A∪C)⊂(B∪C) 」が成り立つことが言えるので,結局「どんな集合
C についても
(A∪C)⊂(B∪C) 」に対して「
A⊂B 」は必要十分条件であることが証明できたことになります.
※元の問題では,C=∪ を持ってきているのに,なぜ上の例ではC=φ の場合を考えるのかと疑問に持たれるかもしれませんが,それはやってみてよい結果が得られたものだけを答案に書いているからです.C についても(A∩C)⊃(B∩C) 」が成り立つときに,C=φ の場合を考えても,φ⊃φ という自明の結果が得られるだけなので,これはスルーします.C についても(A∪C)⊂(B∪C) 」が成り立つとき,C=∪ (全体集合)を持ってきても∪⊂∪ という自明の結果が得られるだけなので,これもスルーします.このようにして,都合の良い結果が得られるものだけを答案に書きます.
この論理(「すべてのCについて○○」に対して「あるCについて○○」は必要条件になり,これを利用すれば捜査の範囲を絞ることができるということ)は慣れないと難しいので,元の問題のヒントに加筆しておきました.
■[個別の頁からの質問に対する回答][一般角 について/16.8.24]
言うことなしの最高です!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/16.8.24]
学習からのミニテストでの習得率の増加は素晴らしいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対偶証明法と背理法 について/16.8.23]
背理法例5について。
なぜ、n/mが互いに素という仮定をつけていいのかがよく分からないのですが、例えば入試にこれが出てきて問題を解こうとするとき、解答者がn/mに互いに素という条件をつける意図は何なのでしょうか?
=>[作者]: 連絡ありがとう.整数の比で表された分数は,もし約分できるものなら約分した形で考えることができます.これが「互いに素」という仮定の意味です(約分しない形のまま扱っていたら分母と分子が確定しません.)
たとえば,
のまま使うと
とすることになりますが,こんなことが許されるなら
もすべてできることなり,n,mが定まりません.この分数では
としてn,mを確定する必要があります.
本音を言えば,高校生なら誰でも知っているように,
が有限個の桁で等しくなるとしたら,その約分した結果のn/mについて両辺を2乗したら「分母も分子も2の倍数でなければならないことになるのは矛盾である」という理屈です.
そこで質問を振り返ってみると,n/mが互いに素という仮定を付けないと(既約分数でないものでもそのまま使っているとすると)n,mが定まらないことになります.
■[個別の頁からの質問に対する回答][2直線の交点を通る直線の方程式 について/16.8.23]
(1)において,2k+1=0 かつ k-7=0 とはならないから の部分ですが,「k-2=0」の間違いではありませんか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][合成関数の導関数 について/16.8.23]
問題 関数y={x-(1/x)}^4の解説の計算結果が間違っている 分子の(x-1)^3➡(x^2-1)^3 一応、導関数の選択肢の方は正しい
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][合成関数 について/16.8.23]
三角関数の合成との違いを教えてください!
=>[作者]: 連絡ありがとう.
○2つの三角関数
と
の合成関数
すなわち
とは
の
の代わりに
を
代入したもの で
になります.
同様にして,
,
,
になります.
○これに対して,「三角関数の合成」は2つの三角関数
と
の1次結合(=定数倍の和差)
が
1つの三角関数で表される ことを示したもので
(ここに
は
となる角)
または
(ここに
は
となる角)
になります.
■[個別の頁からの質問に対する回答][等比数列の和 について/16.8.19]
わかりやすくていろんなパターンがあってありがたかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内接円の半径 について/16.8.17]
問題1の二番の答が違う
=>[作者]: 連絡ありがとう.はじめに書いてありますように[?] をクリックすると解説が出ます.特に不具合はありません.あなたが正しいと考える答えはいくらなのか?
■[個別の頁からの質問に対する回答][接線の方程式 について/16.8.17]
僕は中学生ですが、いつもこのサイトで楽しく学習させて頂いています。問題(5)の答えを入力する欄が3,4桁の答えにしては少し狭いように感じました。最初、欄の大きさからして本当に3,4桁の答えなのかと戸惑ってしまいました。問題(6)のような少し大きめの欄を作って頂ければうれしいです。また、例題(3)の(B)の実演のp^3=1がp3=1になっていました。些細な点ですがどうぞよろしくお願いいたします。
=>[作者]: 連絡ありがとう.いずれも訂正しました.
■[個別の頁からの質問に対する回答][ベクトルの実数倍 について/16.8.17]
ベクトルの実数倍のページの要点のところで、何倍かではなくk倍だと思います
=>[作者]: 連絡ありがとう.より正確さを目指せば,ご指摘のような表現になりますが,k倍にはなりません.次のようには言えないことに注意してください.
ベクトル
の実数倍
は
のとき
を逆向きに
倍したものである.
k自身が負の数だから,正確には次のように言わなければなりません.
ベクトル
の実数倍
は
のとき
を逆向きに
倍したものである.
ところで当サイトの読者層はまちまちですが,その頁は結構な(相当な)基礎・基本の頁で,その頁を読んでいる人はその項目が「分からないから」「自信がないから」読んでいると想定できます.・・・学習塾の講師が教材を収集しているような場合を想定する必要はありません.そうすると,「絶対値記号を使うことによって頭がパニックになって投げ出してしまう人の比率」「あなたのように倍率は自由に指定できるのかと読める余地があると考える人の比率」のどちらが多いかを考えなければなりません.この頁の読者で
を2倍でもよいのかと勘ぐる余裕のある人がそれほどいるとは思いにくいです.
内容的にはその上に例を使って書いているので間違う心配はないのですが,
倍と書く方がストンの頭に入るかどうかの判断になります.(表現から受ける不安定な印象が強い場合には
倍を加筆することになりますが・・・)
■[個別の頁からの質問に対する回答][漸近線の方程式 について/16.8.16]
エックスが入力認識しません
=>[作者]: 連絡ありがとう.その頁でアルファベットの入力を要するのは最後の問題ですが,問題の初めに書いていますように「空欄にはスペースを使わずに半角のアルファベット小文字または数字だけを使用する」ようになっています.
■[個別の頁からの質問に対する回答][分数不等式の解き方 について/16.8.15]
よかった
=>[作者]: 連絡ありがとう.その頁では「画面上でグラフを描く」ために,筆者もそれなりに苦労したかもしれない.
■[個別の頁からの質問に対する回答][漸近線の方程式 について/16.8.15]
答えがでない
=>[作者]: 連絡ありがとう.
を押せば99%まで答案が示されます.残り1%はあなたが考える番です.全部まで筆者が教えてしまったら良くないので,読者が考える余地を残したというのがこの頁の構成です.
■[個別の頁からの質問に対する回答][多項式、分数関数、無理関数の不定積分 について/16.8.15]
無理数の数式が一切表記されません
=>[作者]: 連絡ありがとう.無理関数の表示を定義している関数名と定義の書かれたファイル名がずれてしまいました・・・余計なことに労力を使わせて申し訳ないことです.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.8.15]
p→q を、p⇒qに、した方がいいです。
=>[作者]: 連絡ありがとう.→と⇒はどちらも使うのに対して,その逆向きはコンピュータ上では,←は使えるのに対して二重矢印は環境依存文字(機種依存,フォント依存)となっています.だからこの頁のように両方必要な場合に,二重矢印では毎回図を使わなければならない煩わしさを伴います.
■[個別の頁からの質問に対する回答][余弦定理 について/16.8.13]
「2辺とその間にない角が与えられたとき」の問題は大学入試に出ることがあるのでしょうか?あるなら例題を交えてどの値を求めることがあるのか、また、三角形を2つ描くとはどういうことなのか教えて頂きたいです。
=>[作者]: 連絡ありがとう.
正弦定理の解説 の例2,
正弦定理の問題 でa,B,A; a,b,B; b,c,Cのように辺と角の1組と他の1辺が与えられた問題,
余弦定理の2次方程式 でa,B,Aのように辺と角の1組と他の1辺が与えられた問題がこれに該当します.
教科書や定期試験に普通に出る基本問題なので,大学入試にはそのままの形で単独で出題されることは少ないでしょう.しかし,少子化のために私立大学の40%が定員割れしているという現実から考えると,教科書程度の基本問題でも大学入試に出ることがあるかもしれません.
■[個別の頁からの質問に対する回答][指数が対数のもの について/16.8.11]
すごいわかりやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/16.8.10]
表すが正しい送り仮名です。
=>[作者]: 連絡ありがとう.この問題については以前にも回答しています.参考までに,
文部科学省「送り仮名の付け方」 では,
許容 次の語は,( )の中に示すように,活用語尾の前の音節から送ることができる。
表す(表わす) 著す(著わす) 現れる(現われる) 行う(行なう) 断る(断わる) 賜る(賜わる)
と例示列挙されています.
■[個別の頁からの質問に対する回答][位置ベクトルの応用 について/16.8.10]
数Bのベクトルを最初から順番にやっていて、
今、ベクトルの図形の応用(2)をやっているのですが問題1までわかるのですが、問題2から、突然「→」の無いアルファベットが問題に登場してきて、HELPを見てもよくわかりません。(「内分点の公式」が初耳だったり。)今までの問題はすんなり解けました。
私だけがきちんと理解できてないだけかもしれませんが…>_<
問題2の前に、この問題を解く為の、要点&解説を作って欲しいです。
すごく良いサイトに見つけることができて良かったなと感じています。お世話になっています。
=>[作者]: 連絡ありがとう.問題は「次の各点の位置ベクトルを,
で表しなさい」となっていますので,大文字1つで書かれている
P, Q, R, S, T は点の名前です.この約束事は中学校以来同じものです.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/16.8.10]
問10や問12など組み合わせの公式や同じものがあるときの順列の方法はこの項までにはまだ習っていないので、思いきって、それぞれの項の問題に入れてみてはいかがでしょうか。
=>[作者]: 連絡ありがとう.このサイトの読者は現役:1/3,上級生:1/3,社会人:1/3の割合ですので,復習対応にでも使えるようにしています.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/16.8.10]
じゅず順列の例題に四種類の宝石を「1つずつ」使っての文言を足すべきかと思います。
=>[作者]: 連絡ありがとう.業界の習わしとして「種類」というときには個数の制限を意識しないようですので4個に変更しました.・・・チェックもれです.
■[個別の頁からの質問に対する回答][円の方程式 について/16.8.10]
ここでは円の方程式のことについて説明しておられまきたが、円の方程式は実際に生活の中で使われているのですか?身近で使われていなくても、どういう時に使われている というのがあれば、教えてください。
=>[作者]: 連絡ありがとう.他のところで,中学生ということで同じ質問をしておられますので,こちらでまとめて答えます.
幾つかの例があれがそれを並べると納得してもらえるのですが,ほとんどすべての分野で登場するため,とても列挙できないのが実態だと思います.ただし,「生活の中で」となると,方程式そのものを目にするかどうかは,その人が何を扱っているのかにもよります.
例えば,「中心から半径○○km以内は暴風圏です」とか「半径○mには立ち入らないでください」のような災害や安全に関する情報が提供される場合,一般人が円の方程式そのものを使って自分で判断することを要求されることは少なく,日常生活では○○県◇◇市は該当するかどうかという「結果」が示されます.このように,本当は円を使って東経何度北緯何度を中心とする半径○kmの円を描いて計算していても,生の計算を一般人に要求される場面は,さほど多くはありません.
他の例でいえば,左図のような動物が逃げていくときに,こちらからボールを投げて「当たったことにする」かどうかを中心からの距離で決める場合には,プログラムを作る側は半径がある値よりも小さければ合格,そうでなければ不合格としますが,ゲームをする側は円の方程式を意識しておらず,結果だけを見ています.
ある事柄を使う方法が,全国一律に決まっていないような文化や心理の内容を扱う場合には,研究者ごとに距離を定義して分析する場合もあるでしょう.例えば,ある中学校で国語,数学,英語の得点が
(x, y, z) である生徒について「得点のよく似た卒業生がどこに進学したか」を調べるために,2人の得点の近さ(距離)を
で定義して,そこそこ近い範囲としてとりあえず
などから調べて
(a, b, c) に該当する卒業生を調べるとよいことになります.(普通は,生徒にはそんなデータは見せてもらえませんが,ここでは距離の概念は何にでも使えて文化の分野でも使えるということの例として述べています)
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/16.8.10]
メニューバーが一番下に表示されており、探すのに時間がかかりました。上にあるとより良いです。
=>[作者]: 連絡ありがとう.この教材を作った当時,メニュー(トップメニュー)に戻るというリンクをどこに設置するかについて迷いがありましたが,読者はメニューをたどってくるだろうと想定していましたので,いきなり「お帰りはこちら」では気分を害するかなという判断で,メニューに戻るを下端に置いたように記憶しています.現在では多くの頁で,あなたのようにGoogleから直接来られる方があり,ブラウザの機能としての「戻るキー」ではメニューに戻れないということは認識していますが,ほとんどすべての頁でこの形式になっているため,気が付いた時に直すとして,上端にもメニューに戻れるようにリンクを付けるには,数年かかります.とりあえず,要望のあった頁には付けました.
■[個別の頁からの質問に対する回答][センター試験問題 2次関数 について/16.8.9]
2006年度の最初の問題のエとオの正解が逆になってると思います。エ2がオ3が正解になってしまっています。
=>[作者]: 連絡ありがとう.解答が正しく解説が逆ということで訂正しました.
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/16.8.8]
いつもわかりやすい図を使って教えてくださっていることに本当に感謝しています。
1つ質問があります。問題3の(5)の問題の式のcos(80°-θ)が-cosθになるのがなぜなのか教えて下さい。
補足:どうやら以前にも別の方が同じような質問をされたことを見て知りました。(■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/16.7.10]を参照)この質問からすると同じ問題3の(3)の解説に誤りがあったようだとわかります。確認したところ(3)はすでに訂正されていましたが、(5)の問題の式と解説は80°のままになっていました。以前の質問者の指摘のように180°の誤りであれば、ご訂正をお願い致します。
さらに気づいたこととして、もし(5)の問題と解説を訂正すると、(4)の問題と全く同じになってしまうように感じました。そうでしたら同じ問題があるのは少し不自然に思います。その点も少しご考慮頂ければと思います。
もう1つは(4)の解説の(原式)=の後の部分で、これだとcosθと-sinθをかけているのかそれともcosθからsinθを引いているのか区別しづらいです。またsin(180°-θ)=sinθだから、(原式)=の後の式の左から3項目のsinθの符号は-になると思いました。詳しく書くと(原式)=-cosθsinθ+sinθcosθ=0になるということです。(4)の解説が(5)の解説と全く同じになるととてもわかりやすいと感じました。長きにわたり文章を書き連ねてしまい申し訳ありませんでした。以上の点についてご考慮頂ければうれしく思います。どうぞ今後ともよろしくお願いいたします。
=>[作者]: 連絡ありがとう.突っ込みどころ満載でボロボロの問題でしたので,訂正しました.→(4)の問題,(5)の180°を訂正
■[個別の頁からの質問に対する回答][置き換えによる展開 について/16.8.4]
高校版の置き換えによる展開の(6)の解説がわかりにくいです。項が3つあり、計算が大変だから置き換えをするのではないのでしょうか?ならばなぜ、x2-x+1をAとするのでしょうか。元に戻した時の計算がまた大変になると思うのですが。x2-×+1を計算する公式などがありましたら教えていただきたいです
=>[作者]: 連絡ありがとう.同じものが2回登場したら置き換えます.x2 -x+1 が2回登場するからx2 -x+1=A と置きます.(a−b+c)2 の公式を使います
■[個別の頁からの質問に対する回答][1階線形 微分方程式 について/16.8.4]
(6)のX'について解説ではX'=(Z'-Z)/y^2となっていますが、X'=(Z'y-Z)/y^2ではないのですか。
=>[作者]: 連絡ありがとう.訂正しました.ついでに省略していた式も埋めておきました.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.8.3]
絵が答え方によって変わってとてもおもしろく思います
でも初めは気付かず困りました
=>[作者]: 連絡ありがとう.この問題では初めの方は正解続きになる可能性がありますので,採点結果の図の意味を追加しました.
■[個別の頁からの質問に対する回答][1階線形微分方程式 について/16.8.3]
とてもわかりやすかったです。参考書などはいきなり難しい言葉で説明されているので、こんなに噛み砕いて丁寧な説明があって助かりました。特に、式の展開や変換がきちんと書かれていて良かったです。参考書はものすごく省かれてるので、なぜその式に行き着くのかわからないことが多いのですが、ここでは全て理解できました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][Excel:重回帰分析(2) について/16.8.3]
○カテゴリーデータが何をさすのか
○「一般にn個のカテゴリーデータを区別するにはn-1個の列を準備し」・・・なぜ-1なのか
○「 1個の列が全部0のもので最後の1つの属性を表わす」なぜか
○ 一文が長いので、短い文に修正していったら読みやすくなるのではないか。
=>[作者]: 連絡ありがとう.
1番目の質問について:
この頁(統計データの種類) を見てください.
2番目の質問について:その上に男女の別を区別する方法,「高校」「大学」「専門学校」のように3つの属性を区別する方法を例にとって示しています.
3番目の質問について:どれにも該当しないものが1つ表せるからです.
4番目の質問について:これ以上短くするのは無理です.
■[個別の頁からの質問に対する回答][放物線の移動 について/16.8.2]
正解か不正解かわからないので
文字表記でお願いしたい。
=>[作者]: 連絡ありがとう.全問不正解の場合を除けばすぐにわかります.
■[個別の頁からの質問に対する回答][N進法 について/16.8.2]
わかりやすいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][放物線の移動 について/16.8.2]
問題12について。与式をx=-1に関して対称移動したのち、y=1に関して対称移動した式はy=(x+4)+1ではないでしょうか?答にはy=(x+4)+3となっています。
元の方程式の頂点のy座標が1ですし…
間違っている場合は修正お願い致します。
=>[作者]: 連絡ありがとう.問題の方を変更しました.
■[個別の頁からの質問に対する回答][展開公式1 について/16.8.2]
x+6÷x+2の解き方がわからないので教えて欲しいです
=>[作者]: 連絡ありがとう.展開公式の頁を見ておられますが,
多項式の除法(割り算) の頁を見てください.
■[個別の頁からの質問に対する回答][順路の問題 について/16.8.2]
問題に
「経路に含まれる最も長い距離が○m以上のものは何通りか」
を入れて欲しい
=>[作者]: 連絡ありがとう.この形の順路の問題では,どの順路も合計が同じ長さで,最も長い線分も同じ個数だけ含まれます.だから,経路に含まれる最長距離に差異が生じることはありません.差異が生じるのは遠回りを認めた場合で,遠回りを認めてしまうと順路は無限個できます.
■[個別の頁からの質問に対する回答][双曲線関数 について/16.8.1]
このようなwebページを作っていただきありがとうございます.私は主にパターン認識の勉強をしているのですが,ところどころ数学の操作でわからないところがあれば参照しています.
もう少し,文字の間に余白があると見やすくなると思います.
=>[作者]: 連絡ありがとう.画面上の「文字間の間隔」「改行幅」は普通の教材ではすぐにでも変更できますが,この頁では分数関数を多用しておりその表示のために基準線よりも何ピクセル上に分子を書き,何ピクセル下に分母を書くかということが,改行幅に依存しています.そのため簡単には変更しにくい事情があります.改行幅を150%に変更しましたが,これ以上だとブラウザによっては分子と横棒が重なり醜くなるようです.文字間隔の方は広げ過ぎると間延びするのでこれくらいかなとも思いますが.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/16.7.31]
問題の(6)番の(X3-X2+X-1)(Χ3+Χ2-Χ+1)の後ろの式、
(X3+X2-X+1)を(X3+X2-X+1)に直さないと解けないですよね?
解説の中ではX2-になっているので多分間違いだと思います。
=>[作者]: 連絡ありがとう.「(X3+X2-X+1)を(X3+X2-X+1)に直」すとはどういうことなのか,質問の意味が伝わりません.x3 +x2 −x+1=x(x2 +x−1)+1 のような変形を考えておられるのかなとも思えますが,そうではなくそのまま使うということです.
■?[?さん/16.7.31]
このPCだけかもしれないですが、進み具合がおかしくなって高校の問題をしても色がつかず、中学数1にだけ異様に増え、送信ができない状態になってしまいました
=>[作者]: 連絡ありがとう.(都道府県も名前も伏字にしなければならないほどの事情とは?)
■[個別の頁からの質問に対する回答][理科における有効数字の表し方 について/16.7.29]
加減の方法も教えてください
=>[作者]: 連絡ありがとう.加減の方は簡単な基本とは言えません.精度の異なる幾つかの数字を加減するときは,一番精度の悪いものの勝ちになります.たとえば,mの単位まで図れる高度計とmmの単位まで図れる物差しを使って山の高さを図ろうとしても,精度の悪い方(m)の単位までしか使えません.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.7.28]
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.7.28]
もっと多く例を出してほしい
=>[作者]: 連絡ありがとう.その頁は角度の単位だけを扱っていますが,
それに続く頁 ,
その次の頁 ...などがすべてラジアンを使った練習になっています--三角関数を考える中で弧度法の単位も練習するというのが実際に即した練習の仕方です
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの定義 について/16.7.28]
後半で英語との対比が他のテキストにあまり記載の少ない内容で、訳す方の苦労もわかります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][絶対値 について/16.7.28]
グラフの利用の問3(2)、エ)3<xのときについてです。(x^2-3x)-x=2(x-1)を整理した式、x^2-6x+1=0に解の公式を使うと、自分で計算するとx=3+√8になるのですが、答はx=3+√7となっています。自分で計算してもこの答にはたどり着けないので、答が間違っている場合は修正を、この答で合っている場合はHELPの追加をお願い致します。
=>[作者]: 連絡ありがとう.(x^2-3x)-x=2(x-1)を整理するとx^2-4x=2x-2 になりますので,x^2-6x+2=0に解の公式を適用してx=3±√7. そのうちでx>3となるのはx=3+√7となります.
■[個別の頁からの質問に対する回答][度数分布表をexcelで作成する方法 について/16.7.27]
なぜ関数を変なフォントで書くのですか?
見にくいだけです。
=>[作者]: 連絡ありがとう.Excelの初期設定(=普通の場合の設定)では,ワークシートの表示はMS Pゴシック,ノーマル字体,大文字の英字になると思いますので,分かりやすくするためにその設定に合わせています.Excelのhelpもこの設定で書かれており,明朝体や小文字にすると分からない人が増えると考えられます.(質問者のExcel画面はどんなフォントで表示されているのか?)
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/16.7.27]
例題1の解説についての些末な質問です。
1/4を√の中身にかけているのはわかるのですが、その結果におけるt^2の係数は4ではなく16では無いでしょうか
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][行列の対角化とは について/16.7.26]
ボタンを押すと開くなどの形で計算過程も書いてほしい。
=>[作者]: 連絡ありがとう.言われる意味は分かりますが,この頁も次の頁も「対角化とは」という感じの言わば受付窓口のようなものなので,この場面で伏字の解説をしていると,話が通じなくなります.演習問題の頁に進んでからゆっくり考えてください.
■[個別の頁からの質問に対する回答][剰余の定理 について/16.7.24]
社会人です
すべてに目を通せたわけではありませんが
多項式が一次式で割り切れる場合に
わざわざ整式の割り算をしなくても係数計算で因数分解できますが、そのときの商の暗算が理解できません
特にaX2+bX+cの一次係数であるbの出し方がわかりません
ご教授くださいm(__)m
=>[作者]: 連絡ありがとう.
例えば,
f(x)=x3 −1 の場合
f(1)=0 だからf(x) はx−1 で割り切れるといえる.x3 −1=(x−1)(ax2 +bx+c) とおくx3 の係数は1 ,右辺でx3 になるのはx×ax2 ,したがって,a=1 −1 ,右辺で定数項になるのは−1×c ,したがって,c=1 x3 −1=(x−1)(x2 +bx+1) …(*)とおく0 ,右辺は−1x2 +bx2 ,したがってb=1 0 ,右辺はx−bx ,したがってb=1 で合う
以上により,
x3 −1=(x−1)(x2 +x+1)
ポイントは(*)のように,両端のわかるものは数字にしておき,未知数の数を減らして体制を立て直して見やすくするところ
もう一つ別の例
f(x)=x3 +x2 −7x+2 の場合
f(2)=0 だからf(x) はx−2 で割り切れるといえる.x3 +x2 −7x+2=(x−2)(ax2 +bx+c) とおくx3 の係数は1 ,右辺でx3 になるのはx×ax2 ,したがって,a=1 2 ,右辺で定数項になるのは−2×c ,したがって,c=−1 x3 +x2 −7x+2=(x−2)(x2 +bx−1) …(*)とおくx2 ,右辺は−2x2 +bx2 ,したがってb=3 −7x ,右辺は−x−2bx ,したがってb=3 で合う
■岩手[テディベアさん/16.7.24]
この欄で、質問をしてよいのかどうかわかりませんが、・・・質問させて下さい。
会社員で事務仕事をしている中年女性です。電卓を叩いて消費税の計算をしていた時に、不思議に感じられることに出会いました。
税込みでいくらになるか、というとき、税込みで20,000円ならば、元値が
20,000÷1.08=18518.5185185・・・となりますが、どうして108で割ると循環小数になるのかご教示下さい。他の数字で計算みたり、素因数分解ぐらいはしてみましたが、わかりません。高校で数学が好きだった程度のレベルです。
=>[作者]: 連絡ありがとう.10進法の小数に直す場合,既約分数に直した時に分母に2と5以外以外の素因数が残るものはすべて循環小数になります.有限小数になるのは,既約分数の形で分母が2と5だけでできている場合だけなので,むしろ有限小数となるのは珍しいともいえます.
(このようなことが起こるのは10進法を使うからで,3進法や16進法を使う場合には全く別で話が逆になる場合があります.)
(1) 分母が素因数2だけで成り立っている場合の例
(2) 分母が素因数5だけで成り立っている場合の例
(3) 分母が素因数2と5で成り立っている場合の例
(*) 分母が2,5以外の素因数を含んでいる場合の例
右辺は初項が
公比が
の無限等比級数だから
右辺を
と書いていることになります.
右辺のかっこ内は初項が
公比が
の無限等比級数だから
右辺を
と書いていることになります.
以上の話は10進法で表すために起こったことで,(
N進法の小数 の頁参照)3進法などで表すと立場が逆になり
(1) 分母が素因数3だけで成り立っている場合の例
のように有限小数になるのに対して
(*) 分母が3以外の素因数を含んでいる場合の例
右辺は初項が
公比が
の無限等比級数だから
右辺を
と書いていることになります.
そこで,最初の問題に戻りますと
は既約分数にしたときに分母に2と5以外の素因数3が含まれるので,循環小数になります
■[個別の頁からの質問に対する回答][回転の1次変換 について/16.7.24]
点の回転は分かったのですが、グラフ、つまりy=f(x)を回転させる時にどうなるかわかりません。例題も含めて説明してくださるとありがたいです。
=>[作者]: 連絡ありがとう.1次変換では元の図形が直線図形となっているもの(線形=直線や長方形)の像を扱うのが基本です.これは,サブメニューの
直線の像,領域の像 を読んでください.
元の図形が直線図形でないもの(非線形な図形)についても,形式上は簡単に解けますが,結果がどのような図形を表しているのかわかるためには,2次曲線など別の単元の知識を要するため,どちらかといえば発展学習になります.
旧座標を
x, y ,新座標を
X, Y で表すとき,
←→
だから
から旧座標を消去して新座標のみの方程式にすると
が新座標の方程式となります.
例えば,双曲線
xy=1 のグラフを原点の周りに45°回転してできる図形の方程式を求めるには
旧方程式:
xy=1
新座標と旧座標の関係
←→
だから
旧座標を消去して新座標のみの方程式にすると
が新座標の方程式となります.
双曲線
xy=1 のグラフを原点の周りに−45°回転してできる図形の方程式は,同様にして
となります.
元の図形が
のような楕円である場合,これを原点の周りに45°回転してできる図形の方程式を求めると
などとなって,どのような図形であるか想像するのは難しく,発展学習となります.
■[個別の頁からの質問に対する回答][空間における直線の方程式 について/16.7.22]
質問に丁寧に返信なさっているようですが、このサイトに載っている問題以外の個人的な模試などの数学の質問は受け付けてないですか?
=>[作者]: 連絡ありがとう.それぞれの頁にある問題以外については回答していません.
■[個別の頁からの質問に対する回答][分散分析 について/16.7.21]
とても、助かりました。掲載ありがとうございます。最終的には分析ツールに頼ったのですが、
一元配置法の説明の中の下記の文章において、
「=SUMPRODUCT(不偏分散の範囲,自由度の範囲)」
の、不偏分散の範囲,自由度の範囲がどこに該当するのか理解することができませんでした。すみません。私の見落としかもしれませんが、図の方に色をつけていただけると分かるのではないかと思います。また、利用させていただきます。
=>[作者]: 連絡ありがとう.(自分で書いた文章ですが,約10年経過して読み直してみると,解読するのに1時間ほどかかりました.)
(2)の後で(3)の前にある短縮法のことを訪ねておられるものと解釈しました.この短縮法は表の中に対応するものはありません.理屈は次の通りです.
偏差平方和は,その定義通りに求めれば,平均を求めて,差の平方の和を求めることになります:B21+C21+D21=E21:16.9+31.5+14.6=63.1
しかし,Excelの組み込み関数 VAR(B2:B9)は偏差平方和を自由度6で割ったものになっているので,これに6を掛けると偏差平方和に戻せます.
そこで,表にはない24行目BCD列ににVAR(B2:B9),VAR(C2:C9),VAR(D2:D9)とすると,=SUMPRODUCT(B24:D24,B23:D23)により63.1の値が得られることに,この値を自由度の和15で割ると4.20になります.
■[個別の頁からの質問に対する回答][正規分布 について/16.7.21]
問題(7)の考え方で、「上位から20%すなわち, p(u) = 0.3 となる u」というのがどうしても理解できません...
このp(u)=0.3というのはどこから導き出せば良いのでしょうか?よろしければ回答お願いします。
=>[作者]: 連絡ありがとう.質問内容が明快で論理的に描かれているので,回答するにも気持ちがいいです.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.7.20]
表示が崩れているところは無いです。
トップページに戻るボタンの場所をもっと分かりやすくしていただけると嬉しいです。
分かりやすい解説ありがとうございます。
=>[作者]: 連絡ありがとう.「トップ頁に戻る」をどこに置くと見やすいかという問題は迷うところですが,どの頁も同じような構造なので,今後の課題です
■[個別の頁からの質問に対する回答][根号の計算 について/16.7.20]
問題4の解答欄の表記が分かりづらいです。
答えは|a-1|/2でしょうか?違ったらヘルプをつけて下さると助かります
=>[作者]: 連絡ありがとう.分数の一部を空欄にするために複雑な処理をしており,そのためにブラウザによっては横棒が表示されていなかったようですので訂正しました.
■[個別の頁からの質問に対する回答][t検定 について/16.7.20]
わかりづらいです。
=>[作者]: 連絡ありがとう.このような分量の多い頁をわずか1分で流し読みするのは無理です.高卒以上の方のようですが,他にも10頁以上瞬間的に見ておられますが,そんなに短時間で読むのは誰でも無理です.もっと腰を落ち着けて1つの頁を分かるまで読んだ方が身につくことも多いと考えられます.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.7.19]
わかりやすい!丁寧!ありがと!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][データの種類 について/16.7.19]
データの尺度に関しては初心者でしたが、とてもわかりやすかったです。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/16.7.19]
宣伝が多すぎ言いたいのはそれだけ
=>[作者]: 連絡ありがとう.有料サイトにするよりは,無料サイトにしたほうが誰でも利用できてよいと考えますが・・・それよりも,あなたは解説を3回見たようですが,問題を解いた形跡がない
■[個別の頁からの質問に対する回答][逆行列の求め方 について/16.7.17]
簡便で見易くて、参考になります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆行列の求め方 について/16.7.17]
逆行列って不思議ですね、、、!
とてもわかりやすかったです!!
ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の定義 について/16.7.17]
本の解説より解りやすく練習問題も理解し易いと思います。(40代後半男)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率の基本 について/16.7.16]
これらの問題のです解答は存在しないのですか?
=>[作者]: 連絡ありがとう.問題に答えると,解説と解答が出ます.・・・[解説]というボタンをクリック
■[個別の頁からの質問に対する回答][逆行列の求め方 について/16.7.14]
2) A~Aの対角成分以外の成分は,次のようになる
がよく分からない。
=>[作者]: 連絡ありがとう.ところでA&spos;を考えると,その展開式になっており,2つの列が同じならば行列式は0になる・・・と読みます.
■[個別の頁からの質問に対する回答][展開公式 について/16.7.12]
すごくわかりやすい、しかし色彩豊かすぎて目がチカチカします
=>[作者]: 連絡ありがとう.そうかもしれん
■[個別の頁からの質問に対する回答][t分布 について/16.7.11]
放送大学で統計を選択しましたが、このサイトのおかげでばっちりです! ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][軌跡の方程式1 について/16.7.11]
非常にわかりやすいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/16.7.10]
(3)解説
公式(2) sin(90°-θ)=cosθにθ=10°を代入すると
sin85°=sin(90°-10°)=cos10°
↓
公式(2) sin(90°-θ)=cosθにθ=10°を代入すると
sin80°=sin(90°-10°)=cos10°
(4) 問題
sin(90°-θ)cos(90°+θ)-sin(180°-θ)cos(80°+θ)
↓
sin(90°-θ)cos(90°+θ)-sin(180°-θ)cos(180°+θ)
(4)解説
sin(90°-θ)=cosθ
cos(90°+θ)=-sinθ
sin(180°-θ)=sinθ
cos(80°+θ)=-cosθだから
↓
sin(90°-θ)=cosθ
cos(90°+θ)=-sinθ
sin(180°-θ)=sinθ
cos(180°+θ)=-cosθだから
=>[作者]: 連絡ありがとう.ご指摘の通り,入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][双曲線関数 について/16.7.09]
まとまっているので、短時間で習得でき(昔を思い出せ)て、とても助かりました。長すぎず短すぎずちょうどよいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/16.7.08]
間違えたときに、[?]と言われてもこっちが分からないから解説が欲しい
=>[作者]: 連絡ありがとう.画面は教材と読者の対話になっており,読者が[?]をクリックすると解説が出るようになっています.
■[個別の頁からの質問に対する回答][不等式と領域 について/16.7.08]
(3)-2 (x-3)の二乗+(x-4)の二乗>25については、境界線は含まないと思います。
=>[作者]: 連絡ありがとう.丁寧に読んでくれてありがとう.ご指摘の通り入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][重複順列 について/16.7.07]
分かりやすくてとてもいい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ド・モアブルの定理 について/16.7.05]
携帯用ページを開いています。
【aのn乗根】の【例2】の計算についてです。
cosπ/6+isinπ/6,cos(π/6+2π/3)+isin(π/6+2π/3),cos(π/6+4π/3)+isin(π/6+4π/3)の計算結果がそれぞれ-√3+i/2,-i,√3+i/2と表記されているのですが、計算したところ、順に√3+i/2,-√3+i/2,-iになるかと思います。
そちらで確認が取れ次第、修正のほどよろしくお願いします。
加えて、同じく【aのn乗根】から。
(解説)の一番最後の"(右図参照)"と書かれているのですが、恐らく【例2】と【例3】の間に表記されている図形かと思いますが、携帯用のページだと、そこに表記されているので、せめて、(解説)と【例1】の間に表記するように修正願います。
以上二点修正よろしくお願いします。
=>[作者]: 連絡ありがとう.ご指摘の通りですので訂正しました・・・こちらの記録では約3時間半かけて熱心に読んでくれた様子がうかがえます.
■[個別の頁からの質問に対する回答][組合せ について/16.7.04]
文章問題を入れてください
=>[作者]: 連絡ありがとう.その頁の上端のメニューから文章題の頁を選んでください
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.7.03]
おかげさまで、必要条件、十分条件の区別がつくようになりました!めっちゃ助かりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの直行条件 について/16.7.03]
数字がずれている所が多々ありますよ。
=>[作者]: 連絡ありがとう.windows10にしてEdgeを使うとそうなりますが,今日から1か月くらいで数百~数千頁の教材について,Edge対応の作業に入る予定です.
■[個別の頁からの質問に対する回答][円順列・じゅず順列 について/16.7.02]
7人のうち4人を選んで円形に並べる
この問題がわかりません
教えてください
=>[作者]: 連絡ありがとう.7人のうち4人を選ぶ方法が
通りあり,その各々について4人の人を円形に並べる方法は,円順列の公式そのもので,3!通りあるから,結局 35×6=210通りになります.
■[個別の頁からの質問に対する回答][対数計算 について/16.7.02]
メニューに戻る、に加えてページの上に戻るボタンもあると、いいと思います
=>[作者]: 連絡ありがとう.頁が長いとそういうものもあってもよいかもしれません
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式 について/16.7.02]
色の使い分けが少し見えづらいところがあります。
色弱の方は少し違った見え方になると思うので、字の太さや色の使い分けは少し変更してはどうでしょう?
(赤文字の上に青の斜線等)
=>[作者]: 連絡ありがとう.赤と緑の組合せは読みにくい人がいるということで避けていますが,ネットで調べると赤と青の組合せもそれに次いで読みにくい場合があるように書かれています.ただ,カラーはRGBの組合せなので,どれも使わないと水墨画の世界になってしまいます.
■[個別の頁からの質問に対する回答][楕円の方程式 について/16.6.30]
対応が親切です。また利用します
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階差数列 について/16.6.30]
∑の上が今までは、n だったのが階差数列になってからn-1 になってよくわからなかったけど、ちゃんとそのことについて詳しく書いてあって嬉しかったです。ちゃんと理解できました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆関数 について/16.6.28]
もう少し問題を増やしてほしい
=>[作者]: 連絡ありがとう.この頁にはすでにかなりの例題と問題が載っています.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.6.26]
中三です。
2問目まではできなかったけど、3問目から全問正解でした。
理解できてスッキリしました。
ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/16.6.26]
実測分布と理論分布を比較するにあたり、統計的に判定する方法を知りませんでした。おかげさまで、妥当な検証をすることができます。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][全微分方程式 について/16.6.26]
本項にはたいへんお世話になっております。誠にありがとうございます。
全微分方程式、完全微分形の例題4の青いところが-2xyではなく、-2yであると思います。
小さなことではありますが、気付いたので申し上げさせて頂きます。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][指数法則 について/16.6.25]
間違いの指摘や多い誤答例、正答率も表記されておりとてもわかりやすかったです!ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/16.6.25]
問題正解したときにもっと派手に祝福を!w
=>[作者]: 連絡ありがとう.頑張って正解したときは,派手に祝福された方がやるきが起こるというのはその通りだと思う.ただ,これも大げさ過ぎると読者の気分によっては一歩間違うと「馬鹿にされている」と受け止められる場合があり,陽気な読者から気分的に落ち込んでいる読者まで幅があるので,さじ加減がむずかしいのです.
■[個別の頁からの質問に対する回答][組合せ について/16.6.23]
本当にわからないです。泣きそうです。
=>[作者]: 連絡ありがとう.あなたの動きは,初めに10秒ほど解説を見て,次に問題をやらずに終了しています.もっと気長に解説を読んで,イメージをつかんでから,とりあえず問題を1題クリックすると,意外にできることに気付くはずです.とりあえず間違ってみると展望が開けてきます.では頑張ってください.
■[個別の頁からの質問に対する回答][複素数の計算(解説) について/16.6.22]
どれも解りやすく丁寧で助かります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][平方完成の変形 について/16.6.22]
■[個別の頁からの質問に対する回答][同時確率分布と周辺分布 について/16.6.22]
とてもわかりやすかったです、ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/16.6.21]
とてもわかりやすく、ためになりました。
でも、iPadで見ているのですが画面が真ん中に寄り、見にくいです。改善よろしくお願いします。
=>[作者]: 連絡ありがとう.筆者はiPadのことはよく分かりませんが,この教材のような縦長のものは,当然縦持ちで読んでもらえると考えていましたが,iPadユーザは普通,こういう形でも横向きで読むということでしょうか.(真面目な疑問です)
■[個別の頁からの質問に対する回答][循環小数 について/16.6.21]
気にいった所 : 循環小数を分数に直す方法がよく分かった
わかりにくい問題 : 「有限小数は、有限小数による表記と循環小数・・」の部分が理解できない。そもそも、循環小数は無限ではないのか?
=>[作者]: 連絡ありがとう.(参考) の初めに書いていますように,
1=0.9999・・・
このように,すべての有限小数は有限小数で表す「表記法」と循環小数で表す「表記法」があるということです.
ご質問の点についてストレートにお答えすると,すべての有限小数は無限小数として書き直せるということです.
■[個別の頁からの質問に対する回答][t分布 について/16.6.21]
統計自体に興味が無いのと教わった教授が悪いのか意義を感じられないのでどこが悪いなどは特にないと思います。むしろテキストとしてはわかりやすかったですありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][回転体の体積 について/16.6.21]
一つ目の問題x軸とじゃなくてy軸とじゃないですか
=>[作者]: 連絡ありがとう.y軸の周りの回転の場合は
になります(第3問参照).一つ目の問題はx軸の周りの回転です.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/16.6.20]
大変解り易かったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組合せ について/16.6.20]
組分けの重複されている、区別されていないについての説明をもっと詳しく
=>[作者]: 連絡ありがとう.加筆しました.
■[個別の頁からの質問に対する回答][三角関数のグラフ について/16.6.19]
背景青ってグラフ見にくくないですか?
=>[作者]: 連絡ありがとう.前景色は細い線や小さな点でも見えるように明るい色を使うので,背景色は暗色を使うことが多くなります.昔の黒板には真っ黒というのもありましたが,最近は暗緑色が多くなっています.ところで,赤緑系統の組合せは見えにくい人がいるらしいのでその組合せは避けていますが,夜空の雰囲気の青(この背景色は青ではなく暗青色)は色は暗くても雰囲気は明るいので,筆者は気にいっています.暗緑でも実験しましたが色数が増え過ぎ,赤との配色の組合せの雰囲気が悪いのであまりよくないです.
■[個別の頁からの質問に対する回答][漸化式と一般項(等比形) について/16.6.18]
分かりやすいです! 文字のズレを解消して下さいm(_ _)m
=>[作者]: 連絡ありがとう.iPadで見たときに文字のズレがあると言っておられるようですが,筆者はiPadを持っていませんので確認できません.ズレている箇所を教えてください.
■[個別の頁からの質問に対する回答][円の方程式 について/16.6.18]
わかりにくい問題 : x2-2x=(x-1)2-1
x2-4x=(x-2)2-1
x2-2x=(x-1)2-4
=>[作者]: 連絡ありがとう.4と1が入れ替わっているということで訂正しました.
■神奈川県[Prof.N.Hkさん/16.6.18]
http://www.geisya.or.jp/~mwm48961/koukou/complex_plane1.htm
の問題1の最初の問題、4+5iで、4+4Iのプロットが正答となっています。
また、下で私が言いたかったことは、2^(n-1)-1が正答として認識されない、ということです。
=>[作者]: 連絡ありがとう.この問題は結構複雑な問題です.おそらく,あなたは5月から6月上旬までの間にWindows 10に変更されて,そのときにブラウザをその標準のEdgeに変更されているはずです.(※その最重要なことを書くべきです!!)そのためにスタイルシートの取り扱いがFirefoxと同様になったものと考えられます.筆者の場合は,Windows10で使えなくなると困るソフトが幾つかありますので,7月中旬までこの変更は行いません.したがって,Edgeのテストはそれ以降になります.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/16.6.17]
問題を回答したときに○×が出るのがよかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][弧度法の単位・ラジアン について/16.6.15]
解説がとても丁寧なので、わかりやすく
活用させていただいております!
より多くの問題を解きたいので
問題の数を増やしていただきたいです!
お願いいたします
=>[作者]: 連絡ありがとう.興味を持っていただくのはとても重要なことですが,数学の場合は1つ「点知識」ではなく「知識のつながり」が重要です.弧度法の単位についてそこそこ理解できるようになったら,その弧度法を使った正弦関数,余弦関数の値を求める教材などが続いていますので,そちらをやっていただく方が身につくことが多いでしょう.学習の進め方として1箇所だけ濃い学び方よりは,1つの単元,1つの科目がだいたい分かることの方を目指すとよいでしょう.
■[個別の頁からの質問に対する回答][常用対数 について/16.6.15]
常用対数の説明の中に 「この表を覚える必要はない.特に,今日では(コンユータ)で簡単に計算できる。」とありますが「コンピュータ」ではないのでしょうか?
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.6.15]
明日テストがあるんですが、いい点をとるにはどのようなことに気をつけたらいいと思いますか?
教えて下さい!
私は数学がとても苦手で、克服しようと頑張っているのですが、なかなか克服することができません。数学を得意分野にするにはどのような勉強をすればいいのですか?
=>[作者]: 連絡ありがとう.様々な観点から言えることがあると思いますが,問題が大き過ぎて広過ぎて1問1答は適した質問ではありません.とりあえず地道にやればその分は身につくと言えます.
■[個別の頁からの質問に対する回答][指数法則 について/16.6.15]
すぐに合っているかどうかがわかるのがすごくいいところだと思いました。自分は全部やってから答え合わせをするのでこのサイトはとてもいいものだと思います!これからも使わせていただきます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.6.14]
わかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][マクローリン展開 について/16.6.14]
1/(2-x)の微分で何でマイナスが前に出てこないのか知りたい
=>[作者]: 連絡ありがとう.その頁で扱っている問題と無関係な問題には原則としてお答えしないようにしています.特に,各自で解かなければならない宿題や課題の答を尋ねている場合には,代わりに解いてしまうと弊害がありますので答ません.ただし,あなたの場合は「何でマイナスが・・・」と尋ねているのでその部分については答えます.y=(2−x)−1 → y'=(−1)(2−x)−2 (−1) だからマイナスは前に出ています.2つあるから消えるだけです.
■[個別の頁からの質問に対する回答][円順列・じゅず順列 について/16.6.12]
できれば、1~9までが書かれたトランプで円形に並べる方法が何通りあるのか?
こういうのがあればいいと思います。
=>[作者]: 連絡ありがとう.原理的には何も難しくはないのですが,9個も並べると数字が大きくなり過ぎて扱いにくい難点があります.この問題の場合は,8!なのでまだできなくもないのですが,52枚のトランプを円形に並べる方法という問題になると51!=1551118753287382280224243016469303211063259720016986112000000000000 となって,数学の学習というよりは体力作業に変わってしまいます.
■[個別の頁からの質問に対する回答][ 3項間漸化式の一般項 について/16.6.12]
広告がきちんと目にはいる場所においてあるのですが、拡大してみれば広告が全然気にならなくなるので広告に気が紛らわされることなく勉強できます。そして参考書より解りやすい説明ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重複組合せ について/16.6.12]
重複組合せは○と棒を使った説明とともに公式を暗記していただけでした。
Hというアルファベットを用いる背景、多項式のところ、目が醒めるような思いでした。
説明もわかりやすいです。
(数学好き24歳男性)
=>[作者]: 連絡ありがとう.あなたが「重複組合せの記号には,なぜH を使うのか」という解説に興味を持っていただけたということがよく分かりました.
■[個別の頁からの質問に対する回答][重積分:変数変換.ヤコビアン について/16.6.12]
その場合において,積分変数dxは,単純にdtに変わるのではなく,図1に示されるようにg’(t)tdに等しくなります.
⇒g'(t)tdではなくg'(t)dtですよね...
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■[個別の頁からの質問に対する回答][4次方程式 について/16.6.11]
こんばんは.補足です.あえて載せていないのならすみません.相反方程式のところで,降べきの順に整理された方程式の係数が 1 → 1 → 3 → 2 → 4 のように,左から 1 番目の係数が左から 2 番目の係数の 2 乗に,もしくは左から 5 番目の係数が左から 4 番目の係数の 2 乗になっていてもこの方法は使えます.
=>[作者]: 連絡ありがとう.あえて載せていないとまではいいませんが,なにしろ複2次式から説きはじめているので,そこまで書き切れないというのが実情です.また,この頁は4次方程式に限定して解説しているので,奇数次の相反方程式も取り上げていませんが,また別の機会があれば・・・という感じで保留しています.なお,「左から 1 番目の係数が左から 2 番目の係数の 2 乗に」かつ「左から 5 番目の係数が左から 4 番目の係数の 2 乗に」なっていてもだと思う.
■[個別の頁からの質問に対する回答][直交行列 について/16.6.11]
Ⅰ→Ⅱの証明の箇所で,t(AB)=tAtB となっていますが,t(AB)=tBtAの間違いかと思います.
=>[作者]: 連絡ありがとう.確かにその部分は入力ミスでしたので訂正しました.
■[個別の頁からの質問に対する回答][積の法則 について/16.6.10]
難しすぎます。
=>[作者]: 連絡ありがとう.このサイトでは学習者の今までの学習履歴に関係なく教材を公開していますので,1つの教材を見たときに「易し過ぎる」「ちょうどよい」「難し過ぎる」と感じる3種類の読者がありえます.ただこの頁は,高校の教科書に書かれている普通の内容を著作権を害しないように配慮しながら平凡に教材化したもので,この頁の内容が難し過ぎるとなると,中学生なのか?と思ったりもしますが,ほぼすべての問題をクリアしておられるようなので失礼しました.おっと,問題6のフォントがおかしいようなので訂正します.
■[個別の頁からの質問に対する回答][2進法,3進法,n進法 について/16.6.10]
理屈は分かるが、32進数、64進数には出合ったことはない。
=>[作者]: 連絡ありがとう.一般には分かりにくいので日常生活でムケムケの形で登場することは少ないですが,あなたが送信されたこのメッセージもBase64という64進法で送られているようです=パソコン通信などで使われていた制御コードを含まずに,文字や写真を安全なテキストで送るためにA-Z,a-z,0-9,+/を64種類の文字に当てはめる方法です.
■神奈川県[Prof.N.Hkさん/16.6.9]
http://www.geisya.or.jp/~mwm48961/kou2/sasum101.htmで、
Σ[k=1→n-1]2^(k-1)の正答は2^(n-1)-1ですよね?
正答が見当たらないのですが…
=>[作者]: 連絡ありがとう.よく見てください.あるはずです.
■[個別の頁からの質問に対する回答][行列の対角化とは について/16.6.9]
Pが急に出てきてわからなくなりました
=>[作者]: 連絡ありがとう.・・・という性質を持った行列をPとおくというように,「式に名前を付けるときに」急に出てくるのは当然のことで,以下の文脈を分かろうと努力するのもあなたの自由で,分かろうとしないのもあなたの自由だと思う.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/16.6.9]
基本公式⑴の解説の7行目に間違いがあります
ただし,π/2≦y≦π/2の場合は,cosy≧0
この範囲は、「-π/2≦y≦π/2」のはずです。
=>[作者]: 連絡ありがとう.前の方にマイナスの符号が抜けているということで訂正しました.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/16.6.8]
計算過程がわかりやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階差数列 について/16.6.8]
とても分かりやすく、例題もあって良いです。明日試験なのですが、寝る前に再度確認出来ました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数関数(有理関数)の不定積分 について/16.6.8]
いつもこのサイトにお世話になってる高校生です。
不具合(?)報告なのですが、AndroidのChromeでこのサイトを見ると、積分記号が半角文字3,4文字分程左にずれていて、横の等号に重なってしまい読みにくく感じたので、可能でしたら修正をしてもらえたらと思います。よろしくお願いします。
=>[作者]: 連絡ありがとう.微妙なさじ加減(何とアナログな!)で難しいのですが,とりあえず修正しました
■[個別の頁からの質問に対する回答][不定積分の部分積分 について/16.6.8]
(6)の途中の-1/4を外に出したら+1/4∮…だと思うんですけど
=>[作者]: 連絡ありがとう.(6)の途中の-1/4というのが2箇所あってどの(6)か迷いましたが問題2の方だろうと決めて回答します.
■[個別の頁からの質問に対する回答][同時確率分布と周辺分布 について/16.6.6]
わかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][順路の問題 について/16.6.6]
すごく良いと思うが、もっと、解説を先に与える前にヒントをした方がいいと思う。
すぐに答えを与えてしまうと伸びるものも伸びないと思う。
長文失礼いたしました
=>[作者]: 連絡ありがとう.言われていることはもっともですが,この頁の問題のように,問題と解答の間の論理的な距離が近い場合には,解説でない示唆や暗示の程度の段階を作れるとは限りません.論理的に何重にも組み立てて行かなければならない場合には,そういうことも言えます.
■[個別の頁からの質問に対する回答][展開公式 について/16.6.5]
解説が解りやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1階線形 微分方程式 について/16.6.5]
回答が重なっていて見にくいところがありました。
=>[作者]: 連絡ありがとう.PCのsafariで解答が重なる所があるということで,行間を少し広げました.
■[個別の頁からの質問に対する回答][円の方程式 について/16.6.5]
問2を全問解いたあとに表示されるHelpを押しても反応しません。
=>[作者]: 連絡ありがとう.その頁のHELPは,問題を指定すれば解説が出るようになっています.(全部の解説を表示するととても長くなるため).だから,問題を指定した後,まだ解答する前ならHELPが出ます.
■[個別の頁からの質問に対する回答][不定積分の漸化式 について/16.6.4]
=sinn-1x(-cosx)+∫(n-1)sinn-2x cos x(-cos x) dx
ここふごうミスってません?
=>[作者]: 連絡ありがとう.確かに符号が逆になっていましたので訂正しました
■[個別の頁からの質問に対する回答][双曲線の方程式 について/16.6.3]
2焦点が(1,1),(-1,-1)の双曲線を知りたいです
=>[作者]: 連絡ありがとう.2焦点が
となる双曲線を原点の周りに45°回転させるとよい.
ところで,この問題は2つの漸近線のなす角を指定しないと,結果が決まらないが,ここでは最も簡単な直角の場合を示してみる.
となる直角双曲線の方程式は
次にこれを原点の周りに45°回転するには,
によって旧座標
(x, y) から新座標
(X, Y) に変換するとよいから,
代入して新座標の方程式を求めると
これを整理すると
となって,中学校1年で習う反比例のグラフになる.
■[個別の頁からの質問に対する回答][高次方程式2 について/16.6.3]
【問題 A.2.2】で答えと解説の答えが一致してません
=>[作者]: 連絡ありがとう.選択肢の方で分母の根号が余計でしたので訂正しました.なお,
wxMaxima では,方程式→高次方程式の解を求める→(x-1)*x*(x+1)*(x+2)=24 により,解を確かめることができます.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/16.6.3]
回答に一つだけ当てはまらない場合の方がよく考えれると思います
=>[作者]: 連絡ありがとう.ジョーカーがある形がお気に入りということですが,時間があれば考えてみます
■[個別の頁からの質問に対する回答][行列の積 について/16.6.3]
とてもわかりやすく問題もいいものです
わがままかもしれませんがもっとのせてほしいです
エクセル頑張ってみます
=>[作者]: 連絡ありがとう.ワープロ文書と異なり1つずつがプログラムなので,追加するのは結構大変です
■[個別の頁からの質問に対する回答][複素数の計算 について/16.6.2]
丁寧で分かりやすくてとても助かってます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/16.6.2]
当てはまる例と使えないときの例のどちらも書いてあってとてもわかりやすいです。確認問題でアウトプットできるところもありがたいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/16.6.1]
数Ⅲのまだ微積をやっていなかったため、入試の過去問を解いていても全くわからなかった三角関数の積分がこちらのページでわかりました!ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数のグラフ について/16.5.31]
y=sin4x^3
=>[作者]: 連絡ありがとう.高校生がこのグラフを書かされることはないので,高卒以上の方だと思いますが,他に相談できる人がないのでお願いしますぐらいの一言があるべきケースかなと
Excelでグラフを書くには,A列にA1=0,以下増分0.1で6.3ぐらいまでフィル.次にB1に =sin(4*a1)^3としてこれをB63までコピー.平滑線付き散布図
wxMaxima では,プロット→2次元プロット→関数 sin(4*x)^3 x 下端 0 上端2 OK
■[個別の頁からの質問に対する回答][ベクトル,行列の簡単な復習 について/16.5.29]
すごいわかりやすい
=>[作者]: 連絡ありがとう.ちゃんと読んでもらった感じです.この連絡があったので教材をチェックしたら,たまたまIEで行列の表示のおかしいところが見つかったので訂正しておきました.
■?[?さん/16.5.29]
①放物線の移動 問2の1 答えが どうしても ア2 イ0.5 になります。ヒントを見ても同じ答えになります。どうしたらいいでしょう。解答もあれば そこからも学べるので、もっと学習しやすいです
② グラフの移動が上手く出来なくて いつも × になります。ショックです。
=>[作者]: 連絡ありがとう.ヒントにありますように,頂点の座標が(1,3)から(3,2)へ移動してから(3,-2)に至るのだから,(1,3)から(3,2)へx軸方向の移動は「2」で,y軸方向の移動は「−1」です.ヒントを少し詳しくしました.
■[個別の頁からの質問に対する回答][重要な極限値(1) について/16.5.28]
xを0に限りなく近づけると
sinx/xの値が1に限りなく近づく
ことの証明について。
貴方は、証明の中で円の面積がπr^2で表されることを前提にしていますよね。
しかし、遡って考えると、 円の面積の公式は「cosxを積分するとsinxになる」ことをもとに作られていて、それは今回の命題が真であった時に初めて成り立ちます。
つまり、貴方の証明は、その最中にこれから
証明することを使ってしまっているので、
間違っていると思います。
=>[作者]: 連絡ありがとう.「cosxを積分するとsinxになる」ことをもとに作られているという所が間違っています.他の方法があります.
■[個別の頁からの質問に対する回答][確率の乗法定理 について/16.5.28]
改善されててうれしい!
とても使いやすかった!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/16.5.28]
分数の因数分解も教えてください
=>[作者]: 連絡ありがとう.分数係数の場合の因数分解は通分すればタスキ掛け因数分解の問題に書き換えられます.分数係数のままで因数分解するものや無理係数のままで因数分解する問題も追加しておきます.
■[個別の頁からの質問に対する回答][三角関数の導関数 について/16.5.28]
とても参考になりましたし、問題や回答方式も良くて分かりやすかったです。言うことがあるとすれば、三角関数の微分の証明を三角形の図などを交えたりして解説してほしいです。
=>[作者]: 連絡ありがとう.図でやる方法も参考に付けておきます.
■[個別の頁からの質問に対する回答][全微分方程式 について/16.5.27]
すごくみやすくてわかりやすいです.
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/16.5.27]
問題10のところは答えが間違っていると思います.そしてその過程にも字の間違いがあると思います.
=>[作者]: 連絡ありがとう.最後の方までていねいに読んでくれてありがとう.途中経過でr=±1に間違いがありましたので訂正しました.解答の方はおかしくないように思う.この問題のように計算が長くなると,計算見違いが起りやすくなるので,wxMaximaで一般解と初期条件を入れた解の求めた式の入力方法,出力結果も書いておきました.
■[個別の頁からの質問に対する回答][リッカチ形 微分方程式 について/16.5.26]
参考書だけでは足りない部分まではっきり書いててすっごく勉強になりました.
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベルヌーイ形 微分方程式 について/16.5.26]
参考書だけではなぜそうなるかという過程などが足りなかったんだけど,これを見てその過程を学べてもっと確かにわかることができました.
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/16.5.25]
解説が欲しい
=>[作者]: 連絡ありがとう.間違った場合,==?== というマークが表示されますのでそれをクリックすると解説が出ます.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/16.5.24]
x^4-2x^2+1
=(x^2-1)^2
=(x+1)^2(x-1)^2
まだ分解出来ます
=>[作者]: 連絡ありがとう.まだ因数分解できますが,問題は「もうこれ以上因数分解できない形を探しなさい」ではなく,「等しいものを選びなさい」となっています.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.5.24]
答えが合ってるのに「間違え」と表示されるので改善してほしいです
=>[作者]: 連絡ありがとう.どの問題に,自分はどう答えて,解答は何であるのに「間違え」と表示されると書かないと,何を質問されているのか話が通じません.実際のところ,あなたは問題3で立ち往生していていますとなぜ書かないのですか.そのことを隠してしまっては,何も進みません.次に,問題3のHELPで示されているのは,読者の便宜に供するための係数で,たとえばそこに +1y と書かれていても,まさかそのまま答案に書いているようでは,中学1年生の文字式の基本が習得できていないことになります.+1y とか +1x は +y , +x と書くべきことは中学校の常識です.また, -1y は -y,-1x は -x と書かなければならないことも当然のことです.(1x,1y のような答案を正解にすれば,定期試験や入試であなたが不利益を被ります)
■[個別の頁からの質問に対する回答][放物線の方程式 について/16.5.23]
参考になりました。ありがとうございます
=>[作者]: 連絡ありがとう.管理人の私は最近,どの頁でも第1問の解説はよく読まれるかもしれないと考えています.たぶん,あなたもそのあたりを重点的に読んだ?
■[個別の頁からの質問に対する回答][統計データの種類 について/16.5.23]
尺度の分類が覚えられません。よい方法がありますか?
=>[作者]: 連絡ありがとう.私の場合は,まず両極端を外します・・・比較できない=名義尺度,何でもできる=比例尺度.次に,等間隔=間隔尺度,等間隔でない=順序尺度
■[個別の頁からの質問に対する回答][二重根号 について/16.5.22]
分数のバーと根号が重なって見にくいときがある
=>[作者]: 連絡ありがとう.Chromeで読んだら根号の分数や分数の根号で少し重なるところがあると理解しました.実際のところこのプログラムは10年程前にInternet Explorerに合わせて作ったもので,ブラウザのシェアが変化するとなかなか大変です・・・分数関数の表示プログラムと根号の表示プログラムを合成する方法を見つけたところまではよかったのですが,フォントサイズごとにブラウザごとにバージョンごとに合うようにするのはなかなか難しいので,少々重なる所はお愛嬌としてにっこり笑って見逃してください.
■[個別の頁からの質問に対する回答][展開公式1 について/16.5.22]
すごくわかりやすい!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][軌跡の方程式1 について/16.5.22]
丁度、休んでいた時の内容で、問題の解き方が解らなかったので、使わせていただきました。アニメーション付きなのは
解りやすく、とても良いと思います。とても助かりました。
=>[作者]: 連絡ありがとう.授業を休んだところを補充するために使うのはよい使い方だと思います.
■[個別の頁からの質問に対する回答][積の法則 について/16.5.20]
素因数分解を理解していなかったので、例4が困った。別のページで素因数分解から始めた。
問題8までやれば、例4も理解できた。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階乗 について/16.5.20]
無理数の階乗を知りたかったので、残念でした。
=>[作者]: 連絡ありがとう.初めの方に書いていますように,階乗は0以上の整数に対して定義され,負の整数,小数,分数などには定義されません.当然,無理数,複素数,ベクトル,行列に対しても定義されません.そもそも階乗は「初めの数」と「次の数」という概念だけで構成できる数の列について,「初めの数」から「その数」までのすべての数の積で定義されますが,例えば,小数の1.9に対して,「前の数」は1.8とは限りません.1.89, 1.899, 1.8999, ...かもしれません.このようにして小数を持って来ると,何を掛けるのかが決まりません.分数でも同様です.正の整数以外には階乗は定義できません(0!だけは,順列,組合せの公式を自由に使うための例外です).
■[個別の頁からの質問に対する回答][二項分布 について/16.5.19]
大学の講義よりもはるかにわかりやすい解説がなされていて、とても役立ちました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数平面 について/16.5.19]
問題3の点が1メモリ分下にずれていて、HELPを見るまで気づかず悩んだ。
=>[作者]: 連絡ありがとう.あなたがお使いのWindows10標準のMicrosoft Edge(Webkit系)というブラウザで,一昔前のFirefoxのように,次の文字のスタート位置が1文字分下がる特徴があるということでしたら,そのバグが訂正されるまで一定の対応が必要になるかと思いますが,その症状の報告は初めて聞きました.設定・仕様を各会社の都合に合わせて変更していると,体が持たない!?ブツブツ・・(互換モードIntenet Explorer, Firefox, Chrome, Safari, Opera, Sleipnirのいずれでも問題なく,現在までにその症状が報告されたのはEdgeだけです)
(追伸)2016.5.24 Internet Explorer11にEdgeエミュレーションモードがあったので,これを使ってEdge対応にしました・・・根号の位置もずれていた・・・該当箇所多数なので少しずつ直す予定
■[個別の頁からの質問に対する回答][負の指数 について/16.5.18]
とても分かりやすかったです。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][補集合 について/16.5.18]
採点後の解説がわかりやすい
=>[作者]: 連絡ありがとう.管理人も,分かりやすくするためにそれなりに苦労しているのです
■[個別の頁からの質問に対する回答][正弦定理(解説) について/16.5.18]
わかりやすかった
=>[作者]: 連絡ありがとう.すでに,そこそこ理解しておられるためか,初めの部分と例1,2のあたりに絞って読んでもらえたものと考えています.
■[個別の頁からの質問に対する回答][樹形図、辞書式配列 について/16.5.17]
問題数が少ない。
=>[作者]: 連絡ありがとう.問題を解かれた形跡がありません.この頁が答案を採点する機能があるということを分かってもらえるように,問題1の上に「クリックしてください」の文章を入れておきました.
■[個別の頁からの質問に対する回答][展開公式 について/16.5.17]
問題を毎回変えてくれるところが嬉しいです、
が、もう少し問題数があると嬉しいです(`)
=>[作者]: 連絡ありがとう.4日ほど前にも感想を書いていた人がいましたが,この頁は空欄書き込みなので入力が大変で最後まで持たない人が多いです.特に問題3に赤字で書いておきましたが,最後の方は白紙答案が多い.そんな中でもう少し問題数があると嬉しいとは,やるき十分だな
■[個別の頁からの質問に対する回答][円の接線の方程式 について/16.5.16]
解説がわかりやすくて助かりました🎉
又、練習問題を解いて定着を図れるところもよかったです✨
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/16.5.16]
わかりづらい
=>[作者]: 連絡ありがとう.もう少し具体的に書いてもらえると,回答したり対応したりできるのですが・・・
■[個別の頁からの質問に対する回答][共通部分と和集合 について/16.5.16]
解説や図を交えてからの問題を解くというながれで
理解することができました。ありがとうございます
=>[作者]: 連絡ありがとう.こちらの記録を見ても,きっちり勉強されたように思う.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.5.15]
たすきがけ因数分解ですが、答えを書いた際+やマイナスが半角でないと正解しません。
全角で書いても正解になるようにしてくれれば嬉しいです。
=>[作者]: 連絡ありがとう.InternetExplorerとFirefoxでは全角文字が入らないようになっていましたが,Safari(iHoneも)やChromeでは全角文字も書こうと思えば書ける状態になっていたようです.設定を変更しました.
■[個別の頁からの質問に対する回答][展開公式1 について/16.5.15]
解説のところや重要なところが文字の色が目立つ色になっていて見やすいです。
=>[作者]: 連絡ありがとう
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.5.15]
9は、十分条件じゃないんですか?
=>[作者]: 連絡ありがとう.≪9≫の問題の解答は十分条件だという質問だと解釈しましたが,そこにヒントが書いてありますので,それを読んでください.
■[個別の頁からの質問に対する回答][行列の積 ABの定義 について/16.5.14]
わかりにくい問題 : 右から左から
=>[作者]: 連絡ありがとう.一番先頭の解説から5行までを読んでいただいていないようで,この頁の内容がすべて吹き飛んでいますA にB を右から掛けたものAB とA にB を左から掛けたものBA は違うのだということをその頁で解説しています.これらが普通の数字と同じように当然等しいはずだと思い込んでおられる場合には,この頁に書いてある内容は何も頭に入りません.
■[個別の頁からの質問に対する回答][簡単😉 について/16.5.13]
簡単😉
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/16.5.13]
入力めんどいです
=>[作者]: 連絡ありがとう.確かにそうだと思う.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.5.11]
理解が進みました!
感謝いたします。
幸運をお祈りいたします☆
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開の順序 について/16.5.11]
とってもいいです❗
=>[作者]:
■[個別の頁からの質問に対する回答][逆行列の求め方 について/16.5.10]
逆行列の3X3をやってるのに当たらない。
何で?????
=>[作者]: 「当たらない」という言い方は適当ではありません.それが,答えが合わないという意味でしたら,問題とあなたの答,模範解答の3種類を示さなければ,話が成り立ちません・・・何も材料がないのに通りすがりのおじさんに「なぜ答が合わないのでしょうか」と尋ねている場面を想像してみると,この場面設定はおかしいことに気付くはずです・・・これだけなら,あなたが間違っているか,模範解答が間違っているか,両方とも間違っているかのいずれかですという以外に答え方がありませんので,質問の仕方を変えてください.
■[個別の頁からの質問に対する回答][複素数の和差積 について/16.5.9]
等しい物を見つけていくとジョーカーが出て来るというゲーム形式が、素晴らしいです!楽しみながら出来ました!
=>[作者]: 連絡ありがとう.余裕をもってできたという印象を受けます.約9分で完了しています.
■[個別の頁からの質問に対する回答][対数の計算 について/16.5.9]
問題2 累乗根
ヒント
Log3 9√3=log3(3^2・1/2)=log3 3^5/2
Log3 9√3=log3(3^4・1/2)=log3 3^5/2
^4が^2になっています。
=>[作者]: 連絡ありがとう.9=32 だから,元のヒントで合っています.それにしても,あなたはこの頁を3時間半も勉強したように記録されており,忍耐力に関心しました.
■[個別の頁からの質問に対する回答][外分点の位置ベクトル について/16.5.9]
外分店のm<nのときの公式証明がとてもやくにたちました。
どこの参考書もサイトもm<nのときの証明を端折ってるので自分で証明ができなくて困ってました。
ベクトルの方向が逆になることを見落としてて、証明できなくてほんとに困ってました。
このサイトのようにちゃんと証明しているサイトはありがたいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/16.5.9]
三角関数の合成のところにて、符号がどちらも「-」になっているので、誤字の訂正を宜しくお願いします。
=>[作者]: 連絡ありがとう.この頁全体が三角関数の合成公式なので,式は非常にたくさんあり,どの式なのかを絞って述べていただかないと分かりません.あなたが時間をかけて見ていたのは「紛らわしい公式との区別」【例題1】あたりかと思いますが,そこには何も誤字はありませんが
■[個別の頁からの質問に対する回答][平方完成の変形 について/16.5.8]
とても役に立ちましたありがとうございます。
改善点として挙げるとすれば、前の問題の解説と次の問題の問題文が少しかぶっていることでしょうか。
そこを直せば完璧だと思います。
=>[作者]: 連絡ありがとう.管理人の画面では前後の問題でかぶっているということはないのですが,機種によって少し違いがあるかもしれませんので,間隔を少し広げておきます.
■[個別の頁からの質問に対する回答][二重根号 について/16.5.8]
解き方がとてもわかりやすかったです
ただやりたい項目をピンポイントで出来ないのはすこし煩わしいです
私の場合二重根号の6項目をやりたかったのでそれ以前のページの内容は理解出来ていたので...
勉強をこのサイトをベースにやるのなら全く問題ないと思います。むしろこの方がちゃんと理解できているか確認しながら進めると思います!
私はわからないところがあって探しにきたので、そうすると知りたいところを開くまでに時間がかかりすぎます。
=>[作者]: 連絡ありがとう.筆者自身でもプログラムを点検するために該当箇所にたどり着くのが大変なので,やりたい個所を出してほしいという要望はよく分かります.(あなたは約40分かかって目的の頁にたどり着いています.)ただこの教材は下から積み上げていく構成にするとどうなるのかという仮説の基に作っているので,ジャンプする設定にするには別の頁を作らなければならないかもしれません.少し考えます.
■[個別の頁からの質問に対する回答][数学的帰納法(不等式の証明) について/16.5.8]
数列の苦手な息子が特に数学的帰納法の不等式に苦しんでいて、このサイトにたどり着きました。市販の参考書には書かれていない、なぜこの処理をするのかということが書かれていて、解き方のコツがわかったようです。ありがとうございました。次は群数列です。
=>[作者]: 連絡ありがとう.頑張ってください.
■[個別の頁からの質問に対する回答][等比数列の和 について/16.5.7]
うーん、公比が同じでも、
こんなに答えが違うんですね~
難しかったです。
忘れた頃に再挑戦します。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の積 について/16.5.7]
4(5), 積は (-12 7 -18)になり、その(1,2)成分は 7 だと思うのですが、違うのでしょうか。
=>[作者]: 連絡ありがとう.申し訳ない.全く違う計算を書いていました・・・いったい何の計算だったのか・・・訂正しました
■[個別の頁からの質問に対する回答][同次形 微分方程式 について/16.5.7]
積分記号とその後ろの式の高さが違っちゃうので,積分記号だけ浮いてしまっているような感じになってます.
分数はyが先の下にはみ出す事がありますが,それ以外は美しいです.
=>[作者]: 連絡ありがとう.教科書では「積分記号とその後ろの式の高さが違う」のが普通で,逆にそうでない教科書は見たことがありません.TeXで数式を文中に埋め込むために同じ高さに表示するのは略式と考えるべきでしょう.御指摘の意味が通じませんが,とりあえず他のバージョンの積分記号にしておきました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/16.5.6]
定数係数2階線形微分方程式のrが複素数の時、実数のみに直す時の説明が少し分かりにくかった
=>[作者]: 連絡ありがとう.「rが複素数の時、実数のみに直す時の説明が少し分かりにくかった」と述べておられますが,あなたはそこそこ分かっているせいか,初めから解説を読まずにいきなり問題を解き,rが複素数の時の説明を5秒ほどしか読んでいません.そこが問題の1つです.おそらくもう一つはオイラーの公式
eix =cos x+isin x (もしくは
ド・モアブルの定理 )が理解できていないのです.その部分をもう一度理解してから,読まれるとよいでしょう.
■[個別の頁からの質問に対する回答][不定積分の置換積分 について/16.5.6]
4プロセスの説明では不定の置換積分の原理が分からなかったのですがこのサイトを見ることにより、理解することができました。
このサイトの例題ですが、空白が少ないというか、その式の前後だけ見れば考えなくても解けてしまう、という仕様になっているように感じ、人により、効果が半減してしまう気がしました。
=>[作者]: 連絡ありがとう.4プロセスというのが数研出版の参考書だということがようやく分かりました.ところで,左の学習進行状況[横は時間(秒),縦は進み具合(ピクセル数)]から見ると,あなたはコンスタントに進んでおり,途中で例題1を2回見直したのは何か気になることがあったからで,おそらくバリバリの現役で,学力・持久力とも十分あるのです.しかし,管理人が何年かこのサイトを運営する中で分かったことは「サーチエンジンから入って来る人は,分からないことがあるから調べごとをしている」という事実です.中には高校中退の人もあり,文化系で卒業した人,定年退職後ようやく気になっていた教科の学習時間ができたという人もあります.そうすると「教材は,分からない人を前提に作るべし」という結論に達するのです.あなたのようにそこそこ分かっている人は,当サイトから見れば模範生のようなもので,分かることまで書いてあるところはにっこり笑って見てもらえばよいのです.
■石川県[井上さん/16.5.5]
三次式がかなり自分にとって難しい
=>[作者]: 連絡ありがとう.高校で3次式の展開や因数分解を学んだときには,初めは項数が多いので戸惑いますが「作業は分けて処理する」のが基本です.高校で○十年間教えていた管理人でも,前から順にスラスラと答案を書こうとすると計算間違いすることがあります・・・最終的に4個ないしは5個の係数を合わさなければならないときでも「一度にやっているのではなく」1つずつ作った部品を組み立てているだけです.このように3次式を処理するには,「仕事は分けてやる」「1つずつの係数を正確に作る」ことがポイントです.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/16.5.5]
とてもわかりやすいです(≧∇≦)
間違った時しかHELPが見られないので、正解した時も解き方が見られるようにしてほしいです‼
=>[作者]: 連絡ありがとう.要点を見直したりしながらよく勉強できていると思う.とくに最後の方の2題に時間をかけてやった感じです.正解の場合でも解説が読めるようにしました.
■[個別の頁からの質問に対する回答][展開公式1 について/16.5.4]
とっても分かりました。大人でも
子供にも教えてあげたいと思います。
=>[作者]: 連絡ありがとう.3次の展開公式あたりがお目にとまったように思う.
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間 について/16.5.4]
例題2の計算が間違ってます
=>[作者]: 連絡ありがとう.途中経過の式に余計な係数が付いていましたので訂正しました.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/16.5.4]
回答すると解説で次の問題が読めませーん
=>[作者]: 連絡ありがとう.Safariでチェックしましたが,解説と問題が重なる箇所は見当たりませんでした.それよりもあなたの場合,問題1は2分半ほどかけて熱心に解いていますが,それよりも後ろの方は解説も読まず問題も解かずに放棄してしまっているのが気がかりです.
■[個別の頁からの質問に対する回答][展開公式1 について/16.5.4]
気にいった所 : 右側の問題全問解けたので解説は読んでない
わかりにくい問題 : 今のところ大丈夫です
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][共通部分と和集合 について/16.5.3]
すごくいい問題でした
=>[作者]: 連絡ありがとう.
■三重県[あーたそさん/16.5.3]
わかりやすくて良かった!
=>[作者]: 連絡ありがとう.
■?[?さん/16.5.3]
[x+1/xの値について/16.5.3]
大変 良く理解できました! 有り難うございます!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開の順序 について/16.5.3]
(3xー2)(3x+5)の答えを教えてください。
=>[作者]: 連絡ありがとう.その頁にある問題についてはお答えしますが,各自で解かなければならない宿題などの問題には答えていません.
この頁 を見てください.
■[個別の頁からの質問に対する回答][x+1/xの値 について/16.5.3]
数1 Xn+1/Xn の値 7*の問題
x-1/x=a とするとX2-1/X2 の値は
X2-1/x2 = (X-1/X)2 +2 では解けないんですか?
2乗と分数が上手く入力出来ないので わかりにくい書き方でスミマセン
=>[作者]: 連絡ありがとう.中学3年と高校1年で登場する展開公式で
というのがあります.(
の符号に注意.)
これにより
になります.
にはなりません.
そこで問題を解くために,
の公式を使って
とします.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/16.5.1]
数字が消えているときが存在する
=>[作者]: 連絡ありがとう.「Chromeで見たら数字が消えている場合がある」と述べておられるものと解釈しましたが,第何問など場所を特定していただかないと調べられません.なお,点検作業の中でChromeで見たら改行位置の違う箇所があったので1箇所訂正し,薄い文字色を濃く変更しました.
■[個別の頁からの質問に対する回答][二項分布 について/16.5.1]
わかりにくかった もっと言えば教える意志を感じられなかった。 自分は学校の勉強だけでは理解が追い付かないためインターネット検索を利用しているのにこのページはまるですべての数学知識を持ち合わせているのを大前提に置いて作成されているように感じた。 まったくの初心者向けと言いながら専門用語が行き交う文章はいかがなものだろうか
=>[作者]: 連絡ありがとう.あまり攻撃的な文章は取り上げないようにしていますが,今日は時間に余裕があるので回答します.
■[個別の頁からの質問に対する回答][正弦定理 について/16.5.1]
完璧です。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][部分集合,集合の包含関係 について/16.4.30]
(2)A){0,2,4,8,16,32}だと思います
=>[作者]: 連絡ありがとう.
20 =1 , 21 =2 , 22 =4 , 23 =8 , 24 =16 , 25 =32になります.
この頁参照
■[個別の頁からの質問に対する回答][ 複素数の計算 について/16.4.30]
突然失礼します。虚数の計算順序を忘れてしまい、こちらにたどり着き、質問させていただきます。
(2+√-2)^2 を計算する時、そのまま展開し始めるのか、(2+√2i)^2としてから展開するのかご教授頂きたく。よろしくお願いしますm(_ _)m
=>[作者]: 連絡ありがとう.ご質問の計算順序について,どの順序でなければならないという決まりはありませんが,結論から言えば「 i に書き変えてから行う方がよい」でしょう.
(その理由)i を用いた式の計算規則: (ア) 普通の文字と同じように加減乗除ができ,同類項を整理することもできる. (イ) ただしi
2 が登場したら −1に置き換える.は覚えますが,次のような負の根号についての計算規則は,通常覚えないので,負の根号のまま変形するのは不利です.
のとき
…(1),
…(2),
…(3),
…(4)
(1)(2)は簡単ですが(3)(4)は紛らわしいもので,これらの証明自体 i に直して行いますので,結局 i に直して行う方が楽になります.
■神奈川県[Prof.N.Hkさん/16.4.29]
http://www.geisya.or.jp/~mwm48961/kou3/vector102.htm
で、なぜ{(→+→)/2 + (→+→)/2 + (→+→)/2} /3 が (→+→+→)/3
a b b c c a a b c
になるのですか?普通にやれば
(→+→+→)/6 になると思うのですが…
a b c
=>[作者]: 連絡ありがとう.
において分子の
は2回ずつ登場しているので,
となり,
になるということです.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/16.4.28]
解答を認識しないときがある
=>[作者]: 連絡ありがとう.PCのChromeでチェックしましたが,正常に作動しています.たとえば,1つの問題で誤答→別の誤答と選択した場合,画面の表示は全く変わらない仕様になっています.
■[個別の頁からの質問に対する回答][対数の定義 について/16.4.28]
文系大学1年生です。学科の都合上一から数学2を勉強していますが、とても分かりやすく且つ楽しく学べました。ありがとうございました。
=>[作者]: 連絡ありがとう.がんばってください.なお,管理人の都合で,今日から学習者がどこら辺をどのくらい時間をかけて読んでいるかを大まかに分析するプログラムを埋め込みました.あなたが,第1回回答者ですが,時系列に沿って教材頁内を順調に移動していることが手に取るように分かり,管理人も喜んでいます.今日は記念すべき日でした.
■神奈川県[Prof.N.Hkさん/16.4.27]
相当どうでもいいかもしれませんが、http://www.geisya.or.jp/~mwm48961/kou2/iti_vector2.html
のスモールシーベクトルが、設問文でラージシーベクトルになっています。
=>[作者]: 連絡ありがとう.ご指摘の通りでしたので訂正しました.
■[個別の頁からの質問に対する回答][絶対値記号2つの外し方 について/16.4.27]
助かります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][逆三角関数 について/16.4.27]
逆三角関数の予習で利用致しました。
計算練習が出来たお陰で、基本的なイメージが掴めました。
これから微分にチャレンジします。
ありがとうございました。
=>[作者]: 連絡ありがとう.連絡があった頁を見たら,選択肢が改行されておかしくなっているものがあることに気付き,訂正しました.
■[個別の頁からの質問に対する回答][正弦定理 について/16.4.26]
A’=180°-A
の証明へのリンクお願いします。
=>[作者]: 連絡ありがとう.もちろんその内容も前提にはなっていますが,前提となることは非常にたくさんあります.教材を前から順に読む限り参照は「多くの生徒が忘れている」と考えられる項目に絞っています.
■[個別の頁からの質問に対する回答][関数の連続,極限関数 について/16.4.26]
書き込みができないときがある
=>[作者]: 連絡ありがとう.PCのChromeで確かめましたが,不具合はありませんでした.「書き込みできないときがある」とは,書き込みできるときがあって,書き込みできないときが時々あるという感じなので,空欄にマウスがうまく合わないのかもしれませんので空欄を少し大きくしました.
■[個別の頁からの質問に対する回答][正弦定理 について/16.4.26]
三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけ なのになぜ関数電卓などで任意の数でsin cosできるのがわからない
=>[作者]: 連絡ありがとう.実に深く本質に迫るよい質問だと思う.
そもそも三角比の値,例えば
sin 30°はその角度が
30° であるときの「直角三角形の辺の長さの比」で定義されているので,左図のような三角形ではキラキラ輝いておいしい役割を演じている辺の長さの3と2で辺の比を求めても,
sin 30°の値には関係していません.
見かけを無視して,茶色で示したような直角三角形を考えて,この直角三角形で辺の比を求めていることになります.
⇒見たままの形で辺の比が三角比になるのは直角三角形の場合だけ.それ以外では,直角三角形の骨組みを別に書いて求めていると考えるとよい.
⇒どうやって求めるのか?分度器を使って
30° の図を描き,斜辺の長さが1になるようにしてから縦の長さを読めばよい.分かりやすいのはここまでですが,それだけでは小数第4位とか小数第6位までなど詳しい数字が求められないので,今日ではコンピュータを使って(ただし角度の単位はラジアン)
により必要な桁数まで求めます.関数電卓では角度の単位を度に書き直した公式が組み込んであると考えるとよい.
角度を「度の単位」「半角文字」で書きこんで、下の[計算する]ボタンを押してください→ sin 計算する
■[個別の頁からの質問に対する回答][展開公式1 について/16.4.25]
問題3の⑶と⑷の違いがよく分かりません
=>[作者]: 連絡ありがとう.解説が付いているのでそれを読んでもらえば分かると思いますが,(a+b)(a2 −ab+b2 ) になっているのでa3 +b3 と変形できますが(a+b)(a2 −2ab+b2 ) になっているのでa3 +b3 とは変形できないということです.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/16.4.24]
すごくわかりやすかったです!
僕はこれで東大目指します!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/16.4.24]
選択式なのでいちいち打たなくていい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][楕円の方程式 について/16.4.24]
全体を通して、丁寧に説明されていて見やすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][余弦定理 について/16.4.24]
よくわからん
=>[作者]: 連絡ありがとう.感想が短すぎて,中学生が読んでいるのか大学生が読んでいるのか,どの個所のことなのか書かないと返答のしようがありません.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.4.22]
今晩、固有値、固有ベクトルの意味が初めて分かりました。図解されている他のサイトも見ましたが。60歳代後半の文系人間で、
高校では行列を学ばなかった世代なので。解析学のほうは、フーリエ級数の入り口あたりまでをおおむね理解しているつもりです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角比の相互関係 について/16.4.22]
新課程対応 三角比の相互関係は今は3つの式を習います。
=>[作者]: 連絡ありがとう.「今は」ではなく,昔から3つですが,3つ並べると3個目が覚えられない生徒が多いのでどう教えるとよいかという問題について,まず2つに絞るとよいという教え方を提起しています.教科書には通常3個書かれていますが,4個目はできなくてもよいということではありません.数学の公式は相互に関連しているので,これだけ覚えたらよいという形ではなく必要に応じて「作れる」ことも重要です.
■[個別の頁からの質問に対する回答][複素数の計算 について/16.4.18]
役立っています ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/16.4.17]
とても分かりやすかったです。
ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開の順序 について/16.4.17]
分かりやすかったです!
とても役立ちました!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式 について/16.4.16]
黄色い矢印が意味がわからなくって止まってしまってアルファとベータ二分のエイプラスビィトか暗記してしまいました。もっと黄色い矢印になるまでの家庭が知りたいです
=>[作者]: 連絡ありがとう.あわてずにゆっくり読みましょう.α,βの式は証明できていますがA,Bの式はまだ証明できていませんので,α,βの式からA,Bの式を作るにはどうしたらよいかと考えます.
■[個別の頁からの質問に対する回答][不定形の極限 について/16.4.16]
わかり易かった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/16.4.16]
小数点がつけられない。
解答が出てこない
=>[作者]: 連絡ありがとう.小数点を使わなければならない問題はありません.採点すれば解答は出ます.PCのChromeで確認済みです.
■[個別の頁からの質問に対する回答][割り算について成り立つ等式 について/16.4.16]
3] 2x3-9x2+ax を整式 x2 -3x+b で割ると -x+3 余るとき,定数 a , b の値を求めよ。という問題でなぜa-2b-9=-1となるのでしょうか?同様になぜ3b=3となるのでしょうか?
=>[作者]: 連絡ありがとう.申し訳ないのですが,問題を読んでおられないか,恒等式の取り扱いについて慣れておられないのではないでしょうか.
余りが -x+3 という問題で,余りが Ax+B になるときに,A=-1かつB=3になることについては,なにも省略はありません.この説明について,「なぜ」と尋ねることは,まともな議論ではありません.
同様にして,余りが -x+3 という問題で,余りが (a−2b−9)x+3b になるときに,a-2b-9=-1かつ3b=3になることについては,なにも省略はありません.この説明について,「なぜ」と尋ねることは,まともな議論ではありません.
軽い日常会話の例でいえば,2016年4月16日現在の日本の総理大臣が安倍信三であるときに,現在日本の総理大臣の姓はなぜ阿倍で,名はなぜ信三になるのですかと尋ねることは,まともな議論ではありません.
あなたがそんなことを尋ねているとは思えません.
恒等式の係数比較法の頁 を見てください.
■[個別の頁からの質問に対する回答][実数係数方程式の虚数解 について/16.4.15]
解法3は初めて見ました。少しズルっぽいですがとても便利そうなので使わせていただきます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/16.4.14]
もう少し式同士の空白を開けてほしい。
上の式が目に入ってこんがらがる。
=>[作者]: 連絡ありがとう.この頁は画像を使用していないため1行書き加えるだけで行間を広げられました.他の頁ではこのコマンドにIEが対応しないため簡単にはいかないようです.
■[個別の頁からの質問に対する回答][円と直線の位置関係 について/16.4.13]
例1の答案Aで不等式の文字がxではなくkだと思います
=>[作者]: 連絡ありがとう.結構大きなポカミスでした.訂正しました.
■[個別の頁からの質問に対する回答][指数関数,対数関数の導関数 について/16.4.13]
参考になる情報ありがとうございます。
「○ これらの極限値は,次の極限値で表わすことができる.」次の数式にn乗が抜けているようです。
参考になれば幸いです。
=>[作者]: 連絡ありがとう.iPhoneでチェックしましたが,n乗は見えています.電波事情か何かで表示が遅いのかな?(iPadで遅い事があるという話は,たまにネットに書かれている)
■[個別の頁からの質問に対する回答][母平均,母比率の推定 について/16.4.11]
P(X≦m-1.67σ’)=0.5-0.4525=0.0475
この説明の1,67が判りません
=>[作者]: 連絡ありがとう.右の欄に説明していますが,標本平均は
の正規分布をなすと見なせます.
ここで,
となるkの値は1.67だから
になります.(その値145が,平均値から標準偏差の何倍離れているかを調べます)
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/16.4.11]
練習問題で理解度を確認でき良い。有難うございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間 について/16.4.11]
例題3等の 計算経路をもう少し詳しくお願いします
=>[作者]: 連絡ありがとう.結構詳しい説明になっていると思いますが・・・・
■埼玉[魚成さん/16.4.10]
対偶証明法と背理法の問題1
x,yの[ ア ]ならば [ イ ]となる. よって対偶により示された.は
x,yは か、x,yが のほうが文脈がいいかと思います。
=>[作者]: 連絡ありがとう.例えば「象は鼻が長い」という文は,主語が2つあって「象は長い」とも「鼻が長い」とも読めるので,引っかかることがあります.「象について言えば,鼻が長い」と読めばセーフです.単純に「象の鼻は長い」とすれば問題は起こりません.これと同様に,「x,yは少なくとも1つは1以下」とすると主語が2つになり,「x,yは両方とも(が)1より小さい」としてもおかしくなります.正解の文脈で見ると「x,yの両方とも(が)1より小さい」とすれば納まっていることが分かります.
■長崎県[新一年さん/16.4.9]
同(二文字)2
の答えはどこにありますか? 答えを選択して10問解きましたが、その後がよくわかりません
=>[作者]: 連絡ありがとう.選択問題で数回の試行で正解に達することが分かっているのに,やってみる時間が無駄だという主張をしておられるものと判断しました.
■[個別の頁からの質問に対する回答][対数の定義 について/16.4.9]
73歳の私でも理解できました。有り難う御座いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/16.4.6]
色味が良くないです。図も見にくいです。文章中の色分けに規則性がなく、読みづらいです。内容はわかりやすく、Excel での計算方法も明記されているので助かりました。
=>[作者]: 連絡ありがとう.前半について:確かにご指摘の通り.作者が読んでも疲れる・・・ただし,直すのは今後の課題です
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.4.5]
問題文のあとに、はっきりとした答が書いていないので、正しい答がなんなのかよくわかりません。
解答を見たときに始めに赤い文字で大きく答を表示してから解説をして欲しいです。
=>[作者]: 連絡ありがとう.記述問題ではなく単なる選択問題(4択)なので必ず正解に達します.分からないはずはありません.解答自体は4通りしかなく,この項目では解答が重要なのではなく,途中の考え方が重要で,それがヒントとして書いてあります.
■[個別の頁からの質問に対する回答][直線の像,領域の像 について/16.4.3]
問題8の解答と説明の答えが違っていた
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.4.3]
入門から標準までとても良い問題だと思います。
さらに多くの問題を載せていただけるとありがたいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.4.3]
こういう感じのやつ、すごく楽しいです!
=>[作者]: 連絡ありがとう.おそらく簡単にできた方の感想かなと受け止めました.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.4.2]
分ったつもりでいて、いざ演習題を解こうとするとき、固有ベクトルの導出で躓いてました。一般固有ベクトルへの良いステップでした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数学的帰納法 について/16.4.2]
「右に続く」がどこに続いているのかわかりにくい。左を途中まで右を読んでまた左の途中から読むような記事配置になっているようで、どことどこがつながっているのかよくわからない。
急に将棋や電球の話が出てきて、「続き」がここであってるのかがわかりにくい。
普通に上から下に流すだけの読ませ方でよいと思う。
=>[作者]: 連絡ありがとう.縦横2次元の配置を好まれない方は,上下1次元配置の
携帯用 を見てください.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.4.2]
分ったつもりでいて、いざ演習題を解こうとするとき、固有ベクトルの導出で躓いてました。一般固有ベクトルへの良いステップでした。
=>[作者]: 連絡ありがとう.情報量過多の現代,商品の効能書きをいちいち読んでいてはこちらの体が持たない,という生活スタイルに慣れてしまってしますが,数学やプログラミングの場合は「一言」読みそこなったら,すべて終わってしまう場合があります.白か黒かというような世界は住みにくいです.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.4.1]
問題演習で、内容が定着しました。
非常に良いと思います。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の2倍角公式,半角公式 について/16.3.31]
前の項で、式の導出を覚えたので、
とても解きやすかったです。
※問題が親切すぎると感じるほどでした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/16.3.31]
公式→例題→演習の流れが、非常に定着しやすいのですごく良いです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1次変換の定義 について/16.3.31]
例1の回答が間違ってますよ。
g・fとf・gの回答が逆です。
=>[作者]: 連絡ありがとう.途中経過は正しくて結果が逆ということで了解しました.行列を表示する関数を作ったときに,どの機種のどの範囲のブラウザまで表示できるかなどを気にしていたため,「数学」の話は飛んでいたようです.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/16.3.31]
難しかったです。
導出の仕方を理解するのに半日かかりました。
数学が苦手なので、
左記の簡略説明からだと、たどり着きにくかったのかも。。。
その後、自分でいろいろ調べたので、
おかげさまで公式は身に付きました。
あやうく心が折れるところでした。
=>[作者]: 連絡ありがとう.高校の授業で現役バリバリの生徒が1週間くらいかけて習う内容を,数学が苦手の人が独学・半日で理解したというのですから,自分を褒めてもよいでしょう.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.3.30]
たすき掛けの因数分解の問題で、自分は数学が苦手だけど、とてもわかりやすく、しっかりと理解する事が出来ました。本当にありかとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/16.3.29]
仕事で必要だったため、利用させていただきました。
理論などは難しくて理解できませんが、とりあえずエクセルでの計算はできるようになりました。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/16.3.28]
初めて三角関数の合成がわかりました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][無理関数 について/16.3.28]
もしかしたら、例の(3)と(4)の定義域が間違っているかもしれないです。
無理関数は、よく分からないので難しく感じます。
=>[作者]: 連絡ありがとう.例の(3)(4)はこれでよいはずです.根号(2次無理数)を含む式の定義域は,(根号内)≧0で考えます.
■[個別の頁からの質問に対する回答][相加平均.相乗平均.調和平均 について/16.3.28]
3つの数の2乗平均のところが間違えていると思うのですが。。。
=>[作者]: 連絡ありがとう.3乗になっていたので訂正しました.
■[個別の頁からの質問に対する回答][分数関数 について/16.3.27]
難しかったけど、楽しかったです。
剰余の定理をすっかり忘れていて苦戦しました!
問題2のxyの平方完成の利用が思い付かなかったです。
=>[作者]: 連絡ありがとう.正確には平方完成とは言わないと思いますが,平方完成風の変形は少々マニアックなので問題2の4.についてはもっとノーマルな考え方も書いておきました.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/16.3.27]
大変分かりやすく解説されており、理解が進みました。
1点質問があります。「基底」とは、「空間Vを生成する1次独立なベクトルの組」そのものを指すのか、組を構成している各々のベクトルのことを指すのか、どちらが正しい理解なのでしょうか(おそらく各々のベクトルのことを指すのかと)。
ご教授頂けると幸いです。また、それについてもこのウェブサイトに解説を入れて頂けると良いかと考えます。
=>[作者]: 連絡ありがとう.○4 基底と次元の所に書きましたが,「空間Vを生成する1次独立なベクトルの組を空間Vの基底という」ので,あなたの理解とは異なります.みんなで協力すれば空間を生成できるが,1つずつでは何もできないという感じかな.後半は理解できません・・・この頁全体が解説です.
■[個別の頁からの質問に対する回答][1階線形 微分方程式 について/16.3.26]
これほど綺麗にまとめるのは大変な労力であると思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内接円の半径 について/16.3.26]
ヘロン公式の記憶方法:父母2人,a母,b父,c子供。Q完整家庭。(Q-a):失母,(Q-b):失父,(Q-c):失子。s:家庭四種類完全,根号。
=>[作者]: 連絡ありがとう.ただし,誰かが足りないというような家族構成の問題を,数学教育のような社会改善とは直接関係のない単なる論理的な材料に使うことは歓迎できません.逆の使い方,すなわち,数学の話を社会教育を進めていく上で1つの話題として使うのはかまわないと思います.
■[個別の頁からの質問に対する回答][対数不等式 について/16.3.26]
おもしろかったです!
例3の底が1より小さいのに大きいと文章だけに間違っていました。
修正いただけますとうれしいです!
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][たすき掛け因数分解(2文字) について/16.3.26]
正解or不正解だけを知らせるのではなく、しっかりと解答&解説を付けた方がその場で理解が深まってとても良いと思います。
=>[作者]: 連絡ありがとう.PC用と携帯用の2つあってメンテが大変ですが,
こちらの方 には解説が付いていますので見てください.(PCはどちらも見られます)
■[個別の頁からの質問に対する回答][置き換えによる展開 について/16.3.26]
すごく助かります!
中学生でもめっちゃわかります
=>[作者]: 連絡ありがとう.
■埼玉[魚成さん/16.3.26]
期待値の問題ですがミスですか?
全員同じ手を出す(パパパなど)のが【 3 】通り では?
(6) 紙=パー,石=グー,鋏=チョキ,以下パグチと略す
手の出し方の総数は N=33=27 通り
(ア)1人勝ちとなるのは,パググのような出し方で
勝者の手の決め方が 3 通り(敗者の手は自動的に決まる)
勝者の決め方が 3C1=3 通り
n=9 通りだから,確率は .13n
(イ)2人勝ちとなるのは,パパグのような出し方で
勝者の手の決め方が 3 通り(敗者の手は自動的に決まる)
勝者の決め方が 3C2=3 通り
n=9 通りだから,確率は .13n
(ウ)アイコ(勝者0人)となるのは,
全員同じ手を出す(パパパなど)のが 1 通り
3種類の手が出るのが 3!=6 通り
n=9 通りだから,確率は .13n
勝者の人数の期待値は
E=0·.13n+1·.13n+2·.13n=1 …(答)
=>[作者]: 連絡ありがとう.結果はよいのですが途中経過にミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][高次方程式 について/16.3.24]
4次方程式の解き方も教えて欲しいです。
=>[作者]: 連絡ありがとう.前回の指導要領改訂(H11年)で,高次方程式は3次までと複2次式までとなったときに,4次以上を扱わなくしていましたが,今回の改訂(H21年)ではこの限定はなくなったようです.ただ,筆者は手の込んだ高次方程式は,次のような理由から今後あまり重視されないように思います(本質的な問題と本質的でない事情が混ざっています).(1)今日では高次方程式はコンピュータで解くことができ,人的な労力を投入する値打が下がってきたと思う (2)伝統的な方程式の理論に時間をかけるよりは,統計を駆使したデータサイエンスに重点が移ってきた (3)定期試験で4次方程式の問題を出してしまうと,1題解くために15分から20分ほど使ってしまうため,他の問題が出せなくなる.基本の理解は3次方程式までで調べられる (4)入試に関しては,数値係数の4次,5次方程式は解き方が決まっていて,受験者の創意工夫が測りにくい・・・(言い方に気をつけて言うと)浪人してでも入りたいような大学は,そんな問題は出さない.推薦入試や適性検査のような基本知識を大量に扱う試験で,小品の1つとして出す程度だと思う.
■[個別の頁からの質問に対する回答][剰余の定理 について/16.3.24]
良かったところとしてずっと疑問に思っていた点が書いてあった事です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/16.3.22]
上の高1メニューの赤枠の位置が違う。
=>[作者]: 連絡ありがとう.疲れが出てしまったようで申し訳ない.
■[個別の頁からの質問に対する回答][合成関数の導関数 について/16.3.22]
×2x^2-3
○2x-3
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][微分方程式:変数変換による解き方 について/16.3.22]
あまり初歩的な本では見ない内容なので非常に助かりました。
できれば、(v)あたりの直線が平行、交わるといった箇所のイメージ、物理的意味や、なぜそうなるかを加えていただけるとよりわかりやすいと思います。
=>[作者]: 連絡ありがとう.2つの直線
ax+by+c=0 , a'x+b'y+c'=0 について
a:a'=b:b' となっているとき,例えば
2x+4y=5 …(1)
3x+6y=7 …(2)
において,(1)の傾きは −2/4=−1/2 で(2)の傾きも −3/6=−1/2 となって,(1)(2)は平行です.
a , a' が0でなければ,2直線
a'x+b'y+c'=0 , ax+by+c=0 の傾きはそれぞれ
−b/a , −b'/a' になるので,これらが等しければ平行になります.
すなわち,平行←→
←→
b:a=b':a' これは
a:a'=b:b' と書いても同じ
ところで,y切片も一致すると単に平行であるだけでなく一致します.(全く同じ直線になります)
そこで,
a:a'=b:b'=c:c' ならば一致,
a:a'=b:b'≠c:c' ならば平行,
a:a'≠b:b' ならば平行でない(交わる)とまとめることができます.ただし,どれか1つが0であるときは,対応するものも0であると決めると分母が0になる場合を分ける必要がなくなります.(たとえば
a=0 のときは
a'=0 とする)
■[個別の頁からの質問に対する回答][展開公式 について/16.3.19]
頭をつかいました。
=>[作者]: 連絡ありがとう.基本とはいえども,作業量が多いので大変です.
■[個別の頁からの質問に対する回答][対数の計算 について/16.3.18]
超楽しかったです!
分数の問題もあったんですね!!
ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数計算1 について/16.3.18]
基礎の問題ばかりで、理解しやすかったです。
欲を言うと、もう少し計算が複雑な分数や少数があると
嬉しいです。
楽しかったです。ありがとうございました!
=>[作者]: 連絡ありがとう.頁の上端にサブメニューを作っていますので,その次の項目を見てください.
■[個別の頁からの質問に対する回答][2文字のたすき掛け因数分解 について/16.3.17]
いきなり難しくなり、答えを見てもヒントを見ても、わからず逃げ出したくなりました
=>[作者]: 連絡ありがとう.その頁は2文字たすき掛けの最後にやる「腕試し問題」なので,その頁から始めるのは無理です.・・・ちょうど今,因数分解あたりのサブメニューを作っていますが,もう何時間も作業をして疲れたので,明日以後にできます.
■[個別の頁からの質問に対する回答][微分係数 について/16.3.17]
例えばf(x)=5/xなど分数の時の問題も欲しいです
=>[作者]: 連絡ありがとう.分数関数の微分は数学Ⅲにあります.頁の先頭に小メニューが作ってあり,「商,分数関数の微分」を選んでいただくようになっています.なお,微分係数f’(a)は導関数f’(x)のxをaに変えたものです.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.3.16]
難度が高いたすき掛けについてよく理解できました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/16.3.14]
わかりにくかったです
=>[作者]: 連絡ありがとう.卒業生のようですが,あまり飛び離れた箇所を読むのではなく,もう少し系統的に読まれた方が分かるかもしれません.月日の間隔も,余りに開いていると知識がつながりにくくなります.
■[個別の頁からの質問に対する回答][定積分の基本 について/16.3.13]
(1)
5∫1dxx+1
5∫1dxx = ┌│└log|x|5┐│┘1=log5-log1=log5
+1が不要だと思うのですが。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][割り算の原理 について/16.3.12]
危険な落とし穴というところで「A÷B =Q…RであってもA÷Q=B…Rとはならない」と書いてありますが、成り立つ場合もあるので「とはならない」ではなく「になるとは限らない」にした方がいいと思います。
=>[作者]: 連絡ありがとう.正確に言えばご指摘の通りです.ここのところをグリグリに言っておかないと,多くの生徒が罠にはまってしまうので,ついつい勢い余ったのかな・・・訂正しました.
■[個別の頁からの質問に対する回答][展開公式1 について/16.3.12]
みにくい
=>[作者]: 連絡ありがとう.5W1Hのうちの5Wが抜けているので,意味が通じません.通常,「みにくい」とは「みにくいアヒルの子」の使い方で「汚い」という意味になりますが,そういう意味でしょうか.とりあえず,配色,文字サイズ,文字間隔の内で配色を変えてみましたが,何度もアクセスしておられるようなので,再読み込み(リロード)しないとその結果は現れません.
■[個別の頁からの質問に対する回答][2次関数のグラフと係数 について/16.3.11]
わからない所ので、すごく助かりました!!本当にありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/16.3.9]
分かりやすかったです
=>[作者]: 連絡ありがとう.特に要望があった訳ではありませんが,見てみたら選択肢の間隔が狭いようなので広げました.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.3.8]
本当に助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/16.3.8]
自分で選んだ項目の色が変わるなどして欲しいです。
=>[作者]: 連絡ありがとう.その頁では選択肢の間隔が狭くて何を選択したのか分かりにくいということがあるようですので,直します.なお,androidで記録が残るのか?という意味でしたら確認できません.
■[個別の頁からの質問に対する回答][基本的な三角比の値 について/16.3.7]
これから高校生。数学頑張ります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率の基本 について/16.3.7]
もう少し難しいのも出してほしい
=>[作者]: 連絡ありがとう.その頁の先頭に書いていますように,高校の確率の基本は中学校の復習から始まります.メニューをたどれば順に難しくなります.
■[個別の頁からの質問に対する回答][定積分の置換積分法 について/16.3.7]
分数が、その上段、下段の文字と重なり、良く見えないところがあります。
=>[作者]: 連絡ありがとう.Windows 上のSafariでは取り立てて重なりは見当たりませんが,Mac上については点検できません.第何問の何行目のどれとどれの間というように具体的に述べていただくと直せます.
■[個別の頁からの質問に対する回答][直交行列とは(定義,性質) について/16.3.6]
分かりました。年のせいかすぐ忘れます。すみません。
知識の確認にとても役立ちました。ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.3.6]
独学にとって分かりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/16.3.6]
分かりづらかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][余弦定理 について/16.3.6]
図と例があって分かりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列式 について/16.3.6]
理解しているつもりでもやってみると一回ではなかなか正解にたどり着かず、やり直しが必要でした。
=>[作者]: 連絡ありがとう.
■大阪[iriさん/16.3.6]
社会人です。高校は美術専攻だったため1年時しか数学の授業がなく数Ⅰ数Aまでしか履修していませんでした。有名な微分積分がわかるようになりたくて中学数学から勉強しなおしています。こちらのサイトがなかったら独学できなかったかもしれません。今、微分を勉強しています。すごく楽しいです。ありがとうございます。
=>[作者]: 連絡ありがとう.独学でやったときに,壁になりやすい個所などがありましたら,気がついたときに教えてください.
■[個別の頁からの質問に対する回答][総和記号 Σ(シグマ)に慣れよう について/16.3.5]
クリックをしても反応しないことがある
=>[作者]: 連絡ありがとう.問題が画面に表示されてから,周辺の付属物の表示に取りかかっている初めの数秒間は,採点関数がまだロードされていないことがあります.「♪~せまい日本.そんなに急いでどこへ行く」
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.3.3]
やりたい問題が手軽に手に入るので、便利だと思いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の対角化とは について/16.3.1]
Pの見つけ方はこれではわからない
=>[作者]: 連絡ありがとう.その頁は行列の対角化とはどういうことかということを述べており,「行列Pを見つける方法については,次の頁で扱う」と書いてあるので,
次の頁 を読んでもらえばよいのですが.
■[個別の頁からの質問に対する回答][ベクトル内積(成分) について/16.2.29]
わかりやすいです。問題もピンポン!!ってなるし、暗算でできるレベルなのでめんどくさ、ってならずに解くことが出来ました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの大きさ について/16.2.29]
もやもやしていた部分が解決しました!
単位ベクトルの事なんてすっかり忘れていました…
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][繁分数式 について/16.2.29]
分かりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分の部分積分法 について/16.2.29]
答えがでない
=>[作者]: 連絡ありがとう.なるほど答が出ないようなので,出るようにしました
■[個別の頁からの質問に対する回答][剰余の定理 について/16.2.28]
目次が欲しい
=>[作者]: 連絡ありがとう.書いているうちに,あれもこれもと分量が増えてしまったようです.
■[個別の頁からの質問に対する回答][展開公式 について/16.2.28]
詳しい解説を載せてほしいです!
問題だけでもすでにありがたいんですが…✨
=>[作者]: 連絡ありがとう.連絡をもらいましたので点検しました.なぜかIEでのみ問題3の(2)以後の解答が表示されていませんが,Safari, Chorome, Firefoxではエラーはありませんでした.あなたの場合は,Safariなので表示されていると思います.・・・それとも,詳しい解説というのは 32 ×2=18というような途中経過の全部のことでしょうか.
■福井県[?さん/16.2.27]
中学で支援員をしています。すっかりなまってしまった頭を回転させなおしているときに、行き当たりました。がんばって思い出します。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][導関数の定義 について/16.2.27]
数字の1をイタリックで書いたフォントを、アルファベットのエルの小文字のイタリック体と、見間違えてしまった。イタリックはやめた方が良いと思います。
=>[作者]: 連絡ありがとう.その頁には l という変数は定義されていません.lim の記号以外で,文字のエルが登場する根拠がありません.l (*)が何と言う文字か区別が難しい事情は変わりませんが,イタリックで書いたl を1 と読む生徒はいません.x と×の区別が付かないのに対して,x は×と区別ができます.a が英語のa だと理解できないことがあります.(学力低下のせいで高校でq という字が書けるだけで英雄待遇を受けるという場面に出くわしたことがあります!)x , log x などの特定の関数記号はできる所からnormal字体に直しています.)・・・(*)はエル
■[個別の頁からの質問に対する回答][t分布 について/16.2.26]
要約の式で、標本不偏標準偏差と標本単純標準偏差の式が逆になっているように思います。
片側検定と、両側検定の使い分けの説明がある方が親切と思いました。=>[作者]: 連絡ありがとう.片側検定と、両側検定の使い分けは,その頁にはあまりはっきりとは書いていません.踏み込めば混乱してしまうかもしれないと躊躇したためです.0 に対して,対立仮説μ≠μ0 に興味・関心があるなら両側検定を使い,対立仮説μ>μ0 とかμ<μ0 に興味・関心があるなら片側検定を使う」.
■[個別の頁からの質問に対する回答][絶対値記号2つの外し方 について/16.2.25]
始めのところa>0|a |= a
=>[作者]: 連絡ありがとう.中学1年の教材の初めの方に書いていますが,絶対値の定義の仕方は幾つかありますが,一番簡単なのは「符号」と「符号なしの数字」に分けたときの「符号なしの数字」が絶対値です.正の数の絶対値は|+3|=3 , |+5|=5, |+7.1|=7.1 のようにそれ自体に等しくなります.(難しく考えなくても符号を取り除いただけ)|0|=0 が成り立つので,これらをまとめるとa≧0 → |a|=a |−3 |=−(−3 )=3 , |−5 |=−(−5 )=5 のように符号が変わる:a<0 → |a |=−a となります.(難しく考えなくても「符号を取り除く」にはどうしたらよいかを考えれば分かる)
■[個別の頁からの質問に対する回答][Google Chartを使った数式の書き方 について/16.2.25]
\times{b}とすると、bの前にSpaceを入れなくてもOKのようです。Spreadsheetで使うには、Spaceがあると誤作動を起こします。偶然見つけました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の計算 について/16.2.25]
答えも書いてほしい
=>[作者]: 連絡ありがとう.解答が必要な後半は書いてあり,前半は「見れば分かる」即答問題なので,特に答は必要ないと思いましたが,どうしても書いてほしいという人がいるならということで,付けました.
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/16.2.24]
とてもわかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/16.2.24]
上から見ていけばこの場合にどういう手法を使えばよいのかがわかりやすく作られていてよかった。
欲を言えば、上部にジャンプメニューを配置し、
見たいところがすぐ見れるようになっていたら
非常に良いと思う。
=>[作者]: 連絡ありがとう.欲を言えばそのようにも言えますが,この頁は全くの初心者向けなので,そもそも何の話か?のあたりから説いています.そこそこイメージができている人から言えば,あなたのようにジャンプすることができるかもしれませんが・・・
■[個別の頁からの質問に対する回答][導関数の定義 について/16.2.24]
わかりにくい問題 : y = √2xの部分
=>[作者]: 連絡ありがとう.そこに書いていますように,その問題は発展問題で,本来数学Ⅱでは無理関数(累乗根)の微分は扱いませんので,見かけは難しく感じるかもしれません.ただし,導関数の定義に従って計算すると,その問題もできることになり,定期試験の応用問題として出される場合もあります.ただし,数学Ⅱまでが出題範囲となっている入学試験などでは出さないでしょう・・・もめるから.
■[個別の頁からの質問に対する回答][複素数の計算 について/16.2.24]
複素数の意味がよくわかりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/16.2.23]
証明の部分も素晴らしいと思います
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][関数の連続性 について/16.2.23]
極座標変換しないで解く方法も教えて欲しい
=>[作者]: 連絡ありがとう.「2変数関数における連続の定義」のところに書いていますように,「どんな近づき方をしても一つの値に近づくときに極限値がある」というので,その下の例に示したように近づき方によっては異なる値になる場合は極限値は存在しません.このように,2変数の場合に「近づき方に依存しない極限値」を求めるには,r→0 とするのが安全で,たまたま他の方法でできる問題があっても,それは危ないものです.
■[個別の頁からの質問に対する回答][F検定→t検定・・・平均値の差の検定 について/16.2.23]
表の中で注目すべき値がカラーになっていて見やすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/16.2.22]
やったーの画像が可愛かったです^_^
=>[作者]: 連絡ありがとう.全部できたときに出すご褒美メッセージは,数学的にはどうということはないように見えますが,やる気を起こす上で重要だと考えて,所々頑張って書いています.
■[個別の頁からの質問に対する回答][数学的帰納法 について/16.2.21]
大阪につく電車の例えは秀逸でした。
これのおかげで、すっきりと頭に落とし込むことが出来ました。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/16.2.21]
とりくみやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.2.20]
トップページ、ホームページへのリンクがわかりづらい。ページ左上くらいにほしい。
=>[作者]: 連絡ありがとう.その課題はありますが,まだ対応できていません.改訂には1年ぐらいかかります.- - 作っているときには,十年以上前にはどんな頁ができるのかはあらかじめ分かりませんので,トップ頁>学年>単元>現在頁・・・前後の頁 といった階層図を作成できるようになったのは,全体ができて以後のことです.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/16.2.20]
【例1】
sin15°の値を求めてください.
この問題では,コンピュータや数表を使った近似値ではなく,根号を使った厳密な値を要求しています.
高校では,0°, 30°, 45°, 60°, 90°, ...の三角関数は覚えなければなりませんが,それ以外の角の三角関数は,通常覚えません.
ここでは,sin15°=sin(40°-30°)のように変形することにより,三角関数の加法定理を使って既知の三角関数で表せるものを扱います.
この文のsin15=sin(45°-30°)ではないでしょうか?
=>[作者]: 連絡ありがとう.質問の意味が不明です.sin15と書くとラジアン単位となり,sin(45°-30°)と書くと度単位になるので,全く異なるものです.sin15°=sin(40°-30°)が正しいです.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/16.2.20]
とてもわかりやすい説明と、手軽に答えられる問題(問題が簡単すぎるという訳ではなく、操作に於いての意味です。)がスムーズな流れで配置されているので、気が付いたら全問解答していたという感覚です。とても取っ付きやすいサイト様だと感じました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階差数列 について/16.2.20]
すごいわかりやすくてびっくりしました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/16.2.20]
覚えやすくまとめられており良かったです。ありがとうございました。覚え方のごろ合わせなんかもあるといいですね♪
=>[作者]: 連絡ありがとう.覚え方のごろ合わせについては,少々考える所があって文中の表現のようになっています.すなわち,私塾などでは正弦について「咲いたコスモス コスモス咲いた」,余弦について「コスモスコスモス咲いた咲いた」などと教えるところもあるようですが,語呂合わせは「元のものをそのまま覚えるよりも,簡単になっていて,印象が強く,情報量が多くなければなりません」.しかし,この私塾のやり方では,どちらがどちらかの区別が付かず,符号も区別できません.印象だけ残りますので,1か月も経てばどちらがどちらなのか分からなくなります.このようにして、筆者としては,サインは「サ行=ストレート,そのまま」,コサインは「カ行=カーブ,クセあり」で符号だけは間違わないように押さえています.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.2.18]
因数分解のやり方を楽しく思い出すことができました!ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][放物線 について/16.2.18]
いつも参考にさせて頂いております。
基本チェックの問題(2)の準線の解答欄(空欄の部分)がy=-1/4のところがx=となっておりました。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/16.2.17]
非常に分かりやすくて勉強になりました。特にカーネルと次元のところがよく分かっていなかったので助かりました。
2節例2のa1ベクトルの第3成分に-を付け忘れているみたいですよ。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][二項分布 について/16.2.15]
■まったくの初心者向け■
基本にもどつての計算は参考になりました。
分散計算で
V(X) =E(X2) - E(X)2
は50/36-25/36となり
5/36ではなく
25/36ではと思いますが。
=>[作者]: 連絡ありがとう.訂正しました.ついでにその上のE(X)も書く場所がおかしいので直しました.
■[個別の頁からの質問に対する回答][検定 について/16.2.15]
◇簡単な例でイメージ作り(1)◇の文中、
σ = np(1-p) = 3.536
とありますが、np(1-p)の平方根をとらないと計算が合いません。
=>[作者]: 連絡ありがとう.N(m, σ2 ) で第2引数は2乗だと教えながら,自分で間違っていたようです.訂正しました.
■[個別の頁からの質問に対する回答][対数計算 について/16.2.14]
とてもわかりやすかったです。
例題が多く、要所が赤で色分けしてあったので、ひとつひとつ確実に消化しながら取り組めました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数学的帰納法 ==(等式の証明) について/16.2.14]
無料でこのような問題を作っていただき、ありがとうございます。数列と組み合わせた問題を作っていただくと、より楽しめると思いました。=>[作者]: 連絡ありがとう.精密な形で証明しようとすれば,数列の問題は何でも数学的帰納法の証明問題になるといえます.
■[個別の頁からの質問に対する回答][マクローリン展開 について/16.2.14]
log(1+x)という形は、他と比べて特殊な形ですがどんな場合に使われますか?
=>[作者]: 連絡ありがとう.
テイラー級数:
を
の近傍に適用したものが
マクローリン級数:
ですが
のグラフは
の所が特異点になっており,f(0)もf’(0)もf”(0)も何もありません.このように
という関数を
の近傍で展開することは「無がむなしいことを言う」ような話です.
これに対して
の近傍で展開すると,教材の公式のようにうまくいきます.
他の例では,
のグラフもf(0)もf’(0)もf”(0)も何もありませんので,同様にして
が示されます.
■[個別の頁からの質問に対する回答][正弦定理 について/16.2.12]
気にいった所 : B) 「師匠が直接管理する」
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3点が同一直線上にあるための条件 について/16.2.12]
とても分かりやすかったです
ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1階線形 微分方程式 について/16.2.12]
1階線形微分方程式 波動方程式の、時間変化する誘導電荷の式導出に、参考にさせていただきました。ありがとうございます
=>[作者]: 連絡ありがとう.難しいのをやっておられるようで,筆者に今後復習の機会があるかどうか・・・
■[個別の頁からの質問に対する回答][階乗 について/16.2.11]
どういうときに階乗を使うのかがわからないから、「おお便利だな!」という感動が薄い感じがします
=>[作者]: 連絡ありがとう.その頁の先頭に書いていますように,順列と組合せの全部に登場します.そこから後のその単元全部です.階乗の計算を習得しないと,そこから後の項目に進めません.
■[個別の頁からの質問に対する回答][3次関数の増減(文字係数) について/16.2.10]
実習1 ≪答案≫(C)何故「2つの解が0以下」、「2つの解が1以上」なのでしょうか?解説をお願いいたします。
=>[作者]: 連絡ありがとう.そこに解説が書いてあるのに,解説をお願いしますと言われたら,普通はイラッとしますが,一応気長に述べると
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/16.2.10]
理解しやすいので試験勉強に利用させてもらっています。ありがとうございます。
第3問の12x^2+xy-6y^2+14x+36y-48での質問です。
(-4x-3y+6)(-3x+2y-8)で
答えを出したのですが、
試験では誤回答として
減点されますか。
xをできるだけプラスの
項で記入して綺麗な状態にしないといけないでしょうか。
=>[作者]: 連絡ありがとう.xの係数を正にするのが普通でしょう.簡単な例で示すと
と書く生徒がいたら,「わざと符号を変えて読みにくくしている」のだとしたら,教育的指導が必要でしょう.「負の符号は避けた方がよいということを知らない」のだとしたら,それも問題ありでしょう.
数学なのだから正しければよいはずだと考える人は,次の答案で正解にしてほしいというかもしれませんが,それは無理でしょう.
このような訳で校内の定期試験では,学習の途中だから「少しでもよい答案が書けるように」減点するかもしれません.しかし,何千人,何万人が同じ試験を受ける模擬試験や入学試験では,結果判定ということに重きを置いており,採点官も多人数になりますので正答の許容範囲を完全に決めます・・・そもそも,入学試験では何通りも書き方があるような問題は,避けるでしょう.
さて,元の質問に戻りますが,A「あなたはその書き方しか思いつかなかったのかどうか」、B「本当にその書き方の方がよいと思うのか」、C「全知全能の採点官に喧嘩を売って不利な結果を得たいのか」,D「奇をてらった答案で目立ちたいのか」という辺りの自分の動機に曇りがないのかということを振りかえってみることも重要です.(若いころの筆者ならDの路線で突っ走ったかもしれない)
■[個別の頁からの質問に対する回答][正弦定理 について/16.2.9]
いろんな問題を出して欲しいあともっとわかりやすくして欲しいです
=>[作者]: 連絡ありがとう.その頁の先頭に書いていますように,その頁は解説の頁で問題は別の頁にあります.次に,正弦定理をいろいろな場面で使えるようになるには,結構複雑な処理が必要になりますので,話が込み入って来るのはやむを得ないことです.
■[個別の頁からの質問に対する回答][階乗 について/16.2.9]
階乗という数式があることをこの年までしりませんでした。数字の後ろに!。
練習問題解けてよかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][t分布 について/16.2.9]
右と左で分けてあるが、特に上部のt分布の説明でそれらがどのように関連しているのかわかりにくかった。
あと歳を取ってきているせいか、一部の文字の色(特に灰色)と大きさが少し私の眼にはつらかった。
いずれにしても感謝してます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][余弦定理 について/16.2.8]
分かりやすいくて良かったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/16.2.8]
正しい解を入力してもはずれと表示されるようです
=>[作者]: 連絡ありがとう.問題欄のはじめに書いてありますように「英字は半角小文字、数字は半角」で入力してください.
■[個別の頁からの質問に対する回答][内接円の半径 について/16.2.6]
中学二年生です。
塾の授業の復習に使っています。分かりやすいです。
いつもありがとうございます。
=>[作者]: 連絡ありがとう.中学で習いますか?
■[個別の頁からの質問に対する回答][二項分布 について/16.2.6]
ちょっと忘れた者にはそのまま効く(有り難うございます)が、すっかり忘れた人には他のページなど(全体の構成がわかりませんが)へ飛んで詳しい説明が見られるなどあるとよいかも。
=>[作者]: 連絡ありがとう.必要なものをメニュー項目からさがしていただく想定になっています.
■[個別の頁からの質問に対する回答][対数計算1 について/16.2.6]
指数が分数の場合の計算を調べた後はとても簡単に理解できました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次関数(文字係数と極値) について/16.2.6]
例題もついていてわかりやすい。
質問対応もしてほしい。
=>[作者]: 連絡ありがとう.この教材全般について,教材で取り上げた問題については,質問があれば答えます.ただし,各自が授業や学習塾,問題集で疑問を持った他の問題を解いてほしいという要望には答えません. - -「入試会場の中からweb書き込みで質問して,その答を答案に書いた」という大きな事件が数年前にありました.また,自分で解かなければ力がつかない宿題をやってもらうようなこともよくない.このような訳でこの教材の中にない問題については回答しないのが原則です. - - とはいえ,箸にも棒にもかからないような,何が分からないのか分からない,どの教材を見てよいのか分からない,というような質問に対しては教材の場所(URL)を教えている場合があります.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/16.2.6]
問題7の2.3は問題としては不適切、もしくは設定不十分と思います
理由としては、回答側としては、この問題がいつ生成されたかが分からないからです。
問題文の「今日」が今まさにこの文章を作っている今日なのか、この問題が作成された(回答者はわからない)今日なのか、判別できないからです
=>[作者]: 連絡ありがとう.物事を深く考える方だということは伝わってきますが,提出された御意見には賛同できません.
■[個別の頁からの質問に対する回答][指数法則 について/16.2.5]
0はどのようにすればlogにできますか?
=>[作者]: 連絡ありがとう.この頁のテーマそのものではなく,対数のテーマだと思いますが
0<a<1 , a≠1 となる任意の実数a についてa0 =1 が成り立ちます.0<a<1 , a≠1 となる任意の実数について0=loga 1 が成り立ちます→0=log2 1 , 0=log3 1 , 0=log4 1 , 0=log5 1 , ...
■[個別の頁からの質問に対する回答][同時確率分布と周辺分布 について/16.2.5]
わかりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組分け について/16.2.4]
すごくわかりやすかったです!!!
どこ見てもわからなくて困ってたので助かりました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][t検定 について/16.2.4]
ものすごく助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階乗 について/16.2.3]
大変わかりやすいサイトで、とても重宝しています。
このページの階乗問題の、問い6のHELPの項目に、
誤りではないかと思う記載がありましたので、ご連絡いたします。
訳文の説明で、したの項が4×3×3×1となっていますが、正しくは4×3×2×1ではないでしょうか?
これからも利用させていただきますので、何卒よろしくおねがいします!
=>[作者]: 連絡ありがとう.タイプミスですので訂正しました.
■[個別の頁からの質問に対する回答][内接円の半径 について/16.2.2]
受験日なのですが分かりやすくて助かりました。
=>[作者]: 連絡ありがとう.会場の外なら見てもよいでしょう.
■[個別の頁からの質問に対する回答][対数計算 について/16.2.1]
問題6(3)の◯が表示されない
=>[作者]: 連絡ありがとう.表示されないことはないのですが,携帯版では「選択肢の間隔が狭い」「個別問題の解説がない」という問題があるようですので,改訂します.
■[個別の頁からの質問に対する回答][組合せ について/16.1.31]
パスカルの三角形を紹介し、「こんな所にも組み合わせがある」と、載せてみるのはどうでしょう。
パスカルの三角形そのものも面白いものですから、数学に興味を抱く人が増えるかもしれません。
=>[作者]: 連絡ありがとう.パスカルの三角形を扱うのも悪くないと思いますが,「こうです」と言ってしまえばそれで終わってしまうと,一方向の言いっぱなしになってしまうので,読者が「遊べる教材」に組み立てるには,どのように仕上げたらよいかと考えているうちに,忘れてしまったようです.そのうちいい考えが浮かべば見当してみます.
■[個別の頁からの質問に対する回答][定積分:基本計算 について/16.1.31]
このサイトが断然分かりやすくて、すぐに理解することができました。助かりました!とっても感謝です。このようなサイトを作っていただき ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.1.30]
教科書よりも、とても分かりやすい解説でした!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.1.30]
実用的な例題などがあって式の組み立て方とその説明があったら言うこと無しです。
=>[作者]: 連絡ありがとう.「実用的な」ということが何を表しているかは別として,弧度法によるグラフや三角方程式,不等式での使われ方については,メニューをたどって該当項目をご覧ください.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/16.1.29]
Exelでのchitest関数の使い方が分かってよかった。
返す値がpの確率となるのはどんな仕組みか簡単に説明して頂けるとありがたい。4分割表でdf1の確率比からどのようにしてpを出しているのでしょうか?
=>[作者]: 連絡ありがとう.その頁の下端(2項分布の正規分布による近似)で解説していますように,各々の自由度に応じてカイ2乗値を計算し,◇簡単な例でイメージ作り(2)◇の1つ上の表でカイ2乗値からpを逆に読むと考えるとよいでしょう.(コンピュータの中には表が組み込まれていると考える)
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/16.1.29]
ラムダが表示されない
(Androidにて)
=>[作者]: 連絡ありがとう.Android でギリシャ文字のフォントがない?- - Times,ひげなしゴシック風,ひげあり明朝風,手書き風の順にその機器で利用可能なものがあれば表示されるはずですが,どれにも該当しないとは?
■[個別の頁からの質問に対する回答][指数法則 について/16.1.28]
すごくわかりやすかった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.1.28]
本当に分かりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列の積 について/16.1.28]
行列の計算ができず、このサイトにたどり着きました。
とても良かったです、簡単に練習できる形式のおかげで、誤って理解していたところを把握できました。やはり文章を読む→練習問題は鉄板でありながら重要ですね……。
文章も丁寧でとても良いです。
助かりました、ありがとうございました。(*´◒`*)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/16.1.28]
統計知識がゼロの人間にはちょっと理解できませんでした…。
=>[作者]: 連絡ありがとう.あなた自身が述べておられるように,統計知識がゼロではその頁は無理です.メニューに沿ってもっと前の方から読んでください.
■[個別の頁からの質問に対する回答][極限値,不定形の極限 について/16.1.28]
∞や+0、-0という表記を高校で扱ってる教科書や問題集でしていなかったので、わかりにくく感じてしまいました。
=>[作者]: 連絡ありがとう.数学Ⅱには∞や+0、-0という記号がなくても数学Ⅲには必ずあります.その意味は頁の初めの方に解説しています.数学Ⅲではこれらの記号から逃げることはできませんので必ずマスターしてください.
■[個別の頁からの質問に対する回答][正規分布 について/16.1.28]
ちょうど大学のテストに使うところだったので、わかりやすいし、例題が多くて自分でもできるようになってきました。
ただ、まだわからないところとしては、
解説のP=2θ?のように一旦置き換える作業がよくわかりません。
私はExcelで直接入力して、式は違うけど答えがあっているので、問題はないとは思いますが、
置き換える作業の意味と効果など、ありましたら教えて頂きたいです。
もしくはそれが普通なのだとしたら無知ですいません。
=>[作者]: 連絡ありがとう.Excelが使える場所にいれば,NORMSDIST() は負の値に対してでも使え,さらにNORMDIST() にすれば,期待値(中央)が0でなく,標準偏差が1でない場合でも使えるので,ことさら変数を変換しなくても直接求められます.
■[個別の頁からの質問に対する回答][負の指数 について/16.1.27]
負の指数の導入が分かりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分散分析 について/16.1.27]
時間がない初心者にとって非常にわかりやすい解説で助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][放物線の移動 について/16.1.27]
問題8の解答が解答欄のチョイスの中にない。
=>[作者]: 連絡ありがとう.問題の符号が逆になっていましたので訂正しました.
■[個別の頁からの質問に対する回答][検定.標本が大きく正規分布が使える場合 について/16.1.26]
順番を追って丁寧に説明されており,非常に分かりやすかったです.助かりました.
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][重積分--積分順序の変更 について/16.1.25]
iMac/Safari 少しですが積分記号と数字が重なって表示されます。全く判別不能という訳ではありません。
=>[作者]: 連絡ありがとう.積分区間が根号のある分数の場合に,本体の式と少し被ることがあるようですが,これは技術的に防ぎにくい.
■[個別の頁からの質問に対する回答][平方根の計算・・・センター試験問題 について/16.1.25]
このページは全体的に分数が崩れていて、全く読み取れません。
このサイトはとてもいいサイトだと思っているので改善のほうをよろしくお願いします。
=>[作者]: 連絡ありがとう.PCのIEということですので調査しましたが,こちらからは全く問題なく読めており,崩れていません.(IE, Safari, Firefox, Chrome, Operaいずれも問題ありません.)この1か月の間にその頁を読んだ100人以上のひとからもそのような苦情は来ていません.
携帯版 の方はどうですか.
■[個別の頁からの質問に対する回答][放物線の移動 について/16.1.25]
問題1の正解不正解のイラストがズレて表示される.問題1の1,2のイラストは左上の'メニューに戻る'の左辺りに,5ミリ位の大きさで表示され,3のイラストは1のところに,4のイラストは2のところに…とういうように2つずつ上にズレている.
タブレットでクロムを使っています.
分かりやすくていつもとてもお世話になっています.ありがとうございます.
=>[作者]: 連絡ありがとう.携帯版に移植した時に,ずれてしまったようですので,訂正しました.
■[個別の頁からの質問に対する回答][≪定数係数の2階線形微分方程式≫(非同次) について/16.1.25]
答えかけよ
=>[作者]: 連絡ありがとう.大学生にしては粗雑な言葉使いが気になるところです.あなたは,360 x 640の画面のAndroidを使って,同じ頁に約15分ずつ4回,計1時間以上見ていながら1題も問題に答えなかったということが分かります.1題でも答えていれば解答は表示されます.
■[個別の頁からの質問に対する回答][確率の基本 について/16.1.24]
これだけは押さえた方がいい👍
といったポイントが欲しいです👀
=>[作者]: 連絡ありがとう.赤枠でぐりぐりに強調してあるのが【要点】です.
■[個別の頁からの質問に対する回答][多項式の除法(割り算) について/16.1.24]
とっても分かりやすい!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円の接線の方程式 について/16.1.24]
わかりやすいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][陰関数の導関数 について/16.1.24]
導入やら解説やらわかりやすかったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組わけ について/16.1.24]
例3の(2)で2!をしていません!
=>[作者]: 連絡ありがとう.おっと,携帯版で例題の解説を増やしたときに,ミスがあったようです.訂正しました.
■[個別の頁からの質問に対する回答][余弦定理 について/16.1.22]
わかれば一気に楽しくなりますが、理解するまでが長いのが数学だと思います。テスト前の確認としてこのページを見さしていただきましたが、とてもわかり易かったと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階乗 について/16.1.22]
すっかり、忘れていました。
数Ⅲ でやったのかなぁ?
微積分、代数・幾何とかの時?
受験科目が数ⅡBまでだったから授業だけで。
知っていて損はないものだと。
解りやすい説明でした
=>[作者]: 連絡ありがとう..
■[個別の頁からの質問に対する回答][行列の対角化とは について/16.1.22]
Pについての議論、特にはPをどのようにとるのかについて触れていただければと思います
=>[作者]: 連絡ありがとう.その次の頁
行列を対角化するには を読んください.
■[個別の頁からの質問に対する回答][解と係数の関係 について/16.1.21]
672Xにじょう-2840X+2652=0
は、どのようにして求めればいいですか?
=>[作者]: 連絡ありがとう.この教材で扱っている問題ではなく宿題か何かの問題のようです.そういう質問にはお答えしません.
参考までに,「何を」求めるのかを書かないと質問になっていません.あなたが質問している頁は「解と係数の関係」の頁です.解と係数の関係なら,その頁を読めば「みた通りに」直ちに答が言えるはずです.(係数を4でくくる必要があるが)
そうではなくて「2次方程式の解」を求めたいというのなら,見ている頁が違います:
この頁 の「解を求めるプログラム」で数字を入れたら答が出ます.
■[個別の頁からの質問に対する回答][ド・モルガンの法則 について/16.1.20]
よくわからなかった問題はないが問題4の答案の傾向が問題5の問題文に被っている。
=>[作者]: 連絡ありがとう.あなたと同じようにPCのChromeでチェックしましたが,ご指摘の症状は確認できませんでした.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/16.1.18]
y=tan-1x とは x=tany (π/2<y<π/2 , -∞<x<∞)となるyの値のことです.
yの範囲は-π/2<y<π/2ですよね
=>[作者]: 連絡ありがとう.マイナスが抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][行列式 について/16.1.17]
結局4次の正方行列の場合の行列式のもとめ方がわかりませんでした。
=>[作者]: 連絡ありがとう.2次の場合にたすき掛けの引き算で,3次の場合にサリュの方法でというように,それだけに通用する方法で済ませていると4次以上の場合ができなくなります.
行列式については,
この頁 や
この頁 にも解説がありますので,ぜひ4次の行列式を3次の行列式から余因子展開によって帰納的に定義する方法をマスターしてください.
■[個別の頁からの質問に対する回答][軌跡の方程式2 について/16.1.17]
自分の答えが
間違っている時
何が間違えているか確認したいので
解答があればなぁ~と思いました。
=>[作者]: 連絡ありがとう.HELPを押せば解答も出ます.
■[個別の頁からの質問に対する回答][t検定 について/16.1.16]
大学の授業の参考になりました!!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/16.1.16]
とても良かったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][≪定数係数の2階線形微分方程式≫(非同次) について/16.1.16]
例が出ていてとても分かりやすく参考になります、ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/16.1.15]
私は72歳です。57年ぶりに二次方程式を解きました。解説がわかりやすく、昔もこのくらい良い教師だったらよかったのに。孫に教えます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/16.1.15]
χ二乗分布は、天下り的に教えられたことが多く、学ぶ気もしませんでしたが、このテキストを読み、確率論的なバックグラウンドと応用のを非常に短時間に学ぶことができました。もうテキストを読まなくても適用できるほど理解できました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/16.1.14]
正規分布に従うXiにおいてその2乗の和がカイ2分布に従うということの証明を探していて、この教材を見つけました。 最初の箇所は特に感覚的に分かりやすいと思いました。 まだ、最後まで読めてませんが、他の本などと比べて分かりやすい印象です。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の不定積分 について/16.1.13]
三角関数の積分の解き方が見やすくパターン化されていて自分の知識を整理するのに役立ちました。
ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][複素数の計算 について/16.1.13]
とても良いページで、重宝しています。ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][簡単な重積分の計算 について/16.1.13]
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/16.1.12]
図が表示されない。
=>[作者]: 連絡ありがとう.PCのIEでチェックしましたが,こちらでは図は表示されており,そちらのPCの状況が分かりません.
■[個別の頁からの質問に対する回答][階乗 について/16.1.11]
どこで使ったらいいのか一切分からないため、文章問題を用意して欲しい
=>[作者]: 連絡ありがとう.先頭に書いてありますように,順列や組合せの問題をすれば階乗計算がたくさん出てきます.メニューでは次の項目です.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/16.1.11]
いつもお世話になっております。
反復試行、例題のサイコロを6回投げるとき、ちょうど1が2回出る確率の答えはお間違いないでしょうか?
当方の計算機ですと、3125/15552 になってしまいます。お忙しいところ、失礼致します。
=>[作者]: 連絡ありがとう.分子の計算で5を1回分掛け忘れていましたので訂正しました.
■[個別の頁からの質問に対する回答][放物線の頂点の軌跡,円の中心の軌跡 について/16.1.10]
== 放物線の頂点の軌跡,円の中心の軌跡 ==
大問4番
4-a^2>0 この条件よりどうして-3<x<1になるのでしょうか。
=>[作者]: 連絡ありがとう.
円の中心の座標は
x=−a−1 …(1)
y=2a+1 …(2)
で,半径は正でなければならないから
D=4−a2 >0 → −2<a<2 …(3)
(1)(2)から
a を消去すると,軌跡の方程式は
y=−2x−1
(1)(3)から
x の値の範囲は
−3<x<1 (直線だから,
x の値の範囲を言えばよく,
y の値の範囲は自動的に決まるので,
−3<y<5 の方は言わなくてもよい)
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/16.1.10]
良い復習になりました!
練習問題もいい感じです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][場合分けのまとめ方 について/16.1.10]
分かりやすい解説ですね!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/16.1.9]
仕事で統計などする必要があり,復習に役立ちました!ありがとうございました
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][内接円の半径 について/16.1.9]
中学生です
解説のS=rsの小文字のsとは何ですか?
=>[作者]: 連絡ありがとう.中学生に「何」という形でもので示すのは難しいです.スモールsはその頁に何回か登場しますように
…(*)
で定義される値です.(3辺の長さを足して2で割ったもの.)言ってみればそれまでですが,なぜそんな式にわざわざ名前を付けてスモールsで表すのか,そんなことをして何がうれしいのか,どんな役に立つのか?というのが質問者の本音でしょう.
その頁の(2)に書いていますように,三角形の面積ラージSは
と書くことができ,(*)のように定義すると
などは,すべて s で表されることになるので
のように s を使って表わせることになります.
さらにその頁の先頭にある式も
と書けることになります.
このように何度も登場する式は,名前をつけて1つの文字で表すと,1回ずつ …(*) と書くよりも便利だという考え方です.
≪要点≫ s は「目に見える特定のもの」を表すというよりは,「何度も登場する式に付けた名前」と考えればよいでしょう.
■東京都[しゅーとさん/16.1.8]
曲線で囲まれた図形の面積
http://www.geisya.or.jp/~mwm48961/kou2/integral_poli1.htm
≪類題:問題と答≫
2. ==== 右図の形になるもの ====
(1)y=x2-3x+2とx軸,および2直線x=0, x=1で囲まれる図形の面積
の問題について
この問題が問うている面積S全体は
図のようにy<=0には存在しません。
0<=x<=1の範囲ではy>=0に存在します。
問いと答えに間違いはないのですが、
説明の流れの中においては、この場所に適切な問いではないと思います。
私の思い違いであれば大変恐縮なのですが、
この指摘が正しかったとすれば、それはこのサイトで学んだ成果です。
=>[作者]: 連絡ありがとう.確かにそのままではグラフがx軸よりも上に来てしまうので,問題の符号を変更しました.
■[個別の頁からの質問に対する回答][対数計算1 について/16.1.7]
まったくわからなかったです。
=>[作者]: 連絡ありがとう.この感想では,管理人としては,「そーか」といしか言えませんが,読者としては,本当は「こんなことができるようになりたかったのに,分からなかった」ということではないのですか?「できたらよいな」と思うこと「まだできないな」という思うことが整理できれば,問題は半分以上解決できたものと考えてもいいです- - 何がどうわからないかを整理することが重要.
■[個別の頁からの質問に対する回答][2次方程式の解き方(まとめ) について/16.1.7]
わかりにくい問題 : (X+4)(X+6)=0
=>[作者]: 連絡ありがとう.高校の不等式などの頁をずーっと検索した結果としてこの頁に来られたようですが,筆者としてはどんな立場の人が,どこまで分かっていて何がどう分からないのかを明らかにしてもらえば,解決策が見出されるはずのところが,これでは材料が全然足りません.だから,ここから先は推定です.
因数分解できている2次方程式の解き方が分からないということのようですが,(ここに来るまでの検索頁を見れば)おそらく高校生以上の方で,中学校の授業を何日も続けて休んでおられて,因数分解と方程式の解がつながらないものと推察しました.あなたが読むべき頁は
この頁 です.
※管理人はただのおじさんです,「あなたの不満を単に排泄するだけ」では助けられません.どこまで分かっていて,何がどう分からないのかというように,あなたの置かれている状況について手掛かりとなる材料を書いてもらえば,そこそこ答えることはできますが,手掛かりがないと助けられません.
■[個別の頁からの質問に対する回答][循環小数の計算 について/16.1.5]
3 ー11を循環少数で表しなさい
=>[作者]: 連絡ありがとう.あなたは質問の書き方を間違っています--この問題は,当サイトに掲載されていない問題で,学校や学習塾などからあなたに「やっておくように」いわれた問題をそのまま写した形になっています.何の関係もない当サイトの管理人に解いてもらうように依頼するには,「表わしてください」と言うべきです.
■[個別の頁からの質問に対する回答][例題対比)2次関数のグラフ[標準形] について/16.1.5]
他のよりわかりやすく、採点もできるのでいいと思う
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/16.1.4]
違うんじゃないですか??
=>[作者]: 連絡ありがとう.何がどう違うのかを述べないと,質問にも意見にもなっておらず,答えようがありません.
■[個別の頁からの質問に対する回答][指数法則 について/16.1.3]
私は中三ですが、教科書や持っている参考書には指数についてさらっとしか説明がなく、もうすぐ受験なのに分からない…と焦っていましたが、すごく分かりやすくて苦手が解消できました。問題はクイズみたいで良いと思います。マルが出たときの嬉しさは何とも言えません。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列・じゅず順列 について/16.1.3]
12番の問題が理解が及びません。より詳しく解説していただけると幸いです。
=>[作者]: 連絡ありがとう.途中経過の式を追加しました.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/16.1.1]
むり!わかんない
=>[作者]: 連絡ありがとう.約30秒で学習を放棄されましたが,やり直す機会が何度もある方ならそれでもよろしいが,これで高校2年以上の三角関数は投げたということなら,残念です.
■[個別の頁からの質問に対する回答][2次不等式 について/16.1.2]
授業で先生に説明されても中々理解できませんでしたが、geisyaで勉強したら、解説がとてもわかりやすくてとてもいい勉強になりました。 一つ、提案なのですが、練習問題を もう少し多くしていただければ幸いです。 よろしくお願いします!
=>[作者]: 連絡ありがとう.「練習問題を もう少し多くについて:そのような要望はあり得ますが,問題が多過ぎてできないという意見もあります.Web上では,統計的に約4分程度で読者の「持久力が切れてしまって」学習を放棄してしまうようです(
この頁の3.2の項目(PDF 485KB) )ので,1つの頁にそのような大量の問題を期待されるのではなく,各自の学力に応じて,もっと簡単な,あるいは,もっと難しい頁に分けて学習してください.
■[個別の頁からの質問に対する回答][展開公式 について/15.12.31]
分母の5や7の上の棒が線と重なって、一瞬何かの記号かと思いびっくりしました笑 見にくいわけではないですが、一応^^;
=>[作者]: 連絡ありがとう.Chrome で見ると確かに重なりがきついようですので,分数の横棒の位置を上にあげました.
■[個別の頁からの質問に対する回答][展開公式1 について/15.12.31]
問題3(3)(4)
(4)は係数がー2だから公式は使えない。(3)の係数もー2だと思ってしまいました。
abの係数がどこかよく分からなかったです。
=>[作者]: 連絡ありがとう.abの係数はabの係数です.(画面の上では,何もついていないので1になっているということです)
■[個別の頁からの質問に対する回答][順路の問題 について/15.12.30]
ややこしいところが少し...
けれど、とても勉強になりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角比の相互関係 について/15.12.30]
全く分からないのでもっと簡単に解ける方法を知りたいです。
=>[作者]: 連絡ありがとう.あなたがこの1週間に見たのはその頁だけのようです.高校の授業を受けたことがあるのか(sinθ,cosθという言葉を聞いたことがあるのか,そもそも,θを何と読むのか分かっているのか)も分かりません.あなたがどのレベルの数学をやっていて,何がどう分からないのかを書かないと回答のしようがありません.- - 例えば小中学生が,たまたま検索で当たった頁に対して「全く分からない」と述べているのなら,回答はしません.
■[個別の頁からの質問に対する回答][条件付き確率 について/15.12.30]
とてもわかりやすく、条件付きが苦手だったのですが、基本は理解できました。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1 について/15.12.30]
ものすごく分かりやすいし
復習で自分が分かっていないとこが明確に分かった、
=>[作者]: 連絡ありがとう.ただ単にお礼を述べているのではなく,読者がどんな内容に興味があるのかがよく分かりましたので,お礼申し上げます. - - 次のように理解しました:教科書レベルの公式に数値を代入するという問題で間違いやすいポイントを指摘することなどにも,興味がある人が多いということが分かりました.
■[個別の頁からの質問に対する回答][カイ2乗分布 について/15.12.29]
いままで有意差ありかなしか判定の数字の意味しかわかっていませんでしたが、このページをみてかなり身近なものに感じられました。手計算でも自由度とpの表をみれば有意差ありなしが計算できるということに感動しました!理論は複雑なんでしょうが、計算自体は難しくないので、なんだか気がぬけたような感じです(笑)。大変たすかりました!ありがとうございます!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][楕円の方程式 について/15.12.28]
入試などに出てきそうな問題を少し入れてくれるとありがたいなと思います
=>[作者]: 連絡ありがとう.入試のことを考えに入れると取り扱いがとても複雑になります.現行のセンター試験のレベル(数ⅠⅡAB)までなら基本問題で扱うことができますが,数学Ⅲはその中に入りませんので,私大一般入試はたは国公立2次試験ということになります.(推薦入試では数Ⅲは入らないのではないか.)ところで,御承知のように少子化が進んで,「国内のほとんどの大学は基本ができれば合格できます」(1).他方では,「いわゆる難関校となると,単に定形的な問題を練習しただけでは解けない問題が出題」(2)され,このような頁では解説し切れません.
■[個別の頁からの質問に対する回答][条件付き確率 について/15.12.27]
解答と解説のつくりかたがインターネットならではで非常に良かったと思いました。
=>[作者]: 連絡ありがとう.どの頁の話かなともう一度点検してみました.特にご指摘がなかったものの,配色がいま一つ見やすいものではないようなので,文字色などを改善しました.
■[個別の頁からの質問に対する回答][2円の交点を通る円・直線の方程式 について/15.12.27]
学習に詰まった際時々活用させて頂いております。
いつもありがとうございます。
当ページの一部に誤りと思われる箇所がありましたので恐れ多くも報告させていただきます。
以下抜粋
-------
[例題1]
2円
(x+3)2+(y-3)2=9 …(1)
x2+y2=9 …(2)
について
(1) 2交点と点 (0 , 0) を通る円の方程式を求めよ.
(2) 2円の交点を通る直線の方程式を求めよ.
[答案]
(1) 求める円の方程式を
(x+3)2+(y-3)2-9+k(x2+y2-9)=0 …(1)
とおく.
(1)が点 (0 , 0) を通るための条件は
32+32-9+k(0-9)=0
9-9k=0
k=1
このとき,方程式は
(x+3)2+(y-3)2-9+(x2+y2-9)=0
2x2+2y2+6x-6y=0
x2+y2+3x-3y=0 …(答)
(2) (1)において k=-1 とおくと,
(x+3)2+(y-3)2-9-(x2+y2-9)=0
x2+6x+9+y2-6y-9-x2-y2+9=0【左辺について(y-3)²の展開について+9が抜けていると思われます。】
6x-6y+9=0
2x-2y+3=0 …(答)
以上この場を借りてご報告させていただきました。
失礼いたします
=>[作者]: 連絡ありがとう.間違っていましたので訂正しました.
■[個別の頁からの質問に対する回答][2点間の距離の公式 について/15.12.27]
一個間違ってませんか?
=>[作者]: 連絡ありがとう.全問チェックしましたが,特にデータミス,プログラムの作動ミスとも感じませんでした
■[個別の頁からの質問に対する回答][円の方程式 について/15.12.25]
気にいった所 : 発想が優しくまた丁寧だと思います。どうもありがとうございます。
わかりにくい問題 : 大変懇切丁寧なので分かりやすかったです。感謝いたします。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率の基本 について/15.12.25]
説明が難しくてあまり理解できませんでした
=>[作者]: 連絡ありがとう.難しかったのは残念.難しいときはイラストを見ながら考えるとよい.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/15.12.24]
良い点:固有値、固有ベクトルとは何かが書いてあり、分かりやすかった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][余弦定理 について/15.12.23]
私、数学で0点取ったことがあるくらい苦手なんですよ。
でもこれなら、なんとか赤点(30点)はとれそうです。
=>[作者]: 連絡ありがとう.筆者も昔は勉強のできる人(IQが高い)がうらやましく思えましたが,今は楽しく生きられる人(EQが高い)がうらやましく思えます.
■[個別の頁からの質問に対する回答][母平均,母比率の推定 について/15.12.23]
良いと思います。書籍化してください。
=>[作者]: 連絡ありがとう.画面なら採点ができ,グラフが表示でき,容易に訂正できますが,印刷物にすると何もできなくなりますので,今のところ出版は考えていません.出版社との打ち合わせなどもそれなりに面倒なものです.
■[個別の頁からの質問に対する回答][楕円の方程式 について/15.12.23]
[右図のように直角三角形を描くと,糸の長さが 2a だから,直角三角形の斜辺は a.
そこで,b2=a2−c2 とおくと,三平方の定理(ピタゴラスの定理)により,b は右図の長さになる]・・この右図が良かったです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/15.12.23]
ものすごくわかり易かったです!
色々なパターンを作って欲しいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][合成変換・逆変換 について/15.12.22]
例題1の行列の合成変換の計算が間違えてる。
=>[作者]: 連絡ありがとう.左辺の式が g○ g になっていましたので訂正しました.その他,Firefoxで行列成分の表示が乱れる箇所がありましたので,ついでに直しました.
■[個別の頁からの質問に対する回答][2直線を表わす方程式 について/15.12.21]
とても分かりやすかったです!
逆にどんな2直線も2元2次方程式で表せるんですかね~?
2直線を2元2次方程式で表せ問題ってあるんですかー?
=>[作者]: 連絡ありがとう.「2直線はx,yの2次方程式で表わせます.」そういう問題を作ることは可能ですが「やさし過ぎるのでめったに出題されません.少なくとも筆者は見たことがありません」.
【例】
(1) 2直線
y=x と
y=−x は各々
y−x=0 と
y+x=0 と書くことができます.論理的には,「
y−x=0 または
y+x=0 」ということになります.だから「
(y−x)(y+x)=0 」すなわち「
y2 −x2 =0 」という2次方程式で書けます.
(2) 2直線
y=ax+b と
y=cx+d は各々
y−ax−b=0 と
y−cx−d=0 と書くことができます.論理的には,「
y−ax−b=0 または
y−cx−d=0 」ということになります.だから「
(y−ax−b)(y−cx−d)=0 」いう2次方程式で書けます.展開するのは容易です.
(3) y軸またはx軸に平行な場合も含めて,一般に2直線は
ax+by+c=0 と
dx+ey+f=0 と書くことができます.論理的には,「
ax+by+c=0 または
dx+ey+f=0 」ということになります.だから「
(ax+by+c)(dx+ey+f)=0 」いう2次方程式で書けます.これを展開すれば,2次方程式になるので,問題としては簡単過ぎることになります.
(*) 上記の(1)において「
y2 −x2 =0 」と「
y2 −x2 =k 」との関係は右図1の略図に示したようになっており,k≠0の場合は2つの直角双曲線を表すのに対して,k=0の場合はその屈曲点がちょうどくっついたものになっています.これに対して(3)は,幾つかの形に対応していますが,ある条件を満たしていれば,右図2の略図に示したように「
(ax+by+c)(dx+ey+f)=k 」はk≠0の場合は2つの斜交双曲線を表すのに対して,k=0の場合はその屈曲点がちょうどくっついたものになっています.(
a,b,c,d の符号によっては楕円や放物線が境目となっている渦を表す場合もあります)
■[個別の頁からの質問に対する回答][行列を対角化するには について/15.12.20]
3行3列の計算方法を詳しくやってほしかった
=>[作者]: 連絡ありがとう.今読んで見ると確かに内容が薄いようですので,その部分を追加しました.
■[個別の頁からの質問に対する回答][順路の問題 について/15.12.20]
問題を見て難しいと感じる人がいるだろうから、道に名前をつけるなら簡単な名前にしたほうが良いと思う
=>[作者]: 連絡ありがとう.この問題で道の名前は問題の難易度に全く影響していません・・・数学としてはそれがすべてです.(ただ,順路の問題としてイメージしてもらうためには,それが道であることが分かればよく,修学旅行などで多くの生徒が親しみを持っていると思われる実在の通り名を使っています.今日は高校駅伝で,これらの通り名を解説者が何度も読んでいます.)
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/15.12.19]
「犬であることは,シェパードであるための必要条件です」について。これってp←qを例示しただけで実際は必要条件じゃないですよね?「犬であることはチワワであるための必要条件」て反例も上がりますし。
=>[作者]: 連絡ありがとう.
どうやら,質問者は必要条件は1つしかないと決めておられるために疑問に迷い込んでおられるようです.まず「必要条件や十分条件は何個でもある」ということを押さえてください.
【例1】x>1 → x>0 」「x>2 → x>0 」,「x>5 → x>1 」「x>5 → x>0 」などが成り立ちますので,「x>1 もx>2 も両方ともx>0 の十分条件」「x>1 もx>0 も両方ともx>5 の必要条件」といえます.
次に「反例」という用語の使い方ですが,反例というのは「その主張がなりたたないような例」をいいます.「p→q」が間違った主張であるときにこれに対する反例は,「pであってかつqでない例」です.このようなものがあればそれを反例といいますが,反例がなければ元の「p→q」は正しい主張になります.
【例1】x>1 → x>0 」の反例を探そうとして「x>1 であって,かつ,x>0 でないもの」すなわち「x>1 であって,かつ,x≦0 であるもの」をどんなに探しても見つかりません.だから,「x>1 → x>0 」という主張は正しい=これに対する反例はないことになります.(「集合A={x | x>1} とB={x | x≦0} の共通部分」が空集合になるということと同じです)
■[個別の頁からの質問に対する回答][正規分布 について/15.12.19]
すげーたすかる
=>[作者]: 連絡ありがとう.連絡を受けた機会にもう一度読み直してみると,前後関係が読みにくい部分がありましたので,一部書き換えました.
■[個別の頁からの質問に対する回答][逆行列の求め方 について/15.12.19]
とても丁寧でわかりやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数の計算 について/15.12.17]
すばらしい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/15.12.15]
ページの見方を教えてください。
左と右の項目の関係がよくわかりません。ページの構成がよくわかりませんので。
=>[作者]: 連絡ありがとう.多くは左側が本文で右側が補足説明,本文が左側に書き切れないときは右に書く場合もあります.=一般の文書と同様に左から右へ,次に上から下へです.
どうしても分からないときは,
携帯版 を見てください.--こちらは上から下だけです.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/15.12.14]
一連の式を書いてほしい
=>[作者]: 連絡ありがとう.途中経過もその解説もていねいに書いてあります.あなたは約10秒ほどこの頁を見ただけで,1題も解答せずに答を探したようです.解答すれば,解説は出ます.昨日も述べましたが同じことを繰り返しますと「このホームページは単なる情報提供のWeb頁ではなく,すべてアプりになっています.あなたが解答すれば,採点結果と途中経過,解説が出ます.見ているだけでは何も出ませんが,解答で幾ら間違ってもあなたに不利なことは何も起りません.管理人はただの個人で,あなたの学力を他社に売るなど個人情報を流出する手段を持っていません.(そもそもあなたが誰であるかも分かりません)
■[個別の頁からの質問に対する回答][不定積分の置換積分 について/15.12.14]
あっててもhelpほしい
=>[作者]: 連絡ありがとう.正解の場合にHELPを出さない根拠は
この頁(ただしPDF 486KB) の3.2の項目ですが,出す出さないの差は微妙なものですので,個別に希望のあった頁については,正誤によらず「解説」を選べるようにします.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/15.12.13]
色が薄くて見づらいですね。
=>[作者]: 連絡ありがとう.申し訳ないのですが,あなたはPC画面の設定を16ビットにしています.その設定では微妙な色合いが飛んでしまいます.
■[個別の頁からの質問に対する回答][Sn →an 関係式 について/15.12.13]
途中式もふくめてもっと詳しく書いてほしい
=>[作者]: 連絡ありがとう.あなたは結構な長時間見ておられますが,このホームページは単なる情報提供のWeb頁ではなく,すべてアプりになっています.あなたが選択肢の内の一つをクリックすれば,採点結果と途中経過,解説が出ます.見ているだけでは何も出ませんが,解答で幾ら間違ってもあなたに不利なことは何も起りません.管理人はただの個人で,あなたの学力を他社に売るなど個人情報を流出する手段を持っていません.(そもそもあなたが誰であるかも分かりません)
■[個別の頁からの質問に対する回答][余弦定理 について/15.12.12]
見づらい 分かりづらい
=>[作者]: 連絡ありがとう.うすい色の配色は少し濃くしました.根気よく読まないと分からない場合はあります.
■[個別の頁からの質問に対する回答][直交行列とは(定義,性質) について/15.12.10]
紫色の文字の部分が見づらいです。
=>[作者]: 連絡ありがとう.たぶんあなたが使っておられるものと同じ iPhone で確かめましたが,紫色に見える文字というのはありません.申し訳ないですが対応できません.
■[個別の頁からの質問に対する回答][2次不等式(D=0) について/15.12.07]
まったくわからないです…
むしろ混乱しました↓
=>[作者]: 連絡ありがとう.十分な準備ができていない場合に,
基本問題(D>0の場合) をやらずに,いきなりD=0,D<0の応用問題をやろうとするとできないことがあります.先に
基本 をやってください.
■[個別の頁からの質問に対する回答][確率の基本 について/15.12.07]
それぞれの答えや解説を付けて欲しいです
=>[作者]: 連絡ありがとう.問題に答えて選択肢のどれかをクリックすれば,解答も解説も出ます.問題に答えずに読んでいるだけでは何も出ません.
■[個別の頁からの質問に対する回答][2次関数のグラフ[標準形] について/15.12.07]
最後の回答表示欄が少し狭い気がする。2~3文字分あると見やすいと思う。
=>[作者]: 連絡ありがとう.確かに Safari で見ると解答欄が狭いようですので訂正しました.
■[個別の頁からの質問に対する回答][余弦定理 について/15.12.06]
作戦盤の表を答案に書くのは良いですが、名前を出すと笑われる。という下りですが、その書き方ではこれを読んでこのテーマを初めて学習してるor再び理解しようとしている人が何も説明せずに表だけ突然答案に書き、「表より余弦定理を使えばいいとわかるので~」っという答案を作ってしまうことが予想できる。が、実際説明なしで突然表を書くのは、答案に三次関数の箱入り性と書くのと同じように説明不十分意味不明な答案になると思われ減点されると思います。
=>[作者]: 連絡ありがとう.計算用紙も配布されていればそちらに書きますが,計算用紙が配布されていない試験の場合,答案の本文以外に思考の補助として図や表を書くことは何も問題はありません.「三次関数の箱入り性」というのは何のことか分かりません.
■?[MA管理人さん/15.12.06]
ホームページを拝見させていただきました。当方のブログにリンクを張らせていただいてもよろしいでしょうか?
よろしくお願いいたします。
=>[作者]: 連絡ありがとう.今日では,公開サイトに対してリンクを作成することは,通常は承諾なくして行ってよいものと考えられているようです.当サイトについても同様です・・・ただし,昔,ある新聞社からは「リンクはトップページだけにしてほしい」「フレームの中からあたかも自分のサイトの一部であるかのように表示するのは避けてほしい」などと言われたことがありますが,このような条件も最近では曖昧な取り扱いになっているようです.
ただ,このメールにはそちらのブログのアドレスが書かれていませんし,返信用メールアドレスもありませんので,通常はかまいませんとはいいながらも,誰に何を承諾しているのかが決まりません.??
Re:>>昨日は失礼いたしました。送信ボタンを押すと連絡板に掲載されるのかと思い,売名行為になってはいけないとアドレスを書かなかったのですが,確かに正体不明のお伺いになってしまっていました。申し訳ございませんでした。
http://mathaquarium.blog24.fc2.com/blog-entry-121.html
この記事で紹介させていただきました。まだまだ訪問者の少ないブログですが,よろしくお願いいたします。
■[個別の頁からの質問に対する回答][三角関数の性質(まとめ) について/15.12.05]
sin49/6πはどーやったらといたらいいのか。
=>[作者]: 連絡ありがとう.大きな角の三角関数を求めるときは,2π回転するごとに1周するから,2πを取れるだけ取ります(割って余りを求める)
次に,
の公式[度で書けば(1)の先頭の公式:
sin(360°×n+θ)=sin θ ]を使うと
になります.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/15.12.05]
対数関数の(3)
違う問題の解答になってる気がします、
=>[作者]: 連絡ありがとう.いやはや,ビックリ仰天玉手箱です.今日,携帯版に移植したばかりですが,累乗根を表示する関数名が違っていたため,累乗根が消えていました.平謝りの陳謝です.
■[個別の頁からの質問に対する回答][Google Chartを使った数式の書き方 について/15.12.05]
分数等の数式をできるだけ短いURLで表現できないか調べてました。内容は盛沢山でとても良かったです。今後も参考にさせてもらいたいと思います。
ただ、目的(分数)の表示方法だけを探そうと思った時には、少々見つけにくかったです。見出しが強調されてないから?(なんとなくなのですみません)
=>[作者]: 連絡ありがとう.言われることは分かるのですが,その頁は各種記号一覧のようなものなので,一つずつ見出しにしてしまうと,それはそれで分かりにくくなります・・・どこかの学校で誰かがつぶやいたぼやきにこんなものがあったのを思い出します:「この学校は重点教育の柱が多過ぎて,息をする場所がない」
■[個別の頁からの質問に対する回答][条件付確率 について/15.12.05]
入試やテストの前にチラッと確認するには丁度いい
=>[作者]: 連絡ありがとう
■[個別の頁からの質問に対する回答][円の接線の方程式 について/15.12.05]
円上の点Pの座標がどちらもマイナスの時も、そのまま当てはめればいいんですか?
=>[作者]: その通りです.x2 +y2 =25 上の点(−3 , −4) における接線の方程式は−3x−4y=25 3x+4y=−25
■[個別の頁からの質問に対する回答][展開公式 について/15.12.05]
(x+y)3 の解き方を教えてください
=>[作者]: 連絡ありがとう.
たぶん,Web画面上では累乗がうまく書けなかったので
(x+y)3 のことを尋ねておられるのだと解釈しました.
また,中学高校の授業に少しでも出ていたら,この文脈の中で「解き方」とは言わないはずで,展開の仕方というはずですが,他に解釈する余地がないので「展開」と解釈しました.
だから,上に基本公式として
(a+b)3 =a3 +3a2 b+3ab2 +b3 が書いてあるので,文字を入れ替えるだけのことになります.
(x+y)3 =x3 +3x2 y+3xy2 +y3
これが分からないから尋ねておられて,上の回答で納得されるのでしたら,逆にあなたの学習の仕方には大いに問題があります.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/15.12.04]
すごい!やはり基礎が大事!基礎を意識した応用が王道だと再び気づかされました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][楕円の方程式 について/15.12.04]
√のところがはっきりしていてわかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][1の虚数3乗根ω について/15.12.04]
ふつう、ωは(-1+√3)/2だけを表し、(-1-√3)/2はωの2乗と表すと思いますが。
=>[作者]: 連絡ありがとう.ただし,あなたの考えは間違っています.
【例】 東京書籍の教科書「数学Ⅱ」p.41,第一学習社「数学Ⅱ」p.54,科学振興社「ものグラフ 公式集」p.25・・・「1の3乗根のうち虚数であるものの1つをωで表すと」など
⇒このような訳で,
と決めてしまうと証明問題などで半分の場合しか示していないことになります.
【例1】1の虚数3乗根の1つを
とするとき,他方は
となることを示せ.
(まずい答案)
だから, が成り立つ.
⇒この答案は, とすると となる,ということを示していないので,半分以下に減点されることがあります.
【例2】1の虚数3乗根の1つをωとするとき,他方はω
2 となることを示せ.
(まずい答案)
だから ⇒この答案は, とすると となる,ということを示していないので,半分以下に減点されることがあります.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/15.12.03]
薄い灰色の文字がとても見にくいと感じました。
=>[作者]: 連絡ありがとう.色の深さが24bitのパソコンの場合に,灰色のコントラストが弱過ぎることがあるようですので,変更しました.
■[個別の頁からの質問に対する回答][累乗根 について/15.12.03]
参考になりました ありがとうございます^_^
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/15.12.03]
学習の記録がアクセスのたびにクリアとなり表示されない。
=>[作者]: 連絡ありがとう.学習の記録は,ブラウザや設定によって残らない場合があるようです.
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/15.12.03]
なぜA型B型が確率変数でないか分かるのに時間がかかった。事象・数値・確率が○○○のときに数値が確率変数。○×○のときには確率変数はないという言い方の方が分かりやすい
=>[作者]: 連絡ありがとう.白い背景色の欄の※で最初の方に書いているのですが
■[個別の頁からの質問に対する回答][円の方程式 について/15.12.03]
途中の計算の説明がない
=>[作者]: 連絡ありがとう.問題1の解説はその上の文章全部です.問題2はHELPが付いています・・・画面ドット数 320×580 のiPhoneでは画面の下端よりもさらに下に見えるかもしれませんので,画面構成を少し変更してHELPボタンを真ん中に,HELPメッセージを問題の右側に移動しました.
■[個別の頁からの質問に対する回答][余弦定理 について/15.12.02]
例2の答えの部分の√7が抜けてます
=>[作者]: 連絡ありがとう.携帯版に移植したときに,根号を表示する関数のディレクトリ指定が間違っており,根号が表示されていませんでした.訂正しました.
■[個別の頁からの質問に対する回答][逆行列の求め方 について/15.12.01]
の(1, 2)成分は
a12·A11+a22·A21+a32A31
このような式は,行列Aの2つの列が等しいときの展開に対応しており,2つの列が同じ場合の行列式は0になる.
a12·A11+a22·A21+a32A31=0
となる理由をもう少し詳しく教えてください。
=>[作者]: 連絡ありがとう.何年も前に書いた教材で,今読んでみると作者自身も省略の部分が分かりにくいと感じましたので,補足しました.
■[個別の頁からの質問に対する回答][正弦定理 について/15.11.30]
学校のワークの問題でわからないところがあり、解説を見たもののわかりにくく困っていたところ、このサイトにたどり着きました。とてもわかりやすくて良かったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/15.11.30]
とてもわかりやすく解説していてとても良かったです。さらに回答機能があってテスト勉強にとても役立ちました。他のものも利用させていただこうと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数 について/15.11.30]
すばらしいです
定期試験の範囲とドンピシャでとても助かりました
ありがとうございます
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数のグラフと係数の符号 について/15.11.29]
bの答え方がよくわからなかい。
わかりやすく説明してほしい
=>[作者]: 連絡ありがとう.採点すれば解説が出ます.それ以上詳しい解説は考えにくいので,その解説を読む練習をしてください.
■[個別の頁からの質問に対する回答][2次不等式 について/15.11.28]
全ての実数と解なしの見分けかた
=>[作者]: 連絡ありがとう.さらに,図解入りの解説を追加しました.
■[個別の頁からの質問に対する回答][数学的帰納法(不等式の証明) について/15.11.28]
問題の間違いについてです
例題3の
(1)の右辺について、
n=2の時
(右辺)=2・2/2+1=4/3
よって(左辺)=3/2より
(左辺)>(右辺)
になると思います。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][決定係数 について/15.11.27]
決定係数R2の説明の式で、Σ(yk - m )2=Σ(yk - ^yk )2+Σ(^yk - m )2 と (総変動)=(予測値による変動)+(残差による変動) とで右辺の項の順番が逆ではないでしょうか?
=>[作者]: 連絡ありがとう.式と言葉が逆順になっていましたので訂正しました.
■[個別の頁からの質問に対する回答][総和記号 Σ について/15.11.26]
わかりやすい解説ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][マクローリン展開 について/15.11.25]
意味不明 つまり、マクローリン展開とは、何をやっているんですか?
=>[作者]: 連絡ありがとう.この頁を読む人は,その項目を習得する必要があって調べていることが多いです.ここではマクローリン展開の課題を処理しなければならないが,よく分からないという場合です.しかし,「そもそも・・・とは」という形で入ってこられる場合も確かにあり得ますので,頁の初めの方に読み物的な文章を追加しました.
■[個別の頁からの質問に対する回答][指数法則 について/15.11.25]
(4)についてもっと詳しい解説がほしい
=>[作者]: 連絡ありがとう.その頁に(4)は3箇所あります.どの(4)のことなのか書かないと・・・.なお,各々の(4)にはそれなりに解説がついています.もし「負の指数」がよく分かっていないのでしたら,
この頁 とか
この頁 を読んでください.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルをエクセルのソルバーで求めるには について/15.11.25]
○ 次に行列の積(A−λE)——>xwの成分をセルG11~G14に書き込む.・・・「G11~G14を選択・反転させておいて,」の選択・反転させる方法が解らないです。
=>[作者]: 連絡ありがとう.マウスを押したまま引っ張るか,または,Shiftキーを押しながらG14を押すなどすればよいのではないか.
■[個別の頁からの質問に対する回答][《2次不等式》・・・まとめ について/15.11.25]
1問1問解説して
=>[作者]: 連絡ありがとう.その頁は(まとめ)の頁です.基本が済んだ人が(まとめ)にやる頁です.1問ごとに解説が必要な場合は,解説のある頁を見てください.→
D>0 D=0 D<0
■[個別の頁からの質問に対する回答][2直線を表わす方程式 について/15.11.24]
なぜ完全平方式にしなければならないかわかりません。√を含む一次方程式は存在しないのですか?
=>[作者]: 連絡ありがとう.
xについてxをyの式で表した場合(yについてyをxの式で表した場合でも同様だから,ここではxについて解く場合だけを扱う)を考える.「単に係数だけが根号を含んでいる」ようなものは,yの式としては完全平方式になっているので,これは1次方程式に含まれる.だから,次のような式は合格
これは1次式なので直線を表す
そうではなくて,以下のようにyの式として根号が外れない場合は,どうやってもxはyの1次式にならない.(yはxの2次式になる)
そうすると,つぎのようなものも1次式にならない
…(*)
一般に,根号が外れない式である限り,次のような場合,xはyの(yはxの)1次式にはなりません
一般に,根号が外れない場合には,その根号を外すと相手方(x)が必ず2次式になるので,その根号の影響を「引きずっていく」ことになります.
このような曲線は2次曲線と呼ばれ,例えば次の(1)(2)(3)の形を平行移動したものになります.数学Ⅲを選択していれば,2次曲線の単元で習う.
…(1)楕円(上の(*)の式でc≠0のとき)
…(2)双曲線(上の(*)の式でc≠0のとき)
…(3)放物線(上の(*)の式でc=0のとき)
■[個別の頁からの質問に対する回答][3次関数(文字係数と極値) について/15.11.23]
【例題4】の(解答)の2行目
2次方程式x22x+a=0について
となっていますが、
2次方程式x2"+"2x+a=0について
とするべきではないでしょうか
=>[作者]: 連絡ありがとう.2乗の後にプラスが抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][確率の加法定理,余事象の確率 について/15.11.22]
素晴らしい問題をありがとうございます。
ただ≪問題1.4≫の解説のキの式で3が抜けています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][不等式の証明1 について/15.11.20]
最後に練習問題がついてるのは良いと思いました。最後に成り立つ例と成り立たない例が書かれていますが、それは必ずしも書かないといけないものなのか、書いているとより良い、というものなのかを教えて頂けたら幸いです。
とてもわかりやすい解説と、適切な問題のおかげで、不等式の証明を解くことができるようになりました。ありがとうございました。
=>[作者]: 連絡ありがとう.問4~問7のような問題の場合,センター試験のようなマークシート方式では当然のことながら途中経過は見ませんので,根拠は不要です.ここでは,2次試験,模擬試験,校内の定期試験などで論述式になっている場合に,書かなければならないのかという御質問について答えます.
■[個別の頁からの質問に対する回答][極座標 について/15.11.20]
iPhoneで見ると「忘れずに!」の吹き出しで問題が隠れて見えません
=>[作者]: 連絡ありがとう.確かにiPhoneでは表示位置がずれますので,訂正しました.
■[個別の頁からの質問に対する回答][三角関数の値 について/15.11.18]
答えを見せて欲しい
=>[作者]: 連絡ありがとう.ヒントの図はブラウザ毎に表示を変えなければならないので,今お使いの iPhone..AppleWebKit には対応していないかもしれません.
この頁 に解答と考え方の一覧があります.
■[個別の頁からの質問に対する回答][剰余の定理 について/15.11.17]
剰余の定理の問題8の(x-1)2(x+1)の余りを求める問題のF(x)の部分がわかりません・・・
=>[作者]: 連絡ありがとう.「f(x)=(x-1)2 (x+1)Q(x)+a(x-1)2 +2x+1とおく.」という箇所が分かりにくいということのようです.2 (x+1)Q(x)+ax2 +bx+cとおく.」からスタートして,(x-1)2 とx+1で割った余りを調べるのですが,その上に書いた例題のように(x-1)2 で割った余りを調べやすいように,初めから余りの形を扱いやすい形においたものです.しかしこれでは分からないという場合もあり得ますので,その下にさらに「f(x)=(x-1)2 (x+1)Q(x)+ax2 +bx+c」から地道に計算する方法を追加しました.
■?[?さん/15.11.16]
平方完成の変形[問題4](2)の解答が間違ってますよ
=>[作者]: 連絡ありがとう.ただし,都道府県もなく,ペンネームもなく,自分の解答もないのはよくありません.少なくとも自分がどう思うかを書かないと,単なる思い違いと区別がつきません.
■[個別の頁からの質問に対する回答][二重根号 について/15.11.15]
2ページと3ページ目の最後の問題の四角に数字が入力できない。
ほかにも入力できないマスが結構ある。
=>[作者]: 連絡ありがとう.以前にも回答したことがありますが,この欄はタブキーで移動するようになっています.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/15.11.15]
5番ですが、aかbが(虚数?でしたっけ)の場合は←が成立しないのでは?
=>[作者]: 連絡ありがとう.生徒でない方からよくある質問ですが・・・教科書の順序から言えば,この段階では,生徒は虚数を習っていませんので生徒から言えば何も問題はないのですが,卒業生の場合でも,問題の先頭に「問題文中の文字は,すべて実数とします.」と書いてあります.
■[個別の頁からの質問に対する回答][Excelを使った対応のない場合のt検定…例題・問題2 について/15.11.14]
このサイト、とても役に立っています。ありがとうございます。
さて、問題3の回答は「有意差がある」ということですが、計算した結果、|t|=0.95<片側検定t境界値1.70、そしてP=0.18>0.05であるため、「有意差がない」という結論になるのではないでしょうか?
=>[作者]: 連絡ありがとう.このミスは大きい間違いでした・・・結論が逆になるので・・・問題2の型版をコピペしてしまったようです.不注意を反省して訂正しました.
■[個別の頁からの質問に対する回答][媒介変数表示1 について/15.11.14]
メニューが大量なので、数Ⅲをやっている場合に、メニューに戻って一番下までいって探すのが少し面倒です。数Ⅰ、Ⅱ、Ⅲのメニュー(目次)が別のページになっていると更に使いやすいと思います。
=>[作者]: 連絡ありがとう.問題点は認識していますが,他の作業に追われてまだできていません.当面は,「メニューに戻る」を選択するのではなく,ブラウザの機能としての前の頁に戻るを選択していただくと当該学年・当該科目のメニューに戻るはずです.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/15.11.14]
■[個別の頁からの質問に対する回答][底の変換公式 について/15.11.13]
練習問題もあり、分かりやすかった。高校の数学を思い出せた。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/15.11.12]
八番答えあってますか? -4じゃないのですか?
=>[作者]: 連絡ありがとう.八番というのがどの問題かよくわかりませんが,問題1の(8)以外には8のつく問題がないので,これについて答えます.
確かに途中経過は
になりますが,
という重要公式がありますので,
になります.
したがって,
になります.
■[個別の頁からの質問に対する回答][恒等式 について/15.11.12]
定理1(3)のcの項にxが抜けています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作6・・・行列計算,固有値,固有ベクトル について/15.11.11]
maximaの初歩的な操作6・・・行列計算,固有値,固有ベクトルhttp://www.geisya.or.jp/~mwm48961/linear_algebra/maxima6.htm
の始めの2*2行列の代入の解説の部分で、
matrixで代入しているのは[1,2],[3,4]なのですが、
画面のAは[1,3],[3,4]となっているので訂正をお願いします。
このページに限らず、使い方がとても分かりやすく非常に助かっています。
ありがとうございます。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][余弦定理 について/15.11.11]
タブ表示にした時"メニューに戻る"のボタンが見切れている。
最大化した時は表示されている。
=>[作者]: 連絡ありがとう.最大化して表示してください.
■[個別の頁からの質問に対する回答][共役複素数 について/15.11.11]
例(3)※が「実数と胸数」になってる
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][複素数の計算 について/15.11.9]
X+y=8
X+2y+4=3x
の計算
=>[作者]: 連絡ありがとう.あなたが今日調べたのは,この頁だけで,2時間ほどかけています.しかし,調べた頁と質問内容が全然対応していません.
未知数が2つある方程式の解き方を調べるには中学数学の「連立方程式」を見なければなりません・・・複素数とは,要素が2つある数のことのようですが,未知数が2つある方程式のことではありません.
だから,質問内容もつじつまが合いません.「・・・の解き方」と聞くべきです.
とりあえず,この質問に答えるには,
この頁 の下端にある【付録】で
(1)x+(1)y=8
と入力して[解く]というボタンを押してください.
※この頁でこういう質問を引き出せたということを管理人として自負すべきなのかもしれませんが,質問内容を理解するのが困難です.
■神奈川県[Prof.N.Hkさん/15.11.8]
「総和の記号,Σ(シグマ)に慣れよう」http://www.geisya.or.jp/~mwm48961/kou2/siguma11.htm の例12で、
5
Σ k(k+1)=1・2+2・3+4・5+5・6 = ( 2+6 +20+30 = 58 になる)とありますが、
k=1
正しくは、
5
Σ k(k+1)=1・2+2・3+3・4・5+5・6 (=2+6+12+20+30=70)だと思います。
k=1
いかがでしょうか。
=>[作者]: 連絡ありがとう.2015.1.25に訂正済みの内容です.そちらのブラウザの一次メモリか途中経路にあるサーバのキャッシュメモリに古いデータが残っていると思われますので,リロード(再読み込み)して確かめてください.
■[個別の頁からの質問に対する回答][総和記号 Σ(シグマ)に慣れよう について/15.11.8]
問題1
4 4
Σ k とΣ k は同じことを示していますよね。
k=1 k=2
=>[作者]: 連絡ありがとう.問題1には
はありますが,
はありません.
参考までに,
,
になり,異なるものです.
■[個別の頁からの質問に対する回答][三角関数の2倍角公式,半角公式 について/15.11.7]
cosの2倍角の公式がまちがってないですか?
cosα・cosβ-sinα・sinβだと思ったんですけど
間違えていたらすいません
=>[作者]: 連絡ありがとう.符号を直しました.
■[個別の頁からの質問に対する回答][正弦定理・余弦定理 について/15.11.6]
とても解りやすいです 本当にありがとうござます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][漸化式と一般項(階差形) について/15.11.5]
(3)途中式間違ってます。
=>[作者]: 連絡ありがとう.符号を直しました.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/15.11.5]
問題1の解説がわかりません
>(ガムをかんでいる)者は,何歳であっても違反にならない.⇒チェックしない.
ガムを噛んでいるからと言ってその人が未成年であり、かつ影で喫煙している可能性は排除できないのではないですか?
=>[作者]: 連絡ありがとう.良く考えられた質問だと思います.問題は「年齢と行動のうちの一方だけがわかっている次の4人のうちで」としていますので,この場合「行動」は「ガムをかんでいるいる」と分かっていることになります.「他の時間」「以前」にどうであったかは,この問題では問えないので陰で吸っているかどうかは問題になりません.
■[個別の頁からの質問に対する回答][楕円の方程式 について/15.11.3]
重要な基本事項すぐ確認できてよい!
とても見やすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次不等式 について/15.11.3]
テスト前の確認にとても役立てていただきました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ 複素数の計算 について/15.11.3]
印刷時、右端切れる
=>[作者]: 連絡ありがとう.
携帯版 は横幅が狭いので切れないようです.
■[個別の頁からの質問に対する回答][根号計算 について/15.11.2]
数学の授業でみんなやりました!わかりやすかった!=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][根号計算 について/15.11.2]
数字を打った時に数字がとぎれてでてくるのでなおしてもらいたい。
=>[作者]: 連絡ありがとう.その頁には「数字を打つ」欄はありません.他の頁の話はその頁でしてください・・・江戸の敵を長崎で討ってどうする?江戸の話は江戸で・・・
■[個別の頁からの質問に対する回答][必要条件、十分条件 について/15.10.31]
ヒントと問題がかぶってる…
=>[作者]: 連絡ありがとう.たぶん,「スマホでは選択肢やヒントの間隔が狭いと押しにくい」という意味だと解釈しましたので,間隔を広げました.
■[個別の頁からの質問に対する回答][行列の積 について/15.10.31]
練習問題の解答が表示されない。
あっているかがわからない。
=>[作者]: 連絡ありがとう.解説&解答のボタンを付けました.
■[個別の頁からの質問に対する回答][放物線の頂点の座標 について/15.10.31]
本当にわかりやすい!!
今度、県模試を控えてるので復習するのにとても便利でした!!sinθ cosθ tanθのも学びたいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数のグラフ[標準形] について/15.10.31]
解説などとてもわかりやすかったです!問題もひっかかりやすいところを突いてきていて自分がどこまで理解しているのかを自分で確認出来ました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][放物線の移動 について/15.10.29]
大根を切るためにはコノギリはいらないってかいてあるよ。ノコギリじゃない?
=>[作者]: 連絡ありがとう.ミスプリントなので直しました.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルをエクセルのソルバーで求めるには について/15.10.29]
ある統計の本で固有値はExcelでは解けないので,専用プログラムを使用する様な事が載っていて,そのつもりでいたのですが,ソルバを使用して結構実用的な解が得られるのが興味を引きました。もちろんRなら一発でしょうが,Excelはお手軽なので,ちょっとした時は便利かと思いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][行列と1次変換 について/15.10.29]
(8)の公式の(2.2)はcos^2(θ)ではなく、sin^2(θ)ではないでしょうか、計算しましたが、どうしてもcos^2(θ)になりません。私の力不足で申し訳ないのですが、計算過程も載せて頂けないでしょうか。
宜しくお願い致します。
=>[作者]: 連絡ありがとう.(8)の最後の式の2行2列成分はおかしいので直しました.
■[個別の頁からの質問に対する回答][絶対値 について/15.10.28]
具合の悪い所 : 《問題》
■1
||x|-1|-1|=kの解の個数を調べなさい.
↓
《問題》
■1
|||x|-1|-1|=kの解の個数を調べなさい.
=>[作者]: 連絡ありがとう.縦線を1本追加しました.
■[個別の頁からの質問に対する回答][(例題対比)2次関数のグラフ[標準形] について/15.10.28]
最後の問題のy=4x2-3ですが、最初の空欄は4で間違いとなっていましたが何故ですか?
=>[作者]: 連絡ありがとう.iPhoneのSafariで全角文字の4を入力された場合には,自動では半角文字の4には変わりませんので間違いになったと考えられます.
■[個別の頁からの質問に対する回答][対偶証明法と背理法 について/15.10.25]
正解や不正解の将棋の駒がとてもかわいいです。特に不正解のときの、倒れ方がナイス!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式 について/15.10.25]
具合の悪い所 : 要点などを黒字にしてほしい
=>[作者]: 連絡ありがとう.本文が黒系統の文字なので,強調するために要点を青系統にしていますが,機種によってはもっと濃い色の方が見やすいということかな?
■[個別の頁からの質問に対する回答][(例題対比)平方完成の変形 について/15.10.27]
授業であんまりわからなかったけど、わかりやすかった!採点機能がついてるのがいいとおもった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数方程式 について/15.10.26]
すばらしくわかりやすいです。助かります。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/15.10.25]
ずっと謎だらけで苦手だったベクトルが、一気に近く感じました!学校の先生よりも教科書よりもわかりやすかったです!
あと、言葉というか、用語?の意味もかみくだいて説明されてたらもっといいのになと思いました。
=>[作者]: 連絡ありがとう.後半の「用語」については,機会があれば考えます.
■[個別の頁からの質問に対する回答][回帰直線,回帰係数 について/15.10.23]
アンケート項目2のところで、Y=αx+β のとき、αが回帰係数では???
=>[作者]: 連絡ありがとう.統計の書物では定数項,1次の項の順に書くことがあり,これにならって,y=α+βx と書いています.だから,1次の係数はβです.
■[個別の頁からの質問に対する回答][展開公式 について/15.10.21]
問題3の3問目の解説がほしい
=>[作者]: 連絡ありがとう.HELPが付いていますが,それでは足りないという意味のようですので,追加しました.
■[個別の頁からの質問に対する回答][無理関数(2次式の平方根)の定積分 について/15.10.20]
最後の積分式について、A=0のときでも根号は外れず、不連続関数の積分の形になりませんか?
=>[作者]: 連絡ありがとう.A=0のときは,
になりますので,根号は「はずれる」と言うでしょう.x=0を含む区間については,不連続関数になって異常積分(広義積分)になるというのはその通りですが.このようにしてA=0の場合に取り扱いが変わるので,A≠0ぼ場合を述べたものです.
■[個別の頁からの質問に対する回答][円の方程式 について/15.10.19]
できればどんな簡単な問題でもhelpをつけてほしい
=>[作者]: 連絡ありがとう.できればそのようにしたいと考えていますが,頁数が多いため難しそうな所から先にやっています.
■[個別の頁からの質問に対する回答][順路の問題 について/15.10.19]
間違えたら、HELPで解き方と答えをわかりやすく説明してくれるので、とてもいい。すごくわかりやすかった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数のグラフと係数 について/15.10.18]
計7問を解いていくことで、bの符号の求め方がすうっと頭の中に染み入ってきた気がします。
ありがとうございました。
=>[作者]: 連絡ありがとう.ほめ方がうまいな-.
■[個別の頁からの質問に対する回答][展開公式1 について/15.10.16]
解説だけではなく、問題とその答え合わせ(HELP機能)まであり、とても使いやすく、わかりやすかったです。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/15.10.15]
とても良かったです!!!
自分が苦手なところを探すのが少し大変でしたが、解説などもありとても良かったです😊
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][数学的帰納法とは について/15.10.13]
すべての自然数 n について
1+3+5+ … +(2n - 1)=n2 …(1)
が成り立つことを証明したい.
↑左辺に1+3+5+ … +がある以上、絶対に成り立たないと思うのですが。
実際、適当にnに数を代入してみましたが必ず左辺が大きくなります。
それとも何か数学的お約束事があるのでしょうか?
=>[作者]: 連絡ありがとう.「数学的お約束事」に相当するかどうかは別として,「一般項が2n−1である数列の第1項から第n項までの和」を表すときに『規則性が類推し易いように』初めの幾つかの項を書き並べます.これはΣ記号をまだ習っていない読者の便宜のために行うもので,左辺に1+3+5+ … +があるからといっても,n=1のときには3や5はなく,n=2のときには5はありません.
ほとんどの高校生はこの意味が分かるようで,3や5が必ずある訳ではないと注意事項に書いてある教科書を見たことがありません.
あなたが,絶対に成り立たないと考えるのはn=1の場合とn=2の場合だけを調べたからで,n=3,4,5,...と調べていくと見かけにこだわっていても正しいことが分かります.
次のように読みます:n=4 のとき,(左辺)は1+3+5+7 ,(右辺)は42 =16 だから等しいn=3 のとき,(左辺)は1+3+5 ,(右辺)は32 =9 だから等しいn=2 のとき,(左辺)は1+3 ,(右辺)は22 =4 だから等しい(+5 はどこに行ったのかとは言わないn=1 のとき,(左辺)は1 ,(右辺)は12 =1 だから等しい(+3+5 はどこに行ったのかとは言わない
この話は面白いので(間違いが面白いという失礼な話ではなく,『規則性が類推し易いように』書かれた項が気になるかどうかという点で興味深いということ),授業中にこの話を切り出しても余り受けずに生徒はしらけていることが多いです.次の例は上の話と全く同様です.
すべての自然数
n について
が成り立つ.
【例】
n=4 のとき,
だから等しい
n=3 のとき,
だから等しい
n=2 のとき,
だから等しい(
+3 はどこに行ったのかとは言わない)
n=1 のとき,
だから等しい(
+2+3 はどこに行ったのかとは言わない)
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/15.10.13]
helpの所はすぐに答えを出すんじゃなくて
やり方のヒントだけを出して欲しい
=>[作者]: 連絡ありがとう.HELPと解答を2段階に出すことにしました.
■[個別の頁からの質問に対する回答][(各駅停車)二重根号 について/15.10.12]
自分の端末のせいかもしれませんが、一部入力できない欄がありました。
ちなみに自分の端末はandroidのスマートフォンです。
=>[作者]: 連絡ありがとう.この頁の空欄移動にはtabキーの使用を想定していますが,androidにはtabキーはないようです.googleの記事によればどこかでtabキーのコードを見つけて単語登録するとよいと書かれていました.
■[個別の頁からの質問に対する回答][不等式の証明2 について/15.10.10]
例9の1つ目の式と2つ目の式が成り立ってないです。
=>[作者]: 連絡ありがとう.問題文の側に2が抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][多項式の除法 について/15.10.9]
正解した後の入力でも反応が欲しい
今
2*2=4...正解!
↓
答えを変更する
↓
2*2=3...正解!
改善後
2*2=4...正解!
↓
答えを変更する
↓
2*2=3...不正解!
=>[作者]: 連絡ありがとう.自転車が乗れるようになったかどうか,水泳ができるようになったかどうかなどのように実技的な能力は一度身に着くとめったに失われません.正解できた人ができなくなることはめったにありません.そのため,正解後の不正解は想定外です.
■ [個別の頁のアンケートからの質問]/15.10.9]
不等式の証明1 について
問3の解答で仮定が間違っていると思われます。
=>[作者]: 連絡ありがとう.
a と
b が逆になっていましたので訂正しました.
■ [個別の頁のアンケートからの質問]/15.10.8]
確率の基本 について
答えが正解でも、解説を読めるようにしてほしいです。
=>[作者]: 連絡ありがとう.筆者も本当のところは正解でも解説を読んでほしいと思っていますが,
アンケート結果 (その3頁の表2のE)からは,正解したときにHELPや解説が表示されることは,プライドが傷つくなど嫌う人が多いようですので,多くの頁で間違ったとき・助けてほしいときだけ助けるようにしています.ただし,この差異はさほど顕著なものでもないとも解釈できます.
正答でも誤答でも解説が出るようにするには,プログラムを1行書き換えるだけなので,その頁については,「要望があった」ということで対応しました.ただし,この要望は多くの頁に関連していますので,他の頁はそのままです.
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/15.10.5]
分数のある問題の時に1とかが形が崩れ気味で少し読みづらいです。
=>[作者]: 連絡ありがとう.あなたがお使いのChromeでチェックしましたが,こちらから見る限り特に問題は感じませんでした.
■[個別の頁からの質問に対する回答][F検定→t検定 について/15.10.5]
値の読み方が分からず悩んでいたのですが一気に解決しました。ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][積の法則 について/15.10.4]
正の約数の総和について、何故この方法で求めることが出来るのかの記述が欲しい
=>[作者]: 連絡ありがとう.問題6のHELPに書いてありますが,以下に補足します.
(23 +22 +21 +20 )(32 +31 +30 ) …(1)=23 32 +23 31 +23 30 +22 32 +22 31 +22 30 +21 32 +21 31 +21 30 +20 32 +20 31 +20 30 =(72+24+8)+(36+12+4)+(18+6+2)+(9+3+1) …(2)
(1)で計算すれば答案のようになり(2)で計算すればすべての約数の和になります.
■[個別の頁からの質問に対する回答][三角関数の加法定理 について/15.10.3]
選んで消えていくのはとてもシンプルで分かりやすく勉強するのに役立ちました
=>[作者]: 連絡ありがとう.「進んでいる」という達成感を視覚的に表示するための工夫ですが,認めてもらってうれしいです.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/15.10.3]
非常に分かりやすい解説でした。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の合成公式 について/15.10.3]
理論上…のところの、余弦の加法定理ですが、cos(θ-α)になると思います。
=>[作者]: 連絡ありがとう.御指摘の通りですので,加筆訂正しました.
■[個別の頁からの質問に対する回答][弧度法の単位ラジアン について/15.9.29]
上行と下行が、半行程、重なっている箇所が数か所あります。
=>[作者]: 連絡ありがとう.それはエラーではなく,そういうデザインです.
■[個別の頁からの質問に対する回答][F検定→t検定・・・平均値の差の検定 について/15.9.25]
卒業論文を書く時、とても役に立ちました。 ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][確率変数,確率分布 について/15.9.25]
「確率変数」の意味を知りたくてネット上をさまよっていましたが、この頁でようやく救われました。
「間違い例」があるのがとても役立ちました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/15.9.23]
とっても、解りやすく、数Ⅰの基礎力もない者でも、簡単に、着いていくことが、出来ました。おかげで、37年ぶりに、数ⅡBにたどり着けました。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/15.9.23]
練習問題、ページをわけてもっとたくさんあったらもっとうれしい
単純な四則計算は得意だったし好きだったけれど、
小学校途中から入ってくる文章題と図形でつまづき(薄さの違う塩水は混ぜずに捨てるか水分飛ばしてから使え!とか本気で出るたび思ってた)、
中高で加わったグラフに完璧に行き詰まり数学ボイコット、
通年赤点補習組でした。
かれこれ10数年にわたり、数学の存在まじで意味不と思っていたけれど
本当に"自分と合う(自分にレベルを合わせた)解説をしてくれる人がいる"だけでここまで物事への理解度に差がつくものなのかと目からウロコ。
数学のことを喋って(説いて)らっしゃる文章のはずなのに、私にも意味がわかる…!
多分この感動は、"一般の"、数学苦手~とか言いながらも4,50点はとる(4,50点"は取れちゃってる")人間には伝わらないんじゃなかろうか…
数学の教科書に書かれている解説って、本当に日本語なの?な状態でしたから…。
このサイトに中学・高校時代に出会いたかったです。
数学がこんなに、ゲームみたいに楽しんで解けるものだったなんて、ここにくるまで夢にも思わなかった。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.9.21]
一つの単元を完璧にしたいとき、相同問題をたくさんこなして行くことで力になっていくのでこれらの練習問題は円順列・数珠順列を完璧にしたい私に取って全く文句の付け所がない教材でした。また、解答もしっかりしていて、学校で学んだことをしっかり理解していれば、問題なく全て理解することができます。また、解ければ解けるほど自分の自信になっていくので、本当にこのようなサイトは数学受験組の私にとっては有り難いです。最高のテキストでした。こんなに素晴らしいものを無料で提供してくださってありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/15.9.21]
すごくわかりやすいです 素晴らしいです
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/15.9.21]
大学受験を控える者です。すごくありがたいです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][分数の指数(有理数の指数) について/15.9.20]
有理数の指数の基本的な考え方から問題の解き方まで詳しく載っていて分かりやすかったです。 具体的な数字で例題があったり、実際に問題を解くことができるので自分がきちんと理解しているかを確認できました。 特に、間違えた時に途中式を含んだ解説があるのがよかったです。また、問題の種類や数が多かったので理解度が深まったと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/15.9.20]
とてもわかりやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][定積分(多項式,分数関数,無理関数) について/15.9.17]
問題4の積分範囲の数字に誤記載がある。回答では0-1の範囲という想定になっているが、問題文は1-2の範囲で、これでは逆三角関数を使わない限り値は求められない。
=>[作者]: 連絡ありがとう.問題文の方を訂正しました.
■[個別の頁からの質問に対する回答][二重根号 について/15.9.17]
3ページめの(2)から答えの入力欄に入力不可
=>[作者]: 連絡ありがとう.確かにマウスで空欄をポイントすると入らないようです.自分で言うのもおかしな話ですが,その頁のプログラムは直しにくいので,上端に書いてありますように「タブキーで空欄を移動すると楽です」のでよろしく.
■[個別の頁からの質問に対する回答][媒介変数表示3 について/15.9.16]
問6で、正解はy=-4/3x+4/3ですが、
それが選択肢に含まれていなく、1の選択肢(y=-2/3x+4/3)を正解としています。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][3次関数の増減 について/15.9.16]
問1の回答の選択肢に誤植がある。説明の回答と不等号の向きが逆。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][組分け について/15.9.9]
〈〈7〉〉の問題で例えば6人0人0人の場合などご抜けていませんか?
=>[作者]: 連絡ありがとう.問題文に書いてありますように,「どの組にも少なくとも1人の生徒がいるものとします」とは,0人の組は作らないということです.この但し書きは確認のためのもので,この但し書きがなくても,組分けの場合は,通常1人もいない組は組の数に数えません.例えば,あなたが示した例は,{6,0,0}と見るから3組に分けたとも見えるかもしれませんが,{6}と見れば1組,{6,0}と見れば2組,{6,0,0,0}と見れば4組に分けたことになり,1人もいない組を数えてしまうと,何組に分けたのか決まらなくなります.
■神奈川県[Prof.N.Hkさん/15.9.9] ]
ご回答ありがとうございました。さて、http://www.geisya.or.jp/~mwm48961/kou3/integral2.htmの例3で、[x^2-3x]2 0 とありますが、[x^2-3x]1 -1 ではないですか?=>[作者]: 連絡ありがとう.いずれも御指摘の通り,間違いですので訂正しました.
■神奈川県[Prof.N.Hkさん/15.9.8] ]
三角関数の値(http://www.geisya.or.jp/~mwm48961/kou3/sin004.htm)の10問目 tan(θ-π)のヒントがπ-θと同じ位置を表している気がするのですが… θ-π=π+θではないですか?答えもtan(θ-π)=tanθとなっていたので…第3象限でしたらタンジェントの符号は正になりますよね。もし違っていたらすみません。
=>[作者]: 連絡ありがとう.ここでは2つの公式で考えるヒントを示しています.1つはtan(π−θ)=− tan(θ) …(A),もう1つは tan(−θ)=−tan(θ) …(B)
■[個別の頁からの質問に対する回答][内接円の半径 について/15.9.8]
色を使った図の説明や文が多すぎず必要最低限のことだけを言っていいることが良かったです
=>[作者]: 連絡ありがとう.どの頁の話なのかと,ふと元の頁をみてみると,問題2(4)の解答欄がないことに気が付きました.携帯版に移す時に飛んでしまっていたようですので直しました.おかげで助かりました.
■[個別の頁からの質問に対する回答][確率変数 について/15.9.3]
「確率変数」の意味が分からずネットや書物を多数調べましたが説明不足ばかり。きちんとしたテキストでも既知のことのように突然確率変数が出てくるのでその先はちんぷんかんぷんでした。ここでの定義の説明で一挙に謎が解けました。有り難うございます。みんなこのように初めに説明したらいいのに。。。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][2円の交点を通る円・直線の方程式 について/15.8.31]
表わす、じゃなくて表す、です…
=>[作者]: 連絡ありがとう.楽しい算数の時間に国語の指導を受けるのは,カルチャショックです.確かに「表す」の表記の方が多いようですが,「表わす」も使います.
参照 など.たぶん,筆者のよく使う漢字変換システムにクセが付いているせいでしょう.なお,手元の国語辞典(小学館「新撰国語辞典」)では両方可能とされています.しかし,一連の文章で「表わす」「表せない」の2つあるのはまずかったようです.
■神奈川県[?さん/15.8.30]
数1のデータの分析(散布図、相関表、相関係数)の問題4で質問です。-2.611が正解になっていますが、相関係数は-1以上1以下なので、範囲外ではないでしょうか。エクセル(CORREL)で計算したところ、-0.2611になりました。
=>[作者]: 連絡ありがとう.小数点がずれていましたので,訂正しました.
■[個別の頁からの質問に対する回答][条件付き確率 について/15.8.29]
自分がこの単元についてわからなかったのは、 P(AnB)/P(A)のP(AnB)の求め方です。自分はずっと、 P(AnB)は、AでありBである場合の確率を表すのだから、その求め方はP(A)×P(B)ではないのか、と考えていました。こんな勘違いをする人は少数派なのかもしれませんが、できればP(AnB)の求め方を補足していただければ幸いです。
=>[作者]: 連絡ありがとう.
P(A∩B)=P(A)×P(B) となるのは「2つの事象
A, B が独立な場合」だけです.一般の場合には,それは成り立ちません.独立とは限らない一般の場合には,集合の要素の個数
n(A∩B) と全体集合の要素の個数
N を数えて,
を計算することになります.ただし,その頁では
P(A∩B) を求めなくても,
n(A∩B) で計算できることを示しています.
■[個別の頁からの質問に対する回答][展開公式( について/15.8.22]
次の問題の文字を押すと問題が変わることに押してみないと気付けない。あと、戻れ無いため、一順するのかと思ってENDまで押してしまう。最初から並べて表示しておけばいいのでは?
=>[作者]: 連絡ありがとう.(前半の質問について)それを防止するために「忘れずに!」という吹き出しを付けています.(後半の質問について)全部並べると画面構成がごちゃごちゃしてしまい「ひるんでしまう」こと確実です.山登りと同様で,一題ずつ集中するとそのうち終わることができます.「1つ前に戻る」というボタンを付けるのはよい考えですが,現状でもリロード(再読み込み)すればいつでも元の問題を読むことができます.
■[個別の頁からの質問に対する回答][展開公式1( について/15.8.20]
こういうサイトを探していました。教科書持っていないので助かります
=>[作者]: 連絡ありがとう.この教材を作り始めた頃(15年近く前=ミレニアムプロジェクトという言葉がまだ輝かしく見えていた頃=熱狂が失望に変わる前)に,現役生徒を想定して作成していましたので・・・教科書のバーコードをかざせば,誰でもどこでもWeb上の演習教材を読めるはずでしたが,どの教科書会社もそんなことが実現できたとは思えません.・・・「読者は当然教科書を持っているはずだ」⇒「教科書を見ていることを前提として次の課題を」・・・と考えていましたので,解説部分が味もそっけもない頁が多いです.
■[個別の頁からの質問に対する回答][正規分布 について/15.8.19]
全体的によく工夫された作問だと思います。答えが比較的簡単になるようにしてありますが、後半の問題は、もう少し複雑なものもあってよいと思います。(5)で、偏差値の定義(公式)を最初に与えてもよいと思います。とても参考になりました。(ある大学講師より)
=>[作者]: 連絡ありがとう.この頁は非常に多くの人が読んでおり,超基本の読み物にとなっている可能性があります.そのような使われ方では偏差値を特別な項目を起こして別扱いにするよりも,とりあえず正規分布の表が利用できることに絞り,偏差値は正規分布の一例として扱っています.
■[個別の頁からの質問に対する回答][決定係数とは? について/15.8.18]
○ y と ^yn の値の相関係数Rは =CORREL(実測値yの範囲,予測値 ^yn の範囲)で求められる……
→yと^ynの相関係数は常に正で、Excelではこれを重相関Rと呼んでいるようだが(常に正になる)、CORRELで計算する相関係数は正と負の2通りあり、ここで負になる場合を考慮していないと思うのだが…
=>[作者]: 連絡ありがとう.質問者は,(特殊な場合)であるが(一般の場合)という順序で読んでおられるので,奇妙に見えるだけだと考えられます.これを(一般の場合)であるが(特殊な場合)の順に読まれると普通の話になります.
すなわち,相関係数は(一般に2つのn次元ベクトルのなす角[のcos])を表すので正[同じ向き]の場合も負[逆向き]の場合)もあるが,(特殊な場合として,実測値と予測値はほぼ同じ向きのn次元ベクトルになるので2つのベクトルのなす角[のcos]は正になる)と読むのです.
■神奈川県[Prof.N.Hkさん/15.8.18]
進み具合が正しく表示されません。
=>[作者]: 連絡ありがとう.読者の利用環境(PCか携帯かタブレットか,SafariかChromeかFireFoxかIEか,Cookieサイズ)が複雑に分かれますので,学習の記録が想定通りかどうか作者側で点検するのは難しいです.
■神奈川県[Prof.N.Hkさん/15.8.18]
http://www.geisya.or.jp/~mwm48961/koukou/tyoku14.htmで、二直線y=mx+k, y=m'x+k'がある時、mm'=-1となることの証明をしていますが、その証明(A)の、(1)(2)(3)を代入した後の式が、式の右辺が(m-m'^2) となっていますが、正しくは(m-m')^2ではないでしょうか。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][pならばqの真偽 について/15.8.17]
偽→偽、偽→真はいずれも真であるというのはルールとして覚えるしかないのが悔しい。仮定が真の部分は日常的な真偽の判定と同じで直感的に分かるのだけど・・・。そのあたりをもし理解しやすい説明を持っていれば加えていただきたい。(ラッセルの話はよく分からなかった。)
=>[作者]: 連絡ありがとう.p→qあるいは(仮定)→(結論)の話がどうしても分からない場合,(結論)の真偽だけに囚われていないかどうか,もう一度振り返って見られるとよいでしょう.そのように思い込んでしまうと(仮定)の働きを全く無視していることになります.それはqの真偽を見ているだけということになります.その頁に書いている通り「結論が自分の信念に一致するものは真とされやすく,結論が自分の信念と一致しないときは偽とされやすい」と言われており,結論の真偽に左右され過ぎると分からなくなります.
■群馬県[昭和19年生まれさん/15.8.16]
数III[ 二次曲線 ] 放物線の方程式(7) http://www.geisya.or.jp/~mwm48961/kou3/quadratic_3.htm ■4 自然界にある放物線 問題 (2)焦点 (0 ,−2),準線 x=2からの距離が等しい点の軌跡の方程式を求めよ.準線はy=2と思いますが。
=>[作者]: 連絡ありがとう.問題文の方を訂正しました.
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/15.8.16]
helpが出るのがすごく助かってよかった。こういう風な公式確認のサイトをもっと作っていただきたいです。
=>[作者]: 連絡ありがとう.できるだけそういう問題も作るつもりです.
■福島[黙羊さん/15.8.16]
D=0のときの2次不等式の解き方(まとめ)これはD<0 の間違いではないでしょうか?
=>[作者]: 連絡ありがとう.これとはどれなのか意味が通じません.もしその頁全体を指しているのならば,2次関数のグラフから読み直してください.
■群馬県[昭和19年生まれさん/15.8.16]
ボケ防止に挑戦しています。有難うございます。http://www.geisya.or.jp/~mwm48961/koukou/polar_coord2.htm【例11】r=2sin(θ−π/6) について問題文ではr=2sin(θ−π/6) ですが解答では三角関数の加法定理で展開して展開する式がr=2sin(θ+π/6)になっていますが。
=>[作者]: 連絡ありがとう.問題文の方を訂正しました.
■[個別の頁からの質問に対する回答][極限値,不定形の極限 について/15.8.14]
他の文字は定数とみなします。 という部分なのですが、スマホから閲覧すると極限値の式がお互いに重なって見辛いです。。。採点式の問題が作られていて丁寧なサイトだなあということは感じました。
=>[作者]: 連絡ありがとう.御指摘の箇所をiPhone で点検しましたが,特に問題点は感じませんでした.あなたがお使いのAndroidを筆者は持っていませんので,そちらの見え方は点検できませんでした.
■[個別の頁からの質問に対する回答][転置行列,対称行列,対角行列,三角行列 について/15.8.12]
二次形式で変換するときに、転置行列が逆行列に一致する理由がわかりませんでした。
=>[作者]: 連絡ありがとう.この教材にはそういうことは書いてありませんし,一般にそういうことは言えないと思います.特に,「二次形式で変換する」とはどういうことなのか通じません.概して,質問内容が正確に伝えられるように疑問点を整理できれば,調べるべき項目を絞り込むことができ,多くの問題は解決するでしょう.
この回答が双方向につながることは考えにくく,1回きりでまとめなければならないので,推定で述べますと,
二次形式の性質とは関係なく,例えば「回転を表す1次変換」は
で表され,その転置行列
は逆行列
と一致しますが,これは回転を表す1次変換の性質です.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/15.8.11]
yにマイナスがある場合どの数字にマイナスをつければよいかわからない時があります。マイナスを付ける数字の判断方法はありますか?
=>[作者]: 連絡ありがとう.質問の意味が分かりませんので,具体例を示してください.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(同次) について/15.8.11]
問題(2)の y”−4y’+5y=0 のだが解の公式によりr=2±2iが間違っているr=2±i=>[作者]: 連絡ありがとう.訂正しました
■神奈川[Prof.N.Hkさん/15.8.8]
http://www.geisya.or.jp/~mwm48961/koukou/bunten03.htmの(2)で、分子に"-"を入れるように注釈をつけたほうがよいと思います。一度分母に"-"を入れて×になったので…
あと、「個別のページからの質問」とありますが、そこに入る方法を教えてください。PC版です。
=>[作者]: 連絡ありがとう.(前半)お読みになって気付かれなかったかもしれませんが,問題文に「また、負の分数の符号は分子に付けるものとします.」と書いてあるのはその意味です.
■[個別の頁からの質問に対する回答][行列の積 ABの定義 について/15.8.9]
参考になります。
採点後のgifがよく見えません。
Macで Safari, Chrome, Firefoxのいずれでも
行列の積の意味がよくわからないので追記頂けるとありがたいです。
何を表すんでしょうか?
=>[作者]: 連絡ありがとう.(前半について)1題でも正解すれば良く見えるはずです.この質問があるのは,全部間違った場合だけです.
(後半について)たとえば,ベクトルや行列は何を表すのか,ベクトルの内積,行列の内積は何を表すのかという質問に対して,これが答ですというと分かりやすくはなりますが,単なる例であって本来問われている内容にに対して正確に答えたことにはならないでしょう.なぜなら,数学の定義は,ある性質をもったものをこのように書くと言った約束事なので,日常生活における「このこと」を表していますというような対応関係にはないからです.
たとえば,筆者は高校生の時,ベクトルは矢印に対応していて,ベクトルの内積は仕事量(エネルギー)に対応するといった説明がとても気に入っていましたが,今日の生徒向けにはそのような説明では合わない,むしろ表計算で列の表題がベクトルの名前で,列のデータがベクトルの成分,2つの列の成分の積の和(SumProduct)がベクトルの内積だといったほうが,社会生活での通常の使用法に合うと考えています.
行列の積については,「例えば」次のような場合が積に対応するでしょう.
(1) 行列自体がデータを表している場合
パン ジュース おにぎり
A店 10 5 7
B店 5 8 10
C店 8 10 5
D店 6 15 5
価格 重さ
パン 100 50
ジュース 80 100
おにぎり 120 150
価格 重さ
A店 2240 2050
B店 2340 2550
C店 2200 2150
D店 2400 2550
(行の表題,列の表題を除いて:以下同様)左の行列がA店~D店のパン,ジュース,おにぎりが売れた個数とする.次の行列はパン,ジュース,おにぎりの1個当たり価格と重さとする.このとき,これら2つのを行列の積の定義に従って求めたものは右側の行列になり,パン,ジュース,おにぎりの総価格と総重量になります.(行列の積の従った掛け方:例えばパンの個数にパンの価格を掛けることには意味がありますが,パンの個数にジュースの価格を掛けてもうれしくない)
(2) 行列が変換(演算子)を表している場合
は原点の周りの角αの回転を表し,
は原点の周りの角βの回転を表す.
このとき
において行列の積
は原点の周りに角α回転してから角β回転する変換を表し,各成分を三角関数の加法定理で計算すると
に等しくなるから,1回でα+βだけ回転したのと同じになる.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/15.8.6]
高3でとても数学が苦手な者です。
特に三角関数が壊滅的で公式を何度も覚えようとしましたが覚えられず困っていました。
ですが、この頁を見て自分でも紙に書きながら勉強をしたら(理解力が壊滅的で時間は多少かかりましたが…笑)、覚えることができました。
私でも理解できたことに驚いています。
問題もついていてとても充実した頁でした。
ありがとうございました!
=>[作者]: 連絡ありがとう.長年教えてきた流儀をweb教材にしたものです.気に入ってもらえてうれしいです.関連のないものを無理やり覚えるとすぐ忘れるので,関連を付けて作り方を再現していくというところがミソかな.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/15.8.3]
例2はr=4ではなくてr=2だと思う。
=>[作者]: 連絡ありがとう.訂正しました
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/15.8.3]
例6の解答の下から2行目の式で、
y=-の次に3が抜けているのではないかと思います。
=>[作者]: 連絡ありがとう.訂正しました
■[個別の頁からの質問に対する回答][二重根号 について/15.8.2]
一か所だけ、答えが入らない(記入できない)箇所がありました。
=>[作者]: 連絡ありがとう.自分で言うのもおかしな話ですが,かなり複雑なプログラムなので,場所を特定して頂かないと再現困難です.なお,各頁では毎回同じ問題が表示されているのではなく,見る人によって異なる問題が表示されています.
■熊本県[Yuuさん/15.8.2]
http://www.geisya.or.jp/~mwm48961/kou3/mobile/differ_eq3_m.htm
このページの、問題7の、答えのy2の係数の2というのはどこから来てるのでしょうか?
-1の間違いですか?
それともどこからかもってきたのでしょうか?
よろしくお願いします。
=>[作者]: 連絡ありがとう.2が不要でしたので訂正しました.
なお,wxMaximaで解くには,ode2('diff('diff(y,x),x)-3*'diff(y,x)+2*y=4*x-%e^x*cos(x), y, x); とすることにより
が得られ,特殊解+一般解の形が得られます.
■熊本県[Yuuさん/15.8.2]
http://www.geisya.or.jp/~mwm48961/electro/dif_eq_bernoulli.htm
問題一
答は4のはずなのに、2を押すと◯で、4を押すと×になる
=>[作者]: 連絡ありがとう.訂正しました.
なお,wxMaximaで解くには,ode2('diff(y,x)+2*y=%e^x*y^3, y, x); とすることにより
が得られ,この式を変形すると解の式になります.
■[個別の頁からの質問に対する回答][三角方程式 について/15.8.1]
cosA=-√3/2の答が間違っていませんか
=>[作者]: 連絡ありがとう.特にあやしい点はありません.
■東京と[ Jさん/15.8.2]
http://www.geisya.or.jp/~mwm48961/kou3/trigonometric24.htm
このページの加法定理の式が間違っています。
【例題1】の下辺りで
cosθcosα+sinθsinα=cos(θ+α)
とありますが、
cosθcosα-sinθsinα=cos(θ+α)
だと思います。
=>[作者]: 連絡ありがとう.訂正しました.
■熊本県[Yuuさん/15.8.2]
http://www.geisya.or.jp/~mwm48961/electro/dif_eq_bernoulli.htm
このページ例題2番の部分積分分解の展開が間違い。
答えのsinの係数として2がでてくるはず。
=>[作者]: 連絡ありがとう.訂正しました.
なお,wxMaximaで解くには,ode2('diff(y,x)-y/2/x=y^3*sin(x),y,x); とすることにより
が得られ,あなたの答が合っていることが分かります.
■[個別の頁からの質問に対する回答][いろいろな因数分解 について/15.7.31]
(a-b+c)(a+b+c)の解説が、?マークを押しても出てきません。
=>[作者]: 連絡ありがとう.その頁は「因数分解」の頁です.展開式からスタートして因数分解した式を答えることを想定しています.プログラム上,逆順に答えても対応していれば正解にしていますが,それは「展開」の問題として答えていることになります.その頁のHELP(?で示されるもの)は展開式から因数分解した式を求める方法を述べています.因数分解した式に対する解説ではありません.(こちらの方は気長に展開していけばいずれできるはずです)
■[個別の頁からの質問に対する回答][媒介変数表示 について/15.7.31]
ボクが高校2年生のとき、33年前になりますが数学は成績が悪かったが、とても面白く数学を教えてくれた先生だったので数学がとても好きになりました。おかげで数学をそれ以来嫌いにならずに、幼稚園正のとき以来の夢だったエレクトロニクスの世界で今でも生きています。高校のときに学んだサイクロイドやトコロイドは今でも非常に興味深くこのサイトに行き当たってとてもラッキーでした。大変感謝しております。
=>[作者]: 連絡ありがとう.ロマンとかモティベーションといわれるものは非常に重要だと思う.特に,若い時代のロマンは,一生追い続けるものの原形になっているかもしれません.
■[個別の頁からの質問に対する回答][確率の基本 について/15.7.31]
38人の中で同じ誕生日がいる確率。少なくとも1組はいるものとする。こたえは何になりますか?
=>[作者]: 連絡ありがとう.(1) 各自のレポート課題など,この教材にない問題を尋ねていますので回答しません.(2) 問題が間違っています=問題が正しく書けたら,ほとんど解決したのと同じようなものです.「少なくとも1組はいるものとする」のに「同じ誕生日がいる確率」を問うことは無意味です.また,日が同じでよいのか月日が同じでなければないのか指定されていません.月日の一致まで要求するのなら,1年を356日とするのか366日とするのか指定すべきです.こういう問題は,確率を面白く教える本やweb記事に出ていますが,分母分子が巨大な桁数になるため,基本で分からなくなっている人に,計算を要求することは無理です.
■[個別の頁からの質問に対する回答][逆三角関数 について/15.7.30]
tan(arcsin1/3)の問題で、sinx=1/3,cosx=2√2/3 ですが、sinx/cosx =2/2√2 となるのは何故ですか? 普通に計算すると1/2√2になると思います。
=>[作者]: 連絡ありがとう.途中経過の分子を訂正しました.なお,wxMaximaで検算するにはtan(asin(1/3));により,直ちに結果が得られます.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/15.7.30]
問題4のHELPの中、解説はあってますが番号だけが間違ってます
正誤判定は間違ってないので、番号だけ4→1でいいかと思います
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][maximaの初歩的な操作 について/15.7.29]
いつもお世話になっております。
RやMaximaのページも大変に貴重な情報で助かりますが、次のページに進んだり、全体を俯瞰するのが難しいです。特に、「メニューに戻る」すると、トップページの先頭に戻ってしまうため、下の方にあるカテゴリにアクセスするのが難しいです。googleなど検索ページから個別のページにたどり着いた時はカテゴリを探すのができないかもしれません。
一つの目次ページから全てのページがぶら下がる形ではなくて、いくつかのカテゴリはサブ目次ページを作ってはいかがでしょうか。例えば、Maxima、R,Javascript、大学レベルのカテゴリはそれぞれ別のWebページを作って、その中に項目を立てたほうが良いように思います。
よろしくご検討下さい。
=>[作者]: 連絡ありがとう.各頁からメニュー頁に戻る場合を考えた場合,御要望のような構成にすると全体像が理解し易いこともありますが,作者としては,他のジャンルのそういうメニュー頁でいつも困っているので,サブメニューはなるべく作らないと決めています.具体的には,ある項目はどのサブメニューにあるのかという判断を間違った場合には,どんなに探しても該当項目はないことになります.中学以上の数学というような広い範囲を扱う場合に,該当項目がどのサブメニューに含まれるかが正確に言えるのは,すでにそこそこ分かっている人だけです.例えば,3次方程式の解き方が,中学以上のどの科目に入るか,それともこの教材の中にはないのか,それが分からないからWebで検索している人に,前もって分かっていないければだめだといっても話が始まりません.このようにして,メニュー頁には「可能な限り細目の一覧」が見えるようにするほうが,利用者から見れば有利です.当教材はこの考え方で構成しています.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/15.7.25]
tanの半角の公式のところnが多いと思います。
とてもわかりやすかったです!
=>[作者]: 連絡ありがとう.表題のtan がローマ字漢字入力方式のnnの癖を引きずってましたので訂正しました.
■静岡[やまださん/15.7.23]
このサイトは、筆者様の善意で管理されてるのですか?だとしたらとてもありがたいです。いつも活用しています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][組合せ(文章題) について/15.7.20]
http://www.geisya.or.jp/~mwm48961/kou2/mobile/s1combi3_m.htm の問題8の答えが、問題9の答えになっていて、8.9どちらを解いても、問題9のマルバツが表示されます。
=>[作者]: 連絡ありがとう.失礼しました.携帯版に移し替えるときに,プログラムミスがありましたので,訂正しました.
■[個別の頁からの質問に対する回答][複素数平面 について/15.7.19]
全て分かりやすい!いつもお世話になっております
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][負の指数 について/15.7.18]
問題の答え部分が多くあるのが良かったです 間違い易いところが要点でしっかり説明してあった
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][条件付き確率 について/15.7.18]
説明がわかりやすくてよかったです。問題があっててもhelpが見れるともっといい!
=>[作者]: 連絡ありがとう.正解の場合に解説を示すかどうかについては,否定的な回答が多かったので,現在は間違ったときだけ表示していますが,この頁については「見たい」という要望があったということで検討します.
■[個別の頁からの質問に対する回答][全微分方程式 について/15.7.17]
とてもわかりやすかったです。ちょうど今回の試験範囲と一緒で大変助かりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][正規分布 について/15.07.17]
(6)の数学偏差値 50 + 0.867×10 ではなく 50 + 0.867 x 15ではありませんか? (7) 上位から20%すなわち, p(u) = 0.3 ではなく p(u) =0.2ではありませんか?
=>[作者]: 連絡ありがとう.(6)について数学:得点x=75,m'=65,σ'=15,z=0.867⇒75=m'+zσ'数学:m=50,σ=10,z=0.867⇒偏差値s=m+zσ-50+0.867×10=58.67
■[個別の頁からの質問に対する回答][母平均の推定・信頼区間 について/15.07.17]
問題3の(解答)信頼区間の幅の式が間違っていませんか?
2.0ではなく1.0だと思うのですけれど。
=>[作者]: 連絡ありがとう.右辺がタイプミスでしたので訂正しました.
■[個別の頁からの質問に対する回答][2次関数のグラフと直線(文字係数) について/15.07.16]
2.3.7.8
の問題で、
b~2-ac
となっているのがわかりません。
b~2-4ac
の間違いではないでしょうか?
=>[作者]: 連絡ありがとう.b が偶数のとき,すなわちb=2b' のとき,D=b2 −4ac=4b'2 −4ac=4(b'2 −ac) となるので,判別式の符号はD'=b'2 −ac で調べられます.
■[個別の頁からの質問に対する回答][確率の基本 について/15.07.16]
確率の基本 問題5.2の答え、あるいは問題は間違っていませんか?
解説は、AとBが隣り合わない確立になっていないでしょうか。
=>[作者]: 連絡ありがとう.特におかしいところはありません.もし,隣り合わない確率を求めているのなら 5.1 の結果から 3/5 になるはずです.
■[個別の頁からの質問に対する回答][二次関数の移動 について/15.07.16]
正解にたどり着くまで答えはわかんないですか?
解説とか答えとか出てこないんですか?
問題とか説明は凄くいいんですけど答えがわからないと…
あと、たぶん、合ってるのに-が認識されなくて不正解になってるのではないかと思いました。、
=>[作者]: 連絡ありがとう.10年ほど前に作ったときは,上の解説を読めばわかるはずだと思いましたが,今は,ネットで調べる人は「分からないから調べている場合が多い」と考えていますので,要望通りHELPを追加しました.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/15.07.12]
間隔尺度と比率尺度の違い(間隔尺度は和差はできるが、積商ができない)が分からない。2つの違いに具体的な例はないか。
=>[作者]: 連絡ありがとう.筆者は,統計の分野をあまり得意としていないので,この教材は読者のモティベーションを高めて,専門書に向けるワンステップぐらいのものです.だから,筆者と読者の距離は,学者と生徒の関係ほど絶対的に離れておらず,一緒に勉強しようぐらいの距離です.このことを前提に,幾つか補足を述べます.
例えば,
(1) ある政策に対する意識調査において100人にアンケート調査した結果が次の表のようになったとする.
反対 どちらかと言えば反対 どちらとも言えない どちらかと言えば賛成 賛成
20 30 25 15 10
このような調査の結果をまとめるとき,新聞報道では『「反対」「どちらかと言えば反対」と回答した人の数は50%で,「賛成」「どちらかと言えば賛成」と回答した人25%の2倍ありました』などと,名義尺度であることを意識した記述になり,「反対+どちらかと言えば反対」及び「賛成+どちらかと言えば賛成」はあくまでカテゴリーの併合として扱われています.このように扱う限り,
名義尺度 として無理なく処理されていると考えられます.
(2) 日本の高等学校から生徒の成績を調査書として大学に送付するとき,成績は5段階で表されますが,例えば100人の生徒の数学Ⅰの成績の分布が次の表のようになったとします.
この成績において,評価4の生徒は評価1,2,3の生徒よりも学力が高いとは言えますが(
順序尺度 にはなっていますが),評価4の生徒は評価2の生徒の2倍できるということは表しておらず,評価1の生徒の4倍できるとも言えません.だらか,
比例尺度 としては使えません.
しかし,推薦入試の基準として評定平均値(各教科ごとの科目の平均[数学Ⅰ,A,Ⅱ,B,Ⅲなら5科目の平均]の全教科の平均)が3.5以上というように使うことがあり,足し算の処理は行っていることになります.(平均として教科・科目数で割ることが気になるなら,総和で考えればよいでしょう)
(3) ある新製品の食品を現在の食品と比較したときの印象を100人の客にモニター調査した結果が次の表のようになったとします.
非常に悪い 悪い どちらとも言えない よい 非常によい
20 30 25 15 10
この結果においても,正確に言えばこの尺度は「非常に悪い<悪い<どちらとも言えない<よい<非常によい」という
順序尺度 の条件は満たしていますが,この水準が等間隔であるかどうかは疑問があります.しかし,多くの新製品のうちでどれを採用するかと時間との闘いの中に置かれているときに,『「非常に悪い」「悪い」回答した人の数は50%で,「よい」「非常によい」と回答した人25%の2倍ありました』などと,まどろっこしく正確に記述しているようでは,ライバル店との競争に負けてしまうので,「とりあえず便宜的に」次のように点数化して平均得点の高いものを採用しようというのは自然な流れになります.
(*2) 非常に悪い:-2悪い:-1 どちらとも言えない:0 よい:1 非常によい:2
20 30 25 15 10
このようにして,幾つかの新製品の得点平均値を比較して -0.5, -0.3, 0.2, 0.7, 1.2 などとなれば,1.2のものを採用することになります.「とりあえず便宜的に」でもこのようにしないと企画会議として客観的なデータを示せない.
また,分散(平均との差の2乗の平均)が大きいものは,好きな人は好きで,嫌いな人は嫌いと好き嫌いが分かれるものだから,性別,年齢別,季節別など,さらに条件を絞って分析しないと危ういと言える.こうなると2乗して平均しているのだから,もとの数値が比例尺度の条件を満たしていなければ言えもしない結論を述べていることになりますが,「とりあえず便宜的に」評価が分かれるものは取り扱い注意だという意味なら,目安としては使い方を間違っていないと考えられる.
(*1)(*2) は同じ分布に対して「とりあえず便宜的に」間隔尺度の数値を割り当てたものですが,(*1)の平均値は(*2)の平均値 +3.0となっており,(*1)の分散は(*2)の分散と同じになります.この場合でも,「非常によい」という印象は「よい」という印象の2倍のよさを表していないことは当然のことです.
■[個別の頁からの質問に対する回答][重積分...積分領域が変数に依存する場合 について/15.07.12]
重積分問4について、最後の定積分の答えが9/4ではないと思います。私は19/12になりまたがいかがでしょうか?
=>[作者]: 連絡ありがとう.たぶん,あなたの側のちょっとした計算ミスだと思います.
参考までに,
wxMaxima (←この頁にインストール方法を書いています)を使って検算するには,wxMaximaを起動してから,はじめにEnterキーを押し,
integrate(integrate(x,y,x^2,x+2),x,-1,2);
と書き込んでから,Shift+Enterを押します.これにより,9/4が得られます.
■[個別の頁からの質問に対する回答][2次関数の最大値・最小値 について/15.07.12]
問題が簡単すぎます。
=>[作者]: 連絡ありがとう.あなたがこの日見た頁は,メニューも含めて11頁で中学校の問題も含む基本問題ばかりです.だから簡単な問題ばかりであるのは,簡単な頁ばかりを選んだからです.
■[個別の頁からの質問に対する回答][リッカチ形微分方程式 について/15.7.9]
院試勉強としてリッカチ形の問題を解きたいと思って検索したらこのページに辿り着きました。
一目見て勉強しやすそうな体裁だと思え、解答も理解しやすかったので感謝しています。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][階乗 について/15.7.9]
勉強になりました!
意外に大人で初めて(習ったのか聞いてないのかも不明)なことも多いので、すごく助かります!(^ ^)
=>[作者]: 連絡ありがとう.
■神奈川県[Prof.N.Hkさん/15.7.9]
http://www.geisya.or.jp/~mwm48961/kou3/bunsuushiki2.htmの[よくある間違い1]の整理の2回目で、分母が(x+2)(x+4)から(x+3)(x+4)になっているのは誤りでしょうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/15.07.02]
テストの時などは、答えが出たら形を整理しなければいけないんですか?
=>[作者]: 連絡ありがとう.同類項の係数は整理してまとめてなければなりませんが,そこから先,きれいに整理「降べきの順」「サイクリックな順」などに直すべきかどうか
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/15.07.01]
固有方程式を解くとき、「はきだし法を用いて解くと、上手くいく」と習いましたが、上手なやり方がわかりません。なにか良い方法はないでしょうか。また、基本変形をする際、やってはいけないことはなんでしょうか。
=>[作者]: 連絡ありがとう.固有方程式を掃き出し法で解くには,文字を含む係数のままなので,掃き出し法が自由自在に操れるくらいに上達していないと・・・また,連立方程式を解くときは,行基本変形だけでやることが重要で,列基本変形を混ぜてしまうと,変数x,yなどの値が入れ替わってしまいます.
■[個別の頁からの質問に対する回答][商,分数関数の微分 について/15.06.30]
こぶいたい、いたいこぶがみえにくいくらいで、あとはとてもわかりやすいです。いつもありがとうございます。
=>[作者]: 連絡ありがとう.こぶの図を少し大きくしました.
■[個別の頁からの質問に対する回答][(例題対比)放物線の頂点の座標 について/15.06.30]
高校時代つまずいた経験があるため、それが今、解いてみてクリアできたので高い評価にさせていただきました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][ベクトルの内積 について/15.06.30]
ベクトルの内積 の所の 例 の 図1のaIはIaIの間違えではないですか?
=>[作者]: 連絡ありがとう.行の折り返しの区切りがずれていましたので訂正しました.
■[個別の頁からの質問に対する回答][マクローリン展開 について/15.06.28]
すぐ答え合わせができてすごく勉強になりました!ありがとうございます。
Googleで検索してたまたまこのページに入ったので、そういうときに、教材全体がどんなものかという情報へのリンクがあるといいのではと思いました。
=>[作者]: 連絡ありがとう.教材全体の情報は,「メニューに戻る」というリンクをたどっていただいてメニュー項目一覧表を見ていただくのが最短かと考えられます.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/15.06.28]
http://www.geisya.or.jp/~mwm48961/electro/graph_3eq_1.htm
例題4が計算間違っているように思いますがいかがでしょうか?
導関数を出すあたりからずれていってるようです。
=>[作者]: 連絡ありがとう.問題文で −3x2 の3が不要でしたので訂正しました.
■[個別の頁からの質問に対する回答][重積分 について/15.06.24]
問2,3,5は、選択肢4が2つあります。「簡単な重積分の計算」でも、問2,3で選択肢4が2つあります。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][sinθ+cosθ について/15.06.24]
本当に何も分からない人が見ても出来るかが不安。
質問出来ないのだから小学生に教えるくらいわかり易くした方がいいと思った。
○○だから××だとわからない人もいると思う。
「○○と△△は等しいから代入して××になる」くらい優しい方がいい。
=>[作者]: 連絡ありがとう.申し訳ないのですが,あなたは発展学習のマークのついているその頁だけを読んでおり,基本の頁を読んだ形跡がありません.「本当に何も分からない人」に1つの頁で一から全部説明することは無理です.
■[個別の頁からの質問に対する回答][対数の計算 について/15.06.19]
電子計算機で多きな桁数のかけ算、割り算などができます。、、、誤字「大きな桁数」
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][組合せ について/15.06.18]
本当に分からなかったので
助かりました!!
ありがとうございます!!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.06.17]
(1) n=3で同じものが3個ある場合
順列
1
円順列
1
じゅず順列
1
(2) n=3で同じものが2個ある場合
順列
3!÷2!=3
円順列
1
じゅず順列
1
(3) n=3で全部異なる(同じものがない)場合
順列
3!=6
円順列
6÷3=2
じゅず順列
2÷2=1
数珠順列の場合、奇数個且つ左右対称のパターンがある場合単に2で割ってはいけないという問題も載せるべきではないでしょうか。
=>[作者]: 連絡ありがとう.公式まる暗記ではなく,深く考えていると思います.ただ,この話に踏み込むとかなり複雑になります.
結論から言うと,あなたが質問しておられる例は「偶数・奇数」違いではなく「同じものがある場合」の取り扱いになり,同じものがある場合の,「順列」「円順列」「じゅず順列」の対応関係はかなり複雑で個別に判断せざるをえません.もっと根本的には,円順列の公式 (n−1)! は,すべて異なるものがn個ある場合を前提としていますので,同じものがある場合には使えません.
--次の例は,青字は(円順列)=(順列)÷nや(じゅず順列)=(円順列)÷2が成り立つ場合,赤字はこれらが成り立たない場合--
次の例で,(6)は合計で円順列が3,じゅず順列が2になります.(7)は合計で円順列が2,じゅず順列が2になります.
このようにして,同じものがある場合にはパターンごとに順列から円順列を作る規則,円順列からじゅず順列を作る規則が変わることになり,結局,
順列÷n=円順列,円順列÷2=じゅず順列となるのは,黄色の背景色で示した「全部異なる場合」だけになるということが分かってもらえばOKです.
※(順列)で示したのは,対応する順列とは何かということを言葉では言いにくいもの
(4) n=4で同じものが4個ある場合
(順列)
1
円順列
1
じゅず順列
1
(5) n=4で同じものが3個ある場合
(順列)
4!÷3!=4
円順列
1
じゅず順列
1
(6) n=4で同じ色2個が隣り合っている場合--1--
(順列)
3!=6
円順列
2
じゅず順列
1
n=4で同じ色2個が向かい合っている場合--2--
(順列)
6
円順列
1
じゅず順列
1
(7) n=4で同じものが2個ずつ隣り合っている場合--1--
(順列)
2
円順列
1
じゅず順列
1
n=4で同じものが2個ずつ向かい合っている場合--2--
(順列)
2
円順列
1
じゅず順列
1
(8) n=4で全部異なる(同じものがない)場合
順列
4!=24
円順列
24÷4=6
じゅず順列
6÷2=3
■[個別の頁からの質問に対する回答][絶対値記号付の不等式 について/15.06.17]
学校での授業とは違い、自分のペースで進められるし、説明がわかりやすいです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][3次関数のグラフ・ について/15.06.16]
3重解の注意書きのホームの例は分かりやすかったのですが、「単にx軸と交わっているのとは違います.」とはどう違うのかがいまいちピンときませんでした。
=>[作者]: 連絡ありがとう.どこまで通じたのか微妙です.「単にx軸と交わっている」場合は「接していない=横切っているだけ」という違いがあります--レールの例でいえば,直進できない.
■神奈川[Prof.N.Hkさん/15.6.18]
http://www.geisya.or.jp/~mwm48961/kou2/s1combi4.htm、順路の問題3で、答は10!/(6!4!)-6!/(3!3!)より、190通りではないですか?
数Aはまだ完全に学習できていないので何とも言えませんが…
=>[作者]: 連絡ありがとう.
この頁(携帯版) には解説をつけています.なぜか携帯版へのリンクをつけ忘れていましたので,PCでご覧になると自動転送はされなかったようです.
計算の仕方として,総数10!/(6!4!)=210通りは合っていますが,Pを通る順路の数え方は「A→P間が6!/(3!3!)=20通り,その各々についてP→B間が4!/(3!1!)=4通りだから,80通り」となります.したがって,Pを通る順路を引くと130通りが答になります.
■[個別の頁からの質問に対する回答][隣り合う並び方・隣り合わない並び方 について/15.06.13]
練習問題たくさんあってとても良かったです。ありがとうございました。
ただ、8番のhelpの最後のほうで4!-5×4×6となっていたのですが、4!×5×4×6ではないでしょうか、私の見間違いでしたらすみません
=>[作者]: 連絡ありがとう.間違いですので訂正しました.--少しだけ言い訳:ホームページ上で,−や×のような記号は,&と;ではさんだ特殊な書き方として,−,×のように書くところが,上の文章に引きずられて混ざってしまったようです.
■[個別の頁からの質問に対する回答][(例題対比)2次関数のグラフ[標準形] について/15.06.12]
今まであまり二次関数がよくわかってなかったけど、自分で解く問題とかあって、すごくわかりやすかったです‼︎
これで、授業にもついていけそうです!本当にありがとうございました*\(^o^)/*
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][展開公式1(例題→選択問題) について/15.06.10]
[IX]のこじつけの覚え方がクスッとできて、なかなか良いところ
=>[作者]: 連絡ありがとう.少しでも記憶に残るようなワンポイント・コピーが思いつけばと・・・それなりに苦労が・・・
■群馬県[昭和19年生まれさん/15.6.9]
3項間漸化式の一般項のpageで
http://www.geisya.or.jp/~mwm48961/electro/recurr_series3_m.htm
で上の欄の
基本 初歩 要点 重解形 無理数虚数形 例と答 テスト
の「例と答」のpageの
(7)の模範解答です。
=>[作者]: 連絡ありがとう.an が飛んでいましたので追加しました.
■群馬県[昭和19年生まれさん/15.6.9]
http://www.geisya.or.jp/~mwm48961/electro/recurr_series3_m.htm
(2’)のA(n+1)=1/2+1/2^n-1ではなく
A(n+1)=1/2*A(n)+1/2^n-1
と思いますが。
=>[作者]: 連絡ありがとう.ご質問の頁は7つのサブ頁に分かれています.(2')はほぼどの頁にもありますがA(n+1)=1/2+1/2^n-1という式がどこにあるのか見つかりませんが?
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/15.06.09]
簡潔に分かりやすくまとめられていて、今までよく理解できていなかったところもスッキリしました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][相加平均・相乗平均 について/15.06.09]
根号内の数に根号が重なってることがある。根号内が分数だと、分子の真ん中にちょうど根号が重なって見にくい
=>[作者]: 連絡ありがとう.その頁はまだモバイル対応になっていません.数学,英語×中学,高校の4種類の教材を順次モバイル対応にしていますので,しばらく(数か月)お待ちください.
■[個別の頁からの質問に対する回答][マクローリン展開 について/15.06.08]
マクローリン展開が苦手な自分にとってちょうどいい問題でした。こういった基礎的問題は、苦手意識の克服と自信の養成に有効だと思います。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/15.06.08]
リッカート尺度が本当に間隔尺度と言えるのでしょうか?
=>[作者]: 連絡ありがとう.そのように疑問を持っていただけると教材としてそこそこねらいが達成できたことになります.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.06.07]
とてもいい問題ばかりです。試験前にいい勉強になりました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][連立方程式の解き方 について/15.06.04]
元芸者が大学受験のために活用してます。ありがとうございます。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][最大公約数,最小公倍数,ユークリッドの互除法 について/15.06.04]
問題3に誤りあり
45→54?
=>[作者]: 連絡ありがとう.問題文のタイプミスがありましたので訂正しました.
■??[??卒業生さん/15.6.02]
.....この通信欄で連絡が取れるのか、半信半疑ですが送ってみます。..........
=>[作者]: 連絡ありがとう.メールアドレスがないと返信はできません.
■[個別の頁からの質問に対する回答][平方根の計算・・・センター試験問題 について/15.05.30]
センター試験2010年度の問題のアに√がついていますが√なしが正しいと思うのですが…
=>[作者]: 連絡ありがとう.間違っていましたので訂正しました
■京都[亀さん/15.5.29]
初めまして。亀と申します。
複素数平面上で軌跡を求める問題の式変形の方法を参考にさせていただいたのですが、
一か所疑問に思う場所があります。
軌跡の方程式
http://www.geisya.or.jp/~mwm48961/koukou/complex_trace1.htm
こちらのページでアポロニウスの円について以下のように書かれてありました。
|z-α|=k|z-β|を満たす点P(z)の軌跡は,
「A(α), B(β)を1:kに内分する点と
1:kに外分する点を直径の両端とする円」になる.
しかし、点Pと点Bの距離のk倍が点Pと点Aの距離と与式から読み取れるので
「A(α), B(β)を1:kに内分(外分)…」ではなく、
「A(α), B(β)をk:1に内分(外分)…」が正しいのではないでしょうか。
=>[作者]: 連絡ありがとう.αとβが逆でしたので訂正しました.(ん?近所の人)
■[個別の頁からの質問に対する回答][順路の問題 について/15.05.28]
検問のp q r の位置が、どうしてその場所になるかがわからない。
=>[作者]: 連絡ありがとう.問題番号が書いてありませんが≪9≫の問題とします.
質問者は「いろいろと試行錯誤して失敗してみる」という余裕がないように見えます.問題のパターンは数多くあるので,個別の問題の解き方を「無駄なく覚える」のは無理ですから,一見無駄に見えることをいろいろと試してみることが重要です.
その問題の解説にあるように「もれなく」「重複なく」数えるにはどうすればよいのか,いろいろと失敗してみると分かることがあるので,この規則性を問題に出会った現場で見つけるのです.
ある地点Xを通る道順をn(X)で表すと,n(P)+n(Q)+n(R)が答になるというのがこの問題の結論ですが,他の場所に検問を作ってみると次のようになります.
(*1) P,M,V,Yのように縦に検問を並べると,PもMも通る方法,MもVも通る方法,PもMもVも通る方法などが重複していますので,n(P)+n(M)+n(V)+n(Y)とすると「重複があります」・・1つの道を何回も数えたら実際よりも多く数えてしまうことになります.
(*2) P,H,I,Jのように横に検問を並べても,D,P,L,Tのように右上がりに検問を並べても同様です.D,P,L,Tの検問は,すべての道順をとらえることができないという欠陥もあります(例えば,A→Z→H→J→Bを「もらしてしまう」・・・Aにネズミの家があって,Bに餌があるときにD,P,L,Tのように検問を作っているようでは,だだもれになります).
(*3) P-Q-Rによく似た右下がりに並べた検問で,P-Nという2つの検問を作った場合には,例えば,A→Z→H→J→Bという道順を「もらしてしまう」・・・ネズミが逃げる=実際よりも少なく数えてしまいます.
このようにして,いろいろと試行錯誤しながら,A地点からB地点に行く道順を「もれなく」「重複なく」数えるにはP,Q,Rのように検問を「右下がりに,すきまなく」配置しなければならないことが分かります.
もちろん,(#1) E-J ,(#2) D-I-S , (#3) C-H-N, (#4 )G-H-W-O などでも「もれなく」「重複なく」数えるという条件は満たしていますが,(#1)ではA-D間の道順を計算しようとすると左上に欠けた領域があって計算が複雑になります.(#2)でも同様です.(#3) C-H-Nで計算する計算量は,P-Q-Rとほぼ同じで,この方法なら試験中でも間に合うでしょう.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/15.05.27]
わかりやすい
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/15.05.27]
例2(2)(ⅰ)でx1はどんな実数でも成り立つのに,なぜt≠0なのでしょうか?0を含まない理由の説明を追記していただきたいです.よろしくお願いいたします.
=>[作者]: 連絡ありがとう.固有値と固有ベクトルの定義を復習しますと
与えられた正方行列
A に対して,
が成り立つときに
を固有ベクトル,
を固有値と定義しますので,固有値は0となることがありますが,固有ベクトルはその定義からして零ベクトルとなることはありません.(
を受け入れてしまうと,どんなAについてもどんなλについてもこの式の両辺は零ベクトルになり等号が成り立ちます.そうすると何も固有ではなくなる)
例2(2)(ⅰ)において,
は
のとき
となりますので,固有ベクトルの定義にあてはまりません.したがって,
です.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/15.05.26]
非同次方程式を失敗を許して求める方法はすばらしい。一般の本なんかの無駄な公式を暗記するやりかたから脱却できたのは大きい。(ただなんで3のx^2までの試行で必ず解けるのかがよく分からない。)
=>[作者]: 連絡ありがとう.x^2までの試行で必ず解ける理由を検証しようとすると一層コテコテになってしまうようです.今のところ,読者に負担をかけずに「簡単に検証する」方法を思いつきませんが.
■[個別の頁からの質問に対する回答][分散分析 について/15.05.26]
学習して理解した後であれば十分納得できるのだが、はじめてみたときには2箇所掲載されている「全体+行+列+誤差の図」は何を伝えたいのかまったく分からない。
「4種類の苗を3箇所に植えて成長」云々の例を文字でかいているのだから、その例に沿って各観測値の内訳を視認できるような図にしてもらえると理解の手助けになると思う。
=>[作者]: 連絡ありがとう.言葉だけで伝えるのはなかなか難しく,イラストと併用して理解しやすくするというのが筆者の考え方です.「個々の値を(全体の平均)+(列の効果)+(行の効果)+(誤差)に分けて考える.」書いていますが,扱っている内容自体がそこそこ複雑なものなので,このイラストと文章が結びつくかどうかは読者との相性にもよるかもしれません.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/15.05.26]
間隔尺度の説明にある「和差には意味があるが比率には意味がない.」の部分、実例を示してもらえると理解が容易になると思う。日常の感覚では摂氏の温度も身長体重も同じ計算可能な数字のような扱いをしていて、ともすれば気温20度は10度の2倍熱いような感覚を抱いているので。
=>[作者]: 連絡ありがとう.この話題は最近
この質問 でそこそこ解答しましたが,ストンと納得するかどうかはピッタリの例を示せるかどうかで決まるようです.
客の満足度(B:「非常によい:5,よい:4,普通:3,悪い:2,非常に悪い:1」)の例でアンケート結果をまとめた場合と,(C:「非常によい:2,よい:1,普通:0,悪い:−1,非常に悪い:−2」)でまとめた場合を比較すると,明らかに「分散は一致します」「Bの平均値はCの平均値 +3 」になります.(差には意味がある)
しかし,いずれも比例尺度ではないので,Bで「よい」は「悪い」の2倍の好感度を表す訳ではなく,Cで「非常によい」は「よい」の2倍の好感度を表すとは限りません.このように間隔尺度で測定されたものは,差には意味がありますが比率には意味がありません.
質問者は,特に摂氏に関心を持っておられるようですので,温度の話題に限定すると,摂氏と華氏の温度は次のように対応します.
摂氏 −17.8°C 0°C 10°C 20°C 30°C
華氏 0°F 32°F 50°F 68°F 86°F
摂氏の温度Cと華氏の温度Fとは次の関係があります.
日本で使われる摂氏温度を根拠にして20°Cは10°Cよりも「2倍暑い」といっても,アメリカで使われる華氏を根拠に68°Fは50°Fよりも「1.36倍暑い」といっても,いずれもおかしいでしょう.単に10°C高い,18°F高いというのは正しいでしょう.10°Cが0°Cよりも無限倍暑い(10÷0=∞)と言えば,誰も聞かなくなるでしょう.(←差には意味があるが,比率には意味がない)
同様にして,グリニッジを東西0°とする経度の約束で,日本の明石が東経135°だから,(地球は1時間に15°回転するので)明石はグリニッジよりも9時間早いということには意味がありますが,東経13.5°のベルリンの10倍だけ東にあるとは言えないし,東経0°のグリニッジの無限倍だけ東にあるともいえない.もちろん,ベルリンもグリニッジの無限倍だけ東にあるとも言わない.・・・そもそも比率で使うことを想定していないので.
■[個別の頁からの質問に対する回答][商,分数関数の微分 について/15.05.25]
答えが間違ってると思います.
y=(x+2)/(x+1)のx微分です.
=>[作者]: 連絡ありがとう.間違いを指摘される場合は,あなたが正しいと思う答も示された方がよいでしょう.
ご質問の問題は, なので,そのまま微分した場合には
になります.
しかし,参考書などでのお薦め答案は,これではなく,次に書くように「分数式は富士の山=分子の次数を下げること」(数研の用語)を使って解く方法です.
なので,
になります.
※「変だな」と思うのは「分子が無視されているのではないか」というするどい観察力ですが,さらにするどく見ると,富士の山で変形すると分子の x+2 はなくなることに注意しましょう.
■[個別の頁からの質問に対する回答][不定積分(まとめ1) について/15.05.25]
問題2の解答はln(abs(2x+3))+C ではなく 1/2*ln(abs(2x+3))+C だと思います
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][確率変数 について/15.05.21]
教科書の疑問が解決できてうれしかったです。ありがとうございました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.05.21]
問題と解説、答えがあるのがとても良かった。
独学で勉強をしているのでとても、ためになった。
同じような物をもっと作って欲しい。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][対数計算 について/15.05.21]
「中は外、外は中」で、どこを基準に中と外なのかよく分からない
=>[作者]: 連絡ありがとう.かっこ( )を付けました.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.05.20]
正解しても解説を読めるようにして下さい
=>[作者]: 連絡ありがとう.正解の場合でも解説を示すと「間違っていないときに余計なおせっかいはしないでほしい」と考える読者が多く,学習の妨げとなるようですので多くの頁で正解の場合には解説を示していません.
この頁の (PDF 485KB)「3.2. HELPはどのように出せばよいか」に書いています.
なお,正解してから,再度違っていただくと解説が読めるのは御承知の通りだと思います.・・・作者は,間違ったらどうなるのかを調べるのが毎日の仕事みたいなものです.
■[個別の頁からの質問に対する回答][連立不等式の解 について/15.05.20]
8x2−14x+3<0 の解は、x<1/4,x<2/3 となりませんか。
=>[作者]: 連絡ありがとう.たぶん2次不等式の初歩的な所でつまづいておられます.もっと簡単な例でいうと
x2 <1 の解は
x<−1 , x<1 ではなく,
−1<x<1 です.
※2次不等式の解の不等号の向きは,1次不等式のときのように問題文と同じ向きになるとは限らず,2次関数のグラフで考えるのが基本です.
この頁 参照
■[個別の頁からの質問に対する回答][漸近線の方程式 について/15.05.20]
ヒントを一度出したら消えなくなった
=>[作者]: 連絡ありがとう.その頁では「ヒントを消す」というボタンをまだ作っていませんが,ブラウザの再読み込み(リロード)ボタンを押せば消えます.
■[個別の頁からの質問に対する回答][統計データの種類,尺度水準 について/15.05.19]
1.間隔尺度(interval scale)
例 知能指数,摂氏の温度
(*)の意味はなんですか?
2.間隔尺度の例に摂氏温度がありますが、摂氏温度の「0」は、水が1気圧下で凝固点とされていますが、これは比例尺度の定義にある、原点0の決め方が定まっていることにないらないのですか。
3.間隔尺度の説明に、<和差に意味があるが比率に意味がない>の意味が判りません。だからどうだというのですか?単に分類上の目印(赤と白は色がちがう、葉っぱの形が違うように)以上の意味があると思われるのですが・・・。すとんと落ちないという感じがして気持ち悪です。
=>[作者]: 連絡ありがとう.(*)は下に■答のない問題■(*)として参照しています.
「2.3.」について,
まず,「比例に意味がない」からお話しすると,日本で使われる摂氏°Cやアメリカで使われる華氏°Fは,それを使っている集団が(伝統的な事情で)適当に定めた原点と間隔に従っていると言えるでしょう.摂氏0°Cは華氏0°Fとそろっていません.1°Cの間隔と1°Fの間隔も同じではありません.したがって,それを使っている集団の中での「単なる約束ごと」でしょう.
比例に意味がないというのは,例えば,今日は30°Cでとても暑くて,昨日の温度15°Cの「2倍だ」とは言えません.しかし間隔(差)には意味があって,30°Cは20°Cよりも10°Cだけ高く,40°Cは30°Cよりも10°Cだけ高いとは言えて,水の重さを決めたら,20°Cの水を30°Cにするに要する熱量と30°Cの水を40°Cにする熱量は同じだと言えます.
さて,その頁の下の欄には絶対温度が比例尺度に該当すると書いています.これと比較すると摂氏が比例尺度ではないことが分かりやすくなるでしょう.
分子運動の平均速度をv、絶対温度をTで表すと
となるので,分子の運動エネルギーは絶対温度に比例しますが,摂氏の温度にも華氏の温度にも比例しません.絶対温度が2倍になると分子運動のエネルギーは2倍(平均速度は√2倍)になりますが,摂氏の温度や華氏の温度が2倍になっても分子運動のエネルギーは2倍にはなりません.
もっと身近な例を使うと,元号や西暦では年の間隔(差)には意味があるが,原点はその年号を使う集団の中での約束事によって決まっており,比率には意味がない.例えば昭和40年生まれの人は昭和20年生まれの人よりも2倍遅く生まれた訳ではないが、20年遅く生まれたとは言える.西暦1000年に作られた建物は西暦500年に作られた建物よりも2倍遅く作られた訳ではないが500年遅く作られたとは言える.
元の話に戻すと,摂氏0°Cの原点は日本にいれば周り中みんな使っているので特別な意味があるように見えますが,ただの約束事です.
それよりも,統計を学ばれているのなら,(*)客の満足度(A: 非常によい:4,よい:3,悪い:2,非常に悪い:1)の例で客の満足度が「2倍」よかったということはあり得ませんが,4と3と2と1の間隔が(心理的に)等間隔であると(それなりにでも)言えなければ,そのアンケート調査では平均点ですら意味のないものとなり,スピアマンの順位相関係数のような順序尺度についてでも使えるような計算しかできないというあたりが重要かと思います.(B:「非常によい:5,よい:4,普通:3,悪い:2,非常に悪い:1」でアンケート調査するとAの調査とは結果は全く変わります.実際上は平均点や分散を平気で使うことが多いですが,AかBのどちらがよいか,その調査に応じて判断は必要でしょう.)
■[個別の頁からの質問に対する回答][対数計算 について/15.05.19]
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/15.05.15]
数ある微分方程式の記事の中で
一番わかりやすかったです
=>[作者]: 連絡ありがとう.作者もこの説明方法が気に入っているので,たぶん,気分的に通じるところがあるのだと思います.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.05.15]
なぜ、さいころや立方体の問題で、円順列の式になるのかおしえてほしい
=>[作者]: 連絡ありがとう.左の図のように,上と下を固定しても,側面を回転すると重なるものがあるからです.
■[個別の頁からの質問に対する回答][円順列,じゅず順列 について/15.05.15]
説明によく使われる「固定する」の意味が理解できず困っています。この言葉があると「固定していいの?」という疑問がいつもつきまといます。固定して考えてよい理由(説明)を期待しています。
=>[作者]: 連絡ありがとう.その頁の一番初めの図を見ましたか?その図で,もし固定しなければ「回転してできるものは全部別のものとして数えることになり,4!=24通りになります.」これに対して,円順列とは「回転して重なるものは同一物とみなす」という数え方なので,初めの4個の図は1つのものを表していることになります.
■[個別の頁からの質問に対する回答][和の法則 について/15.05.15]
この答えがわからなくって教えてください! 大小2個のサイコロを同時に投げる時、次の場合は何通りあるか。 1、目の和が9以上の奇数。 2、目の和が6以下の3の倍数
=>[作者]: 連絡ありがとう.原則として,このホームページの教材にある問題については質問にお答えしますが,読者作成の問題については,宿題であったりその他必ず本人がやらなければならない問題であるかどうか区別ができませんので,答えていません.ただ,この頁を読んだ人がそのような質問をするのは,本当にこの頁の問題をやったのか?と疑問があります.もしこの頁の問題をやっていれば数字が変わったぐらいならできるはずだからです.
■[個別の頁からの質問に対する回答][逆三角関数の微分法 について/15.05.15]
大学の授業の予習用として使用しました。
教科書よりもわかりやすく良かったです!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/15.05.15]
優しい解説で、解りやすかったです。特に、tanが、解りやすかったです。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/15.05.15]
とても良い感じでした。高校生だった時に、これがあれば、よかったのにと思いました。
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][基本的な三角比の値 について/15.05.12]
問題1の答えを表示してほしい
=>[作者]: 連絡ありがとう.選択問題では他の候補に当たれば,すぐに正解に達することができますので,必ずしも解答は表示していません.(5秒もかからないでしょう)
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/15.05.12]
どこから1が出てきて
どこから2が出てくんのか
それが書いてないと理解不能。
理由がかいてねーとせっかくの説明が台無し。
当たり前のことが意外にわからなくて苦手になる人も多いので書いていただけると助かります
=>[作者]: 連絡ありがとう.分からないストレスをぶつけていただくのはかまいませんが,1とか2という数字はこの頁の中に何度も登場しますので,質問の箇所を特定していただかないと答えようがありません.
■[個別の頁からの質問に対する回答][階乗 について/15.05.11]
分母と分子のどちらにも『!』が付いている計算の仕方が曖昧でしたが、これを見てよくわかりました(^ ^)
=>[作者]: 連絡ありがとう.視覚から入ると速攻性があるようです.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/15.05.9]
すごく分かりやすかったです!
ありがとうございました!
お陰でたすき掛けが、分かるようになりました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][二次方程式の解の公式 について/15.05.09]
解の公式を導く過程で、
繰り返して同じ式がある。
=>[作者]: 連絡ありがとう.おかしいので直しました.
■群馬県[昭和19年生まれさん/15.5.9]
いつもボケ防止で問題を楽しんでいます。
http://www.geisya.or.jp/~mwm48961/electro/integral_length1_m2_5.htm
下から2行目
上から24行目
はdxはdθシ-タと思いますが
=>[作者]: 連絡ありがとう.3か所訂正しました.
■[個別の頁からの質問に対する回答][行列を対角化するには について/15.05.08]
解答を省略しすぎであると思う。
例えば、固有ベクトルを求めるときの解答の道筋がまったく示されていなかったり、行列PやDをなぜ解答にあるようにおくのかの説明がまったくなかったりする点である。
また、固有値や固有ベクトルや対角行列が物理的にどのようなことを表すのかが示されていないので、実際のデカルト座標系での点の関係をイメージすることもできない。
行列の対角化について、もっと基礎から学べるような配慮が必要である。
=>[作者]: 連絡ありがとう.教材に対する要求水準を上げていただくことは歓迎ですが,1つの頁,1コマの授業にそんなにたくさんの項目を詰め込んでしまうとほとんどの生徒が分からなくなってしまいます.数学は「点学習」ではなく「線学習」の方がよく,もっとはっきり言えば「網学習」にすべきです.メニューがありますので「 固有値,固有ベクトルの定義」「固有値,固有ベクトルの求め方」「行列の対角化とは」「行列を対角化するには」と,順を追って読んでください.
■[個別の頁からの質問に対する回答][展開公式1 について/15.05.06]
答えはどこですか?
=>[作者]: 連絡ありがとう.4択の問題なので,初めは間違っても数秒以内に正解に達するはずです.
■神奈川[ろんいえさん/15.5.6]
いつも高校数学サイトを利用させていただき、ありがとうございます。
ミスがあると思われますので報告します。
http://www.geisya.or.jp/~mwm48961/kou3/prob_trance1.htm
・右の段のはじめの赤い【例】問題の最後の行
誤:3^2×5=45 正:15^2=225
・下の方の「基準化」の問題4
誤:解答の選択肢が全ておかしいのではないでしょうか。
以上、初めて(久しぶりに?)やる単元なので、私が間違っているかもしれません。
大変勉強になりました。45歳。
=>[作者]: 連絡ありがとう.間違いでしたので,訂正しました.(いずれも,上の段の式をコピペして次の式を作ったために,ミスがあったようです)
■[個別の頁からの質問に対する回答][ベクトルの直交条件 について/15.05.06]
a=(-3.4.1)b=(-3.2.k)
a-b,bが直交するときのkの値
答え候補
(1,-3)
(-1,3)
(-2,2)
(-2,2)
(-3,3)
答えあいません、ご教授お願いします
=>[作者]: 連絡ありがとう.答が合わないときはHELPが出るようになっています.HELPの通りですが・・・
■[個別の頁からの質問に対する回答][3次関数の増減(文字係数) について/15.05.02]
一つ一つの式の意味するところがまったく分からない。判別式からどうやって軸を求めるのか特に分からない
=>[作者]: 連絡ありがとう.おそらくですが,基本がわからないままに応用問題をやろうとされている所に無理があります.先に,
2次方程式の解と定数の大小問題 をやるべきです.判別式と軸とは関係ありません.
■[個別の頁からの質問に対する回答][展開公式 について/15.05.02]
問題がむずかしいー もっとカンタンのもんだいにして
=>[作者]: 連絡ありがとう.例えば中学校の教材が分からないままに高校の教材をやろうとしている場合に,普通の人の2倍の時間を掛けて2倍の教材を消化すればできるという研究もありますが,実際には各自には1日に24時間しかないので,英語も数学も・・・も2倍だけやってクリアするというのは,現実的には無理です.このような場合には,中学校の学習を振り返ってから高校の学習をやる方が近道となります.
■[個別の頁からの質問に対する回答][接線の方程式 について/15.05.02]
問題2 (1)の
>(3)(4)より, p = q = 0 ・・・(5)
>p = 89, q = 3227 ・・・(6)
>以上から,
の部分で、何がどうなって「以上から」になるのか分からない
=>[作者]: 連絡ありがとう.(5)のとき(1)からy=3p2 x−2p3 → y=−x になって,(6)のとき(1)からy=3p2 x−2p3 → y=37/27x−1024/729 としてもよいしy=(2q−1)x−q2 → y=−x になって,(2)からy=(2q−1)x−q2 → y=37/27x−1024/729 となるのだから,何も問題がないと考えますが?
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/15.4.30]
例10の回答2行目の式が間違っているような気がする、正しくは「y=2(x2+2ax)+a2」じゃないだろうか?
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][3次関数の最大値・最小値(文字の区間,文字係数を含む場合) について/15.4.30]
問2のグラフがX=0のときY=0になってない理由がよく分からない
=>[作者]: 連絡ありがとう.申し訳ない.視力の低下のせいかグラフを描くプログラムに +1 が余計についていましたので(問題1のプログラムを引きずっていたようです)訂正しました.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/15.4.27]
増減表の意味がよく分からない
=>[作者]: 連絡ありがとう.もっと基本の問題からやってください.たとえば
この頁
■[個別の頁からの質問に対する回答][3次関数(文字係数と極値) について/15.4.27]
a<0の場合は極値があるときでも,極値よりも外の区間で減少となるので,aは負であってはいけません.
以上により,少なくともa>0でなければなりません.…(1)
このくだりの意味がよく分からない
=>[作者]: 連絡ありがとう.問題は「
すべての区間で単調増加となるような定数aの値の範囲 を求めてください」となっており,a<0の場合は左図のように,減少となる区間がどうしてもできるから,だめだということです.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/15.4.23]
例1の答え、「2ca」になってますが、アルファベット順だと思うので、「2ac」ではないでしょうか?
=>[作者]: 連絡ありがとう.解説に書いてあるように,
ab, ac, bc (辞書式配列,アルファベット順)と書くか,
ab, bc, ca (輪環の順,サイクリックの順)と書くかは正しい・間違いの違いではなく,見やすく点検しやすければどちらでもよいでしょう.
なお,数学Iの教科書で3文字
a, b, c の場合は,ほとんど輪環の順に書かれていますが,輪環の順は,グー・チョキ・パーのように「三すくみ」「巴形」になっている場合:
(x+y+z)2 のような場合にしか登場しません.2文字,4文字,...の場合に輪環の順は使わないので,「サイクリック」は実際上は3文字専用の書き方となります.(左図参照)
※どれも2次なので降べきの順では対等.そこで厳密に「アルファベット順」に書けば,
(a+b+c)2 =a2 +2ab+2ac+b2 +2bc+c2 …(1)となりますが,これでは見にくく点検しにくいので,『1文字の式を先に書いて』
(a+b+c)2 =a2 +b2 +c2 +2ab+2ac+2bc …(2)とすると,『文字数順』かつ「アルファベット順」となって折衷物になりますが少し見やすくなります.さらに,
(a+b+c)2 =a2 +b2 +c2 +2ab+2bc+2ca …(3)と書くと,もっと「見やすく」「点検しやすく」=「間違いにくく」なると考えればよいでしょう.
■[個別の頁からの質問に対する回答][隣り合う並び方・隣り合わない並び方 について/15.4.23]
もしかしたら、<うまい方法>は間違ってませんか? (問題7、8の答えも)その方法を使って例2を解こうとすると元の答えと異なりませんか? 私の勘違いなら、すみません。
=>[作者]: 連絡ありがとう.この<うまい方法>というのは,筆者が思いつきで言っていることではなく,教科書・参考書に普通に書かれているものです.おそらく「元の答と違う」というのは<大変な方法>というのを正しく行えなかったためだと考えられます.
[例2]を<うまい方法>で解くと
女子3人の並べ方が3!=6 通り4×2=12 通り6× 12=72 通り …一致
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/15.4.17]
簡単すぎる。もっとたくさんの応用問題を取扱ってほしい。
=>[作者]: 連絡ありがとう.左半分の基本問題の方をされたということなので,右半分の応用問題の方もされたらよいではないかと・・・
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/15.4.17]
高一の娘が泣きついて来たので、忘れた記憶を呼び戻すために参考にさせてもらいました。あのころ、こんなサイトに出会えていたなら、もう少し頑張れたかも、と思いました。大変参考になりました。
=>[作者]: 連絡ありがとう.がんばってください.
■[個別の頁からの質問に対する回答][ベクトルの平行条件・垂直条件 について/15.4.17]
この式に何の意味があってどう役に立つのかよく分からない
=>[作者]: 連絡ありがとう.
筆者とよく似た人がいるのだなと感心しました.筆者も高校時代にはそのように考えましたが,この問題に対する「答」というものはないことに注意してください.○○問答のようなものです.
通常,教科書では各章の初めにその章の内容が数学全体とどのように関係しているかを示す概観的な話があります.eラーニングにおいても,はじめにその学習をすれば何ができるようになるのかを述べて目標を掲げることによって学習に向かう動機付けを図ることが重要であるとされています.少し前のExeclには,アドベンチャーxx社という架空の会社の社員としてExcelを使って仕事をする立場になったとして,ある章の学習をすれば何ができるようになるのかを初めに述べるというスタイルのチュートリアルが付録につていたことがありました(うろ覚えなので正確ではないかもしれません.現在はWeb上の
この頁 などでビデオ教材として公開されているようです).まさに,このようにして新しい章の学習に向かわせるのだという手本のような印象を受けました.
しかし,このような概観的な話は各章レベルのことで,各単元,各項目,各公式ごとにそんなことをしても同じことの繰り返しになるだけでなく,細目についてまでおおげさな目標が示せるとは限りません.昔,筆者が高校で教えていた頃には,なぜか新しい章に入るときは,いくら頑張って演説してもほぼ全員が睡眠学習になってしまって誰も聞いていないということが多かったような記憶があります.これは無理もない話で,大局的なお話など試験には出せず生徒の得点には結びつかないので,「この話は聞かないようにしよう」とフィルターにかける心理が働くようでした.そんなことをするよりも,個別の項目で「これは出るぞ」とうだけで簡単に授業に集中してもらえるのです.
さて,本題に戻って「この式に何の意味があってどう役に立つのかよく分からない」という疑問は,数学の体系上の論理的な関係を尋ねているというよりは,「自分にとってどんな意味があるのか」という疑問に裏打ちされていると考えられます.ところが,数学の,数学Bの,ベクトルの,そのまた内積の,そのまた成分表示おける平行と垂直条件を知ることが「国民的素養として必要なことだ」と証明できるとすると,とても具合の悪いことになるのです・・・そんなことが証明できたら,中卒の人はどうなるのか,数学Bを選択しなかった人はどうなるのか,逆・裏を考えてみたらすぐ分かります.(言葉に出して言うのも失礼に当たります).だから,人間として必要なことだというような大げさなことは元々証明できるはずがありません.たぶん「それをやれば,より豊かな生活ができるようになるでしょう」「それができるようになれば,できる分野が広がるでしょう」ぐらいの話です.・・・本人がどんな人生を歩んで,その時々の業種・職種で重要な局面がどう変化するかが分からないのに,あらかじめこの場面で使いますなどと言えるはずがありません.
ただ,ベクトルの平行・垂直条件を成分で取り扱うというようなことは基本中の基本で,これ以降の数学の学習をする場合には,至る所に水や空気のように登場するので,学校や会社で何かのレポートをまとめるような場合にこれが分からないと土台から崩れてしまう可能性があります.例えば,多次元のデータがあるときにあるデータと他のデータが相関があるかないかは,それらのベクトルが垂直であると見なせるかどうかで判断できると聞いた時に,「ちんぷんかんぷんの話をしている」と考えるか,「だいたいのイメージだけは分かる」のとではその後の仕事ができるかできないかの違いになって来るかもしれません.
■[個別の頁からの質問に対する回答][負の指数 について/15.4.17]
全体的にわかりやすかったです
=>[作者]: 連絡ありがとう.がんばってください.
■[個別の頁からの質問に対する回答][Excel:重回帰分析(3) について/15.4.17]
t2乗値が2以下、ではなく、ここでは(エクセルの出力は「t」だと思います)t値でいいのではないか?
=>[作者]: 連絡ありがとう.t 値は正負の値をとるので,t 値が...よりも小さいとは言えず,|t|<... ということになります.ただ,この頁では詳しくは書けませんでしたがt2 の値はF 値に等しくなり,意味のある数値となるので,通常t2 値で判断するようです.参考書によってはこの値をt2 >Fin =2 , t2 <Fout =2 などと書いて,入れる,外すの判断を表しているようです.
■三重[おっさんさん/15.4.17]
お伺いしたいことがあります。
ご存じの事と思いますが、sin,cos,tan等は変数では無いので直立体の文字を使うことになっていますが敢えて斜字体を使って見える理由をお聞かせ頂きたいのです。
=>[作者]: 連絡ありがとう.ご覧になった頁では,斜体になっていたということですが,全体では両方あります.確かに教科書では直立体になっていますが画面構成上,Web頁上で特に
a , x をブラウザで表示できるフォントで分かりやすく示すために斜体を使っています.sin, logなどが登場するたびにフォントFaceを切り替えることもできますが,分数や根号の中に登場する場合に個別に切り替えていると繁雑になるだけでなく,縦横とも表示位置がずれてしまうため式の中で表示する場合にはやむなくそのまま使っています.
なお,分数,根号,定積分などの数式を表示する方法には,上記のような筆者独自の方法以外にGoogleの方式やMathJax(jsMath+MathML)の方式があります.各々の方式についての筆者の感想については,
この頁 を参照してください.
■[個別の頁からの質問に対する回答][三項間漸化式の一般項 について/15.4.14]
無理数の絡んだ証明がまったく理解できない
=>[作者]: 連絡ありがとう.三項間漸化式で特性方程式の解が無理数になる場合のような問題は,応用問題中の応用問題です.あなたが現役なのか浪人中なのか卒業生なのかよく分かりませんが,もっと普通にやらなければならない問題があるはずです.この頁の問題は,余裕ができたときに再度やってください.
■岡山[檜高さん/15.4.11]
重複順列の問題はないのですか?
どこにも見当たらないので戻ると赤塗りになっているので見落としているのかな、と気になりました
=>[作者]: 連絡ありがとう.その頁には採点する問題はありませんが,ぎっしりと書かれた例題を読むのには,どんなに速く読んでも1分はかかるはずです.そこで,その頁を読んだ時間が1分未満なら赤で表示,1分以上なら青で表示しています.まともに読めば5分でも読めないでしょう.
■[個別の頁からの質問に対する回答][円順列・じゅず順列 について/15.4.9]
14のヒントがよくわかりません
=>[作者]: 連絡ありがとう.解説図を追加しました.
■[個別の頁からの質問に対する回答][基本的な三角比の値 について/15.4.8]
解説が欲しいです
=>[作者]: 連絡ありがとう.三角比の定義の図を付けます.
■[個別の頁からの質問に対する回答][漸化式と一般項(等比形) について/15.4.8]
漸化の意味するところが解説を読んでもまったく分からない
=>[作者]: 連絡ありがとう.メニューの右欄にあることから分かりますように,漸化式の問題は教科書的な基本問題ではありません.この頁に手を付ける人は左側の欄の基本項目がそこそこ分かることを前提にしていますが,検索などから直接やって来る場合もありますので,簡単な説明をしておきますと↓.
前の項を使って次の項を定義すると,次々に数列の各項が定まりますが,このような隣り合う項の関係式のことを漸化式といいます.教科書の表題としては数列の帰納的定義となっている場合もあります.
例えば
a1 =1 …(1)n+1 =2an +1 …(2)
のように初項(1)と二項間漸化式(2)によって,数列 {
an } が帰納的に(前の項を使って次の項が順次)定義されていれば,
a1 =12 =2a1 +1=33 =2a2 +1=74 =2a2 +1=15
のように,数列の各項は次々に求まり,この数列 {
an } が定まるはずですが,2,3項求めるなら簡単ですがnで表すのはなかなか大変です.このような漸化式から一般項
an =2n −1 を求めるのが「漸化式から一般項を求める」ということの意味です.
■[個別の頁からの質問に対する回答][3項間漸化式の一般項 について/15.4.8]
例と答えの(3)が何度やっても解けない
=>[作者]: 連絡ありがとう.[?] を押せば途中経過が出ます.
■[個別の頁からの質問に対する回答][3次以上の因数分解(例題→選択問題) について/15.4.7]
高校の課題でつまずいていた問題がなんとなくですが解けるようになりました!説明や例題があったので、とても分かりやすかったです(^^)
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][F検定→t検定 について/15.4.7]
一番上のブロック内、(2)にタイポと思われる個所があります。「データの個数が等しいときも等しいときもある」→「データの個数が等しいときも異なるときもある」?
=>[作者]: 連絡ありがとう.ご指摘の通り,タイプミスですので訂正しました.
■[個別の頁からの質問に対する回答][■例題対比)2次関数のグラフ[標準形] について/15.4.7]
カリフォルニア在住です。日本の教材はわかりやすく、まとめ方がうまいです。ありがとうございました!
=>[作者]: 連絡ありがとう.
■[個別の頁からの質問に対する回答][固有値・固有ベクトルの求め方 について/15.4.6]
よくわかります。ありがとうございます。固有値、固有ベクトルの意味する直観的な説明があると理解が深まるかと思います。
=>[作者]: 連絡ありがとう.あなたの意見を取り入れて,図を追加しました.
■[個別の頁からの質問に対する回答][必要条件・十分条件 について/15.4.6]
無料でここまで丁寧な教材があったとは。感激です(T ^ T)
=>[作者]: 連絡ありがとう.では頑張ってください.
■埼玉県[よっちゃんさん/15.4.6]
3乗根√1.5×2√3÷3乗根√9√6がこちらのサイトを駆使してもわかりません。
最後の三乗根は全体にかかっています。
=>[作者]: 連絡ありがとう.ご質問の意味が正確には伝わりませんが,このサイトにある問題ではなくて読者独自の問題の解き方が分からないということを述べておられると解釈しました.この場合は,全部教えるといろいろとトラブルになることがありますので,解き方と途中までの計算を示して,残りは各自でやってもらうようにしています.
まず,元の問題は
だとします.
(1) これをExcelで解くには,=1.5^(1/3)*2*3^(1/2)/(9*6^(1/2))^(1/3) と入力します.結果は小数で示されますが,数字の並び方を見ると「ひとよひとよに」「ひとなみに」など見れば分かる根号を表していることが分かります.
(2) 筆算でやるには
を「分数の指数で表してから」「2と3の指数に分ける」という方向で変形します.
などと変形します.
■埼玉県[よっちゃんさん/15.4.6]
詳しく書いていただきありがとうございました!とても分かりやすい説明で、そしてこの考え方は自分には思いつきませんでした、ありがとうございました。
=>[作者]: あなたの疑問はその頁だけでなく,少し後ろにある
分数の指数 の頁を読めば分かるはずです.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/15.4.4]
教科書読んでもよくわからなかったけど、丁寧に説明されていて、とてもわかりやすかったです。ありがとうございます。
=>[作者]: 連絡ありがとう.それはよかった.幸運を祈る.
■[個別の頁からの質問に対する回答][定積分(多項式,分数関数,無理関数) について/15.4.3]
最後の√ax+b=tの置換積分を行う問題(2)の答えは、27/14 では?
=>[作者]: 連絡ありがとう.計算間違いがありましたので訂正します.なお,あなたの答も少し違うようです.
■[個別の頁からの質問に対する回答][展開公式1 について/15.3.29]
薄い字や薄い色が見にくいので、見やすくして頂けると、有り難いです。
=>[作者]: 連絡ありがとう.コントラストの強いギラギラとした配色は目が疲れやすいので,ソフトな配色にしています.薄い色の文字は,どちらかと言えばあまり重要ではない付け足しの内容が多いです.
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/15.3.25]
例題5の微分3乗ではなく2乗だと思います。そこを修正して頂ければ素晴らしいサイトだと思います。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][展開公式 について/15.3.25]
解説を問題より上に持ってきて欲しいです。
=>[作者]: 連絡ありがとう.この頁作成当時は,解説→問題という順方式の流れ[A]と,問題→解説という逆方式の流れ[B]のどちらが身に付きやすいかに関心があって,[B]の方式の頁も幾つか作ってみたようです.基本がほとんど思い出せない人は[A]の方式でなければ無理ですが,少し勉強して結果が身に付いたかどうかチェックするには[B]方式によって,まず自分の課題・弱点を見つけてから,解説を読み,問題に戻るという流れにより弱点を埋めることができまるという構想です.ただ実際に教材として公開してみると,ほとんどの人が[A]方式を好むらしいので,[B]方式の頁は減らしています.
■[個別の頁からの質問に対する回答][
このページではないのですが、正方行列のn乗のところの問題で、チェックを付ける問題ありますよね? 上から二番目の問題の図が多分間違ってます。
=>[作者]: 連絡ありがとう.どの頁の話なのか分かりませんが,それらしい頁を推定してみるとt A=A
■[個別の頁からの質問に対する回答][決定係数とは? について/15.3.22]
「自由調整済決定係数」が「補正R2」であることが、あとから説明されるので、最初混乱します。^yが読めないので、引っかかります。読み方を書いてくれるとありがたいです。
=>[作者]: 連絡ありがとう.ここでは,自由度調整済決定係数は広く使われる用語として扱い,補正R2というのはこれに対するExcel出力の表中だけで使われる記号として扱っています.他の統計ソフトや参考書で補正R2と書かれるとは限りません.
後半の質問について,一般に数学記号は「書かれたもの,書き方」は世界共通ですが,「読み方」はこれが正しく,これは正しくないという形に硬く決められているものではないと考えています.昔,ある教科書会社が高校教員向けに数学記号の読み方アンケート調査の結果を集計したことがありますが,極端に言えば人によって読み方が違うが,比較的多い読み方,明治以来の日本語独特の読み方,英語の直訳に近い読み方などに大別されるようです.
は「yハット」とか「yカレット」と読む人が多いと思います.(
ディーyディーxのように上から順に素読みしてハットy,カレットyが好みの人もいるかもしれません)
■[個別の頁からの質問に対する回答][展開公式 について/15.3.22]
問題3が表示されずにエンドになってしまったそこを直して欲しい
=>[作者]: 連絡ありがとう.なるほど携帯版で問題3の(3)が分数関数表示プログラムの指定の仕方にミスがあって,スクリプトエラーのために途中終了してしまうようです.訂正しました.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/15.3.21]
答案の傾向が問題に重なってしまって問題が醜くなっているこの問題の解決を求めます
=>[作者]: 連絡ありがとう.PCで点検する限り何も問題はないのですが,スマホで見ると確かに「かぶる」ようですので,少しは見やすくしました.
■群馬県[昭和19年生まれさん/15.3.20]
■sinxに関する不定積分のpageで
1/sinxの積分で
右欄最上列
(cos x)^2は(cos x/2)^2と思いますが。
=>[作者]: 連絡ありがとう.訂正しました(独自方式の分数表示なので,分子の中の分母を表示するのが大変でしたが,一応直せました)
■[個別の頁からの質問に対する回答][2次関数の頂点の座標 について/15.3.19]
解説なけりゃ間違ってもわかりませんよ!あるのかもしれないですけど見つけにくすぎです!!!わかりませーん!
=>[作者]: 連絡ありがとう.どうも回答者は答を先に見たいようですが,自分の解答を先に書けば(間違った場合に)必要に応じて=?= のそこそこ派手な目印が出て,これを押せば解説が出るようになっています.この目印が「派手過ぎる」と回答者が馬鹿にされたような印象を持つことがあり,逆に「地味過ぎる」と見落とす場合がありますので,ほどよく目立つ色と大きさとは?という問題になります.
■[個別の頁からの質問に対する回答][置き換えによる展開 について/15.3.18]
(3)間違ってませんか?
=>[作者]: 連絡ありがとう.解き方(途中経過)は下に書いてあります.質問者の利用環境として,Android のMobile Safariで日本語漢字変換モードになっていませんか?
■[個別の頁からの質問に対する回答][行列の対角化とは について/15.3.14]
次のページにいくリンクがない。
=>[作者]: 連絡ありがとう.下端の左側にあります.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/15.3.13]
もっとたくさんのもんだいがやりたいです。
=>[作者]: 連絡ありがとう.画面に書いてありますように,それぞれの問題は回答者の必要に応じて「ほぼ無限に」出ます.(⇒問題と答は自動生成です.コンピュータ相手の,この「しつこさ」に,とことん付き合う人がいるとは思えませんし,本当に「最後まで」やる人がいるとも考えられません.):[それなりの自信作です]
■[個別の頁からの質問に対する回答][展開公式Ⅰ について/15.3.13]
とてもわかり易くて勉強がはかどりました!!
ですが公式にあてはまるあてはまらないの意味がわからなくて一番最後の問題が解けませんでした、、
理解力の低い私でもわかるようなそこの簡潔でいいので
説明が欲しいです(;´Д`)
=>[作者]: 連絡ありがとう.大きくは変わりませんが少し解説を追加しました.
■[個別の頁からの質問に対する回答][根号の計算 について/15.3.12]
イコール(=)がマイナス(-)表示している
=>[作者]: 連絡ありがとう.質問者と同じ環境(PCのChorome)で確かめましたが,場所を特定していただかないと,連絡内容が分かりません.
■[個別の頁からの質問に対する回答][空間における直線の方程式 について/15.3.12]
例題5の解答16~17行目のベクトルvのy,z成分が間違っているように思ったのですが、私の思い違いでしょうか?
=>[作者]: 連絡ありがとう.ご指摘の通り,転記ミスがありましたので訂正しました.
■[個別の頁からの質問に対する回答][複素数平面 について/15.3.112
気にいった所 : 複素数平面のグラフにプロットできるのが楽しくていいと思いました。
わかりにくい問題 : 分かりづらかった部分はとくにありませんが、回答は選択形式ではなく、自分で記入できるものもあると、もっと頭で考えることにつながると思います。
=>[作者]: 連絡ありがとう.web教材を長年提供する中で,現在の自分の考え方をまとめたものは
この頁 にあります.プログラム学習の原理のうち「積極反応の原理」に「空欄埋めの方が選択問題よりもよい」とう主張があることは認識していますが,筆者は情報機器のダウンサイジング(小型化)の帰結として,今後の多くのユーザから見て「空欄埋め問題」よりも「選択問題の方が使いやすい」と考えています.その結果,回答者に対しては大変申し訳ないですが,筆者は,多くの問題について記入問題を選択問題に変更する方向で書き換え中です.
※この理由を説明するには,文字数が足りませんが・・・子供は大人を小さくしたものではない,子供は完全な大人を不完全にしたものではない,というのは発達心理学の常識ですが,このロジックのアナロジーとして,デジタルWeb教材は印刷教材を画面に表示したものではないということは多くの人が認めることです.では何がどう違うのか.その部分については定説はありませんが,筆者の考えでは,各々の媒体(紙に印刷された教材,情報機器の画面にパラパラ漫画のように表示される教材)では,それぞれに適した作り方が違うようなのです.筆者の選択が正しかったか間違っていたかは,今後10年~20年後のWeb教材の大勢がどうなるか見てもらうのが一番かと思います(20年後?・・・おっと筆者はたぶん生きていない.質問・ご意見は筆者が生きているうちにお願いします.)
■[個別の頁からの質問に対する回答][回転移動の1次変換 について/15.3.11]
横に広がってて読みづらい
縦に細長いほうがスマホからだと読みやすい
=>[作者]: 連絡ありがとう.現在,スマホ版を準備中ですが,数千頁のすべての教材を対応させるには約1年ほど要します.
■[個別の頁からの質問に対する回答][(例題対比)平方完成の変形 について/15.3.11]
平方完成についてまずは説明から入って例題で確認でき、問題演習ができるという流れが良かったです。また他のサイトと比べて細かいところまで説明がなされていて共感が持てました。
章末問題をつくってくれるとありがたいです。
=>[作者]: 連絡ありがとう.章末問題・・・なかなか余裕がないので,とりあえず要望があるということを覚えておきます.
■[個別の頁からの質問に対する回答][平方完成(基本) について/15.3.10]
3つ行があるのは教えて欲しかった
=>[作者]: 連絡ありがとう.横幅が720のAndroidがあることは,あまり意識していませんでしたので,等倍で表示していました.参考になるコメントでしたので,少し設定を変更しました.
■[個別の頁からの質問に対する回答][(例題対比)確率の求め方 について/15.3.10]
分数のときどっちが分母の正誤で、どっちが分子の正誤なのかわかりにくい
=>[作者]: 連絡ありがとう.センター試験などの解答欄と同様に,分子→分母の順になっています.
■[個別の頁からの質問に対する回答][余弦定理 について/15.3.9]
a95mm b125mmcの角度が53°でc寸法の計算式を教えて下さい
=>[作者]: 連絡ありがとう.このサイトの教材にある問題についてはお答えしますが,読者個人の問題については原則としてお答えしていません.(過去には,入試会場からの質問で大きな社会問題になった話も聞いており,また本人自身が解かなければならない課題の場合もあり,こちらでは見分けがつきません.)c2 =a2 +b2 −2ab cos C に値を代入します.53°の余弦の値を使うには数表を見るかまたは次のようにExcelで計算するとよいでしょう.cos(53°)=cos(RADIANS(53))=0.601815023.c^2=95^2+125^2-2*95*125*COS(RADIANS(53))=10356.8932 =SQRT(10356.8932) とすれば結果が得られます.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/15.3.9]
問7間違っている気がします!違ってたらごめんなさい!
=>[作者]: 連絡ありがとう.途中経過でy''−3y'+2y=ex cos x としており,y''−3y'+2y=−ex cos x としていないので,話がややこしくなっていますが,選択肢がわに1/2の係数が足りなかったようですので訂正しました.
■[個別の頁からの質問に対する回答][ベクトルの平行条件,垂直条件 について/15.3.8]
回答してから誤ってソフトウェアキーボード上の開くをタップしてしまうと、更新されて回答した内容が消えてしまう。
=>[作者]: 連絡ありがとう.iPhoneなどの機器について,筆者の方ではよく分かりませんが,それぞれの機器のくせとして今後の参考にしていただくとよいと思います.
■[個別の頁からの質問に対する回答][直交行列とは について/15.3.7]
(Ⅲ→Ⅳ)の証明の下から3行目は、「ベクトルp1・ベクトルp2=0が示せる」の誤植ですね・・・
また、「両辺を比較すると」の部分は「両辺を2乗して比較すると」とした方が親切だと思います。
全体としては、とても分かりやすい説明になっていて、助かりました!
=>[作者]: 連絡ありがとう.前半は誤植でした.後半は確かにそうですが,絶対値の比較は通常2乗比較にするので,計算の方法に踏み込んで記述するかどうかはどちらかと言えば好みの問題かもしれれません.
■[個別の頁からの質問に対する回答][同じものがあるときの順列 について/15.3.3]
6番の問題で正解のはずの35をタップしても×と出ます。もしかしたら私のスマホが悪いのかもしれませんが確認のほどよろしくお願いいたします。
今回初めて使わせていただいたのですがとてもわかりやすかったです。問題も解説が読めてよかったです。ただ、ある節ごとに問題を設けるのではなく、全ての節に問題が欲しいと感じました。
=>[作者]: 連絡ありがとう.(前半について)6番の問題は,記入式の問題を選択式の問題に書き換えたときに,問題番号がずれたようですので訂正しました.
■千葉県[いぬすけさん/15.3.2]
高校数学 置き換えによる展開(6)の解説は
x2−x+1=A と考えると
{x3−(x2−x+1) }{x3+(x2−x+1) }とありますが問題の方は(6) (x3−x2+x−1)(x3+x2−x+1)
となっています、左側の括弧内はプラスxマイナス1
右側の括弧内はマイナスxプラス1
これでは置換えできませんので問題の左側の括弧内の訂正をお願いします
=>[作者]: 連絡ありがとう.掛け算の記号×と紛らわしくないようにエックス(x )をイタリック体にしているので判別できると思いますが,掛けるの×ではなく文字のエックス(x )です.
■[個別の頁からの質問に対する回答][二次関数の頂点 について/15.2.27]
解答があるとよいです
=>[作者]: 連絡ありがとう.解答を付けました.
■[個別の頁からの質問に対する回答][相加平均.相乗平均.調和平均 について/15.2.25]
三乗根を示す3とその前につく数字の指数が殆ど同じ位置にあるため見分けがつきづらいです
=>[作者]: 連絡ありがとう.教材作成者が言うべきことではないのですが「実に同感です」.以前から,これら2つが組み合わされている式が正確に見分けがつくのかどうか疑問に思っていましたが,HTML上で数式を表示するシステムを比較してみますと
Google Chart APIによる数式:
と
,
と
と
当サイトの独自方式
a3 と
a ,
a2 と
a23 と
a
⇒ そこそこ区別できている感じですが,独自方式の場合に隣り合う場合は少し離すことが考えられます..
■[個別の頁からの質問に対する回答][曲線の長さ について/15.2.25]
λ3-17λ2+90λ-168=0
が間違え
90λでなく94λ
=>[作者]: 連絡ありがとう.90→94訂正しました.
■大阪府[荘周さん/15.2.25]
http://www.geisya.or.jp/~mwm48961/electro/integral_length1_m3.htm
問題(2)において,シータの範囲が問題と回答で異なっている.
=>[作者]: 連絡ありがとう.問題の方を訂正しました.
■[個別の頁からの質問に対する回答][複素数平面 について/15.2.24]
複素数平面の問題3で、赤点の場所が(虚軸の方が)0.5ずれて表現されているようで、問題が解けません。
=>[作者]: 連絡ありがとう.とても言いにくいことですが,Firefoxだけはレイヤーの表示位置が下にずれる癖があり,バージョンによってもこのずれかたが変わるようです.とりあえず応急処置として,現在普及しているIE,Firefox,Chrome,safari,Operaについて正常に表示されるようにしたつもりです.
■[個別の頁からの質問に対する回答][/15.2.23]
いつも活用させていただいております。
ここのページに関連するものでなくて申し訳ないのですが、数1の根号に関するページが開けません。
改善お願いします。
=>[作者]: 連絡ありがとう.「数1の根号に関するページ」というのが沢山あって,どの頁のことなのか分かりませんでした.いろいろ調査しましたが,あなたがご覧になった頁で「数1の根号に関するページ」は??でしたので,教材のURLをお知らせください.
■[個別の頁からの質問に対する回答][相加平均.相乗平均.調和平均 について/15.2.21]
(1+2+……+n)/n≧(√1×2×……×n)^1/n
の証明を知りたい
=>[作者]: 連絡ありがとう.教材では図示する都合でn=3の場合を書いていますが,これをnにします.次の方針で証明するとよい.
は対数関数上の青で示した点
は多角形内部の赤で示した点
対数関数は上に凸だから青は赤よりも上(以上)にある.
ゆえに
※青で示した点は対数関数のグラフ上にあることは分かりやすいですが,赤で示した点(多角形の重心)を作図する方法は,解説が長くなるので教材の本文では省略しています.次のように順に組み立ていくと分かるかもしれません.
まず,点が2つの場合:
は対数関数上の青で示した点のy座標,
は中点.対数関数は上に凸だから,青が上
次に,点が3つの場合:
は対数関数上の青で示した点のy座標,
は
と
を1:2に内分する点になるから,多角形(水色)の内部
さらに,点が4つの場合:
は対数関数上の青で示した点のy座標,
は
と
を1:3に内分する点になるから,多角形(水色)の内部
このようにして,
は対数関数上の青で示した点,
は多角形内部の赤で示した点となり,対数関数は上に凸だから青は赤よりも上(以上)にあることが言えます.
■[個別の頁からの質問に対する回答][階乗 について/15.2.19]
q6の問題に対する選択肢に正解がない
=>[作者]: 連絡ありがとう.あれ~.あり得ない話で申し訳ないです.訂正しました.
■[個別の頁からの質問に対する回答][不定積分(まとめ1) について/15.2.19]
問題を選択したときの黄色いバーが縦にずれることが多い気がします
=>[作者]: 連絡ありがとう.PCのchromeでの見え方について,問題点を理解しました.chrome固有の現象ならかなり難しそうな予感がしますが,検討してみます.
■[個別の頁からの質問に対する回答][対数計算 について/15.2.18]
問題3(2)のおわりのケイサンのしかたと答えを教えてください
=>[作者]: 連絡ありがとう.他の頁での要望として,helpで解答を示されると勉強にならないという意見が大勢になってきましたので,helpから解答を消しましたが,この頁については答も復活させました.問題3(2)だけに限定される意味が分かりませんので問題3に全部について復活.右図が変形のポイントです.
■北海道[たけるさん/について/15.2.18]
いつも拝見させて頂いております。ありがとうございます。
以下の設問のHelpの説明がおかしいと思ったのですが、いかがでしょうか?
■集合と条件,必要条件,十分条件,センター試験問題[3](3)
(2006年度センター本試験問題[数学I・A]第1問[2])
http://www.geisya.or.jp/~mwm48961/kou3/cond101.htm
上記設問の反例として
a+b=1,ab=1を上げておりますが、この解は複素数となり実数となりません。
問題文よりa,bは実数であることが求められているため反例としては
ふさわしくないと考えました
a = 1/2 + √3/2i , b = 1/2 ー √3/2i または
a = 1/2 ー √3/2i , b = 1/2 + √3/2i と、なります
反例としては a=√2 , b= - √2(ともに無理数)のようなものが適当と考えます
この場合 a+b = 0 ,ab = -2(ともに有理数)となるからです
=>[作者]: ていねいに読んでくれてありがとう.「Aのとき,p→q」は「Aかつp→Aかつq」のことなので,これが真であることを示すには,図の×印の部分が空集合になることを示せばよい.偽であることを示すには,図の×印の部分に入る要素が少なくとも1つあることを示せばよい.
そこで,「Aかつq」であって「Aかつ~p」の例としてあなたの意見を採用して,helpを書き換えました.
■[個別の頁からの質問に対する回答][必要条件・十分条件 について/15.2.16]
問6において、c=0の場合aとbの値が異なる事があるので問6の解答は十分条件だと思います。
=>[作者]: 連絡ありがとう.c=0の場合は,両辺にc=0を代入すると分かるようにa=bになります.a=b ×← →○ac=bc というのがあります.こちらの問題では,あなたがお考えのように「c=0の場合aとbの値が異なる事がある」ので十分条件となります.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/15.2.14]
例-右辺が三角関数のもの1
の連立方程式は自分のブラウザからだと
−2A+6B=1
と見えるのですが右辺は=20の誤記ではないでしょうか?
=>[作者]: 連絡ありがとう.ご指摘の通り誤記ですので訂正しました.
■[個別の頁からの質問に対する回答][数列,関数の極限 について/15.2.14]
大変わかりやすいので、大学の課題をする際に参考にさせていただいています。
H19年のⅢ1なのですが、問題では②は分子が(-2)^n となっていたはずです。
=>[作者]: 連絡ありがとう.冒頭に書きましたように引用問題ですので,「(1.)試験会場で見た問題」「(2.)
現在公開されている問題 」「(3.)当教材に引用した問題」の3種類の整合性についてですが,(2.)と(3.)の整合性は確かめました.(1.)と(2.)の整合性については,現在となっては分かりませんが,ご指摘のように②が
であった場合は,ここで紹介している問題よりも格段にハイレベルな問題となります.
その場合には,絶対値の対数の極限値をスターリングの公式を使って求める方法など考えられます.また,
のように収束する等比数列と比較する論法に持ち込む方法が考えられます.(結果は変わりません.)
ここでは,先に述べましたように,現在確かめられる問題(2.)は引用(3.)の通りなので,特に訂正等は行いませんのでご了解願います.
■[個別の頁からの質問に対する回答][定積分の漸化式 について/15.2.13]
等号がうまく表示されず、マイナスと区別しにくい。
=>[作者]: 連絡ありがとう.あなたがお使いのPCのChromeで確かめましたが,ご指摘の不具合は特に感じませんでした??
■[個別の頁からの質問に対する回答][余弦定理 について/15.2.12]
初めてアクセスしました。
(余弦の定理を勉強するためです)
印刷が出来るバージョンが設定されているといいななんて思うのはわたしだけでしょうか。。。
わかりやすかったです!
ありがとうございました
=>[作者]: 連絡ありがとう.この話は前にお答えしたことがありますが,よくある質問のようですので再掲します.
■[個別の頁からの質問に対する回答][固有値 について/15.2.12]
固有値が0の場合の物理的意味って何ですか?ベクトルが点に変化するという解釈でいいのでしょうか。
=>[作者]: 連絡ありがとう.そのように理解していただいていいと考えます.
■[個別の頁からの質問に対する回答][マクローリン展開 について/15.2.12]
重要な関数の所で、logの一番最後に書かれている項の分母はnなのでは?
=>[作者]: 連絡ありがとう.勢い余って階乗記号が付いてしまったようですので,訂正しました.
■[個別の頁からの質問に対する回答][相加平均.相乗平均.調和平均 について/15.2.5]
例5の右辺 abc が抜けていませんか?
=>[作者]: 連絡ありがとう.抜けていましたので訂正しました.
■[個別の頁からの質問に対する回答][決定係数 について/15.2.1]
初めてこのページを拝見しました。仕事で重回帰を使いはじめましたが、私立文系の私にとっても、これまでみたどのテキストよりも分かりやすく、かつシンプルに解説されているため、非常によく理解できました。ありがとうございます。
1点回のみ質問です。私の理解不足かもしれませんが、解説に書いてある、「回帰による偏差 (y - ^y ) ,残差 (^y -m )」の記述は逆のようにも思えたのですが、いかがでしょうか。
=>[作者]: 連絡ありがとう.教科書によっては,回帰による偏差という言い方になっている場合と他の言い方になっている場合がありますのでややこしいですが,残差が (y - ^y ) という方はそろえなければいけませんので,訂正しました.
■[個別の頁からの質問に対する回答][漸化式と一般項(階差形) について/15.2.1]
問題の(4)について
a1=24だと思います。
=>[作者]: 連絡ありがとう.例題の解説が違っていましたので,そちらの方を訂正しました.
■[個別の頁からの質問に対する回答][全微分方程式 について/15.2.1]
例題1の8行目∂F/∂yはーyです。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][余弦定理 について/15.1.30]
ちゃんと何度も読み返しましたが、どうしてその答えにたどり着くかがわかりませんでした。皆、公式はわかると思います。その公式からどう計算して答えになるのか、が知りたいのです。
=>[作者]: 連絡ありがとう.どの問題の話かを書いていただかないと答えようがありません.
■[個別の頁からの質問に対する回答][1次独立,1次従属,基底,次元,核,階数 について/15.1.29]
どうしてIm(A)を求めるときに2つの基底にするようになったのかが分かりません。
あと、基底の説明が具体的過ぎて問題集の問題にうまくあてはめられません。
=>[作者]: 連絡ありがとう.前半に対しての回答:質問の箇所がはっきりしませんので,推定で回答します.A がある演算について「閉じている」という場合の定義には,要素が2つ(または3つ)使うようになっています.例えば,正の整数全体の集合N={1,2,3, . . .} は和の演算について閉じています.(m,n∈N ならばm+n∈N だから)N={1,2,3, . . .} は差の演算について閉じていません.(m,n∈N のときm−n∈N とは限らない.例えば3−5=−2 は正の整数ではない)
■[個別の頁からの質問に対する回答][3次方程式の実数解の個数(文字係数) について/15.1.29]
いつも使わせてもらっています
ありがとうございます
問1の解は
-1<a<3 ではないでしょうか
=>[作者]: 連絡ありがとう.計算間違いがありましたので,問題文と選択肢を訂正しました.
■?[Spicyさん/15.1.27]
数II [ 三角関数 ]
練習問題3 の
第8問の sin(2α+β)sin(α-2β) の正解が間違っているような気がします。
確認お願いします。
=>[作者]: 連絡ありがとう.解答欄の選択肢がHELP情報と合っていないようですので訂正しました.
■東京都[kotarhoさん/位置ベクトルについて/15.1.25]
位置ベクトルの定義の問題で、示された点をピンポイントでクリックしても、間違いだと判断されています。
=>[作者]: 連絡ありがとう.この頁は2009年11月アップの作品で,まだスマホ対応になっていなようです.順次,対応させていますのでしばらく(ファイル総数は数千なので,数か月かかります)お待ちください.
■[個別の頁からの質問に対する回答][3次関数のグラフ について/15.1.25]
具合の悪い所 : 横の広告が途中で切れてます
=>[作者]: 連絡ありがとう.教材の幅が800ドットで,これに最も近い広告の幅が728ドットなので,やむを得ず72ドット分の不自然な隙間ができます.
■[個別の頁からの質問に対する回答][総和記号Σ について/15.1.25]
統計学のテキストを手にしたので解らない部分を検索してたらたどり着いて、時々参考にさせていただいております。おかげさまでテキストで曖昧な説明だったり物足りなかったりする部分を補っていただいております。ありがとうございます。
一つだけ気になったところが・・・ここではなくて、
○Σ記号に慣れよう!(1)
の例題12なのですが、3・4が抜けていて答えは70だと思われます。
もし、違っていましたらごめんなさい。
合っているようでしたら訂正頂ければ幸いです。
それと、お手数ですが、
○Σ記号に慣れよう!(1)
の証明の部分をもう少し詳しく載せていただけないでしょうか?どうして、Σが= nΣk=1 ak+ nΣk=1 bk このような形になるのか展開が理解しにくいのです。私の理解力が足りないのだとは思うのですが時間を割いていただければ幸いです。
よろしくお願いいたします。
=>[作者]: 連絡ありがとう.前半はタイプミスですので訂正しました.後半は,これ以上詳しく分けることはできないので,「簡単な例」を追加しました.
■[個別の頁からの質問に対する回答][最大公約数・最小公倍数 について/15.1.22]
気にいった所 : とてもわかりやすかったです=>[作者]: 連絡ありがとう.タイプミスですので訂正しました.ついでに文章と図の間に,見やすいように線も入れました.
■[個別の頁からの質問に対する回答][接線の方程式 について/15.1.9]
わかりにくい問題 : 問題2(1)
解説の
>(3)(4)より, p = q = 0 ・・・(5)
>p = 8/9, q = 32/27 ・・・(6)
どういう計算でこうなるのかが判らない
=>[作者]: 連絡ありがとう.おそらく電車の中で携帯で読んでいるのでなく,PCで読んでおられるので,手元に鉛筆やボールペンぐらいはあるでしょう.3p2 =2q と変形するだけで,すべて分かります.労力を惜しむと分かる話も分からなくなる可能性あり
■北海道[明日さん/14.12.25]
X3乗-4x2乗-11x+30の因数分解の解き方教えてください。
=>[作者]: 連絡ありがとう.このサイトの特定の頁の教材について疑問がある場合はお答えしていますが,各自の問題については原則としてお答えしていません.ヒントだけ示しておきます.x3 −.....+30=(x−a)(x2 ....+..) と書けるとき,a は30 の約数になります.f(x)=x3 −4x2 −11x+30 とおいて,30 の約数(正負とも)を順に代入して0になるものを調べます.・・・1, 2 , 3, 5 , −1, −2, −3 , −5 a (x−a ) の形で因数になりますので注意しましょう.では頑張ってください.
■[個別の頁からの質問に対する回答][
具合の悪い所 : (原式)=−2x+1−2x−1=−4x (減少する)
増加ずるじゃないんですか?
=>[作者]: 連絡ありがとう.なんとなく読んだのでなく,よく考えられたた質問だと思います.ただ,内容的には教材の記述で合っています.x<0 のとき,確かに−4x>0 ですが,「グラフは」右下がりなので減少です.
■[個別の頁からの質問に対する回答][F検定→t検定 について/14.12.17]
統計のみのメニューが欲しいです!
また、ページの一番上にグローバルナビが欲しいです!
いつも参考にさせて頂いております!ありがとうございます。
=>[作者]: 連絡ありがとう.スマホからメニューを探すと下端まで移動するのが大変なようですので,とりあえずサブメニューを作りました.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/14.12.17]
問題6の解答 間違ってません?!
=>[作者]: 連絡ありがとう.解答は大丈夫のようですが,HELPの中の(1)(2)の1と0が逆のようですので訂正しました.
■[個別の頁からの質問に対する回答][必要条件と十分条件 について/14.12.16]
【答案の傾向】の文書がはみ出して読めない
=>[作者]: 連絡ありがとう.確かにFirefoxで読むと文字が重なるようですので,訂正しました.
■[個別の頁からの質問に対する回答][次数最低の文字で整理 について/14.12.13]
頭の中で答えを考えるから答えを簡単にだせるようにしてほしい
=>[作者]: 連絡ありがとう.普通の場合,この頁を読むのはその項目がよく分からない場合です.そうした場合に,暗算でやるのは無理があります.問題の上に計算用紙でやってくださいと注意書きを入れました.
■滋賀[会社員さん/14.12.12]
すばらしいサイトをありがとうございます。
高校生ではありませんが、統計のところを活用させていただいています。
以下、間違いではないかと思うのでご連絡させて頂きます。
■母平均の推定・信頼区間
(http://www.geisya.or.jp/~mwm48961/linear_algebra/conf1.htm)
【例題4】の解答で、途中の計算が間違っているように思います。
157.5-0.8162≦μ≦157.5+0.8162
156.683≦μ≦158.316
156.7≦μ≦158.3…(答)
ではないでしょうか。
■Excelを使った対応のない場合のt検定…例題・問題
(http://www.geisya.or.jp/~mwm48961/statistics/ttest_question2.htm)
問題3の解答で、
分散のp値の不等号が逆だと思います。
|t|はt片側境界値よりも「小さい」
t検定のp値の不等号が逆で、有意水準5%で有意差なし
ではないでしょうか。
=>[作者]: 連絡ありがとう.これは,うっかりミスといった軽いものでなく,疲れのせいかもしれません.いずれも訂正しました.
■[個別の頁からの質問に対する回答][展開公式1(例題→選択問題) について/14.12.12]
abの係数が-1の時は使えて-2の時は使えないとありますが、例題は両方ともabの係数は-2ですが片方は使えてもう片方が使えない理由がよくわかりません。もう少し詳しく教えてください。
=>[作者]: 連絡ありがとう.問題3の(3)は(a+b)(a2 −ab+b2 ) の形になっているから公式が使えますが,問題3の(4)は(a+b)(a2 −2ab+b2 ) の形になっているから公式が使えないということです.b2 =4 →b=2 が係数に入っているだけです.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/14.12.8]
わかりにくい問題 : 例2の(2)の(i)、
x1=tになる理由がよく分からなかったです
=>[作者]: 連絡ありがとう.1行追加しました.
■[個別の頁からの質問に対する回答][絶対値記号2つの外し方 について/14.12.7]
HELPのァはx2=14になってしまうのですが?
=>[作者]: 連絡ありがとう.第何問の話ですか?
■埼玉県[ミラルさん/14.12.7]
なんか学校でやったのと違うもんだいがある。
エクセルを使った度数分布表なんてやらなかった
=>[作者]: 連絡ありがとう.社会生活で出あう問題の一つの解決方法として教材を作らせてもらいました.
■[個別の頁からの質問に対する回答][三角不等式 について/14.12.4]
具合の悪い所 : 問4の答えが合わない
=>[作者]: 連絡ありがとう.問題が間違いで,グラフも間違いでしたので訂正しました.(トホホ~)
■[個別の頁からの質問に対する回答][負の指数 について/14.11.27]
☆印刷をして使えるPDFも作ってくれたらありがたいです。
=>[作者]: 連絡ありがとう.かなり前にはPDFファイルにしたこともありますが,PDFファイルは非常にファイルサイズが大きくなり,双方向応答型の機能はなくなりますので現在はやっていません.印刷物として必要な場合は,ブラウザから単に「印刷」を選択し,出力先としてプリンタではなく「ファイル」を選べばPDFファイルができます.(小さなチェックボックスにレを付けるだけです.)「正解などが表示された状態」「表示されていない状態」の各々で印刷を選ぶと練習用と採点用ができます.
■[個別の頁からの質問に対する回答][定数係数の2階線形微分方程式(非同次) について/14.11.20]
具合の悪い所 : 印刷するときに広告が邪魔なので印刷するときに広告が消えるようにしてくれると嬉しいです
=>[作者]: 連絡ありがとう.WYSIWYG=What You See Is What You Get(画面と印刷の一致)という国際的な技術を外す方法は思いつきません.
■[個別の頁からの質問に対する回答][集合 1 について/14.11.20]
わかりにくい問題 : (3)8項目回答のうちの左列の上から3番目が何故違うのかがわからなかった。2はAの集合ではない、という意味で合ってるのかなと最初思った。
=>[作者]: 連絡ありがとう.∈は,(要素)∈(集合)の関係に使います.これに対して⊂は,(集合)⊂(集合)の関係に使います.したがって,2⊂Aが間違いであるのは,2が集合でないのに⊂を使っているからです.
■群馬県[昭和19年生まれさん/14.11.16]
http://www.geisya.or.jp/~mwm48961/koukou/area_closed_curve3.htm
【問題1】
dy/dx=2costとありますが
dy/dx=2cos2t
と思います。
=>[作者]: 連絡ありがとう.訂正します.
■群馬県[昭和19年生まれさん/14.11.4]
http://www.geisya.or.jp/~mwm48961/koukou/area_closed_curve1.htm
問題4
+5は-5と思いますが。
=>[作者]: 連絡ありがとう.つまらん間違いがいろいろあって・・・
■[個別の頁からの質問に対する回答][逆・裏・対偶 について/14.11.4]
具合の悪い所 : 否定の⁻がつく部分のほとんどが上か下かはランダムでずれて映る
=>[作者]: 連絡ありがとう.Firefoxのヴァージョン32.xx, 33.xxからレイヤーがずれる不具合が直ったらしいので,逆向きにずらすプログラムを外しました.
■愛知県[浩二さん/14.11.4]
極座標の(問題1)の3番目と4番目は問題の間違いではないですか?
たとえば、 3cos(θ+π/4)=r は、rcos(θ+π/4)=3 ではないのですか?
=>[作者]: 連絡ありがとう.極座標の頁をいくら探しても該当の箇所がありませんでしたが,極方程式の頁にご指摘の箇所がありました.
■?[?さん/14.11.1]
http://www.geisya.or.jp/~mwm48961/koukou/complex_line1.htm
問題2(1)の答えは左上ではないか
=>[作者]: 連絡ありがとう.右の解説と採点プログラムが一致していませんでしたので訂正しました.(2)のz→Wもついでに訂正
■[個別の頁からの質問に対する回答][積和の公式.和積の公式 について/14.10.26]
具合の悪い所 : 問題4(1)って答え合ってますか?
和積の公式の(1)をもちいるのではないでしょうか?教えてください
=>[作者]: 連絡ありがとう.結果は合っていますが,途中のsin,cosの表記に間違いがありましたので訂正しました.
■[個別の頁からの質問に対する回答][(例題対比)連立方程式 について/14.10.25]
わかりにくい問題 : ×が入力できない
=>[作者]: 連絡ありがとう.ご利用になっているFirefoxで実際に点検しましたが,x の値は該当箇所のすべてについて入力でき,x という文字を入力する箇所もすべて入力できるようです??と言う訳でご指摘の内容が理解できませんでした.
■[個別の頁からの質問に対する回答][
教科書ではcombination、₂C₁の形で表示されているので、大変分かりやすいですが、この様にも表示して頂きたいのと、iPhoneなどの画面に自動的に調節される様にして頂けると理由し易くなると思います。
この様なサイトを作って頂けたことを心より感謝致します。
=>[作者]: 連絡ありがとう.前半については意味が理解できません.そのような表記は見たことがない??後半については考え中です.
■[個別の頁からの質問に対する回答][漸化式と一般項(階差形) について/14.10.22]
具合の悪い所 : 「?」を押しても何も起こらない
=>[作者]: 連絡ありがとう.mobile版と2つのプログラムがあって,混ざっていたようですので訂正しました.
■[個別の頁からの質問に対する回答][たすき掛け因数分解 について/14.10.21]
具合の悪い所 : 4x2-5x-21
=>[作者]: 連絡ありがとう.分からないという声なき声だと解釈して,helpボタンを付けました.
■[個別の頁からの質問に対する回答][閉曲線で囲まれた図形の面積3…(媒介変数表示) について/14.10.20]
具合の悪い所 : 積分記号と定積分の範囲が重なる。
=>[作者]: 連絡ありがとう.確かにスマホ上のSafariではそうなるようです.PC向けに作った教材をスマホ用に作り直すとなると,数年はかかるかもしれません.
■[個別の頁からの質問に対する回答][2次関数の頂点(展開形) について/14.10.17]
このページではないですが解答の説明が出ると説明文が次の問題にかかって字が見えにくいことがあります。
=>[作者]: 連絡ありがとう.何千頁もありますので,具体的にどの頁の話なのか指摘していただかないと,点検・訂正は無理です.
■群馬県[昭和19年生まれさん/14.10.14]
細かいことばかりですが
空間における平面の方程式
[問題2]
点(3, 2, −1)を通り,平面x+y+2x+3=0に平行な平面の方程式を求めてください。
問題文
2xは2zと思います。
=>[作者]: 連絡ありがとう.点検もれタイプミスでした.訂正します.
■群馬県[昭和19年生まれさん/14.10.14]
空間における直線の方程式
[問題12]ヒント
(p-6)/2=(q-4)4=(r-10)/2
が
(p-6)=(q-6)2=(r-10)
と計算されていますが。
=>[作者]: 連絡ありがとう.1行余計にコピーしているようですので,訂正しました.
■群馬県[昭和19年生まれさん/14.10.13]
空間における直線の方程式
例6
a+3b=c
−a+2b=−3c
の解は
b=-2c/5
a=-1c/5
ではなく
a=11c/5
と思いますが。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/14.10.09]
わかりにくい問題 : 問題4 (2)
=>[作者]: 連絡ありがとう.読んでいる人は「その項目が分からないから調べている」ことが多いので,分からないことを前提とした画面構成にした方がよいと,最近考えるようになりました.
■[個別の頁からの質問に対する回答][2次式の因数分解 について/14.10.01]
このページではなく、2次式の因数分解のページで回答すると、表示される説明文が次の問題にかぶって見づらいです。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][円順列・じゅず順列 について/14.09.28]
具合の悪い所 : 広告の位置がおかしい
=>[作者]: 連絡ありがとう.PCのSafariとiPhoneのSafariでチェックしましたが,特に問題点は感じませんでした.iPadはチェックできません.
■[個別の頁からの質問に対する回答][展開公式1 について/14.09.27]
わかりにくい問題 : VIIIとIXのこじつけの覚え方、言いたい事はわかるのですが、逆の方が良いのではと思いました。
高校生であれば、すでに異符号同士が引き合い、同符号が反発するという事を感覚的に理解していますので、1年と3年だけが仲が悪い(反発する)と覚える方がすんなりと入ってくるのではと思います。
まあ既に前の覚え方で覚えてしまった人は混乱するでしょうが…。
=>[作者]: 連絡ありがとう.本人がストンと納得できるロジックを選ぶのがよいと思います.
■群馬県[昭和19年生まれさん/14.09.26]
漸化式と一般項の
類題4-2で
α・5(n-1) -β(n+1)
表示が少しずれていると思います。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][Web上の数式表示方式の比較 について/14.09.24]
例10は MathJax でも実装可能です。以下を参照してみて下さい。
http://spacelike.cocolog-nifty.com/blog/2014/09/post-bbc2.html
当該ページの動作でOKですね?
コードは当該ページのソースを開いて下さい。
=>[作者]: 連絡ありがとう.最近作った頁ですが,こんな頁を読んでくれる人がいるんだ~(驚き).研究の上,当該文書を訂正します.
■埼玉県[ミラルさん/14.09.22]
正弦定理
解説だけのページが赤く残る
=>[作者]: 連絡ありがとう.その頁は解説だけなので,読んだかどうかを判断するためにタイマーを使っています.どんなに速く読んでも5分はかかると思いますが,少なく見積もって「1分以上」読んでいれば完了となって「青」に変わります.・・・再び見たときも,最後に見た時間の長さで決まります.
■[個別の頁からの質問に対する回答][最大公約数,最小公倍数,ユークリッドの互除法 について/14.09.22]
気にいった所 : Ⅱの解き方を解説するところがわかりやすいと思いました。=>[作者]: 連絡ありがとう.512は計算間違いでしたので訂正しました.
■埼玉県[ミラルさん/14.09.17]
[問題3]
次の空欄を埋めよ.
(1)
y=−3(x−5)2−1 のグラフは,y=x2 のグラフを x 軸の正の向きに ,y 軸の正の向きに だけ平行移動したもので,頂点の座標は ( , ) である.○○○○○
採点する やり直す
【答案の傾向】
≪正答率≫⇒69%に下がりました.
≪主な誤答≫⇒初めの3だけ答えて残りが白紙という答案が13%ありました.
≪ここがポイント≫
⇒y=−3(x−5)2−1のグラフは,y=−3x2のグラフを平行移動して作ります.y=3x2のグラフをどのように平行移動しても「形」(下に凸という形)が合いません.
≪主な誤答≫⇒初めの-3だけ答えて残りが白紙という答案が13%ありました.では?
解説だけのページが赤く残るところがある。
=>[作者]: 連絡ありがとう.−3は訂正しました.残るところという形ではなく,どの頁かということをURLを右クリック&コピー&貼り付けするなど「頁が分かるように」示してください.
■埼玉県[ミラルさん/14.09.15]
■1次不等式の解き方
____________________○ 初めに左の欄から問題を1つ選び,続いて右の欄から解を1つ選べ.正答のときは,○に変り,誤答のときは変化しない.
____________________○ 右の欄にはジョーカーが1つあり,ジョーカーだけになればその頁は完了.
問題 次の各不等式の解を右の欄から選べ.(全部で4頁あります!)
[ 第4頁 / 全4頁中 で解答を先にクリックすると反応しなくなる
=>[作者]: 連絡ありがとう.その問題は「初めに左の欄から問題を1つ選び,続いて右の欄から解を1つ選べ」と書いているように,初めに左の欄を選ばないと答えられないようになっています.これは4頁だけではなくどの頁でも同じです.もし右の欄を先に選んだら,その操作は無効になり,左の欄を選び直せばできます.
■[個別の頁からの質問に対する回答][最大公約数,最小公倍数,ユークリッドの互除法 について/14.09.15]
ありがとうございます。分からないより「話題」の色が薄いので見にくいです。
=>[作者]: 連絡ありがとう.色調は機器によって変わるようですが,少し濃くしました.
■[個別の頁からの質問に対する回答][3次以上の因数分解 について/14.09.14]
わかりにくい問題 : Ⅲの証明の最後の二行が(a+b+c)でくくって導いたと理解するまで少し時間がかかったので(a+b+c)の色を変えてみるとよりりかいしやすいかと思います。
=>[作者]: 連絡ありがとう.そのアイデアを採用させてもらいます.(読者の多くは「分からないから」調べ学習をしているということをつねに意識するようにしていますが,しばしば,筆者のペースで「分かっているはずの箇所を省略してしまう」ことがあります.読む側,聞く側からすれば,それが分からなくなる大きな要因かもしれません.・・・全部教え込んでしまったら,読者が考える余地がなくなってしまうので,低いハードルだけは残して置く方がよいが,この低いハードルは,問題にはあってもよいが,解説には不要みたいです.)
■埼玉県[ミラルさん/14.09.08]
数I [ 三角比と図形 ] 正弦定理 正弦定理
って数I [ 三角比と図形 ] 正弦定理 正弦定理(問題)と表示したほうがよいのでは?
=>[作者]: 連絡ありがとう.なるほど,題名が被っているようなので,解説と問題にします.
■[個別の頁からの質問に対する回答][積の法則 について/14.09.05]
気にいった所 : 初めてに近いですが,すばらしいです。作者のプロフィールなどあれば,なぁと思うことです。
わかりにくい問題 : 問題7のhelpが欲しいでした。
本格的にこのサイトでやろうと考えました,すばらしいです。しかも無料!?
=>[作者]: 連絡ありがとう.作者のプロフィールと言えるほどのものはないのですが,このサイトに関する作者の考え方については
この頁(PDF:486KB) 参照.問題7のhelpは誤答の場合に表示されます.(なぜ,誤答の場合に表示されるのかという理由も左記の論文に記述しています)
■埼玉県[ミラルさん/14.08.28]
三角関数の加法定理,倍角公式,3倍角公式,半角公式
[問題4] 正しく対応させなさい。(初めに左側を,次に右側を選びなさい。正しく対応していれば消えます。)
消えたのがまた出て残ってるのに扇子が出る。
=>[作者]: 連絡ありがとう.たぶん同じ機器の同じブラウザで何度もチェックしましたが,ご指摘の不具合は起らないようです.6月21日に訂正していますが,キャッシュに古いデータが残っていないかどうか,一度リロードしていただくと状況が変わるかもしれません.
■[個別の頁からの質問に対する回答][
問題の解説が欲しいです
=>[作者]: 連絡ありがとう.少し派手気味のHELPを追加しました.
■[個別の頁からの質問に対する回答][空間における直線の方程式 について/14.08.25]
一式 は 二行目の文字の中で読めません。
=>[作者]: 連絡ありがとう.今はやりのTwitter風つぶやきのように短い文章なので,解読するのにとても時間がかかりました.
■[個別の頁からの質問に対する回答][独立な試行の確率,反復試行の確率 について/14.08.18]
わかりにくい問題 : 解答傾向が表示されない。
=>[作者]: 連絡ありがとう.今年の春にプログラムを変更したときに,間違った箇所がかなりあるうちの1つでした.(→「直して間違った」トホホ)訂正しました.
■埼玉県[ミラルさん/14.08.18]
■正規分布
第9問 / 全9問]
[第4問 / 全4問
終わらない(ずっと次の問題がクリック可)
=>[作者]: 連絡ありがとう.[第9問 / 全9問]と[第4問 / 全4問]は意味を考えればわかるとも言えますが,最後の問題になったときに,[*** END ***]と表示するか[次の問題]のボタンを消してしまうと確かにはっきりとわかるので,後者の案で変更しました.
■ 神奈川[ あttさん/14.08.17]
いつも拝見させていただいております。ありがとうございます。
検索サイトから、ある数学の単元のページにやってきて、そこからメニューにいく場合、一番下まで行く必要があるので、長いページだと少し不便かなと感じました。もし可能ならページの一番上にパンくず(?目次の階層みたいなもの)か「メニューに戻る」のリンクがあると便利かなと感じました。恐縮ですがご検討お願いします。 (追記、リンク在るページもありますね失礼しました。)
=>[作者]: 連絡ありがとう.各頁の上端か下端にメニューに戻るのリンクを作っていますが,長い年月の間に作ったもので,数千頁ありますので,今から揃えるのは大変です.今から作る頁について,上端からも下端からも戻れるというのはよいアイデアかな.(階層はなく1枚のメニューに全部ぶら下がっています.階層が深いのはよくないという考え方です)
■[個別の頁からの質問に対する回答][根号の計算 について/14.08.16]
解答がところどころ崩れる
3・4の解説ほしい
=>[作者]: 連絡ありがとう.式の見え方については,あなたと同じPCのIE11でかなりチェックしているので,このぐらいが現在のベストエフォットかな.3・4の解説については,問題文が詳しい解説になっているので,これ以上書けることが思いつきません・・・屋上屋を掛ける(=慎重に慎重にやり過ぎて,屋根の上にさらに屋根をかけて雨漏りを防ぐ態度):体育館の屋根があるのに,大相撲で土俵の上にさらに屋根を付ける[あれはあれで伝統の流儀だが,他の場面で真似したら変]ようなイメージ
■ 東京都[ msrさん/14.08.15]
常用対数の問3の途中式が間違っています。
log[10]6=0.7781となっているのに40·log[10]6=40×0.7881となっています。
計算結果は正しい答えかと思います。
=>[作者]: 連絡ありがとう.小数第2位が入力ミスでしたので訂正しました.
■[個別の頁からの質問に対する回答][3次以上の因数分解(例題→選択問題) について/14.08.14]
気にいった所 : 左に少し文字がはみ出ている
=>[作者]: 連絡ありがとう.読者が使用している機器やブラウザによる見え方の違いについて,いろいろ調べています・・・直せる所は直した方がよいので・・・.Macのノートで1280 x 800 の画面だと,左端が切れるということかな?
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/14.08.14]
問題4
∫wn2xe−3xdx
の解がおかしい?
最後から2行目→最後の行の変換が計算間違い
答えのカッコの中は(x+3)ではなく、(3x+1)が正しいのでは?=>[作者]: 連絡ありがとう.訂正しました.
■埼玉県[ミラルさん/14.08.13]
tab移動ができるのとできないのがあるのはなぜ?
=>[作者]: 連絡ありがとう.この解説は,多少技術的なものになります.
■[個別の頁からの質問に対する回答][双曲線の方程式 について/14.08.13]
入力欄に半角英数字で入力できますか→できない
=>[作者]: 連絡ありがとう.iPhoneで入力方式を切り替えるには,「ABC」「☆123」「あいう」がトグルスイッチ(巡に回る仕掛け)になっているところを「☆123」に合わせるとよいようです.
■埼玉県[ミラルさん/14.08.07]
∑に関する説明の追加をおねがいする
=>[作者]: 連絡ありがとう.まず
この頁 を見てください.
■[個別の頁からの質問に対する回答][余弦定理 について/14.08.06]
IPad miniで見ていますが、ページの左端が切れて表示されます。
=>[作者]: 連絡ありがとう.iPadはよく分からないのですが,画面を横にしても見えないのですか?
■埼玉県[ミラルさん/14.08.07]
和の記号∑についての説明
左側クリック(間違えて)しかたないからその下をクリック
⇒土がつきました
これをなんとかしてほしい
=>[作者]: 連絡ありがとう.「振り出しに戻る」の設定はゲームてきですが,良いようで良くないところもあるので,「正解のときは消えて,誤答のときは何も起らない」設定に変更しました.
■埼玉県[ミラルさん/14.08.04]
ベクトルの2点赤から変わらず
=>[作者]: 連絡ありがとう.ベクトルの2点というのがどの頁のことなのかわかりませんが,「2点を結ぶベクトル」については問題に正解すればメニューの色は変わるようです.
■[個別の頁からの質問に対する回答][
整数で答える場所、つまり√のかかっていない部分はクリック出来ないので、タブキーで移動するしかできない。
=>[作者]: 連絡ありがとう.訂正しました.
■埼玉県[黒き死神改めミラルさん/14.08.04]
不等式の証明1
問3(3)反応しずらい
相加平均 相乗平均 調和平均
問3(2)反応しづらい
=>[作者]: 連絡ありがとう.ご使用のPCの反応が速いため,誤答→誤答となったときに,変わっていないように見えるということだと考えられます.(誤答→正答,正答→誤答の場合は,はっきりわかります.)
■[個別の頁からの質問に対する回答][
b, c , A が与えられているとき、直角三角形 AHC の3辺の長さが求
まるので、 HB , HC の値から三平方の定理を使って BC を求めま
す。
などの下地が白いところの文章が灰色で若干見にくいです
=>[作者]: 連絡ありがとう.本当はその箇所は下地が黄色なのですが,スマホのOperaで読んでおられるということで色調が違うものになっているのかもしれません.当該個所の文字色を1段黒くしました.
■埼玉県[黒き死神さん/14.07.31]
三角形の辺の長さ問い4反応せず
=>[作者]: 連絡ありがとう.入力した単語の綴りにミスがありました(documentのdが吹き飛んでいてエラーになっていました).何年もこの状態だったようですが訂正できました.
■埼玉県[黒き死神さん/14.07.30]
1.放物線の移動3の色が変わらない。
2.高校数学の通信欄が一度送ると送れなくなる。
3.↑間違えて送ったときに送れない。
4.間違えて送ってしまいました すみません
=>[作者]: 連絡ありがとう.<1.放物線の移動3の色>こちらでテストすると,正常に作動するようです.(By MS-IE.11)<2.3.高校数学の通信欄が一度送ると送れなくなる。>見破られてしまいましたか.実はその通りです.公開型のサイトの場合,世の中にはいろいろな主義主張の方がおられて,自分の主張に管理人が屈服するまで何千回となく,自分の主張を限りなく送り続ける方(確信型とかスト□□□型という感じの方)がごくわずかにおられることがあります.特に,このような初歩的な数学サイト向けには,「自分の発見した学説を掲載せよ!」という連絡がしばしば送られてきますが,とても対応しきれません.このような訳で,通信欄送信後に,一定時間経過しないと送信できない設定にしていますが,「お怒りがおさまる程度の時間が経過すると」(しばらくとはどれくらいかは未公開)元に戻りますので,悪しからず・・・炎上には反論で対応せず.ただ沈黙あるのみ.<4.>了解
■埼玉県[黒き死神さん/14.07.28]
3次以上の因数分解が赤から変わらない。
=>[作者]: 連絡ありがとう.申し訳ないことです.2014.4月以後の設定変更で「ミスがあったかもしれないな」と薄々は感じながらも,変更頁数が多過ぎて(それだけではなく,健康事情や家庭事情など作業に集中できない事情もあって)全数検査(何千頁あるのかも数えていません)ができていません.苦情があった頁を優先的に訂正していますので,クレーム歓迎です.
■[個別の頁からの質問に対する回答][固有値,固有ベクトルの求め方 について/14.07.27]
わかりにくい問題 : Operaを使っています。
=>[作者]: 連絡ありがとう.現在集計中ですが,PC上のブラウザの中でOperaだけはフォントの処理が独自の仕様になっており,数式をうまく表示することはできないようです.当サイトに関する限り原因ははっきりしており,Opera以外のブラウザは「Times系のフォントがあればそれで表示する」という指定を処理できますが,Operaだけは「はじめに指定されたフォントが理解できなければ(Times New Romanという個別のフォント名は理解できるがTimes一族のどれかで使えるものがあればそれを出すという指定が理解できない場合に)第2希望以下に指定されたフォントと無関係にとんでもないフォントを出す」という仕様になっているらしく,これは当サイトのような個人の努力では直せない問題だと考えられます.(アンケートの回答を見て,今までにいろいろと工夫してみましたが,スタイルシートだけに関係する部分は簡単に直せますが,ダイナミックに学習者の応答に応じてスタイルシートがらみのデータをその場で書き換えて行くとう構成上,いろいろ都合があって,Operaだけは対応困難です)
■兵庫[すかまさん/14.07.26]
変数分離型の微分方程式の例3の(3)式、log|y|+log e^Aではなくlog|x|+log eAになってしまってますね。
=>[作者]: 連絡ありがとう.yはxに直しましたが,他のご指摘は?です.誤解がないように元の文章を少し変更しなした.
■[個別の頁からの質問に対する回答][次数最低の1文字について整理 について/14.07.26]
◎cについて整理すると
⇒ (a2-b2)c+(a3-ab2) ⇒ 1次式の因数分解になる(1次式の因数分解などと大きな声で言うのも恥ずかしい。1次式では定数の係数でくくる変形だけがある。)
⇒ (a2-b2)(c+a) …(1)
ここがイマイチ理解できません。
(a2-b2)(c+a)ここに至るまでの過程
があると嬉しいです
=>[作者]: 連絡ありがとう.1行追加しました.
■[個別の頁からの質問に対する回答][展開公式1 について/14.07.22]
数字を見ると拒絶反応が出ます。算数も難しいと思う私でも分かるような方法ってありませんか?
=>[作者]: 連絡ありがとう.世間の俗説では,数学とは数の学問だと考えられていますが,今日いわれている解釈では数学と数字は何の関係もありません.むしろ,数学とは構造とか関係の学問だといった方が実態に近いかもしれません・・・たとえば,幾何学(図形)とか記号論理学(真偽を調べる--コンピュータ科学に広く使われる)には,根本的には数字は必要ない.・・・とはいえ,中学生や高校生が遭遇する数学には,実際には数字がどうしようもなくたくさん登場します.算数や方程式の解き方は,アラビアの錬金術師たちの苦心の跡を引きずっている伝承文化なのかもしれません.(♪~あー人は昔々・・・アラビアの砂漠で夜空の星を見ながら,こんな計算の仕方を考えていたのかもしれません)
■[個別の頁からの質問に対する回答][空間における直線の方程式 について/14.07.16]
[問題2]に誤植があるのではないでしょうか?問題とHELPの方向ベクトルが相違してます
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][(各駅停車)二重根号 について/14.07.15]
5頁目(2)に出題された問題、√{1+2√(6+4√2)}に置いて、恐らく正しい問題式は√{1+√(6+4√2)}かと思われます。
=>[作者]: 連絡ありがとう.複雑な問題で手直しが大変でしたがおそらく直りました.・・・この問題は固定されおらず,プログラム生成になっています.だから,人によっては違う問題が出されていますが,確かに4回に1回ほどご指摘の問題が出ます.ご指摘の訂正でもなおかつ解答が正しきなりませんので,√{− 1+2√(6+4√2)}に訂正しました.
■埼玉県[黒き死神さん/14.07.05]
■問題1 左の式の値に等しいものを右から選びなさい.
(ルール:左から一つクリックし,続けて右から「対応するもの」をクリックすると消えます.間違えば「ふりだしにもどる」.) 何度も間違えると左側上4つが選択できなくなる。
=>[作者]: 連絡ありがとう.この欄からの投稿の場合,どの頁のことなのかを明示していただかないと分かりませんが,アクセスログからは,前回と同様に累乗根のことかもしれないと判断して回答.ご指摘の現象は確認できませんでした--- Mozilla/5.0 like Gecko がFirefoxだとして,Firefoxでも調べましたが確認できず
■埼玉県[黒き死神さん/14.07.05]
rnの極限
3 一番右の選択肢反応せず。
=>[作者]: 連絡ありがとう.訂正しました.
■[個別の頁からの質問に対する回答][指数関数、対数関数の不定積分 について/14.07.02]
部分積分法の右辺二つ目が間違っている(微分、積分してる式が逆)
=>[作者]: 連絡ありがとう.訂正しました.
■埼玉県[黒き死神さん/14.07.04]
多項式の除法(割り算)
にて解答入力後、広告をクリックしてから戻ってくると入力されているのに判定されず、最初から入力することになる。
=>[作者]: 連絡ありがとう.申しわけないのですが,広告に触った時の動作については,筆者だけは確認できないことになっています.その場合は,再読み込みでスタートということでお願いします.
■埼玉県[黒き死神さん/14.06.27]
N進法の問題が全部で何問あるか先に表示してほしい。
=>[作者]: 連絡ありがとう.実はランダムに限りなく出題され,重複する場合もありますので,何題あるといえないため表示していません.そこで,読者の側から見て「何連勝したら」よいのかという目安の回数を新たに書きましたのでよろしく.
■[個別の頁からの質問に対する回答][複素数の計算(解説) について/14.06.21]
虚数 iに0をかけたらどうなるのですか?
=>[作者]: 連絡ありがとう.少しだけ注釈を追加しました.
■[個別の頁からの質問に対する回答][三角関数の加法定理,倍角公式,3倍角公式,半角公式 について/14.06.21]
問題で正解し消えた後に右側を選んでから消えたところを再度押すとまた表示されるようになる
=>[作者]: 連絡ありがとう.ご指摘のように「倒されたものが生き返る」プログラムミス(バグ)があるようですので,訂正します.・・・この頁は,毎日1000人以上が読んでいる超人気頁ですが,「倒されたものが生き返るかどうか」と試した人はめったにないのか,今まで指摘がなく筆者も気が付きませんでした.
■[個別の頁からの質問に対する回答][展開公式1 について/14.06.09]
答えのせてほしい
=>[作者]: 連絡ありがとう.この頁の問題は,左の解説から非常に近い所で出題しており,選択問題なので答は必ず分かります.(運が悪くても,クリック4回で当たりますが,そんなに答にこだわらずに,まず例を見て「真似をする」ことが重要です)
■[個別の頁からの質問に対する回答][データの代表値(平均値,中央値,最頻値) について/14.06.09]
問題2以降
何の平均値を求めるのか問題文から読み取れない
=>[作者]: 連絡ありがとう.すべての値が書かれている場合だけでなく,度数分布表に表されている場合の平均値,中央値,最頻値の求め方について,【例2】【例3】などを参考にしてください.当面の課題として,度数分布表に慣れることが重要です.
■[個別の頁からの質問に対する回答][ド・モルガンの法則 について/14.05.26]
問題を回答すると解説が表示されますが、それが次の問題に重なって読み辛い
=>[作者]: 連絡ありがとう.とりあえず,初めに「解説を読まない」ことを選択できるようにしました.
■[個別の頁からの質問に対する回答][http://www.geisya.or.jp/~mwm48961/koukou/center_root1.htmについて/14.05.26]
|2abx-a2 |<b2 が-b2 <2abx-a2 <b2 になる経緯がよく分からない
=>[作者]: 連絡ありがとう.例えば,|x|<3 ⇒ −3<x<3 を参考にすれば,a>0 のとき−a<x<a ⇒ −a<x<a という変形ができます.b2 >0 が成り立つので,|2abx-a2 |<b2 ⇒ -b2 <2abx-a2 <b2 になります.
[個別の頁からの質問に対する回答]⇒[http://www.geisya.or.jp/~mwm48961/koukou/expo_log_integral1.htmについて/14.05.24]
問題の(2)の∫2^xdxの答えにaが入っているのですが、そこは『2』ではないのでしょうか?
=>[作者]: 連絡ありがとう.ご指摘の通りですので,訂正しました.
■兵庫県[abcさん/14.05.14]
便利に利用させていただいています。2点間違い報告です。
/kou3/base2_2.htm 2進数の演算ページにて、
base2_2_4.gif の割り算の説明が、×掛け算と割り算でできます→掛け算と引き算
問題9 10111(2)→110111(2) (HELP内も含む)
だと思います。
=>[作者]: 連絡ありがとう.ご指摘の通りですので,訂正しました.
■神奈川[AKIRAさん/14.05.05]
統計検定の勉強で利用させてもらってます。
ありがとうございます。
リンク先の、一番下部の例題(4)'の解答間違っておりませんか?
http://www.geisya.or.jp/~mwm48961/statistics/sample1.htm
解答
1.96×6.76/√(n)≦0.5となるには
1.96×6.76≦√(n)
175.6≦n
176人以上
こちらの指摘間違いでしたら申し訳ありません。
=>[作者]: 連絡ありがとう.右辺の0.5を処理するを忘れていたようです.訂正しました.
■長野県[CEGIPOさん/14.04.26]
【三角関数のn倍角の公式の表現方法について】
このHPで三角関数の2倍角,3倍角(?),4倍角(?)の公式を拝見いたしました。
そこでn倍角に拡張して考えると...
(以下、a^bはaのb乗、iは虚数単位とします)
ド・モアブルの定理
cos(nθ)+isin(nθ)=(cosθ+isinθ)^n...[A1]
をまず考えます。
そこで、n倍角の公式の上手い表現方法があります。
それはド・モアブルの定理の共役複素数版
cos(-nθ)+isin(-nθ)=(cos(θ)+isinθ)^(-n)
を利用するというものです。
右辺=(cosθ+isinθ)^(-n)
={(cosθ+isinθ)^(-1)}^n
={(cosθ-isinθ)}^n
左辺=cos(nθ)-isin(nθ)
より
cos(nθ)-isin(nθ)=(cosθ-isinθ)^n...[A2]
で両辺に現れるのが確かに
[A1]式に対応する共役複素数になっています。
[A1]+[A2]/2より
cos(nθ)={(cosθ+isinθ)^n+(cosθ-isinθ)^n}/2...[B1]
[A1]-[A2]/2より
isin(nθ)={(cosθ+isinθ)^n-(cosθ-isinθ)^n}/2...[B2]
整理して
sin(nθ)=-i{(cosθ+isinθ)^n-(cosθ-isinθ)^n}/2...[B3]
さらにcosθ≠0の時は、[B3]/[B1]より
tan(nθ)
=-i{(cosθ+isinθ)^n-(cosθ-isinθ)^n}
=/{(cosθ+isinθ)^n+(cosθ-isinθ)^n}
= -i{(1+itanθ)^n-(1-itanθ)^n}
=/{(1+itanθ)^n+(1-itanθ)^n}...[B4]
まとめると、
cos(nθ)={(cosθ+isinθ)^n+(cosθ-isinθ)^n}/2
sin(nθ)=-i{(cosθ+isinθ)^n-(cosθ-isinθ)^n}/2
tan(nθ)
= -i{(1+itanθ)^n-(1-itanθ)^n}
=/{(1+itanθ)^n+(1-itanθ)^n}
となります。n=1~1000000...まで一貫して使える便利な記法だと思います。
(未確認ですが、n=0,n=-1~-1000000...でも成り立つと思います)
=>[作者]: 連絡ありがとう.変形は正しいと思います.(ただし,tanの式の=/{のところは =がいらない.2箇所)
頑張って研究してもらったのに,言い方によっては水を差すような発言になるとまずいのですが,どちらかといえば
[この頁] の途中経過に使っていますように,
cos nx= , sin nx= の形で,普通に使うと思う.
■東京都[bunmpkinさん/14.04.24]
数1 根号計算 問題3のア)は減少ではなく 増加ですね。
=>[作者]: 連絡ありがとう.x<−1/2 のとき,y=−4x は正ですが,関数は減少です.もしこれがy'=−4x となっていたら,ご指摘の通り増加になりますが,ここではy=−4x のグラフを考えると減少だということが分かります.(たぶん,すでに微分を習っておられて,深読みされたのかもしれません)
■東京都[bunmpkinさん/14.04.24]
数1 3次以上の因数分解の右上の{Ⅰ}}Ⅱ}の例の式(2x-3)(x二乗+(2x)3+3二乗)の右の( )内の最初のxは(2X)ですね。 問題4の(1)の答の右の(x二乗ー3x
-4)は(x+1)(x-4)に因数分解できます。
=>[作者]: 連絡ありがとう.第1点は入力ミスなので訂正します.第2点は,だからその式は解答にならないようになっています.
■沖縄[静寂さん/14.04.19]
数Ⅲの複素数平面の【例】の(4)は点Dだと思います
=>[作者]: 連絡ありがとう.訂正します.
■北海道[pkd:fhjさん/14.04.13]
数学Ⅰの数と式 基本回答2⃣がわかりません
よければ解説願います
=>[作者]: 連絡ありがとう.どの頁の話なのか分かりませんので,画面上にURLを表示して,右クリック→コピーの上,質問文に貼り付けてください.
■東京都[asdさん/14.04.09]
数Ⅱ「理科における有効数字の表し方 」の光速が間違っています。
30万km/sです。
=>[作者]: 連絡ありがとう.単位が間違っていましたので訂正しました.
■千葉[平郎さん/14.02.22]
和積・積和の公式の問題で間違いがあるかと思われます。http://www.geisya.or.jp/~mwm48961/kou3/trigonometric23.htm
問題3の(4)の答えの確認をよろしくお願いします。
=>[作者]: 連絡ありがとう.符号が逆になっていたようですので,訂正しました.
■広島[牢人さん/14.02.10]
「軌跡の方程式2」の例題2の解答で、
一般に (x-a)2+(y-b)2=r^2 は円を表わす.
この形に直すためには
(2x-4)(2x-4)+(2y-2)(2y-2)^2=2
の両辺を2で割っただけでは
(x-1)(2x-4)+(y-1)(2y-2)^2=2
になり変形不十分
さらに2で割ると
(x-1)(x-2)+(y-1)(y-1)^2=1 になる.
要するに,(4)を 4 で割ればよい.
とありますが、
一番目の式の右辺は2ではなく4
(x-1)ではなく(x-2)
(2y-2)^2ではなく(2y-2)
(y-1)^2ではなく(y-1)
だと思います。
今まで軌跡の求め方がいまいち理解できなかったのですが、このサイトでだいぶ納得できたように思います。
「【要点】 軌跡の方程式の求め方」が分かりやすかったです。
=>[作者]: 連絡ありがとう.ご指摘の点はすべて不注意による入力ミスですので,訂正しました.
■大阪府[あいうさん/14.01.24]
「導関数の定義」のページについて、
解説の「2.f(x) = x2 のとき」のくだりの最後、f’(a) = 2xじゃなくて2aじゃないでしょうか? あと、質問なんですが、問題がf(x)=・・・の時、計算がf’(x)=・・・、y=・・・の時dy/dx=・・・になってますが必ずこのようにしなくてはならないのでしょうか?
=>[作者]: 連絡ありがとう.前半は入力ミスなので訂正します.後半は,f’(x),df(x)/dxのどちらでもよく,y’, dy/dxのどちらでもよい.しかし,問題がf(x)のときにy’とか,問題がyのときにf’(x)とかは対応しません.
■神奈川[こぽんぽさん/13.12.15]
よく利用しています。
さて、数Aの必要条件・十分条件のセンター2012年本試験の問題に順番間違いが
あります。
2番と3番が入れ違っています。回答2番が、「m≦k かつ n≦k」と
なっています。
=>[作者]: 連絡ありがとう.問題の順序がちがっていましたので,訂正しました.
■東京[しみずさん/13.11.23]
了解いたしました。助かっております。
JScriptで次のページを組んで検証していたためにお邪魔してすみません。
スクリプトは自由に改変・発表してかまいません。
http://homepage3.nifty.com/01117/kai2.htm
=>[作者]: 了解しました.
■東京[しみずさん/13.11.22]
カイ2乗検定,ポアソン分布ページの
(3) カイ2乗検定[ポアソン分布との適合性]の
ヒントの表の理論月数の計が合いません。
また、回数0のカイ2乗値はおかしくないですか?
=>[作者]: 連絡ありがとう.観測月数の方は実際の月数を数えたものなので,必ず整数になりますが,理論月数の方は曲線に当てはめたときの理論値なので,本来は小数となる月数を四捨五入によって丸めたものです.このため,ご指摘のように合計が120になっていません.(微妙な問題ですが,このような形で文章化するとき,確かに鋭い読者から疑問を持たれる場合がありますので,小数を四捨五入した結果として合計が合わなくなってしまった場合,欄外にその旨注釈を付ける方法が1つ考えられます[A].また,文書としての整合性を重視して,合計が合うようにしてしまう・・・個々の確率のうちで加減しても最も影響を受けにくい「最大項」=ここでは1回の33を34にしてしまうという方法がもう一つ考えられます.[B]・・・公表する統計で百分率の合計が100%にならないときなどに使う)
■神奈川[oioiさん/13.11.17]
=>[作者]: 連絡ありがとう.ご指摘の通りで,間違っていましたので訂正しました.
■島根[あさん/13.11.12]
http://www.geisya.or.jp/~mwm48961/linear_algebra/independent1.htm
を理解の参考とさせてもらいました。ありがとうございます。1点気になるところがあり、
例2 次のベクトルの組が1次独立かどうか調べよ.では、det(A)=16となり一次独立ではないでしょうか?
x=1, y=1, z=-1で右辺は(0 2 0)になるはずです
=>[作者]: 連絡ありがとう.その下に書かれている(*1)の求め方の記述が正しく,例2の行列の成分中 (2,1)成分の符号が逆になっていましたので,訂正しました.
■東京[olimpicさん/13.10.19]
ちょっとした間違いの報告です
http://www.geisya.or.jp/~mwm48961/kou2/s1sc205.htm
このページの最後の問題の解説において
b-c=x^2-4-(4x+4)=x^2-4x+8=(x-2)^2+4>0 となっているところに計算ミスがあります
b-c=x^2-4-(4x+4)=x^2-4x-8 が正しい
b-cの正負はxの値によって場合わけしなくてはならないので
代わりにa-c=(x^2+2x+4)-(4x+4)=x^2-2x=x(x-2)>0 なぜならx>2
a-b>0 a-c>0 ⇒ aは最大辺になる
以下の証明は同じで結果は変わりません
=>[作者]: 連絡ありがとう.訂正しました.
■?[?さん/13.9.25]
初歩的な質問だと思います。すみません。
逆三角関数
http://www.geisya.or.jp/~mwm48961/electro/inv_trigono1.htm
(y=sinx、y=cosx、y=tanx の説明の部分のグラフが表示されていません。)
についての質問です。
技術士第一次試験問題のHELPをクリックして、解き方を見ても、α、βの
変域の設定をどの様にすれば良いのか分かりません。
現在、『大学生の微積分』という本で、勉強をしています。
微積分の知識はほとんど無くて、上記の本の問題を書き写しながら、
分からない初歩的な事を、インターネットなどで調べながら進めています。
現在、学習しています問題は、上記の本の
問題14(1)
sin^-1(5/13)-2cos^-1(4/5) = cos^-1(204/325)
の証明です。
解説は、
sin^-1(5/13)=α、cos^-1(4/5)=β とおくと
0<α<(4/π)、0<β<(4/π)で…
と続くのですが、この変域の設定が、全く理解が出来ず、
ヒントとして、
「α-2βの書くの変域を考える必要があるので、4/πと比較して
このようにした。」とありますが、これも理解が出来ません。
上記の様な質問にはお答え頂けないかも知れませんが、
浅尾様がお作りのページで、上記の変域のことを分かり
やすく説明されているページがあれば、そのページを見たいと
思いますので、そのページのURLだけでも教えて頂けませんか?
よろしくお願い致します。
=>[作者]: 連絡ありがとう.他の本に出ている問題は,原則としてお答えしません.転記ミスなども,気になるところです:4/π⇔π/4は正しく転記できていますか?証明すべき式の右辺の符号は合っていますか??
■東京[olimpicさん/13.9.13]
山の高さ(http://www.geisya.or.jp/~mwm48961/koukou/sctl001a.htm)について。
正解として受け付ける数値は342になっていますよね。
windows7付属の電卓で次のように計算します
(1000*tand(10))/(tand(20)-tand(10))*tand(20)=342.02014332566873304409961468226
小数点第一位で四捨五入した値342を入力すると正解になります。
しかし、付属の電卓で計算すると丸め誤差によって結果は341.89238になります。
小数点第一位で四捨五入した値341.9を入力しても正解になりません。
付属の電卓の三角関数の計算結果の小数点以下の桁数を増やすとよいかもしれません。
補足ですが、小数点第一位で四捨五入した値を求めているのに
342.0を入力すると不正解になることも不適切ではないかと思いました。
=>[作者]: 連絡ありがとう.丸めの誤差とか,あまり他の要因で答が変わるのは確かに余りよくないかも.今,余裕がないので後日検討します.
■神奈川[虚時九さん/13.8.27]
指数関数グラフ(y=a^x)で、a=0 の時と、a<0 の時はどのようになるのでしょうか?
a=0 は x=0 で1 x<0 で無限大 x>0 で0でしょうか?
a<0 は xが整数以外の時はどうすればよいのでしょうか? ご示唆お願いします。
=>[作者]: 連絡ありがとう.高校では,指数関数y=a^xにおいては,a>0, a≠1の場合だけを扱います.
■千葉県[さるさん/13.4.11]
「ド・モアブルは出たり入ったり」のようなことを読んだ覚えがあります。いろいろあるのでしょうが、何やら迷惑な話ですね。今回は3点ほど。
http://www.geisya.or.jp/~mwm48961/kou3/quadratic_1.htm、初めの説明文の「頂点」(青字)の直前のB’(-b,0)→B’(0,-b)
http://www.geisya.or.jp/~mwm48961/kou3/quadratic_3.htm、最後の問題、準線の方程式の最後のx
http://www.geisya.or.jp/~mwm48961/kou3/quadratic_4.htm、«基本事項のチェック»(2) 最初の式のx項の分母の4→9
=>[作者]: 連絡ありがとう.すべて訂正しました.
■千葉県[さるさん/13.4.3]
[Excelで定積分を計算するには]は、グラフ作成のプロセスの中で微積分の要素の意味や要素間の関係を具体的に確認できて、とてもよかったです。2点ほど指摘を。=>[作者]: 連絡ありがとう.すべて訂正しました.(2つ目の間違いが常用対数を使ったせいだと気付かれたのには脱帽)
■千葉県[さるさん/13.3.30]
数Ⅲ[導関数] 漸近線の方程式2 は、「漸近線といえば双曲線」程度の認識だったのでとても興味深かったです。グラフがあると視覚的に確認できていいですね。=>[作者]: 連絡ありがとう.すべて訂正しました.
■千葉県[さるさん/13.3.23]
このサイトを利用していて、よく思います。「高校数学ってこんなに難しかったっけ?」なまじ流れの中で答えを出せていただけ、本質を理解するまでには至らなかったのだと痛感しています。(その不安は当時からありましたが。)
[http://www.geisya.or.jp/~mwm48961/kou3/exp_log1.htm、4.指数関数、対数関数の微分計算、例1]で x-2 が途中から x-1 になっています。答えはあっているようです。
[http://www.geisya.or.jp/~mwm48961/kou2/d_general2.html#、22、問題1]の答えは、1/2(sin(α+β)+sin(α-β))を使って 4cos(8x)-cos(2x) もあると思います。
とりあえずご報告まで。
=>[作者]: 連絡ありがとう.1つ目:ご指摘の通りで,訂正しました.2つ目:確かにそれも行けます.(ただし,選択問題では正しいものを1つ選ぶことになります.)
■?[?さん/13.3.18]
逆関数の項目 問2の2問目のヘルプで
ff=I となればよいから
a(ax+b)+b=x が恒等式
⇔ (a^2-1)x+(a+1)b=x が恒等式……ここ=0ではないでしょうか?
=>[作者]: 連絡ありがとう.移項したら右辺のxがなくなるはずなので訂正しました.
■千葉県[さるさん/13.3.15]
素晴らしいサイト、ありがとうございます。特にExcelとの絡みが好みです。
(各駅停車)ベクトルの内積、6ページ目の問2、一辺が2の立方体の面の対角線どうしの内積の問題で、答えが2とありましたが、4が正しいと思います。正しくなかったらごめんなさい。
=>[作者]: 連絡ありがとう.間違っていましたので訂正しました.なお,一度読まれた場合,パソコンのキャッシュに古いデータが記憶されますので,手動でリロード(再読み込み↓↑)していただく必要があるかもしれません.
■北海道[yosshiさん/13.3.3]
詳しく教えていただき、ありがとうございました。そういう逸話があったとは、知らず勉強になりました。とってもすばらしく、わかりやすい問題なのでいつも活用しています。今後ともよろしくお願いします。そして、お互いに数学が分かりやすくなるようにがんばりましょう!
=>[作者]: 連絡ありがとう.
■北海道[yosshiさん/13.3.2]
いつもお世話になっています。質問(間違いと思われる箇所の指摘)なのですが、数Bの数列「規則を見つける問題(文字)」の(7)で、ヒントが月の頭文字ですと言うので英単語での月はmoonなので、Mをいれましたが、不正解になりました。ほかにあるのか教えてもらえませんか?
=>[作者]: 連絡ありがとう.おそらくとてもまじめな方なのかなと想像します.
■群馬県[里見さん/13.3.1]
「必要条件・十分条件(等式)」についてです。
12 整数nについて
n^2が3の倍数であることは,nが3の倍数であるための ( )条件
とありますが、nは実数なので、
n=2√3のとき
n^2=(2√3)^2=12
n^2は3の倍数ですがnは3の倍数ではないので、
必要十分条件ではなく必要条件ではないかと思います。
まだ中学生でわからないことが多いですが、確認をお願いします。
=>[作者]: 連絡ありがとう.「整数nについて」と指定されているときは,nが整数である場合だけを考え,n=2√3のような場合は考えません.
■大阪[スナさん/12.12.10]
7
男子5人,女子3人の合計8人が1列に並ぶとき女子が互いに隣り合わない並び方は何通りあるか.
=>[作者]: 隣り合う並び方・隣り合わない並び方 の第7問のやり方についての質問ということらしいので,解説します.
まず,男子5人を並べる方法は 5!=120 通り…(1)
(
5 P
5 =5×4×3×2×1=120通りとしてもよい)
その各々について,両端を含めて隙間は6箇所あり,女子をこの隙間に並べる.
1人目の女子の入り方は6通り,2人目の女子の入り方は5通り,3人目の女子の入り方は4通り⇒6×5×4=120通り…(2)
(
6 P
3 =6×5×4=120通りとしてもよい)
(1)(2)より120×120=14400…(答)
(2)の計算をするときに,1人目の女子の入り方が6通り:
①男1②男2③男3④男4⑤男5⑥
であるのに対して,2人目の女子が入るときは1人目の女子が入った場所以外の5通りとするところがポイント.
①男1●男2③男3④男4⑤男5⑥
たとえば,上の図のように1人目の女子が②の場所に入っときに2番目の女子が同じ場所に入ると「女子同士が隣り合ってしまう」.だから,残りの5通りの入り方がある.同様にして,3人目の女子は前の2人の女子が入った場所以外の4通りになる.
■京都[kenjiさん/12.12.04]
いつもお世話になっております.
間違いと思われる個所を見つけましたので報告いたします.
http://www.geisya.or.jp/~mwm48961/kou3/bibun1.htm
ページ右側について,
2.f(x) = x2 のとき
f’(x) = limh→0(x+h)2-x2h = limh→02x+h2h = 2x
とありますが,
f’(x) = limh→0(x+h)2-x2h = limh→02xh+h2h = 2x
の間違いと思います.
(hが抜けています.)
よろしくお願いいたします.
=>[作者]: 連絡ありがとう.訂正します.
■沖縄県[mappyさん/12.11.29]
数学検定2級に1次免除で、2次満点合格できました!
=>[作者]: 連絡ありがとう.質問内容から考えて「かなりやっておられるようだ」とは思っていましたが,学習の成果があがってよかったです.おめでとう!
■神奈川県[Mickさん/12.11.9]
http://www.geisya.or.jp/~mwm48961/kou3/quadratic_2.htm の ■2 焦点の働きと軌跡 の中で、(c^2-a^2)x^2-a^2y^2=a(c^2-a^2) の右辺は a^2(c^2-a^2) では?
=>[作者]: 連絡ありがとう.2乗が抜けているということで訂正しました.
■埼玉県[YellowDetteiuさん/12.11.4]
http://www.geisya.or.jp/~mwm48961/kou2/para_episode3.htm の[問題2](2)で、主な誤答に「軸:x=2」が挙げられていますが、y = −2x^2+8x = -2(x-2)^2+8
でx=2は正答ではないでしょうか。 また、数学ではないですが、自分の環境では高校英単語の成績が保存されません。(IE9とfirefox16.0.2+アドオンIETab2 4.1.3.1で、http://www.geisya.or.jp/~mwm48961/hsword/eng_highschool_a1.htmで確認)
=>[作者]: 連絡ありがとう.
■群馬県[nsさん/12.09.23]
いつも勉強させていただいております。群馬県のnsです。
http://www.geisya.or.jp/~mwm48961/koukou/imaginary_number4.htm
の問題4の(2)と(3)の問題について不明な点がありました。
ご質問させてください。
問題4の(2)の答えは「商はx-1,余りは3」となっていますが、
2x^3-8x^2+13x-7 = (x-1)(2x^2-6x+7)となり、
正しくは「商はx-1、余りは0」がではないでしょうか。
また問題4の(3)の答えは3となっていますが、(2)を受けて
0が正しいのではないでしょうか。
=>[作者]: 連絡ありがとう.訂正します.
■沖縄県[mappyさん/12.09.12]
http://www.geisya.or.jp/~mwm48961/kou2/safrc101.htm
の問題(特に、階乗)の解説がほしいです。
=>[作者]: 連絡ありがとう.解説の表示方法を考えてみます.
■栃木県[おちゅんさん/12.09.08]
つい先ほど、偶然こちらのサイトを初めて拝見させて頂きましたが、図での説明(動径が表す一般角θ)がとても解りやすく理解の手解きとなりました。また、タッチ式での問題もとても便利です。あらゆるパターンを何度でもTRYできるので、非常に効率よく反復できます!感激しました!w しばらく利用させて頂きます。大の数学嫌いとしては、どうしてこうなるのか~、ということを、図なども交えて詳しく解説してくれているところがとても有難いです!ケアレスミスポイントや、注意すべき例外点がチョロチョロ足されているところも有難いです!今後も期待しております!(?)
=>[作者]: 連絡ありがとう.一層の充実に努めます.
■沖縄県[mappyさん/12.08.19]
http://www.geisya.or.jp/~mwm48961/koukou/sbim04.htm
の問題3の問3の判別式が間違っていると思います。
=>[作者]: 連絡ありがとう.DとD’が違っていましたので訂正しました.
■沖縄県[mappyさん/12.08.18]
http://www.geisya.or.jp/~mwm48961/koukou/imaginary_number3.htm
の(9)の答えは、
1+i
ではなく、
-1+iだと思います。
=>[作者]: 連絡ありがとう.これは少しまずいミスでした.問題の方の符号を訂正しました.
■沖縄県[mappyさん/12.08.18]
http://www.geisya.or.jp/~mwm48961/koukou/imaginary_number2.htm
の問題1の(5)の答えは、
-6√6i
ではなく、
-6√6
だと思います。
=>[作者]: 連絡ありがとう.入力ミスですので訂正します.
■沖縄県[mappyさん/12.08.04]
http://www.geisya.or.jp/~mwm48961/kou3/trigonometric24.htm
の問題5のy=√2sinθ+cosθはy=√3sinθ+cosθだと思います。
=>[作者]: 連絡ありがとう.入力ミスですので訂正します.
■沖縄県[mappyさん/12.08.03]
http://www.geisya.or.jp/~mwm48961/kou2/inductive_method3.htm
の例題1の(I)の
よって,n=1のとき(A)が成り立つ
は
よって,n=3のとき(A)が成り立つ
だと思います。
=>[作者]: 連絡ありがとう.入力ミスですので訂正します.
■沖縄県[mappyさん/12.07.11]
http://www.geisya.or.jp/~mwm48961/kou2/d_triangle2.html で、
lim sinx/x = 1
x→0
となることを、積分法で定義される面積を使うことは、循環論法になりませんか?
⌒
AH<AB<PBとなることを利用すれば、
sinx<x<tanxとなり、
1<x/sinx<1/cosx
1<sinx/x<cosx
x→0
ゆえに、
sinx/x=1(x→+0のとき)
といったように、証明できませんか。
=>[作者]: 連絡ありがとう.(モデムの故障で,機器の取り寄せ,プロバイダの確認などに合計1週間もかかってしまって,回答が遅くなりました.)
はじめに結論から:AH<ABは言えそうですが,AB<PBは簡単ではない.
※sinx/x→1に関係する循環論法については,受験参考書などでよくみるのは,sinx/x→1を使って(sinx)'=cosxを証明するのだから,(sinx)'=cosxを使ってsinx/x→1を証明するのは循環論法だという議論です.
確かに,ほとんどの教科書ではその組み立てになっていますので,見え見えに(sinx)'=cosxを使ってsinx/x→1を証明すると循環論法が目立ってしまいますが,あなたのように積分から持ってくるのはかなり遠いので,そこまで気づく人はめったにいないかもしれません.私は一応,物理出身なので数学専攻の人がどう言うか予想できないという断り書きの上で以下の個人的感想を読んでください.
(1) 高校では,生徒の発達段階に応じて理解しやすいように,面積を使ってsinx/x→1を証明しますが,数学の立場から言えば「幾何学を使って解析学の定理を証明している」ことになり論外な話です.解析学では解析学としてsinxは図など使わなくても,無限級数とか微分方程式の解として定義できるので,その定義からsinx/x→1や(sinx)'=cosxを示せば,幾何学とは無関係に証明できることになります.
(2) 今日では,積分は微分の逆演算として導入されますが,私が高校生の頃は定積分は無限級数の和として定義され,定積分を簡単に求める手段として不定積分を使うという数学史の流れに忠実な導入方法でした.したがって,親学問の数学から言えば,微分によって積分が定義されるのではなく,別のものとして発展したものにうまく接点が見つかったというように考えればよいと思います.
そこで,あなたの疑問は今日的な教え方のために生じたもので,数学自体にある問題ではないと考えられます:
高校の教科書は親学問と矛盾しないように注意深く配慮しながらも,(1)で述べたように「生徒の発達段階に応じて理解しやすいように」工夫しなければならない要素があります.はじめから無限級数で正確に定義して,ほとんどの生徒が分からないようにしてしまえば元も子もないことははっきりしています.
今日の教科書では,例外なく微分の逆演算として不定積分を導入し,これを用いて定積分を定義しますが,(2)で述べたようにそれは親学問の流れとは違うようです.だから,親学問では何も矛盾はなくても,たまたま高校での教え方の順序のために,循環論法に見えるのだと考えられます.
(※この件について,筆者は自信満々ではありません.ただし,定積分から循環論法をもってこられた推論力はすごいと思います.)
■沖縄県[mappyさん/12.07.08]
http://www.geisya.or.jp/~mwm48961/kou2/prccen01.htm
の《もとの問題1》の(2)の
Aから2個取り出す方法は
4C2=6通り.
は
Bから2個取り出す方法は
4C2=6通り.
だと思います。
=>[作者]: 連絡ありがとう.(モデムの故障で,機器の取り寄せ,プロバイダの確認などに合計1週間もかかってしまって,回答が遅くなりました.)
■高知県[JYさん/12.07.03]
早速のお返事感謝いたします。
丁寧に説明していただき、ありがとうございます。
高校の参考書にも、そのようなことが書かれていると知って驚きました。
特にA側の参考書では、極限関数という特殊な関数に限って定義を変えてしまっているので、それはそれでマズイと思いますが(数学における定義はどんな状況であれ、変わるものではありません)。
ただ、正確にはx=aにおける関数の連続性は、前に申し上げた通り''aを含む開区間(x, y)で定義された関数''に対して定義されるものです。
高校ではそうではないと言われれば、それまでなのですが・・・。
お騒がせいたしました。
=>[作者]: 高校では親学問(数学)と矛盾しないように注意しながらも,直感的に理解させる程度にとどめることが求められており,単純明快に定義して当てはまるか当てはまらないかで考えるのがよいようです.ではまた.
■高知県[JYさん/12.07.03]
早速のお返事ありがとうございます。
申し訳ありません、どの項のことか書いていなかったのですが
数Ⅲ[関数] の 関数の極限、極限関数 の定義の条件(2)についてです。
連続関数という言葉を使ってしまったので、混乱を招いてしまったのかもしれません(x=?においての連続性と言うべきでした)。
恐らく1点で不連続というのは、関数が定義されてないから不連続ではなくて、1/xのような関数の場合、x=0の1点でどのように関数を決めても不連続になるから、それを不連続点として扱おうという意味だと解釈しています。
通常の高校生向けの参考書では、例えば(x^2-1)/(x-1)のような関数であっても、x=1は不連続点だと考えているのでしょうか。
=>[作者]: 手元の問題集,参考書などで関数の連続性について調べてみると,
■高知県[JYさん/12.07.02]
初めまして。JYと申します。大変恐縮ではございますが、多くの学生さんもこのサイトを参考にされているようですので、気づいた点をご報告させて頂きたいと思います。
もし、作者様の意図していることと違っていたら申し訳ありません。
連続関数の定義についてですが、f(a)の存在を連続の定義に入れていますが(私にはそう見えたので)、そうしてしまうと少しまずいのではないかと思います。というのも、正確には関数の連続性というのは、aを含むある開区間(x,y)で定義された関数に対して議論されるもので、1/xのようなx=0のところでは定義されてない関数に対しては連続かどうかの議論はできないと思います。
=>[作者]: 連絡ありがとう。本来,関数の連続性は定義域の中で考え,関数が定義されていない点では,連続かどうか議論しません.したがって,y=logx などにおいてはx≦0においては連続かどうかという議論もしません.しかし,1点だけで定義されていないときは,この点を不連続点として扱うのが普通です.このことが明示的に書かれている参考書もあります.
■東京都[りっちゃんさん/12.05.18]
たすき掛けの問題がよかったです。また、作ってください。
=>[作者]: 連絡ありがとう。自分で言うのも何ですが,ちょっとした苦心の作かも.
■沖縄県[mappyさん/12.05.13]
x^3+y^3+x^3 - 3xyz
の三項目です。
=>[作者]: 連絡ありがとう。分かりました.xとzの入力ミスということで訂正しました.
■北海道[yosshiさん/12.05.14]
複素数と方程式の解説、問題を作ってほしいです。よくわからないのでお願いします。
=>[作者]: 連絡ありがとう。複素数の内容は数学Ⅱの高次方程式の項目に少し作っています(数学Ⅱのメニューの下端にあります)が,具体的には複素数のどのような問題のことでしょうか.(複素数平面やド・モアブルの定理は学習指導要領から出たり入ったりでH25.4から変わるようですが,ご質問の内容は数学Ⅱの複素数ですよね?)この数学Ⅱの複素数については,もう少し教材を充実させなければいけませんが,今すぐという約束は無理なので「そのうちに」ということで・・・
■沖縄県[mappyさん/12.05.13]
http://www.geisya.or.jp/~mwm48961/kou2/sqrt2002.html
の対称式の問題5が、x^3+x^2y++xy^2+y^3
になっています。ヒントの式も間違っています。
=>[作者]: 連絡ありがとう。3項目にプラスが2つ付いているということで訂正しました.
■沖縄県[mappyさん/12.05.13]
http://www.geisya.or.jp/~mwm48961/kou3/factor1.htm
の、8番目の問題で、
x^3+y^3+x^3 - 3xyz=(x+y+z)(x^2+y^2+z^2 - xy - yz - zx)
は、
x^3+y^3+z^3 - 3xyz=(x+y+z)(x^2+y^2+z^2 - xy - yz - zx)
だと思います。
=>[作者]: 連絡ありがとう。元の内容と訂正内容がどう違うのかがよく分かりません.何回か読んだのですが・・・
■東京[YKさん/12.05.09]
http://www.geisya.or.jp/~mwm48961/koukou/saabs001.htm
《問題》 ■1
||x|-1|-1|=kの解の個数を調べなさい.
オ) k>1のときの解は無限個なのではないでしょうか?
お手数ですが解説お願いいたします。
=>[作者]: 連絡ありがとう。グラフを見れば,k>1のとき y=||x|-1|-1| と y=k とは2箇所で交わっているので,解の個数は2個になります.
■東京[YKさん/12.05.07]
http://www.geisya.or.jp/~mwm48961/koukou/saabs001.htm
問題
(2)
-1<x≦1/2のとき,2|x+1|+|2x-1|
を簡単にすると
-1<x<1/2 の誤りではないでしょうか?
=>[作者]: 連絡ありがとう。結論から言いますと間違いではありません。
その頁のそこまでの解説を読むと,絶対値記号が次のように外せることが分かります.
1) |x+1|の外し方
ア.x<−1のとき−(x+1)
イ. x≥−1のときx+1
⇒この問題では−1≤xの場合と書かれているから,イの場合分けを使ってx+1になります.
2) |2x−1|の外し方
ア. x<1/2のとき −2x+1
イ. x≥1/2のとき 2x−1
⇒この問題ではx≥1/2の場合と書かれているから,アの場合分けを使って−2x+1になります.
(x=1/2の場合も含めてもよい)
以上により,(原式)=2(x+1)−2x+1=2x+2−2x+1=3
■東京[YKさん/12.05.07]
いつもお世話になってます。質問です。
http://www.geisya.or.jp/~mwm48961/kou2/sqrt2001.html
(定理1)
a,bが有理数のとき,a+b√2=0 ←→a=b=0
←→
この記号の意味は何でしょうか?
問題1のヒント
a+16-(2a+4)√2=b-10√2
と変形すると,a,bが有理数であるから
a+16=b,2a+4=10
a,b有理数だとどうして√2と係数の部分が消えるのでしょうか?
解説何度もよんで他のサイトもみたのですがわかりません。
お手数ですが解説お願いします。
=>[作者]: 連絡ありがとう。
前半の回答:
←→は右向き矢印も左向き矢印も両方とも成り立つ(必要十分,同値ともいう)ことを表します.
例えば,「a=1→a>0」は右向き矢印だけが成立し左向きは成立しないことを表します.
これに対して,「a+1=3←→a=2」は「a+1=3」ならば「a=2」も成立し,「a=2」ならば「a+1=3」も成立することを表します.
後半の回答
それがまさに定理1の内容です.「a,bが有理数のとき,a+b√2=0 ←→a=b=0」の定理を右向きに読むと
a+b√2=0 ならばa=0かつb=0というように2つの式に分けられるのです.
(このときにa=0かつb√2=0と変形するのは,高校生がよくやる未熟な変形でb=0とすることろが重要です)
■沖縄県[mappyさん/12.05.05]
http://www.geisya.or.jp/~mwm48961/koukou/bunten01.htm
の外分点の画像
http://www.geisya.or.jp/~mwm48961/koukou/gaibun01.gif
は、??
だと思います。
=>[作者]: 連絡ありがとう。訂正しました。
■沖縄県[mappyさん/12.04.22]
http://www.geisya.or.jp/~mwm48961/koukou/saabs001.htm#mebun
の例10
次の関数の最小値を求めなさい.
y=4|x|-3|x-1|+2|x-2|-|x-3| =>[作者]: 連絡ありがとう。訂正しました。
■?[Qさん/12.04.06]
数1の式の展開(4)の問題の答えが間違っています。確認お願いします。
=>[作者]: 数1の式の展開(4)という項目はありません.項目名と小問番号を書くか、または、URLを書くようにしましょう(ブラウザの一番上の欄で右クリックしてコピー→連絡欄に貼り付け)。また,間違っているというときは、自分の考えも書きましょう。・・・間違っていることはありますが、どの問題がどう間違っているのかを伝えないと直せません。
■沖縄県[mappyさん/12.04.01]
http://www.geisya.or.jp/~mwm48961/kou3/exp_log1.htm
の
2. 指数関数,対数関数の導関数
で、
(2)において,a^h-1=t とおくと,
h→0 のとき,a^h→0 だから,t→0
の
a^h→0
は
a^h→1
だと思います。
=>[作者]: 連絡ありがとう。訂正しました。
■長野県[けにいさん/12.03.11]
誤殖がありました。「まとめのチェックテスト」→「場合の数, 順
列, 組合せ」→「(7) 多項定理」の答えは -12831 です。解説の下
の方
イ) p = 2 のとき,q = 3, r = 2
このとき係数は 7!/(2! 3! 2!) (- 2)^3 3^2 = -2520
が違っており、正しくは -15120 です。よろしくお願いします。
=>[作者]: 連絡ありがとう。訂正しました。
■埼玉[まなぶさん/12.03.4]
お世話になっております。早速ですが、■定積分 問題2(1)は誤りかと思います。 ご確認ください。
=>[作者]: 連絡ありがとう。表示されている式を訂正しました。
■宮崎県[れもさん/12.02.19]
いつもお世話になります。数II[円][考え方]2円の交点を通る円の方程式 の問題3の
答えが合っていない気が致します。(自力で解くと虚数解になる。-2x+y-10に、答えの(x,y)=(5,0)を代入しても0にならない。)
ご確認よろしくお願いします。
=>[作者]: 連絡ありがとう。問題の符号と係数を訂正しました。
■東京都[heinerさん/12.02.07]
三角関数の不定積分で二つ質問があります。
1.問題2の(3)の解説で1/(1-t^2)をー1/(t^2-1)に変換する必要があるのでしょうか?このため後で|sinx-1|→|1-sinx|の別の変換が必要になっています。なお、1/(1-t^2)のままで計算すると答が1/2log{(1+sinx)/(1-sinx)}+Cとなり、解説の答とlogの係数の符号及び分子・分母が逆になります。logの場合どちらでも正しいと思いますが、表示の決まりがありますか?
2.問題3の(2)の解説でf=s=e^-2x/2とありますが(-)記号が抜けています。計算の過程では(-)が付いています。
=>[作者]: 連絡ありがとう。1.について:最高時の係数を負の数にすると間違いやすいので、直す方がよいでしょう--そうしなければならない訳ではないが、そのまま行うと半分以上の高校生が符号で間違うという「実績」があります。2.訂正しました。
■東京都[heinerさん/12.02.07]
三角関数・不定積分の最後の問題(13)sin5xcosxはcos5xcosxですね。解説を見てわかりました。
=>[作者]: 連絡ありがとう。問題の入力ミスを訂正しました。
■東京都[heinerさん/12.02.06]
指数関数・対数関数の不定積分の最後の問題(3)の答えの一番右側の式はー(x^2+2)ではなくー1/2・(x^2+2)ですね。解説は正しく表記されています。
なお、小生が部分積分法でやると1/2(x^2+2)log(x^2+2)ー1/2x^2+Cとなりました。実質的に同じ答えと思いますが、正解と見做されますか?
=>[作者]: 連絡ありがとう。{ }が抜けているということで訂正しました。後半はOKです。
■東京都[heinerさん/12.02.03]
分数関数不定積分(1)の例題(2)!!)-3の答えは
-1/2・(2x+3)^-2ではなく、1/2・(2x+3)^-1だと思います。
=>[作者]: 連絡ありがとう。計算間違いでしたので訂正しました。
■東京都[heinerさん/12.01.28]
数Ⅲ・商の微分の最初の定義のところで、大分母としてのhが抜けているのではないでしょうか?
=>[作者]: 連絡ありがとう。ご指摘の通り抜けていましたので、訂正しました。
■東京都[リベンジさん/12.01.26]
いつもお世話様です。数日前に今までの記録が消えてしまい、新たに問題を解いたところ、反映されなくなりました。その上、解いた覚えのない中一数学の問題を「26頁」やったことになっていて、「まだ進み具合を送信できない」状態です。どうしてなのかさっぱりわかりません。このままご挨拶もなく消えていくのは本意ではありませんので、こちらで一言お礼を申し上げたいと思います。管理人様には素晴らしいサイトをありがとうございました。おかげさまで楽しく勉強させていただきました。進み具合は送ることができなくなりましたが、これからも数学を学んでいきたいと思います。本当にありがとうございました。参加されている皆さんもお元気で。頑張ってくださいね。
=>[作者]: 採点、記録、送信などすべてのプログラムが自作であるため、プログラムの作動について、手掛かりが少ないので答切れません。残念ですが・・・
■北海道[とんびさん/11.12.19]
数Bの「平面上のベクトル」で、位置ベクトルの応用1について、問題1と2の最後の問題、問題1でいうと「LN」、問題2でいうと「U」が選択できません。確認していただけますか。
=>[作者]: 連絡ありがとう。プログラムにミスがありましたので訂正しました。
■広島県[pahさん/11.12.15]
先ほど連絡させて頂きましたが、同じく数Ⅰの連立方程式の問題1の他の問題でも分母がきちんと認識されておりません。
ご確認ください。
=>[作者]: 連絡ありがとう。訂正しました。
■広島県[pahさん/11.12.15]
数Ⅰの連立方程式
問題1 [2]
3(x+1)≧2(x-2) …(1)
x-1>4(x+1) …(2)
ですが、解答欄に7,5,3と正解を入力しても3の所が正解となりません。
また、やり直すをクリックした場合に7と5の欄は空欄となりますが3の部分は空欄にならないため、入力がきちんと拾えてないのかと思います。
=>[作者]: 連絡ありがとう。訂正しました。
■神奈川県[nanasiさん/11.11.19]
分数関数 問題3の(4)の解答なのですが、
正解は「y=6/x+1 +2」となっていますが、正しくは「y=6/x+1 -2」ではないでしょうか?
(こちらの勘違いだったらごめんなさいm(_ _)m)
=>[作者]: 連絡ありがとう。正解は「y=6/x+1 -2」で、実際に「y=6/x+1 -2」と表示されていますので特に問題はないようですが、気になる点が1つあります。
■愛知県[かなさん/11.10.27]
sin46.8の問題なんですけど
解答欄に0.7289とうっても正解になりません(T_T)
しかし、右にある電卓の計算結果と一致していました。
エラーでしょうか?こちらの間違いだったらごめんなさい(T_T)
すごく活用させていただいています!ありがとうございます。
=>[作者]: 0.7193と0.7314を4:1に内分する値は、(1×0.7193+4×0.7314)/5=0.72898となり、右にある電卓で計算しても、0.7289686274214114となります。いずれも「小数点以下第4位まで計算」するには「小数第5位を四捨五入する」ので0.7290になります。
■北海道[OLLONさん/11.10.19]
高校数学・数Ⅰの『根号計算』で、問題4の答えが分かりません。
宜しくご指導頂けると助かります。
=>[作者]: こちらのミスで、分数と根号を表示する関数を書き換えたときに、解答と入力欄の照合関係が切れていましたので、訂正しました。
■北海道[yosshiさん/11.09.03]
隣り合う並び方の問題で、6番の「男子2人、女子4人が一列に並ぶとき、男子が隣り合わない並び方は何通りあるか」について、どうやって、答えを出すのですか?
=>[作者]: 連絡ありがとう。ヒントにもありますが、この問題の解き方は2つ考えられます。
■東京[やまさん/11.08.27]
今マックのパソコンでこのサイトをつかってるんですが、多項式の部分で最初の多項式の割り算のとこと商と積のところはサイトが閲覧できるのですが、そこから下がinternet explore 専用ページとなって開けません。以前ウィンドーズを使っていたのでこのことに気付かなくて、、、なんとかしてマックのsafariかfirefoxから閲覧できる方法はないでしょうか?このサイトが唯一の救いなのでぜひどうにか可能にしていただきたいです!
=>[作者]: 連絡ありがとう。現在のブラウザの普及状況は第二次ブラウザ戦争、ポスト第二次ブラウザ戦争などと言われることもあり、IEの支配による平和が崩れた結果としてプログラマには過酷な時代になってきたようです。可能な限りクロスブラウザを目指しますが、頁数が多いため簡単には書き換えられません。
■中国上海[小狼さん/11.07.21]
今剰余の定理(解説)のページを見ているところですげど、2次式で割ったときの余りの例1の3式がちょっと間違いです、私は2a+b=9だと思います。
=>[作者]: 連絡ありがとう。タイプミスですので、訂正します。
■青森県[ぱんけーきさん/11.06.06]
はじめまして、たまたまケアレスミス?を見付けました。媒介変数表示の解説部分で下記の(4)の箇所です。
■ 要点 --媒介変数の消去 (x,y関係式; 軌跡の方程式の求め方)
例○1 次の媒介変数表示をx,yの関係式に直しなさい。
x = -t +3・・(1)
y = 2t + 1・・(2)
(t は全実数)・・(3)
__________________
(1)より t = 3 - x
これを(2)に代入
y = (3 - x) + 1= -x +4 ・・・答・・(4)
既に気づかれたでしょうが、2t→tとなっていました。
私は少し前から閲覧利用させて頂いている者です。とても有難く思っております。僭越ながら、よろしくお願いします。
=>[作者]: 連絡ありがとう。訂正します。
■北海道[yosshiさん/11.05.31]
久しぶりです。高校になったばかりのyosshiです。今度分からない所で質問させて下さい!宜しくお願いします。
=>[作者]: 質問は構いませんが、どんな質問でも回答するわけではありません・・・入試問題に回答して事件になった例は、記憶に新しいところです。
■岐阜県[あかつきそうさん/11.05.12]
母平均の推定・信頼区間 例題4は
標本平均は157.5 では?
=>[作者]: 連絡ありがとう。訂正します。
■ニュージーランド[kiwiさん/11.04.10]
(無理関数と分数指数)の問題プログラムですが、
"累乗根の形"の枠にある一度選択した緑●を再度押すと正解の処理になるようです。
選択した両者の答えが同一だったら正解。という処理故のバグかと思います。
お時間がありましたらご確認くださいませ。
私はニュージーランド暮らしで、数学を日本語で習う機会がないので非常に助かっております。
=>[作者]: 連絡ありがとう。採点のロジックにバグがあるようですので訂正します。
■大阪[あさん/11.03.26]
勉強のため、サイト拝見させていただきました。
正規分布のページの右のカラムについてですが、
■正規分布
0 ≦ X ≦ m+uσ となる確率
とありますが、
m ≦ X ≦ m+uσ となる確率
ではないですか?
=>[作者]: 連絡ありがとう。間違っていましたので訂正しました。
■静岡県[ポテさん/11.02.26]
数学の授業でいつも役立ってます。ありがとうございます。数Ⅱ 多項式の除法 ■問題■ 問4(2x2+3x2 -11x+3)÷(x2+3x - 1)になっていまが1番はじめにある(2x2)は2x3ではないですか??
=>[作者]: 連絡ありがとう。間違っていましたので訂正しました。
■埼玉[learnerさん/11.01.08]
ご回答ありがとうございました。全くの勘違いで質問をしてしまいました。お恥ずかしい限りです。ご迷惑をおかけして申し訳ございませんでした。今後ともよろしくお願いい致します。
=>[作者]: 了解しました。
■埼玉[learnerさん/11.01.07]
サイトを拝見させていただいております。恐縮ですが質問をさせていただきます。
「ベクトル内積の定義」《問題》につきまして、答が9に相当する(つまりクリックすると消える)問題の答がなぜそのようになるのかがわかりません。ご説明いただければ幸いです。
=>[作者]: 連絡ありがとう。
ご質問の問題は、AB=3, BC=4, AC=5の「直角三角形」のことだと考えられますので、これについて答えます。
■1 まず、次の計算は基本ですからできるようにしてください。
ここで、
AB=3 , AC=5 , cos A=
だから
AB·AC·cos A=3·5·
=9
■2 次に右図のように
AC , cos A の値そのものは書かれていないときも、
AB·AC·cos A=[AB][AC·cos A] と見ると、
AC·cos A=b となることから、
AB·AC·cos A=ab となります。
このように、AC·cos A は、AB の線に投影した(符号付きの)長さ[有向線分]になります。初めの質問では[AB]·[AC·cos A]=3·3=9 とします。 ■神奈川県[yamakoさん/10.12.12]
三角関数の半角の公式を拝見しました
とても参考になりました
tanαの2乗の公式ですが(tanα)*(tanα)=(1-cos2α)/(1+cos2α)
=>[作者]: 連絡ありがとう。tan^2(α/2)の公式になっていましたので、至急訂正します。
■福岡[くーさん/10.08.31]
サイトとは関係ない問題なのですが参考書で「dy/dx + Ay = B」でAとBが定数のとき
「y=B(1-e^-Ax) / A」となっておりどうしたらこうなるのかが分かりません。
よろしければ教えてください。
=>[作者]: 「y=B(1-e^-Ax) / A」→「dy/dx + Ay = B」は微分すれば分かります。「dy/dx + Ay = B」→「y=B(1-e^-Ax) / A」は成り立ちません。あなたは、初期条件を写し忘れています。
■福岡[くーさん/10.07.31]
ありがとうございました。何となくですがeが何なのか理解できたと思います。
=>[作者]: 同じ趣旨の内容になりますが,y=ex やy=loge x の微分や(その逆の)積分の問題をやるとa=e 以外では込み入った計算になってとても大変で,a=e のときが一番扱いやすくなると考えれば,高校の範囲までは片付きます.y=ex だけが定義されていて他のy=ax などはそれを使ってy=ekx の形に書けると考えます.( ax =exlog a [対数の底が省略されていればe ] )
■福岡[くーさん/10.07.30]
ネイピア数に関して質問ですがネイピア数というのが一体何なのかがよく分かりませんでした。
どうしてeを使うのか、どういうときに使うのか、教えてください。
=>[作者]: この頁 に書きましたが,eが何なのかということについては様々な側面があります:数列の極限としての性質,微分(積分)に関する性質など.このことがその頁に書いてあります.
しかし,枝葉を取り除くと「
a=e の場合に限って
y=ax →
y’=ax となる」性質が最も重要です.(
y=ax →
y’=ax となるような(最も便利な)値
a を
e と書くことに決めたと考えてもよい.微分がなければ底は
10 で十分間に合う.微分に便利なように
e の値を決めたと考える.)
■福岡[くーさん/10.07.06]
数III[ 数列の極限 ]の各項目に貼ってある画像ですが一部見れなくなっています。(自分だけかもしれませんが・・・)
IE8を使っていますが何とかみれないでしょうか?
=>[作者]: 連絡ありがとう.数か月前に設定変更したときに,点検漏れがあったかもしれませんので直します.まだ直っていないところがあればお知らせください.
■兵庫県[Andyさん/10.07.03]
ありがとうございました。白1,黒1のところでつまづいていました。今後とも宜しくお願いします。
=>[作者]: 了解
■兵庫県[Andyさん/10.07.02]
問題の特定が不十分で申し訳ありませんでした。ホームページの問題です。表題が「確率のセンター試験問題」、出典は「 2002年度数1A追試験第1問(2)---一部引用」となっています。「 http://www.geisya.or.jp/~mwm48961/kou2/prob3000.html」のページで見ることができると思います。宜しくお願いします。
=>[作者]: Aが勝つのは2人の取り出した玉の個数の合計が(ア)0個のとき(イ)2個のとき(ウ)4個のとき のいずれか
■兵庫県[Andyさん/10.07.01]
申し訳ありません、教えて下さい。「[独立試行の確率/白玉・黒玉]A,Bの二人がそれぞれ袋をもっている。Aの袋には黒玉が3個と白玉が2個,Bの袋には黒玉が2個と白玉が3個入っている。(2)の後半、 二人の取り出した黒玉の個数の合計が,偶数ならばAの勝ち,奇数ならばAの負けとする。ただし,0は偶数に含めるものとする。Aが勝つ確率は?」という問題です。解説を基にトライしましたが正解にたどりつきません。(A,B)=(白2,白2)(黒0,黒2)(黒1,黒1)(黒2,黒0)の各々の確率の出し方を教えて下さい。
=>[作者]: 問題が見つかりません.(2)というのはこのホ-ムページの問題ですか?A,Bが玉を取り出す方法が指定されていないので計算できませんが・・・
■兵庫県[Andyさん/10.07.01]
ありがとうございました。とてもよくわかりました。今後とも宜しくお願いします。
=>[作者]: 了解
■兵庫県[Andyさん/10.06.28]
初めてお便りさせていただきます。兵庫県在住のAndyと申します。数学のセンスがないことは重々承知しています。そこをギチギチと努力で道を拓こうとしています。私のセンスのない質問に苦笑されているのが目に浮かぶのですが、どうぞ宜しくお願いします。
隣り合う並び方・隣り合わない並び方
「7 男子5人,女子3人の合計8人が1列に並ぶとき女子が互いに隣り合わない並び方は何通りあるか.」についてです。
男子5人を並べる方法は5!=120通り
男子の端または間は、6か所あり、この6か所から任意の(女子の座る)3か所を選ぶ方法は、
6C3=120通り
女子3人の並ぶ方法は3!=6通り
120×120×6=86400通り の誤りをご教示下さい。
そもそも、全体が8!=40320通りしかないので、この答が間違っているのはわかるのですが、
どこで道を踏み外したのでしょうか。宜しくお願いします。
=>[作者]: ( 6C3の計算が間違っており,6P3の計算になっています.そのため3!倍だけ大きな値になっています.)
■福岡[くーさん/10.06.23]
ありがとうございます。
書き込んだ内容が反映されていなかったので送信失敗したと思い同じような内容の質問を二回してしまいました。
すみませんでした。
=>[作者]: 分かってもらったということで,了解しました.
■福岡[くーさん/10.06.23]
ご返事ありがとうとざいます。
グラフの描き方は分かるのですがなぜあのような赤いラインの範囲を取るのかがわかりません。どうやって範囲を決めているのでしょうか?
=>[作者]: 例えば ア t<2のときは2t<4になるので,期間の右端2tは4(折り目となる山のx座標)よりも左になるなどと考える.(そのことが答案に書いてある)
■福岡[くーさん/10.06.23]
ありがとうございます。あのグラフになる理由が分かりました。
しかしなぜtがあのような範囲を取るのかがよく分かりません。
=>[作者]: -t≦x≦2tという範囲は,「どうして」ではなく「問題に書いてある」ことなので・・・あとはその範囲がどうなるかは区間の端2tの値に応じて,図形が変わるところで分類します.
■福岡[くーさん/10.06.22]
絶対値のところで
関数f(x)=||x-4|-5|に対し答えよ。という問題の(2)の解答ですが
「右の図のようになるのは…」と書かれていますがなぜそのような図になるのかが分かりません。どうしてあのような範囲になるのでしょうか?
=>[作者]: その前のところに,■2・・グラフを利用する方法・・《解説つづき》と書いてあります.
■東京[シロさん/10.06.21]
毎日勉強させてもらっています。
n
Σ2-K (-kは指数です)
K=1
答えは 2n-1 /2n のようですが、計算過程を教えてください。
=>[作者]: 答えの表し方が不完全で意味を解読するのが大変でしたが,次のように解釈できます.
(指数を ^ で表すものとする.例えばxの2乗はx^2,xの(-n+1)乗はx^(-n+1)で表すものとする.)
n
S=Σ2^(-k)とおくとS=2^(-1)+2^(-2)+2^(-+)+…+2^(-n)
K=1
2S=1+2^(-)+2^(-2)+…+2^(-n+1)
辺々引くと
-S=-1+2^(-n)
S=1-2^(-n)=(2^n - 1)/2^n
■滋賀[HIROTOさん/10.04.24]
数A 補集合 問題(3)のことなんですが=>[作者]: はじめに,記号の間違いを指摘:U∋A,Bと書くとUは集合を要素とする集合となって話がややこしくなるので,「A,Bが全体集合Uの部分集合である」ことを表すときはU⊃A,Bと書く方がよい.(数学基礎論で有名なラッセルの矛盾のような危ない話は避けた方がよい)
■埼玉[ちはるさん/10.04.11]
わかりました、ありがとうございました!
=>[作者]: 難しかったようですが,必ず乗り越えなければならないハードルです.
■埼玉[ちはるさん/10.03.29]
すごく数学が苦手で、基本的なところかもしれないのですが質問させてください。
絶対値のところの例(2)で答案にイ) x≧-2のとき, x+2とありますが
これはx>0のとき|x|=xよりですよね?でもx=-2だとx<0になるので|x|=-xになるんじゃないかと思うのですが、これはどうしてなんでしょうか。よろしくお願いします。
=>[作者]: そこのところを分かってもらうための問題です.このハードルがなかなか超えられないことが多いのです.⇒ その上に[重要]と囲みで書いていますが,中身全体が+になるか-になるかで判断することが重要です. | |記号の中身全体: x+2 の符号 を見て,x+2 ≧0より|x+2|=x+2すなわち0とします.例3も読んで,この変形に慣れてください.
■山梨[ゆっけさん/10.02.27]
疑問ですが、p⇒qのときP⊂Qならば、Pは十分条件、Qは必要条件といいますが、日本語的に考えると、QはPよりも多くの要素を十分にもっているから十分条件、逆にPはQよりも要素が少なくてQの要素が必要だから必要条件、という考えをもちました。
十分条件と必要条件のページに、普段使っている「十分」と「必要」という言葉と意味が違うとありましたが、意味的にどう捉えていいか分かりません。
何か、よい考えはありますか? 回答宜しくお願いします。
=>[作者]: 嫌われるのを承知ではっきり言いますと,日本語的に考えたり自分の思考に合うように調整すると「多義的」になり客観的に正確な定義を維持できなくなります.あくまで,「x∈Pならばx∈Q」が成り立つとき,PはQの十分条件というように「ある要素がある集合の要素になっているときに他の集合の要素になっているかどうか」で考えないといけません.言葉としては十→要と形式的に決めるだけです.
■三重[?さん/10.02.25]
数学Aの逆・裏・対偶のページの、p→qにおける真理表の対偶の部分が「pの否定→qの否定」になっています。正しくは「qの否定→pの否定」ではないでしょうか。
=>[作者]: 連絡ありがとう.訂正します.
■?[?さん/10.02.19]
必要・十分条件の問題で
「x=1 は x2+3x-4=0 であるための()条件」というのがありこれは
x=1 → x2+3x-4=0は○
x2+3x-4=0 → X=1は反例のX=-4があるので×
よって十分条件というのでした。これはx=1 ⊂ x2+3x-4=0ということですよね?
もしこれが
「x2+3x-4=0 は X=1 であるための()条件」という問題だったら
x2+3x-4=0 → X=1は反例のX=-4があるので×
x=1 → x2+3x-4=0は○
よって必要条件になってx2+3x-4=0 ⊂ X=1になるのですか?
=>[作者]: 最後が間違っています.x2+3x-4=0 ⊃ X=1になります.
■?[?さん/10.02.18]
基本的な質問ですいませんが
Q→Pが真であるとき、QをPであるための十分条件、QをPであるための必要条件でQ⊂Pの関係があるんですよね?
Q→Pが偽ならどうなるんですか?
=>[作者]: 「Q→Pが真であるとき、QをPであるための十分条件」は正しいです.「QをPであるための必要条件でQ⊂Pの関係があるんですよね?」:QがPであるための十分条件のとき,Q⊂Pの関係があります.QがPであるための必要条件であるときはQ⊃Pになります.(教材に書いてある通り 「十→要」が重要です.また卵の黄身が十で全体が要です.)
Q→Pが偽でも,それだけではP,Qの関係は何とも言えません.Q→Pが偽ならばQはPの部分集合でなく,QであってPでないものがあることなります.さらに,PであってかつQでないものがなければPはQの十分条件となります.(卵の図[オイラー図と呼ばれるもの]を書けば簡単ですが,言葉でいえば難しそうに聞こるだけです.)
■?[?さん/10.02.16]
数Aの「独立な試行の確率,反復試行の確率」の問題2の(5)の解説で
5C2・(1/2)^2・(1/2)^4
となってますがなぜ最後の1/2は4乗なのでしょうか?
=>[作者]: 連絡ありがとう.問題の読み間違いで,「第6試合でAが勝つ確率」を出したつもりでしたが,実際の問題文がそうはなっていなかったので食い違いが生じていました.訂正しました.
■福岡[?さん/10.02.11]
数Ⅰの「最大角、最小角」のところの問題3の3の(1)の解答ですが
x=2+√2のとき
(x^2-2x)<(2x-1)=(x^2-x+1)
とありますが詳しい解答をお願いいたします
=>[作者]: 「x=2+√3のとき」のタイプミスですので訂正しました.
■?[?さん/10.02.5]
x>1→x>0は成立しませんけど、
=>[作者]: どのような文脈の中で述べておられるのか書いてありませんが,一般的にはx>1→x>0は成立します.
■いばらき県[いばらKIさん/10.02.3]
こんにちは
http://www.geisya.or.jp/~mwm48961/kou2/para_episode4.htm
[例題3]
■定数項を簡単にして仕上げるの 次の式で
ーa^2+3a - 4が、+a^2+3a - 4になっています。
頂点のy座標は、ーになっていますので大丈夫でした。
=>[作者]: ありがとう.訂正しました.
■東京都[?さん/09.12.11]
http://www.geisya.or.jp/~mwm48961/kou2/log_episode_mouse1.htm対数計算1の要点の下にある例題の解答が2^4=64になっています。
=>[作者]: ありがとう.訂正しました.
■埼玉[zさん/09.12.03]
早速のご回答ありがとうございます。
「10 の倍数は除く」という条件を見落としておりました。申し訳ございませんでした。
=>[作者]: 了解
■埼玉[zさん/09.12.03]
失礼いたします。
■集合の要素の個数2 (3)の解説において166+66 - 2×33=166 となっておりますが、
なぜ33を2倍するのでしょうか。よろしくご回答ください。
=>[作者]: 6の倍数166個と15の倍数66個を足すと,30の倍数(三重に重なっている部分)は2回分足されます.普通ならば1回分だけ引けばちょうど1回数えたことになるはずのところが,問題が「10の倍数を除く」となっているので,30の倍数は1回も数えないようにします.このためには2回はがします.
■東京都[?さん/09.09.17]
http://www.geisya.or.jp/~mwm48961/kou3/bunsuushiki2.htm分数式の和.差で
問題2(3)helpの分子4行目aが抜けていると思うのですが。
あと同ページ 例題2 最後の分母にx-2があります。
=>[作者]: 連絡ありがとう.入力ミスですので訂正しました.
■東京[マス尾さん/09.09.01]
たびたび失礼します。
数学B、ベクトルの成分(内積)にて、第一列の第三行目の問題が、
クリックする前は、a=(1,2) b=(-1,3)なのですが、
クリックすると、a=(2,-3) b=(4,0)に変わるようです。
恐れ入りますが確認のほどよろしくお願いいたします。
=>[作者]: プログラムミスですので訂正しました.
■東京[マス尾さん/09.08.30]
失礼します。
数学Bの、位置ベクトルの応用4にて。
(4)の問題で、Pベクトルを表した後の変形で、分子の部分が、
5÷(2a+3c) となっておりますが、
5÷(2a+3b) だと思うのです。
恐縮ですが、確認お願いいたします。
=>[作者]: 入力ミスですので訂正します.
■東京都[?さん/09.08.26]
解説ありがとうございます。問題の正解に辿り着けてスッキリしました。
御指摘のように教科書を持っていません。てっきりy=ax^2+bx+cを平方完成するのかと
思ってやってみてたんですが???な状態になってました。
=>[作者]: とりあえずよかったです.教材の手直しはまだです.
■東京都[?さん/09.08.24]
ここのページの問題の解き方がわからないので教えて頂けませんでしょうか?
http://www.geisya.or.jp/~mwm48961/koukou/s12jg701.htm
=>[作者]: 連絡をありがとう.
■埼玉[utokioさん/09.08.16]
検索サイトからこのHPの内容の一部にたどり着くことがあります。
私はFirefoxユーザなのですが,
一度ページの内容が表示された後、「IE専用でした」などというページに変化し
戻るボタンをおしても、元いたページに戻ることができず大変不便な思いをします。
何とかならないのでしょうか?
=>[作者]: 連絡をありがとう.
■福岡[天狼さん/09.08.15]
とても役に立ちました。似たような問題のヒントがあるので復習にも、問題に詰まったときにも助かりました。
=>[作者]: 連絡をありがとう.最近は例題を見ながら解ける頁を多くしています.
■?[?さん/09.08.10]
http://www.geisya.or.jp/~mwm48961/koukou/sa_in21.htm
2文字のたすき掛け因数分解の問題で
12x^2-xy-6y^2-21x+20y-6がわからないのでhelpをみると
helpの問題が12x^2-10xy-12y^2-9x+20y-3になっていて
12x^2-xy-6y^2-21x+20y-6の答えがわかりません。
=>[作者]: 連絡をありがとう.問題とHELPのシンクロがはずれているようですので訂正します.
■神奈川[マイコジャクソンさん/09.06.27]
恒等式の問題1の第4問の左辺分母の第2項の符号が逆になってはいないでしょうか。
=>[作者]: 連絡をありがとう.訂正しました.
■三重県[nbr-krkさん/09.04.10]
お世話になっています.経済的に余裕のない家庭で受験勉強をしている者としては本当に助けて頂いています.参考書などを使っても思うように進まなかったり,集中できなかったり...困っていました.このサイトに出会えてから希望が湧いてきました.本当にありがとうございます.これからもよろしくお願いします.
=>[作者]: 連絡をありがとう.作者としては社会奉仕のつもりでやっていますが,外から見ればパソコンマニアが趣味でやっているようにも見えるため,このようにストレートに言ってもらえるとやはりうれしいです.
■京都[勉強中さん/09.04.05]
http://www.geisya.or.jp/~mwm48961/kou3/circle1.htm
上記ページ中の
x2 - 4x+4+y2 - 6x+9=16 となり,定数項をまとめると
x2+y2 - 4x - 6x - 3=0 になる.
の -6x は -6y の間違いです。
=>[作者]: 連絡をありがとう.間違いですので訂正しました.
■福岡県[ぷりっぷりのおしりさん/09.03.17]
23才の社会人です。ゲームの分析をするためにエクセルの講座を参考にさせて頂きました。ありがとうございます。
多少見にくくなっても構わないので、すべての講座をIE以外のブラウザでも見られるようにして頂けるとより便利になるような気がしました。ちなみに私はgoogle chromeです。
=>[作者]: 連絡をありがとう.当サイトではアクセス解析で把握できるブラウザの多いものに対応するようにしています.2009.2.17~2009.3.17までの当サイトヒット回数 1,069,465 件中の各ブラウザのシェアは IE7 (48.69%) ,IE6 (42.65%) ,Firefox 3.0 (3.64%),Safari (2.02%),Netscape 4 (1.35%),IE5(0.53%),Opera (0.48%),Firefox 2.0(0.36%),PLAYSTATION 3 (0.05%),Mozilla (0.05%),Firefox 1.0 (0.04%),Netscape 7 (0.04%),不明 (0.03%),Firefox 1.5 (0.03%),Google (0.01%),Sleipnir (0.01%),SoftBank (0.01%),NTT DoCoMo (0.01%),Netscape 3 (0.01%) ,以下0.00%台でした.(IE7の集計中にはIE8が少し含まれるらしい)
■長野[たろさん/09.02.20]
http://www.geisya.or.jp/~mwm48961/koukou/sbim04.htm=>[作者]: 連絡をありがとう.問題の方でxの係数を訂正しました.
■三重[ギリギリスさん/08.05.11]
二項定理の問題を載せてほしい
=>[作者]: 連絡をありがとう.ちょうど今,高校数学の項目で足りない部分を埋めようと考えていたところなので,すぐ対応します.
■滋賀県[一会社員さん/08.06.11]
拝啓
はじめまして。
χ二乗検定の所の説明についてですが、下記の例の時に
例1
日本人のABO式血液型の分布はおよそA型40%,B型20%,AB型10%,O型30%だといわれている.ある村で献血に応じた者のうち先着100人の血液型は次の表のとおりであった.(ただしデータは架空のもの)
血液型 A型 B型 AB型 O型 計
度数 37 25 12 26 100
この村の住人の血液型分布は,日本人全体の血液型分布とほぼ同じと見なしてよいか?
(考え方)
もし,完全に一致していたら,次の表の期待度数で示される人数となるはずであるが,標本調査の場合には少々の凹凸はありうる.どの程度の差異ならば偶然として許容されるかと考える.
血液型 A型 B型 AB型 O型 計
観測度数 37 25 12 26 100
期待度数 40 20 10 30 100
χ二乗値= 2.41となりますが
実際,標本を10倍に増やしたときを考えた下記のデータだと
血液型 A型 B型 AB型 O型 計
観測度数 370 250 120 260 1000
期待度数 400 200 100 300 1000
χ二乗値= 24.1
となり、χ二乗値が10倍大きくなりませんか?
そうすると、たとえばAさんは100人のデータにて検定し、仮に有意差がなかったとし、
Bさんは1000人のデータを取って検定した時に、χ二乗値が10倍の値となり有意差が
出るということが生じるのではないでしょうか?
どこか間違っているのでしょうか?
それとも、χ二乗検定を用いるときには、何か制限条件があるのでしょうか?
お教え願います。
=>[作者]: 連絡をありがとう.さて,私の教材は,仕事ですぐに報告書を作らなければならないような方が直ちに場面を理解して,そこそこの報告書が書けることを念頭に置いていますので,理論的な説明(力量的にも無理かも?)は避けて,実務ができることを目指しています.(「なぜ,この方法でできるのかという数学的根拠は難しい」とさらりと流して,深入りしていません.)文面からは,カイ2乗値の数学的な根拠づけについての理論的な質問のように受取りましたが,比率が同じならばカイ2乗値は同じであるべきだとお考えではないでしょうか.まさに,その部分がこの問題の核心です.要約の直前に書いていますように「日常生活では,・・・割合で表わした表・・・を元に「少し違う」「あまり違わない」といった議論をすることがあるが,カイ2乗を用いた検定は,割合ではなく,度数を用いて計算することが重要」で,標本の大きさ(データの個数)が小さいときには,比率は結構ばらつくものですが,標本の大きさ(データの個数)が大きくなると,比率が偶然的にはずれる確率はほとんどなくなるということです.カイ2乗値の定義自体は,ガンマ関数を用いて定義される連続関数ですが(統計の教科書に書いてあります),これで比率の検定ができることを「今すぐ分かりやすく」説明する方法を思いつきませんので深入りしていません.上の例では,標本の大きさが100のときなら偶然としてあり得る差異でも,標本の大きさが1000のときなら確率的に偶然では起こらないくいちがいということになります.・・・「上のように比率が同じで,人数が10倍になればカイ2乗値が大きくなり有意差が出る」というのは何も間違っておらず,その通りだと思います.
(※追加) もう少し日常生活で経験する例を思いつきましたので,参考にしてください:そのページの下にサイコロの問題がありますが,単純化して次の形にするとします.サイコロを6回投げて,1,2,,,の目が出る回数が各々2,0,1,1,1,1回となるのは,日常生活でよくあることです(カイ2乗値は2).しかし,サイコロを60回投げて,1,2,,,の目が出る回数が各々20,0,10,10,10,10回となるようなことはめったになく(カイ2乗値は20),サイコロを600回投げて,1,2,,,の目が出る回数が各々200,0,100,100,100,100回となるようなことはまずあり得ない(カイ2乗値は200).後二者ではサイコロが正しく作られていないと言えます.
このページ の実験2で感じをつかんでください.
■神奈川県[心チャソ@りそりそさん/08.05.11]
ほとんど悪いところはありませんでした。
ですがもう少し問題数があればいいなぁ~!!と思いました。
=>[作者]: 連絡をありがとう.感想については,言われる通りかもしれないと考えつつも,高校数学独特の現状があって思案中です.すなわち,今の高校数学は,一応検定済みの教科書を使っていることになっていますが,多様化が進みすぎて何かポイントを絞った教材を作ってもほとんどの人に合わなくなります.例えば十種類に分化していれば,どこかの需要層に合う教材を作ると残り九割の人には,少し難しいとか簡単の程度ではなく,「難し過ぎまたは簡単過ぎて論外」なものになってしまう現状があると思います.これは現役の生徒を考えた場合のことですが,むしろ社会人・文系大学生向けの簡単復習というスタイルで行くと需要に合わせやすいように思われますので,今のところその方向で考えています.(ユーザのドメイン種別(.ac , .ad など)や時間帯などからこのように考えをまとめましたが,教材全体に波及するのは早くても数年後です.)
■?県[銭形さん/08.03.26]
拝啓
趣味で数学を思い出しつつ解いている者です。作者様のページにていつも楽しまさせていただいております。ありがとうございます。
大変恐縮かと思いましたが、一点、もしかしたら間違われているのではないかと思われる箇所をお知らせさせていただきます。
数B(今はこう呼ぶのでしょうか?私のころは代数幾何という名前だったと思うのですが。年がばれますね。)・平面上のベクトル、点の存在範囲2の「問題」http://www.geisya.or.jp/~mwm48961/kou2/vector_eq12.htmlのページで、
問題の選択肢にあります、一番上右側の条件(線分ABが正解のもの)は、u=1ではなくu=0 (s+t=1) なのではないかと考えております。
もし私が間違えておりましたら、お手数を取らせまして大変申し訳ございました。
では、これからもご活躍を祈念申し上げます。
敬具
=>[作者]: 連絡をありがとう.間違っていましたので訂正します.
■奈良[ソックスさん/08.03.16]
確率のセンター問題の2004年度数1A追試験第1問(2)---一部引用の(3)の問題の解説のところで2本当たった場合の分子で5C2と書いてありますが、その場合は2等が2本以上当たった場合ではなく、2等以上が2本以上当たった場合じゃないですか?
=>[作者]: 連絡をありがとう.間違っていましたので訂正します.
■愛知[スサノウ飲み琴さん/08.03.16]
http://resistance.20.dtiblog.com/
のサイトをやっている者です。
よくここのサイトを見ては高校数学の予習みたいな感じでやっております。
解説なども分かりやすく、この度このサイトをリンクさせて戴くことになりましたので報告いたしました
=>[作者]: 連絡をありがとう.夕暮れに鏡が池から校舎を眺めながら帰宅を急いだのは,もうずいぶん昔のことになります.3月1日に,何かの会合のときにちらっと見えた限りでは昔と同じ風景でした.
■愛知県[ohkuboyさん/08.01.16]
ご返事の要約で納得です。
Microsoftがヒストグラムを分析ツールとFrequency関数で上限を'以下'、ピボットテーブルで上限を'未満'と統一性のない使用にしたこととヒストグラムの公式ヘルプに前者を'未満'と誤記していることが質問となった最大の原因です。このため、当方もピボットテーブルがどちらの仕様か気になったのです。多分、他の読者も気にして確認するでしょう。
蛇足ですが、例としての積分の話は連続関数です。議論の対象となった境界上にデータがあるヒストグラムや分割表などは境界値上で不連続関数になり話が逸脱していると思います。
Microsoftの公式ページにピボットテーブルの利用が紹介されていました。
=>[作者]: ほぼ納得いただけたということで安心しました.
■愛知県[ohkuboyさん/08.01.11]
300個程度の接近した大量データのヒストグラム作成の場合に適用して、以下の危険性に気が付きました。=>[作者]: ていねいに読んでいただき、ありがとうございます.少しテストしてみて、記述の仕方を考えてみます.
f(x)dx= f(x)dx+ f(x)dx f(x)dx=0 ■奈良県[うおさん/08.01.09]
返答の「数学的にはないときは0と解する」のは、結局場合分けをしているのに過ぎません。私の見つけた等式は、数列の一般項表示で初項を別扱いするのが理論的には無意味である・回避可能であると言う事実を示しているのです。”解釈”など不必要なのです。また、お示しになった二つの例も論点がずれています。その二つの例、共に変数の変域の範囲を集合上で考えています。一方、高校で使用されているΣ記号の使用は、全てが一次元ベクトル的なのです。この事実を自覚して、露骨に表現された文を読んだ記憶はありません。この一次元ベクトル(有向線分)的性質を尊重する立場を取れば、符号つきの値、つまりΣ(k=1~n)kはーΣ(k=n~1)kに等しいと考える・みなすことの方が、ずうっと自然です。”微積分の基本定理:定積分の値は原始関数の値の差に等しい”事とも合致して美しさすら感じます。
=>[作者]: うまく証明されていますし,特に矛盾は感じません.誰もが一度は疑問に感じてそのままにしていることを深く追求されていることに感心します.採点者の多数がその方式を採用するようになれば,紹介することもできると思います.
■奈良県[うおさん/08.01.03]
大誤解・迷信=階差数列使用時にn≧2という制限は重要です。
真実・真相:
すべてのn(n=1,2,3・・・)に対してan = a1+(Σk=1nbk)-bn
こんなに単純な式ですむのに誰も今まで発見できていません。
私は例外なしの単一表示があるはずだと証明しようとしてから
気づくのに10年かかりました。
発見日時:2000年8月26日午後4時頃、仕事場に向かうバスに乗っている時。
住所情報を送って頂ければもっと先まで考え抜いたレポートを送ります。
(2008-01-03.THU 00:24)
=>[作者]: 少しおもしろい話です.正式に習ったわけではありませんが,Σについている末項が初項以上という制限は,この段階の教育用のもので,数学的にはないときは0と解するのが自然です.次のような記号も普通に使われています.akj , f(x)
■愛知県[ohkuboyさん/07.12.17]
なかなか興味あるまとめ方で参考になります。さて、 Excelを用いた統計解析のところでのミスや説明不足と思われる部分を指摘いたします。ご検討ください=>[作者]: この分野について、はじめて連絡をいただき喜んでいます.どう見えているのか、少々気になっていたところです.大量の文書を書きましたので、入力ミスや思い違いもあるかもしれません。御指摘の点については、ゆっくり読み直しますのでしばらくお待ち下さい。(12.19 追加・訂正しました.)
■愛媛県[かなたさん/07.12.01]
いつもお世話になっています。抜け!?を見つけたのでお知らせします。必要十分条件の12番の問題で3(3k)に2乗が抜けています。それではこれからも宜しくお願いいたします。
=>[作者]: 連絡をありがとう.訂正します.
■大阪府[ゆたかさん/07.11.10]
ようやくお届けすることが出来まして、良かったです。
=>[作者]: 入力ミスを見つけてくれてありがとう.ではまた.
■大阪府[ゆたかさん/07.10.31]
5度ほどメールいたしましたが、届きましたでしょうか。念のため別の方お二人に同じものを送信して確認しましたところ、間違いなく着信したとのことです。メールの受取を制限しておられるのでしょうか。メールアドレスは先のアドレスで良かったのですね。
=>[作者]: 1通も届きません.なお,前回のアドレスは合っています.他の方のメールは受け取れます.ユーザとして特に受診制限はしていませんが,プロバイダ間の途中経路で1Mバイト以上の添付ファイルがある場合にリレーしないことがあります.もし画像ファイルを使っておられるのなら,圧縮比を変えてみてはどうでしょうか.
■大阪府[ゆたかさん/07.10.31]
2度メールいたしましたのですが、届きましたでしょうか。メールアドレスは(伏せ字)@(伏せ字)でよろしいでしょうか。
=>[作者]: アドレスは合っていますがメールは来ていません.添付ファイルが大きいと途中経路で切られてしまうことがあるかも.
■愛媛県[かなたさん/07.10.23]
早速のお返事有難う御座います!とても分りやすい説明有難う御座いました。これからもサイト運営がんばってくださいv
=>[作者]: 納得してもらえてよかった.では、また.
■愛媛県[かなたさん/07.10.22]
微分について検索していたらこのサイトにたどり着きました!とても分りやすい説明でフリーとは感動しましたw 1つ分らないことがあったので質問させてください。微分の増減表からグラフを書く時に極大値、極小値、y軸との交点だけとって描けば良いのでしょうか?それだと値をとったところ以外(両端)は適当になってしまうような気がするのですが・・・
=>[作者]: 増減表からグラフの概形(およその形)を描くには,極大値,極小値(あなたの言われるようにx=0の代入ですぐ分るy軸との交点)を元に,後はできるだけ「なめらかに」描けば十分です.もちろん,もっと正確なものを求めるにはx=1, 2, 3 , ・・・などと点を増やしていけばよいのですが,正確なグラフを描くには,x=1.1 , 1.2, 1.3 , ・・・なども気になり出すときりがありません.そこで,当面の「概形」としては,極大値,極小値がグラフの中に描かれていて,それらをなめらかに結んでおればよいとします.(さらに,凹凸,漸近線も習えば,変曲点,漸近線の方程式,x軸との交点など必要に応じて材料を増やしていけますが,グラフの概形として,最小限必要なものは極大値,極小値です.増減が変化する点が最も重要な点と考えます.)
■大阪府[ゆたかさん/07.10.20]
少しずつ学習させていただいてますが、気になるところが幾つかあります。数学的記述がありますので、当欄では入力できないでおります。
=>[作者]: 画像ファイル,word,一太郎で「中学数学」の下端にあるアドレスに送っていただければ受け取れます.
■山梨[まさやさん/07.10.15]
ご丁寧にありがとうございました。
=>[作者]: 納得してもらったようでよかった.
■山梨[まさやさん/07.10.08]
いつもHPに助けられている高校3年生です。まことに勝手ながら「行列の対角化」について教えてください。学校では少しの内容しか触れなかったので・・・。よろしくお願いします。
=>[作者]: 行列の対角化は,大学1,2年の線形代数学で固有値問題として扱うものなので,前提となる事項も分量が多く,固有値問題自体もかなり分量のある話になります.高校3年生で幾ら時間があっても足りない状況で,そこに突入してしまうのはあまり賢明な策ではないので,高校生として求められる程度にあっさりと処理するために,
このページ ,特に(1)の [ 説明 ] (をクリックすると解説が出ます)程度で当面納得しておくのがよいと思います.
■大阪府[ゆたかさん/07.09.19]
ベクトルの内分点の内分点の解説に誤りがあります。△ABP:△BCP:△CAPの面積比は,6t:1.5t:3t=12:3:9=4:1:3 と
ありますが、6t:1.5t:3t=12:3:6=4:1:2となるのでは。
=>[作者]: 連絡をありがとう.訂正します.
■新潟県[ふくちゃんさん/07.08.21]
平均の差(F検定→t検定)を見させて頂きました。大変解り易く、非常に参考になりました。ありがとう御座います。これからもこちらのHPで統計の勉強を参考にさせてください。
=>[作者]: 連絡をありがとうございます.こちらも長い間高校で教えていましたが,確率分布の単元が選択になって久しく,めったなことでは教える機会がなかったため(10年に1回当たれば幸運の方?),復習しながらの教材作成ということで十分こなれていないところがありますが,今後改善する予定です.御指摘の入力ミスは点検します.
■京都府[tmさん/07.08.12]
http://www.geisya.or.jp/~mwm48961/kou2/log_eq1h.htmlの[重要]
のところはMMじゃなくてMNじゃないんですか?
=>[作者]: ていねいに見ていただいてありがとう.間違いですので訂正します.(高1?)
■福島県[hikaru4169さん/07.06.01]
∑の計算で,シグマの後に( )をつけるのは,加法,減法のみで乗法,除法は必要ないのでしょうか?
=>[作者]: 基本はそのように考えるとよいと思います.他の意味に間違われないように,念入りに( )を付けるのは自由です.
ak bk
= a1 b1 + a2 b2
+ … +an bn ,
ak
bk = (a1 + a2
+ … +an )(b1
+ b2 + … +bn )
=
+
+ … +
,
=
などです.
■青森県[ユウさん/07.03.01]
関数の連続性の説明を見てようやく理解できたのですが、学校の問題集に載ってある問題で、どうしてもわからないものがあるんです。f(x)=[sinx]
(x=π/2) と f(x)=[cosx] (x=π/2) の違いがよく分かりません。解答を見てもなぜそうなるのかが載っていないため困っています。できたら図で説明してもらえると助かります。お願いします。
=>[作者]: (本当はその問題集を見せてもらわないと言いにくいことですが)
f(x) = [ sinx
] のグラフは
となるから,
f(π/2)= 1,f(x)= 0 となり,
f(x)≠ f(π/2) により
x= π/2 で不連続.
次に,
g(x)
= [ cosx ] のグラフは
となるから,
g(π/2)
= 0 ,
g(x)
= 0 ,
g(x)
= -1 となり,
g(x)
は存在しないから,
g(x)
≠ g(π/2) となり,
x
= π/2 で不連続.
●==メニューに戻る
 =>[作者]:連絡ありがとう.どの問題の話かが書かれていませんが,凸という言葉の意味を「開いている」という意味に誤解していませんか.
=>[作者]:連絡ありがとう.どの問題の話かが書かれていませんが,凸という言葉の意味を「開いている」という意味に誤解していませんか.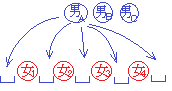 =>[作者]:連絡ありがとう.左図のイメージで積の原則にそって確実に押さえるとよいでしょう.空席が5つあって,男Aの座り方は5通り,その各々について男Bの座り方は4通り,その各々について男Cの座り方が3通りだから5×4×3です.空席の方が男の子よりも多いので,男の子が座らない空席もあります.
=>[作者]:連絡ありがとう.左図のイメージで積の原則にそって確実に押さえるとよいでしょう.空席が5つあって,男Aの座り方は5通り,その各々について男Bの座り方は4通り,その各々について男Cの座り方が3通りだから5×4×3です.空席の方が男の子よりも多いので,男の子が座らない空席もあります.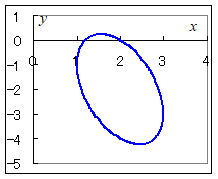 =>[作者]:連絡ありがとう.-1≦x≦-3ということはありません(-1が-3よりも小さい[以下]ということはない).左図のようになりますので,元の答案で正しいです.2次不等式の解き方があなたの弱点ですので簡単に復習しておくとよいでしょう.
=>[作者]:連絡ありがとう.-1≦x≦-3ということはありません(-1が-3よりも小さい[以下]ということはない).左図のようになりますので,元の答案で正しいです.2次不等式の解き方があなたの弱点ですので簡単に復習しておくとよいでしょう.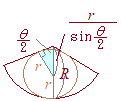 =>[作者]:連絡ありがとう.扇形の角度を0<θ≦πとし半径をRとして,内接円の半径rをRとθで表すことはできます.あなた自身が解かなければならない宿題かもしれなので,考え方のみ伝え,答は書きません.
=>[作者]:連絡ありがとう.扇形の角度を0<θ≦πとし半径をRとして,内接円の半径rをRとθで表すことはできます.あなた自身が解かなければならない宿題かもしれなので,考え方のみ伝え,答は書きません.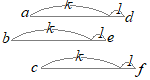 正確さを度外視してイメージだけで言えば,直線 (1)+k×(2) は,(1)と(2)をk:1に内分(または外分)する直線なので,k=±∞の場合に(2)に近付きます.
正確さを度外視してイメージだけで言えば,直線 (1)+k×(2) は,(1)と(2)をk:1に内分(または外分)する直線なので,k=±∞の場合に(2)に近付きます.
 =>[作者]:連絡ありがとう.なるほど,教える側は交点と漸近線を混同しないように,実際に交わるのが交点で,「限りなく近づいていくが交わらないのが漸近線」という部分を強調しますが,実は漸近線と元の曲線は交わっても構いません.
=>[作者]:連絡ありがとう.なるほど,教える側は交点と漸近線を混同しないように,実際に交わるのが交点で,「限りなく近づいていくが交わらないのが漸近線」という部分を強調しますが,実は漸近線と元の曲線は交わっても構いません. =>[作者]:連絡ありがとう.同じものが含まれているような場合の円順列,じゅず順列の計算は,実際上は「根性物語」が計算方法だと思います.
=>[作者]:連絡ありがとう.同じものが含まれているような場合の円順列,じゅず順列の計算は,実際上は「根性物語」が計算方法だと思います.
 例えば,円
例えば,円 そこで,「ベクトルの和を考えときは,終点に始点を接ぎ木して和を作ります」が,問題の図で終点に始点が接ぎ木してあるとは限らず,自分で移動させて作るのです.
そこで,「ベクトルの和を考えときは,終点に始点を接ぎ木して和を作ります」が,問題の図で終点に始点が接ぎ木してあるとは限らず,自分で移動させて作るのです.
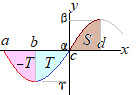 =>[作者]:連絡ありがとう.変数変換が1対1でないときにどうなるのかということについて,ゆっくり考えてみるのはよいことだと思います.そこの部分は踏み込んで書いていませんので,納得してもらえなかったかもしれません.
=>[作者]:連絡ありがとう.変数変換が1対1でないときにどうなるのかということについて,ゆっくり考えてみるのはよいことだと思います.そこの部分は踏み込んで書いていませんので,納得してもらえなかったかもしれません.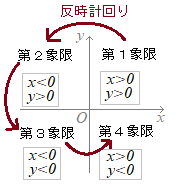 =>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.
=>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.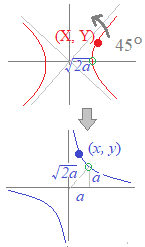 =>[作者]:連絡ありがとう.
=>[作者]:連絡ありがとう.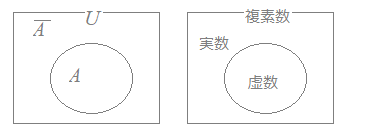 集合をオイラー図で描くとき「境界線の外と中,境界線をまたいだら背反関係になっていることを表す」「ただし,四角の中に丸がある場合や,丸の中に丸がある場合は内側にある丸は部分集合であることを示す(=背反関係ではない)」という約束で絵を描きます.
集合をオイラー図で描くとき「境界線の外と中,境界線をまたいだら背反関係になっていることを表す」「ただし,四角の中に丸がある場合や,丸の中に丸がある場合は内側にある丸は部分集合であることを示す(=背反関係ではない)」という約束で絵を描きます. 左図1のように描くと,あなたの見方とは近いかもしれません・・・左図1のうちで純虚数の丸を取り除いた図が東京図書の数学Ⅱの教科書に出ています.
左図1のように描くと,あなたの見方とは近いかもしれません・・・左図1のうちで純虚数の丸を取り除いた図が東京図書の数学Ⅱの教科書に出ています. 質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,
質問者が気分を害されるかもしれませんが,質問されているようにs,tの範囲が独立に定まる場合は,
 方程式に書き換えて交点のx座標を求めておく.
方程式に書き換えて交点のx座標を求めておく. =>[作者]:連絡ありがとう.ベクトルは「大きさ」と「向き」をもつ量として定義され,「大きさ」と「向き」さえ等しければベクトルとして等しいといいます.
=>[作者]:連絡ありがとう.ベクトルは「大きさ」と「向き」をもつ量として定義され,「大きさ」と「向き」さえ等しければベクトルとして等しいといいます.
 g)
g) h(x)=f(g(h(x)))はx→h(x)→g(h(x))→f(g(h(x)))のように右から順に作用していきます.
h(x)=f(g(h(x)))はx→h(x)→g(h(x))→f(g(h(x)))のように右から順に作用していきます. (f
(f h)(x)=g(f(h(x)))はx→h(x)→f(h(x))→g(f(h(x)))の順,
h)(x)=g(f(h(x)))はx→h(x)→f(h(x))→g(f(h(x)))の順, g
g f)(x)=h(g(f(x)))はx→f(x)→g(f(x))→h(g(f(x)))の順です.
f)(x)=h(g(f(x)))はx→f(x)→g(f(x))→h(g(f(x)))の順です.
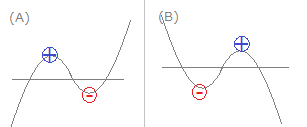
 =>[作者]:連絡ありがとう.興味を持っていただいたということはありがたいことですが,質問内容をもっと絞ってください.
=>[作者]:連絡ありがとう.興味を持っていただいたということはありがたいことですが,質問内容をもっと絞ってください.
 を押せば99%まで答案が示されます.残り1%はあなたが考える番です.全部まで筆者が教えてしまったら良くないので,読者が考える余地を残したというのがこの頁の構成です.
を押せば99%まで答案が示されます.残り1%はあなたが考える番です.全部まで筆者が教えてしまったら良くないので,読者が考える余地を残したというのがこの頁の構成です.
 連絡ありがとう.他のところで,中学生ということで同じ質問をしておられますので,こちらでまとめて答えます.
連絡ありがとう.他のところで,中学生ということで同じ質問をしておられますので,こちらでまとめて答えます.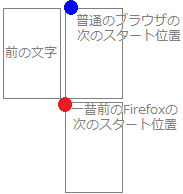 =>[作者]:連絡ありがとう.あなたがお使いのWindows10標準のMicrosoft Edge(Webkit系)というブラウザで,一昔前のFirefoxのように,次の文字のスタート位置が1文字分下がる特徴があるということでしたら,そのバグが訂正されるまで一定の対応が必要になるかと思いますが,その症状の報告は初めて聞きました.設定・仕様を各会社の都合に合わせて変更していると,体が持たない!?ブツブツ・・(互換モードIntenet Explorer, Firefox, Chrome, Safari, Opera, Sleipnirのいずれでも問題なく,現在までにその症状が報告されたのはEdgeだけです)
=>[作者]:連絡ありがとう.あなたがお使いのWindows10標準のMicrosoft Edge(Webkit系)というブラウザで,一昔前のFirefoxのように,次の文字のスタート位置が1文字分下がる特徴があるということでしたら,そのバグが訂正されるまで一定の対応が必要になるかと思いますが,その症状の報告は初めて聞きました.設定・仕様を各会社の都合に合わせて変更していると,体が持たない!?ブツブツ・・(互換モードIntenet Explorer, Firefox, Chrome, Safari, Opera, Sleipnirのいずれでも問題なく,現在までにその症状が報告されたのはEdgeだけです) =>[作者]:連絡ありがとう.4プロセスというのが数研出版の参考書だということがようやく分かりました.ところで,左の学習進行状況[横は時間(秒),縦は進み具合(ピクセル数)]から見ると,あなたはコンスタントに進んでおり,途中で例題1を2回見直したのは何か気になることがあったからで,おそらくバリバリの現役で,学力・持久力とも十分あるのです.しかし,管理人が何年かこのサイトを運営する中で分かったことは「サーチエンジンから入って来る人は,分からないことがあるから調べごとをしている」という事実です.中には高校中退の人もあり,文化系で卒業した人,定年退職後ようやく気になっていた教科の学習時間ができたという人もあります.そうすると「教材は,分からない人を前提に作るべし」という結論に達するのです.あなたのようにそこそこ分かっている人は,当サイトから見れば模範生のようなもので,分かることまで書いてあるところはにっこり笑って見てもらえばよいのです.
=>[作者]:連絡ありがとう.4プロセスというのが数研出版の参考書だということがようやく分かりました.ところで,左の学習進行状況[横は時間(秒),縦は進み具合(ピクセル数)]から見ると,あなたはコンスタントに進んでおり,途中で例題1を2回見直したのは何か気になることがあったからで,おそらくバリバリの現役で,学力・持久力とも十分あるのです.しかし,管理人が何年かこのサイトを運営する中で分かったことは「サーチエンジンから入って来る人は,分からないことがあるから調べごとをしている」という事実です.中には高校中退の人もあり,文化系で卒業した人,定年退職後ようやく気になっていた教科の学習時間ができたという人もあります.そうすると「教材は,分からない人を前提に作るべし」という結論に達するのです.あなたのようにそこそこ分かっている人は,当サイトから見れば模範生のようなもので,分かることまで書いてあるところはにっこり笑って見てもらえばよいのです.
 =>[作者]:連絡ありがとう.実に深く本質に迫るよい質問だと思う.
=>[作者]:連絡ありがとう.実に深く本質に迫るよい質問だと思う. において,(1)の傾きは −2/4=−1/2 で(2)の傾きも −3/6=−1/2 となって,(1)(2)は平行です.a , a'が0でなければ,2直線 a'x+b'y+c'=0 , ax+by+c=0の傾きはそれぞれ−b/a , −b'/a'になるので,これらが等しければ平行になります.
において,(1)の傾きは −2/4=−1/2 で(2)の傾きも −3/6=−1/2 となって,(1)(2)は平行です.a , a'が0でなければ,2直線 a'x+b'y+c'=0 , ax+by+c=0の傾きはそれぞれ−b/a , −b'/a'になるので,これらが等しければ平行になります.
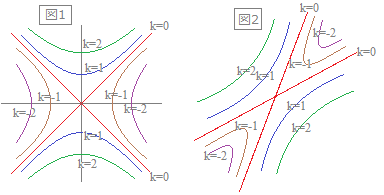 【例】
【例】
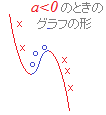
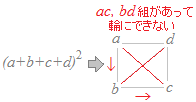 なお,数学Iの教科書で3文字a, b, cの場合は,ほとんど輪環の順に書かれていますが,輪環の順は,グー・チョキ・パーのように「三すくみ」「巴形」になっている場合:(x+y+z)2のような場合にしか登場しません.2文字,4文字,...の場合に輪環の順は使わないので,「サイクリック」は実際上は3文字専用の書き方となります.(左図参照)
なお,数学Iの教科書で3文字a, b, cの場合は,ほとんど輪環の順に書かれていますが,輪環の順は,グー・チョキ・パーのように「三すくみ」「巴形」になっている場合:(x+y+z)2のような場合にしか登場しません.2文字,4文字,...の場合に輪環の順は使わないので,「サイクリック」は実際上は3文字専用の書き方となります.(左図参照)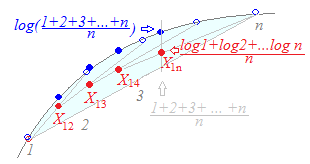 =>[作者]:連絡ありがとう.教材では図示する都合でn=3の場合を書いていますが,これをnにします.次の方針で証明するとよい.
=>[作者]:連絡ありがとう.教材では図示する都合でn=3の場合を書いていますが,これをnにします.次の方針で証明するとよい. =>[作者]:連絡ありがとう.他の頁での要望として,helpで解答を示されると勉強にならないという意見が大勢になってきましたので,helpから解答を消しましたが,この頁については答も復活させました.問題3(2)だけに限定される意味が分かりませんので問題3に全部について復活.右図が変形のポイントです.
=>[作者]:連絡ありがとう.他の頁での要望として,helpで解答を示されると勉強にならないという意見が大勢になってきましたので,helpから解答を消しましたが,この頁については答も復活させました.問題3(2)だけに限定される意味が分かりませんので問題3に全部について復活.右図が変形のポイントです.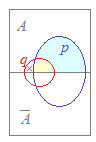
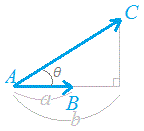 ご質問の問題は、AB=3, BC=4, AC=5の「直角三角形」のことだと考えられますので、これについて答えます。
ご質問の問題は、AB=3, BC=4, AC=5の「直角三角形」のことだと考えられますので、これについて答えます。 =>[作者]: 「Q→Pが真であるとき、QをPであるための十分条件」は正しいです.「QをPであるための必要条件でQ⊂Pの関係があるんですよね?」:QがPであるための十分条件のとき,Q⊂Pの関係があります.QがPであるための必要条件であるときはQ⊃Pになります.(教材に書いてある通り 「十→要」が重要です.また卵の黄身が十で全体が要です.)
=>[作者]: 「Q→Pが真であるとき、QをPであるための十分条件」は正しいです.「QをPであるための必要条件でQ⊂Pの関係があるんですよね?」:QがPであるための十分条件のとき,Q⊂Pの関係があります.QがPであるための必要条件であるときはQ⊃Pになります.(教材に書いてある通り 「十→要」が重要です.また卵の黄身が十で全体が要です.) となるから,
f(π/2)= 1,f(x)= 0 となり,f(x)≠ f(π/2) により x= π/2で不連続.
となるから,
f(π/2)= 1,f(x)= 0 となり,f(x)≠ f(π/2) により x= π/2で不連続.
 となるから,g(π/2)
= 0,
g(x)
= 0,
g(x)
= -1 となり,
となるから,g(π/2)
= 0,
g(x)
= 0,
g(x)
= -1 となり,