ベクトルの成分

→ 携帯版は別頁

平面ベクトル（２次元ベクトル）の成分表示

[解説]
　ベクトルは「大きさ」と「向き」をもつ量です。ベクトルを表す１つの方法は，矢印を用いて図形で表す方法です。

　図形を用いずにベクトルを表す方法として，成分で表す方法があります。成分は単なる数字なので大きさは表せますが，向きをも表すには，平面のベクトルでは数字を２つ使います。
　すなわち，始点から終点に向けて，どちら向きにいくら移動したかを，ｘ方向の移動量(符号付き)，ｙ方向の移動量(符号付き)の組で表します。

- 図１ -

【例】
図１において

$\vec{a}=(3,\hspace{2}4)$
$\vec{b}=(2,\hspace{2}3)$

です。

ベクトルは「どこに書いてあるか」を問わないことに注意しましょう。つまり，始点がどこであるかには無関係に，始点から終点に向けて，どちら向きにどれだけ移動しているかだけを問題にするのがベクトルです。

図１において，同様に

$\vec{c}=(-3,\hspace{2}2)$
$\vec{d}=(-4,\hspace{2}3)$
$\vec{e}=(-1,\hspace{2}-4)$

です。
図１の $\vec{a}$ や $\vec{d}$ のように，原点を始点として表したベクトルでは，終点のx,y座標とベクトルの成分表示に「全く同じ記号」を使います。
（ベクトルの話をしているのか，点の座標の話をしているのかは，前後の文脈から分かりますので，混乱は生じません。・・・初めは不思議に思うかもしれませんがやってみれば分かります・・・）

[要点]
・ベクトルの成分表示では，点の座標と同じように数字の組　(x, y)の形を用います。ただし，このx,yは始点から終点に向けての移動量を表し，一般には終点の座標とは一致しません。
・始点を原点に重ねた場合には，ベクトルの成分表示は，終点の座標と一致します。

※　ベクトルの成分表示は，教科書では通常，基本ベクトル表示と呼ばれるものから導入しますが，ここでは，直接的に矢印図と成分を結びつけました。
　高校の数学で，基本ベクトル表示は，根本的な内容の導入の際に一時的に登場するだけで，その後は出てきませんので，ここでは省略しました。
　基本ベクトル表示を学びたい方は，教科書をご覧下さい。

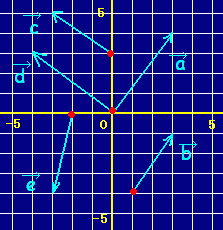
≪問題≫　次の図で水色の矢印で表されているベクトルの成分を答えなさい.（下の選択肢の中から正しいものをクリック）
[第1問 / 全8問]

ベクトルの成分は

解説を読む解説を隠す次の問題

始点から終点に向かうには，ｘ軸の正の向きに2，ｙ軸の正の向きに3だけ進めばよいから(2, 3)
　または，終点の座標が(4, 6)で始点の座標が(2, 3)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(4,6)-(2,3)=(2,3)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに4，ｙ軸の正の向きに2だけ進めばよいから(4, 2)
　または，終点の座標が(8, 4)で始点の座標が(4, 2)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(8,4)-(4,2)=(4,2)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに−3（左向きに3），ｙ軸の正の向きに1だけ進めばよいから(−3, 1)
　または，終点の座標が(−5, 6)で始点の座標が(−2, 5)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(-5,6)-(-2,5)=(-3,1)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに2，ｙ軸の正の向きに−4（下に4）だけ進めばよいから(2, −4)
　または，終点の座標が(7, −6)で始点の座標が(5, −2)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(7,-6)-(5,-2)=(2,-4)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに−3（左に3），ｙ軸の正の向きに−2（下に2）だけ進めばよいから(−3, −2)
　または，終点の座標が(−1, −5)で始点の座標が(2, −3)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(-1,-5)-(2,-3)=(-3,-2)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに0（横移動なし），ｙ軸の正の向きに5だけ進めばよいから(0, 5)
　または，終点の座標が(−3, 7)で始点の座標が(−3, 2)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(-3,7)-(-3,2)=(0,5)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに3，ｙ軸の正の向きに0（縦移動なし）だけ進めばよいから(3, 0)
　または，終点の座標が(9, 0)で始点の座標が(6, 0)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(9,0)-(6,0)=(3,0)$ と考えます始点から終点に向かうには，ｘ軸の正の向きに−5（左に5），ｙ軸の正の向きに0（縦移動なし）だけ進めばよいから(−5, 0)
　または，終点の座標が(−5, 3)で始点の座標が(0, 3)だから，ベクトルを $\vec{a}$ とすると $\vec{a}=(-5,3)-(0,3)=(-5,0)$ と考えます

←メニューに戻る