|
← PC用は別頁
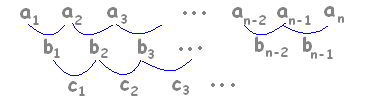
【解説】 数列の「各項の差」からなる数列を元の数列の階差数列と言います。 【例】 次の数列{bn}は,数列{an}の階差数列です. 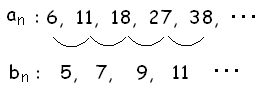 元の数列よりもその差から作った階差数列の方が簡単な規則性を持っていることが多いので,階差数列で規則性を見つけて,元の数列の一般項を求めることができます。
○【階差数列の定義】
(1)の解説元の数列を{an}, 階差数列を{bn}で表わすとき
bn = an+1−an …(1)
○【階差数列から元の数列を求める公式】 n≧2のとき 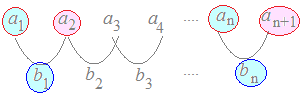 (後の項)−(前の項) でできる数列が階差数列 {bn} なので
b1=a2−a1
b2=a3−a2 b3=a4−a3 
一般に bn=an+1−an になります. 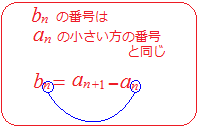
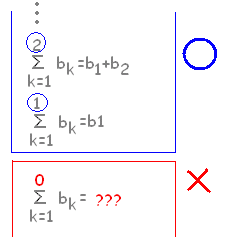
○ n=1のときan=a1は当然のようですが,n=1の場合
だけ他とは異なる計算になりますので,分けて書くことは重要です. ○ n≧2のとき
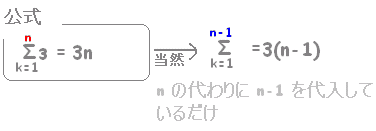
※この公式は,「階差数列の一般項は分かる」が「元の数列の一般項が分からない」場合に,
始発駅a1と地下通路b1 , b2 , b3 , ...が分かっているときに,地下通路を1区間行けば第2の駅に達します.「階差数列」から「元の数列」を求めるという場面を考えると,使い道が分かります. 始発駅から,地下通路を2区間行けば第3の駅に達します. 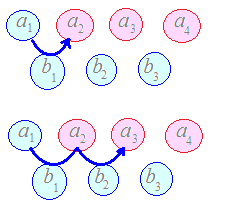 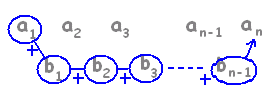 an=a1+(b1+b2+···+bn−1 ) Σで書けば 
|
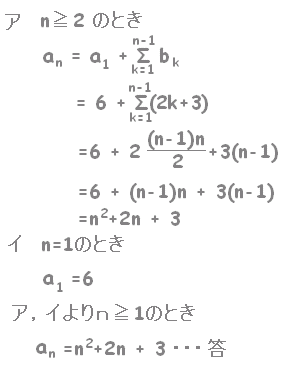

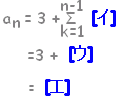
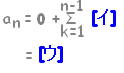
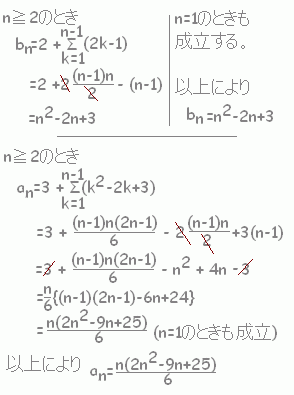
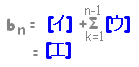 (n=1のときも成り立つ。)
(n=1のときも成り立つ。)
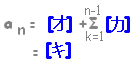 (n=1のときも成り立つ。)・・答
(n=1のときも成り立つ。)・・答