|
■階差数列
[解説] 数列の「各項の差」からなる数列を元の数列の階差数列と言います。 例 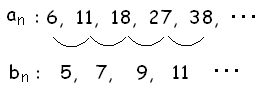 [階差数列の定義] 元の数列を{ an },階差数列を{ bn }で表わすとき
答案作成の途中経過では,n≧2の場合とn=1の場合を分けなければなりません。 n=1のときはa1でその値は問題文に書かれています。 ※ n≧2とn=1を統一して,n≧1で共通の関数形となるのがほとんどです。 |
補足説明
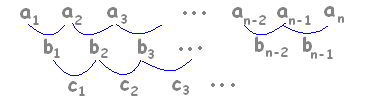
元の数列がn次式で表わされるとき,その階差数列は n-1次式になります。左の例では元の数列anは2次式,階差数列bnは1次式です。
例 階差数列の項番号は,元の数列の小さい方の番号と同じです。 次の数列において, 6+5=11 6+5+7=18 6+5+7+9=27 6+5+7+9+11=38 です。 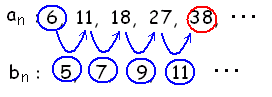
実際の和を表わさないこのような形式的な和は,高校では使わないということです。 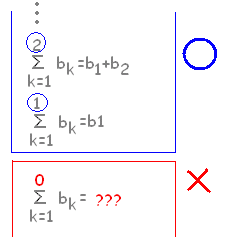 |
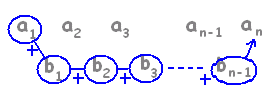
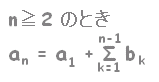 ※ 植木がn本あるときのロープの数はn−1本(植木算)であることに注意すると,Σはn−1項までの和となります。
※ 植木がn本あるときのロープの数はn−1本(植木算)であることに注意すると,Σはn−1項までの和となります。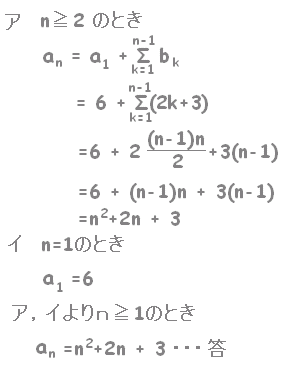

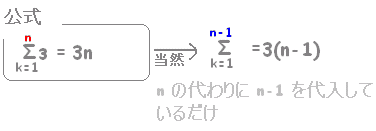
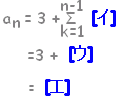
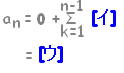


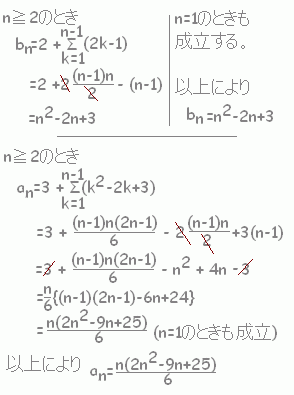
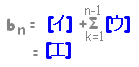 (n=1のときも成り立つ。)
(n=1のときも成り立つ。)
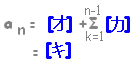 (n=1のときも成り立つ。)・・答
(n=1のときも成り立つ。)・・答