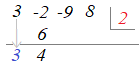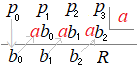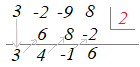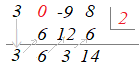|
�i�g�����@�Ƃ́j
�}�P
�Ⴆ��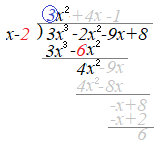
�@�g�����@�ł́C�}�Q��}�R�̂悤�ȕ\�����܂��D�i�}�Q�������j
�}�Q
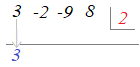
�}�R
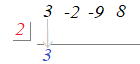
�@�g�����@�̐}�ɂ�x3, x2, x�̂悤�ȕ����̕����͏������Ɂu�W���������~�ׂ��̏��ɕ��ׂ����̂��g���܂��v�D �@�}�P�̊���Z�ŏ�[�ɏ�����鏤�́C�g�����@�ł͉��[�ɌW���������ׂď����܂��D �@���̐}�ł́C��̍s�������鎮�̌W������ׂ����́C���g�ɂ�x−a�̂Ƃ�a�Ə����܂��D �@���̊��鎮�̒萔��−a�Ɣ�ׂ�ƁC�g�����@�̑��g�Ɋe�����́u�������̕������t�ɂ����v�Ƃ������Ƃ��ŏ��̒��ӎ����ł��D
�����̑��g�ɂ�x−a�̂Ƃ�a�Ə����Ƃ����̂́C���ł��Ȃ����ׂȂ��Ƃ̂悤�Ɏv���܂����C���ʂ̊���Z�ł͒��̌v�Z�������Z�ɂȂ�̂ɑ��āC�g�����@�ł͑����Z�ɂȂ�u���炭��v�������ɂ���܂��D
|