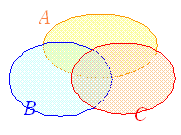|
���Ɨ��Ȏ��s�̊m���C�������s�̊m��������
�y�Ɨ��Ȏ��s�̊m���z�s�v�_�t
A , B ���Ɨ��ł���Ƃ��CA �� B ���N����m����
�y��P�z�@����������Q���ĂP��ڂɂR�ȉ��C�Q��ڂɂS�ȉ��̖ڂ��o��m��
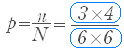
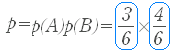
�@�����܂łɏK�����l�����ŁC�}1�̂悤�ɂP��ځC�Q��ڂ̋N���蓾�邷�ׂĂ̏ꍇ�� N=36 �ƍl����Ƃ��́C
�ˁ@���̂悤�ɁCA , B ���Ɨ��ł���Ƃ��CA �� B ���N����m����
�@���P�̂悤�Ɍv�Z���āC P = = �Ƃ���D �@�������C���̖��ł��P��ڂɏo��ڂ͂Q��ڂɏo��ڂɉe�����Ă��Ȃ��̂ŁC �@���Q�̂悤�ɂP��ڂɂR�ȉ��ƂȂ�m���i �j�ƂQ��ڂɂS�ȉ��ƂȂ�m���i �j�̐ςł����߂邱�Ƃ��ł���D
���
�@�P��ڂɋ���(2 , 4 , 6)���o��m���� �C�Q��ڂɋ���(2 , 4 , 6)���o��m���� �ł����͓Ɨ��������@���������2����Ƃ��Q��Ƃ������̖ڂ��o��m�� p=�~=
## �Ɨ��łȂ��ꍇ ##
�@�ԋʂR�C���ʂQ�������Ă���܂���C�ʂ��P�����o���C���o�����ʂ͌��ɖ߂��Ȃ��ꍇ�ɁC�ԋʂ��Q��o��m������i�����o�Ƃ����j  �i�A�j�@�P��ڂɐԋʂ��o���Ƃ��C�܂̒��͐ԋʂQ�C���ʂQ�̌v�S�ɂȂ邩��C �@�Q��ڂɐԂ��o��m���� �i�C�j�@�P��ڂɔ��ʂ��o���Ƃ��C�܂̒��͐ԋʂR�C���ʂP�̌v�S�ɂȂ邩��C �@�Q��ڂɐԂ��o��m���� �ˁ@���̂悤�Ɏ��o�����ʂ����ɖ߂��Ȃ��Ƃ��́C�P��ڂ� A ���N���邱�ƂƂQ��ڂ� B ���N���邱�Ƃ͓Ɨ��ł͂Ȃ��D �ˁ@���o�����ʂ����ɖ߂��Ƃ��́C�u�Ɨ��Ȏ��s�̊m���v���K�p�ł��邪�C���o�����ʂ����ɖ߂��Ȃ��Ƃ��́u�Ɨ��Ȏ��s�̊m���v���K�p�ł��Ȃ��D
���@���̖������܂łɏK�������@�ʼn����ɂ́C
�P��ڂ̋ʂ̏o����5�ʂ�C���̂��ꂼ��ɂ��ĂQ��ڂ̋ʂ̏o����4�ʂ� �� N=20 �ʂ� �@�P��ڂɐԂ��o��̂�3�ʂ�C���̊e�X�ɂ��ĂQ��ڂɐԂ��o��̂͂Q�ʂ� �� n=6 �ʂ� p = = �Ƃ���D ���@���̖��ŁC�P��ڂɎ��o�����ʂ����ɖ߂��Ƃ��i�������o�Ƃ����D�j�́C�P��ڂ̋ʂƂQ��ڂ̋ʂ͂��݂��ɉe�����ꂸ�C�ԐԂƏo��m���� p = �~ = �ŋ��߂���D |