|
�����̕łɓo�ꂷ��y���z�́C���v�Вc�@�l���{�Z�p�m��̃z�[���y�[�W�Ɍf�ڂ���Ă���u�Z�p�m��ꎟ�����ߋ���� ���ʉȖ�A ���w�v�̈��p�ł��D�i=���\���ꂽ���앨�̈��p�j
���y����z�͌l�̎��Ăł����C�v�������މ��ɂ������āu���̓]�L�~�X�v�u�l�����̊ԈႢ�v�u�v���O�����̍쓮�~�X�v�Ȃǂ��܂܂��ꍇ�����蓾�܂��D �@�������ɂ��Ă̎��ⓙ�́C������҂�ς킹�邱�ƂȂ��C���v�������ނ̍쐬�ҁi<���>�j�ɑ��čs���Ă��������D
�y�t�O�p���z
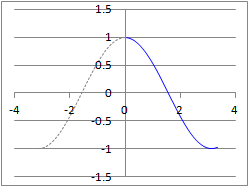
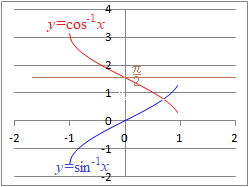
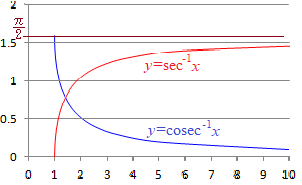
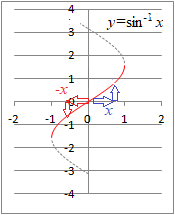
�� y=sinx�̃O���t�́C���̐}�̂悤�ɂȂ�܂��D 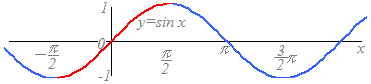
�Ex�͈̔͂ɐ������Ȃ���C��̗^����ꂽy�̒l�ɑ��āCsinx=y�ƂȂ�x�̒l�͖����ɑ��݂��܂����C
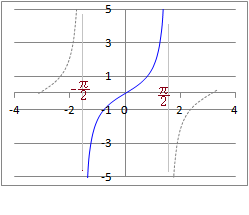
�� y=cosx�̃O���t�́C���̐}�̂悤�ɂȂ�܂��D−��x��
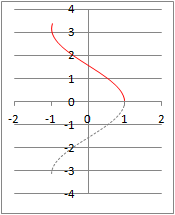
�i�ԂŎ����������j�ɐ�������Cx�̒l�͂����P�ʂ�ɒ�܂�܂��D�E���−��x���ɂ����āCsinx=�������l����l�Ƃ����Cx=sin−1���ŕ\���܂��D�i�A�[�N�T�C�� �A���t�@�Ɠǂށj
�@�����I�Ȓ��ӂƂ��āCsin−1�����Ƃ�
�W�Ȃ��Csinx�̋t����\����p�̋L���ƂȂ��Ă���Csinn���̋t����sin−2���Ə����ȂǂƐV���ɒ�`���Ȃ�����sin−2���Ȃǂ͒�`����Ă��܂���D
�y��z�icos−1���Ctan−1���ɂ��Ă����l�j (1) sin=������Csin−1=�ł��D (2) sin−1�Ƃ́Csin��=�ƂȂ�p���̂��Ƃł��D �i−�������j
�@���l�ɂ��āCsin−1�Ƃ́Csin��=�ƂȂ�p���̂��Ƃł��D�i−�������j

�Ex�͈̔͂ɐ������Ȃ���C��̗^����ꂽy�̒l�ɑ��āCcosx=y�ƂȂ�x�̒l�͖����ɑ��݂��܂����C
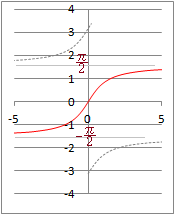
0��x����
�i�ԂŎ����������j�ɐ�������Cx�̒l�͂����P�ʂ�ɒ�܂�܂��D�E���0��x�����ɂ����āCcosx=�������l����l�Ƃ����Cx=cos−1���ŕ\���܂��D �y��z (1) cos=������Ccos−1=�ł��D (2) ��=cos−1 �� cos��=�i0���������j �@���l�ɁC��=cos−1 �� cos��=�i0���������j �@���������āC cos−1+cos−1=��+��=+= �Ȃǂƌv�Z�ł��܂��D ���������e�X��l�ɂ����Ċm�肷��悭�C��+���̒l�͈̔͂͂������g���ĒP���Ɍv�Z����悢�D |
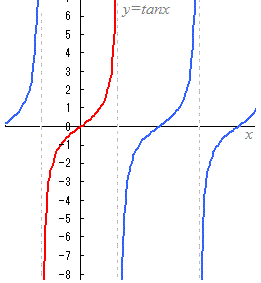
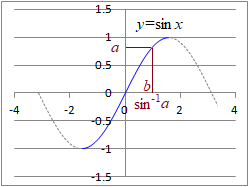
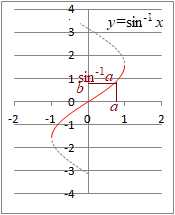
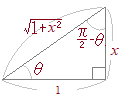
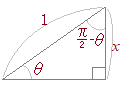 �O�p���̌���
�O�p���̌���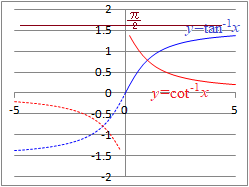
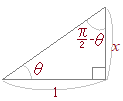
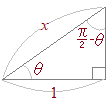 ���̎���
���̎���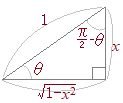 �i����j
�i����j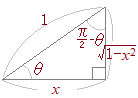
 �i����j
�i����j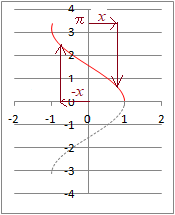 �i����j
�i����j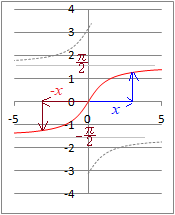 �i����j
�i����j