← PC用は別頁

== ２円の交点を通る円・直線の方程式 ==
【内容】
　この頁では，次のような問題の解き方を扱う．

(1)　２円
________(x+3)2+(y−3)2=9 …(1)
________x2+y2=9 …(2)
の２つの交点と点 (0 , 0) を通る円の方程式を求めよ．

(2)　x2+y2−9+k(x2+y2−2x−6y−10)=0
は，定数 k の値にかかわらず定点を通ることを示し，定点の座標を求めよ．
【要点】
○　２つの円
________x2+y2+ax+by+c=0 …(1)
________x2+y2+dx+ey+f=0 …(2)
が２点で交わるとき，方程式
________x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0
は，定数 k の値にかかわらず２交点を通る円を表す．
○　ただし，k=−1 のときは，２交点を通る直線を表す．
○　k=0 のときは，円(1)を表す．円(2)はこの形式では表せない．
○　方程式
h(x2+y2+ax+by+c)+x2+y2+dx+ey+f=0 も同様
○　h=0 のときは，円(2)を表す．円(1)はこの形式では表せない．

［解説］
○　２つの円
________x2+y2+ax+by+c=0 …(1)
________x2+y2+dx+ey+f=0 …(2)
が２点で交わるとき，方程式
________x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0…(A)
は，定数 k の値にかかわらず２交点を通る円を表す．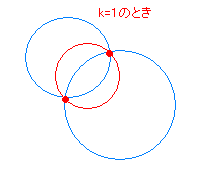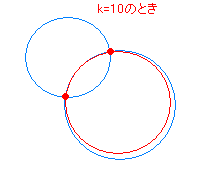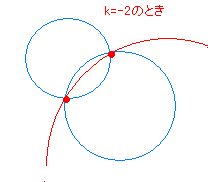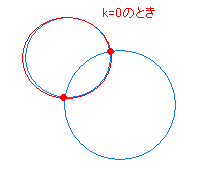
この定理を２段階に分けて解説する．

(I)　まず， 3x2+3y2−2x+4y=0 のような方程式は，
両辺を 3 で割ると
________x2+y2−x+y=0

________(x−)2+(y+)2=

のように変形できるので「円を表す」．
○　一般に，Ax2+Ay2+Bx+Cy+D=0 のように x2 と y2 の係数が等しい方程式は，両辺を A で割ると， x2 と y2 の係数が両方とも 1 になるので，（平方完成したときに右辺が正の数になる限り）「円を表す」．
○　したがって，x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0 は，
________(k+1)x2+(k+1)y2+ … =0
と変形できるから，k+1 が 0 になる場合を除けば「円を表す」．(*1)

(II)　次に，２つの円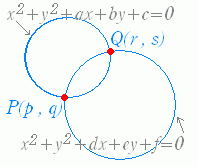
____x2+y2+ax+by+c=0 …(1)
____x2+y2+dx+ey+f=0 …(2)
の交点の座標を各々 (p ,q) , (r , s) とおくと，これらは(1)(2)を満たすから
___p2+q2+ap+bq+c=0
___p2+q2+dp+eq+f=0
が成り立つ．
したがって，p2+q2+ap+bq+c+k(p2+q2+dp+eq+f)=0 …(3)
が成り立つ．（0+0k=0 は成り立つ．）
　同様にして， (r , s) についても
r2+s2+ar+bs+c+k(r2+s2+dr+es+f)=0 …(4)
が成り立つ．
　(3)(4)は，x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0 が「２交点を通る」ことを示している．

　以上の(I),(II) の内容を続けて言うと，「円を表す」「２交点を通る」となり，「２交点を通る円を表す」
［補足説明］
(*1)
○　元の２円(1)(2)が共有点を持たない場合や１点で接する場合でも方程式(A)は円になるが，「２交点と･･･を通る円の方程式を求めよ」という問題は作れないから，「２交点で交わる場合しかこの問題は出ない」と考えてよい．

○　実際に (x−p)2+(y−q)2=R （ R>0 ）の形になることを示さなくても，x2+y2+…=0 のグラフが異なる２点 (p ,q) , (r , s) を通っているのなら，虚円でも点でもなく円であると断定してよい．

○　k=−1 のときは，方程式は 0x2+0y2+a’x+b’y+c’=0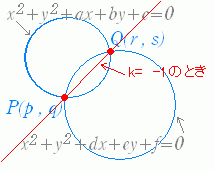
すなわち a’x+b’y+c’=0 の形になり，これが異なる２点 (p ,q) , (r , s) を通っているのなら，それは２交点を通る直線を表す．
（無限の彼方に中心があって半径が無限大の円を考えるとよい．）

（以下の説明はややハイレベルなので，読まなくてもよい）
○　左図の動画において x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0 が通過する場所についての目安
1)　たとえば x2+y2<9 すなわち x2+y2−9<0 は次の図の灰色の部分を表し，x2+y2>9 すなわち x2+y2−9>0 は白色の部分を表す．
2)　同様にして (x−3)2+(y + 3)2<16 すなわち (x−3)2+(y + 3)2−16<0 は次の図の灰色の部分を表し，(x−3)2+(y + 3)2>16 すなわち (x−3)2+(y + 3)2−16>0 は白色の部分を表す．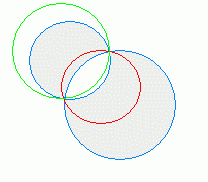

3)　そこで

k=−

の値が「正」になる点は，−正÷負または−負÷正の場合だから，点 (x , y) は右図の灰色の部分にある．同様にして，k の値が「負」になる点は−正÷正または−負÷負の場合だから，点 (x , y) は右図の白色の部分にある．
　そこで，k>0 のとき，２交点と灰色の部分を通る円は右図の赤で示したような円になり，k<0 のとき，緑で示したような円になる．


［例題1］
　２円
________(x+3)2+(y−3)2=9 …(1)
________x2+y2=9 …(2)
について
(1)　２交点と点 (0 , 0) を通る円の方程式を求めよ．
(2)　２円の交点を通る直線の方程式を求めよ．

［答案］
(1)　求める円の方程式を
________(x+3)2+(y−3)2−9+k(x2+y2−9)=0 …(1)
とおく．
(1)が点 (0 , 0) を通るための条件は
________32+32−9+k(0−9)=0
________9−9k=0
________k=1
このとき，方程式は
________(x+3)2+(y−3)2−9+(x2+y2−9)=0
________2x2+2y2+6x−6y=0
________x2+y2+3x−3y=0 …（答）
(2)　(1)において k=−1 とおくと，
________(x+3)2+(y−3)2−9−(x2+y2−9)=0
________(x2+6x+9)+(y2−6y+9)−9−x2−y2+9=0
________6x−6y+18=0
________x−y+3=0 …（答）
［例題2］
__x2+y2−8x+4y−5+k(x2+y2−25)=0　は定数 k の値にかかわらず２つの定点を通ることを示し，定点の座標を求めよ．
定数 k の値にかかわらず a+kb=0 が成立する
⇔　a+kb=0 が k の恒等式
⇔　a=b=0
［答案］
定数 k の値にかかわらず x2+y2−8x+4y−5+k(x2+y2−25)=0 が成立するためには，
________x2+y2−8x+4y−5=0 …(1)
________x2+y2−25=0 …(2)
が必要条件

連立方程式(1)(2)を解く
(1)-(2)
________−8x+4y+20=0
________y=2x−5 …(3)
(3)を(2)に代入
________x2+(2x−5)2−25=0
________x2+4x2−20x+25−25=0
________5x2−20x=0
________5x(x−4)=0
________x=0 , 4
x=0 のとき(3)より y=−5
x=4 のとき(3)より y=3
ゆえに (x , y)=(0 ,−5) , (4 , 3)　（必要）

逆に， (x , y)=(0 ,−5) , (4 , 3) のとき
________x2+y2−8x+4y−5=0 …(1)
________x2+y2−25=0 …(2)
が成り立つから
定数 k の値にかかわらず x2+y2−8x+4y−5+k(x2+y2−25)=0 が成立する．（十分）

以上により，定点の座標は (0 ,−5) , (4 , 3) …（答）
［例題3］
　円 x2+y2+kx+ky−k−5=0 は定数 k の値にかかわらず２定点を通ることを証明しなさい．
※　「円」と「直線」の組合せでも同様の性質が成り立つ．
定数 k の値にかかわらず x2+y2+ax+by+c+k(dx+ey+f)=0 が成立
⇔　 x2+y2+ax+by+c+k(dx+ey+f)=0 が k の恒等式
⇔　x2+y2+ax+by+c=0 …(1) __dx+ey+f=0 …(2)

⇒　k に関係のある式と k に関係のない式に分けるところがポイント　：　x2+y2−5+k(x+y−1)=0 と変形しておく．
［答案］
　定数 k の値にかかわらず x2+y2−5+k(x+y−1)=0 が成立するならば，
________x2+y2−5=0 …(1)
________x+y−1=0 …(2)
(1)(2)より，(x , y)=(−1 , 2) , (2 ,−1) （必要条件）

　逆に (x , y)=(−1 , 2) , (2 ,−1) のとき，
________x2+y2−5=0 , x+y−1=0 となるから
________x2+y2−5+k(x+y−1)=0
は
________0+0k=0
となり，定数 k の値にかかわらず成立する．（十分条件）

　以上により，２定点 (−1 , 2) , (2 ,−1) を通る．
［例題4］
　円 x2+y2−2x−4y−5=0 と直線 y=x−1 の２交点と点 (1 , 2) を通る円の方程式を求めよ．
［答案］
　求める円の方程式を x2+y2−2x−4y−5+k(x−y−1)=0 とおく．
点 (1 , 2) を通るから
________1+4−2−8−5+k(1−2−1)=0
________-10 -2k=0
________k=−5
このとき，円の方程式は
________x2+y2−2x−4y−5−5(x−y−1)=0
________x2+y2−7x+y=0 …（答）


【問題1】
　２円
________x2+y2−6x+2y+5=0 …(1)
________x2+y2=5 …(2)
について
(1)　２交点と点 (0 , 0) を通る円の方程式を求めよ．
(2)　２円の交点を通る直線の方程式を求めよ．
________(1)　円の方程式は　x2+y2−x+y=0
________(2)　直線の方程式は x+y+=0
採点する やり直す ヘルプ
【問題2】
__円 x2+y2−2y−9+k(x2+y2−4x+2y+3)=0　は定数 k の値にかかわらず２つの定点を通る．この定点の座標を求めよ．
________________（次の空欄において，ア＜イとする．）
________( , )
________( , )
採点する やり直す ヘルプ
【問題3】
　円 x2+y2−2kx+ky+10k−25=0 は定数 k の値にかかわらず２定点を通る．この定点の座標を求めよ．
__________（次の空欄において，ア＜イとする．）
________( , )
________( , )
採点する やり直す ヘルプ

...（携帯版）メニューに戻る

...メニューに戻る

■［個別の頁からの質問に対する回答］[２円の交点を通る円・直線の方程式について／17.1.28］
2円の交点を通る円・直線の方程式の ［解説］ ○　２つの円 x2+y2+ax+by+c=0 …(1) x2+y2+dx+ey+f=0 …(2) が２点で交わるとき，方程式 x2+y2+ax+by+c+k(x2+y2+dx+ey+f)=0…(A) は，定数 k の値にかかわらず２交点を通る円を表す． ここ、2交点を通る円ではなく、図形ではないですか？ k=-1のとき直線になるので。
＝＞［作者］：国語表現の好みの話をしておられるのなら対応しません．「ただし，k=−1 のときは，２交点を通る直線を表す」と書いてあるのですから何も問題はありません．
　これを「(A)は三角形を表すか，四角形を表すか，ただ2点を結んだ曲がった曲線を表すかまったくわかりません．アッハッハー，とにかく図形を表します．」と書けば，この文章は読者に対してほとんど情報を与えません．そんな文章なら書く必要がありません．
　これに対して，日本国憲法第四十五条「衆議院議員の任期は、四年とする。但し、衆議院解散の場合には、その期間満了前に終了する。」のように原則を書き，例外を示すと明快になりますが
　衆議院議員の任期は、そんなもの決まっていません，アハッハー
衆議院が四年以内に解散されなかった場合は四年とする。
衆議院解散の場合には、その期間満了前に終了する。
と書く方が好まれるとは限りません．