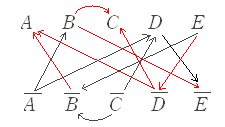
| (1) あるイベントの参加者について次のことが分かっている. ○ 入場料を支払う人は白いリボンを着けておらず,青のチケットも持っていない.このとき,次のうち確実に言えるものはどれか. 1.青のチケットを持っている人は招待客でない. |
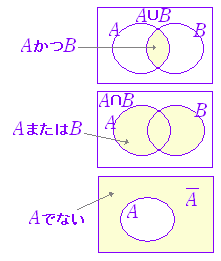
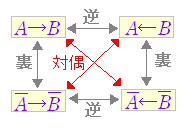
※ある条件 A とこれを満たす集合 A は厳密には別の概念であるが,以下においては混乱が生じるおそれがないので同じ記号で表わす. A : 青のチケットを持っている, B :入場料を支払う, C :招待客, D :当日受付, E :白いリボンを着けているとすると,問題文から次の赤の矢印が成り立ち,その対偶として青の矢印が成り立つ. 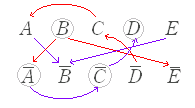 3.C → E は成り立たない. 4. → は成り立たない. 5. → は成り立たない. |
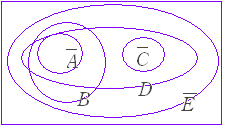
| (2) ある朝食のメニューについて次のことが分かっている. ○ サラダが付いていないメニューには,トーストが付いている.このとき,次のうち確実に言えるものはどれか. 1. サラダが付いているメニューには,コーヒーは付いていない. |
※ 店独自の考えがあるかもしれないので,常識で組合わせを判断してはいけない. A : トーストが付いている, B :サラダが付いている, C :赤だしが付いている, D :納豆が付いている, E :コーヒーが付いているとすると,問題文から次の赤の矢印が成り立ち,その対偶として青の矢印が成り立つ. 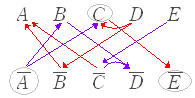 2. → は成り立たない. 3.E → は成り立たない. 5. → B は成り立たない. |
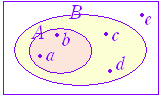
| (3) ある朝食のメニューについて次のことが分かっている. ○ サラダが付いているメニューには,コーヒーが付いている.このとき,次のうち探しても見つかる見込みのないメニューはどれか. 1. トーストが付いていて納豆が付いていないメニュー |
※ 店独自の考えがあるかもしれないので,常識で組合わせを判断してはいけない. A : サラダが付いている, B :コーヒーが付いている, C :トーストが付いている, D :納豆が付いている, E :赤だしが付いているとすると,問題文から図になる. 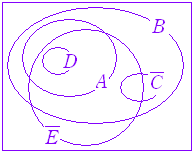 2.D∩= 3.∩= だから,このようなメニューは存在しうる. 4.E∩ を満たすメニューは存在しうる. 5.E∩C を満たすメニューは存在しうる. 以上より,答は2. |
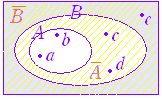
| (4) ある朝食のメニューについて次のことが分かっている. ○ 納豆が付いているメニューには,トーストもサラダも付いていない.これらのメニューで,一方が付いていれば他方も必ず付いている組合わせは次のうちどれか. 1. トーストとコーヒー |
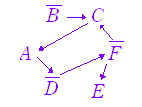
※P → Q → R → P のように条件の連鎖がサイクルになるとき,これらは互いに必要十分条件で,これを満たす集合は等しくなる.すなわち, P → Q → R → P ならば P=Q=R A : サラダが付いている, B :納豆が付いている, C :トーストが付いている, D :赤だしが付いている, E :コーヒーが付いているとすると,問題に示された相互関係及びその対偶を図示すると次の図のようになる. 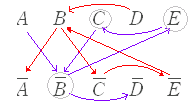 (なお,「付いていない」ものとの組合わせ()は問われていない.また,B== も言えるが,ないもの2つの組も問われていない.) |