|
(参考) 次のような公式もある. ここで だから ここで だから 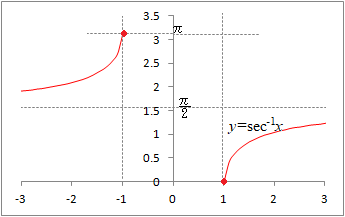 |
(英語の書物では, ここで だから この関数は,x≦−1, 1≦xで定義され,傾きはつねに負になる. 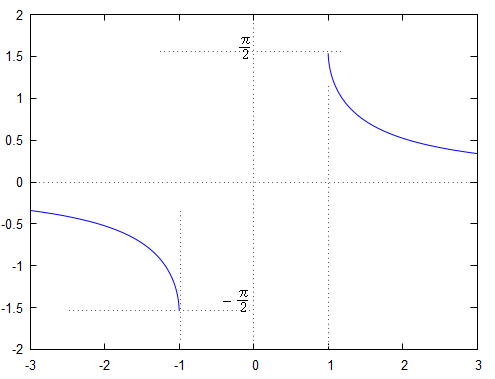 |
|
■逆三角関数の微分法
【基本公式】
(解説)y=sin−1x → = …(1) (−1<x<1) y=cos−1x → = − …(2) (−1<x<1) y=tan−1x → = …(3) (−∞<x<∞) (1)← y=sin−1x とは x=siny (−≦y≦ , −1≦x≦1)となるyの値のことです. yの関数x=sinyをyで微分すると =cosy ところで,三角関数の相互関係によりsin2θ+cos2θ=1だから cosy=±=± ただし,−≦y≦の場合は,cosy≧0 したがって = 逆関数の微分法により == ここで,分母が0となる値を除いて,定義域を−1<x<1とする.
合成関数の微分法を使ってx=sinyをxで微分すると考えてもよい.
両辺をxで微分すると 1=(siny) 合成関数の微分法 = により (siny)=(siny) =cosy だから 1=cosy ゆえに == |
※ 逆三角関数sin−1x , cos−1x , tan−1xの定義については [→この頁]参照 (2)← y=cos−1x とは x=cosy (0≦y≦π , −1≦x≦1)となるyの値のことです. yの関数x=cosyをyで微分すると = − siny ところで,三角関数の相互関係によりsin2θ+cos2θ=1だから siny=±=± ただし,0≦y≦πの場合は,siny≧0 したがって = − 逆関数の微分法により == − ここで,分母が0となる値を除いて,定義域を−1<x<1とする.
y=sin−1xの場合と同様に,合成関数の微分法を使って示してもよい.
(3)← y=tan−1x とは x=tany (−<y< , −∞<x<∞)となるyの値のことです. yの関数x=tanyをyで微分すると = ところで,三角関数の相互関係によりsin2θ+cos2θ=1だから tan2y+1= したがって =tan2y+1=x2+1 逆関数の微分法により ==
y=sin−1xの場合と同様に,合成関数の微分法を使って示してもよい.
|
|
【例題1】
(解答)y=sin−1 (−4<x<4)の導関数を求めてください. y=sin−1t , t=とおくと 合成関数の微分法により ==== |
【例題2】
(解答)y=x sin−1x (−1<x<1)の導関数を求めてください. 積の微分法により =(x)’sin−1x+x(sin−1x)’=sin−1x+ |
|
【例題3】
(解答)y=cos−12x (−<x<)の導関数を求めてください. y=cos−1t , t=2xとおくと 合成関数の微分法により == − ·2= − |
【例題4】
(解答)y=tan−1(2−x)の導関数を求めてください. y=tan−1t , t=2−xとおくと 合成関数の微分法により ==·(−1)= − |
|
○正しい番号を選択してください.
○番号をクリックすれば採点結果が表示され,解説を読むことができます.
y=sin−1t , t=とおくと
合成関数の微分法により === →1
|
y=sin−1t , t=3xとおくと
合成関数の微分法により == ·3= →4
|
|
y=sin−1t , t=とおくと
合成関数の微分法により == ×(− )= − →4
|
y=cos−1t , t=とおくと
合成関数の微分法により == − ×= − →1
|
|
y=tan−1t , t=とおくと
合成関数の微分法により == ×= ×= →4
|
y=tan−1t , t=とおくと
合成関数の微分法により == ×(− )= − × = − →2
|
|
(参考) 次のような公式もある. ここで だから ここで だから  |
(英語の書物では, ここで だから この関数は,x≦−1, 1≦xで定義され,傾きはつねに負になる.  |
|
■[個別の頁からの質問に対する回答][逆三角関数の微分法について/17.5.17]
大学生ですが、高校の内容で分からないところがあったときに見ています。ネットの情報なのでスマホさえあればいつでも解説と例題を見ることができ重宝しています。更に大学範囲や例題が増えるととても嬉しいです。これからもよろしくお願いします。
■[個別の頁からの質問に対する回答][逆三角関数の微分法について/17.5.8]
=>[作者]:連絡ありがとう. 解けなどという文面ではなく、求めてくださいと書いてあるので嬉しい。本当に嬉しい。
=>[作者]:連絡ありがとう.自分の担当している生徒や受験生に対しては,教えるものと学ぶものという上限関係がはっきりしているので,伝統的な数学本のスタイルで「解け」といってもおかしくないのですが,Web上の一時的な関わりではそれほど明確な上下関係はないので,敬語もありかなという感じです.ただし,教材作成に18年近くかかっていますので昔風に「解け」という文章も残っています. |