現在地と前後の項目

正の角・負の角/動径の表わす一般角/三角関数の定義 /(第2象限) /(第3象限) /(第4象限) /(まとめ)/弧度法の単位：ラジアン/三角関数の値(よく使う角度)/sin(π+θ)など/三角方程式　/三角不等式/三角関数のグラフ(sinθの平行移動)/(cosθの平行移動)/sin(θ－α)のグラフ（解説）/(振幅)/(周期)/(周期と振幅)/三角関数のグラフ(総合1)/三角関数のグラフ(総合2)/加法定理，倍角公式，３倍角公式，半角公式/加法定理の練習問題/２倍角公式.半角公式/加法定理の数値計算/積和.和積の公式/練習問題2/練習問題3/練習問題4/合成公式/三角不等式/三角関数（まとめ）/[センター]積和の公式/[センター]合成公式/三角関数公式一覧/三角関数公式プラス/三角形の証明・形状問題/センター試験.三角関数(2015年～)/

■　動径の表わす一般角

■　解説

　右図1において，始線OXから「+30°回ったとき」「-330°回ったとき」「+390°回ったとき」･･･いずれの場合も，動径OPに一致する．

　このように，角度を決めれば動径が定まるが，動径を決めても角度は１つには定まらない．
（動径：角度の対応は1：多になっている．）		 図1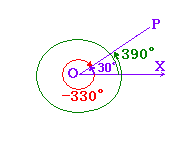
　右図2のように，動径OPが表わす１つの角度をαとするとき，何回転かすると動径は一致するから，
θ=α+360°×n　( n は整数)
で表わされる角度はすべて同じ動径を表わす．

　動径OPの表わす１つの角度をαとするとき
θ=α+360°×n　( n は整数)
を動径OPの表わす一般角という．


例
上の図１において動径OPの表わす一般角は
θ=30°+360°×n ( n は整数)
（※　参考→）








○　要点
１つ見つけて，+360°×n 　( n は整数)　を付けると動径OPの表わす一般角となる．
 図2

（※参考）
もちろん，θ= - 330°+360°×m ( m は整数)でもよく，
θ= 390°+360°×k ( k は整数)でもよい．

ア)　n が整数全体を動くとき，θ=30°+360°×n ( n は整数)で表わされる角度は，
n ··· -1 0 1 2 ···
θ ··· - 330° 30° 390° 750° ···

イ）　m が整数全体を動くとき，θ= - 330°+360°×m ( m は整数)で表わされる角度は，
m ··· -1 0 1 2 ···
θ ··· - 690° - 330° 30° 390° ···
ア）イ）で表わされる角度の全体は，一致する．
（m=n+1　［nは全整数⇔mは全整数］　となっている．）
ウ）　θ= 390°+360°×k ( k は整数)のときも同様．
■　問題
　左の図の動径が表わす一般角を右から選びなさい．
※正しい選択肢をクリック
※間違った場合［解答］ボタンをクリックすれば，答えが赤枠で表示されます．
[第1問 / 全12問]



次の問題












←メニューに戻る
■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります