■Excelを用いたベクトルの計算

○はじめに
　ベクトルを表す方法としては
(1) 矢印ベクトル
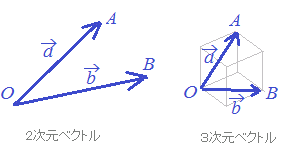
右図１のように矢印を使って図形的に表したもの
(2) 成分ベクトル
=(3, −4), =(2, 5, −1)のように成分を並べて表したもの
の２種類があります．
　(1)の矢印ベクトルは図形的に考えるときに便利ですが，２次元までが限界で３次元のベクトルは投影図として擬似的に表したものとなっています．４次元以上のベクトルを図形的に考えるのは無理です．
　以下においては，主に(2)の成分ベクトルを扱うものとし，矢印ベクトルは必要なときだけ参考にします．

　物理的に考えると，３次元ベクトル=(3, −2, 5)などが空間ベクトルを表していて，４次元ベクトルはこれにさらに時間座標を追加したものか？などと難しく考えるかもしれませんが，数学的には４次元以上のベクトルも単に成分の個数が多くなっているだけで，特別な事は何もありません．100次元，200次元，...などは普通の話です．（コンピュータを使えば簡単にできます）
図１


○ベクトルは列ベクトルで表すのが基本
　高校の数学でベクトルを成分で表示するときは=(3, −2), =(3, −2, 5)のように
• ベクトルの成分は行ベクトルとして横に並べてカンマで区切る．
• ベクトルの名前には矢印を付ける．
のが普通です．
　しかし，コンピュータでベクトルを扱うときは（Excelに限らず他のソフトでも）
• ベクトルの成分は列ベクトルとして縦に並べる．（区切りの記号のカンマはいらない）
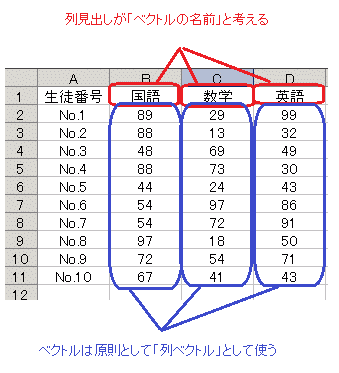
• ベクトルの名前は列のラベルとして付け，特に矢印はいらない．
　右図２の例で国語の得点は，数学記号では
=(89,88,48,88,44,54,54,97,72,67)
という10次元のベクトルになりますが，Excelでは列ベクトルとして右図のように入力します．このとき，国語，数学，英語というラベルが各々のベクトルの名前になります．
（データベ−ス的な見方をすれば列がフィールド，列ラベルはフィールド名になりますが，これらがベクトル，ベクトルの名前に対応します．右図で１行分の横の並びはデータベース的な見方をすれば１件のレコードですが，各々が数学でのx座標，y座標，...もしくはx1座標，x2座標，...になります．） 		図２
○ベクトルの演算
　2+3のようなベクトルの演算の結果を成分で表したいとき，例えば図２のベクトルで国語の２倍と数学の３倍を加えたベクトルＥ列に表示するには，
• セルＥ２に =2*B2+3*C2 と書き込みます．
• セルＥ２をコピーし，Ｅ３からＥ11までに貼り付けます．（相対参照の式が貼り付けられます）
⇒ 各成分の演算によってベクトルの演算を表すということです．
（この演算結果を表すベクトルの列ラベルは，何を表しているか分かるように付ければよい）

【例題１】ＢＭＩ指数は，体重をkg単位で身長をｍ単位で表したときに，体重÷身長2で定義され，肥満度を表す目安に使われます．右の表１の９人についてＢＭＩ指数が最も高い人を探してください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．灰色の部分も付いてきますが，その部分はExcelに貼り付けてからExcel上で削除してください．）


○ベクトルの大きさ
　数学ではベクトル=(x1 , x2 , x3 , ...)の大きさ||は次のように定義されます．
　||=

　Excel上で各々の値の２乗を求めるには，例えば =B2 * B2 のように計算してもできますが，
「２乗の和を求める関数」 SUMSQ(範囲)
を利用すると，まず
||2=x12+x22+x32+...
が求まりますので，次に
「正の平方根を求める関数」 SQRT(値)
を使って||とできます．
SQRT(SUMSQ(範囲))


【例題２】右の表２で，10人分の言語能力，理数能力，運動能力を列ベクトルと見なしたとき，ベクトルの大きさが最も大きいものを選んでください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．）

表１
　 A B C D
1 生徒 身長 体重 BMI指数
2 No.1 161.5 50.8 　
3 No.2 176.0 55.2 　
4 No.3 168.9 59.4 　
5 No.4 153.9 53.2 　
6 No.5 157.0 58.1 　
7 No.6 158.2 59.3 　
8 No.7 168.2 55.4 　
9 No.8 173.5 55.9 　
10 No.9 178.0 56.0 　


（解答）
セルD2に =C2/(B2/100)^2 と書き込み，これをコピーしてD3からD10までに貼り付けます．（２乗の演算 ^ は掛け算，割り算よりも優先して行われます）
小数第１位までの表示で，順に
19.5 ,17.8 ,20.8 ,22.5 ,23.6 ,23.7 ,19.6 ,18.6 ,17.7
となり，No.6の人のＢＭＩ指数が最も高くなります．

表２
生徒番号 言語能力 理数能力 運動能力
No.1 2.3 2.9 3.3
No.2 4.8 4.5 3.3
No.3 4.2 4.3 3.9
No.4 4.8 4.3 4.3
No.5 3.9 3.6 3.2
No.6 2.5 2.2 3.3
No.7 4.4 2.9 2.7
No.8 3.4 4.4 4.9
No.9 2.3 2.2 4.9
No.10 3.7 3.2 3.9
　 　 　 　
　 　 　 　
（解答）
上記の表をExcelワークシートの左上端（A1）に貼り付けるものとします．
言語能力（B列）のデータの下端に =SQRT(SUMSQ(B2:B11)) と書き込み，これをC列，D列にもコピー&貼り付けすると，各々11.8，11.2，12.1 となって，運動能力のベクトルの大きさが最大となります．
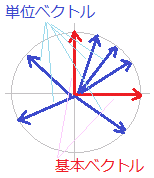
○単位ベクトル
　大きさが１のベクトルを単位ベクトルといいます．右図３のように，単位ベクトルは無数にあります．
　単位ベクトルと間違いやすいものに基本ベクトルがあります．基本ベクトルは，座標軸の正の向きに向いている単位ベクトルのことで，２次元の基本ベクトルは=(1, 0)，=(0, 1)の２個だけ，３次元ベクトルの単位ベクトルは=(1, 0, 0)，=(0, 1, 0)，=(0, 0, 1)の３個だけです．
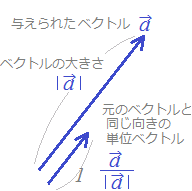
　ベクトルを定数倍すると，方向が変わらずに大きさだけ何倍かされます．（正の数を掛ければ同じ向きに何倍かされ，負の数を掛けると逆向きに何倍かされます．）そこで，与えられたベクトルと同じ向きの単位ベクトルを作るには，その大きさ||で割ればよいことになります．
と同じ向きの単位ベクトルは
ベクトルの割り算というものは定義されていませんが||は単なる数なので，
は，単に各成分をベクトルの大きさ（長さ）で割ったものを表しています．
【例】
　=(3, 4)の大きさは=5だから，=(3, 4)を5で割るとと同じ向きの単位ベクトル（大きさ１のベクトル）になります．
=( , )
Excel上では小数で表示され(0.6, 0.8)となります．

　３次元ベクトル=(1, 1, 1)の大きさは=だから，=(1, 1, 1)をで割るとと同じ向きの単位ベクトル（大きさ１のベクトル）になります．
=( , , )
Excel上では小数で表示され(0.577, 0.577, 0.577)などとなります．
 図３
図４
【例題３】上の表２で，言語能力を表すベクトルと同じ向きの単位ベクトルを求めてください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．）

（解答）
　はじめに，言語能力を表す列ベクトル（B列にあるものとし，表題「言語能力」は１列目にあるものとする）の大きさを求めます．
　右図でB13のセルに =SQRT(SUMSQ(B2:B11)) と書きこみます．
　次に，言語能力のベクトルを単位ベクトルに直したものをE列に書き込むものとして列見出しを「言語u」とし，E2に
=B2/$B$13
と書きこみます．これをコピーし，E3からE11までに単純に貼り付けると右図のように単にベクトルができます．
（割り算となる分母のE13はコピー&貼り付けのときに変化しないように絶対参照$B$13とします：ファンクションキーF・4を押します．）
検算を兼ねて，E列のベクトルの大きさが１になるかどうか確かめておくとよいでしょう．
 （解答続き）
生徒番号 言語能力 理数能力 運動能力 言語u
No.1 2.3 2.9 3.3 0.19
No.2 4.8 4.5 3.3 0.41
No.3 4.2 4.3 3.9 0.35
No.4 4.8 4.3 4.3 0.41
No.5 3.9 3.6 3.2 0.33
No.6 2.5 2.2 3.3 0.21
No.7 4.4 2.9 2.7 0.37
No.8 3.4 4.4 4.9 0.29
No.9 2.3 2.2 4.9 0.19
No.10 3.7 3.2 3.9 0.31
　 　 　 　 　
　 11.8 11.2 12.1 1.0
○ベクトルの内積
　２つのベクトル=(x1 , x2 , x3 , ...)，=(y1 , y2 , y3 , ...)の内積は
· =x1 y1+x2 y2+x3 y3+ ...
で定義されます．（対応する成分の積の和になります）
右図５のように，Excel上で要素数が等しい「列と列」「行と行」の積の和を求めるには，
=SUMPRODUCT(範囲1，範囲2)
が利用できます．
(1) =SUMPRODUCT(範囲1，範囲2)で指定する２つの範囲の要素数は等しくなければなりません．
(2) =SUMPRODUCT(範囲1，範囲2)で指定する２つの範囲は「列と列」「行と行」のようにセルを同じ向きに選んだものでなければなりません．
（=SUMPRODUCT(範囲1，範囲2)は，行列の積のように行と列を掛けることには使えません．行と列を掛けたいときは，行列の積を求める関数=MMULT(行の範囲，列の範囲)を使います．）

【例題４】右の表３で，項目１の列ベクトルと項目２の列ベクトルの内積を求めてください．また，標本１の行ベクトルと標本２の行ベクトルの内積を求めてください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．）

（解答）
　以下，データはワークシートの左上端（A1〜D7）に貼り付けるものとします．
　項目１の列ベクトルと項目２の列ベクトルの内積は =SUMPRODUCT(B2:B7,C2:C7)で求めることができ（小数第１位まで表示すると）−0.69になります．
　標本１の行ベクトルと標本２の行ベクトルの内積は =SUMPRODUCT(B2:D2,B3:D3)で求めることができ（小数第１位まで表示すると）1.92になります．
 図５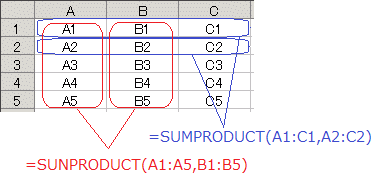


表３
　 項目１ 項目２ 項目３
標本1 0.7 -1.2 1.6
標本2 1.6 0.8 1.1
標本3 1.2 0 -0.6
標本4 0.5 -1 0.9
標本5 0.9 0.3 0.7
標本6 0.9 -1 -1.9
○数学にはなくて統計にはあるもの
　数学では１つのベクトル=(x1 , x2 , x3 , ...)の平均，分散，標準偏差というようなことは考えませんが，統計で扱っている列ベクトルなどは同種のデータを並べたものなので平均，分散，標準偏差などを考えるのが普通です．

○変数の基準化
　右図６のように横軸に項目１，縦軸に項目２をとって２次元の散布図によってデータの差異を比較したいときに，各項目のスケール（単位など）や散らばり具合が違うと数字の大きい方の項目の影響を受けやすく，本質的でない要素によって比較が左右されてしまう．このようなことを避けるために，各項目の「平均が0」「標準偏差が1」となるように変数変換を行うことを基準化といいます．
　元のベクトル（統計では変数と呼ばれることが多い）の平均をm，標準偏差をσとするとき，元の値（ベクトルの各成分xi）から平均を引いて標準偏差で割ってできる新しい変数が基準化された変数Xiになります．
Xi=
【例】
　右の表４がワークシートの左上端（A1〜E10）にあるとき，元のベクトル（変数）身長（cm），体重（kg）を基準化するには
(1) 元の変数の平均，標準偏差を求めておきます．（B9に=AVERAGE(B2:B7)，B10に=STDEVP(B2:B7)，これらをコピーしてC列にも貼り付けます．）
(2) 新たに変数を作り，身長ｓ，体重ｓなどとラベルを付けます．
(3) D2に=(B2-B$9)/B$10と書きこみます．この計算式をコピーし，D3〜D7，E2〜E7に貼り付けます．
※上記の(3)は=STANDARDIZE(B2,B$9,B$10)によっても行うことができます．この場合でも，あらかじめ平均と標準偏差は求めておく必要があります．
※検算を兼ねて，できた基準化変数の平均が0，標準偏差が1になっているかどうか確かめておく方がよいでしょう．

【例題５】次の表の身長と体重のデータを基準化してください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．）
生徒番号 身長 体重
No.1 167.3 68.4
No.2 150.1 50.5
No.3 159.1 69.9
No.4 158.5 70.4
No.5 165.6 74.3
No.6 156.1 78.1
（解答）
　平均は各々159.5，68.6，標準偏差は各々5.8，8.7 となり，これらを使って (元の値−平均)÷標準偏差 を計算すると，右の表５のようになります． 		図６

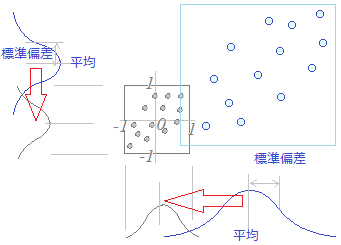表４
生徒番号 身長 体重 身長s 体重s
No.1 170.6 67.8 0.84 -0.07
No.2 165.2 72.1 0.13 0.58
No.3 163.8 60.3 -0.05 -1.20
No.4 175.7 78.9 1.51 1.60
No.5 155.9 70.5 -1.10 0.34
No.6 154.1 60.0 -1.33 -1.24
　 　 　 　 　
平均 164.2 68.3 0.0 0.0
標準偏差 7.6 6.6 1.0 1.0






表５
生徒番号 身長 体重 身長s 体重s
No.1 167.3 68.4 1.36 -0.02
No.2 150.1 50.5 -1.62 -2.08
No.3 159.1 69.9 -0.06 0.15
No.4 158.5 70.4 -0.16 0.21
No.5 165.6 74.3 1.07 0.65
No.6 156.1 78.1 -0.58 1.09
　 　 　 　 　
平均 159.5 68.6 0.0 0.0
標準偏差 5.8 8.7 1.0 1.0

○ベクトルのなす角
　２つのベクトルのなす角は，２次元ベクトル，３次元ベクトルについては右図７のように矢印ベクトルの図を用いて考えることができます．（４次元以上のベクトルではこのような図を描くことはできませんが，成分を用いて計算することはできます．）
　２つのベクトル=(a1 , a2 , a3 , ... )，=(b1 , b2 , b3 , ...)の内積は，２つのベクトルのなす角θを用いて
· =||·||cosθ …(1)
成分を用いて
· =a1b1+a2b2+a3b3+... …(1)
と表すことができ，これら(1)(2)が等しいことから，
cosθ=
=
となります．
（この値は角度θではなく，角度の余弦であることに注意．高校数学の初歩では「角度θを求めなさい」という問題も出されますが，Excel上では必要に応じて逆三角関数ACOS(値)により弧度法の角度に直すことができ，さらにDEGREES(ラジアン)により60分法の角度に直すことができます.）

【例題６】右の表６はあるコンビニ・チェーン店の深夜の時間帯におけるパン，おにぎり，ジュースの売れ行きを支店別に集計したものとします（ただし，架空データ）．変数（列ベクトル）パンとジュースのなす角を求めてください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．）
（解答）
　cosθ=0.98，θ=0.20（ラジアン），θ=11.46°

○ベクトルのなす角と相関係数
　２つの変数（ベクトル）の関連性は通常，相関係数によって調べられます．
　これを矢印ベクトルの図で言えば，２つの変数（ベクトル）がほぼ同じような向きを向いているとき，これらの変数（ベクトル）はよく似た傾向があると考えることになります．ただし，右図８のように原点の取り方や縮尺の大小により，元のデータからそのまま角度を計算すると，見かけだけよく似ているものと区別がつきませんので，２つのベクトルの相関を調べるときは，各々のベクトルを基準化した（平均0，標準偏差1のデータに直した）ベクトルでその角度を測ります．
【例】
　表６のデータを基準化したデータが表７です．このとき，表７から角（の余弦）を求めると
パンsとおにぎりs･･･ −0.847
パンsとジュースs･･･ 0.740
おにぎりsとジュースs･･･ −0.595
となって，パンsとジュースsがよく似た売れ行きをしていることが分かります．
※元のデータの（基準化ベクトルでも同じ）相関係数は，ここで求めた基準化したデータのなす角（の余弦）になっています．
図７



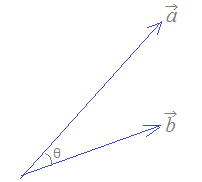表６
店舗 パン おにぎり ジュース
A店 24 11 23
B店 14 22 14
C店 18 8 16
D店 24 9 15
Ｅ店 12 19 14
Ｆ店 11 25 12
図８

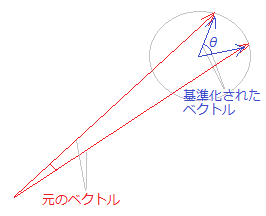表７
店舗 パンs おにぎりs ジュースs
A店 1.288 -0.704 2.098
B店 -0.597 0.956 -0.477
C店 0.157 -1.157 0.095
D店 1.288 -1.006 -0.191
Ｅ店 -0.974 0.503 -0.477
Ｆ店 -1.163 1.409 -1.049
○ベクトルの垂直条件
【要点】
　２つのベクトルが垂直 ⇔ 内積が0
Excel上では
　２つの列ベクトルが垂直 ⇔ SUMPRODUCT(列１,列2)=0
（解説）
　２つのベクトルのなす角がθ=90°であることはcosθ=0と同じであるので，ベクトルの垂直条件は内積を用いて·=0と書くことができます．
·=||·||cosθ
だから
θ=90° ⇔ cosθ=0 ⇔ ·=0
ここで
·=a1b1+a2b2+a3b3+...
だから
θ=90° ⇔ a1b1+a2b2+a3b3+...=0
数学では·=0であっても，理論上は||=0の場合や||=0の場合もあると言いますが，統計データでは||=0や||=0（すべての成分が0）であるかどうかは見れば分かります．
【例】
　右の図10において，調査項目１と調査項目２のなすベクトルが垂直であるかどうかは，
=SUMPRODUCT(A2:A10,B2:B10)
が0になるかどうかによって調べることができます．

○２つの変数の独立・無相関
　数学で垂直，直交（直角に交わる）ということを，統計では独立，無相関といいます．
  • ２つの変数（ベクトルの成分）に正の相関があるとき（一方が増えると他方も増える，一方が減ると他方も減るという関係があるとき）
    右図11のとのような関係になります
    ベクトルのなす角θは0°〜90°
    相関係数は正
    内積は正
  • ２つの変数（ベクトルの成分）に負の相関があるとき（一方が増えると他方は減る，一方が減ると他方は増えるという関係があるとき）
    右図11のとのような関係になります
    ベクトルのなす角θは90°〜180°
    相関係数は負
    内積は負
  • ２つの変数（ベクトルの成分）が無相関であるとき（一方が増えても減っても他方は変化しないという関係があるとき）
    右図11のとのような関係になります
    ベクトルのなす角θは90°
    相関係数は0
    内積は0
【要点】
　２つのベクトル（変数）が独立，無相関，垂直，直交であるための条件
SUMPRODUCT(列１,列2)=0
 図９


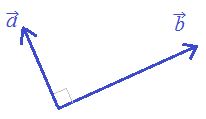図10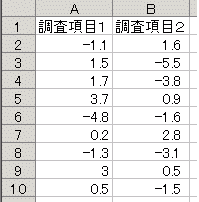







図11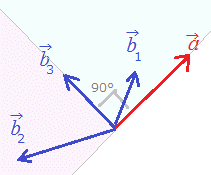
【問題】右の表８のデータについて，以下の問いに答えてください．
（右の表を画面上でドラッグ→コピーし，Excel上に単純に貼り付けるとデータを転記できます．以下においては，ワークシートの左上端に貼り付けられたものとして解説）
以下，選択肢の中から最も近い値を選んでください．
(1)項目１が表すベクトルの大きさを求めてください．
(2)項目１が表すベクトルをその大きさで割って単位ベクトルに直したとき，No.1の成分を求めてください．
(3)項目１が表すベクトルと項目２が表すベクトルの内積を求めてください．
(4)項目１が表すベクトルを基準化したとき，No.1の成分を求めてください．
表８
生徒番号 項目１ 項目２ 項目３
No.1 9.0 -5.6 -8.2
No.2 7.6 2.2 3.4
No.3 8.6 5.6 -2.1
No.4 5.2 -9.5 4.5
No.5 6.4 -3.5 7.0
No.6 1.3 8.7 4.1
No.7 -7.6 2.7 7.6
No.8 -1.8 0.7 0.4
No.9 -0.7 2.7 1.3
No.10 -7.8 -8.5 2.9
(5)項目２が表すベクトルと項目３が表すベクトルのなす角の余弦（cosθ）を求めてください．
(6)項目２と項目３を基準化したとき，それらのベクトルのなす角の余弦（cosθ）を求めてください．
(7)元の項目３のNo.1の値を少し変えると，項目２と項目３は「ほぼ垂直」になります．項目３のNo.1の値が次のどの値となるとき垂直に近くなりますか．（難しく考えずに，内積を表す式を作っておいて，選択肢の値を試しに代入してください．）
○メニューに戻る