|
2点を結ぶベクトルを与えられたベクトルを使って表す問題では,
「定数倍」で伸ばしたり縮めたりすることも併用しながら,「接ぎ木」の要領で,「分からない=求めたい道」を「分かっている道を通る迂回路に置き換える」とよい.
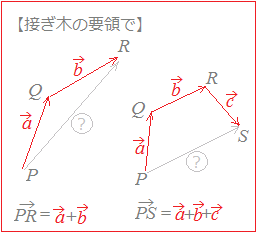
【例】 右図1において→OA=, →OB=とするとき,次の各ベクトルを, で表すには (1)→AB
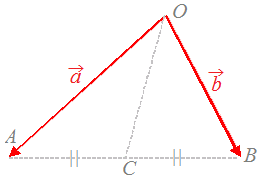
分かっている道,すなわち赤色で示された道を通ってAからBへ行くには,A→O→Bと進むとよいから,
(2)→OC○まず,→AOと進む:これはの逆向きだから − ○次に,→OBと進む:これはに等しい. 以上を「接ぎ木」の要領で足すと, →AB=−+
(1)の問題で→ABも分かっている道,すなわち赤色になるので,分かっている道を通ってOからCへ進むには ○まず,→OAと進む:これはに等しい. ○次に,→ABが分かっているから,これを倍すると→ACになる.
→AC=(−+)
以上を「接ぎ木」の要領で足すと,
→OC=+(−+)=
|
図1
 ※2点を結ぶベクトルについては(終点の位置ベクトル)−(始点の位置ベクトル) − と覚える立場もありますが,これは頭の中の別の引き出しに入るはずだから,数学が不得意な人は1つの原理(接ぎ木の要領でう回路をつないでいく)に絞る方が確実にできると考えられます. ※同様にして,ベクトルの和を平行四辺形の対角線として覚える方法もありますが,1つの原理(接ぎ木の要領でう回路をつないでいく)で押し通して,三角形の2辺で考えるとよい. ※同様にして,2点の中点の位置ベクトルを
と覚える立場もありますが,左の解説のようにやれば幾つもの異なる原理を使い分けなくてもできます.
【要点】
○ 分かっている道をたどって「接ぎ木の要領で迂回路に置き換える」 ○ 大きさと向きが同じなら「どこに書いてあっても」同じベクトル |
|
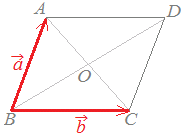
問題1右図2においてABCDは平行四辺形で,Oは対角線AC,BDの交点とする.→BA=, →BC=とするとき,次の各ベクトルを, で表してください.
(正しいものを選択肢から選んでください.) (1)→CD解説 |
図2
 |
|
(2)→CA解説 |
分かっている(赤で示された)道を通ってCからAに行くには ○ まず,CからBに行く:→CB=− ○ 次に,BからAに行く:→BA= 以上を接ぎ木の要領で足すと,→CA=→CB+→BA=−+ (このままの形でもよいが,必要に応じて−の形に変形してもよい.) |
|
(3)→BD解説 |
分かっている(赤で示された)道を通ってBからDに行くには ○ まず,BからAに行く:→BA= ○ 次に,AからDに行く:→AD=→BC= 以上を接ぎ木の要領で足すと,→BD=→BA+→AD=+ |
|
(4)→AO解説 |
分かっている(赤で示された)道を通ってAからOに行くには ○ →AO=→ACだから,→ACを求めればよい. ○ →AC=→AB+→BC=−+ したがって,→AO=(−+)= |
|
問題2右図3においてABCDは平行四辺形で,Oは対角線AC,BDの交点とする.→DA=, →AB=とするとき,次の各ベクトルを, で表してください.
(正しいものを選択肢から選んでください.) (1)→AC解説 |
図3
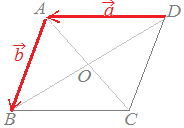 ○ まず,AからBに行く:→AB= ○ 次に,BからCに行く:→BC=→AD=− 以上を接ぎ木の要領で足すと,→AC=→AB+→BC=+(−)=− |
|
(2)→BD解説 |
分かっている(赤で示された)道を通ってBからDに行くには ○ まず,BからAに行く:→BA=− ○ 次に,AからDに行く:→AD=− 以上を接ぎ木の要領で足すと,→BD=→BA+→AD=−+(−)=−− |
|
(3)→CO解説 |
○ →CO=→CAだから,→CAを求めればよい. ○ →CA=→CB+→BA=− したがって,→CO=(−)= |
|
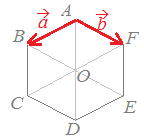
問題3右図4においてABCDEFは正六角形です.→AB=, →AF=とするとき,次の各ベクトルを, で表してください.
(正しいものを選択肢から選んでください.) (1)→CD解説 |
図4
 |
|
(2)→DE解説 |
→DE=−→ABだから →DE=− |
|
(3)→BC解説 |
→BC=→BO+→OC=→AF+→ABだから →BC=+ |
|
(4)→CE解説 |
→CE=→CD+→DE=→AF+(−→AB)だから →CE=− |
|
(5)→DF解説 |
→DF=→DE+→EF ここで →DE=− また(3)の結果から→EF=−→BC=−− したがって→DF=(−)+(−−)=−2− 別解:→DF=→DC+→CF=−−2 |
|
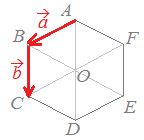
問題4右図5においてABCDEFは正六角形です.→AB=, →BC=とするとき,次の各ベクトルを, で表してください.
(正しいものを選択肢から選んでください.) (1)→AF解説 |
図4
 |
|
(2)→EB解説 |
→EB=→ED+→DA+→ABだから →EB=+(−2)+=2−2 |
|
(3)→EC解説 |
→EC=→EF+→FCだから →EC=−+2 |
|
(4)→EA解説 |
→EA=→ED+→DAだから →EA=−2 |