|
○ 三次元空間において1点P0(x0 , y0 , z0 )を通り,方向ベクトル=(a, b, c)に平行な直線の方程式は
== …(1)
○ ただし,方向ベクトル=(a, b, c)のうち,いずれか1つの成分が0であるとき,例えば,b=0のときは
=, y=y0 …(1’)
○ 方向ベクトル=(a, b, c)のうち,いずれか2つの成分が0であるとき,例えば,b=0, c=0のときは
【例1】y=y0, z=z0 …(1”)
(1)式において,分子のx,y,zの係数は1として使うようになっています.だから
==
のような方程式は,
==と変形することにより,
点(, 0, 1)を通り,方向ベクトル=(, 2, −5)に平行
な直線と解釈することになります.方向ベクトルの大きさは自由に指定できるので,=(3, 4, −10)に平行とすることもできます.
点P0(1, −2, 3)を通り,方向ベクトル=(4, 5, −6)に平行な直線の方程式は == 【例2】 点P0(2, 4, −3)を通り,方向ベクトル=(1, 0, −2)に平行な直線の方程式は x−2= , y=4 【例3】 点P0(1, 2, 3)を通り,方向ベクトル=(0, 0, 5)に平行な直線の方程式は x=1, y=2 ≪解説≫ ○ 点P0(x0 , y0 , z0 )を通り,方向ベクトル=(a, b, c)に平行な直線上にある1点をP(x, y, z)とおくとき,その位置ベクトル=→OP=(x, y, z)は
=→OP0+t (tは実数)
で表されます.例えば,t=0のときは,=→OP0となって,点P0を表します. 例えば,
t=1のときは,=→OP0+
となって,各々図に示した点を表します.t=2のときは,=→OP0+2 t=3のときは,=→OP0+3 このようにして,tがすべての実数値をとるとき,=→OP0+tはこの直線上のすべての点を指します. 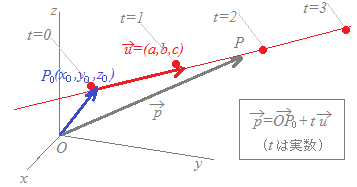 を成分に分けると
==…(1)
となります.右に続く→
|
○ 方向ベクトル=(a, b, c)のうち,いずれか1つの成分が0であるとき,例えば,b=0のときは,(1)式で分母が0となって,そのままでは使えません.
=, y=y0 …(1’)
となります.
※ 一般に,三次元空間(自由度3)において,1つの制限(方程式による縛り)を入れると,自由度が1つ減って2次元(平面や曲面)になります.方程式2つなら,自由度が2つ減って1次元(直線や曲線)になります.
(1’)のグラフはy軸に垂直な(y軸を串刺しにしたような)平面y=y0(=一定)上にあって,x,zの関係が
=で表される直線ということになります.
(1)式は=, = という連立方程式を省略的に表したもので,方程式2つになっています. このように,三次元空間における直線の方程式は,1つの方程式では表せず,「連立方程式」で書くことになります.(1’)は,その連立方程式を分けて書いたものです. 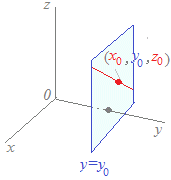
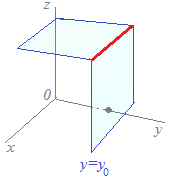 このとき,y, zは定数となって,グラフはy軸に垂直な平面とz軸に垂直な平面の両方を満たします(それらの交線上にあります).x座標は,x=x0+at (a≠0)から,tが実数全体を変化するとき,xは実数全体を変化します.すなわち「xは任意の値をとります」.すなわち,制限がありません.
このとき,y, zは定数となって,グラフはy軸に垂直な平面とz軸に垂直な平面の両方を満たします(それらの交線上にあります).x座標は,x=x0+at (a≠0)から,tが実数全体を変化するとき,xは実数全体を変化します.すなわち「xは任意の値をとります」.すなわち,制限がありません.
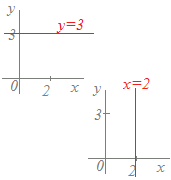 このような,任意の値をとる変数(制限のないもの)は,方程式(制限の式)としては,何も書きません.
このような,任意の値をとる変数(制限のないもの)は,方程式(制限の式)としては,何も書きません.例えば,x-y平面上でy軸に垂直な右図の直線の方程式は,単にy=3と書き,xについては何も書きませんが,それはxは任意の値をとる(制限がない)ということです.y=3でありさえすれば,(0,3), (1,3), (2,3), ..などはすべてこの直線上にあります. 同様にして,x-y平面上でx軸に垂直な直線の方程式は,単にx=3と書き,yについては何も書きませんが,それはyは任意の値をとる(制限がない)ということです.x=2でありさえすれば,(2,0), (2,1), (2,2), ..などはすべてこの直線上にあります. ※ ==の形の方程式を変形するときの注意点 (1) 1つの分数(第1辺,第2辺,第3辺だけ)を約分などで変形するときは,他の分数には影響しません ==→== ==→== (2) 各辺に同じ数を掛けたり,同じ数で割ったりすることはできます ==→== (3) 方程式の見かけが違っていても,同じ直線を表している場合があります ==→==
(1,2,3)を通り,方向ベクトル(3,4,5)に平行な直線は,(1+3,2+4,3+5)を通り,方向ベクトル(3,4,5)に平行な直線と考えることもできます.
(4) 3つの辺から成り立っている方程式では,「移項」という考え方はしない方がよいでしょう.(第3の辺の取り扱いが分かりにくくなります)これは −1=−1=−1→== のように,各辺から1だけ引く変形と対応しています. x+a=y+b=z+c → x+a−b=y=z+c ?? 【要約】 ⇒ 「1つの分数の分母と分子で約分する」「3つの辺に同じ数を足す,引く,掛ける,同じ数で割る」などが安全な変形です |
||||||||
|
以下,正しい番号を選択してください.
[問題1]
点(2, 1, −3)を通り,方向ベクトル=(3, −2, 1)に平行な直線の方程式を求めてください. 1==z−3 2==z+3 33(x+2)=2(y+1)=z+3 43(x−2)=2(y−1)=z−3 解説
通る点の座標が(2, 1, −3)で,方向ベクトルが(3, −2, 1)だから
==
すなわち
==z+3
になります.
→2
|
通る点の座標が(3, 0, −1)で,方向ベクトルが(−2, 3, 0)だから
= , z=−1
すなわち
= , z=−1
になります.
→1
|
||||||||
|
(x, y, z)=(0, 4, −5)+t(3, 0, 0) (tは実数)
を成分に分けると
→3
|
[問題4]
媒介変数表示
に対応する直線の方程式(x, y, zの関係式)を求めてください. 1== 2== 3== 4== 解説
通る点の座標が(p, −q, r)で,方向ベクトルが(u, v, −w)だから
==
すなわち
==
になります.
→2
|
||||||||
|
【例題1】
点(4, −2, 0)を通り,直線= , y=1に平行な直線の方程式を求めてください. 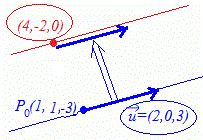 (解答) (解答)
≪ポイント≫
点(4, −2, 0)を通り,方向ベクトル(2, 0, 3)に平行な直線の方程式を求めればよいから
= , y=−2
直線の方程式 = , y=1 は,方向ベクトルを取り出すためだけに使う!点(1, 1, −3)は関係ない!
【例題2】
2直線=y= とy=x+2, z=−1 のなす角を求めて ください. 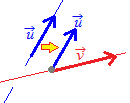 (解答) (解答)
≪ポイント≫
方向ベクトルは各々=(2, 1, −2), 2直線が交わらない場合(空間的に「ねじれの位置」にあるときや「平行」な場合)でも,2つの方向ベクトルのなす角を2直線のなす角という =(1, 1, 0)だから
||==3
·=||·||cosθ||== ·=2+1+0=3 から cosθ== θ= |
以下,正しい番号を選択してください.
点(0, −1, 3)を通り,方向ベクトル(2, 3, −1)に平行な直線の方程式を求めればよいから
==
→2
(1)は
==
と変形すると,方向ベクトル=(, 3, 1)
(2)は方向ベクトル=(0, −4, −3) だから
||==2
cosθ==−||=5 ·=−15 θ= →4
|
|
○ 三次元空間において2点P0(x0 , y0 , z0 ) , P1(x1 , y1 , z1 )を通る直線の方程式は
==
≪解説≫
「x,y,zがいろいろあって,混乱する〜」などと,初歩的な弱音を吐いていてはだめです.実際には,変数は赤で示した3個だけで,他のものは単なる係数です.
2点P0(x0 , y0 , z0 ) , P1(x1 , y1 , z1 )を通るということから,1点P0(x0 , y0 , z0 )を通り,方向ベクトル=(x0−x1 , y0−y1 , z0−z1 )に平行な直線と読み替えると,この公式になります.なお,方向ベクトルのうち1つまたは2つの成分が0になるときの取り扱いは,上で述べたことと同様です. |
【例題3】
(解答)2点P0(3, 4, −2) , P1(3, 6, 1)を通る直線の方程式を求めてください. 方向ベクトルは→P0P1=(3−3 , 6−4, 1−(−2) )=(0, 2, 3)だから = , x=3 (別解) 点P1(3, 6, 1)を通り,方向ベクトル→P0P1=(0, 2, 3)に平行な直線と考えて = , x=3 と答えてもよく,方向ベクトルを→P1P0=(0, −2, −3)として = , x=3 などと答えてもよい. |
|
点P0(−1, 2, 3)を通り,方向ベクトル→P0P1=(5, −7, 3)に平行な直線だから
→3
|
点P0(1, 4, 3)を通り,方向ベクトル→P0P1=(−3, 0, 2)に平行な直線だから
→2
|
|
≪媒介変数表示を使いこなそう!≫
【例題4】
1点P0(1, 0, 2)から直線==までの最短距離 を求めてください. 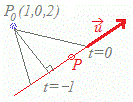 (解答) (解答)直線==上の点Pの 座標(x,y,z)は,媒介変数tを用いて次のように表すことができます.
|P0P|2=(4t+7)2+(3t−1)2+(2t+2)2 と,tの2次関数で表すことができますので,その最小値を求めればよいことになります. |P0P|2=...=29(t+1)2+25 となるので,t=−1のとき,|P0P|2=25,すなわち|P0P|=5となります.
→P0P⊥のとき,P0Pは最小となるので,内積→P0P·=0から求めると,もう少し簡単に計算できます.
4(4t+7)+3(3t−1)+2(2t+2)=0より 29t=−29 t=−1 このとき,P(4, −4, 2),P0P===5 |
直線==上の点Pの座標(x,y,z)は,媒介変数 tを用いて次のように表すことができます.
−2(−2t−1)+2(2t)+3(3t+5)=0より 17t+17=0 t=−1 このとき,P(1,−2,2),OP===3 →3
|
||||||||
|
【例題5】
2直線==z−2 , ==の両方に垂直に 交わる直線の方程式を求めてください. 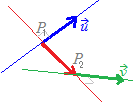 (解答) (解答)直線==z−2上の点 P1(x1 ,y1 ,z1 ) は,媒介変数sを用いて次のように表すことができます.
P2(x2 ,y2 ,z2 ) は,媒介変数tを用いて次のように表すことができます.
※ 単に垂直であるだけでなく,実際に交わっていることから,P1(x1 ,y1 ,z1 ),P2(x2 ,y2 ,z2 )が各々の直線の方程式を満たすといえます.
このとき,2直線の方向ベクトル=(3, −1, 1) , =(−3, 2,4)に対して,→P1P2=(−3t−3s−3, 2t+s−16, 4t−s+4)が垂直となればよいから ·→P1P2=0 ⇔3(−3t−3s−3)−(2t+s−16)+(4t−s+4)=0…(1) ·→P1P2=0 ⇔−3(−3t−3s−3)+2(2t+s−16)+4(4t−s+4)=0…(2) (1)→−7t−11s+11=0 (2)→29t+7s−7=0 これを解くと,s=1, t=0 P1(3,8,3), P2(−3,−7,6)となるから,これら2点を通る直線の方程式は == 方向ベクトルの大きさ(≠0)は自由に定めることができるから ==3−z |
直線=y−4=z−2上の点P は,媒介変数sを用いて 次のように表すことができます.
変数tを用いて次のように表すことができます.
このとき,2直線の方向ベクトル=(2,1,1) , =(−5, 2, −4)に対して,→PQ=(−5t−2s−6, 2t−s−1, −4t−s+1)が垂直となればよいから ·→PQ=0 ⇔2(−5t−2s−6)+(2t−s−1)+(−4t−s+1)=0…(1) ·→PQ=0 ⇔−5(−5t−2s−6)+2(2t−s−1)−4(−4t−s+1)=0…(2) (1)→−12t−6s−12=0 (2)→45t+12s+24=0 これを解くと,s=−2, t=0 P(1,2,0), Q(−1,3,3)となるから,これら2点を通る直線の方程式は =y−2= →4
|
||||||||
|
【例題6】
点(2,0,4)を通り,2直線x−1==2−z , 3−x== の両方に垂直な直線の方程式を求めてください. 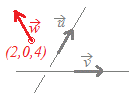 (解答) (解答)直線x−1==2−zの方向ベクトルは =(1,3,−1),直線3−x== の方向ベクトルは=(−1,2,3)とおける. 求める直線の方向ベクトルを=(a,b,c)とおくと ·=0 ⇔a+3b−c=0…(1) ·=0 ⇔−a+2b+3c=0…(2) ※ この問題では,単に垂直であればよく,実際に交わっているとは限りません.
この方程式を解く(未知数が3個で,方程式が2個だから,不定解となる.そこで例えば1文字cについては「解かない」と決めて,分かりやすくするために「かっこ」に入れておく)a+3b=(c)…(1’) −a+2b=(−3c)…(2’) 解をcで表すと a=(c) , b=(−c) したがって =(c , −c , c) 方向ベクトルの大きさ(≠0)は自由に定めることができるから =(11,−2,5)とすると,求める直線の方程式は =−= |
直線x−2= , z=4の方向ベクトルは =(1,3,0),直線= , y=2の方向ベクトルは =(2, 0, −1)とおける. 求める直線の方向ベクトルを=(a,b,c)とおくと ·=0 ⇔a+3b+0c=0…(1) ·=0 ⇔2a+0b−c=0…(2) a+3b=0…(1’) 2a−c=0…(2’) 不定方程式(1’)(2’)の解をaで表すと b=(−a) , c=(2a) したがって =(a, −a , 2a) 方向ベクトルの大きさは自由に定めることができるから, =(3,−1,6)とすると,求める直線の方程式は == →3
|
||||||||
|
【例題7】
直線3−x==に関して点P0(3,4,5)と対称な点 の座標を求めてください. 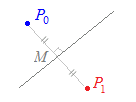 (解答) (解答)求める点をP1(p,q,r)とおくと,線分P0P1の(1つの)垂直二等分線が 直線3−x==になればよい. そのためには, ベクトル→P0P1=(p−3,q−4,r−5)が 直線3−x==の方向ベクトル=(−1,2,3)に垂直…(*) かつ 線分P0P1の中点(,,)が直線 3−x== 上にあればよい.…(#) (*)→−(p−3)+2(q−4)+3(r−5)=0 −p+2q+3r=20…(1) (#)→3−== == == == これより,2(p−3)=−(q+8) → 2p+q=−2…(2) 3(q+8)=2(r+1) → 3q−2r=−22…(3) (1)(2)(3)よりp=0, q=−2, r=8 P1(0, −2, 8) |
[問題12]
直線x−3==z−5に関して原点O(0, 0, 0)と対称 な点の座標を求めてください. 1(2, −4, 6) 2(1, −2, 3) 3(−3, −2, −5) 4(6, 4, 10) 解説
求める点をP(p,q,r)とおくと,線分OPの(1つの)垂直二等分線が
直線x−3==z−5になればよい. そのためには,ベクトル→OP=(p, q, r)が 直線x−3==z−5の方向ベクトル=(1, 2, 1)に垂直…(*) かつ 線分OPの中点(,,)が直線x−3==z−5 上にあればよい.…(#) (*)→p+2q+r=0…(1) (#)→−3==−5 == これより,2p−12=q−4 → 2p−q=8…(2) q−4=2r−20 → q−2r=−16…(3) (1)(2)(3)よりp=2, q=−4, r=6 P(2, −4, 6) →1
|
||||||||
|
【例題8】
点P0(3,4,5)に関して直線3−x==と対称な直線 の方程式を求めてください. 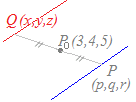 (解答) (解答)直線3−x==上の動点を P(p,q,r),求める直線上の動点をQ(x,y,z)とするとき,PQの中点がP0になればよい.
PQはこれらの直線とは垂直になるとは限らない点に注意
P(p,q,r)とQ(x,y,z)の中点の座標は
(,,)これが,P0(3,4,5)に一致すればよいから =3, =4, =5 P(p,q,r)は 3−p== を満たすから 3−(6−x)== x−3== |
直線==z−4上の動点を
P(p,q,r),求める直線上の動点をQ(x,y,z)とするとき,PQの中点がP0になればよい. P(p,q,r)とQ(x,y,z)の中点の座標は (,,) これが,P0(−1,2,3)に一致すればよいから =−1, =2, =3 P(p,q,r)は ==r−4 を満たすから ==(6−z)−4 ==2−z ==z−2 →2
|