|
■行列の積 ABの定義 [行ベクトルと列ベクトルの内積] ●行と列の掛け方 内積については,左からは行ベクトルを 右からは列ベクトルを掛けるものとします。 (左右を逆にしたものは定義されません。) ●要素数
|
内積が定義できるものの例
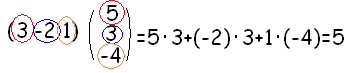 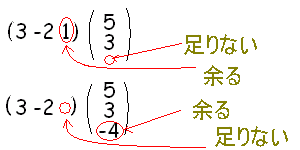 |
| [行列の積]
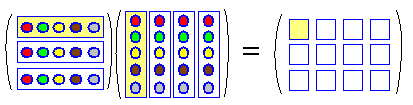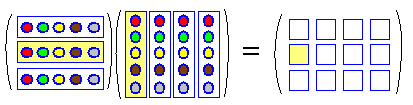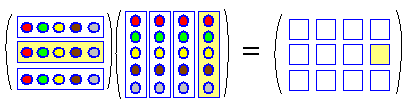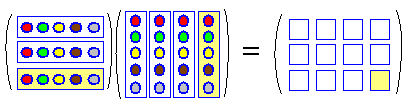
●[m×n型][n×p型]=[m×p型] 積が定義されるためには,左の列数と右の行数が等しくなければなりません。  ●成分は,成分は,i行とj列の積がi行j列成分 となります。 |
 |
|
■行列の積 ABの定義 [行ベクトルと列ベクトルの内積] ●行と列の掛け方 内積については,左からは行ベクトルを 右からは列ベクトルを掛けるものとします。 (左右を逆にしたものは定義されません。) ●要素数
|
内積が定義できるものの例
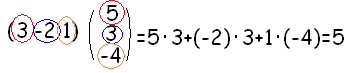  |
| [行列の積]
●[m×n型][n×p型]=[m×p型] 積が定義されるためには,左の列数と右の行数が等しくなければなりません。  ●成分は,成分は,i行とj列の積がi行j列成分 となります。 |
 |
[要約] (1) 行・列=行列 (2) 型は「しりとり」
| 例
右の行列B1〜B9のうち,2×3行列 また,2×3行列 |
B1= B4= B7= 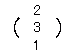 ,B8= ,B8=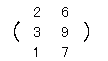 ,B9= ,B9=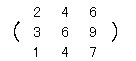 |
|
1
右の行列B1〜B9のうち,3×2行列 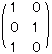 |
 Cは3行2列の行列だから,これに右から掛けることのできるものは,2行?列の行列になります. ⇒ B4,B5,B6の3個にチェックをつければ正解
Cは3行2列の行列だから,これに右から掛けることのできるものは,2行?列の行列になります. ⇒ B4,B5,B6の3個にチェックをつければ正解
|
| 2
右の行列B1〜B9のうち,3×2行列 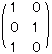 |
 Cは3行2列の行列だから,これに左から掛けることのできるものは,?行3列の行列になります. ⇒ B3,B6,B9の3個にチェックをつければ正解
Cは3行2列の行列だから,これに左から掛けることのできるものは,?行3列の行列になります. ⇒ B3,B6,B9の3個にチェックをつければ正解
|
例
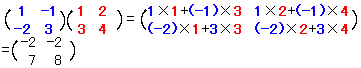 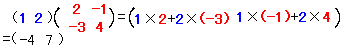 |
| 3 |
 [ア]=4−2=2
[ア]=4−2=2[イ]=−5+6=1  [ウ]=3−4=−1
[ウ]=3−4=−1[エ]=−3+4=1 [オ]=5−6=−1 [カ]=−5+6=1  [キ]=8−3=5
[キ]=8−3=5[ク]=4−1=3  [ケ]=1+0+3=4
[ケ]=1+0+3=4[コ]=1+2+0=3 [サ]=0+2+3=5 |
|
4 各々正しいものを選んでください. |
2×2行列 と 2×1行列 の積は,しりとりの仕組みで中の組を落としていくと2×1行列になります
左の行列の2行目 |
|
2×3行列 と 3×2行列 の積は,しりとりの仕組みで中の組を落としていくと2×2行列になります
左の行列の1行目 |
|
|
3×2行列 と 2×3行列 の積は,しりとりの仕組みで中の組を落としていくと3×3行列になります
左の行列の2行目 |
|
|
1×2行列 と 2×2行列 の積は,しりとりの仕組みで中の組を落としていくと1×2行列になります
左の行列の1行目 |
|
|
1×2行列 と 2×2行列 と 2×3行列の積は,しりとりの仕組みで中の組と組を落としていくと1×3行列になります
左端の行列と中の行列を掛けて,できた行列に右端の行列を右から掛けると だから (1,2) 成分は7になります |
|
■[個別の頁からの質問に対する回答][行列の積について/18.6.12]
昭和の初期に生まれた84歳の老人です。ふとしたことから行列、ベクトルに興味をもち、これまた偶然にこのサイトに出会いました。(もちろん高校時代に行列やベクトルなど教科書にありませんでした。)説明が非常にわかりやすく、よく理解できました。ありがとうございました。最後のページの行列の積の問題をやり全問正解だったとき自分で拍手をしてしまいました。これからも時間があったら少しずつ勉強してみようと思っております。よろしくお願いいたします。
■[個別の頁からの質問に対する回答][行列の積について/18.3.21]
=>[作者]:連絡ありがとう.この教材の管理人が行列を習ったのは今からほぼ半世紀前です.50歩100歩かも. 行 列 行 列 と頭の中で念仏の様に唱えながら解きました
行は漢字に横の線があるから横 列は縦の漢字があるから縦とも覚えてみました
■[個別の頁からの質問に対する回答][行列の積について/18.1.22]
=>[作者]:連絡ありがとう.各自の内的なロジックで身に着いていくのだと思う. わかりやすかったです。
■[個別の頁からの質問に対する回答][行列の積 ABの定義について/17.10.7]
=>[作者]:連絡ありがとう. すごく参考になります!ありがとうございました!
■[個別の頁からの質問に対する回答][行列の積について/17.9.26]
=>[作者]:連絡ありがとう. 私は、行列について初心者でしたが、
分かりやすかったです。
■[個別の頁からの質問に対する回答][行列の積 ABの定義について/17.3.3]
=>[作者]:連絡ありがとう. 行列に関してほぼ知識なしの状態でこのページにたどり着きましたが、ちゃんと理解できました。すごく分かりやすかったです。
■[個別の頁からの質問に対する回答][行列の積について/17.2.8]
=>[作者]:連絡ありがとう. windows8.1、IEの環境ですが、4(2)と(3)の数字が上下消えていて読めなくなっておりました(他は問題ありませんでした。こちらの機種(NECのタブレットPC)のせいかもしれませんが、念のため報告します。
■[個別の頁からの質問に対する回答][行列の積について/17.1.12]
=>[作者]:連絡ありがとう.原因となる箇所は特定できるのですが,区切り文字のスペースを入れるとエラーになる場合と,区切り文字のスペースを入れないとエラーになる場合があって,やってみないと分からないという感じです.(2)はスペースあり:エラー,なし:正常,(5)はなし:エラー,あり:正常とちょうど逆にすると直りました. (5)の式を示す画像が正しく表示されておりません。修正していただけると嬉しいです。
=>[作者]:連絡ありがとう.このエラーが時々起こることは認識していましたが,今原因が特定できました(たぶん).直っています. |