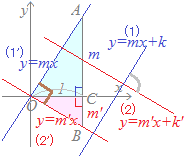
 ※OA⊥OBのとき,2直線OA, OBは,互いに「垂直である」「直角である」「直交する=直角に交わる」ともいう 2直線 y=m'x+k' …(2)
y=mx+kとy=m'x+k'とが垂直 ←→ mm'=−1
[例外] x軸に平行な直線y=kと y軸に平行な直線x=cとは 互いに垂直
[1]
直線y=2x+1と 直線 だから互いに垂直 ※切片の値1, 3は関係ない [2] 直線 直線 だから互いに垂直 ※切片の値−2, 5は関係ない
[3]
直線y=2xと 直線 だから互いに垂直ではない ※切片の値0, 4は関係ない [4] 直線y=2x−3と 直線y=−2x+6とは 2×(−2)=−4≠−1 だから互いに垂直ではない ※切片の値−3, 6は関係ない
【解説】
  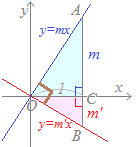 右図のような(1)と(2)が垂直であるかどうかを調べたいときに,(1)の代わりに(1)を上下に平行移動した直線(1')を使っても結果は変わりません.同様にして(2)の代わりに(2)を上下に平行移動した直線(2')を使っても結果は変わりません. このようにして,切片が0となる2つのグラフy=mx…(1') とy=m'x…(2') で調べると有利です. 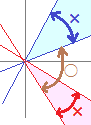 左図のように,2つの直線y=mx…(1') とy=m'x…(2') について傾きm, m'が2つとも正のとき(右上がりのとき)や2つとも負のとき(右下がりのとき),これらのなす角は90°よりも小さくなりますので,2直線が垂直になることはできません.
左図のように,2つの直線y=mx…(1') とy=m'x…(2') について傾きm, m'が2つとも正のとき(右上がりのとき)や2つとも負のとき(右下がりのとき),これらのなす角は90°よりも小さくなりますので,2直線が垂直になることはできません.したがって,2直線y=mx…(1') とy=m'x…(2')が垂直になることができるのは,m, m'の一方が正の値(右上がりの直線)で他方が負の値(右下がりの直線)になっている場合です. ここでは右図のように,m>0, m'<0の場合を考えてみます. 以下において
(A)三平方の定理を使う方法
の3つ示して見ます.(1つ分かればよい)(B)相似図形を使う方法 (C)ベクトルの垂直条件を使う方法
(A)
図2のように原点を通る2直線OAとOBが垂直になるには,△AOBが∠AOB=90°の直角三角形になればよい. AC=m, OC=1だから,△AOCについて三平方の定理により BCは長さだからBC=−m'.△BOCについて三平方の定理により また,例えば,m=5>0, m'=−3<0の場合に,温度計で5°と−3°の温度差が5−(−3)とするように AB=m−m'…(3) △AOBについて∠AOB=90°となる条件を三平方の定理により求めると (1)(2)(3)を代入すると 2=−2mm' したがって mm'=−1 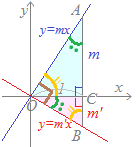 (B)
(B)△AOB=90°のとき,
∠AOC+∠BOC=90°
これらから,△AOC∽△OBCとなるから
∠AOC+∠OAC=90° だから∠BOC=∠OAC また, ∠AOC+∠BOC=90° ∠OBC+∠BOC=90° だから∠AOC=∠OBC
OC:CA=BC:CO
1:m=−m':1 mm'=−1
(C)
[例外]ベクトルを習っているときは,ベクトルの垂直条件を考えれば簡単にできます. ベクトル
1+mm'=0
mm'=−1 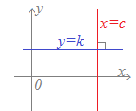 上記の(A)(B)(C)はいずれも2直線の方程式がy=mx+kとy=m'x+k'の形に書ける場合を扱っていますが,一方がy軸に平行な場合には,この形には書けません.
上記の(A)(B)(C)はいずれも2直線の方程式がy=mx+kとy=m'x+k'の形に書ける場合を扱っていますが,一方がy軸に平行な場合には,この形には書けません.そこで,一方がy軸に平行な直線x=cのときは,直線のグラフを思い浮かべてx軸に平行な直線y=kは垂直であると判断します.(これらは原点を通るかどうかには関係なく,式の形から直ちに答えるとよい) 【例】 [1] 直線y=1と直線x=3とはx軸に平行な直線とy軸に平行な直線だから互いに垂直 ※y切片の値1,x切片の値3は何でもよい [2] 直線2x+4=0と直線3y−1=0とはy軸に平行な直線とx軸に平行な直線だから互いに垂直 ※x切片の値−2,y切片の値 |
|
《問題》 次のうち,垂直な直線の組を選びなさい. ○初めに左欄の方程式一つクリックし,続けてこれと垂直な直線を右欄からクリックすると,合っていれば消えます.間違えば消えません. ○間違ったときは,右の欄を連打してもやり直しにはなりません. ○間違ったときは,「HELP」と「再開する」のボタンが表示されます.「HELP」を見る場合でも見ない場合でも「再開する」ボタンを押せば解答を続けることができます. HELP 再開する |
|
y=2x+1の傾きは2です
|
