(参考)
1) 和差⇒積の公式により,同種の三角関数(
 \( \sin A \)
\( \sin A \)と
 \( \sin B \)
\( \sin B \),
 \( \cos A \)
\( \cos A \)と
 \( \cos B \)
\( \cos B \))の和[差])の変形ができる
 \( \sin A+\sin B=2\sin\dfrac{A+ B}{2}\cos\dfrac{A-B}{2} \)
\( \sin A+\sin B=2\sin\dfrac{A+ B}{2}\cos\dfrac{A-B}{2} \)
 \( \sin A-\sin B=2\cos\dfrac{A+ B}{2}\sin\dfrac{A-B}{2} \)
\( \sin A-\sin B=2\cos\dfrac{A+ B}{2}\sin\dfrac{A-B}{2} \)
 \( \cos A+\cos B=2\cos\dfrac{A+ B}{2}\cos\dfrac{A-B}{2} \)
\( \cos A+\cos B=2\cos\dfrac{A+ B}{2}\cos\dfrac{A-B}{2} \)
 \( \cos A-\cos B=-2\sin\dfrac{A+ B}{2}\sin\dfrac{A-B}{2} \)
\( \cos A-\cos B=-2\sin\dfrac{A+ B}{2}\sin\dfrac{A-B}{2} \)
1’) 異種の三角関数(
 \( \sin A \)
\( \sin A \)と
 \( \cos B \)
\( \cos B \)など)の和差)の変形公式はない
 \( \sin A\pm\cos B=?? \)
\( \sin A\pm\cos B=?? \)
2) 角度が同じなら,振幅が違っても,合成公式がある.
&chco=990000) \( a\sin A+b\cos A=\sqrt{a^2+b^2}\sin(A+\alpha) \)
\( a\sin A+b\cos A=\sqrt{a^2+b^2}\sin(A+\alpha) \)
&chco=990000) \( a\sin A+b\cos A=\sqrt{a^2+ b^2}\cos(A-\beta) \)
\( a\sin A+b\cos A=\sqrt{a^2+ b^2}\cos(A-\beta) \)
3) 以上の内容に反して??(以上の内容を踏まえて??),三角関数の種類を変えると,変形公式が使えることがある.
&chco=990000) \( \sin A+\cos B=\sin A+\sin(\dfrac{\pi}{2}-B) \)
\( \sin A+\cos B=\sin A+\sin(\dfrac{\pi}{2}-B) \)など
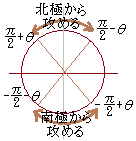
※南極から攻めてもよい
これにより,元の問題が加法定理,合成公式を併用するのに対して,1つの変形で解答する別解を作れる
(ただし,途中経過,キ,ク,ケ,コは,当然埋められない)
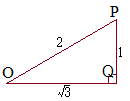 (1)のア,イの結果から,右図のように
(1)のア,イの結果から,右図のように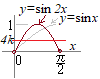 (#1)(#2)より
(#1)(#2)より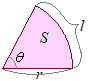 半径が
半径が ※南極から攻めてもよい
※南極から攻めてもよい