== Excelを使った対応のない場合のｔ検定…例題・問題 ==…例題・問題

■対応のない場合のｔ検定
　２群の母集団平均を比較したいときに，第１群のデータと第２群のデータが「同一被験者に対する２つの条件での観測結果」「各組が兄弟の身長データ」「各組が数学の得点の等しい生徒の英語の得点」などのように，単にデータ件数が同数であるだけでなく第１群のデータと第２群のデータの間に対応がある場合は，「対応のある場合のｔ検定」を用いることができる．
　これに対して，２群のデータ相互の間には個別の対応がない場合は「対応のない場合のｔ検定」を用いる．
　対応のない場合のｔ検定は，２群の標本数が等しい場合にも等しくない場合にも使えるが，２群の分散が等しいと見なせる場合と等しいとは見なせない場合とでは適用する公式が異なるので，対応のない場合のｔ検定を行うためには，初めに分散が等しいと見なせるかどうかの検定（Ｆ検定）を行う．
例１
　右図２は20匹の鶏のうち半数の10匹に飼料１を，残りの10匹に飼料２をそれぞれ１か月間与えたときの体重増加（ｇ）を表しているものとする．
　これら２種類の飼料による体重の増加には有意差があるかどうか検定してください．
　図２のデータはExcelワークシートの左上端に貼り付けるものとする．（標本の番号NoはＡ列，飼料１の欄はＢ列，飼料２の欄はＣ列に，これらの見出しは第１行，No1のデータは第２行に，...，No10のデータは第11行に来るものとする．）
　読者がデータを転記するときも，図２のデータを画面上でドラッグ→反転表示→右クリック→コピー→Excelのワークシート左上端に貼り付けるものとする．（以下の問題についても同様）
(*) 飼料１のデータと飼料２のデータはたまたま同数になっているが，これは以下の検定の進め方に関係ない．それぞれの横の並びのデータには何も対応がないということが重要．（20匹の鶏のうち半数を飼料１に残り半数を飼料２に割り当てただけだから．）
(1) Ｆ検定を行う
「対応のない場合のｔ検定」を行うためには，あらかじめこれら２群のデータの分散が等しいと見なせるかどうか調べなければならない．
Excel2010, Excel2007のとき
　データ→データ分析
Excel2002のとき
　ツール→分析ツール

→Ｆ検定：２標本を使った分散の検定→
・変数1の入力範囲(1)として B1:B11と書きこむ
（または入力欄の右にあるをクリックし，B1からB11までドラッグする．）
・変数2の入力範囲(2)として C1:C11と書きこむ
（または入力欄の右にあるをクリックし，C1からC11までドラッグする．）
・上記のように変数1，2の入力範囲が飼料1，飼料2というラベルを含んでいる場合は，ここで［ラベル］にチェックを付ける．
（入力範囲をB2:B11およびC2:C11としたときはこの［ラベル］にはチェックを付けない．その場合は，左にある欄が分析ルールの出力結果において「変数1」として，右にある欄が「変数2」として表示されるが，分析ツールを利用するときはラベルを含めるようにする方が見やすく分かりやすい．ただし，ラベル自体を数値の1とか2とかにすると，データ範囲と混同した時にエラーが検出されないので，ラベルには必ず文字列を使用するようにする．）
・α欄は有意水準で，デフォルトで0.05が書きこまれている（有意水準5％で検定することを表している．有意水準1％の検定を行う場合はこの数字を0.01にする．）
・何度も検定を行うときに，出力オプションを新規ワークシートや新規ブックにしているとワークシートやExcelファイルがどんどん増えてややこしくなるので，データの右側などの見やすい範囲に出力するようにするためには，「出力オプション」で「出力先」を選ぶと右の空欄が書き込めるようになるので，そこに出力したい範囲の左上端のセル番地を書きこむ．この場合，すでにあるデータが上書きされるおそれがあるときは警告が出る．
→OK
右図３のような出力結果が得られる．
図１
図２
No 飼料１ 飼料２
1 84.8 99.6
2 89.3 91.3
3 89.0 92.5
4 89.4 87.7
5 77.4 91.2
6 90.3 99.4
7 89.9 91.1
8 84.5 88.8
9 86.4 91.8
10 76.1 93.9

※Excelの「分析ツール」を利用するためには
Excel2010の場合
ファイル→オプション→アドイン→（下端の管理欄がExcelアドインとなっているときにその右の［設定］をクリック）→分析ツールにチェックを付ける→ＯＫ
Excel2007の場合
メニューのうち［ホーム］の左にある丸いOfficeボタンをクリック→下端にあるExcelのオプション→アドイン→（下端の管理欄がExcelアドインとなっているときにその右の［設定］をクリック）→分析ツールにチェックを付ける→ＯＫ
Excel2002の場合
ツール→アドイン→分析ツールにチェックを付ける→ＯＫ


図３
F-検定: 2 標本を使った分散の検定　　
　 　 　
　 飼料１ 飼料２
平均 85.71 92.73
分散 26.681 15.75122222
観測数 10 10
自由度 9 9
観測された分散比 1.693900297 　
P(F<=f) 片側 0.222230302 　
F 境界値 片側 3.178893105 　
　
【出力結果の読み方】
⇒　観測された分散比が1.69でＦ境界値片側が3.18であるから，Ｆ値が境界値よりも小さく分散には有意差が認められず，等分散とみなせる．
（または，Ｐ片側が0.22で5％（0.05）よりも大きいから，分散には有意差が認められず，等分散とみなせる．）


図４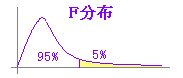
　Ｆ検定は通常分散の大きい方を分子，小さい方を分母として片側検定で行い，上のようなＦ分布曲線において上側5％の区間（黄色の部分）に入るほど大きければ分散に有意差がある（分散が等しくない=不等分散）とみなす．（印刷物：統計の参考書などについているＦ分布表では分子の分散が大きい場合のみ掲載されている．）
　図３の例では26.681/15.75122222=1.693900297が5％境界値よりも小さいので有意差がないと判断する．この分散比は左欄に置いたデータの分散を右欄に置いたデータの分散で割ったものとなっているので，教科書通りにＦ検定を行うためには，分散の大きい方のデータを左欄に置かなければならない．
　		 　しかし，どちらの分散が大きいかはやってみないと分からないので，あらかじめ分散を計算することなくＦ検定を行ったとき，左欄の分散が右欄の分散よりも小さくなってしまった場合には，次の図のように分散比が0に近いほど（小さいほど）分散に有意差があることになる．（分散比が１に近ければ２つの分散は等しいと見なせるが，分子が小さくなるほど分散比は0に近づく．）
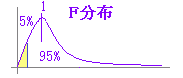　次の図５は図２のデータにおいて分散が大きい方のデータ飼料１を右欄に，分散が小さい方のデータ飼料２を左欄に置いてＦ検定を行ったときの出力結果

図５
F-検定: 2 標本を使った分散の検定　　
　 　 　
　 飼料２ 飼料１
平均 92.73 85.71
分散 15.75122222 26.681
観測数 10 10
自由度 9 9
観測された分散比 0.590353518 　
P(F<=f) 片側 0.222230302 　
F 境界値 片側 0.314574906 　
　図５の例では15.75122222/26.681=0.590353518が5％境界値よりも大きいので有意差がない．この分散比0.590353518は図３の分散比とは0.590353518=1/1.693900297という関係になっている． 　
(2) ｔ検定を行う
　上記の例では等分散となったので，「分差が等しい場合のｔ検定」を行う．
Excel2010, Excel2007のとき
　データ→データ分析
Excel2002のとき
　ツール→分析ツール

→t 検定：等分散を仮定した２標本による検定→
・変数1の入力範囲(1)として B1:B11と書きこむ
（または入力欄の右にあるをクリックし，B1からB11までドラッグする．）
・変数2の入力範囲(2)として C1:C11と書きこむ
（または入力欄の右にあるをクリックし，C1からC11までドラッグする．）
・上記のように変数1，2の入力範囲が飼料1，飼料2というラベルを含んでいる場合は，ここで［ラベル］にチェックを付ける．
（入力範囲をB2:B11およびC2:C11としたときはこの［ラベル］にはチェックを付けない．
・「母集団平均が等しい」という帰無仮説に対応するためには，仮説平均との差異の欄を0にする．（平均の差が0という仮説を検定する）
（この欄は空欄のままでもデフォルトで0が入る）
・α欄は有意水準で，デフォルトで0.05が書きこまれている（有意水準5％で検定することを表している．有意水準1％の検定を行う場合はこの数字を0.01にする．）
・何度も検定を行うときに，出力オプションを新規ワークシートや新規ブックにしているとワークシートやExcelファイルがどんどん増えてややこしくなるので，データの右側などの見やすい範囲に出力するようにするためには，「出力オプション」で「出力先」を選ぶと右の空欄が書き込めるようになるので，そこに出力したい範囲の左上端のセル番地を書きこむ．この場合，すでにあるデータが上書きされるおそれがあるときは警告が出る．
→OK
右図６のような出力結果が得られる．

【出力結果の読み方】
⇒　ｔ値が-3.4で両側検定の境界値が2.1であるから，|ｔ|>2.1となって平均に有意差がある．
　この分析ツールでは左欄（飼料1）の平均が右欄（飼料２）の平均よりも小さいときにｔ値が負（逆ならば正）で表示され，［ｔ境界値両側］よりも絶対値が大きければ外側に来る．
（または，Ｐ両側が0.003で5％（0.05）よりも小さいから有意差がある．）
※新しい飼料２を作って，従来の飼料１よりも増量効果があるかどうかに関心があるような場合は飼料２の平均が大きいという帰無仮説をおいて片側検定を行うことになる．（片側検定か両側検定かはデータの値で決まるのでなく，分析者が何に関心があるのかによる．）
帰無仮説 H0：μ1=μ2
対立仮説 H1：μ1<μ2

　この場合は，出力結果のうち片側の方を見ることになる．片側検定の境界値は両側検定のときよりも内側に来るので有意差は認められやすくなる．（上記の出力結果のうち，t 境界値 片側 1.734063592，t 境界値 両側 2.100922037 を見ると片側の方が小さい．） 　		 図６
t-検定: 等分散を仮定した２標本による検定　　
　 　 　
　 飼料１ 飼料２
平均 85.71 92.73
分散 26.681 15.75122222
観測数 10 10
プールされた分散 21.21611111 　
仮説平均との差異 0 　
自由度 18 　
t -3.407918685 　
P(T<=t) 片側 0.00156801 　
t 境界値 片側 1.734063592 　
P(T<=t) 両側 0.00313602 　
t 境界値 両側 2.100922037 　
　
※ |ｔ| の値は外側に行くほど大きくなる．
図７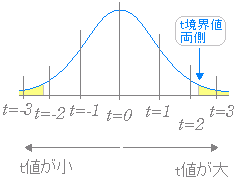

（ア）　|ｔ値|>ｔ境界値 両側
（イ）　p値<0.05
のいずれかで有意差があると判断できる．

図８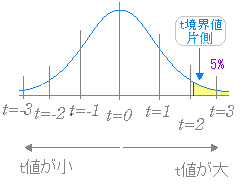

問題１
　右の表はある学級の生徒25人（男子15人，女子10人）の数学の得点であるとする．男子と女子とで平均値に有意差があるかどうか検定してください.
空欄を埋めてください．なお，小数は第3位を四捨五入して小数第2位まで求めてください．
○分散比（>1となるようにとる）は
片側検定のＦ境界値は
上記２つの数値を比較して，Ｆ値が境界値よりも小さいことから有意水準5％で有意差はない．分散は等しいと見なせる．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=>0.05
だから有意水準5％で有意差はない．分散は等しいと見なせる．
そこで，等分散の場合のｔ検定を行うと
○t=
両側検定のｔ境界値は
上記２つの数値を比較して，|t|がｔ片側境界値よりも大きいことから有意水準5％で有意差がある．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=<0.05
だから有意水準5％で有意差がある．
採点する やり直す
　
No 男子 女子
1 65 54
2 69 68
3 69 68
4 66 55
5 66 55
6 51 55
7 63 56
8 46 55
9 63 52
10 73 56
11 64 　
12 61 　
13 72 　
14 59 　
15 74 　



問題２
　右の表は２つのクラスＡ，Ｂの生徒についてある値を測定した結果だとします．これら２つのクラスの平均に有意差があるかどうか検定してください.
空欄を埋めてください．なお，小数は第3位を四捨五入して小数第2位まで求めてください．
○分散比（>1となるようにとる）は
片側検定のＦ境界値は
上記２つの数値を比較して，Ｆ値が境界値よりも大きいから有意水準5％で有意差がある．分散は等しいとは見なせない．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=<0.05
だから有意水準5％で有意差がある．分散は等しいとは見なせない．
そこで，不等分散の場合のｔ検定を行うと
○t=
両側検定のｔ境界値は
上記２つの数値を比較して，|t|がｔ片側境界値よりも大きいことから有意水準5％で有意差がある．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=<0.05
だから有意水準5％で有意差がある．
採点する やり直す
No Ａクラス Ｂクラス
1 15.3 13.9
2 14.9 14.2
3 14.5 14.1
4 14.4 14.3
5 14.0 14.1
6 13.9 13.7
7 14.1 14.7
8 14.7 13.9
9 15.3 14.1
10 14.6 13.8
11 　 14.3


問題３
　右の表はある教科を旧方式で指導した学級と新方式で指導した学級のテスト結果だとします．新方式の指導方法には効果があると言えるかどうか検定してください.
空欄を埋めてください．なお，小数は第3位を四捨五入して小数第2位まで求めてください．
○分散比（>1となるようにとる）は
片側検定のＦ境界値は
上記２つの数値を比較して，Ｆ値が境界値よりも小さいから有意水準5％で有意差が認められない．分散は等しいとは見なせる．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=>0.05
だから有意水準5％で有意差が認められない．分散は等しいとは見なせる．
そこで，等分散の場合のｔ検定を行うと（新方式で効果があるかどうかだから新方式の平均点が高いかどうかを調べる片側検定とする）
○|t|=
片側検定のｔ境界値は
上記２つの数値を比較して，|t|がｔ片側境界値よりも小さいことから有意水準5％で有意差がない．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=>0.05
だから有意水準5％で有意差がない．
採点する やり直す

　
No 旧方式 新方式
1 79 63
2 77 64
3 74 89
4 65 83
5 78 69
6 71 68
7 81 77
8 78 74
9 70 80
10 79 82
11 87 72
12 62 88
13 68 84
14 65 85
15 89 89



①Excel2007～2010, web上にあるフリーのExcel onlineで行う場合
②フリーの統計ソフトRで行う場合
*** 作業例 ***
表１
No 飼料１ 飼料２
1 84.8 99.6
2 89.3 91.3
3 89.0 92.5
4 89.4 87.7
5 77.4 91.2
6 90.3 99.4
7 89.9 91.1
8 84.5 88.8
9 86.4 91.8
10 76.1 93.9
【例1】
　　右図２は20匹の鶏のうち半数の10匹に飼料１を，残りの10匹に飼料２をそれぞれ１か月間与えたときの体重増加（ｇ）を表しているものとする．
　これら２種類の飼料による体重の増加には有意差があるかどうか検定してください．
F検定→T検定の２段階で行う場合
①Excelの分析ツールを使う場合
データ→データ分析→F検定
⇒次のように出力される
F-検定: 2 標本を使った分散の検定
	飼料１	飼料２
平均	85.71	92.73
分散	26.681	15.751..
観測数	10	10
自由度	9	9
観測された分散比	1.693..	
P(F<=f) 片側	0.222..
F 境界値 片側	3.178..
⇒p値=0.22>0.05だから有意差は認められない
データ→データ分析→t-検定: 等分散を仮定した２標本による検定
⇒次のように出力される
t-検定: 等分散を仮定した２標本による検定
	飼料１	飼料２
平均	85.71	92.73
分散	26.681	15.7512..
観測数	10	10
プールされた分散	21.216..
仮説平均との差異	0	
自由度	18	
t 	-3.407..	
P(T<=t) 片側	0.001..
t 境界値 片側	1.734..	
P(T<=t) 両側	0.003..
t 境界値 両側	2.100..
⇒p値=0.003<0.05だから有意差が認められる
もしくは，|t|値=3.407>2.100だから有意差が認められる
【結果のまとめ方】
　表1は20匹の鶏のうち半数の10匹に飼料１を，残りの10匹に飼料２をそれぞれ１か月間与えたときの体重増加（ｇ）を表している．
《表1》 体重増加の平均と分散
飼料1飼料2
個体数1010
平均85.7 *92.7 *
分散26.715.8
「ｔ検定の結果，体重増加の差は有意であった（両側検定：t(18)=3.40, p=.003）．したがって，これら２つの飼料による体重増加には有意差が認められる．」
*p<.05, **p<.01
 ①Excelのワークシート関数で行う場合
　関数FTEST(A群, B群)は，A群とB群の分散の差異が認められない「両側確率」を返す．
　F検定を両側検定で行うと，分散に差異がある場合だけでなく，一致し過ぎる「≒0」場合も検出する．
　しかし，ほとんどのF検定で，分散に有意差があると見なすときは，一致する場合は含めないので，F検定は片側検定で行う．
　右図のように，片側確率が5%以下であるかどうかを検定するには
FTEST(A群, B群)/2
とするとよい．
　結果⇒0.222..
p値>0.05だから等分散という仮定は棄却されない．
=TTEST(A群, B群, 2, 2)
• 第3引数は，片側検定のとき1，両側検定のとき2･･･この問題では，「2」の両側検定を指定
• 第４引数は，ｔ検定の種類を指定する．この問題のような「等分散が仮定できるｔ検定」の場合は「2」
※なお，前，後というラベルを「含める」「含めない」は両方同じに揃えると自動で判別される．
　結果⇒0.0031..
　p値だけで判断するときは，ここまででよいが，一般的な報告書のようにｔ値も付けるには
=TINV(上記のp値, 自由度)
とする．=TINV(0.0031,18)
　結果⇒3.408..
　結果をまとめるには，この他に各群の平均と不偏分散[標本の個数N−1で割る方]が必要であるから，=AVERAGE( ), =VAR( )で求めておく．
【結果のまとめ方】
　前述と同様
②Rによる場合
F検定を行う
Rのvar.test( )関数は，第３引数以下を略すると両側検定になるが，F検定を通常の意味に使うには，第１引数に示される群を分子としたときの片側検定にすべきだから，名前タグalternative="greater"を指定して，前の群が大きくなる片側検定とする． 

> food1<-c(84.8,89.3,89,89.4,77.4,90.3,89.9,84.5,86.4,76.1)
> food2<-c(99.6,91.3,92.5,87.7,91.2,99.4,91.1,88.8,91.8,93.9)
> var.test(food1,food2,alternative="greater")

        F test to compare two variances

data:  food1 and food2
F = 1.6939, num df = 9, denom df = 9, p-value = 0.2222
alternative hypothesis: true ratio of variances
 is greater than 1
95 percent confidence interval:
 0.5328585       Inf
sample estimates:
ratio of variances 
            1.6939
⇒p値=0.22..>0.05だから分散の有意差は棄却されない．または，比率の95%信頼区間に「1」が含まれるから，有意差は棄却されない．
等分散を仮定した２標本によるt検定を行う 
> t.test(food1,food2,var.equal=TRUE)

        Two Sample t-test

data:  food1 and food2
t = -3.4079, df = 18, p-value = 0.003136
alternative hypothesis: true difference in means
 is not equal to 0
95 percent confidence interval:
 -11.347707  -2.692293
sample estimates:
mean of x mean of y 
    85.71     92.73
⇒p値=0.003<0.05だから平均値には有意差が認められる．
もしくは，95%信頼区間に「0」が含まれないから，差が0に等しいと言えない．
なお，t値も使って結果を出すには，関数qt(確率, 自由度)を使う．この問題のように，両側検定でt境界線を求めるには，確率として0.025を使う．
qt(0.025, 18)
⇒−2.10
⇒|t|値=3.40>2.10だから有意差が認められる．
【結果のまとめ方】
　前述と同様
　

Welch検定で行う場合
①Excelの分析ツールを使う場合
データ→データ分析→t-検定: 不等分散を仮定した２標本による検定
⇒次のように出力される
t-検定: 分散が等しくないと仮定した２標本による検定
	飼料１	飼料２
平均	85.71	92.73
分散	26.681	15.751..
観測数	10	10
仮説平均との差異	0	
自由度	17	
t 	-3.407..	
P(T<=t) 片側	0.001..
t 境界値 片側	1.739..
P(T<=t) 両側	0.003..
t 境界値 両側	2.109..
⇒p値=0.003<0.05だから有意差が認められる
もしくは，|t|値=3.407>2.100だから有意差が認められる
【結果のまとめ方】
　表1は20匹の鶏のうち半数の10匹に飼料１を，残りの10匹に飼料２をそれぞれ１か月間与えたときの体重増加（ｇ）を表している．
《表1》 体重増加の平均と分散
飼料1飼料2
個体数1010
平均85.7 *92.7 *
分散26.715.8
「ｔ検定の結果，体重増加の差は有意であった（両側検定：t(17)=3.41, p=.003）．したがって，これら２つの飼料による体重増加には有意差が認められる．」
*p<.05, **p<.01
※Welch検定を用いたことは，自由度が18よりも小さいことで分かる．
①Excelワークシート関数で行う場合
=TTEST(A群, B群, 2, 2)
• 第3引数は，片側検定のとき1，両側検定のとき2･･･この問題では，「2」の両側検定を指定
• 第４引数は，ｔ検定の種類を指定する．この問題のような「不等分散のｔ検定」の場合は「3」
※なお，前，後というラベルを「含める」「含めない」は両方同じに揃えると自動で判別される．
　結果⇒0.0033..
　p値だけで判断するときは，ここまででよいが，一般的な報告書のようにｔ値も付けるには
=TINV(上記のp値, 自由度)
とする．=TINV(0.0031,17)
　結果⇒3.4040..
【問題点あり】
このようにワークシート関数で計算するには「自由度」を使わなければならないが，Welch検定の自由度は，分析ツールの場合とは異なり，自動では計算されないので，次の公式に代入して自分で計算するしかない．

この問題では，16.88≒17
また，両側検定ｔ値の境界値は=TINV(0.05,17)⇒2.10..による
　結果をまとめるには，この他に各群の平均と不偏分散[標本の個数N−1で割る方]が必要であるから，=AVERAGE( ), =VAR( )で求めておく．
【結果のまとめ方】
　前述と同様
②Rによる場合
> food1<-c(84.8,89.3,89,89.4,77.4,90.3,89.9,84.5,86.4,76.1)
> food2<-c(99.6,91.3,92.5,87.7,91.2,99.4,91.1,88.8,91.8,93.9)
> t.test(food1,food2,var.equal=FALSE)

        Welch Two Sample t-test

data:  food1 and food2
t = -3.4079, df = 16.88, p-value = 0.003378
alternative hypothesis: true difference
 in means is not equal to 0
95 percent confidence interval:
 -11.368381  -2.671619
sample estimates:
mean of x mean of y 
    85.71     92.73
⇒p値=0.003<0.05だから有意差が認められる
もしくは，95%信頼区間に「0」が含まれないから，差が0に等しいと言えない．
　なお，t値も使って結果を出すには，関数qt(確率, 自由度)を使う．この問題のように，両側検定でt境界線を求めるには，確率として0.025を使う．
qt(0.025, 17)
⇒−2.10..
⇒|t|値=3.41>2.10だから有意差が認められる．
【結果のまとめ方】
　前述と同様
（気になること）
ここまでやってくると，どの方法でやっても，そこそこ一致するように見えるが，小数第４位５位あたりで「微妙に合わない」
Welch検定の場合

①Excelツール①Excel関数②R
p値0.0033500.0033780.003378
|t|値3.4079193.4040863.4079
t境界値2.1098162.1098162.109816
自由度1716.8816.88

等分散検定の場合⇒全部一致する

①Excelツール①Excel関数②R
p値0.0031360.003140.003136
|t|値3.4079193.407923.4079
t境界値2.1009222.1009222.100922
自由度181818
　

表2
No Ａクラス Ｂクラス
1 15.3 13.9
2 14.9 14.2
3 14.5 14.1
4 14.4 14.3
5 14.0 14.1
6 13.9 13.7
7 14.1 14.7
8 14.7 13.9
9 15.3 14.1
10 14.6 13.8
11
14.3
【例2】
　　右の表2は２つのクラスＡ，Ｂの生徒についてある値を測定した結果だとします．これら２つのクラスの平均に有意差があるかどうか検定してください.
F検定→T検定の２段階で行う場合
①Excelの分析ツールを使う場合
データ→データ分析→F検定
⇒次のように出力される
F-検定: 2 標本を使った分散の検定
	Ａクラス	Ｂクラス
平均	14.57	14.1
分散	0.246..	0.078
観測数	10	11
自由度	9	10
観測された分散比	3.163..	
P(F<=f) 片側	0.043564..	
F 境界値 片側	3.020382..
⇒p値=0.435<0.05だから分散に有意差が認められる
もしくは，観測された分散比=3.163>F境界値片側=3.02038だから不等分散と見なせる．
データ→データ分析→t-検定: 分散が等しくないと仮定した２標本による検定 ⇒次のように出力される
t-検定: 分散が等しくないと仮定した２標本による検定
	Ａクラス	Ｂクラス
平均	14.57	14.1
分散	0.246..	0.078
観測数	10	11
仮説平均との差異	0	
自由度	14	
t 	2.636927722	
P(T<=t) 片側	0.009760438	
t 境界値 片側	1.761310115	
P(T<=t) 両側	0.019520876	
t 境界値 両側	2.144786681
⇒p値=0.0195<0.05だから平均値に有意差が認められる
もしくは，t値=2.6369>t境界値両側=2.1447だから有意差が認められる．
【結果のまとめ方】
　表2は２つのクラスの平均値と分散である．
《表2》 Ａ，Ｂ２つのクラスの平均値と分散
ＡＢ
生徒数1011
平均14.57 *14.1 *
分散0.2460.078
「ｔ検定の結果，Ａ，Ｂ２つのクラスの平均値に有意差が認められる（両側検定：t(14)=2.637, p=.020）．」
*p<.05, **p<.01
①Excelワークシート関数で行う場合
　関数FTEST(A, B)は，AとBの分散の差異が認められない「両側確率」を返す．
　F検定を両側検定で行うと，分散に差異がある場合だけでなく，一致し過ぎる「≒0」場合も検出する．
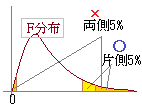　しかし，ほとんどのF検定で，分散に有意差があると見なすときは，一致する場合は含めないので，F検定は片側検定で行う．
　右図のように，片側確率が5%以下であるかどうかを検定するには
FTEST(A, B)/2
とするとよい．
　結果⇒0.043564..
p値<0.05だから等分散という仮定は棄却される．
=TTEST(A, B, 2, 3)
• 第3引数は，片側検定のとき1，両側検定のとき2･･･この問題では，「2」の両側検定を指定
• 第４引数は，ｔ検定の種類を指定する．この問題のような「等分散が仮定できないｔ検定」の場合は「3」
※なお，前，後というラベルを「含める」「含めない」は両方同じに揃えると自動で判別される．
　結果⇒0.0196285..
　p値だけで判断するときは，ここまででよいが，一般的な報告書のようにｔ値も付けるには
=TINV(上記のp値, 自由度)
とする．=TINV(0.0196285,14)
　結果⇒2.634108..
両側検定のt 境界値も付けるには=TINV(0.05,14)⇒2.144786681
【問題点あり】
このようにワークシート関数で計算するには「自由度」を使わなければならないが，Welch検定の自由度は，分析ツールの場合とは異なり，自動では計算されないので，次の公式に代入して自分で計算するしかない．

この問題では，13.88≒14
　結果をまとめるには，この他に各群の平均と不偏分散[標本の個数N−1で割る方]が必要であるから，=AVERAGE( ), =VAR( )で求めておく．
【結果のまとめ方】
　前述と同様
②Rによる場合
F検定を行う
Rのvar.test( )関数は，第３引数以下を略すると両側検定になるが，F検定を通常の意味に使うには，第１引数に示される群を分子としたときの片側検定にすべきだから，名前タグalternative="greater"を指定して，前の群が大きくなる片側検定とする． 
> a<-c(15.3,14.9,14.5,14.4,14,13.9,14.1,14.7,15.3,14.6)
> b<-c(13.9,14.2,14.1,14.3,14.1,13.7,14.7,13.9,14.1,13.8,14.3)
> var.test(a,b,alternative="greater")

        F test to compare two variances

data:  a and b
F = 3.1638, num df = 9, denom df = 10, p-value = 0.04356
alternative hypothesis: true ratio of variances
 is greater than 1
95 percent confidence interval:
 1.047489      Inf
sample estimates:
ratio of variances 
          3.163818
⇒p値=0.04356<0.05だから有意差が認められる
もしくは，比の95%信頼区間に「1」が含まれないから，比が1に等しいと言えない．
等分散を仮定した２標本によるt検定を行う．関数t.test( )において第３引数以下を省略すれば，Welch検定になる． 
> t.test(a,b)

        Welch Two Sample t-test

data:  a and b
t = 2.6369, df = 13.884, p-value = 0.01963
alternative hypothesis: true difference in means
 is not equal to 0
95 percent confidence interval:
 0.08741704 0.85258296
sample estimates:
mean of x mean of y 
    14.57     14.10
⇒p値=0.01963<0.05だから平均値には有意差が認められる．
もしくは，95%信頼区間に「0」が含まれないから，差が0に等しいと言えない．
なお，t値も使って結果を出すには，関数qt(確率, 自由度)を使う．この問題のように，両側検定でt境界線を求めるには，確率として0.025を使う．
qt(0.025, 13.884)
⇒−2.146469
⇒|t|値=2.6369>2.146469だから有意差が認められる．
【結果のまとめ方】
　前述と同様
Welch検定で行う場合
　この問題では，､第１段階のF検定を行わずに，不等分散の場合のT検定を行うと，①Excelツール，①Excel関数，②Rを使う場合のいずれの場合も,上記の結果と同じになる．
（気になること）
　ここまでやってくると，どの方法でやっても，そこそこ一致するように見えるが，小数第４位５位あたりで「微妙に合わない」
　原因の１つとして，Rでは小数のままで自由度を扱うが，Excelでは四捨五入して整数にするということがあるかもしれん．⇒p値，t値，t境界線に影響

①Excelツール①Excel関数②R
p値0.0195208760.0196285240.01963
|t|値2.6369277222.6341086672.6369
t境界値2.1447866812.1447866812.146469
自由度141413.884
　

【例3】
表3
No123456789101112131415
男子656969666651634663736461725974
女子54686855555556555256
　上の表3はある学級の生徒25人（男子15人，女子10人）の数学の得点であるとする．男子と女子とで平均値に有意差があるかどうか検定してください.
　この問題では，F検定で等分散の仮定が棄却されないので，従来方式でF検定→T検定と進める場合と，初めからWelch検定で行う場合に用いるT検定の種類が異なる．しかし，実際に行ってみると結果はほとんど変わらない．
Welch検定で行う場合
②Rで行う場合
>  t.test(b,g)
        Welch Two Sample t-test
data:  b and g
t = 2.4819, df = 22.669, p-value = 0.02093
alternative hypothesis: true difference in means
 is not equal to 0
95 percent confidence interval:
  1.105512 12.227822
sample estimates:
mean of x mean of y 
 64.06667  57.40000
⇒p値=0.02093<0.05だから平均値には有意差が認められる．
もしくは，95%信頼区間に「0」が含まれないから，差が0に等しいと言えない．
なお，t値も使って結果を出すには，関数qt(確率, 自由度)を使う．この問題のように，両側検定でt境界線を求めるには，確率として0.025を使う．
qt(0.025, 22.669)
⇒−2.07033
⇒|t|値=2.4819>2.07033だから有意差が認められる．
また，報告書に分散も付けるには，関数var(変数)が使える．
var(b)⇒59.49524, var(g)⇒32.48889
【結果のまとめ方】
　表3はある学級の生徒25人（男子15人，女子10人）の数学の得点の平均と分散である．
《表1》 数学の得点の平均と分散
男子女子
人数1510
平均64.1 *57.4 *
分散59.532.5
「ｔ検定の結果，平均点の差は有意であった（両側検定：t(22.669)=2.4819, p=.02093）．」
*p<.05, **p<.01
※この問題では，等分散を仮定したｔ検定でもWelch検定でも，自由度≒23でほとんど差がない．
　		 ①Excel分析ツールで行う場合
データ→データ分析→t-検定: 分散が等しくないと仮定した２標本による検定 ⇒次のように出力される
t-検定: 分散が等しくないと仮定した２標本による検定	
	男子	女子
平均	64.06666667	57.4
分散	59.4952381	32.48888889
観測数	15	10
仮説平均との差異	0	
自由度	23	
t 	2.481895019	
P(T<=t) 片側	0.010403777	
t 境界値 片側	1.713871517	
P(T<=t) 両側	0.020807553	
t 境界値 両側	2.068657599
⇒p値=0.0208<0.05だから平均値に有意差が認められる
もしくは，t値=2.4818>t境界値両側=2.06865だから有意差が認められる．
【結果のまとめ方】
　前述と同様
※Rの数字とExcel分析ツールの数字は，小数第2位，第3位あたりから微妙に食い違う．この原因として，Rは自由度として小数値を用いているのに対して，Excelは四捨五入した整数値を用いていることが考えられる．
①Excelのワークシート関数で行う場合
TTEST(男子範囲,女子範囲,2,3)⇒確率:p値
第３引数は，片側検定の場合は1,両側検定の場合は2．この問題では2
第４引数は，不等分散の場合は3
⇒ p値=0.020929361が返される． ⇒ p値<0.05だから平均値に有意差が認められる．
なお，ｔ検定の報告書によく示されるようにｔ値やｔ境界値も計算するには，関数TINV( )を利用する．
TINV(確率,自由度)⇒t値
第1引数に，上記で求めたp値を使えば，t値が返される
第1引数に，0.05を代入すれば，ｔ境界値が返される
※ただし，自由度は

の公式を使って，自分で計算しなければならない．意外な弱点でもあるが，これを使えばExcelで小数の自由度が処理できる長所もある.
TINV(0.020929361,22.669)⇒2.487519727
TINV(0.05,22.669)⇒2.073873058
平均や分散は各々aVERAGE(), VAR()で求めておく．
【結果のまとめ方】
　前述と同様
（参考）３種類の検定の比較
Welch検定の場合

①Excelツール①Excel関数②R
p値0.0208075530.0209293610.02093
|t|値2.4818950192.4875197272.4819
t境界値2.0686575992.0738730582.07033
自由度2322.66922.669
　

（気楽な雑談．茶飲み話）･･･よい子の皆さんは眉に唾を付けてください

大人小人
分散uv
人数mn
• 等分散を仮定した場合のｔ検定における自由度は，はっきりしていて，２群の人数m, nに対して，自由度を
ν=(m−1)+(n−1)
とする．
• これに対して，Welch検定の自由度は

とされているが，この式がなかなか煩雑で覚えにくい．そこで，正確ではなくても，だいたいの見当の付け方を庶民感覚で考えてみた．
　バス代のように大人料金と小人料金で全然違う金額を集めるときは，大人の人数を数えて，子人はまとめて大人の何人分になるかと換算してから足せばよいと考える．
　もっと卑近な例では，町内に大豪邸数軒とボロアパート多数があるとき，町内の宅地面積を数えるには，大豪邸の軒数を数えたらよい．
例1

大人小人
分散0.760.35
人数612
　右の例1の場合，Welch検定の自由度は，7.40になるが，大人(6−1)と大人に換算した2.4人で近い数字になる．
例2

大人小人
分散0.750.28
人数126
　右の例2の場合，Welch検定の自由度は，15になるが，大人(12−1)と大人に換算した4人で近い数字になる．
例3

大人小人
分散3.222.00
人数69
　右の例3の場合，Welch検定の自由度は，9.02になるが，大人(6−1)と大人に換算した4人で近い数字になる．
• 等分散を仮定した場合のｔ検定における自由度は，大人も小人も平等に「頭数」を数えていることになる．［平等主義］
• Welch検定の自由度は，大人の人数に換算するとだいたいの数字が出る．［金額重視］
　

F検定→T検定の２段階で行う場合
　この問題について，F検定によって等分散の仮定は棄却されない．そこで，等分散を仮定したｔ検定を行うと，p値=0.02866で有意差が認められる．
　Welch検定の場合と比較して，p値は少し大きくなるが「平均値の有意差が認められる」という結論は同じになる．
「Welch検定だけで行う」「F検定→T検定の２段階で行う」の２つの立場があるが，理論的なことは別として，これら２つの方式で結論が逆になるのはどの様な場合かを数値実験で調べて見た．
（十分な調査をやったわけではないので，結果は鵜呑みにできないという前提で）
• Ｆ検定で等分散の仮定が棄却されず，ｔ検定で２つに分かれて，かつ結果が食い違う具体例を幾つか作る．
• 実際には，どちらの方式でやっても（p値の微妙な差はあるが）5%有意差の有無について同じ結果になるのがほとんどで，逆に食い違う例を作るのは，それなりに根気のいる作業になる．筆者は半日を費やした．
• Welch検定のp値と等分散のｔ検定のp値の大小は，どちらの場合もあるから，どちらの方式で有意差が出やすいと，一律には言えない．
• 標本数が概ね25～30以上になると（大標本になると），z検定となって，差は出にくいから，標本数が20以下の場合を調べる．
　		 分散（標準偏差）の大きい側を太字で示す．
平均138.1 52.4 58.3 55.25 54.0 55.9
平均249.1 43.8 49.5 48.54 49.0 50.2
観測数1168812107
観測数2716413136
分散比0.47 1.79 2.56 2.25 0.37 3.19
分散172.38 95.41 62.21 90.57 17.33 32.48
分散2153.48 53.36 24.33 40.27 46.83 10.17
標準偏差18.51 9.77 7.89 9.52 4.16 5.70
標準偏差212.39 7.30 4.93 6.35 6.84 3.19
F検定0.11 0.16 0.24 0.09 0.07 0.11
不等分散のp0.062 0.051 0.043 0.054 0.043 0.048
等分散のp0.0210.024 0.073 0.048 0.055 0.053

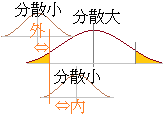　不等分散のpが0.05以下か否かは，分散の大きい側だけで判断して，平均±1.96σの範囲内に相手方の平均があるかどうか見た場合とほぼ一致する．
　等分散のpは標準偏差を按分したもので同様に平均±1.96σの範囲内に相手方の平均があるかどうか見た場合とほぼ一致する．
　表の赤字は有意差あり，下線は有意差なし．
　
確率統計のメニューに戻る 高校数学のメニューに戻る