|
���d�ϕ�--�ϕ������̕ύX
�y�L���z
���@�̈�D�F*1��x��*2, *3��y��*4�ɂ�����d�ϕ� f(x,y)dxdy �i*1, *2�͒萔�ł���ꍇ���Cy�Ɉˑ�����ꍇ������D���l�ɁC*3, *4�͒萔�ł���ꍇ���Cx�Ɉˑ�����ꍇ������D�j
���C�܂�x�ɂ��Đϕ����Ă���C����y�ɂ��Đϕ����s���ݎ��ϕ��i�J��Ԃ��ϕ��j�Ƃ��čs�����Ƃ�
( f(x,y)dx)dy …(1)
�ŕ\���D�@(1)���� dy f(x,y)dx …(1’) �Ƃ����L���ŕ\����邱�Ƃ�����D���̏ꍇ�ɂ����āCx�ɂ��Đϕ��������ʂ́C��ʂɂ�y���܂��ƂȂ��Ă���̂ŁC dy �̕����́C����y���܂��̐ϕ��Ƃ����Ӗ��ɂȂ�D ���@���l�ɂ��āC dx f(x,y)dy …(2’) �́C�܂�y�ɂ��Đϕ����ē�����i��ʂɂ�x���܂��ɂȂ�j���̂��C����x�Őϕ��������� ( f(x,y)dy)dx …(2) ��\���D
��P(2xydy)dx�̐ϕ��̏������������
(2xydx)dy�ɂȂ� 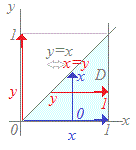 ������
�������@�E�}�̗̈�D�ɂ����āC (1)�@�̏c���Ŏ��������ɉ����āC�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āC0��y��x�̋�Ԃŕϐ�y�Őϕ�����x���܂��Ƃ��ē����鎮�� 2xydy (2)�@���ɁC0��x��1�̋�Ԃŕϐ�x�Őϕ�����Ƃ����̂����̎� (2xydy)dx ���\���Ă�����́D
2xydy=xy2=x3
�@�ϕ��̏�����ύX���āC�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āCx�Őϕ�����Ƃ��́C�}�̂悤�ɐϕ���Ԃ̍��[��y�C�E�[��1�ɂȂ�Dx3dx=x4= �ɂȂ� (1)�@�Ԃ̉����Ŏ��������ɉ����āCy��x��1�̋�Ԃŕϐ�x�Őϕ����ē����鎮�� 2xydx (2)�@������0��y��1�̋�Ԃŕϐ�y�Őϕ������ (2xydx)dy
2xydy=x2y=y−y3
(y−y3)dy=y2−y4=−= �ɂȂ�
��P���̂�����dxx2y dy�Ɠ��������̂�I��ł��������D
1dyx2y dx
2dyx2y dx(�o�TB)
3dyx2y dx 4dyx2y dx HELP
�͂��߂ɁC�L���̊m�F�F
dxf(x,y)dy�Ƃ�(f(x,y)dy)dx�̂���
dyf(x,y)dx�Ƃ�(f(x,y)dx)dy�̂��� 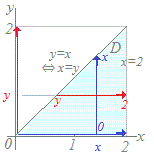 �E�}�̗̈�D�ɂ����āC
�E�}�̗̈�D�ɂ����āC�@�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āC�̏c���ɉ�����0��y��x�̋�Ԃŕϐ�y�Őϕ����āCx���܂��Ƃ��ē����鎮 x2y dy ��0��x��2�̋�Ԃŕϐ�x�Őϕ�����Ƃ����̂����̖��̕\���Ă�����̂ƂȂ��Ă���D
���̏����Őϕ������
�@����́C�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āC�Ԃ̉����ɉ�����y��x��2�̋�Ԃŕϐ�x�Őϕ����āCy���܂��Ƃ��ē����鎮
x2y dxx2y dy=xy2=x4 x4 dx=x5=�ɂȂ� ��0��y��2�̋�Ԃŕϐ�y�Őϕ��������� dyx2y dx �ɓ������D → 3
���̏����Őϕ������
x2y dx=xy=y−y4 (y−y4)dx=y2−y5=�ɂȂ� |
�y���̖��̏o�T�z
(�o�TA) �u�����ϕ��w�U�v�i�����o�� ��b���w�u���V��/�F�엘�Y���j (�o�TB) �u�V�� ����̐��w�R ���W�v�i�X�k�o��/�c��ÍG���j (�o�TC) �u���H�n��b �����ϕ��w�v�i�|����/�x�������Y.���A�g.�Y������Y�����j (�o�TD) �u���w�ւ̃A�v���[�`�v�i�։ؖ[/���؍��ߒ��j
��Qdyf(x,y)dx�̐ϕ��̏������������
dx f(x,y)dy�ɂȂ� 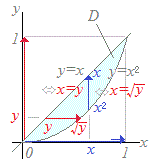 ������
�������@�E�}�̗̈�D�ɂ����āC (1)�@�Ԃ̉����ɉ����āC�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āCy��x���̋�Ԃŕϐ�x�Őϕ�����y���܂��Ƃ��ē����鎮�� f(x,y)dx (2)�@���ɁC0��y��1�̋�Ԃŕϐ�y�Őϕ�����Ƃ����̂����̎� dyf(x,y)dx ���\���Ă�����́D �@�ϕ��̏�����ύX���āC (1)�@�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āCy�Őϕ�����Ƃ��́C�̏c���ɉ����āCx2��y��x�̋�Ԃŕϐ�y�Őϕ����ē����鎮�� f(x,y)dy (2)�@������0��x��1�̋�Ԃŕϐ�x�Őϕ������ dx f(x,y)dy
��Rdx2x2ydy�̐ϕ��̏������������
2x2ydxdy+2x2ydxdy�ɂȂ� (�o�TB)
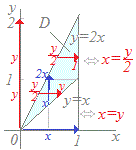 ������
�������@�E�}�̗̈�D�ɂ����āC (1)�@�̏c���Ŏ��������ɉ����āC�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āCx��y��2x�̋�Ԃŕϐ�y�Őϕ�����x���܂��Ƃ��ē����鎮�� 2x2ydy (2)�@���ɁC0��x��1�̋�Ԃŕϐ�x�Őϕ�����Ƃ����̂����̎� dx2x2ydy ���\���Ă�����́D �@�ϕ��̏�����ύX���āC�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āCx�Őϕ�����Ƃ��́C�}�̂悤�ɐϕ���Ԃ̉E�[��y�̒l�ɂ���ĕς��̂ŁC�Q�̗̈�ɕ����ċ��߂�D (1)�@0��y��1�̋�Ԃł́C�Ԃ̐��Ŏ��������ɉ����āC��x��y�̋�Ԃŕϐ�x�Őϕ����ē����鎮�� 2x2ydx �@1��y��2�̋�Ԃł́C�Ԃ̐��Ŏ��������ɉ����āC��x��1�̋�Ԃŕϐ�x�Őϕ����ē����鎮�� 2x2ydx (2)�@������0��y��2�̋�Ԃŕϐ�y�Őϕ������ 2x2ydxdy+2x2ydxdy�ɂȂ� ���i�Q�l�j�ǂ���Ōv�Z���Ă��C���ʂ��ɂȂ�
��Qa>0�̂Ƃ��C���̂�����dxf(x,y)dy�Ɠ�����
1dyf(x,y)dx
2dyf(x,y)dx���̂�I��ł��������D (�o�TA)
3dyf(x,y)dx 4dyf(x,y)dx HELP
�͂��߂ɁC�L���̊m�F�F
dxf(x,y)dy�Ƃ�(f(x,y)dy)dx�̂���
dyf(x,y)dx�Ƃ�(f(x,y)dx)dy�̂��� 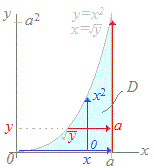 �E�}�̗̈�D�ɂ����āC
�E�}�̗̈�D�ɂ����āC�@�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āC0��y��x2�̋�Ԃŕϐ�y�Őϕ����Ă��� �@x���܂��Ƃ��ē����鎮 f(x,y)dy ��0��x��a�̋�Ԃŕϐ�x�Őϕ�����Ƃ����̂����̖��̕\���Ă�����̂ƂȂ��Ă���D �@����́C�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āC��x��a�̋�Ԃŕϐ�x�Őϕ����Ă��� �@y���܂��Ƃ��ē����鎮 f(x,y)dx ��0��y��a2�̋�Ԃŕϐ�y�Őϕ��������� dyf(x,y)dx �ɓ������D → 3 |
|
��Rdx(x2+y2)dy�̐ϕ�������ύX����ƁC
1dy(x2+y2)dx
2dy(x2+y2)dx���̂ǂ̎��ɂȂ�܂����D 3dy(x2+y2)dx 4dy(x2+y2)dx HELP 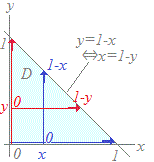 �E�}�̗̈�D�ɂ����āC
�E�}�̗̈�D�ɂ����āC�@�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āC0��y��1−x�̋�Ԃŕϐ�y�Őϕ����Ă��� �@x���܂��Ƃ��ē����鎮 (x2+y2)dy ��0��x��1�̋�Ԃŕϐ�x�Őϕ�����Ƃ����̂����̖��̕\���Ă�����̂ƂȂ��Ă���D �@����́C�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āC0��x��1−y�̋�Ԃŕϐ�x�Őϕ����Ă��� �@y���܂��Ƃ��ē����鎮 (x2+y2)dx ��0��y��1�̋�Ԃŕϐ�y�Őϕ��������� dy(x2+y2)dx �ɓ������D → 2 ���i�Q�l�j�ǂ���Ōv�Z���Ă��C���ʂ��ɂȂ� |
��S(f(x,y)dy)dx�̐ϕ�������ύX����ƁC
1(f(x,y)dx)dy
2(f(x,y)dx)dy���̂ǂ̎��ɂȂ�܂����D 3(f(x,y)dx)dy+(f(x,y)dx)dy 4(f(x,y)dx)dy+(f(x,y)dx)dy HELP 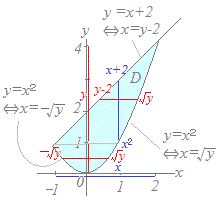 �E�}�̗̈�D�ɂ����āC
�E�}�̗̈�D�ɂ����āC�@�͂��߂�x���Œ肵�āC���ꂼ���x�ɑ��āCx2��y��x+2�̋�Ԃŕϐ�y�Őϕ����ē�����x���܂� f(x,y)dy ��−1��x��2�̋�Ԃŕϐ�x�Őϕ�����Ƃ����̂����̖��̕\���Ă�����̂ƂȂ��Ă���D �@�@�ϕ��̏�����ύX���āC�͂��߂�y���Œ肵�āC���ꂼ���y�ɑ��āCx�Őϕ�����Ƃ��́C�}�̂悤�ɐϕ���Ԃ̍��[��y�̒l�ɂ���ĕς��̂ŁC�Q�̗̈�ɕ����ċ��߂�D (1)�@0��y��1�̋�Ԃł́C�Ԃ̐��Ŏ��������ɉ����āC−��x���̋�Ԃŕϐ�x�Őϕ����ē����鎮�� f(x,y)dx ������C (f(x,y)dx)dy (2)�@1��y��4�̋�Ԃł́C�Ԃ̐��Ŏ��������ɉ����āCy−2��x���̋�Ԃŕϐ�x�Őϕ����ē����鎮�� f(x,y)dx ������C (f(x,y)dx)dy �@�����𑫂������̂����ƂȂ� |