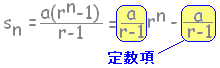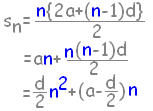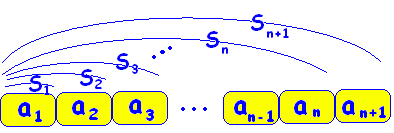
← PC用は別頁
|
■解説 ○［問題の場面］ 数列｛ａｎ｝の初項から第ｎ項までの和Ｓｎが与えられていて，｛ａｎ｝の一般項が分からないとき，Ｓｎからａｎを求めるには？ 
a1 = S1 …(1)
ｎ≧2のとき，an = Sn- Sn-1 …(2)
≪(1)の解説≫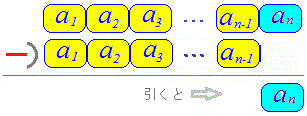  
=== 駅で電車を待っていると分かること ===
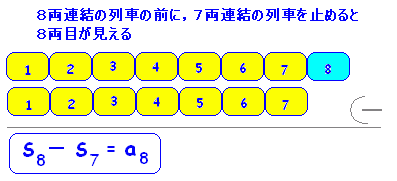
※注意※
よく似ているが，階差数列のときとは事情が違うので注意
階差数列：bｎ
= an+1 - an ← 小さい方の番号
Sn→an： an = Sn - Sn-1 ← 大きい方の番号
【例】
初項から第ｎ項までの和Snが次の式で与えられる数列の一般項ａｎを求めなさい。 Ｓｎ = n2 答案例
※求めるときは，n=1のときと，n≧2のときとを分けて求めなければならないが，結果が１つの式にまとめられるときは，まとめる．
実際，ほとんどの問題は，まとめられる． |
|
■問題
１
初項から第ｎ項までの和Snが Ｓｎ=n2+2n で与えられる数列の一般項ａｎを求めなさい。 (答案) n＝1のとき，ａ１=［ア］ ｎ≧2のとき，ａｎ=Sn - Sn-1=［イ］ ゆえに，ｎ≧1のとき，ａｎ=［ウ］ |
|||||||||
（適当なものを選びなさい。）
|
|
2
初項から第ｎ項までの和Snが Ｓｎ=n3-3n で与えられる数列の一般項ａｎを求めなさい。 (答案) n＝1のとき，ａ１=［ア］ ｎ≧2のとき，ａｎ=［イ］ ゆえに，ｎ≧1のとき，ａｎ=［ウ］ |
|||||||||
（適当なものを選びなさい。）
|
|
３
初項から第ｎ項までの和Snが Ｓｎ=2n で与えられる数列の一般項ａｎを求めなさい。 (答案) n＝1のとき，ａ１=［ア］ ｎ≧2のとき，ａｎ=［イ］ |
||||||
（適当なものを選びなさい。）
 となって，定数項があるはずですが，それがないのは初項が例外ルールとなっているから。この場合，ａ1はｎ≧2の場合と統一できない |
|
４
初項から第ｎ項までの和Snが Ｓｎ=n2+5 で与えられる数列の一般項ａｎを求めなさい。 (答案) n＝1のとき，ａ１=［ア］ ｎ≧2のとき，ａｎ=［イ］ |
||||||
（適当なものを選びなさい。）
 |
| ５
初項から第ｎ項までの和をSnが 2aｎ=Sn + 1 （ｎ≧1）を満たすとき，数列｛ａｎ｝の初めの３項を求めなさい。 (答案)
|
（正しいものを選びなさい。）
|
||||||||||
|
※ S1=a1に注意すると，a1の方程式ができます。 |
|||||||||||
 ...（携帯版）メニューに戻る...メニューに戻る |
|
■［個別の頁からの質問に対する回答］[Sn→ａｎ関係式について／18.8.24］
Sn+1-Snはありですか
＝＞［作者］：連絡ありがとう．仲間うちで使うほどの省略語では，質問の意味が正確に伝わりません． そこに書いてある8両連結の列車を見ると分かるように |
| 鬯ｮ�ｫ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ鬯ｮ�ｦ�ｽ�ｮ髯ｷ�ｻ�ｽ�ｻ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｩ蟷｢�ｽ�｢�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｵ鬯ｩ蟷｢�ｽ�｢�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�､鬯ｩ蟷｢�ｽ�｢髫ｴ荵暦ｿｽ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�･�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮGoogle鬯ｮ�ｫ�ｽ�ｶ�ｽ縺､ﾂ鬮ｫ�ｲ陝ｷ�｢�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢鬯ｮ�ｫ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ |
