|
■ Sn→an関係式 ■解説 ○[問題の場面] 数列{an}の初項から第n項までの和Snが与えられていて,{an}の一般項が分からないとき,Snからanを求めるには?
※a1は特別: S1-S0 とはできない。S0は定義されていない。
※階差数列のときと事情が違うので注意: Sn→an: an = Sn - Sn-1 例
答案例
|
<図で示せば>
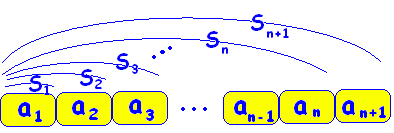
<式で示せば> S1=a1 S2=a1+a2 S3=a1+a2+a3 ・・・ Sn=a1+a2+a3+・・・an-1+an 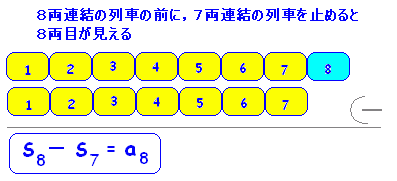 |
|
■ Sn→an関係式 ■解説 ○[問題の場面] 数列{an}の初項から第n項までの和Snが与えられていて,{an}の一般項が分からないとき,Snからanを求めるには?
※a1は特別: S1-S0 とはできない。S0は定義されていない。
※階差数列のときと事情が違うので注意: Sn→an: an = Sn - Sn-1 例
答案例
|
<図で示せば>

<式で示せば> S1=a1 S2=a1+a2 S3=a1+a2+a3 ・・・ Sn=a1+a2+a3+・・・an-1+an  |
|
■問題
1
初項から第n項までの和Snが Sn=n2+2n で与えられる数列の一般項anを求めなさい。 (答案) n=1のとき,a1=[ア] n≧2のとき,an=Sn - Sn-1=[イ] ゆえに,n≧1のとき,an=[ウ] (適当なものを選びなさい。) |
2
初項から第n項までの和Snが Sn=n3-3n で与えられる数列の一般項anを求めなさい。 (答案) n=1のとき,a1=[ア] n≧2のとき,an=[イ] ゆえに,n≧1のとき,an=[ウ] (適当なものを選びなさい。) |
|
3
初項から第n項までの和Snが Sn=2n で与えられる数列の一般項anを求めなさい。 (答案) n=1のとき,a1=[ア] n≧2のとき,an=[イ] (適当なものを選びなさい。) ※参考:数列{an}が等比数列ならば,その和は 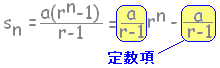 となって,定数項があるはずですが,それがないのは初項が例外ルールとなっているから。この場合,a1はn≧2の場合と統一できない |
4
初項から第n項までの和Snが Sn=n2+5 で与えられる数列の一般項anを求めなさい。 (答案) n=1のとき,a1=[ア] n≧2のとき,an=[イ] (適当なものを選びなさい。) ※参考:数列{an}が等差数列ならば,その和は 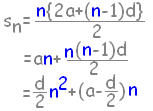
5
初項から第n項までの和をSnが 2an=Sn + 1 (n≧1)を満たすとき,数列{an}の初めの3項を求めなさい。 (答案) a2=[イ] a3=[ウ] |
|
■[個別の頁からの質問に対する回答][Sn→an関係式について/18.8.24]
Sn+1-Snはありですか
=>[作者]:連絡ありがとう.仲間うちで使うほどの省略語では,質問の意味が正確に伝わりません. そこに書いてある8両連結の列車を見ると分かるように |