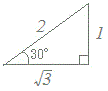|
【例題4】
0°≦θ<360°のときy=sinθ+cosθの最大値,最小値及びそのときのθの値を求めてください.
 (解答) (解答)
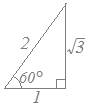
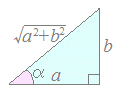
右図のように斜辺の長さが=2となる直角三角形を考えると
cos60°=, sin60°=
となるから
sinθ+cosθ
=2(sinθ +cosθ )
=2(sinθ·cos60°+cosθ·sin60°)
=2sin(θ+60°)
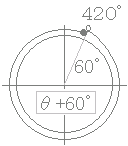 0°≦θ<360°のとき60°≦θ+60°<420°だから
0°≦θ<360°のとき60°≦θ+60°<420°だから
−1≦sin(θ+60°)≦1
−2≦2sin(θ+60°)≦2
θ+60°=90°→θ=30°のとき最大値2
θ+60°=270°→θ=210°のとき最小値−2
|
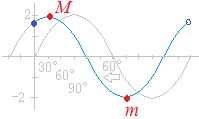 ※教科書や参考書では,右図のように三角関数のグラフを描いて問題を解く方法が示されていることもあります.
※教科書や参考書では,右図のように三角関数のグラフを描いて問題を解く方法が示されていることもあります.
実際に生徒の手の動きを観察していると,グラフを描く方法では
- 30°,60°などの目盛りを打つためにかなりの時間を掛けてしまう生徒が多い.このため,制限時間内に解答にたどりつけないことがある.
- y=rsin(θ+α)のグラフを描くことはハードルが高い.
このような事情が考えられますので,筆者は左図のように(ヘッドホン=耳あて)の図をお薦めします.この図を利用するときに,重要な事は「定義域の変換」だけです.
○ヘッドホン=耳あての図がお薦め
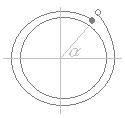
○定義域( θ+α°の取り得る値の範囲)に注意すること
0°≦θ<360°のときα≦θ+α°<360°+α
|
|
【問題4】
0°≦θ<360°のときy=sinθ−cosθの最大値,最小値及びそのときのθの値を求めてください.
(空欄に入るものを下から選んでください)
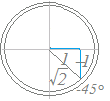 =だから,右のような図を考えると
=だから,右のような図を考えると
sinθ−cosθ=sin(θ−45°)
ここで0°≦θ<360°のときθ−45°の値の範囲は?解答
|
 \( 0^{\circ}\leqq\theta\lt 360^{\circ} \) \( 0^{\circ}\leqq\theta\lt 360^{\circ} \)
の各辺から45°を引くと
 \( -45^{\circ}\leqq\theta-45^{\circ}\lt 315^{\circ} \)
→閉じる← \( -45^{\circ}\leqq\theta-45^{\circ}\lt 315^{\circ} \)
→閉じる←
0°≦θ−45°<360°
−45°≦θ−45°<315°
45°≦θ−45°<405°
0°≦θ−45°<315°
|
θ−45°=90°すなわち θ=135°のとき
最大値 ?解答
|
&chco=aa2200)
は  \( \theta-45^{\circ}=90^{\circ} \) \( \theta-45^{\circ}=90^{\circ} \)のとき最大値  \( \sqrt{2} \) \( \sqrt{2} \)をとる
→閉じる←
1
−1
−
|
θ−45°=270°すなわち θ=315°のとき最小値 ?解答
|
&chco=aa2200) \( y=\sqrt{2}\sin(\theta-45^{\circ}) \) \( y=\sqrt{2}\sin(\theta-45^{\circ}) \)
は  \( \theta-45^{\circ}=270^{\circ} \) \( \theta-45^{\circ}=270^{\circ} \)のとき最小値  \( -\sqrt{2} \) \( -\sqrt{2} \)をとる
→閉じる←
−1
−
−
|
|
【問題5】
0°≦θ<360°のときy=sinθ+cosθの最大値,最小値及びそのときのθの値を求めてください.
(空欄に入るものを下から選んでください)
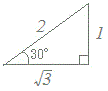 =2だから,
=2だから,
y=2(sinθ·+cosθ·)
=2(sinθ·cos30°+cosθ·sin30°)
=2sin(θ+30°)
ここで0°≦θ<360°のときθ+30°の値の範囲は?解答
|
 \( 0^{\circ}\leqq\theta\lt 360^{\circ} \) \( 0^{\circ}\leqq\theta\lt 360^{\circ} \)
の各辺の30°を加えると
 \( 30^{\circ}\leqq\theta+ 30^{\circ}\lt 390^{\circ} \)
→閉じる← \( 30^{\circ}\leqq\theta+ 30^{\circ}\lt 390^{\circ} \)
→閉じる←
0°≦θ+30°<360°
−30°≦θ+30°<330°
0°≦θ+30°<390°
30°≦θ+30°<390°
|
θ+30°=90°すなわち θ=60°のとき
最大値 ?解答
|
&chco=aa2200) \( y=2\sin(\theta+ 30^{\circ}) \) \( y=2\sin(\theta+ 30^{\circ}) \)
は  \( \theta+ 30^{\circ}=90^{\circ} \) \( \theta+ 30^{\circ}=90^{\circ} \)のとき最大値2をとる
→閉じる←
1
−1
2
−2
|
θ+30°=270°すなわち θ=240°のとき最小値 ?解答
|
&chco=aa2200) \( y=2\sin(\theta+ 30^{\circ}) \) \( y=2\sin(\theta+ 30^{\circ}) \)
は  \( \theta+ 30^{\circ}=270^{\circ} \) \( \theta+ 30^{\circ}=270^{\circ} \)のとき最小値−2をとる
→閉じる←
−1
1
2
−2
|
|
【問題6】
0°≦θ<360°のときy=4sinθ−3cosθの最大値,最小値を求めてください.
(空欄に入るものを下から選んでください)
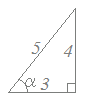 =5だから,右図のような直角三角形を考えるとy=5sin(θ−α)
=5だから,右図のような直角三角形を考えるとy=5sin(θ−α)
ただし,αはcosα=, sinα=となる第1象限の角
ここで0°≦θ<360°のとき
0°−α≦θ−α<360°−α
θ−α=90°すなわちθ=90°+αのとき,最大値
?
解答
|
|
1
1+α
5
5+α
|
θ−α=270°すなわち θ=270°+αのとき
最小値 ?
解答
(このような問題では角αが0°<α<90°に存在することが言えればよく,その詳細な数値まで必要とはされない.)
|
|
−1
−1+α
−5
−5+α
|
 ○ しかし,一般にはa·sinθ+b·cosθのように与えられた係数,a, bがそのままで一つの角度αの三角関数cosα, sinαに等しいことはめったにありません.
○ しかし,一般にはa·sinθ+b·cosθのように与えられた係数,a, bがそのままで一つの角度αの三角関数cosα, sinαに等しいことはめったにありません.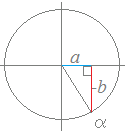 ○ a sinθ−b cosθ (a,b>0)を
○ a sinθ−b cosθ (a,b>0)を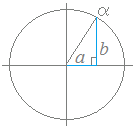 ○ a sinθ−b cosθ (a,b>0)を
○ a sinθ−b cosθ (a,b>0)を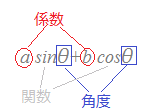 (1) 係数と関数が同じなら,角度が違ってもよい
(1) 係数と関数が同じなら,角度が違ってもよい (解答)
(解答)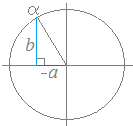 ○
○  (解答)
(解答)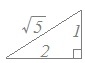 (解答)
(解答)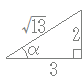

 ※教科書や参考書では,右図のように三角関数のグラフを描いて問題を解く方法が示されていることもあります.
※教科書や参考書では,右図のように三角関数のグラフを描いて問題を解く方法が示されていることもあります.